Improving Feature Learning in Remote Sensing Images Using an Integrated Deep Multi-Scale 3D/2D Convolutional Network
Abstract
1. Introduction
2. Methodology
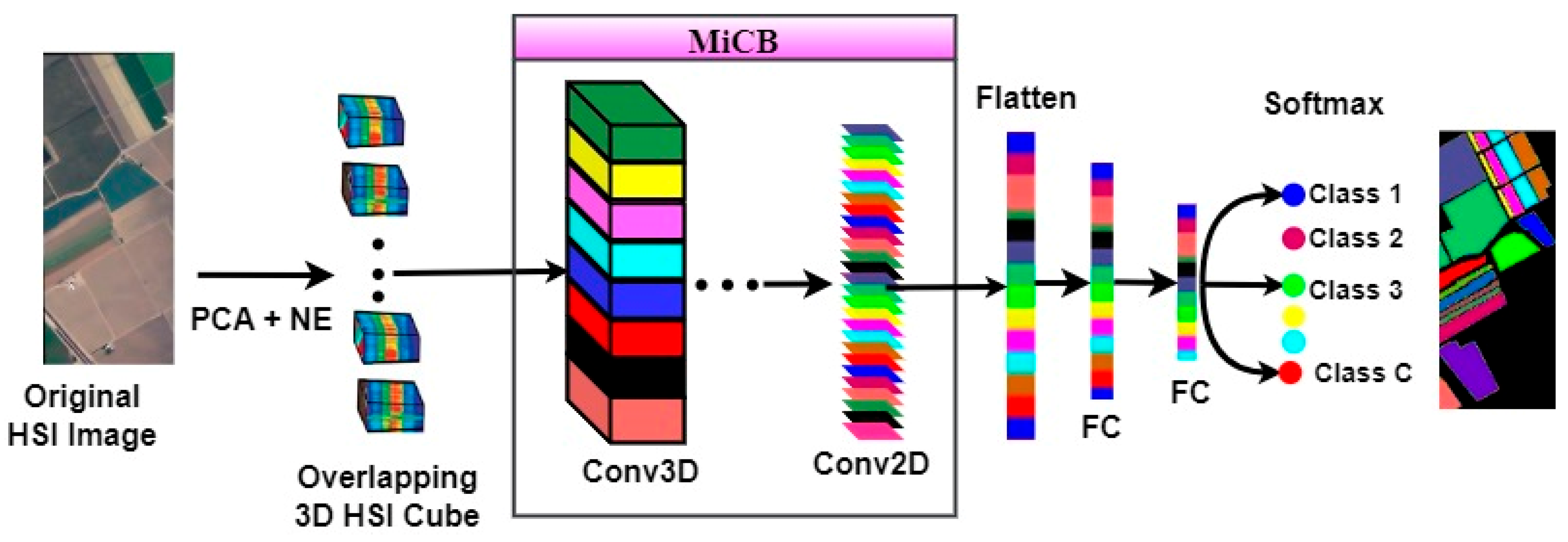
2.1. The Proposed Model
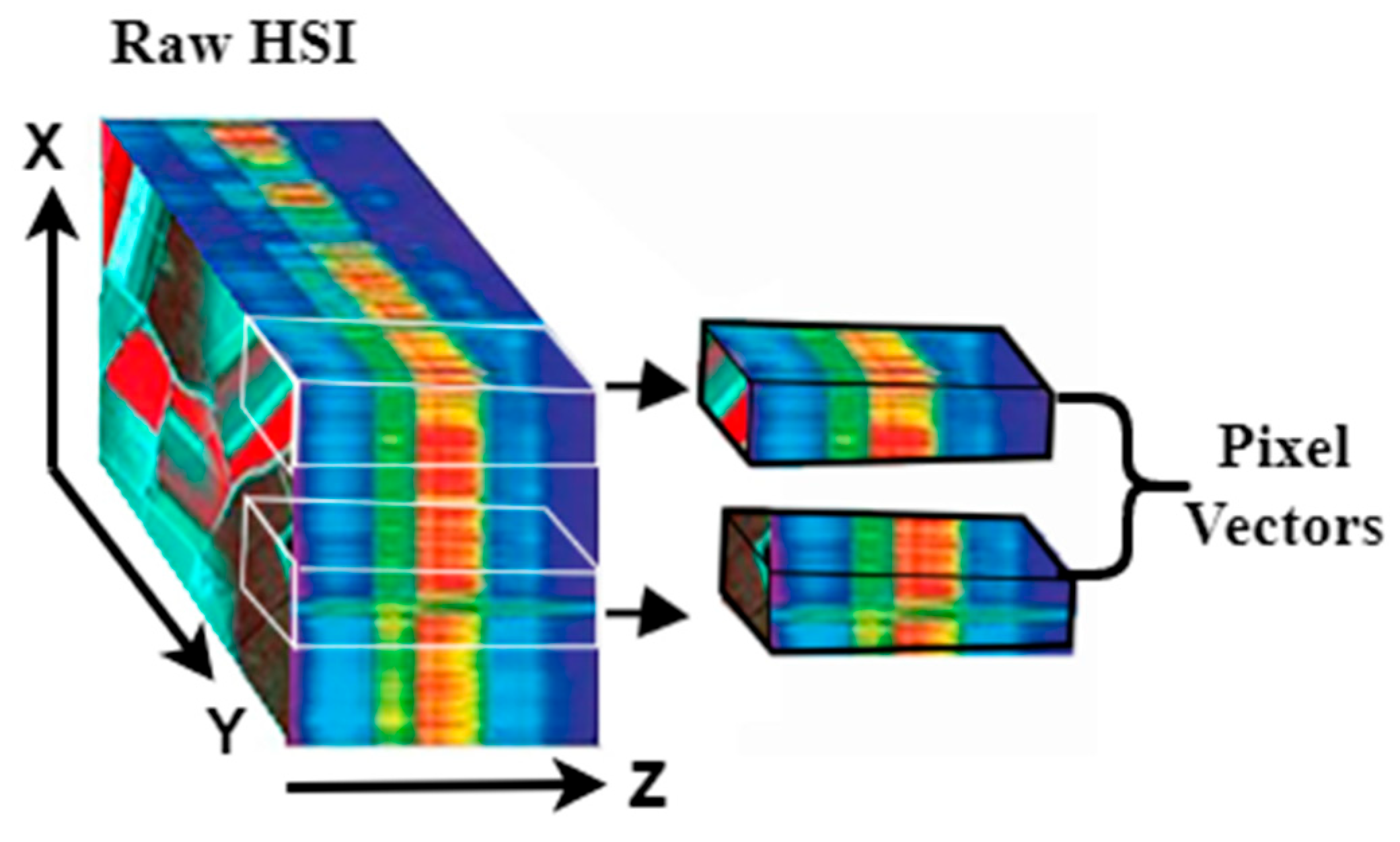
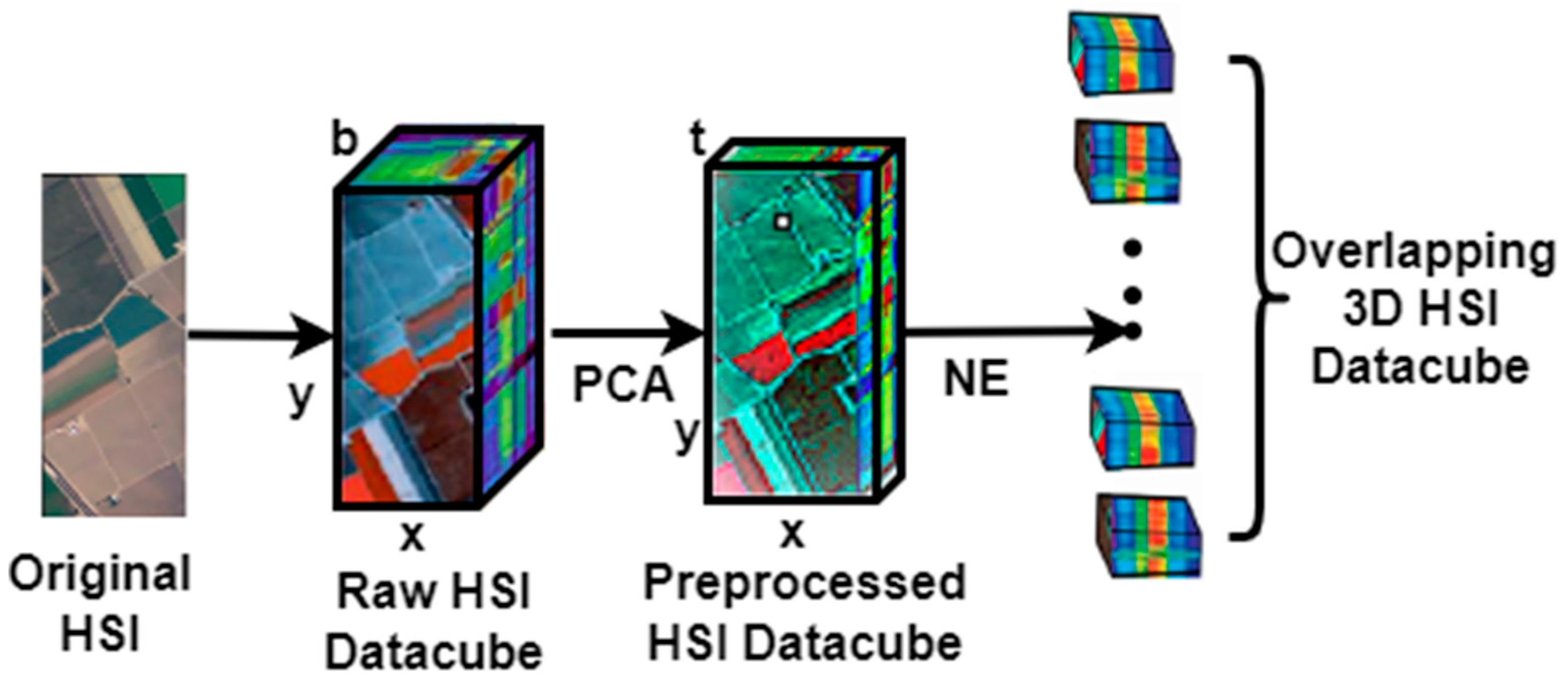
2.1.1. The Pre-Processing Part
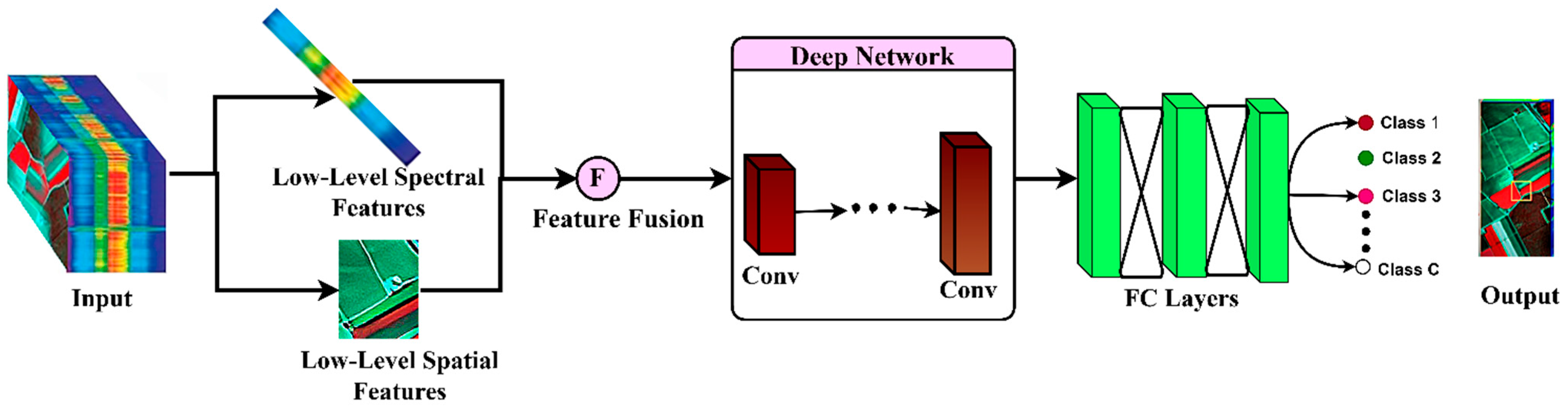
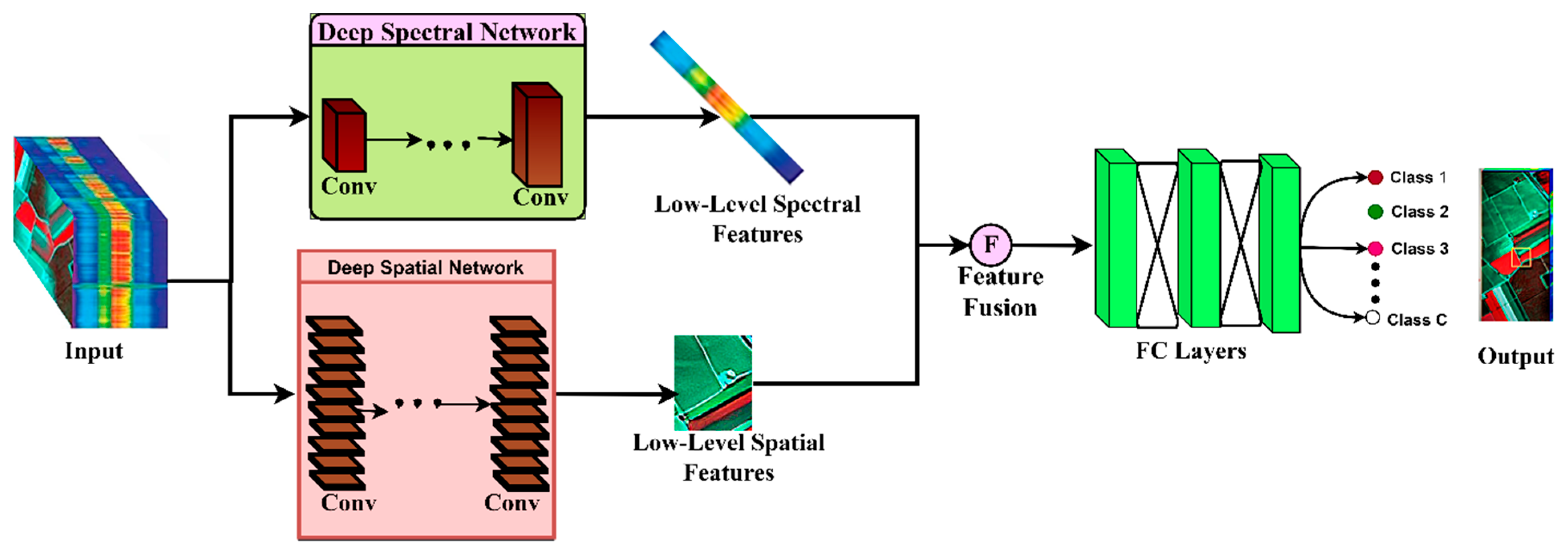
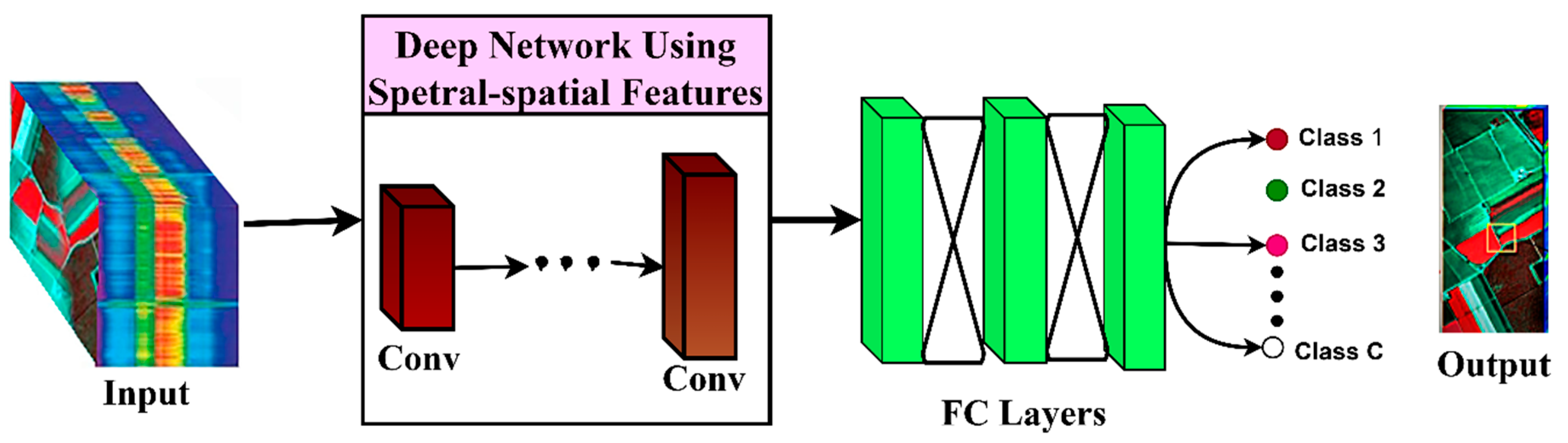
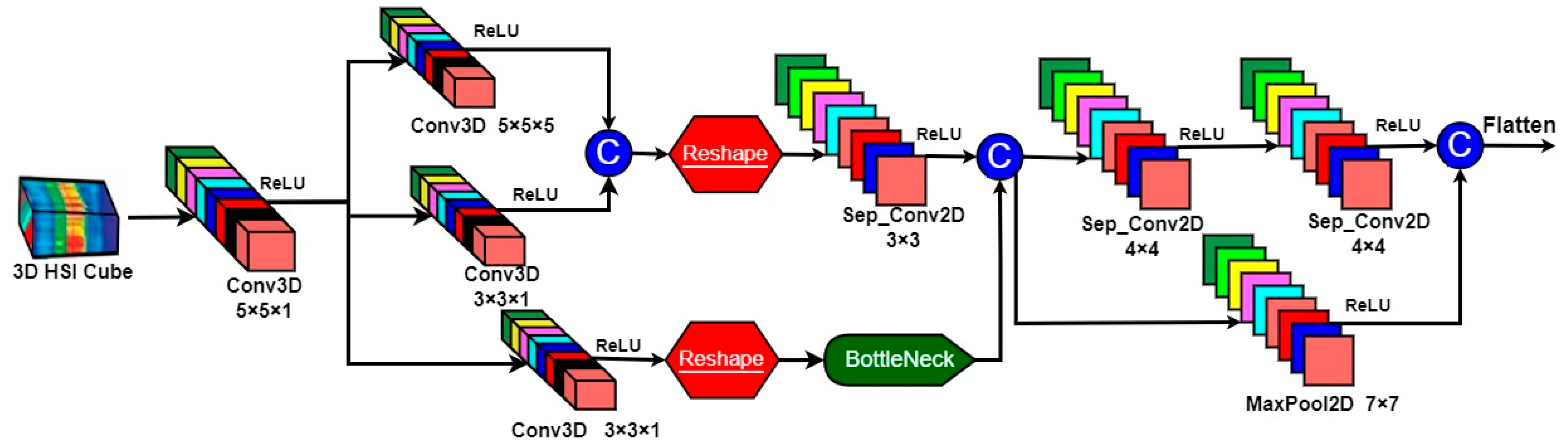
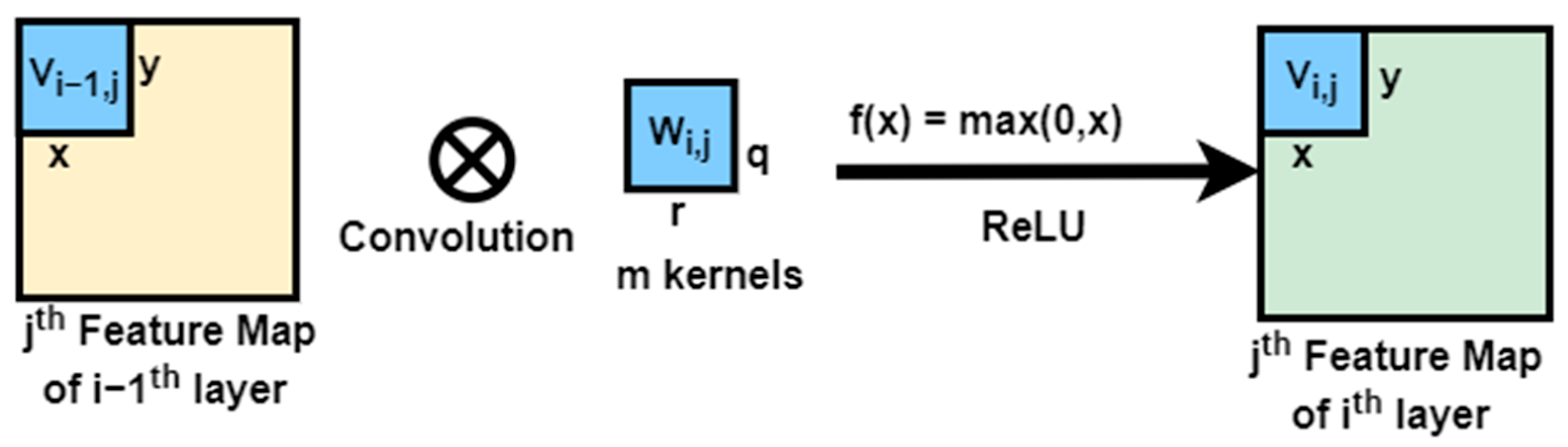
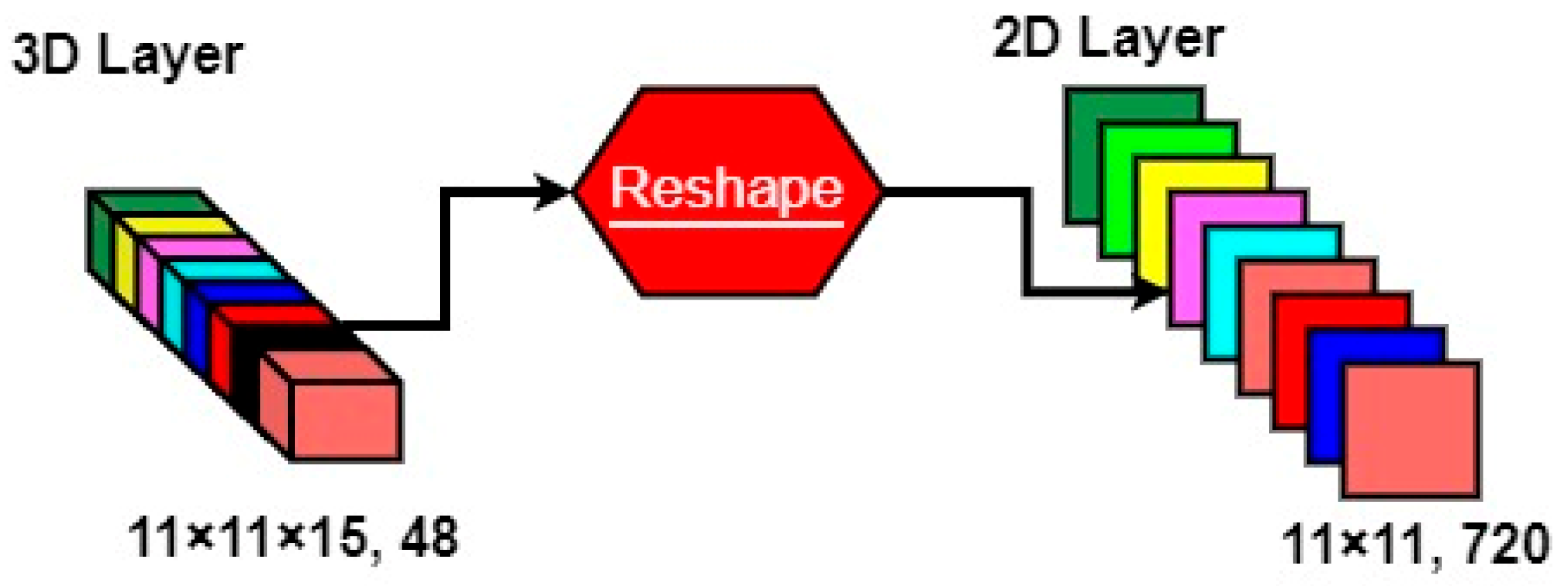
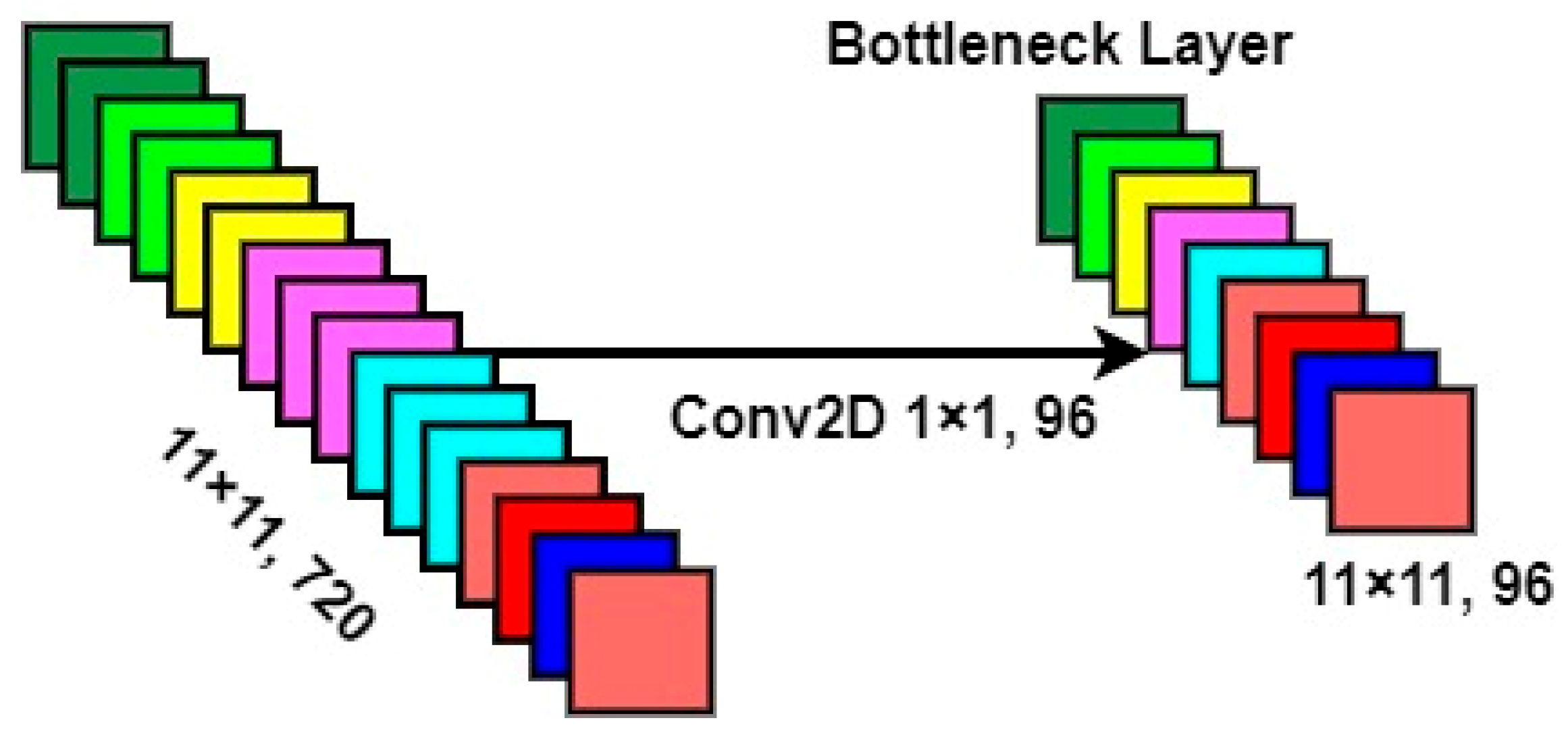
2.1.2. Spectral–Spatial Feature Learning Process
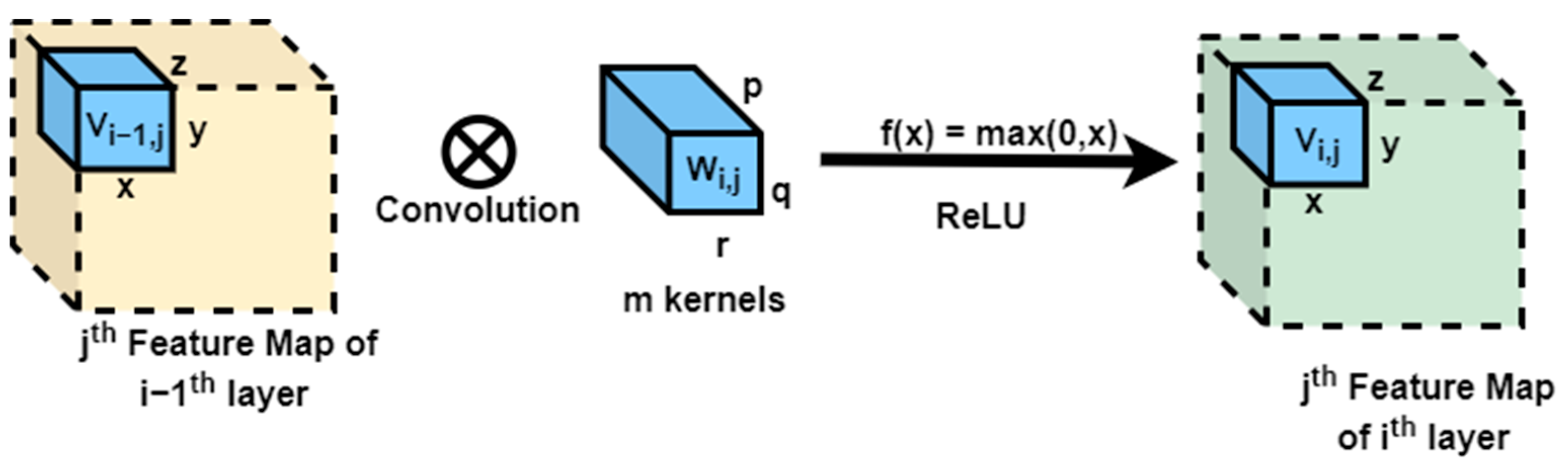
- Figure 9 can be expressed mathematically using Equation (4):
- represents the ReLU activation function.
2.1.3. MiCB Classifier
- is the ground truth label and is the softmax probability for the class.
- The argmin operation finds the class with the least loss value from the target function.
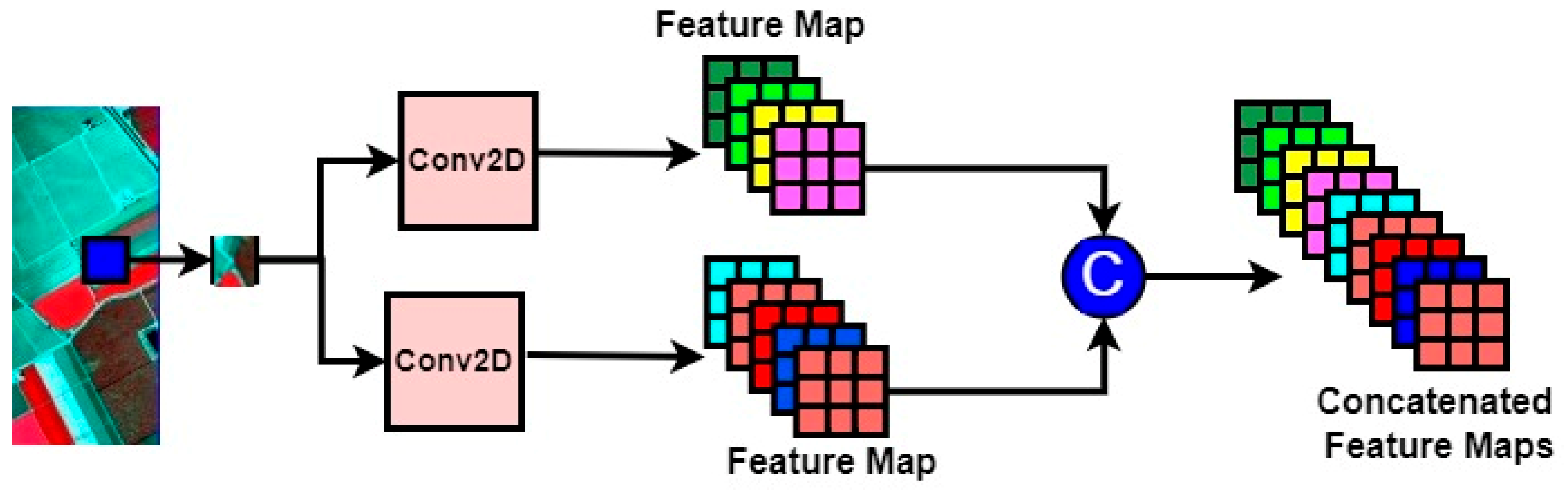
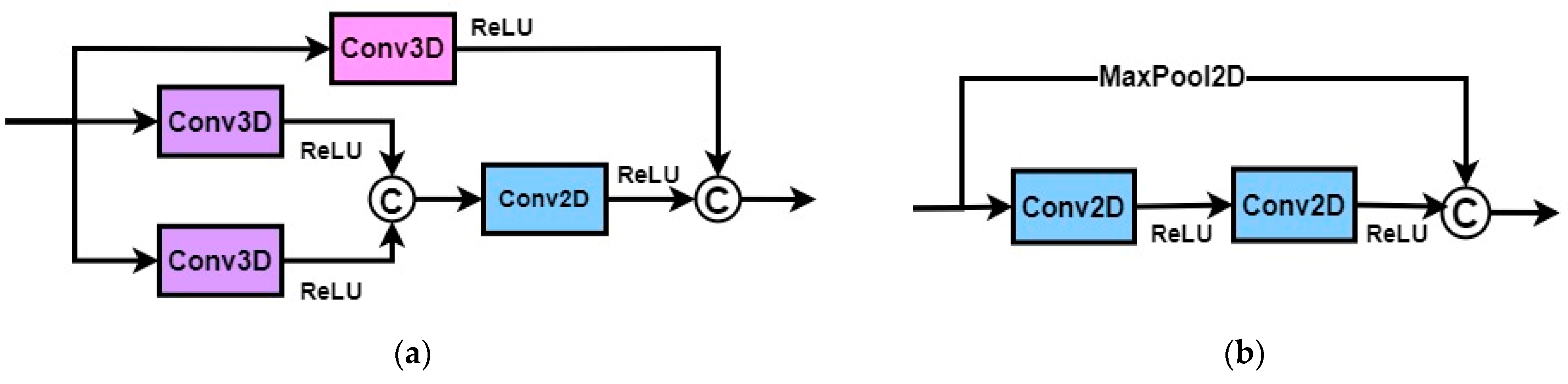
2.2. Simultaneous Convolution of Low-Level High-Level Spectral–Spatial Features
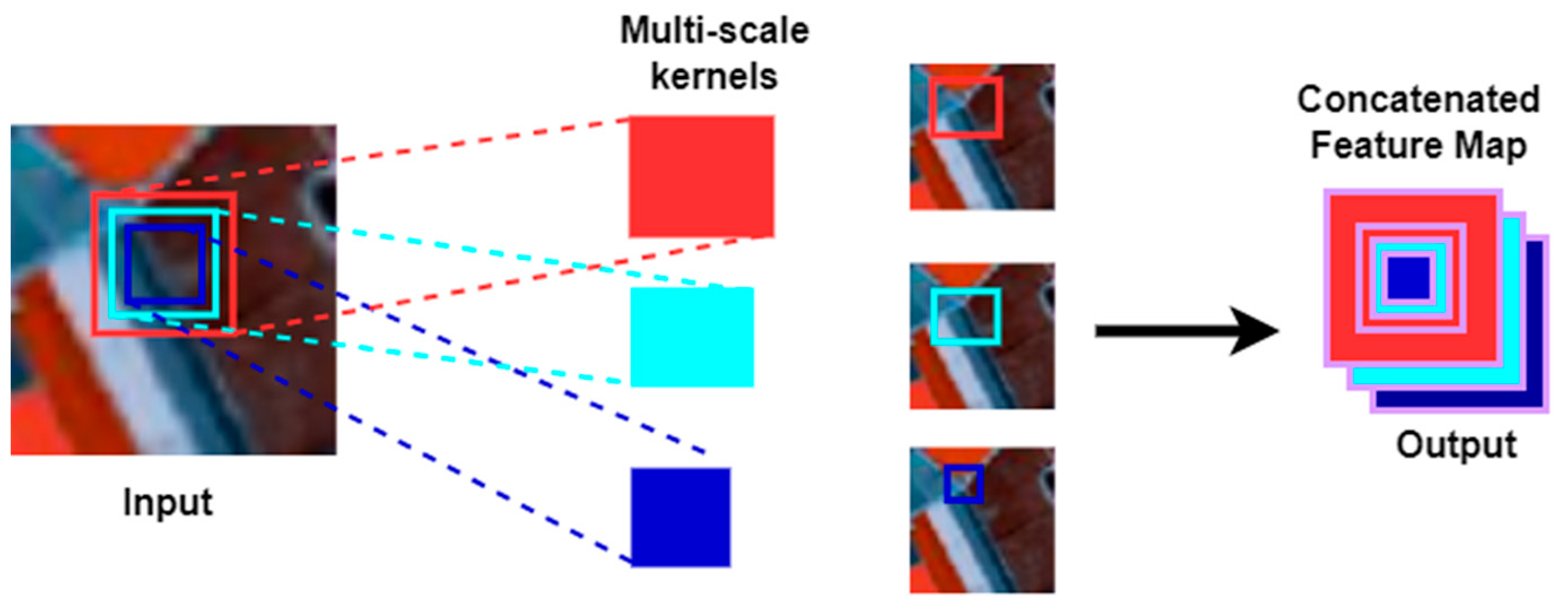
2.3. Multi-Scale 3D Convolution Block
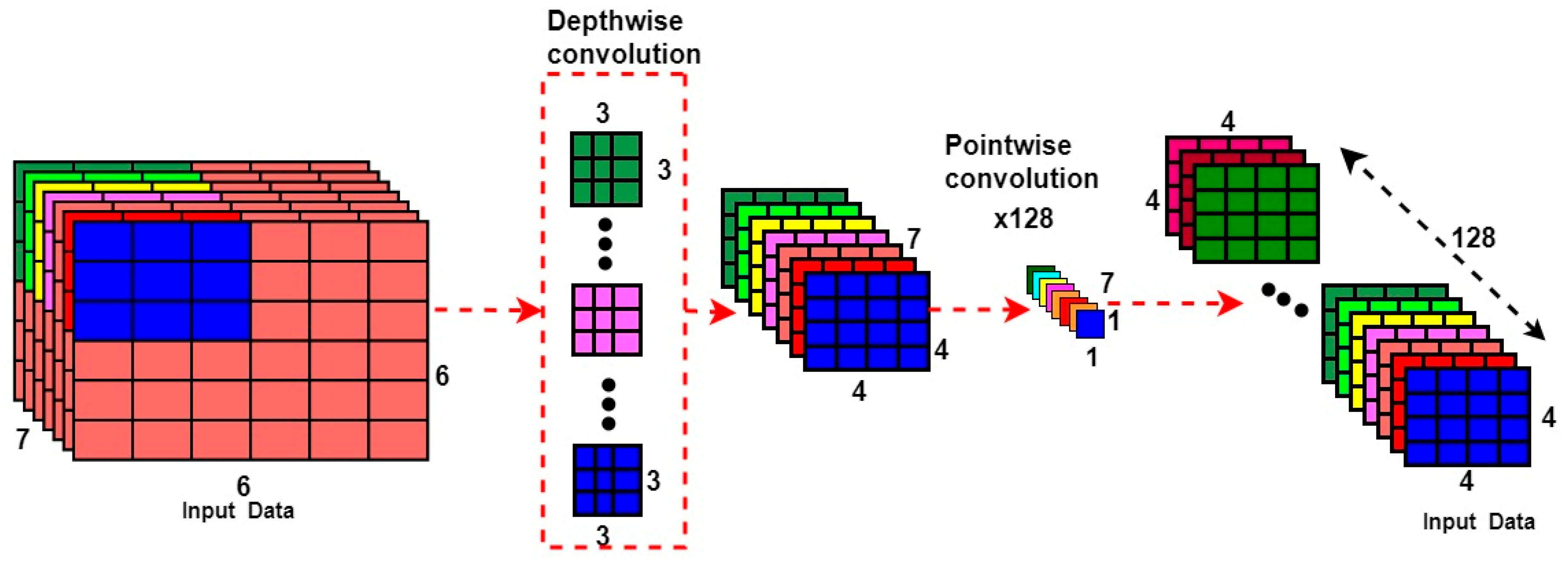
2.4. Depthwise Separable Convolution
2.5. Residual Learning
- denotes the pooled feature map, and is a max pooling function.
3. Experimental Setup
3.1. Dataset Description
3.2. Implementation Details
3.3. Evaluation Criteria
4. Experimental Results and Discussion
4.1. Effect of Varying Window Size
4.2. Ablation Results
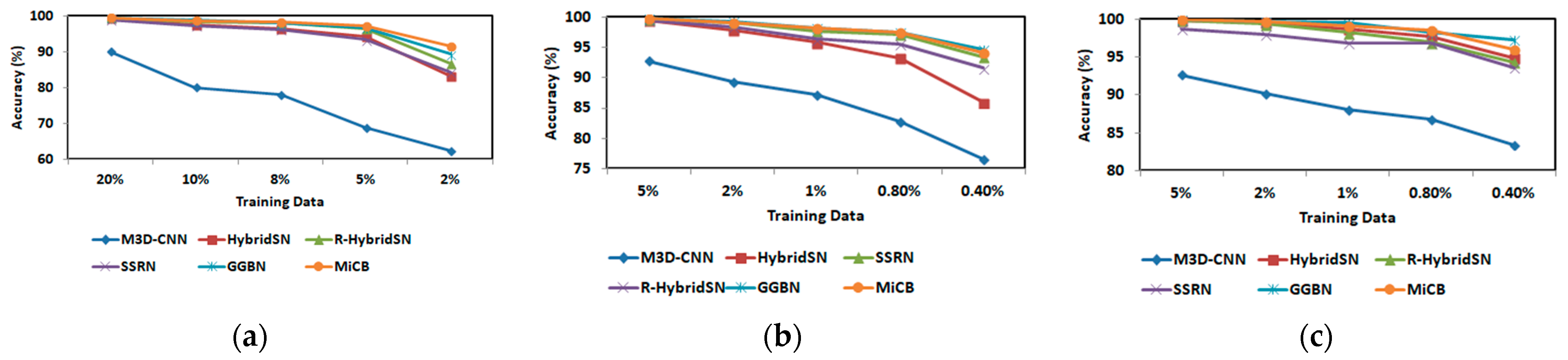
4.2.1. The Summary of Classification Accuracies of the Selected Models Trained Using Very Minimal Sample Data
4.2.2. Computational Complexity of Model A, Model B, and MiCB over IP, UP, and SA Datasets
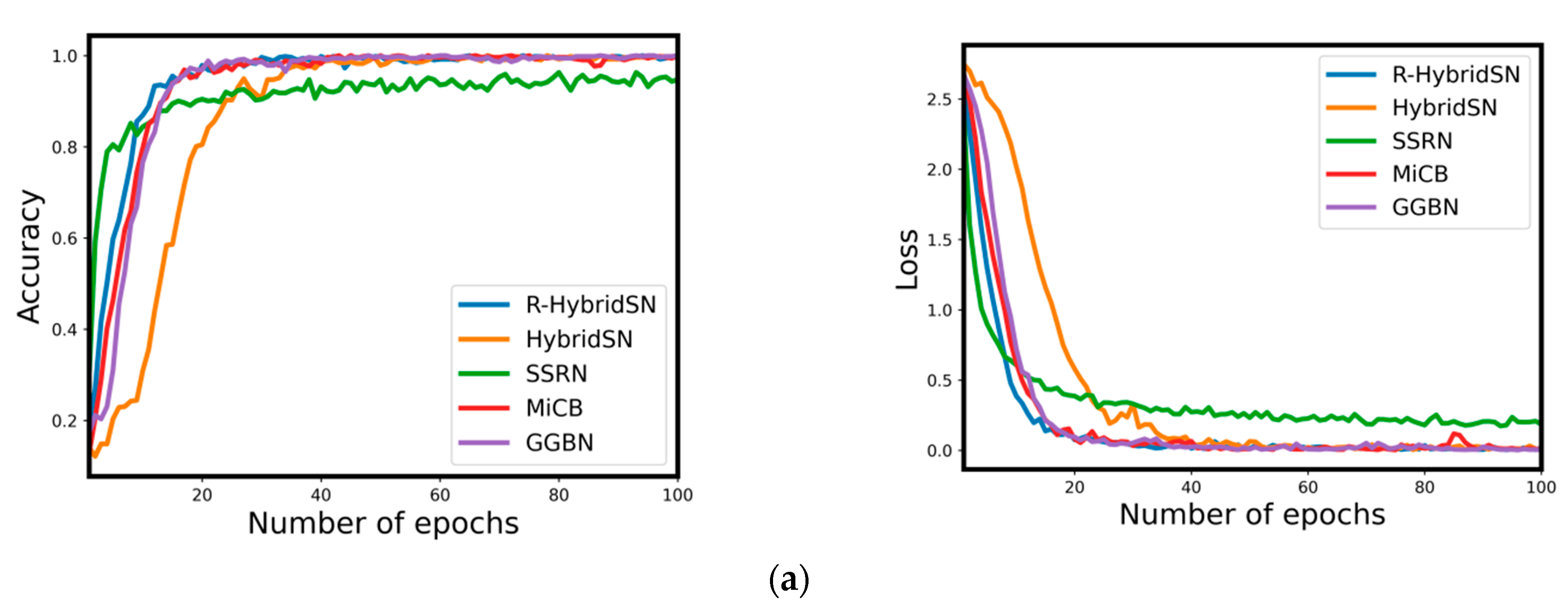
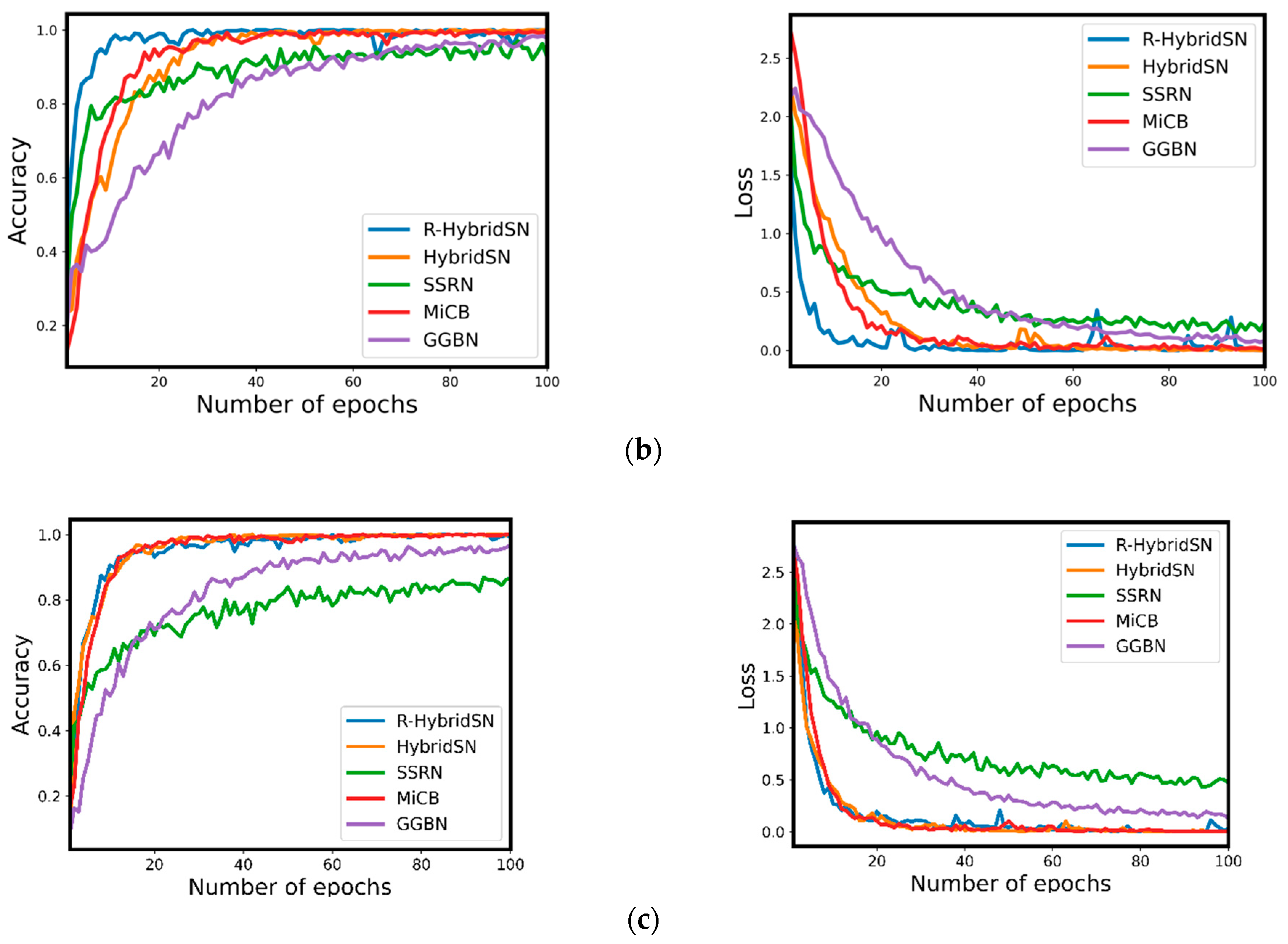
4.3. The Training Accuracy and Loss Convergence Graphs
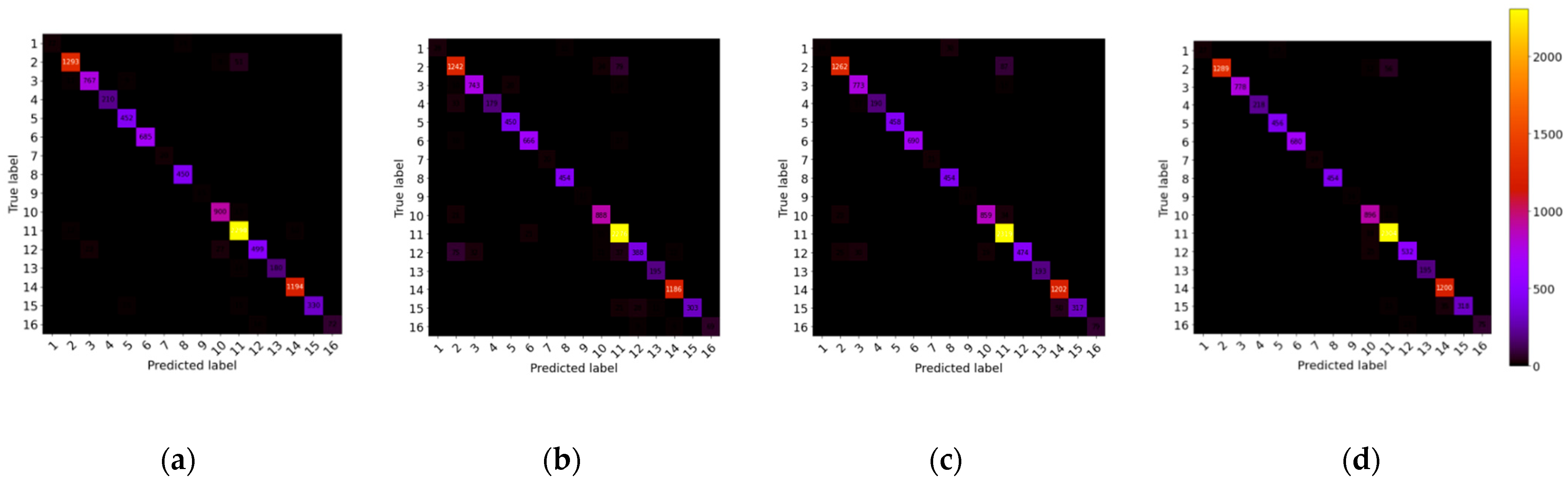
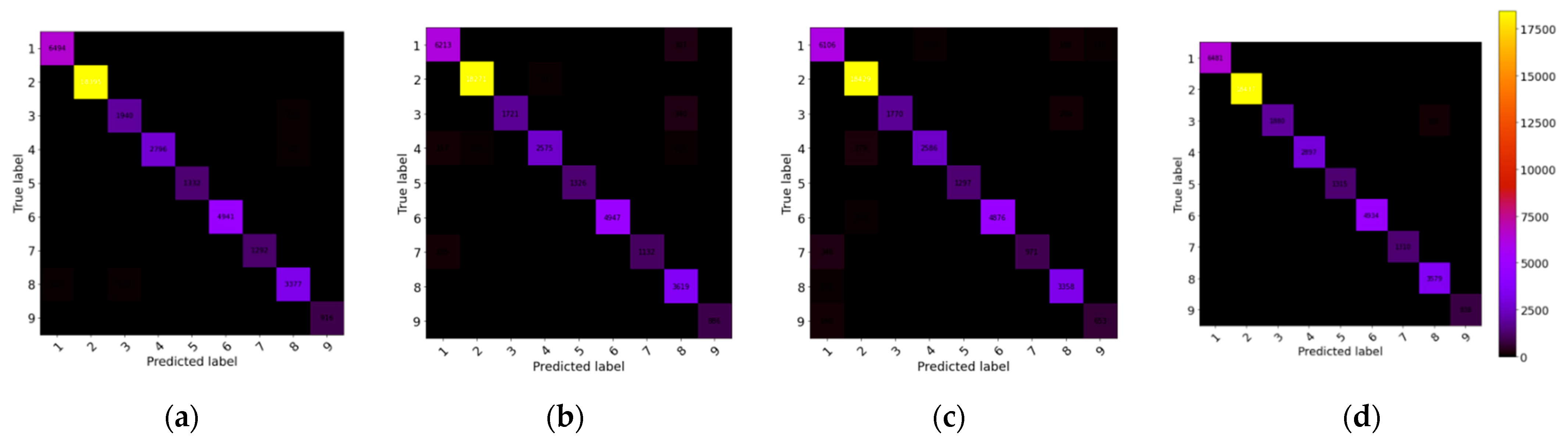
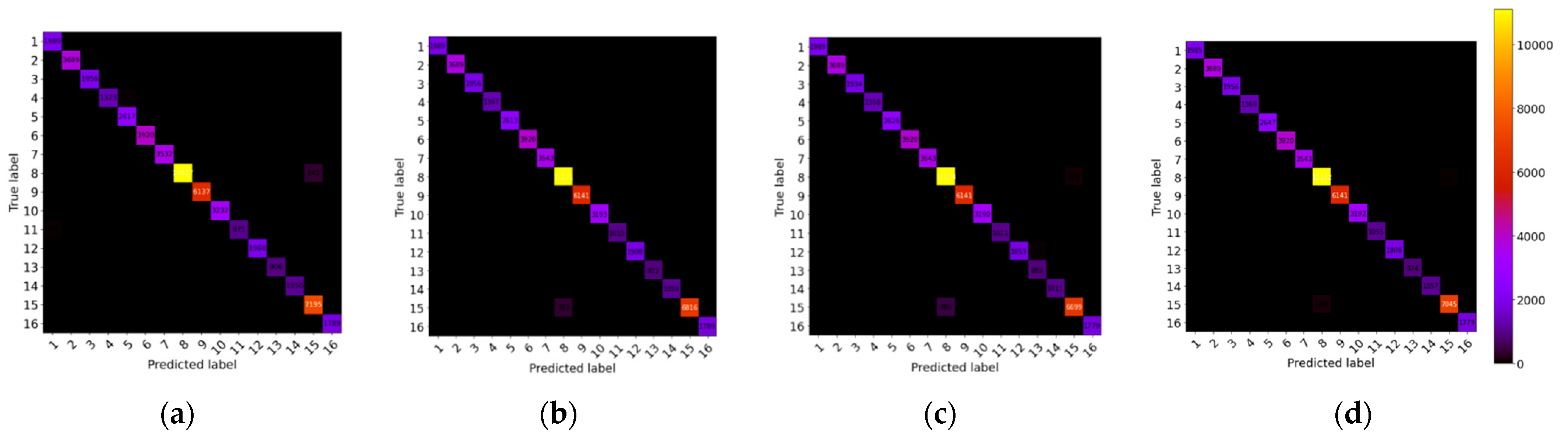
4.4. The Confusion Matrix
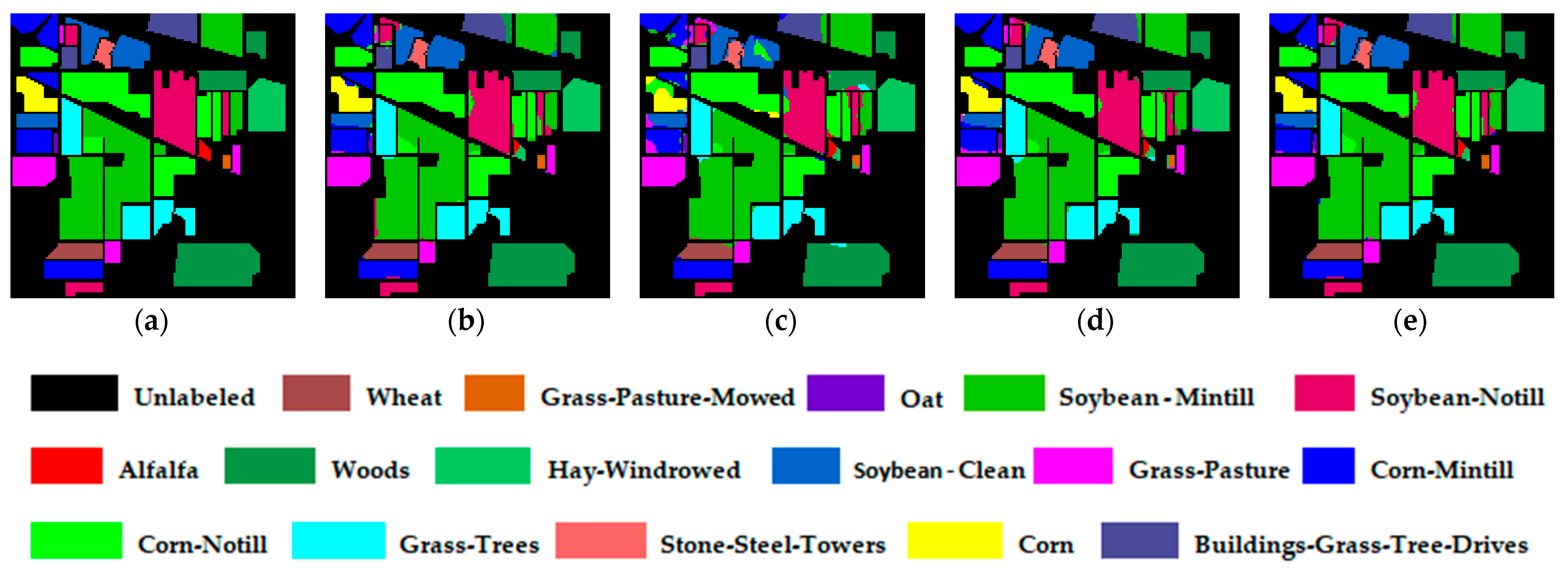
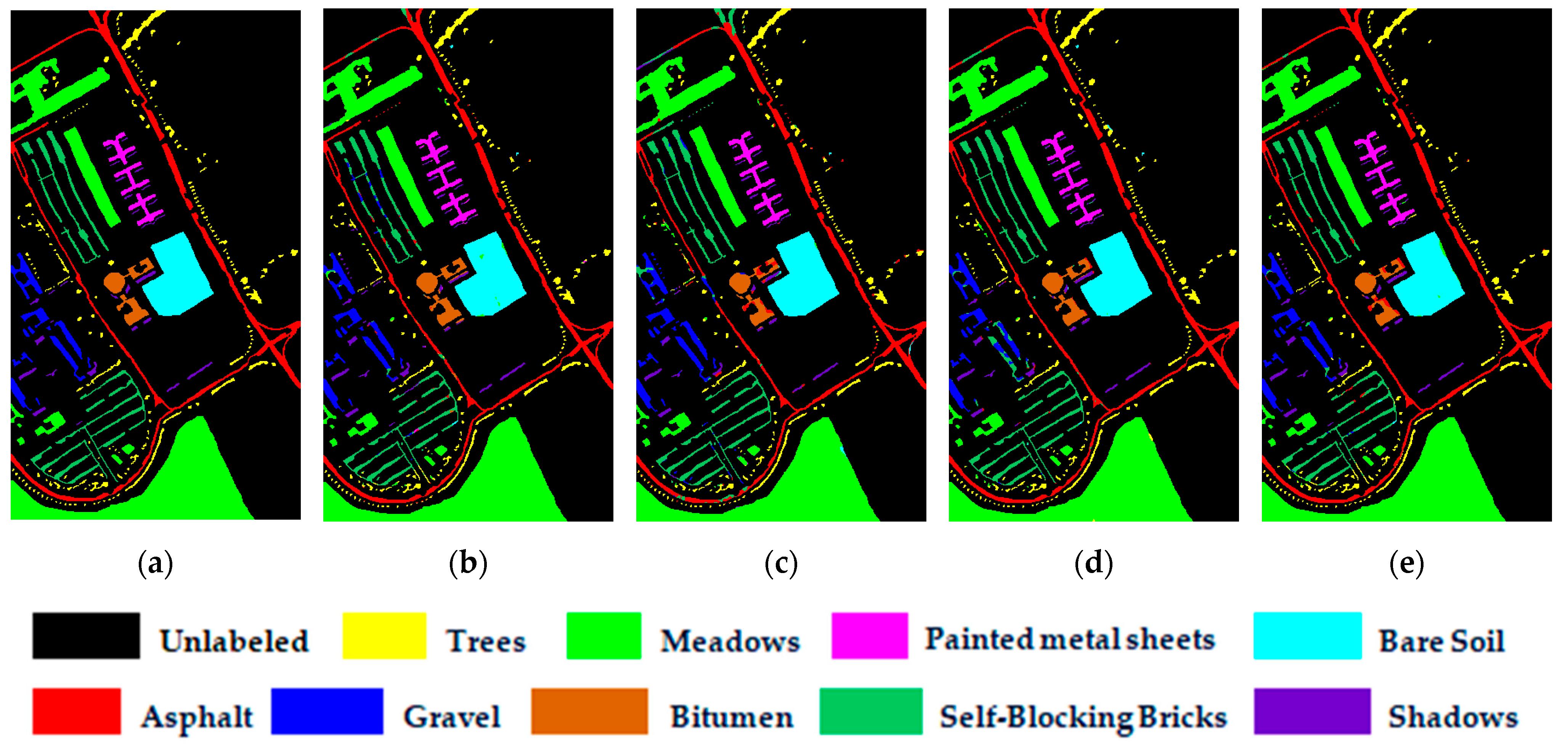
4.5. Classification Diagrams
4.6. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tinega, H.; Chen, E.; Ma, L.; Mariita, R.M.; Nyasaka, D. Hyperspectral Image Classification Using Deep Genome Graph-Based Approach. Sensors 2021, 21, 6467. [Google Scholar] [CrossRef]
- Hao, S.; Wang, W.; Ye, Y.; Nie, T.; Bruzzone, L. Two-Stream Deep Architecture for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 2349–2361. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, Y.; Liu, W.; Wang, Z. A hyperspectral image classification algorithm based on atrous convolution. EURASIP J. Wirel. Commun. Netw. 2019, 270. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Y.; Zhao, X.; Wang, G. Spectral-spatial classification of hyperspectral image using autoencoders. In Proceedings of the 2013 9th International Conference on Information, Communications Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Yue, J.; Mao, S.; Li, M. A deep learning framework for hyperspectral image classification using spatial pyramid pooling. Remote Sens. Lett. 2016, 7, 875–884. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Nyabuga, D.O.; Song, J.; Liu, G.; Adjeisah, M. A 3D-2D Convolutional Neural Network and Transfer Learning for Hyperspectral Image Classification. Comput. Intell. Neurosci. 2021, 2021, 1759111. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear Versus Nonlinear PCA for the Classification of Hyperspectral Data Based on the Extended Morphological Profiles. IEEE Geosci. Remote Sens. Lett. 2012, 9, 447–451. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Zhang, Y. Classification of hyperspectral image based on deep belief networks. In Proceedings of the 2014 IEEE International Conference on Image Processing ICIP 2014, Paris, France, 27–30 October 2014; pp. 5132–5136. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Aptoula, E.; Ozdemir, M.C.; Yanikoglu, B. Deep Learning with Attribute Profiles for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1970–1974. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning Deep Hierarchical Spatial–Spectral Features for Hyperspectral Image Classification Based on Residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Cao, F.; Guo, W. Deep hybrid dilated residual networks for hyperspectral image classification. Neurocomputing 2020, 384, 170–181. [Google Scholar] [CrossRef]
- Wu, P.; Cui, Z.; Gan, Z.; Liu, F. Three-dimensional resNeXt network using feature fusion and label smoothing for hyperspectral image classification. Sensors 2020, 20, 1652. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, H.; Wang, G.; Chen, H. Hybrid Depth-Separable Residual Networks for Hyperspectral Image Classification. Complexity 2020, 2020, 4608647. [Google Scholar] [CrossRef]
- Tinega, H.C.; Chen, E.; Ma, L.; Nyasaka, D.O.; Mariita, R.M. HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 1332. [Google Scholar] [CrossRef]
- Bao, J.; Chen, Y.; Yu, L.; Chen, C. A multi-scale kernel learning method and its application in image classification. Neurocomputing 2017, 257, 16–23. [Google Scholar] [CrossRef]
- Zhou, W.; Lin, X.; Lei, J.; Yu, L.; Hwang, J.-N. MFFENet: Multiscale Feature Fusion and Enhancement Network For RGB–Thermal Urban Road Scene Parsing. IEEE Trans. Multimedia 2022, 24, 2526–2538. [Google Scholar] [CrossRef]
- Elizar, E.; Zulkifley, M.A.; Muharar, R.; Zaman, M.H.M.; Mustaza, S.M. A Review on Multiscale-Deep-Learning Applications. Sensors 2022, 22, 7384. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-Scale 3d Deep Convolutional Neural Network for Hyperspectral Image Classification. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3904–3908. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised Spectral–Spatial Feature Learning via Deep Residual Conv–Deconv Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 391–406. [Google Scholar] [CrossRef]
- Liu, G.; Qi, L.; Tie, Y.; Ma, L. Hyperspectral Image Classification Using Kernel Fused Representation via a Spatial-Spectral Composite Kernel with Ideal Regularization. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1422–1426. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]

| Class No | IP Dataset | SA Dataset | UP Dataset | |||
|---|---|---|---|---|---|---|
| Class Label | Samples (%) | Class Label | Samples (%) | Class Label | Samples (%) | |
| 1 | Alfalfa | 0.45 | Brocoli_green_weeds_1 | 3.71 | Asphalt | 15.50 |
| 2 | Corn-notill | 13.93 | Brocoli_green_weeds_2 | 6.88 | Meadows | 43.60 |
| 3 | Corn-mintill | 8.10 | Fallow | 3.65 | Gravel | 4.91 |
| 4 | Corn | 2.31 | Fallow_rough_plow | 2.58 | Trees | 7.16 |
| 5 | Grass-pasture | 4.71 | Fallow_smooth | 4.95 | Painted | 3.14 |
| 6 | Grass-trees | 7.12 | Stubble | 7.31 | Bare | 11.76 |
| 7 | Grass-pasture-mowed | 0.27 | Celery | 6.61 | Bitumen | 3.11 |
| 8 | Hay-windrowed | 4.66 | Grapes_untrained | 20.82 | Self-Blocking | 8.61 |
| 9 | Oats | 0.20 | Soil_vinyard_develop | 11.46 | Shadows | 2.21 |
| 10 | Soybean-notill | 9.48 | Corn_senesced_green_weeds | 6.06 | ||
| 11 | Soybean-mintill | 23.95 | Lettuce_romaine_4wk | 1.97 | ||
| 12 | Soybean-clean | 5.79 | Lettuce_romaine_5wk | 3.56 | ||
| 13 | Wheat | 2.00 | Lettuce_romaine_6wk | 1.69 | ||
| 14 | Woods | 12.34 | Lettuce_romaine_7wk | 1.98 | ||
| 15 | Buildings-Grass- Trees-Drives | 3.77 | Vinyard_untrained | 13.43 | ||
| 16 | Stone-Steel-Towers | 0.91 | Vinyard_vertical_trellis | 3.34 | ||
| Evaluation | 15 ×15 | 17 × 17 | 19 × 19 | 21 × 21 | 23 × 23 | 25 × 25 | 27 × 27 |
|---|---|---|---|---|---|---|---|
| Kappa | 0.967 | 0.970 | 0.967 | 0.965 | 0.965 | 0.963 | 0.963 |
| OA | 97.14 | 97.35 | 97.13 | 96.90 | 96.95 | 96.76 | 96.71 |
| AA | 90.08 | 92.16 | 91.38 | 89.18 | 91.46 | 91.22 | 91.79 |
| Evaluation | 15 × 15 | 17 × 17 | 19 × 19 | 21 × 21 | 23 × 23 | 25 × 25 | 27 × 27 |
|---|---|---|---|---|---|---|---|
| Kappa | 0.974 | 0.977 | 0.973 | 0.974 | 0.970 | 0.969 | 0.969 |
| OA | 98.03 | 98.23 | 97.96 | 98.07 | 97.73 | 97.66 | 97.66 |
| AA | 96.44 | 96.73 | 95.99 | 96.09 | 95.51 | 94.98 | 94.99 |
| Evaluation | 15 × 15 | 17 × 17 | 19 × 19 | 21 × 21 | 23 × 23 | 25 × 25 | 27 × 27 |
|---|---|---|---|---|---|---|---|
| Kappa | 0.988 | 0.991 | 0.992 | 0.995 | 0.995 | 0.995 | 0.996 |
| OA | 98.93 | 99.20 | 99.28 | 99.51 | 99.54 | 99.56 | 99.64 |
| AA | 98.95 | 99.13 | 99.16 | 99.42 | 99.35 | 99.47 | 99.51 |
| Class Number | Overall Accuracy in Percentage (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| M3D-CNN | HybridSN | R-HybridSN | SSRN | GGBN | Model A | Model B | MiCB | |
| 1 | 27.5 | 61.82 | 45 | 12.99 | 46.36 | 59.09 | 32.14 | 72.73 |
| 2 | 59.15 | 92.25 | 95.45 | 93.04 | 94.78 | 95.15 | 94.85 | 96.05 |
| 3 | 45.07 | 92.97 | 97.36 | 93.72 | 98.38 | 97.97 | 98.70 | 99.24 |
| 4 | 38.49 | 78.22 | 94.8 | 72.38 | 94.49 | 93.27 | 88.57 | 92.38 |
| 5 | 70.33 | 96.6 | 98.85 | 98.16 | 99.15 | 99.69 | 99.38 | 98.79 |
| 6 | 97.2 | 98.11 | 99.32 | 99.86 | 98.02 | 99.55 | 98.66 | 98.52 |
| 7 | 18.52 | 68.52 | 95.56 | 0 | 87.78 | 77.25 | 12.70 | 98.41 |
| 8 | 98.04 | 99.96 | 100 | 99.94 | 99.85 | 99.81 | 99.31 | 99.94 |
| 9 | 25.79 | 83.68 | 65.26 | 0 | 78.95 | 82.71 | 10.53 | 50.38 |
| 10 | 55.85 | 96.12 | 95.9 | 91.01 | 97.82 | 97.04 | 96.36 | 97.26 |
| 11 | 76.2 | 96.66 | 98.09 | 95.63 | 97.98 | 97.86 | 98.21 | 98.73 |
| 12 | 33.89 | 85.44 | 89.15 | 87.9 | 92.97 | 93.45 | 92.01 | 93.12 |
| 13 | 91.23 | 94.97 | 99.74 | 98.53 | 97.64 | 99.71 | 99.49 | 99.34 |
| 14 | 94.68 | 99.34 | 99.26 | 99.82 | 99.03 | 99.97 | 99.14 | 99.77 |
| 15 | 42.37 | 82.92 | 87.66 | 82.09 | 92.29 | 92.45 | 86.22 | 89.96 |
| 16 | 49.32 | 80 | 88.18 | 82.31 | 88.75 | 82.79 | 89.94 | 89.94 |
| Kappa | 0.642 | 0.934 | 0.96 | 0.923 | 0.96 | 0.965 | 0.955 | 0.97 |
| OA (%) | 68.88 | 94.24 | 96.46 | 93.39 | 96.85 | 96.92 | 96.07 | 97.35 |
| AA (%) | 57.73 | 87.97 | 90.6 | 75.28 | 91.51 | 91.67 | 81.01 | 92.16 |
| Class | Overall Accuracy in Percentage (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| M3D-CNN | HybridSN | R-HybridSN | SSRN | GGBN | Model A | Model B | MiCB | |
| 1 | 90.56 | 95.72 | 96.94 | 98.76 | 98.50 | 97.65 | 98.56 | 99.40 |
| 2 | 89.47 | 99.68 | 99.69 | 99.91 | 99.70 | 99.68 | 99.77 | 99.38 |
| 3 | 59.11 | 84.38 | 87.17 | 85.72 | 89.03 | 95.37 | 89.70 | 95.01 |
| 4 | 93.25 | 87.7 | 89.15 | 94.85 | 93.28 | 92.57 | 93.26 | 93.90 |
| 5 | 93.66 | 98.99 | 99.51 | 99.76 | 99.71 | 98.83 | 99.77 | 99.47 |
| 6 | 69.63 | 96.82 | 98.44 | 96.11 | 99.79 | 99.26 | 97.54 | 99.73 |
| 7 | 65.71 | 84.42 | 95.82 | 95.98 | 98.14 | 97.13 | 84.40 | 93.97 |
| 8 | 78.35 | 89.18 | 93.28 | 94.96 | 96.03 | 97.93 | 91.50 | 96.89 |
| 9 | 94.41 | 71.71 | 77.82 | 99.89 | 97.35 | 97.77 | 92.42 | 92.79 |
| Kappa | 0.798 | 0.935 | 0.955 | 0.97 | 0.975 | 0.977 | 0.960 | 0.977 |
| OA (%) | 84.63 | 95.09 | 96.59 | 97.67 | 98.13 | 98.30 | 97.01 | 98.29 |
| AA (%) | 81.57 | 89.84 | 93.09 | 96.22 | 96.84 | 97.35 | 94.10 | 96.73 |
| Class | Overall Accuracy in Percentage (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| M3D-CNN | HybridSN | R-HybridSN | SSRN | GGBN | Model A | Model B | MiCB | |
| 1 | 94.88 | 99.99 | 100 | 100 | 99.95 | 100.00 | 99.98 | 99.99 |
| 2 | 99.61 | 100 | 99.97 | 100 | 100 | 100.00 | 99.97 | 100 |
| 3 | 91.89 | 99.82 | 99.49 | 99.96 | 99.92 | 99.74 | 100.00 | 99.72 |
| 4 | 98.33 | 98.38 | 98.72 | 99.72 | 96.25 | 99.68 | 99.49 | 99.66 |
| 5 | 98.83 | 99.26 | 98.43 | 98.73 | 99.33 | 99.34 | 99.60 | 99.02 |
| 6 | 98.09 | 99.93 | 99.9 | 100 | 99.92 | 99.98 | 99.65 | 99.80 |
| 7 | 97.67 | 99.95 | 99.96 | 99.99 | 99.98 | 99.98 | 100.00 | 99.85 |
| 8 | 82.4 | 97.77 | 98.23 | 95.06 | 99.25 | 99.38 | 98.60 | 98.98 |
| 9 | 98.14 | 99.99 | 99.99 | 100 | 100 | 99.99 | 100 | 100 |
| 10 | 87.6 | 98.36 | 97.9 | 98.33 | 99.08 | 98.48 | 98.49 | 98.54 |
| 11 | 86.72 | 96.06 | 96.46 | 97.42 | 98.75 | 96.49 | 96.85 | 99.24 |
| 12 | 96.99 | 97.44 | 99.09 | 100 | 99.77 | 99.92 | 99.48 | 99.48 |
| 13 | 97.14 | 97.42 | 82.82 | 93.02 | 93.67 | 96.79 | 96.35 | 95.86 |
| 14 | 91.78 | 99.52 | 97.25 | 95.62 | 99.27 | 99.10 | 99.30 | 98.00 |
| 15 | 64.42 | 97.06 | 95.12 | 88.18 | 98.49 | 95.76 | 95.18 | 98.02 |
| 16 | 78.14 | 100 | 99.71 | 99.49 | 99.99 | 99.88 | 99.52 | 99.98 |
| Kappa | 0.867 | 0.985 | 0.98 | 0.966 | 0.992 | 0.989 | 0.986 | 0.991 |
| OA (%) | 88.02 | 98.72 | 98.25 | 96.94 | 99.29 | 99.00 | 98.74 | 99.20 |
| AA (%) | 91.41 | 98.81 | 97.69 | 97.84 | 98.98 | 99.03 | 98.90 | 99.13 |
| Dataset | Model A | Model B | MiCB | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Params | Train Time | Test Time | Params | Test Time | Test Time | Params | Test Time | Test Time | |
| IP | 2,354,700 | 43.01 | 2.95 | 426,108 | 35.08 | 2.07 | 958,428 | 39.96 | 2.47 |
| UP | 2,353,797 | 41.88 | 11.88 | 425,205 | 33.24 | 8.99 | 957,525 | 42.02 | 10.82 |
| SA | 2,354,700 | 47.83 | 14.78 | 426,108 | 40.92 | 11.08 | 958,428 | 45.44 | 12.79 |
| Training Sample Data in Percentage | |||||
|---|---|---|---|---|---|
| Model | 20% | 10% | 8% | 5% | 2% |
| M3D-CNN | 90.03 | 80.10 | 78.04 | 68.88 | 62.28 |
| SSRN | 98.91 | 97.25 | 96.33 | 93.39 | 84.30 |
| HybridSN | 99.30 | 97.66 | 96.37 | 94.24 | 83.14 |
| R-HybridSN | 99.52 | 98.44 | 98.12 | 96.46 | 86.67 |
| GGBN | 99.45 | 98.80 | 98.04 | 96.85 | 89.37 |
| MiCB | 99.52 | 98.75 | 98.43 | 97.35 | 91.59 |
| Model | Training Sample Data | ||||
|---|---|---|---|---|---|
| 5% | 2% | 1% | 0.80% | 0.40% | |
| M3D-CNN | 92.80 | 89.27 | 87.19 | 82.75 | 76.53 |
| SSRN | 99.57 | 99.07 | 97.67 | 97.12 | 93.41 |
| HybridSN | 99.45 | 97.86 | 95.86 | 93.30 | 85.95 |
| R-HybridSN | 99.47 | 98.47 | 96.40 | 95.64 | 91.60 |
| GGBN | 99.74 | 99.34 | 98.13 | 97.46 | 94.66 |
| MiCB | 99.74 | 99.16 | 98.29 | 97.48 | 94.21 |
| Model | Training Sample Data | ||||
|---|---|---|---|---|---|
| 5% | 2% | 1% | 0.80% | 0.40% | |
| M3D-CNN | 92.65 | 90.17 | 88.02 | 86.82 | 83.42 |
| SSRN | 98.7 | 98.02 | 96.94 | 96.87 | 93.64 |
| HybridSN | 99.83 | 99.57 | 98.72 | 97.78 | 94.88 |
| R-HybridSN | 99.82 | 99.36 | 98.25 | 96.97 | 94.33 |
| GGBN | 99.97 | 99.68 | 99.29 | 98.32 | 97.26 |
| MiCB | 99.93 | 99.73 | 99.20 | 98.57 | 96.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinega, H.C.; Chen, E.; Nyasaka, D.O. Improving Feature Learning in Remote Sensing Images Using an Integrated Deep Multi-Scale 3D/2D Convolutional Network. Remote Sens. 2023, 15, 3270. https://doi.org/10.3390/rs15133270
Tinega HC, Chen E, Nyasaka DO. Improving Feature Learning in Remote Sensing Images Using an Integrated Deep Multi-Scale 3D/2D Convolutional Network. Remote Sensing. 2023; 15(13):3270. https://doi.org/10.3390/rs15133270
Chicago/Turabian StyleTinega, Haron C., Enqing Chen, and Divinah O. Nyasaka. 2023. "Improving Feature Learning in Remote Sensing Images Using an Integrated Deep Multi-Scale 3D/2D Convolutional Network" Remote Sensing 15, no. 13: 3270. https://doi.org/10.3390/rs15133270
APA StyleTinega, H. C., Chen, E., & Nyasaka, D. O. (2023). Improving Feature Learning in Remote Sensing Images Using an Integrated Deep Multi-Scale 3D/2D Convolutional Network. Remote Sensing, 15(13), 3270. https://doi.org/10.3390/rs15133270








