High-Resolution Estimation of Methane Emissions from Boreal and Pan-Arctic Wetlands Using Advanced Satellite Data
Abstract
:1. Introduction
- Importance of spatial resolution in soil moisture (SM) data for estimating methane fluxes from wetlands: We examine how the spatial resolution of SM data influences the accuracy of CH4 flux estimations from wetland areas.
- Impact of spatial resolution on the simulated temporal variability of CH4: We analyze the effect of spatial resolution on capturing the local temporal variations in CH4 emissions, which helps us understand the dynamics of CH4 fluxes at different scales.
- Assessment of remote sensing SM techniques compared with hydrological models: We assess the additional value of using remote sensing-based SM techniques compared with a hydrological model for simulating CH4 fluxes. This analysis helps us understand the potential benefits of incorporating satellite-derived SM data into improving CH4 emission estimates.
2. Materials and Methods
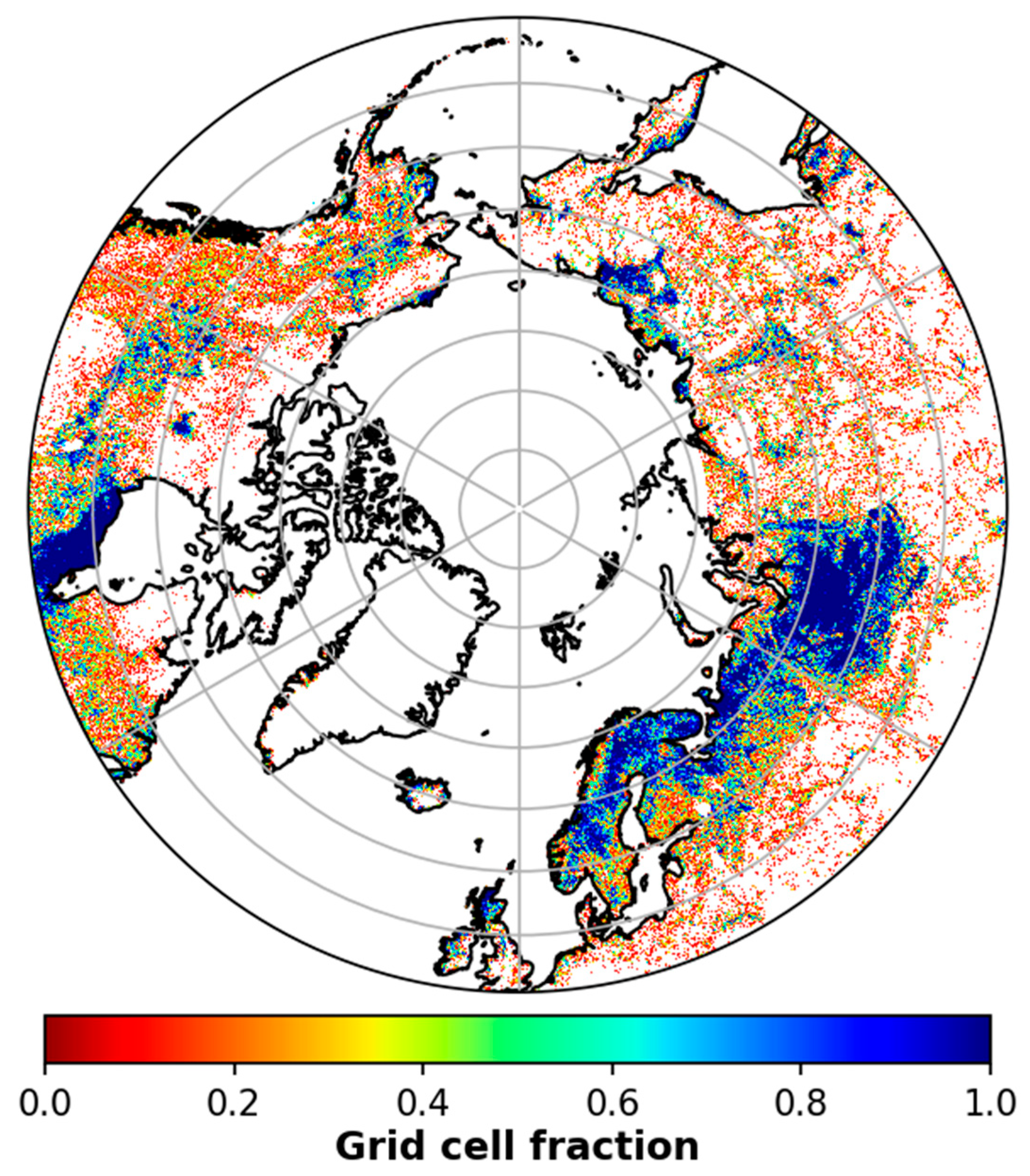
2.1. Study Area and Wetland Map
2.2. Wetland Model Description
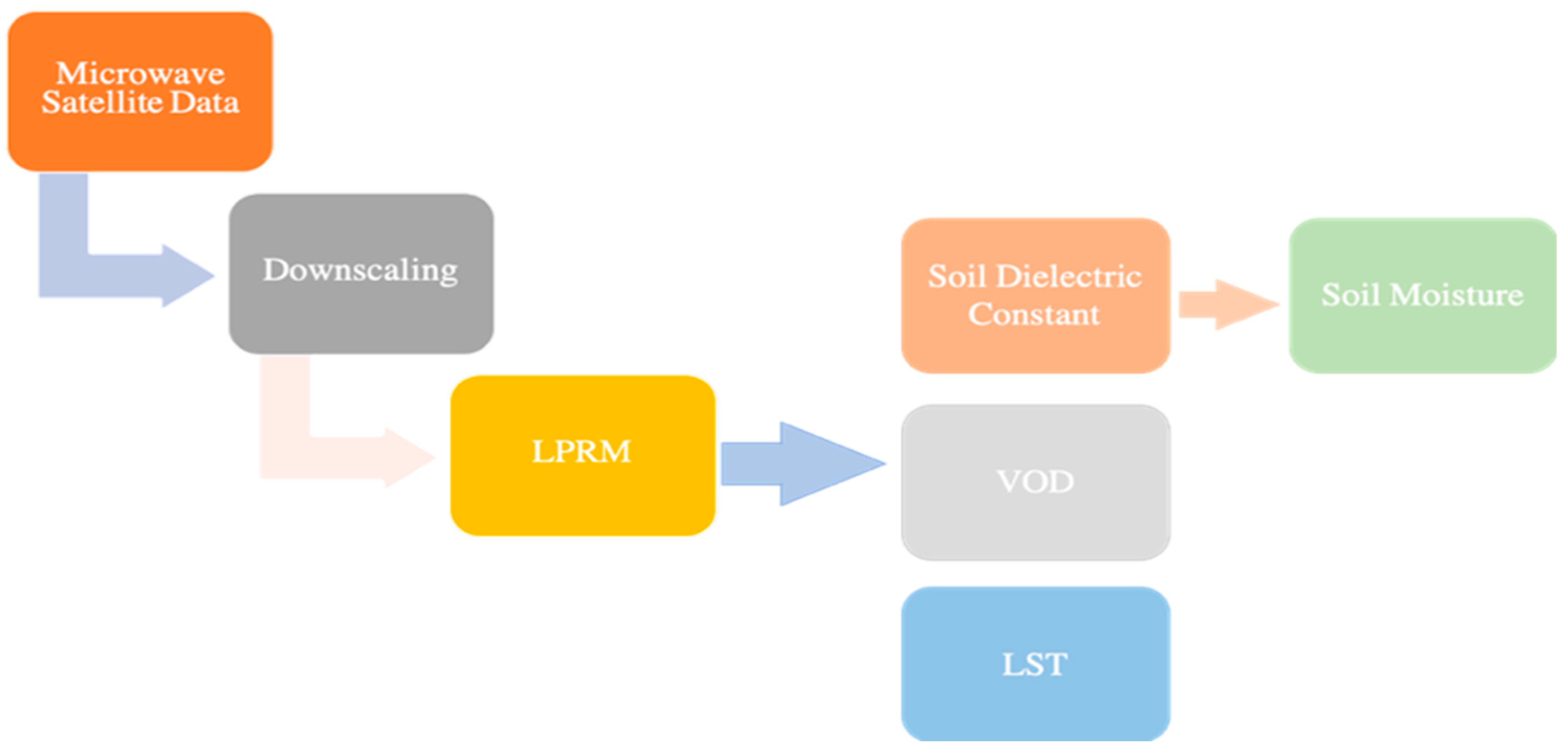
2.3. Soil Moisture Data
2.3.1. PCRaster Global Water Balance
2.3.2. Planet L-Band SM
2.4. Model Calibration and Validation Data
2.4.1. FLUXNET—CH4 Measurements
2.4.2. Model Intercomparison Data Sources
2.5. Model Performance Evaluation
3. Results
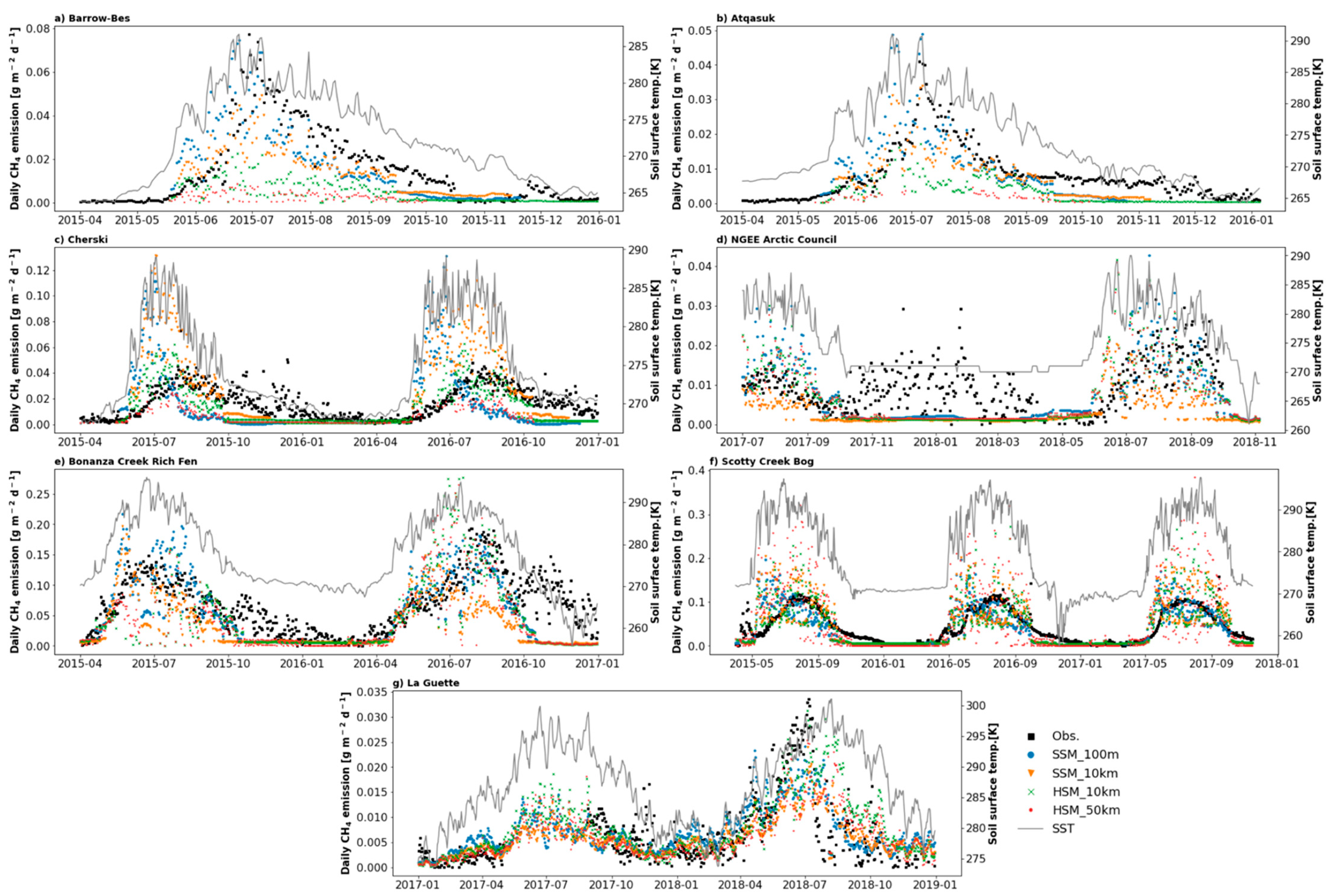
3.1. Methane Emission at Local Sites
3.2. Upscaled CH4 Fluxes
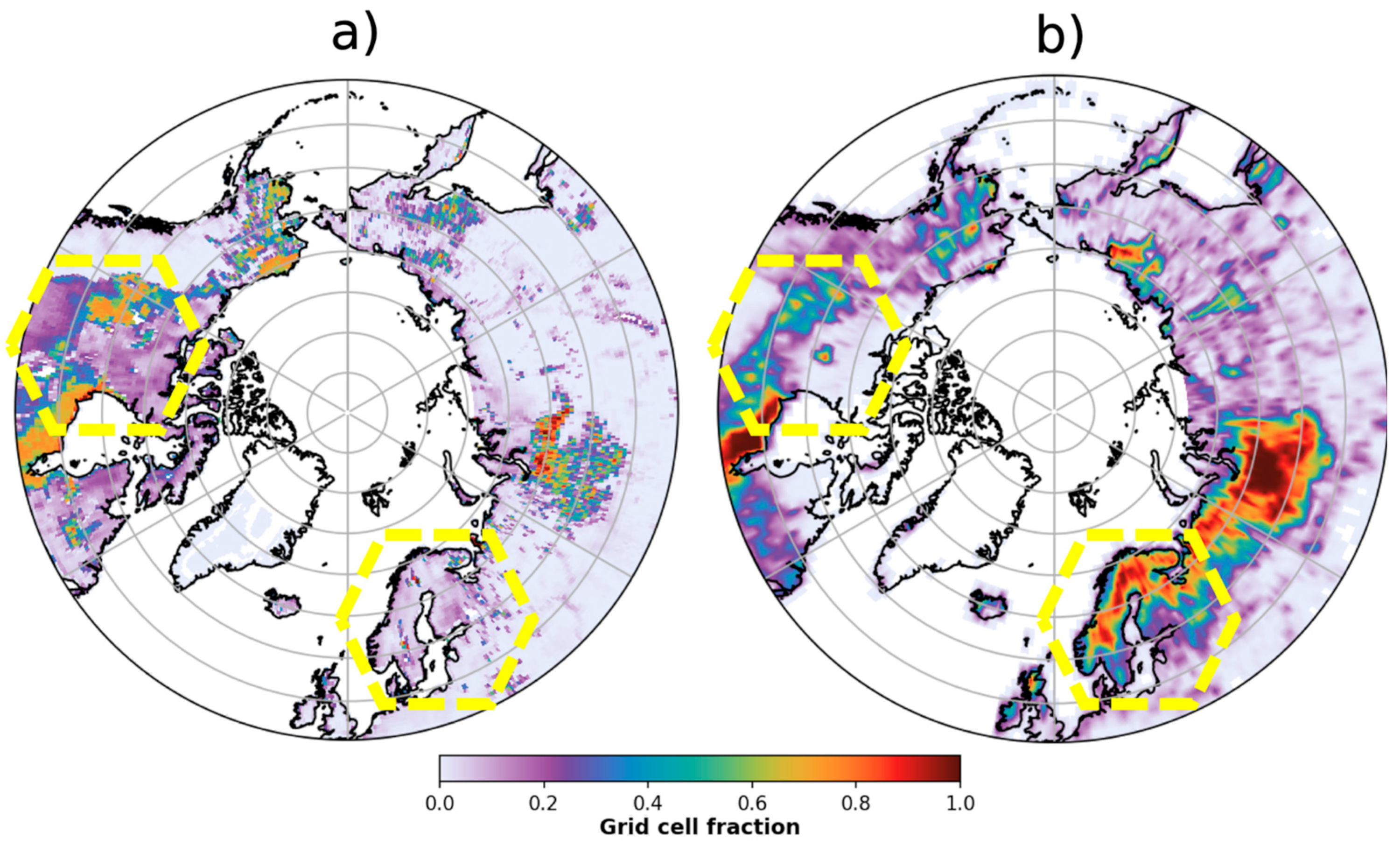
West Siberia Lowlands and Hudson Bay Wetlands
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


Appendix B
| Site Name | SSM_100 m | SSM_10 km | HSM_10 km | HSM_50 km |
|---|---|---|---|---|
| Siikaneva | 0.79 | 0.75 | 0.72 | 0.70 |
| Degero | 0.78 | 0.76 | 0.72 | 0.70 |
| Huetelmoor | 0.67 | 0.51 | 0.46 | 0.54 |
| Zarnekow | 0.78 | 0.76 | 0.76 | 0.66 |
| Lost Creek | 0.45 | 0.21 | 0.13 | 0.12 |
| Barrow-Bes | 0.65 | 0.61 | 0.53 | 0.28 |
| Atqasuk | 0.69 | 0.25 | 0.20 | 0.1 |
| Cherski | 0.34 | 0.26 | 0.21 | −1.37 |
| NGEE Arctic Council | 0.38 | 0.35 | 0.33 | 0.31 |
| Bonanza Creek | 0.46 | 0.25 | 0.2 | 0.16 |
| Scotty Creek | 0.62 | 0.61 | 0.45 | 0.19 |
| La Guette | 0.36 | 0.22 | 0.22 | 0.12 |
| Soil Moisture Data | SSM_100 m | SSM_10 km | HSM_10 km | HSM_50 km |
|---|---|---|---|---|
| KCH4[d−1] | 0.0055 | 0.0043 | 0.0027 | 0.002 |
References
- Chen, H.; Xu, X.; Fang, C.; Li, B.; Nie, M. Differences in the Temperature Dependence of Wetland CO2 and CH4 Emissions Vary with Water Table Depth. Nat. Clim. Chang. 2021, 11, 766–771. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Bernal, B.; Nahlik, A.M.; Mander, Ü.; Zhang, L.; Anderson, C.J.; Jørgensen, S.E.; Brix, H. Wetlands, Carbon, and Climate Change. Landsc. Ecol. 2013, 28, 583–597. [Google Scholar] [CrossRef]
- Nahlik, A.M.; Fennessy, M.S. Carbon Storage in US Wetlands. Nat. Commun. 2016, 7, 13835. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Craft, C.B.; Boon, P.I.; Burgin, A.J.; Neubauer, S.C.; Franklin, R.B.; Ardón, M.; Hopfensperger, K.N.; Lamers, L.P.M.; Gell, P. A Global Perspective on Wetland Salinization: Ecological Consequences of a Growing Threat to Freshwater Wetlands. Ecosphere 2015, 6, 1–43. [Google Scholar]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Zhang, Z.; Zimmermann, N.E.; Stenke, A.; Li, X.; Hodson, E.L.; Zhu, G.; Huang, C.; Poulter, B. Emerging Role of Wetland Methane Emissions in Driving 21st Century Climate Change. Proc. Natl. Acad. Sci. USA 2017, 114, 9647–9652. [Google Scholar] [CrossRef]
- Spahni, R.; Joos, F.; Stocker, B.D.; Steinacher, M.; Yu, Z.C. Transient Simulations of the Carbon and Nitrogen Dynamics in Northern Peatlands: From the Last Glacial Maximum to the 21st Century. Clim. Past 2013, 9, 1287–1308. [Google Scholar] [CrossRef] [Green Version]
- Rosentreter, J.A.; Borges, A.V.; Deemer, B.R.; Holgerson, M.A.; Liu, S.; Song, C.; Melack, J.; Raymond, P.A.; Duarte, C.M.; Allen, G.H.; et al. Half of Global Methane Emissions Come from Highly Variable Aquatic Ecosystem Sources. Nat. Geosci. 2021, 14, 225–230. [Google Scholar] [CrossRef]
- Kirschke, S.; Bousquet, P.; Ciais, P.; Saunois, M.; Canadell, J.G.; Dlugokencky, E.J.; Bergamaschi, P.; Bergmann, D.; Blake, D.R.; Bruhwiler, L.; et al. Three Decades of Global Methane Sources and Sinks. Nat. Geosci. 2013, 6, 813–823. [Google Scholar] [CrossRef] [Green Version]
- Melton, J.R.; Wania, R.; Hodson, E.L.; Poulter, B.; Ringeval, B.; Spahni, R.; Bohn, T.; Avis, C.A.; Beerling, D.J.; Chen, G.; et al. Present State of Global Wetland Extent and Wetland Methane Modelling: Conclusions from a Model Inter-Comparison Project (WETCHIMP). Biogeosciences 2013, 10, 753–788. [Google Scholar] [CrossRef] [Green Version]
- Anthony Bloom, A.; Bowman, W.K.; Lee, M.; Turner, J.A.; Schroeder, R.; Worden, R.J.; Weidner, R.; McDonald, C.K.; Jacob, J.D. A Global Wetland Methane Emissions and Uncertainty Dataset for Atmospheric Chemical Transport Models (WetCHARTs Version 1.0). Geosci. Model Dev. 2017, 10, 2141–2156. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Climate Change 2007 Synthesis Report; IPCC: Geneva, Switzerland, 2007. [Google Scholar] [CrossRef]
- Lu, B.; Song, L.; Zang, S.; Wang, H. Warming Promotes Soil CO2 and CH4 Emissions but Decreasing Moisture Inhibits CH4 Emissions in the Permafrost Peatland of the Great Xing’an Mountains. Sci. Total Environ. 2022, 829, 154725. [Google Scholar] [CrossRef] [PubMed]
- Mi, J.; Li, J.; Chen, D.; Xie, Y.; Bai, Y. Predominant Control of Moisture on Soil Organic Carbon Mineralization across a Broad Range of Arid and Semiarid Ecosystems on the Mongolia Plateau. Landsc. Ecol. 2015, 30, 1683–1699. [Google Scholar] [CrossRef]
- Voigt, C.; Lamprecht, R.E.; Marushchak, M.E.; Lind, S.E.; Novakovskiy, A.; Aurela, M.; Martikainen, P.J.; Biasi, C. Warming of Subarctic Tundra Increases Emissions of All Three Important Greenhouse Gases–Carbon Dioxide, Methane, and Nitrous Oxide. Glob. Change Biol. 2017, 23, 3121–3138. [Google Scholar] [CrossRef]
- Green, J.K.; Seneviratne, S.I.; Berg, A.M.; Findell, K.L.; Hagemann, S.; Lawrence, D.M.; Gentine, P. Large Influence of Soil Moisture on Long-Term Terrestrial Carbon Uptake. Nature 2019, 565, 476–479. [Google Scholar] [CrossRef]
- Zhang, Z.; Chatterjee, A.; Ott, L.; Reichle, R.; Feldman, A.F.; Poulter, B. Effect of Assimilating SMAP Soil Moisture on CO2 and CH4 Fluxes through Direct Insertion in a Land Surface Model. Remote Sens. 2022, 14, 2405. [Google Scholar] [CrossRef]
- Dos Santos, T.; Keppel-Aleks, G.; De Roo, R.; Steiner, A.L. Can Land Surface Models Capture the Observed Soil Moisture Control of Water and Carbon Fluxes in Temperate-To-Boreal Forests? J. Geophys. Res. Biogeosci. 2021, 126, e2020JG005999. [Google Scholar] [CrossRef]
- Chamindu Deepagoda, T.K.K.; Smits, K.M.; Oldenburg, C.M. Effect of Subsurface Soil Moisture Variability and Atmospheric Conditions on Methane Gas Migration in Shallow Subsurface. Int. J. Greenh. Gas Control 2016, 55, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Sutanudjaja, E.H.; van Beek, L.P.H.; Drost, N.; de Graaf, I.E.M.; de Jong, K.; Peßenteiner, S.; Straatsma, M.W.; Wada, Y.; Wanders, N.; Wisser, D.; et al. PCR-GLOBWB 2.0: A 5 Arc-Minute Global Hydrological and Water Resources Model. Geosci. Model Dev. 2018, 11, 2429–2453. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.D.; Guo, Z.; Yang, R.; Dirmeyer, P.A.; Mitchell, K.; Puma, M.J. On the Nature of Soil Moisture in Land Surface Models. J. Clim. 2009, 22, 4322–4335. [Google Scholar] [CrossRef] [Green Version]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T.R. A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef] [Green Version]
- Ahlström, A.; Xia, J.; Arneth, A.; Luo, Y.; Smith, B. Importance of Vegetation Dynamics for Future Terrestrial Carbon Cycling. Environ. Res. Lett. 2015, 10, 054019, Erratum in Environ. Res. Lett. 2015, 10, 089501. [Google Scholar] [CrossRef]
- Zaehle, S.; Sitch, S.; Smith, B.; Hatterman, F. Effects of Parameter Uncertainties on the Modeling of Terrestrial Biosphere Dynamics. Glob. Biogeochem. Cycles 2005, 19, 1–16. [Google Scholar] [CrossRef]
- Knorr, W.; Heimann, M. Uncertainlies in Global Terrestrial Biosphere Modeling 1. A Comprehensive Sensitivity Analysis with a New Photosynthesis and Energy Balance Scheme. Glob. Biogeochem. Cycles 2001, 15, 207–225. [Google Scholar] [CrossRef]
- Booth, E.G.; Loheide, S.P. Hydroecological Model Predictions Indicate Wetter and More Diverse Soil Water Regimes and Vegetation Types Following Floodplain Restoration. J. Geophys. Res. Biogeosci. 2012, 117, 1–19. [Google Scholar] [CrossRef]
- Vainio, E.; Peltola, O.; Kasurinen, V.; Kieloaho, A.J.; Tuittila, E.S.; Pihlatie, M. Topography-Based Statistical Modelling Reveals High Spatial Variability and Seasonal Emission Patches in Forest Floor Methane Flux. Biogeosciences 2021, 18, 2003–2025. [Google Scholar] [CrossRef]
- Treat, C.C.; Jones, M.C.; Brosius, L.; Grosse, G.; Walter Anthony, K.; Frolking, S. The Role of Wetland Expansion and Successional Processes in Methane Emissions from Northern Wetlands during the Holocene. Quat. Sci. Rev. 2021, 257, 106864. [Google Scholar] [CrossRef]
- Treat, C.C.; Bloom, A.A.; Marushchak, M.E. Nongrowing Season Methane Emissions–A Significant Component of Annual Emissions across Northern Ecosystems. Glob. Change Biol. 2018, 24, 3331–3343. [Google Scholar] [CrossRef] [Green Version]
- Albuhaisi, Y.A.Y.; van der Velde, Y.; Houweling, S. The Importance of Spatial Resolution in the Modeling of Methane Emissions from Natural Wetlands. Remote Sens. 2023, 15, 2840. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; De Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of Its Specifications, Validation Results, and Emerging Applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef] [Green Version]
- Parinussa, R.M.; Holmes, T.R.H.; Wanders, N.; Dorigo, W.A.; De Jeu, R.A.M. A Preliminary Study toward Consistent Soil Moisture from AMSR2. J. Hydrometeorol. 2015, 16, 932–947. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS Performance in Terms of Global Soil Moisture Monitoring after Six Years in Operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Fernandez-Moran, R.; Al-Yaari, A.; Mialon, A.; Mahmoodi, A.; Al Bitar, A.; De Lannoy, G.; Rodriguez-Fernandez, N.; Lopez-Baeza, E.; Kerr, Y.; Wigneron, J.P. SMOS-IC: An Alternative SMOS Soil Moisture and Vegetation Optical Depth Product. Remote Sens. 2017, 9, 457. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.K.; Bindlish, R.; O’Neill, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J.; et al. Assessment of the SMAP Passive Soil Moisture Product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- Dorigo, W.; de Jeu, R. Satellite Soil Moisture for Advancing Our Understanding of Earth System Processes and Climate Change. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 1–4. [Google Scholar] [CrossRef]
- Griesfeller, A.; Lahoz, W.A.; Jeu, R.A.M.D.; Dorigo, W.; Haugen, L.E.; Svendby, T.M.; Wagner, W. Evaluation of Satellite Soil Moisture Products over Norway Using Ground-Based Observations. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 155–164. [Google Scholar] [CrossRef] [Green Version]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements Ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Torres, R.; Davidson, M.; Geudtner, D. Copernicus Sentinel Mission at C- and L-Band: Current Status and Future Perspectives. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Online, 26 September–2 October 2020; pp. 4055–4058. [Google Scholar]
- Schmidt, A.J.K. The Value of Using Hydrological Datasets for Water Allocation Decisions: Earth Observations, Hydrological Models, and Seasonal Forecasts; Routledge: Abingdon-on-Thames, UK, 2019; ISBN 9780367429553. [Google Scholar]
- Delwiche, K.; Knox, S.H.; Malhotra, A.; Fluet-Chouinard, E.; McNicol, G.; Feron, S.; Ouyang, Z.; Papale, D.; Trotta, C.; Canfora, E.; et al. FLUXNET-CH4: A Global, Multi-Ecosystem Dataset and Analysis of Methane Seasonality from Freshwater Wetlands. Earth Syst. Sci. Data Discuss. 2021, 13, 3607–3689. [Google Scholar] [CrossRef]
- Copernicus. Climate Data Store 2019. Land Cover Classifcation Gridded Maps from 1992 to Present Derived from Satellite Observations. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-land-cover?tab=overview (accessed on 5 May 2022).
- Falt’an, V.; Petrovič, F.; Ot’ahel’, J.; Feranec, J.; Druga, M.; Hruška, M.; Nováček, J.; Solár, V.; Mechurová, V.; Faltan, V.; et al. Comparison of CORINE Land Cover Data with National Statistics and the Possibility to Record This Data on a Local Scale-Case Studies from Slovakia. Remote Sens. 2020, 12, 2484. [Google Scholar] [CrossRef]
- Defourny, P.; Lamarche, C.; Marissiaux, Q.; Carsten, B.; Martin, B.; Grit, K. Product User Guide Specification: ICDR Land Cover 2016–2020; ECMWF: Reading, UK, 2021; p. 37. [Google Scholar]
- Gedney, N.; Cox, P.M.; Huntingford, C. Climate Feedback from Wetland Methane Emissions. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Walter, B.P.; Heimann, M. A Process-Based, Climate-Sensitive Model to Derive Methane Emissions from Natural Wetlands: Application to Five Wetland Sites, Sensitivity to Model Parameters, and Climate. Global Biogeochem. Cycles 2000, 14, 745–765. [Google Scholar] [CrossRef] [Green Version]
- Rinne, J.; Tuittila, E.S.; Peltola, O.; Li, X.; Raivonen, M.; Alekseychik, P.; Haapanala, S.; Pihlatie, M.; Aurela, M.; Mammarella, I.; et al. Temporal Variation of Ecosystem Scale Methane Emission From a Boreal Fen in Relation to Temperature, Water Table Position, and Carbon Dioxide Fluxes. Global Biogeochem. Cycles 2018, 32, 1087–1106. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Ye, R.; Bridgham, S.D.; Jin, Q. Limitations of the Q10 Coefficient for Quantifying Temperature Sensitivity of Anaerobic Organic Matter Decomposition: A Modeling Based Assessment. J. Geophys. Res. Biogeosci. 2021, 126, 1–18. [Google Scholar] [CrossRef]
- Kimball, J.S.; Endsley, K.A.; Jones, L.A.; Kundig, T.; Reichle, R. SMAP L4 Global Daily 9 Km EASE-Grid Carbon Net Ecosystem Exchange; NSIDC: Boulder, CO, USA, 2021; Volume 6. [Google Scholar]
- Bosmans, J.H.C.; Van Beek, L.P.H.; Sutanudjaja, E.H.; Bierkens, M.F.P. Hydrological Impacts of Global Land Cover Change and Human Water Use. Hydrol. Earth Syst. Sci. 2017, 21, 5603–5626. [Google Scholar] [CrossRef] [Green Version]
- Van Beek, L.P.H.; Bierkens, M.F.P. The Global Hydrological Model PCR-GLOBWB: Conceptualization, Parameterization and Verification; Universiteit Utrecht: Utrecht, The Netherlands, 2006. [Google Scholar]
- Petrescu, A.M.R.; Van Beek, L.P.H.; Van Huissteden, J.; Prigent, C.; Sachs, T.; Corradi, C.A.R.; Parmentier, F.J.W.; Dolman, A.J. Modeling Regional to Global CH4 Emissions of Boreal and Arctic Wetlands. Global Biogeochem. Cycles 2010, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- De Graaf, I.E.M.; Sutanudjaja, E.H.; Van Beek, L.P.H.; Bierkens, M.F.P. A High-Resolution Global-Scale Groundwater Model. Hydrol. Earth Syst. Sci. 2015, 19, 823–837. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Sheng, X.; Wu, M.; Wu, H.; Ning, X. Methane Production Potential and Emission at Different Water Levels in the Restored Reed Wetland of Hangzhou Bay. PLoS ONE 2017, 12, e0185709. [Google Scholar] [CrossRef] [Green Version]
- De Jeu, R.A.M.; de Nijs, A.H.A.; Van Klink, M.H.W. Method and System for Improving the Resolution of Sensor. Data. Patent WO2017216186A1, 21 December 2017. [Google Scholar]
- De Jeu, R.A.M.; Holmes, T.R.H.; Parinussa, R.M.; Owe, M. A Spatially Coherent Global Soil Moisture Product with Improved Temporal Resolution. J. Hydrol. 2014, 516, 284–296. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 Dataset and the ONEFlux Processing Pipeline for Eddy Covariance Data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Knox, S.H.; Jackson, R.B.; Poulter, B.; McNicol, G.; Fluet-Chouinard, E.; Zhang, Z.; Hugelius, G.; Bousquet, P.; Canadell, J.G.; Saunois, M.; et al. FluXNET-CH4 Synthesis Activity Objectives, Observations, and Future Directions. Bull. Am. Meteorol. Soc. 2019, 100, 2607–2632. [Google Scholar] [CrossRef] [Green Version]
- Segers, A.; Houweling, S. Description of the CH4 Inversion Production Chain; ECMWF: Reading, UK, 2019. [Google Scholar]
- Zhang, Z.; Zimmermann, N.E.; Kaplan, J.O.; Poulter, B. Modeling Spatiotemporal Dynamics of Global Wetlands: Comprehensive Evaluation of a New Sub-Grid TOPMODEL Parameterization and Uncertainties. Biogeosciences 2016, 13, 1387–1408. [Google Scholar] [CrossRef] [Green Version]
- Peltola, O.; Vesala, T.; Gao, Y.; Räty, O.; Alekseychik, P.; Aurela, M.; Chojnicki, B.; Desai, A.R.; Dolman, A.J.; Euskirchen, E.S.; et al. Monthly Gridded Data Product of Northern Wetland Methane Emissions Based on Upscaling Eddy Covariance Observations. Earth Syst. Sci. Data Discuss. 2019, 11, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Lehner, B.; Döll, P. Development and Validation of a Global Database of Lakes, Reservoirs and Wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Parker, R.J.; Wilson, C.; Bloom, A.A.; Comyn-Platt, E.; Hayman, G.; McNorton, J.; Boesch, H.; Chipperfield, M.P. Exploring Constraints on a Wetland Methane Emission Ensemble (WetCHARTs) Using GOSAT Observations. Biogeosciences 2020, 17, 5669–5691. [Google Scholar] [CrossRef]
- Thompson, R.L.; Sasakawa, M.; Machida, T.; Aalto, T.; Worthy, D.; Lavric, J.V.; Myhre, C.L.; Stohl, A. Methane Fluxes in the High Northern Latitudes for 2005-2013 Estimated Using a Bayesian Atmospheric Inversion. Atmos. Chem. Phys. 2017, 17, 3553–3572. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.; Zhuang, Q.; Henze, D.K.; Frankenberg, C.; Dlugokencky, E.; Sweeney, C.; Turner, A.J.; Sasakawa, M.; Machida, T. Inverse Modeling of Pan-Arctic Methane Emissions at High Spatial Resolution: What Can We Learn from Assimilating Satellite Retrievals and Using Different Process-Based Wetland and Lake Biogeochemical Models? Atmos. Chem. Phys. 2016, 16, 12649–12666. [Google Scholar] [CrossRef] [Green Version]
- Ito, A. Methane Emission from Pan-Arctic Natural Wetlands Estimated Using a Process-Based Model, 1901–2016. Polar Sci. 2019, 21, 26–36. [Google Scholar] [CrossRef] [Green Version]
- Nakano, T.; Inoue, G.; Fukuda, M. Methane Consumption and Soil Respiration by a Birch Forest Soil in West Siberia. Tellus Ser. B Chem. Phys. Meteorol. 2004, 56, 223–229. [Google Scholar] [CrossRef]
- Zhang, Z.; Fluet-Chouinard, E.; Jensen, K.; McDonald, K.; Hugelius, G.; Gumbricht, T.; Carroll, M.; Prigent, C.; Bartsch, A.; Poulter, B. Development of the Global Dataset of Wetland Area and Dynamics for Methane Modeling (WAD2M). Earth Syst. Sci. Data 2021, 13, 2001–2023. [Google Scholar] [CrossRef]
- Bohn, T.J.; Melton, J.R.; Ito, A.; Kleinen, T.; Spahni, R.; Stocker, B.D.; Zhang, B.; Zhu, X.; Schroeder, R.; Glagolev, M.V.; et al. WETCHIMP-WSL: Intercomparison of Wetland Methane Emissions Models over West Siberia. Biogeosciences 2015, 12, 3321–3349. [Google Scholar] [CrossRef] [Green Version]
- Wecht, K.J.; Jacob, D.J.; Frankenberg, C.; Jiang, Z.; Blake, D.R. Mapping of North American Methane Emissions with High Spatial Resolution by Inversion of SCIAMACHY Satellite Data. J. Geophys. Res. 2014, 119, 7741–7756. [Google Scholar] [CrossRef]
- Warwick, N.J.; Cain, M.L.; Fisher, R.; France, J.L.; Lowry, D.; Michel, S.E.; Nisbet, E.G.; Vaughn, B.H.; White, J.W.C.; Pyle, J.A. Using Δ13C-CH4 and ΔD-CH4 to Constrain Arctic Methane Emissions. Atmos. Chem. Phys. 2016, 16, 14891–14908. [Google Scholar] [CrossRef] [Green Version]
- Thonat, T.; Saunois, M.; Bousquet, P.; Pison, I.; Tan, Z.; Zhuang, Q.; Crill, P.M.; Thornton, B.F.; Bastviken, D.; Dlugokencky, E.J.; et al. Detectability of Arctic Methane Sources at Six Sites Performing Continuous Atmospheric Measurements. Atmos. Chem. Phys. 2017, 17, 8371–8394. [Google Scholar] [CrossRef] [Green Version]
- Overland, J.E.; Wang, M. The 2020 Siberian Heat Wave. Int. J. Climatol. 2021, 41, E2341–E2346. [Google Scholar] [CrossRef]
- Scholten, R.C.; Coumou, D.; Luo, F.; Veraverbeke, S. Early Snowmelt and Polar Jet Dynamics Co-Influence Recent Extreme Siberian Fire Seasons. Science 2022, 378, 1005. [Google Scholar] [CrossRef]
- Peng, S.; Lin, X.; Thompson, R.L.; Xi, Y.; Liu, G.; Hauglustaine, D.; Lan, X.; Poulter, B.; Ramonet, M.; Saunois, M.; et al. Wetland Emission and Atmospheric Sink Changes Explain Methane Growth in 2020. Nature 2022, 612, 477–482. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhuang, Q. Methane Emissions from Arctic Landscapes during 2000–2015: An Analysis with Land and Lake Biogeochemistry Models. Biogeosciences 2022, 20, 1181–1193. [Google Scholar] [CrossRef]
- Olefeldt, D.; Hovemyr, M.; Kuhn, M.A.; Bastviken, D.; Bohn, T.J.; Connolly, J.; Crill, P.; Euskirchen, E.S.; Finkelstein, S.A.; Genet, H.; et al. The Boreal-Arctic Wetland and Lake Dataset (BAWLD). Earth Syst. Sci. Data Discuss. 2021, 13, 5127–5149. [Google Scholar] [CrossRef]
- Thornton, B.F.; Wik, M.; Crill, P.M. Double-Counting Challenges the Accuracy of High-Latitude Methane Inventories. Geophys. Res. Lett. 2016, 43, 12569–12577. [Google Scholar] [CrossRef]


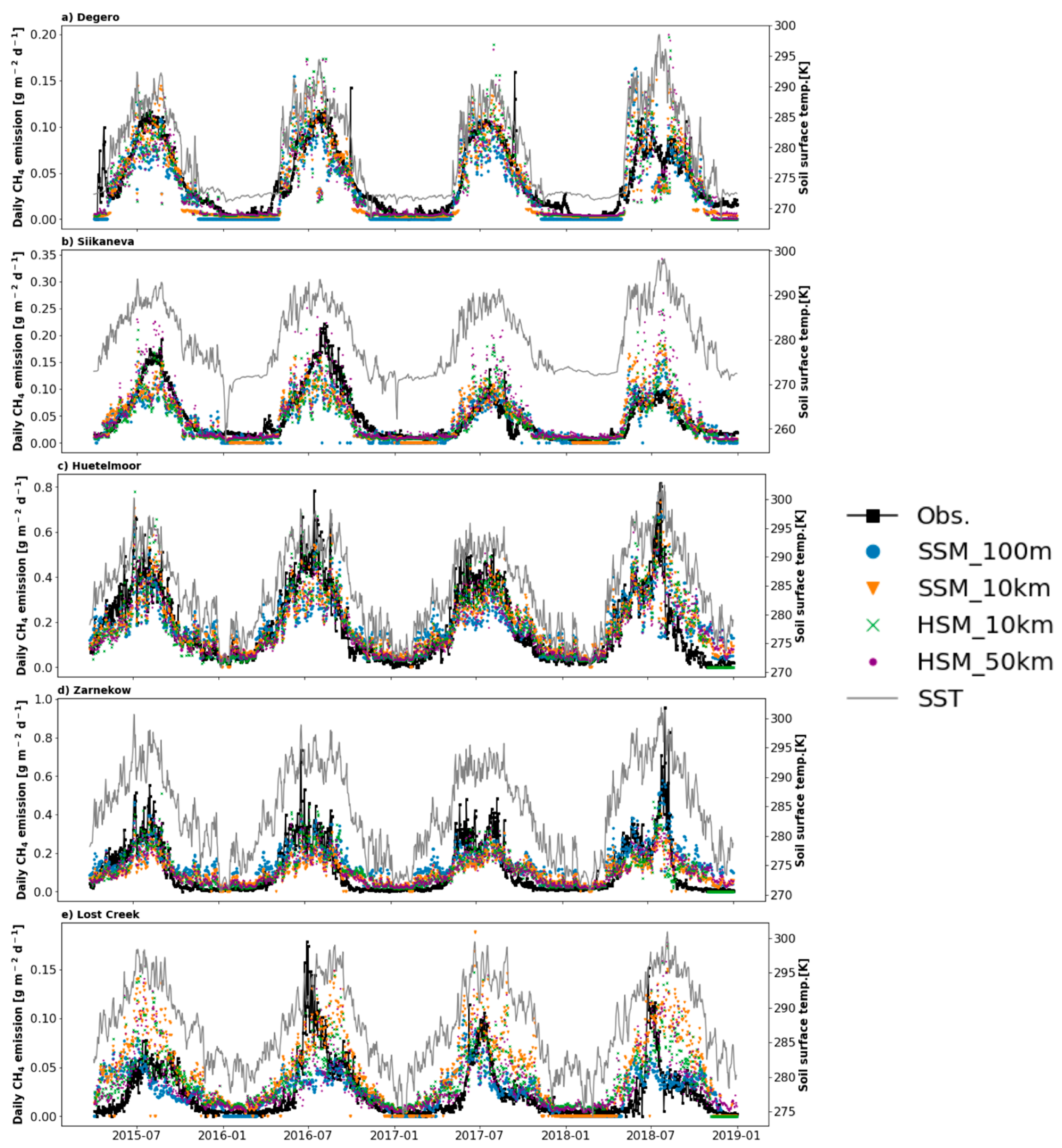
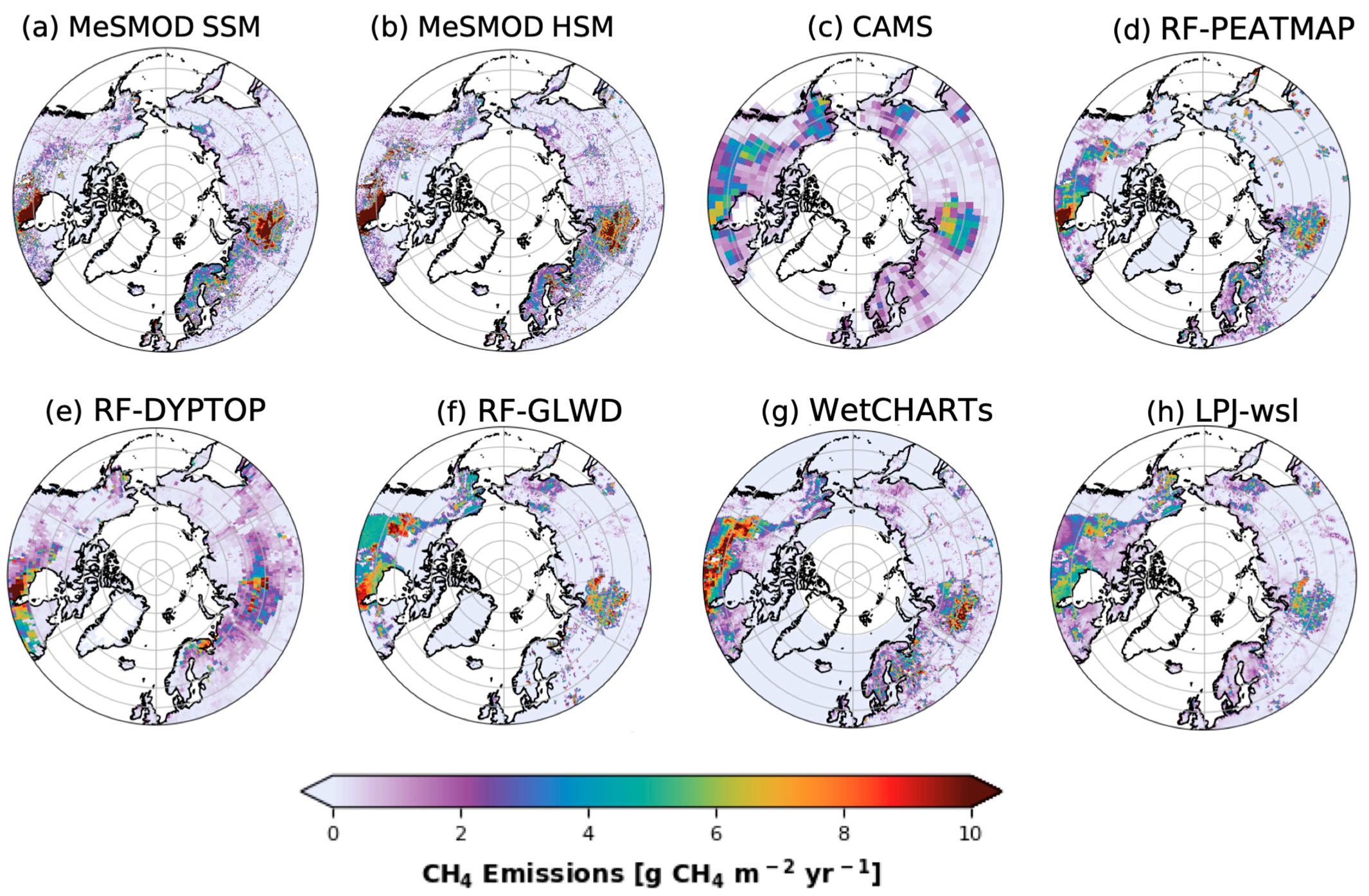
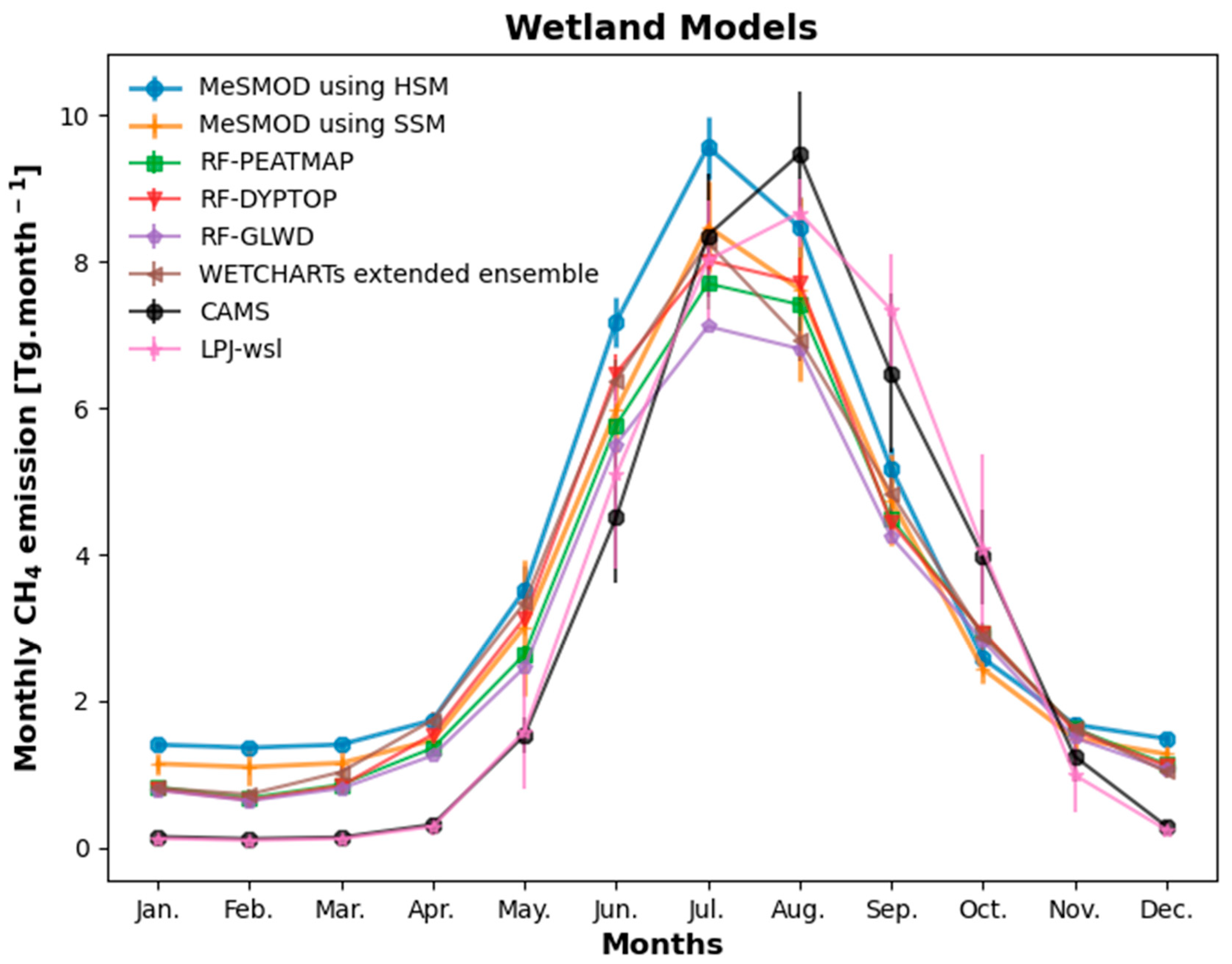
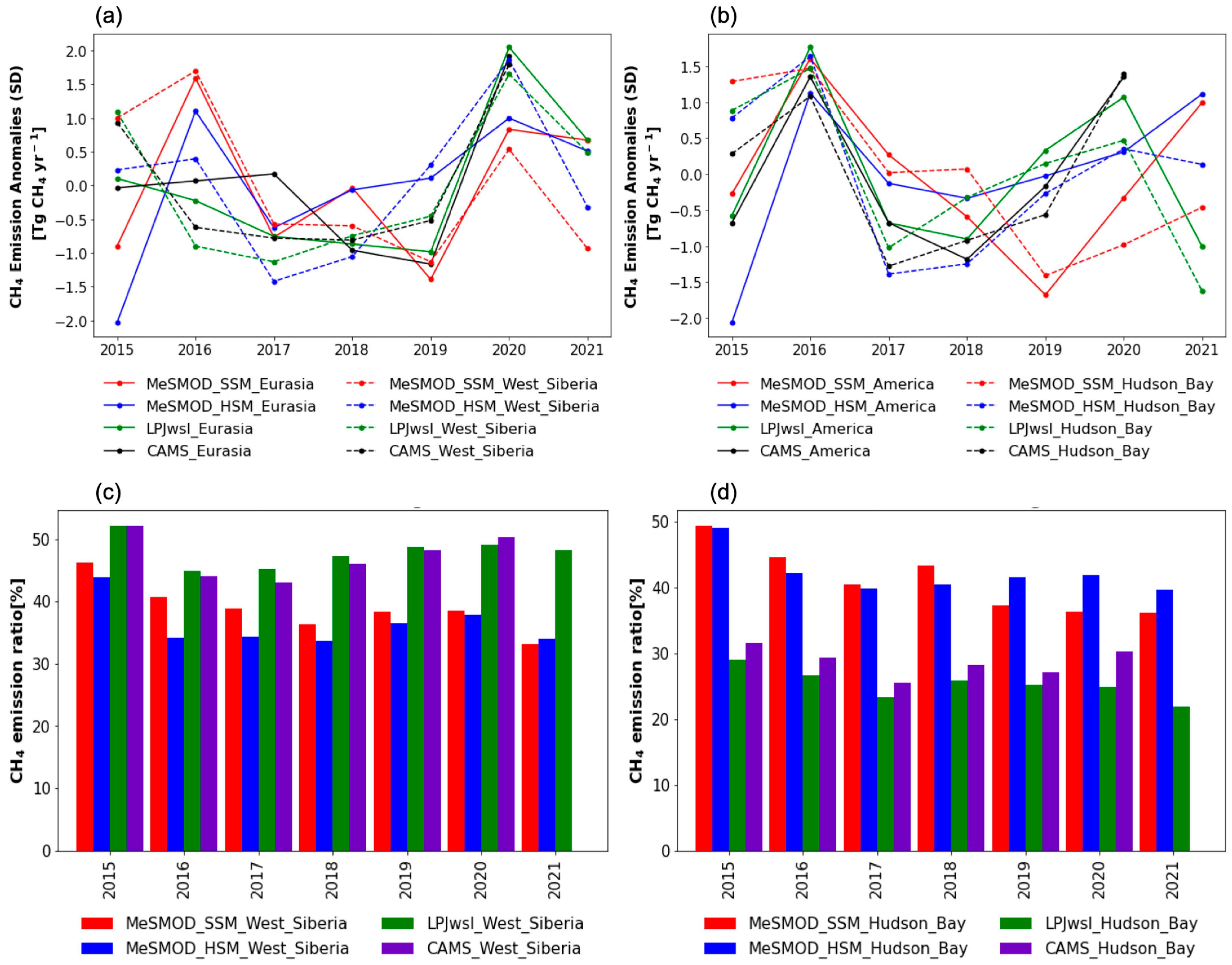
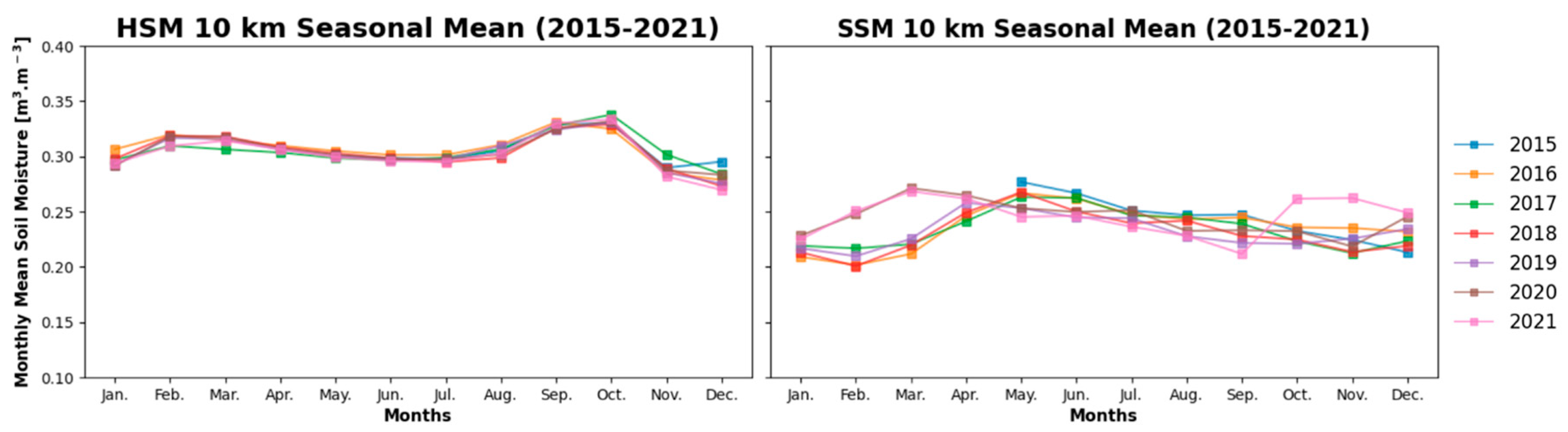
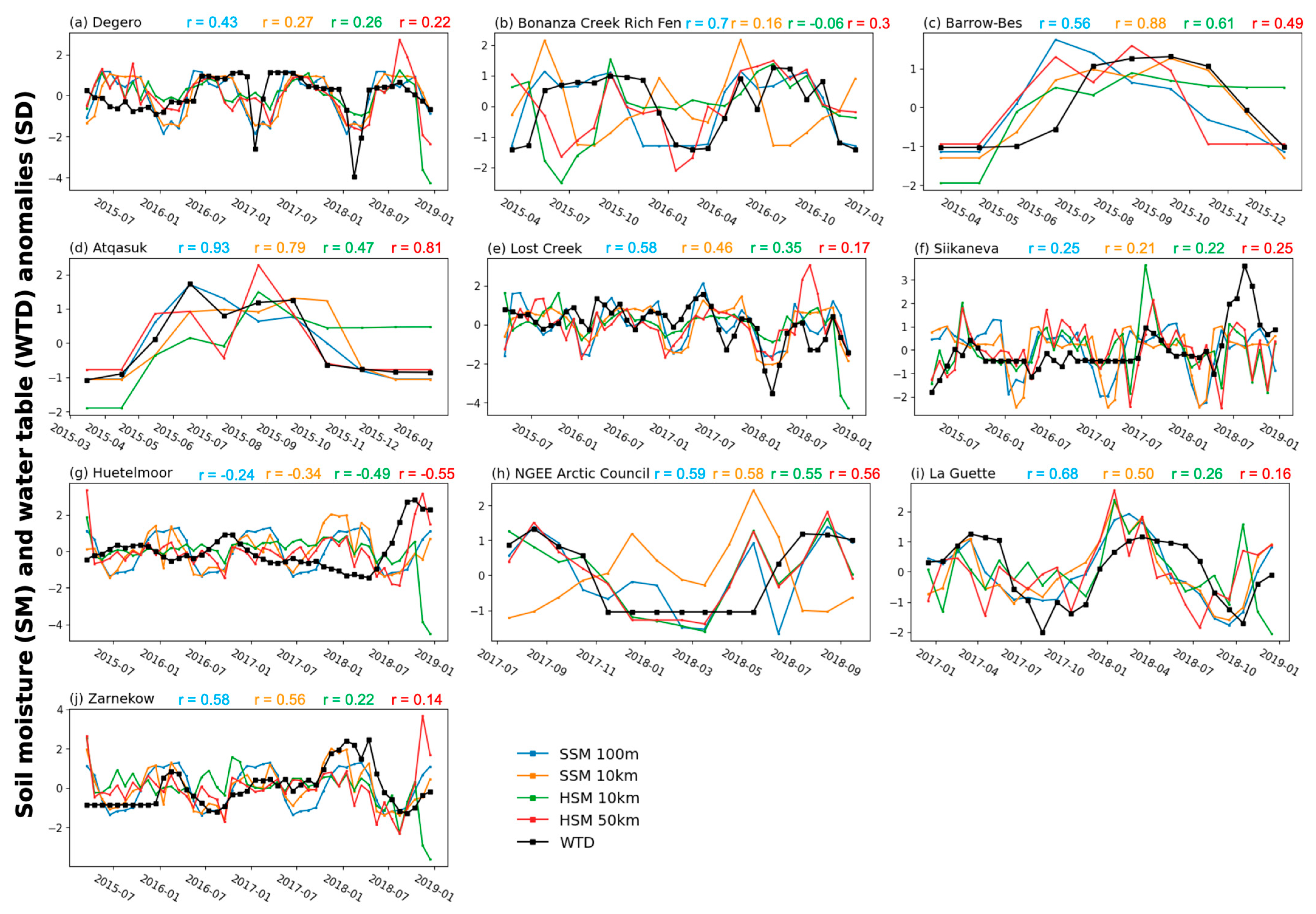
| Group No. | No. | Site ID | Site Name | Coordinates (Degrees) | Data Availability | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lat | Lon | 2015 | 2016 | 2017 | 2018 | DOI | ||||
| Group 1 * | 1 | FI-Sii | Siikaneva | 61.83 | 24.19 | + | + | + | + | https://doi.org/10.18140/FLX/1669640 |
| 2 | SE-Deg | Degero | 64.18 | 19.56 | + | + | + | + | https://doi.org/10.18140/FLX/1669659 | |
| 3 | DE-Hte | Huetelmoor | 54.21 | 12.18 | + | + | + | + | https://doi.org/10.18140/FLX/1669634 | |
| 4 | DE-Zrk | Zarnekow | 53.88 | 12.89 | + | + | + | + | https://doi.org/10.18140/FLX/1669636 | |
| 5 | US-Los | Lost Creek | 46.08 | −89.98 | + | + | + | + | https://doi.org/10.18140/FLX/1669613 | |
| Group 2 ** | 6 | US-Bes | Barrow-Bes | 71.28 | −156.6 | + | https://doi.org/10.18140/FLX/1669665 | |||
| 7 | US-Atq | Atqasuk | 70.47 | −157.41 | + | + | https://doi.org/10.18140/FLX/1669663 | |||
| 8 | RU-Che | Cherski | 68.61 | 161.34 | + | + | https://doi.org/10.18140/FLX/1669655 | |||
| 9 | US-NGC | NGEE Arctic Council | 64.86 | −163.7 | + | + | https://doi.org/10.18140/FLX/1669688 | |||
| 10 | US-BZF | Bonanza Creek | 64.7 | −148.31 | + | + | https://doi.org/10.18140/FLX/1669669 | |||
| 11 | CA-SCB | Scotty Creek | 61.31 | −121.3 | + | + | + | https://doi.org/10.18140/FLX/1669613 | ||
| 12 | FR-LGt | La Guette | 47.32 | 2.28 | + | + | https://doi.org/10.18140/FLX/1669641 | |||
| Site Name | Flux (g CH4 yr/m2) | |||||
|---|---|---|---|---|---|---|
| Observation | SSM_100 m | SSM_10 km | HSM_10 km | HSM_50 km | ||
| Group 1 | Degero | 15.30 ± 0.5 | 11.61 ± 0.5 | 13.32 ± 0.5 | 14.06 ± 0.6 | 13.89 ± 0.5 |
| Siikaneva | 17.52 ± 0.7 | 14.45 ± 0.5 | 16.02 ± 0.6 | 16.26 ± 0.6 | 19.69 ± 0.8 | |
| Huetelmoor | 67.60 ± 2.4 | 66.85 ± 2.1 | 69.69 ± 2.3 | 68.29 ± 2.3 | 64.90 ± 2.5 | |
| Zarnekow | 43.06 ± 1.8 | 50.42 ± 1.6 | 37.96 ± 1.2 | 41.63 ± 1.4 | 40.88 ± 1.3 | |
| Lost Creek | 9.12 ± 0.4 | 9.17 ± 0.32 | 16.69 ± 0.6 | 13.68 ± 0.5 | 12.63 ± 0.6 | |
| Group 2 | Barrow-Bes | 4.05 ± 0.4 | 3.37 ± 0.34 | 2.63 ± 0.44 | 1.09 ± 0.45 | 0.35 ± 0.47 |
| Atqasuk | 2.28 ± 0.19 | 1.88 ± 0.20 | 1.46 ± 0.22 | 0.73 ± 0.07 | 0.11 ± 0.01 | |
| Cherski | 10.77 ± 0.50 | 8.20 ± 0.70 | 14.16 ± 0.90 | 7.87 ± 0.50 | 2.15 ± 0.17 | |
| NGEE Arctic Council | 4.06 ± 0.24 | 3.22 ± 0.23 | 1.51 ± 0.10 | 3.40 ± 0.20 | 3.40 ± 0.12 | |
| Bonanza Creek | 43.62 ± 2.1 | 33.66 ± 2.00 | 22.76 ± 1.40 | 27.29 ± 1.80 | 25.58 ± 1.70 | |
| Scotty Creek | 43.10 ± 1.8 | 36.46 ± 1.8 | 43.35 ± 2.2 | 45.38 ± 2.2 | 52.62 ± 2.8 | |
| La Guette | 3.59 ± 0.23 | 5.17 ± 0.23 | 4.23 ± 0.19 | 5.71 ± 0.27 | 4.63 ± 0.21 | |
| Reference | Model Name | Years | Annual Emission North of 50° N (Tg CH4 yr−1) | |
|---|---|---|---|---|
| Inversion Model | Copernicus Atmosphere Monitoring Service | CAMS v21r1 | 2015 to 2020 | 34 ± 2.50 |
| Process Models | Bloom et al. [68] | WetCHARTs | 2001 to 2015 | 25 ± 3.70 |
| Zhang et al. [17] | LPJ-wsl | 2015 to 2021 | 30 ± 2.70 | |
| Flux measurement upscaling | Peltola et al. [63] | RF-PEATMAP | 2013 and 2014 | 29 (22.3–41.2) |
| RF-DYPTOP | 2013 and 2014 | 28 (21.4–39.9) | ||
| RF-GLWD | 2013 and 2014 | 32 (25.9–49.5) | ||
| This study | MeSMOD_SSM | 2015 to 2021 | 33 ± 2.30 | |
| This study | MeSMOD_HSM | 39 ± 2.0 |
| Model | North-America | Eurasia | HB | WSL |
|---|---|---|---|---|
| CAMS | 23.33 (21.21–26.31) | 16.11 (15.02–18.10) | 6.70 (5.63–7.87) | 7.64 (7.00–9.06) |
| LPJ-wsl | 17.60 (16.44–19.64) | 12.75 (12.06–14.18) | 4.45 (3.59–5.23) | 6.11 (5.53–6.97) |
| MeSMOD_SSM | 14.62 (12.91–16.12) | 17.24 (15.32–19.44) | 4.61 (3.71–5.55) | 6.69 (5.88–7.90) |
| MeSMOD_HSM | 17.24 (15.13–19.4) | 21.52 (17.98–23.44) | 6.49 (6.11–6.94) | 7.77 (7.00–8.79) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albuhaisi, Y.A.Y.; van der Velde, Y.; De Jeu, R.; Zhang, Z.; Houweling, S. High-Resolution Estimation of Methane Emissions from Boreal and Pan-Arctic Wetlands Using Advanced Satellite Data. Remote Sens. 2023, 15, 3433. https://doi.org/10.3390/rs15133433
Albuhaisi YAY, van der Velde Y, De Jeu R, Zhang Z, Houweling S. High-Resolution Estimation of Methane Emissions from Boreal and Pan-Arctic Wetlands Using Advanced Satellite Data. Remote Sensing. 2023; 15(13):3433. https://doi.org/10.3390/rs15133433
Chicago/Turabian StyleAlbuhaisi, Yousef A. Y., Ype van der Velde, Richard De Jeu, Zhen Zhang, and Sander Houweling. 2023. "High-Resolution Estimation of Methane Emissions from Boreal and Pan-Arctic Wetlands Using Advanced Satellite Data" Remote Sensing 15, no. 13: 3433. https://doi.org/10.3390/rs15133433
APA StyleAlbuhaisi, Y. A. Y., van der Velde, Y., De Jeu, R., Zhang, Z., & Houweling, S. (2023). High-Resolution Estimation of Methane Emissions from Boreal and Pan-Arctic Wetlands Using Advanced Satellite Data. Remote Sensing, 15(13), 3433. https://doi.org/10.3390/rs15133433







