Refraction Correction for Spectrally Derived Bathymetry Using UAS Imagery
Abstract
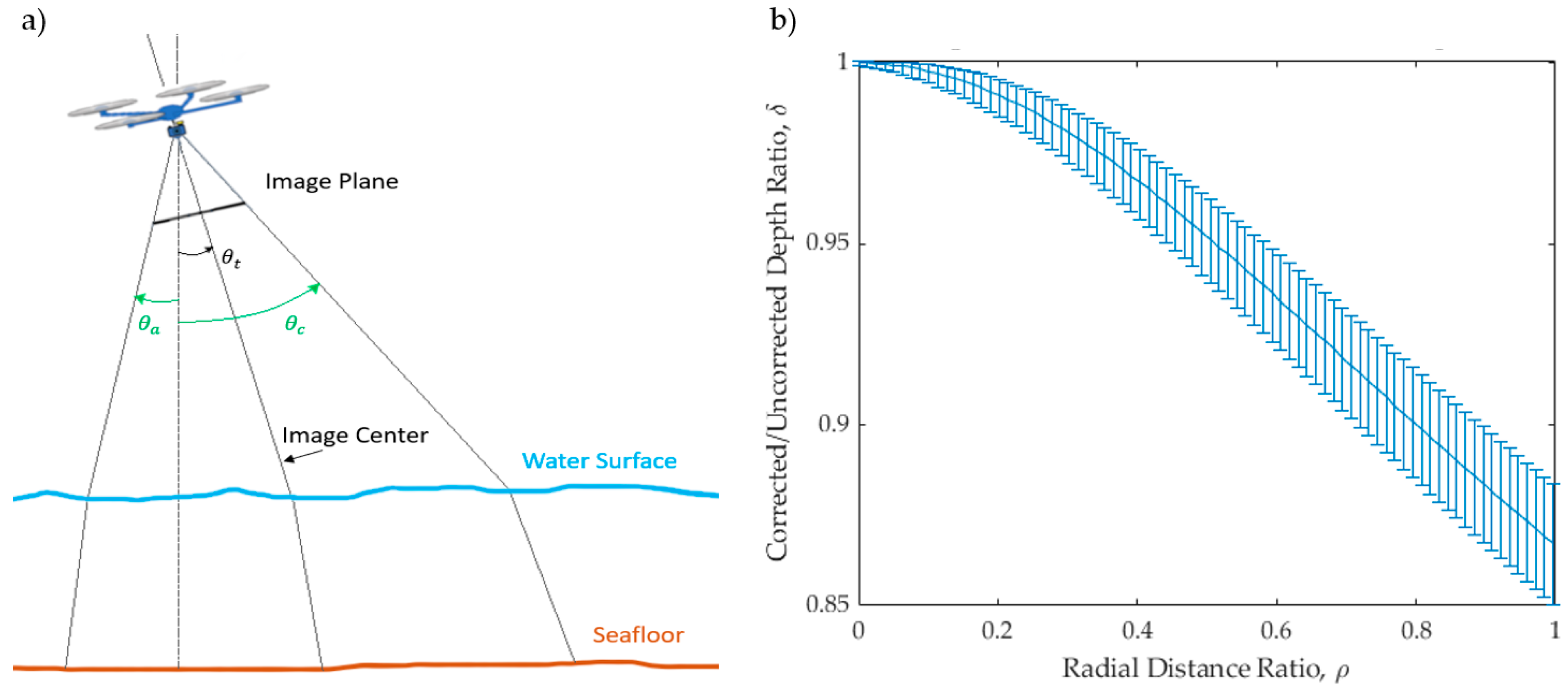
1. Introduction
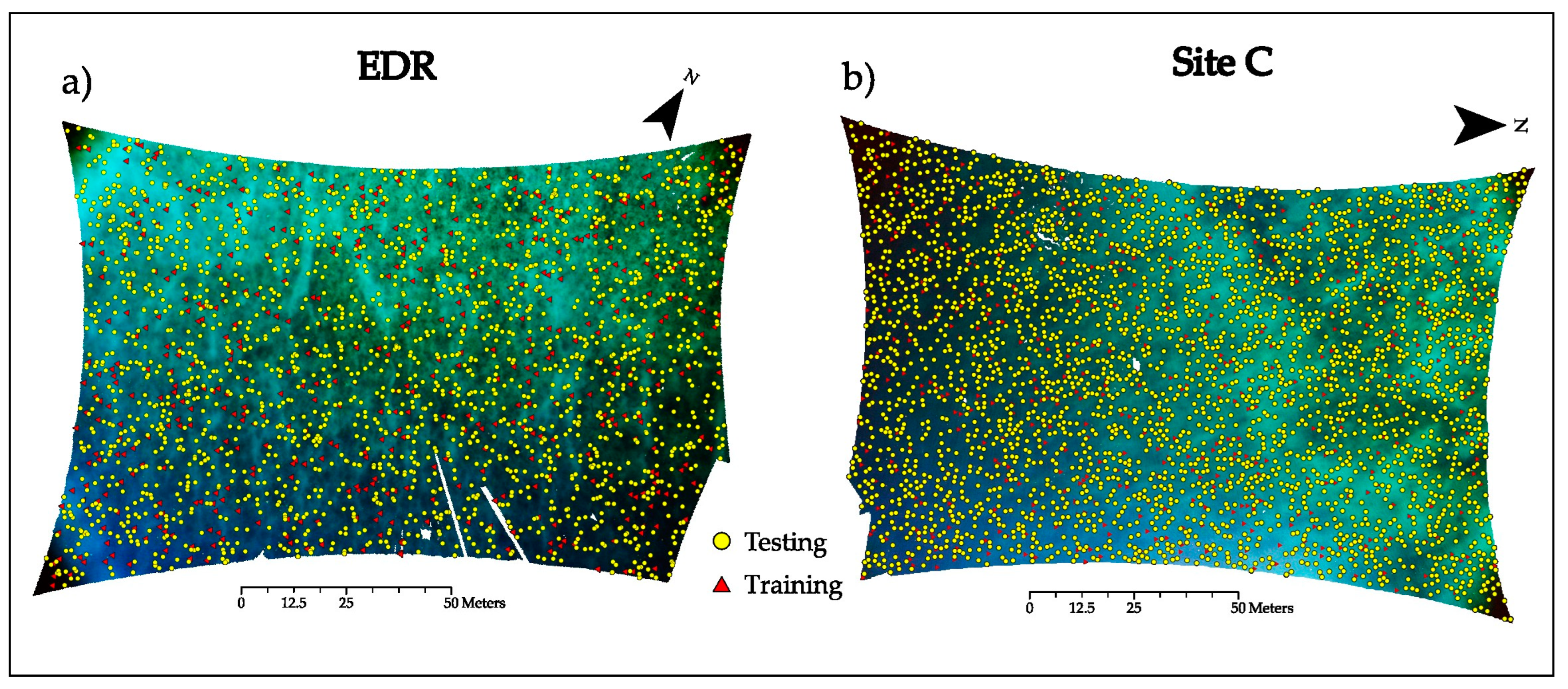
2. Methods
3. Experiment
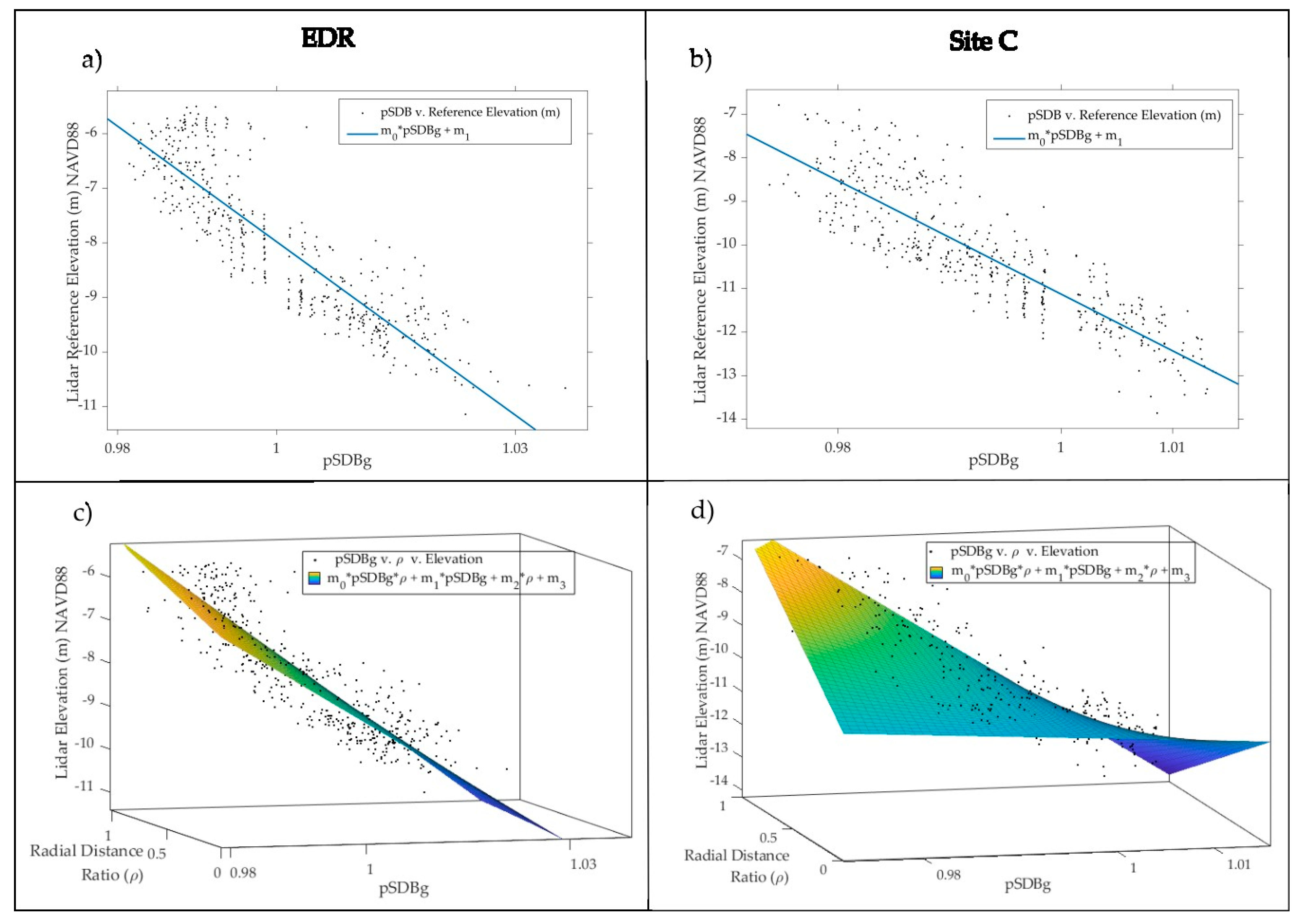
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moore, J.G. The determination of the depths and extinction coefficients of shallow water by air photography using colour filters. Philosophical Trans. Royal Soc. London Ser. A Math. Phys. Sci. 1947, 240, 163–217. [Google Scholar]
- Tewinkel, G.C. Water depths from aerial photographs. Photogramm. Eng. 1963, 29, 1037–1042. [Google Scholar]
- Polcyn, F.C.; Lyzenga, D.R. Remote Bathymetry and Shoal Detection with ERTS: ERTS Water Depth. 1975. Available online: https://ntrs.nasa.gov/api/citations/19750014800/downloads/19750014800.pdf (accessed on 21 June 2022).
- Brewer, R.K. Project planning and field support for NOS photobathymetry. Int. Hydrogr. Rev. 1979, 56, 55–66. [Google Scholar]
- Brown, R.M.; Zied, A.; Arnone, R.; Townsend, F.; Scarpace, F. Water Penetration Photogrammetry. In Feasibility and Evaluation Study; Naval Ocean Research and Development Activity Stennis: Hancock County, MS, USA, 1983; Volume 1. [Google Scholar]
- Zhang, C. Applying data fusion techniques for benthic habitat mapping and monitoring in a coral reef ecosystem. ISPRS J. Photogramm. Remote Sens. 2015, 104, 213–223. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.J.; Barrilero, O.; Laporte, J.; Koetz, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote. Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Purkis, S.J.; Gleason, A.C.; Purkis, C.R.; Dempsey, A.C.; Renaud, P.G.; Faisal, M.; Saul, S.; Kerr, J.M. High-resolution habitat and bathymetry maps for 65,000 sq. km of Earth’s remotest coral reefs. Coral Reefs 2019, 38, 467–488. [Google Scholar] [CrossRef]
- Misra, A.; Ramakrishnan, B. Assessment of coastal geomorphological changes using multi-temporal Satellite-Derived Bathymetry. Cont. Shelf Res. 2020, 207, 104213. [Google Scholar] [CrossRef]
- Herrmann, J.; Magruder, L.A.; Markel, J.; Parrish, C.E. Assessing the ability to quantify bathymetric change over time using solely satellite-based measurements. Remote Sens. 2022, 14, 1232. [Google Scholar] [CrossRef]
- Pe’eri, S.; Madore, B.; Nyberg, J.; Snyder, L.; Parrish, C.; Smith, S. Identifying bathymetric differences over Alaska’s North Slope using a satellite-derived bathymetry multi-temporal approach. J. Coastal Res. 2016, 76, 56–63. [Google Scholar] [CrossRef]
- Mavraeidopoulos, A.K.; Pallikaris, A.; Oikonomou, E. Satellite derived bathymetry (SDB) and safety of navigation. Int. Hydrogr. Rev. 2017, 17, 7–20. [Google Scholar]
- Chénier, R.; Faucher, M.A.; Ahola, R. Satellite-derived bathymetry for improving Canadian Hydrographic Service charts. ISPRS Int. J. Geo Inf. 2018, 7, 306. [Google Scholar] [CrossRef]
- Guenther, G.C. Airborne lidar bathymetry. In Digital Elevation Model Technologies and Applications: The DEM Users Manual; ASPRS Publications: Baton Rouge, LA, USA, 2007; Volume 2, pp. 253–320. [Google Scholar]
- Dietrich, J.T. Bathymetric structure-from-motion: Extracting shallow stream bathymetry from multi-view stereo photogrammetry. Earth Surf. Process. Landf. 2017, 42, 355–364. [Google Scholar] [CrossRef]
- Mancini, S.; Olsen, R.C.; Abileah, R.; Lee, K.R. Automating nearshore bathymetry extraction from wave motion in satellite optical imagery. In Proceedings of the SPIE Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimore, MD, USA, 23–27 April 2012; Volume 8390, pp. 206–217. [Google Scholar]
- Abileah, R.; Blot, J.Y. Bathymetry of the Golfe d’Arguin, Mauritania, derived with the moderate resolution Sentinel-2 satellites. In Proceedings of the IEEE OCEANS 2021: San Diego–Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–7. [Google Scholar]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Towards routine mapping of shallow bathymetry in environments with variable turbidity: Contribution of Sentinel-2A/B satellites mission. Remote Sens. 2020, 12, 451. [Google Scholar] [CrossRef]
- Muzirafuti, A.; Crupi, A.; Lanza, S.; Barreca, G.; Randazzo, G. Shallow water bathymetry by satellite image: A case study on the coast of San Vito Lo Capo Peninsula, Northwestern Sicily, Italy. In Proceedings of the 2019 IMEKO TC-19 International Workshop on Metrology for the Sea, Genoa, Italy, 3–5 October 2019. [Google Scholar]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Review of near-shore satellite derived bathymetry: Classification and account of five decades of coastal bathymetry research. J. Ocean Eng. Sci. 2021, 6, 340–359. [Google Scholar] [CrossRef]
- Slocum, R.K.; Parrish, C.E.; Simpson, C.H. Combined geometric-radiometric and neural network approach to shallow bathymetric mapping with UAS imagery. ISPRS J. Photogramm. Remote Sens. 2020, 169, 351–363. [Google Scholar] [CrossRef]
- Maas, H.G. On the accuracy potential in underwater/multimedia photogrammetry. Sensors 2015, 15, 18140–18152. [Google Scholar]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS bathymetry and analysis of ATLAS’s bathymetric mapping performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Karantzalos, K.; Georgopoulos, A.; Skarlatos, D. Correcting image refraction: Towards accurate aerial image-based bathymetry mapping in shallow waters. Remote Sens. 2020, 12, 322. [Google Scholar] [CrossRef]
- Mandlburger, G.; Kölle, M.; Nübel, H.; Soergel, U. BathyNet: A deep neural network for water depth mapping from multispectral aerial images. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 9, 71–89. [Google Scholar] [CrossRef]
- Rossi, L.; Mammi, I.; Pelliccia, F. UAV-Derived Multispectral Bathymetry. Remote Sens. 2020, 12, 3897. [Google Scholar] [CrossRef]
- Klemm, A.; Pe’eri, S.; Freire, R.; Nyberg, J.; Smith, S. Nautical Chart Adequacy Evaluation Using Publicly-Available Data. In Proceedings of the U.S. Hydrographic Conference, National Harbor, MD, USA, 16–19 March 2015. [Google Scholar]
- Wolf, P.R.; Dewitt, B.A.; Wilkinson, B.E. Elements of Photogrammetry with Applications in GIS; McGraw-Hill Education: New York City, NY, USA, 2014. [Google Scholar]
- Babbel, B.J.; Parrish, C.E.; Magruder, L.A. ICESat-2 elevation retrievals in support of satellite-derived bathymetry for global science applications. Geophys. Res. Lett. 2021, 48, e2020GL090629. [Google Scholar] [CrossRef] [PubMed]
- Casal, G.; Monteys, X.; Hedley, J.; Harris, P.; Cahalane, C.; McCarthy, T. Assessment of empirical algorithms for bathymetry extraction using Sentinel-2 data. Int. J. Remote Sens. 2019, 40, 2855–2879. [Google Scholar] [CrossRef]
- Traganos, D.; Poursanidis, D.; Aggarwal, B.; Chrysoulakis, N.; Reinartz, P. Estimating satellite-derived bathymetry (SDB) with the google earth engine and sentinel-2. Remote Sens. 2018, 10, 859. [Google Scholar] [CrossRef]
- Reguero, B.G.; Beck, M.W.; Agostini, V.N.; Kramer, P.; Hancock, B. Coral reefs for coastal protection: A new methodological approach and engineering case study in Grenada. J. Environ. Manag. 2018, 210, 146–161. [Google Scholar] [CrossRef]
- Geyman, E.C.; Maloof, A.C. A simple method for extracting water depth from multispectral satellite imagery in regions of variable bottom type. Earth Space Sci. 2019, 6, 527–537. [Google Scholar] [CrossRef]
- Hsu, H.J.; Huang, C.Y.; Jasinski, M.; Li, Y.; Gao, H.; Yamanokuchi, T.; Wang, C.G.; Chang, T.M.; Ren, H.; Kuo, C.Y.; et al. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: A case study in the South China Sea. ISPRS J. Photogramm. Remote Sens. 2021, 178, 1–9. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.; Herzfeld, U.; Thomas, N.; Markel, J.; Jasinski, M.; Imahori, G.; Herrmann, J.; Trantow, T.; Borsa, A.; et al. ICESat-2 Bathymetry: Advances in Methods and Science. In Proceedings of the IEEE OCEANS, Hampton Roads, VA, USA, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Sharr, M.B.; Parrish, C.E.; Jung, J. Classifying Valid and Erroneous Depths in Satellite Derived Bathymetry with Random Forest. ISPRS J. Photogramm. Remote Sens. 2023; in review. [Google Scholar]
- Bartels, E.; (Mote Marine Laboratory, Summerland Key, FL, USA). Personal communication, 2023.
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Seogwipo-si, Republic of Korea, 4–6 November 2009; International Convention Center Jeju Korea: Seogwipo-si, Republic of Korea, 2009; Volume 1, pp. 1–6. [Google Scholar]
- Slocum, R.K.; Wright, W.; Parrish, C.; Costa, B.; Sharr, M.; Battista, T.A. Guidelines for Bathymetric Mapping and Orthoimage Generation using sUAS and SfM, An Approach for Conducting Nearshore Coastal Mapping. In NOAA Technical Memorandum NOS NCCOS 265; National Ocean Service (NOS): Silver Spring, MD, USA; National Centers for Coastal Ocean Science (NCCOS): Silver Spring, MD, USA; NOAA: Silver Spring, MD, USA, 2019. [Google Scholar] [CrossRef]
- Over, J.S.; Ritchie, A.C.; Kranenburg, C.J.; Brown, J.A.; Buscombe, D.D.; Noble, T.; Sherwood, C.R.; Warrick, J.A.; Wernette, P.A. Processing Coastal Imagery with Agisoft Metashape Professional Edition, Version 1.6—Structure from Motion Workflow Documentation; US Geological Survey: Reston, VA, USA, 2021.
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using unmanned aerial vehicles (UAV) for high-resolution reconstruction of topography: The structure from motion approach on coastal environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef]
- American Society for Photogrammetry and Remote Sensing (ASPRS). Positional Accuracy Standards for Digital Geospatial Data, 2nd ed.; ASPRS Publications: Baton Rouge, LA, USA, 2023. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P. Accuracy assessment of LiDAR-derived digital elevation models. Photogramm. Rec. 2008, 23, 148–169. [Google Scholar] [CrossRef]
- DeWitt, J.D.; Warner, T.A.; Conley, J.F. Comparison of DEMS derived from USGS DLG, SRTM, a statewide photogrammetry program, ASTER GDEM and LiDAR: Implications for change detection. GIScience Remote Sens. 2015, 52, 179–197. [Google Scholar] [CrossRef]
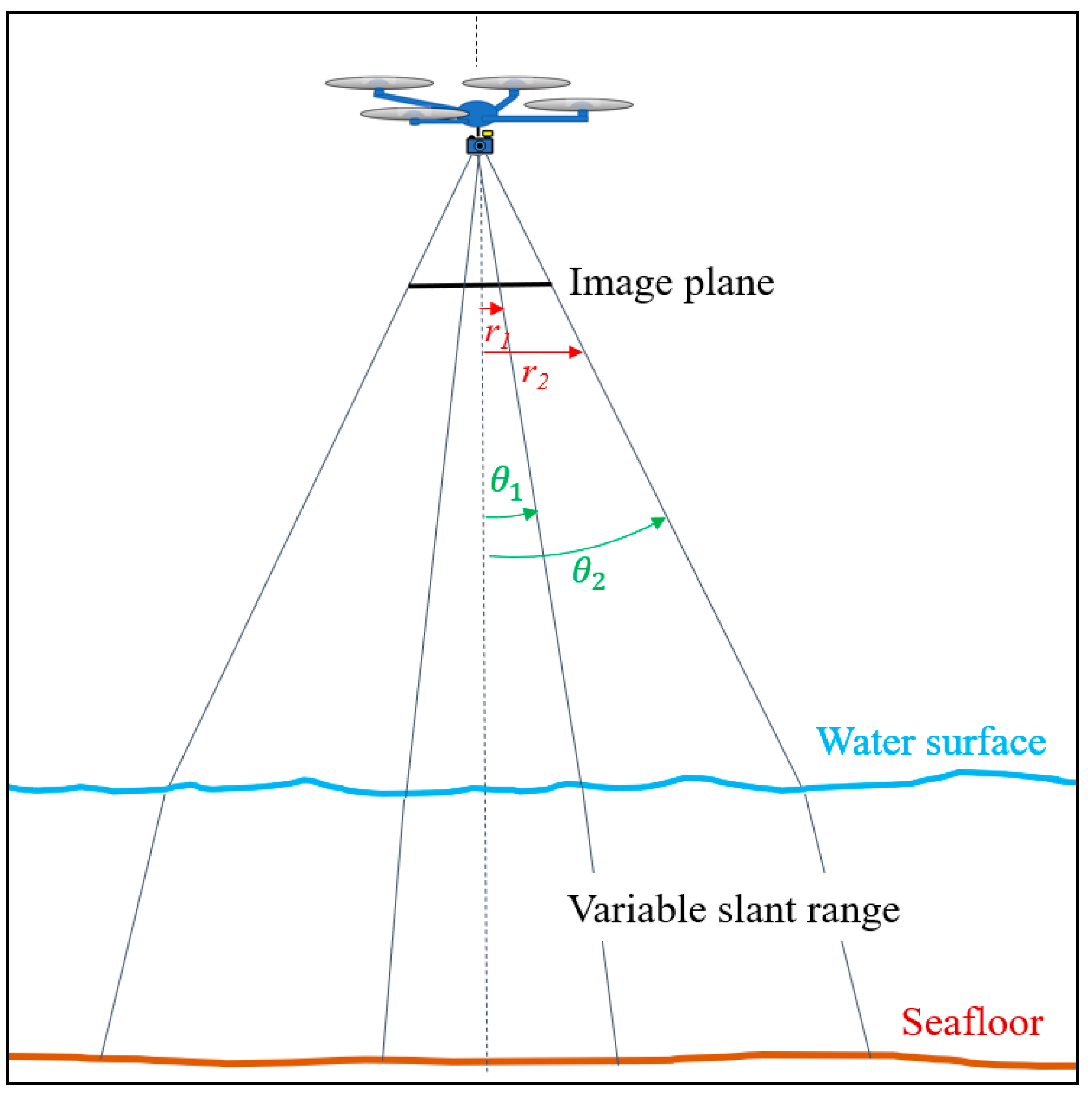
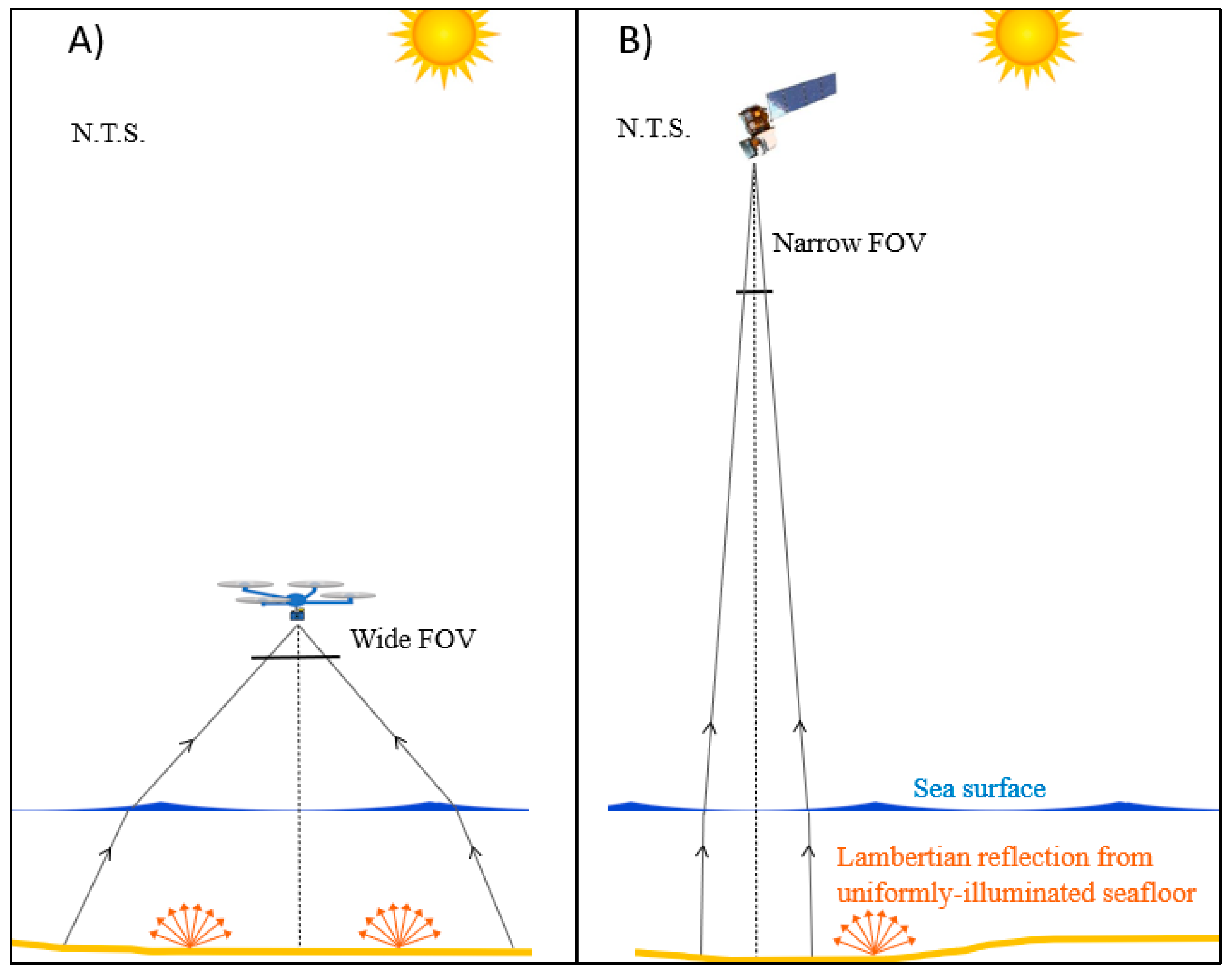

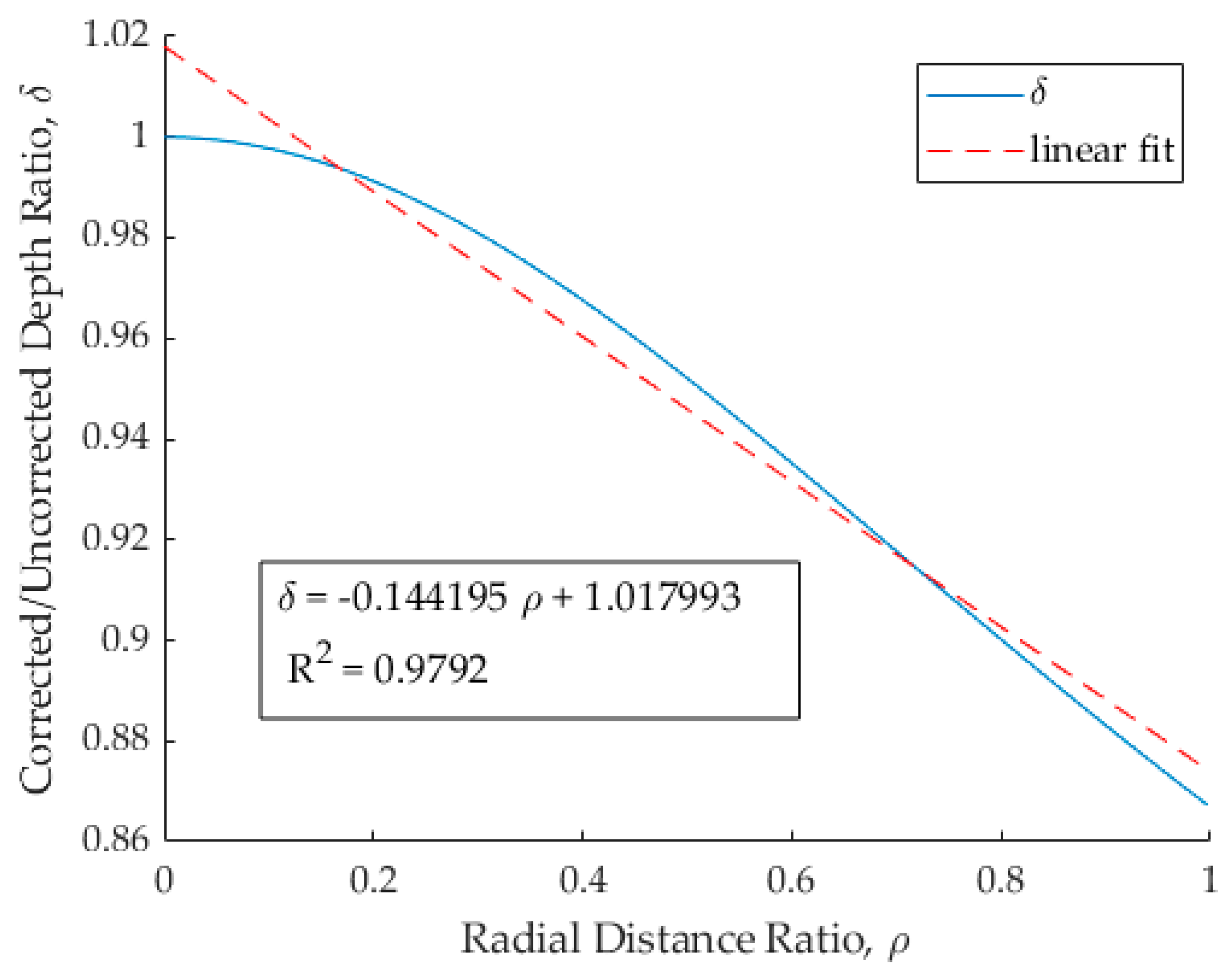

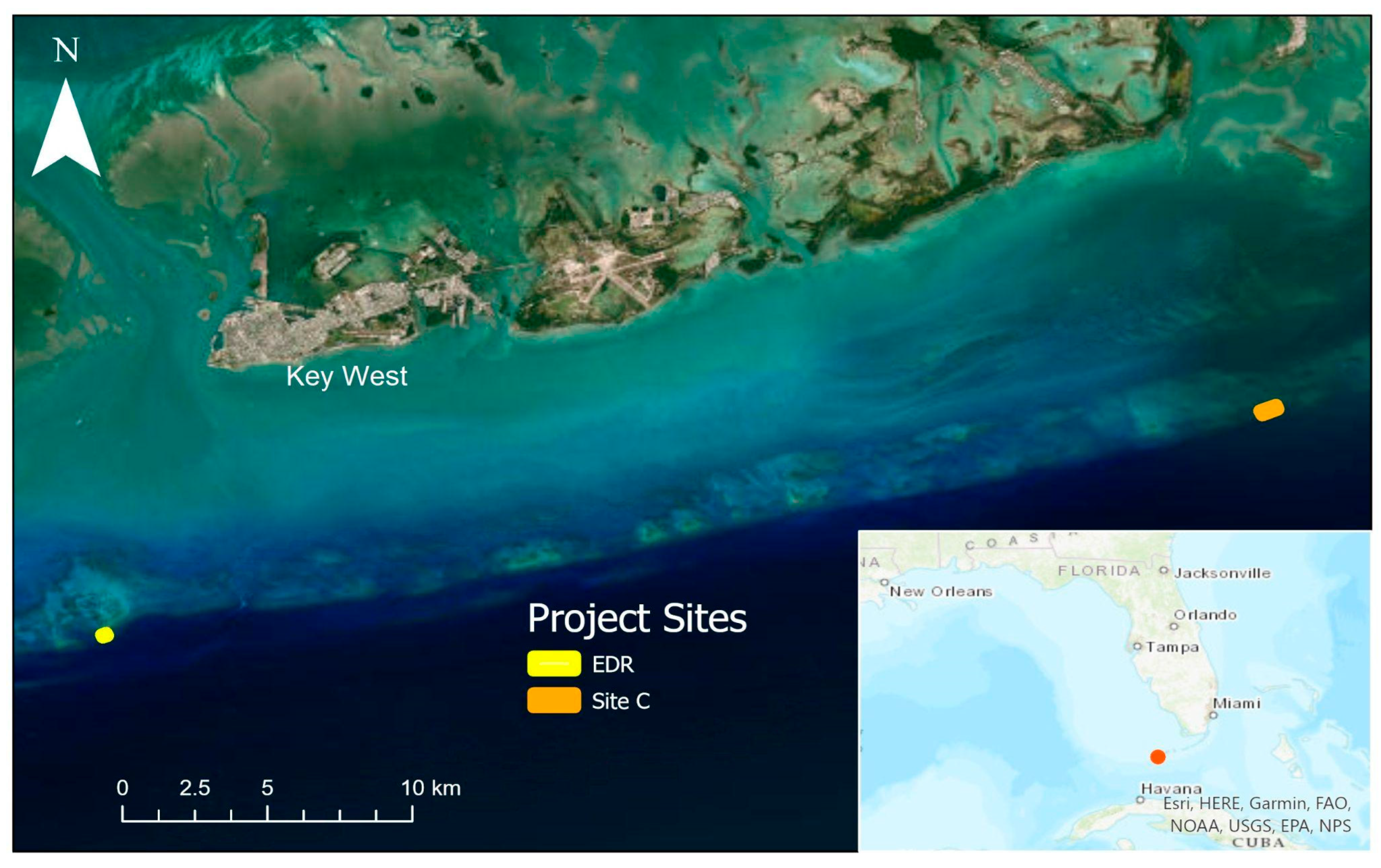


| Sensor | Platform | Field of View | Max Relative Depth Error from Ignoring Refraction Correction (Assuming Vertical Image) | Mean Relative Depth Error from Ignoring Refraction Correction (Assuming Vertical Image) |
|---|---|---|---|---|
| Operational Land Imager (OLI) | Landsat 8–9 satellites | 15° | 0.5% | 0.2% |
| Multispectral Instrument (MSI) | Sentinel-2A and -2B satellites | 21° | 0.9% | 0.3% |
| DJI Phantom 4 Pro integrated camera | UAS | 84° | 13.3% | 5.4% |
| Parameter | EDR | Site C |
|---|---|---|
| Solar altitude | 38°–43° | 38°–43° |
| Solar azimuth | 78°–80° | 78°–80° |
| Kd(490) (diffuse attenuation coefficient of downwelling irradiance at 490 nm) | 0.106 m−1 (Note: based on data from previous day) | 0.110 m−1 |
| SPM (suspended particulate matter) | 0.363 mg/L (Note: based on data from previous day) | 0.456 mg/L |
| Significant wave height | 0.20 m | 0.18–0.19 m |
| Wind speed | 1.6 m/s | 1.4 m/s |
| Atmospheric pressure | 1017.2 hPa | 1015.6 hPa |
| Humidity | 68% | 66% |
| Temperature | 27.9 °C | 27.5 °C |
| EDR (Standard) | EDR (Corrected) | Site C (Standard) | Site C (Corrected) | |
|---|---|---|---|---|
| SSE (m) | 196.9 | 172.4 | 242 | 165.7 |
| R2 | 0.79 | 0.81 | 0.75 | 0.83 |
| RMSE (m) | 0.640 | 0.600 | 0.718 | 0.596 |
| Standard Model: EDR-47 | Refraction-Corrected Model: EDR-47 | Standard Model: SiteC-75 | Refraction-Corrected Model: SiteC-75 | |
|---|---|---|---|---|
| Number of samples, N | 1947 | 1947 | 2963 | 2963 |
| RMSE (m) | 0.694 | 0.663 | 0.735 | 0.629 |
| Bias, μ (m) | 0.069 | 0.017 | 0.024 | −0.013 |
| Standard deviation, σ (m) | 0.561 | 0.538 | 0.734 | 0.629 |
| Mean squared error (MSE) (m2) | 0.481 | 0.440 | 0.540 | 0.396 |
| Skewness of error distribution | −0.534 | −0.135 | −0.562 | −0.252 |
| Error distribution passes normality test (Y/N) | No | Yes | No | No |
| Difference in MSE is statistically significant (Y/N) | Yes | Yes | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambert, S.E.; Parrish, C.E. Refraction Correction for Spectrally Derived Bathymetry Using UAS Imagery. Remote Sens. 2023, 15, 3635. https://doi.org/10.3390/rs15143635
Lambert SE, Parrish CE. Refraction Correction for Spectrally Derived Bathymetry Using UAS Imagery. Remote Sensing. 2023; 15(14):3635. https://doi.org/10.3390/rs15143635
Chicago/Turabian StyleLambert, Selina E., and Christopher E. Parrish. 2023. "Refraction Correction for Spectrally Derived Bathymetry Using UAS Imagery" Remote Sensing 15, no. 14: 3635. https://doi.org/10.3390/rs15143635
APA StyleLambert, S. E., & Parrish, C. E. (2023). Refraction Correction for Spectrally Derived Bathymetry Using UAS Imagery. Remote Sensing, 15(14), 3635. https://doi.org/10.3390/rs15143635






