Abstract
The detection ability of SO2 cameras has been improved effectively, while the calibration is still the main factor that limits their measurement accuracy. This paper presents a nonlinear calibration theory by considering the effect of light dilution due to the path radiance as well as the dependence of plume aerosol on scattering wavelength. This new spectral calibration method is used to retrieve the SO2 column density and emission rate of the Etna volcano. Results show that, compared with the DOAS calibration approach, the inversion error can be reduced by 13% if the new spectral calibration is adopted. The superiority of the proposed method will become more obvious for long-distance detection of optically thick plumes.
1. Introduction
SO2 is one of the most important air pollutants. Despite the short service life of SO2, it easily combines with atmospheric water vapor and forms sulfurous acid, oxidizing into acid rain quickly and efficiently, further damaging forest ecology and the acid balance of the water environment. In addition, SO2 also sharply increases air toxicity and seriously affects human health. Research has shown that SO2 stimulates the respiratory system and deteriorates pulmonary function, thereby weakening the immune system [1,2,3].
The main sources of SO2 are the burning of fossil fuels and the eruption of volcanoes. The annual volcanic eruption process injects tens of millions of tons of SO2 into the troposphere and upper stratosphere and causes huge, widespread, and long-term damage to the global ecological environment, further affecting economic development. As a common natural disaster, the hazard scope of volcanic eruption is extremely wide. The SO2 produced by volcanic eruptions can cause fatal damage to commercial and military aircraft, even at a distance beyond 1000 km [4].
In reality, although the SO2 emitted by volcanic eruption causes disasters and losses, it also serves as a crucial marker for monitoring volcanic activity. In the early stage of volcanic activity, magma breeds in the deep part of the earth and does not deform the surface. Thus, traditional seismic monitoring methods based on the pressure deformation principle of geography can hardly predict volcanic activity in the early stage. However, as an important product of volcanic activity, SO2 escapes from the surface of the volcano during the gestation and migration of magma, suggesting that the changing rule of its content can shed insights into the prediction of volcanic eruptions [5]. In addition, monitoring the change in SO2 column density in the crater offers important scientific significance for studying volcanic dynamics [6], volcanic degassing processes [7,8], spatial evolution of volcanic plumes [9], volcanic plume chemistry [10], and plume diffusion theories [11]. Thus, SO2 is also called “the telegram in the deep part of the earth” by volcanic scientists.
Top international scientific research institutions have successively proposed optical remote sensing technologies and different mechanisms to monitor the emission of SO2 from volcanoes. Examples include the Differential Optical Absorption Spectrometer (DOAS), Passive Multi-Axis Differential Optical Absorption Spectroscopy (MAX-DOAS) [12], Imaging Differential Optical Absorption Spectrometer (I-DOAS), open-path Fourier transform infrared spectrometers (open-path FTIR) [13], DOAS and Raman LIDAR, and thermal infrared cameras (nicAIR IIC) [14]. Among them, LIDAR is an active detecting technology and can accurately and quickly measure the SO2 column density along the laser beam path through the volcanic plume, but it cannot observe the entire volume of plume emission [15]. DOAS and FTIR are superior because of their good portability, high spectral resolution, high sensitivity, and simple operation, but they are limited by spatial resolution and the availability of sample data. I-DOAS can visually display the column density information at any position in the field of view (FOV) via mechanical scanning to ensure the overall detection accuracy; however, due to the problem of low temporal resolution, its application in the remote sensing monitoring of volcanic plumes is seriously limited. IIC can simultaneously achieve high spatial resolution and high temporal resolution, but it is seriously affected by environmental interference and background radiation; moreover, due to the complex process of infrared radiation transmission, it is also limited by the problems of low detection sensitivity and large measurement error [16].
In recent years, the SO2 camera, a new remote sensing method with obvious technical advantages in temporal resolution, spatial resolution, and accuracy, has achieved rapid development. This new technology has been quickly applied to the detection of volcanic activity and the study of the gas-dynamic structure of volcanic plumes since it was proposed [17,18]. With the rapid development of UV cameras and the gradual optimization of UV filter performance, the detection capability of SO2 cameras has been effectively improved. In the last decade, the accuracy and reliability of SO2 cameras have been further enhanced owing to the continuous development of plume transport velocity estimation theory and the gradual optimization of image correction methods [19,20,21,22]. However, the precise calibration of SO2 cameras remains to be a problem limiting their measurement accuracy.
The physical quantity directly measured by SO2 cameras is the SO2 optical density (OD). This parameter requires additional equipment to obtain the conversion relationship between the OD of SO2 and its column density prior to retrieving the SO2 column density image. This process of determining the conversion relationship can be simply described as calibration. The two commonly used calibration methods for SO2 camera systems are the gas cell and DOAS methods. The calibration cell method determines the linear relationship between the OD of SO2 and its column density by inserting multiple SO2 quartz cells with known amounts of SO2 column density in the FOV [23]. This method has been the most straightforward and commonly used since several years ago. However, the frequent switching of calibration cells causes adverse effects on the real-time detection of SO2 UV cameras. Furthermore, the reflection effect of the cell window causes non-negligible errors when determining the calibration function. For the DOAS calibration method, the SO2 column density information at a certain point of the volcanic plume can be directly retrieved by measuring the OD, and then the conversion factor is determined. In contrast to the cell calibration method, DOAS can effectively reduce the influence of volcanic ash during SO2 column density retrieval. However, obtaining the best matching relationship between the measurement position of DOAS and the corresponding pixels of the SO2 camera is difficult during operation, further causing a large system error for the DOAS method.
This study first explains the working mechanism of the SO2 camera, focusing primarily on the transmission characteristics of atmospheric ultraviolet radiation and then establishes the nonlinear model of SO2 camera calibration under the effect of light dilution [24]. This dilution effect refers to the changes in spectral features during propagation due to the presence of path radiance arising from the scattering of solar radiation [25]. On this basis, a new spectral calibration method that can continuously calibrate the SO2 camera in real time is proposed. Then, the new method is used to reprocess the Etna volcanic plume data collected by the Norwegian Air Research Institute with a SO2 camera to more accurately retrieve SO2 column density images, consequently enhancing the reliability of the SO2 camera system.
2. SO2 Camera
2.1. Theory
The SO2 camera, which is based on realistic radiative transfer, consists of a UV-sensitive camera and two UV narrow-band filters [26,27,28]. The design scheme of using double narrow-band filters improves the anti-stray scattering interference ability of the SO2 camera. The emitted plumes of volcanic eruptions, industrial chimneys, or ship exhaust not only contain SO2, but also comprise abundant particulate matter, which can affect the measurement of SO2 OD. Thus, the dual-channel SO2 camera technology can eliminate this adverse effect and eventually improve the measurement accuracy [29,30].
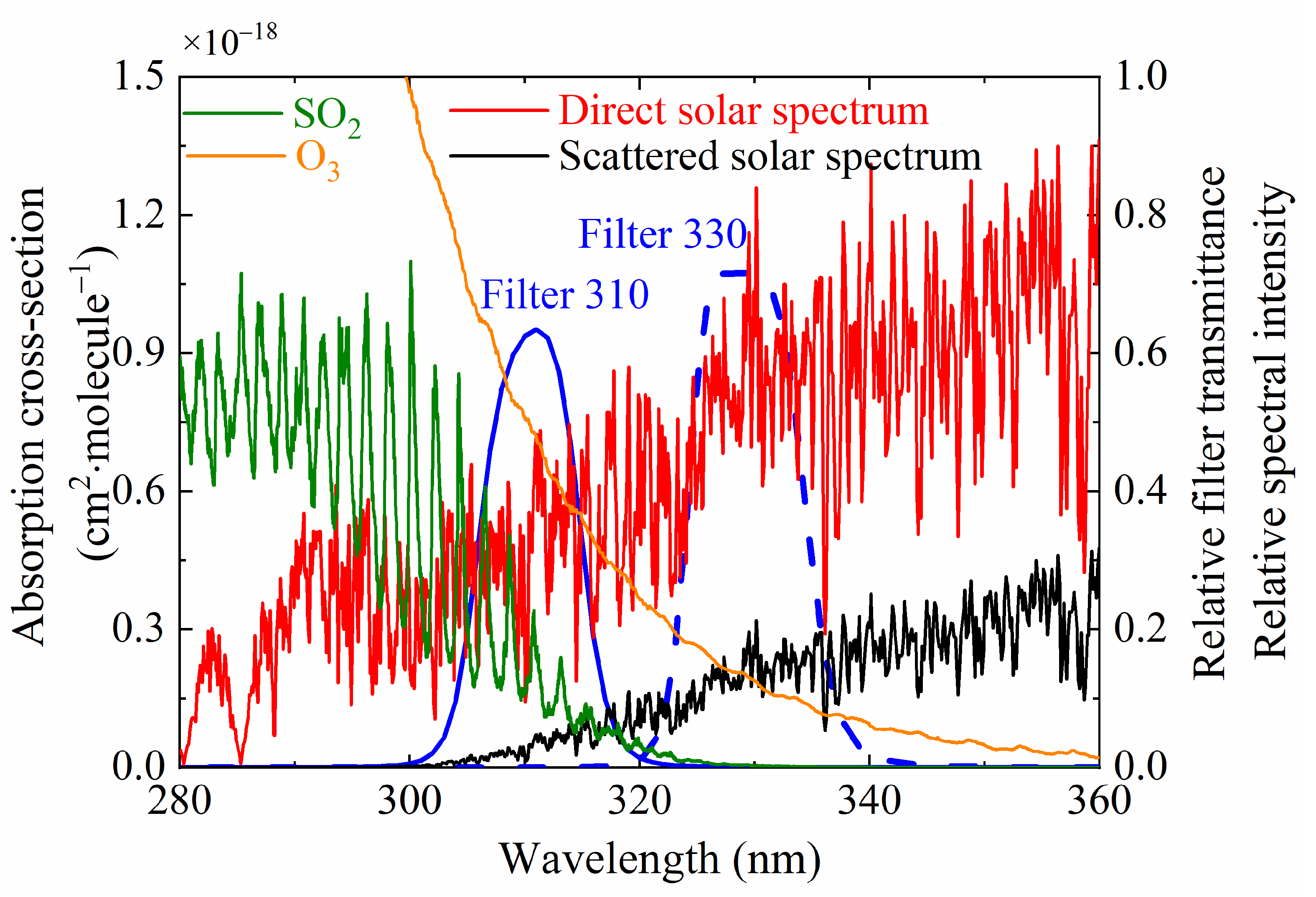
Figure 1 shows the absorption cross-sections of SO2 and O3, the transmission curves of two UV narrowband bandpass filters at 310 and 330 nm, and the relative spectra of direct and scattered solar radiation. SO2 exhibits a significant characteristic spectrum in the UV band within the region of 240–338 nm. For wavelengths shorter than 300 nm, the sunlight signal reaching the ground is almost completely absorbed by the ozone layer. Given the intensity of the solar-scattered signal and the wavelength distribution of the SO2 absorption cross-section, the SO2 camera generally selects a UV bandpass filter with a center wavelength of 310 nm and a transmission bandwidth of 10 nm as the signal channel. For this channel, particle (aerosol) scattering and SO2 absorption reduce the intensity of scattered solar radiation. For the reference wavelength of 330 nm, on the other hand, the scattered solar intensity is affected only by the particle scattering. Thus, pure SO2 OD can be obtained by determining the difference between the signal channel and reference channel.
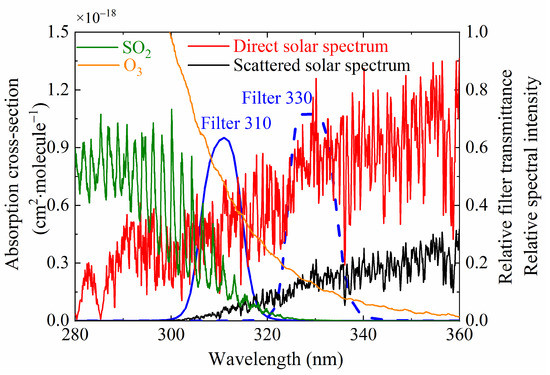
Figure 1.
Transmittance curves of filters at the wavelengths of 310 and 330 nm and the absorption cross-sections of SO2 and O3, and the relative spectra of direct and scattered solar radiation are also shown in the figure.
On the basis of realistic radiative transfer, the 310 nm spectral channel can be expressed as:
where and represent the light intensity before and after passing through the plume, respectively, and and are the OD of SO2 and aerosol OD of the signal channel, respectively.
For the 330 nm channel, the scattered solar light is only subject to the extinction effect of particulate matter, i.e.:
where is the aerosol OD of the reference channel. By synthetically handling the ODs of the two channels, the SO2 OD can be obtained as:
After obtaining the OD of SO2, the column density image of SO2 can be retrieved based on the calibration relationship between the SO2 OD and its column density.
2.2. Light Dilution
The UV camera response is often linear in SO2 column density and the differential optical depth when a standard Beer–Lambert absorption model is assumed. Therefore, the cell calibration method is generally used to retrieve SO2 column density in cases where the camera is close to the plume and the amount of aerosol in the plume can be neglected. However, for volcanic monitoring, the SO2 camera system is usually positioned at a point several kilometers away from the volcano to include the whole plume. In this condition, the scattered photons between the camera and plume come into FOV, which induces a systematic underestimation of the SO2 retrievals.
SO2 cameras with two filters allow for the compensation of aerosol attenuation. However, the Mie scattering of aerosols in the plume is strongly dependent on wavelength [31]. The aerosol OD of the two channels can be expressed as a numerical relation as:
where is the ratio between the scattering cross-sections of the aerosol in the plume for the two different wavelengths.
By substituting Equation (4) into Equations (1) and (2), the SO2 OD can be expressed as:
The scattering intensity of aerosol that varies with wavelength will cause a non-negligible error in the calculation of SO2 OD. Moreover, the light dilution effect can cause large errors. When the distance between the camera and the measured target is sufficiently far, an incremental radiation ID, which increases with the increase in distance L, will be produced due to the atmospheric scattering of photons between the plume and the instruments.
where is the extinction coefficient, is the intensity of the sky background, and is the incremental radiation.
According to Equation (6), the values of incremental radiation of the 310 and 330 nm channels are not equal. In consideration of the light dilution effect, the SO2 OD should be written as [32]:
3. OD Image Acquisition
The data set used in this paper was collected by Jonas Gliß et al. at 07:06 and 07:22 on 16 September 2015, using their self-developed SO2 UV camera in Milo Town, about 10.3 km from Etna volcano plume source. The altitude of Milo Town and the crater is 803 and 3103 m, respectively [33]. The main instrumental information is summarized in Table 1.

Table 1.
Main instrument information.
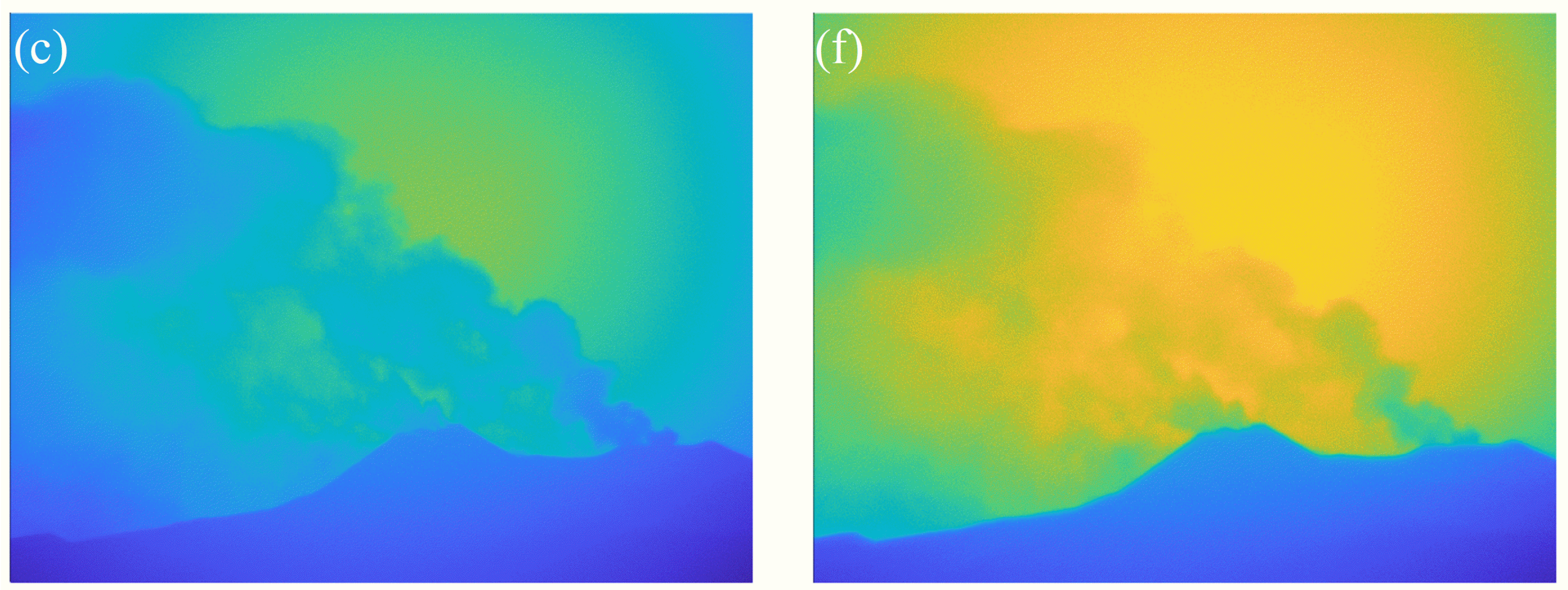
The time for collecting picture information was short (about 15 min), so the solar zenith angle (SZA) did not change significantly, and it was considered that the calibration curve remained almost unchanged during the experiment. Figure 2a,d represent dark current images of channels 310 and 330 nm, respectively. The sky background and plume images corresponding to the two channels can be obtained through dark current correction, as shown in Figure 2b,c,e,f, respectively. The sky background images in both channels were taken by moving the camera FOV above the crater when no volcanic plume was detected, and the dark noise images were obtained after shooting the sky background with a lens hood on the back cover. The exposure time for A and B channel plume images was 33 and 8 ms, respectively.
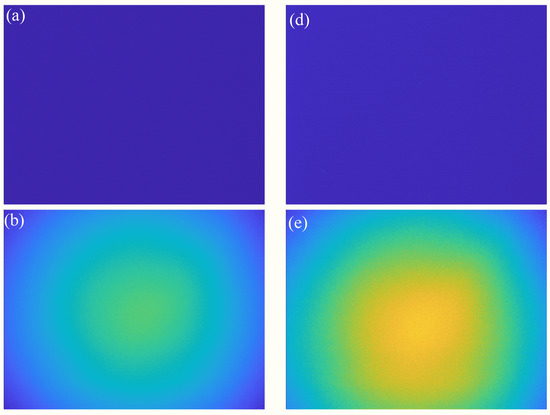
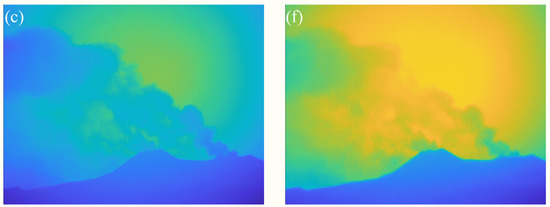
Figure 2.
(a) The dark image of 310 nm; (b) the sky background image of 310 nm; (c) the plume image of 310 nm; (d) the dark image of 330 nm; (e) the sky background image of 330 nm; (f) the plume image of 330 nm.
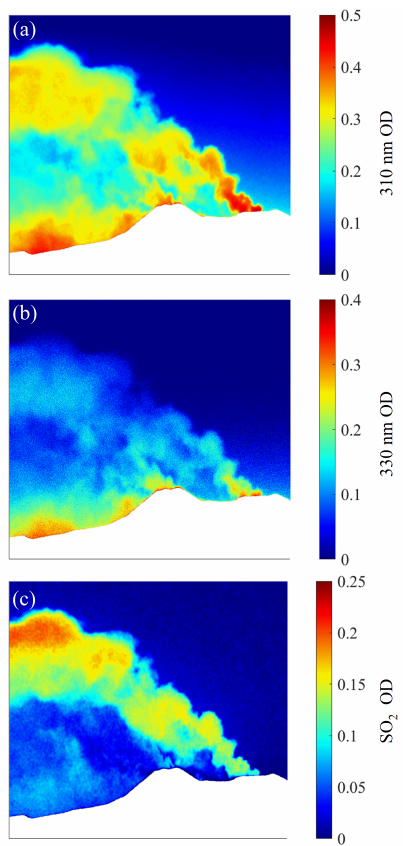
Figure 3a,b present the ODs of 310 and 330 nm channels obtained by using the four-images (4-IM) method after obtaining their corresponding sky background and smoke plume images [24]. On the basis of the working principle of SO2 cameras, the SO2 OD image can be obtained by performing a subtraction operation between the OD images, which is shown in Figure 3c. Note that, in order to stress the details of the plume, the mountain areas have been masked in all images.
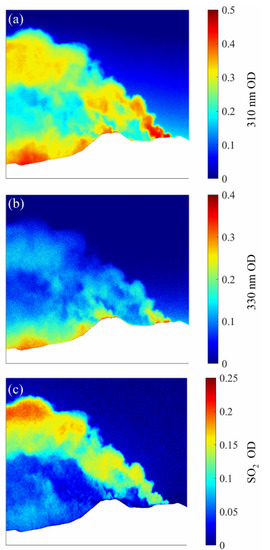
Figure 3.
OD images: (a) the 310 nm channel; (b) the 330 nm channel; (c) the differential channel.
4. Calibration
The intensity of the scattering spectrum reaching the ground is determined by SZA, especially in the ultraviolet wavelength region where O3 has a significant absorption (as shown in Figure 1). For different SZAs, the optical paths passing through the atmospheric ozone layer vary considerably, with different strengths of scattered light reaching the near-surface earth. This situation further differentiates the path lengths through the plume, eventually altering the ODs. Thus, precise real-time calibration for the SO2 camera system must be ensured. At present, DOAS is the most commonly used calibration method due to its advantages in correcting for radiative transfer effects. However, it is quite difficult in engineering practice to obtain the best FOV correlation between DOAS and the UV camera, which inevitably causes systematic errors. Aiming to improve the calibration accuracy, we propose a new method of spectral calibration in this study.
4.1. DOAS Calibration
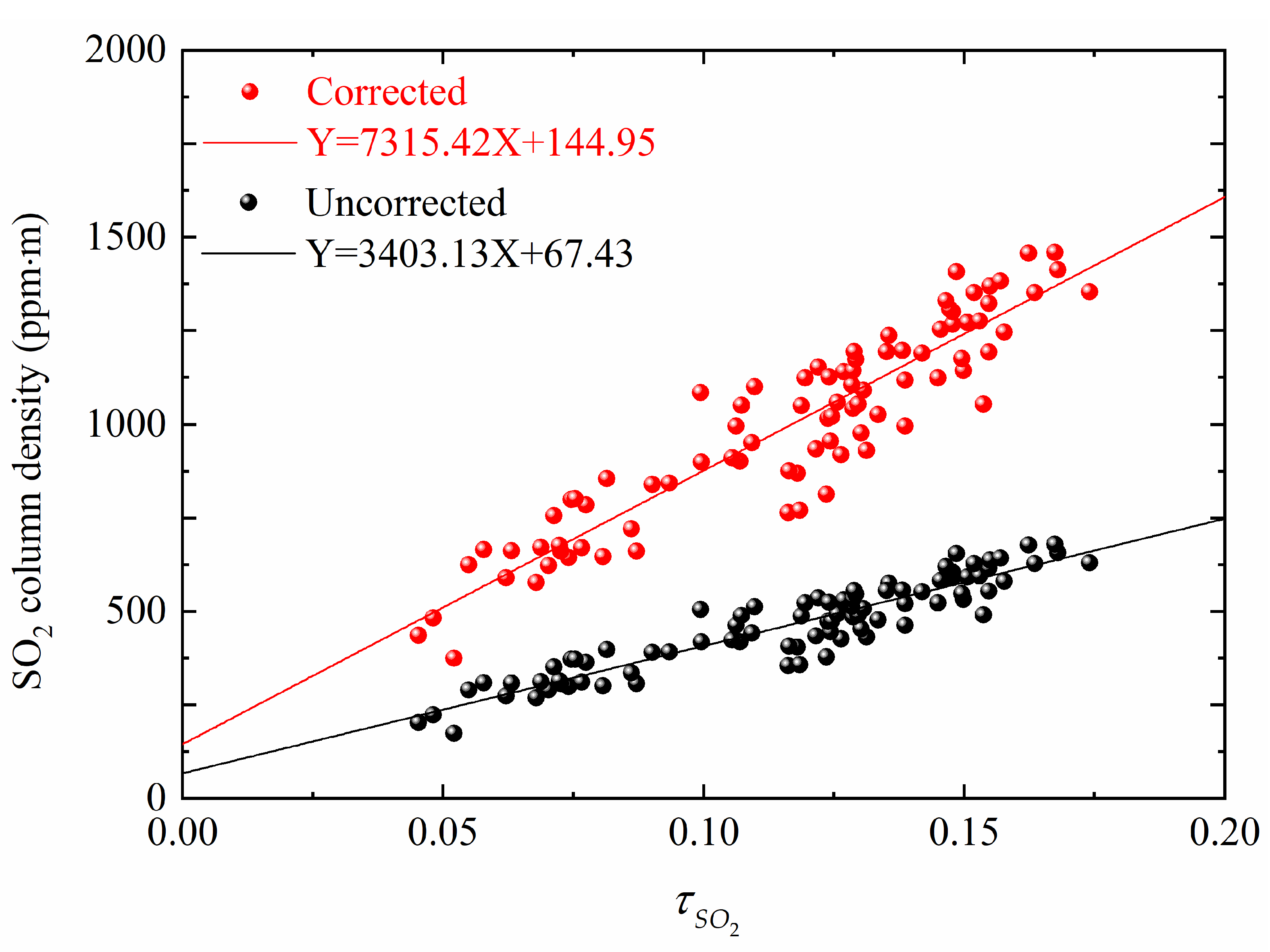
DOAS identifies gas components based on the narrowband absorption characteristics of gas molecules and infers the column density of trace gases according to the narrowband absorption intensity. The calibration curves for the DOAS method can be obtained by fitting the OD images on the same time series with the corresponding DOAS data in a linear function. This approach, which can reduce the impact of particles, gradually becomes the mainstream method of SO2 UV camera calibration. However, the light dilution effect still affects the inversion accuracy, so it needs to be corrected. The DOAS calibration curves uncorrected and corrected by the light dilution effect are shown in Figure 4. During the calibration process, it is necessary to obtain the extinction coefficients of channels A and B, which are 0.0743 and 0.0654 km−1, respectively, to correct the transmission of solar radiation from the plume to the cameras’ FOV. More detailed information on determining the calibration curve of DOAS is described by Gliß et al. [33]. Note that the calibration curve of the SO2 camera obtained with DOAS is sensitive to the position, shape, and exact size of the DOAS FOV. This implies that the identification of the best correlation between SO2 column density and its OD is very difficult, which leads to a nonignorable error between the measurement and the true value. Moreover, applying the specific point to the entire OD image is an inappropriate approach.
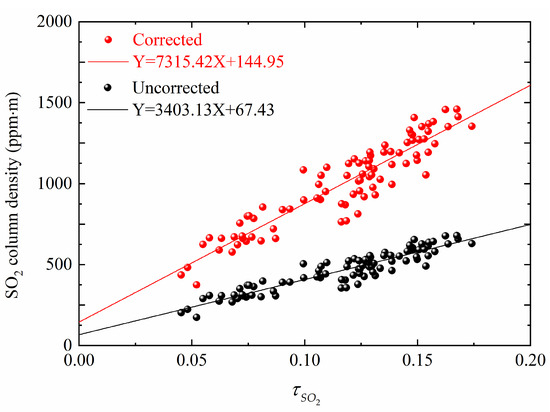
Figure 4.
DOAS calibration curves determined with and without light dilution effect corrected.
4.2. Spectral Calibration
On the basis of the measurement principle of the SO2 UV camera and the theory of light dilution effect, a new method of personalized real-time calibration for all pixels of the camera is proposed for solving the calibration problem of SO2 UV cameras. This method requires the incorporation of a spectrometric channel into the SO2 imaging system for collecting the sky background spectra. Thereafter, the calibration curve of the SO2 camera can be obtained based on the realistic radiative transfer.
For any pixel of the SO2 UV camera, the signal intensity corresponds to the convolution integral of the camera quantum efficiency , the incident solar-scattered light intensity , the SO2 absorption cross-section , the SO2 column density , and the transmission function of the UV bandpass filter [32]. On the basis of known filter transmittance and camera quantum efficiency (both can be obtained from the product delivery report), the calibration curve of the SO2 UV camera at any time can be calculated in real time by measuring the spectral signal of the sky background with a spectrometer.
where is the wavelength of the A or B channel.
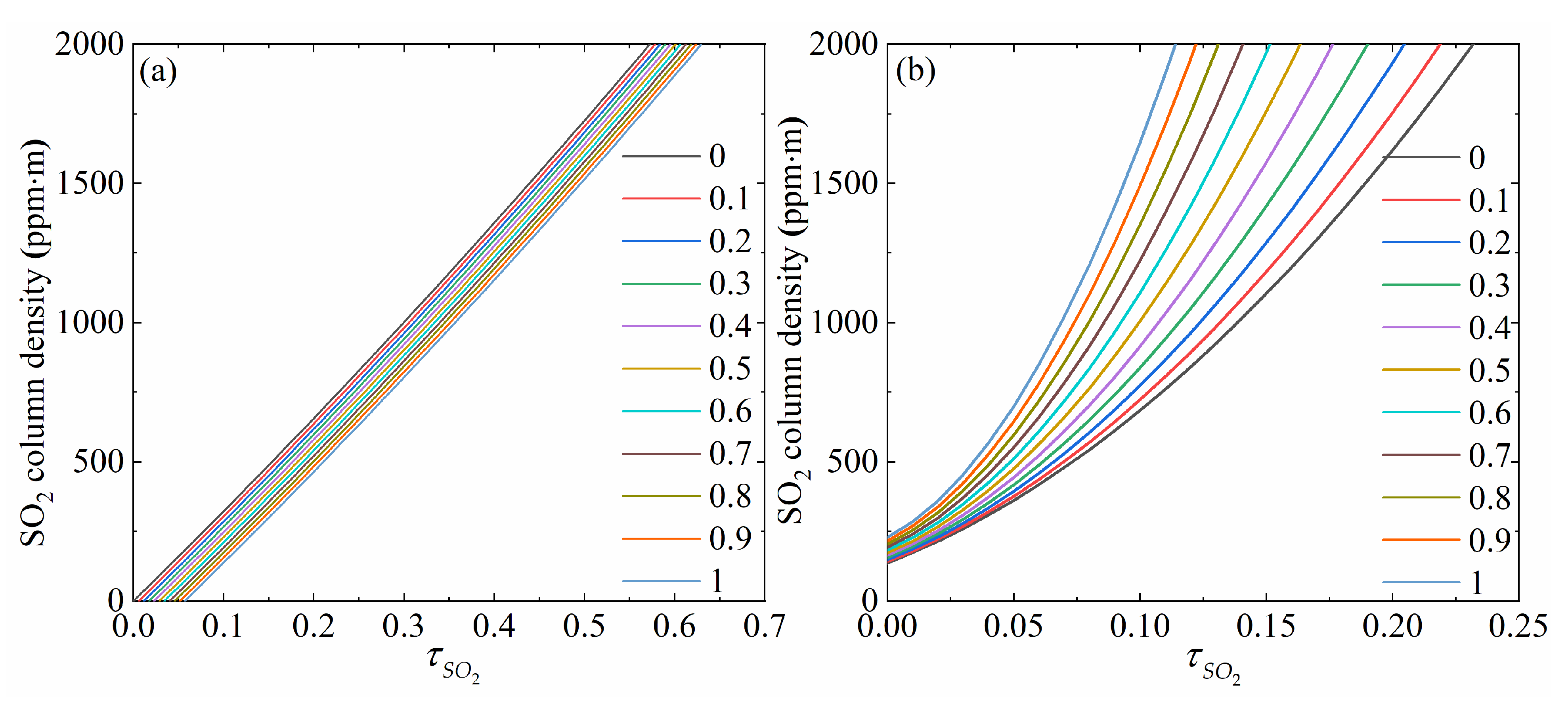
Combining Equations (7) and (8), the functional relationship between the SO2 OD and SO2 column density can be obtained. Based on the study by Lübcke et al. [31] and combining the specific OD values of the A and B band channels, the scattering cross-section ratio K = 1.09 was chosen. Figure 5a,b show the spectral calibration curves under different particle ODs with the light dilution effect uncorrected and corrected, respectively. These calibration curves in Figure 5 were obtained through the constructed MODTRAN radiative transfer model [34], which only quantitatively explains the effect of optical dilution and particle optical thickness on the calibration curves. From the comparison of these two sets of calibration curves, it can be found that the relationship between SO2 OD and its column density follows the Beer–Lambert approximation if the light dilution effect is neglected, which is in good agreement with the black line in Figure 4. The direct linear relationship is destroyed for distant or optically thick volcanic plumes, as the Beer–Lambert model does not account for complex radiative transfer. The larger the aerosol optical thickness, the lower the sensitivity towards SO2. Moreover, the camera sensitivity also decreases with increasing SO2 OD. This means that the column density of both SO2 and aerosol in the plume must be taken into account if accurate calibration curves are desired.
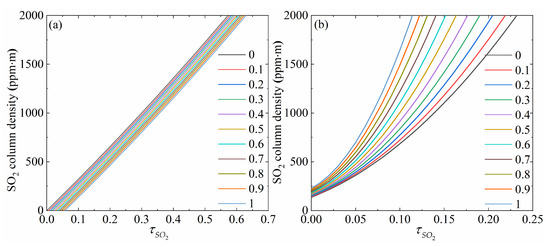
Figure 5.
Spectral calibration curves (i.e., increases by 0.1 each time from 0 to 1): (a) light dilution effect uncorrected; (b) light dilution effect corrected.
Superior to the DOAS approach, the spectral calibration method could customize a personalized real-time calibration curve for each pixel, fully considering the influence of different SO2 and particle content on camera sensitivity. Moreover, the spectral calibration method also takes the influence of incident angles on the effective transmittance of filters into account, which can significantly reduce the underestimation of the column density inversion caused by the nonparaxial effect.
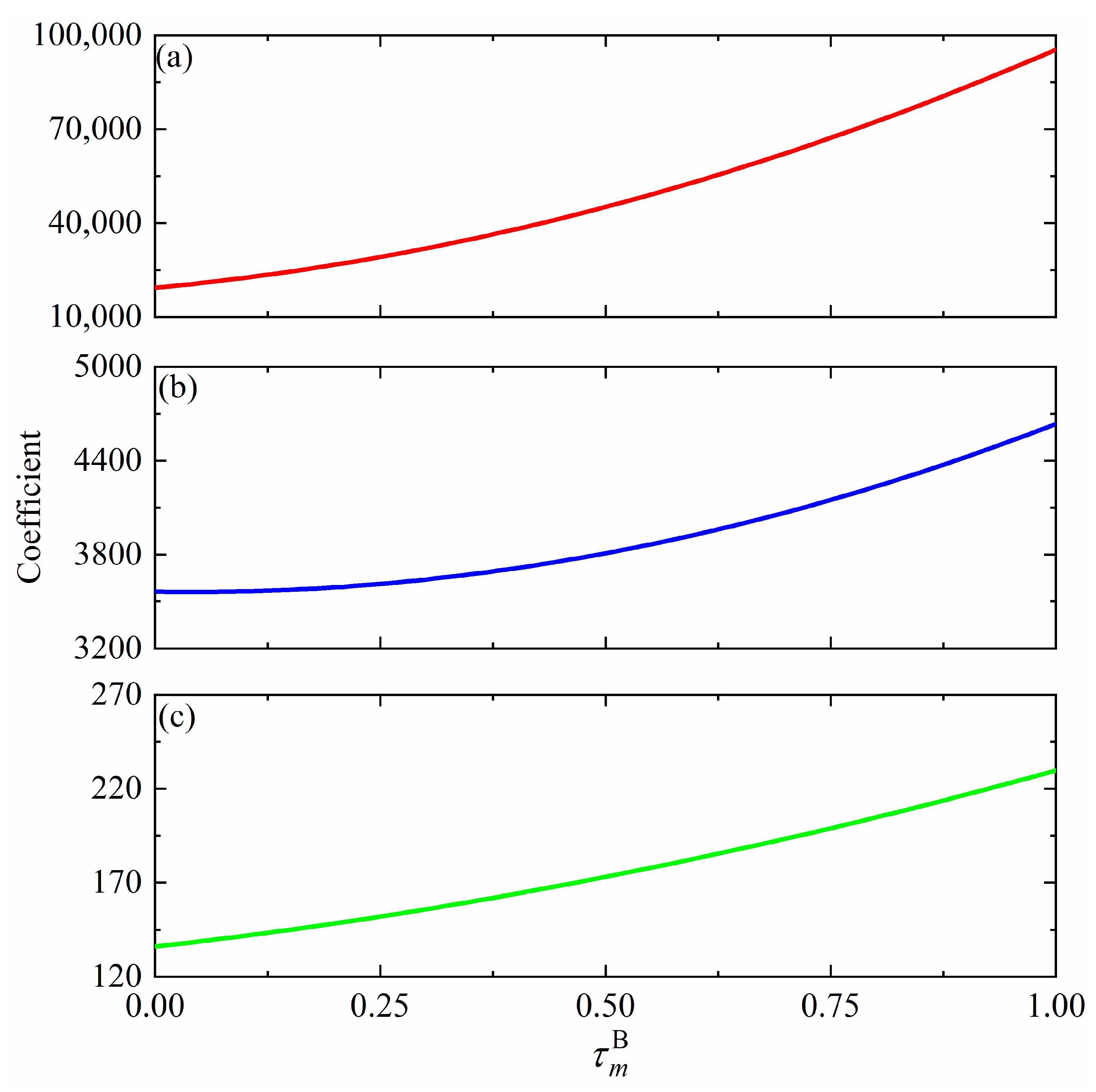
In the experimental process, the actual calibration spectra were measured in real time using the spectrometer. In view of further comparing and analyzing the influence of the particle OD, the calibration curve data are fitted with the quadratic function (). In addition, the coefficients a, b, and c of the real-time calibration curve obtained by the actual measurement spectral calibration method are constantly changing and, according to the theoretical analysis in Figure 5, it can be known that also affects the results of the calibration curve, so there is some kind of relationship between the coefficients a, b, c, and . After several sets of measurements were calculated and analyzed, it was found that the coefficients a, b, and c were quadratically related to , i.e., , , and , as shown in Figure 6. Thus, the accurate inversion of the SO2 column density image under the light dilution effect should obtain the direct numerical relationships between the SO2 column density and SO2 OD and between the SO2 column density and particle OD. However, the sensitivity of the instrument can significantly deviate from the linear relationship (i.e., Beer–Lambert approximation) of the optically thick plumes. The larger the particle OD value, the lower the instrument’s sensitivity towards SO2. The slope of the calibration curves also increases with the widening distance between the SO2 camera and the plume. Thus, should be calculated, with and corresponding to each pixel, to bring the coefficients into the calibration curve.
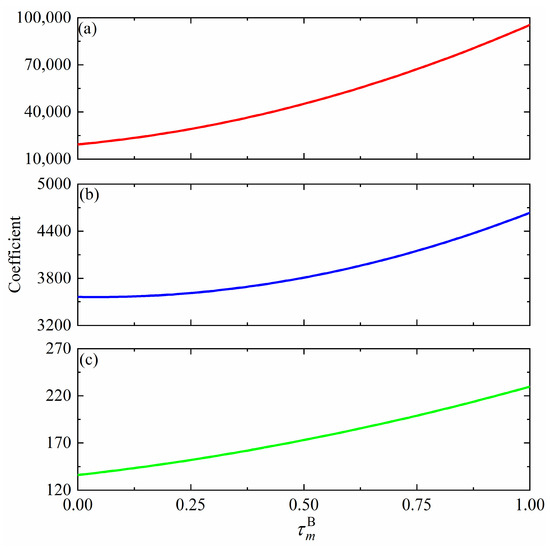
Figure 6.
Functional relationship between and the calibration curve coefficients (a,b) or (c).
5. Inversion
5.1. Column Density Inversion
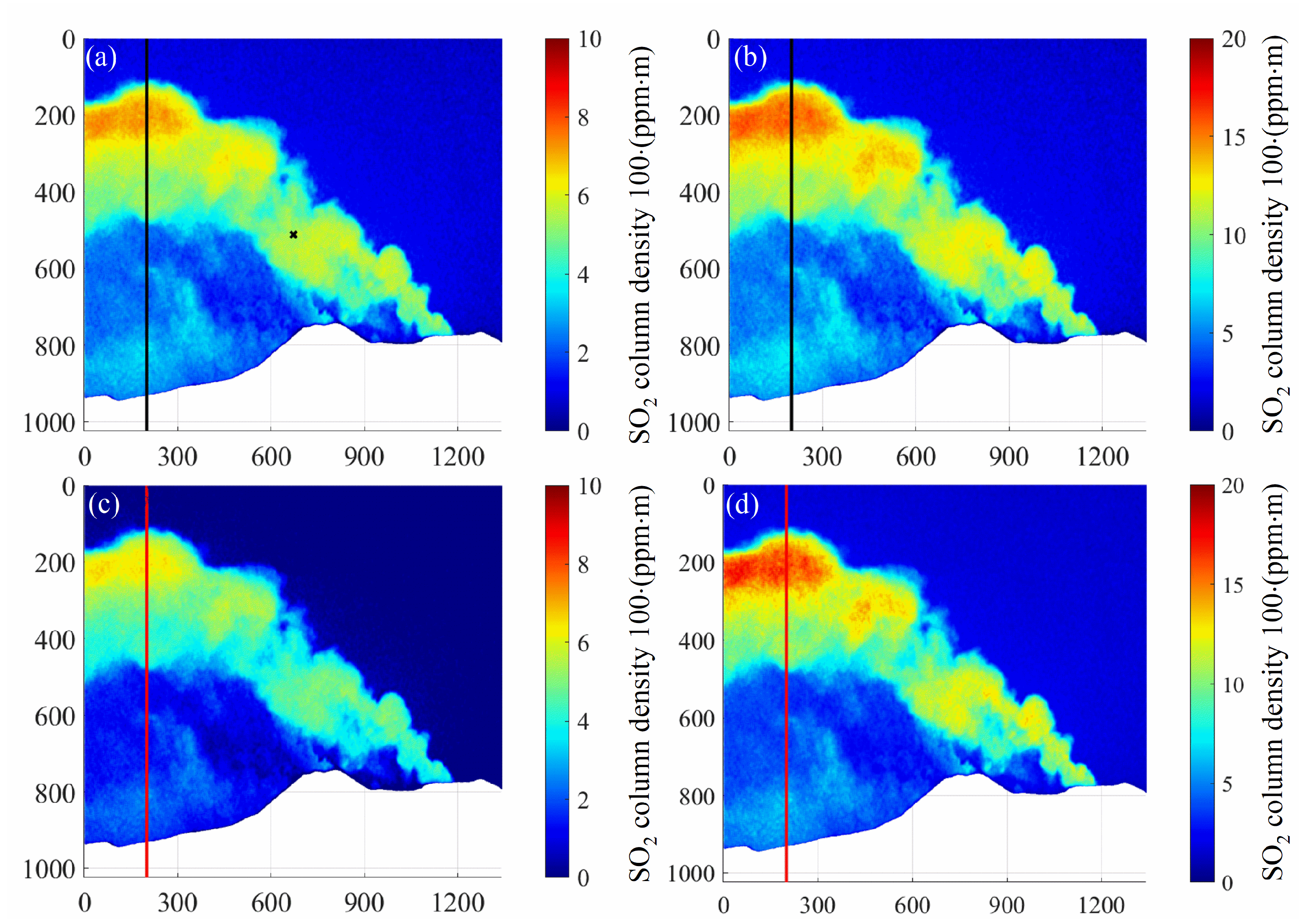
Due to the influence of the light dilution effect and different physical mechanisms, the SO2 column density inversion results with calibration curves obtained from the DOAS and spectral methods will also be different. Figure 7 shows SO2 column density images retrieved by these two calibration methods with and without the light dilution effect. It can be seen that the SO2 column density images retrieved by DOAS (Figure 7a,b) and spectral (Figure 7c,d) calibration methods are consistent on the whole regardless of whether the light dilution effect is considered, which proves the scientificity of the spectral calibration method. Note that the scale range of the column density image corrected by light dilution is twice that of the uncorrected image. In addition, the point calibrated by the DOAS method is located in the center region of the image with the corresponding co-ordinates of (672, 512), as shown by the black cross in Figure 7a.
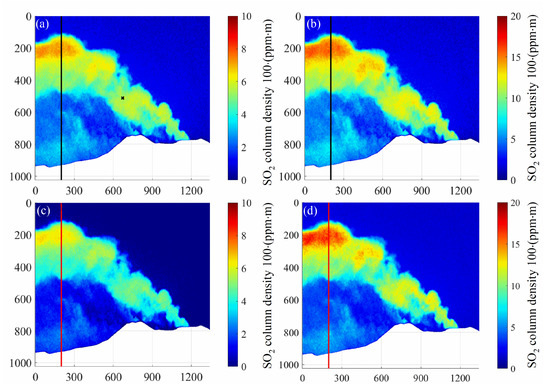
Figure 7.
The SO2 column density image was retrieved by DOAS and spectral calibration methods, and the data used were collected on 16 September 2015 at 7:06:42:37. (a) Uncorrected DOAS calibration; (b) corrected DOAS calibration; (c) uncorrected spectral calibration; (d) corrected spectral calibration.
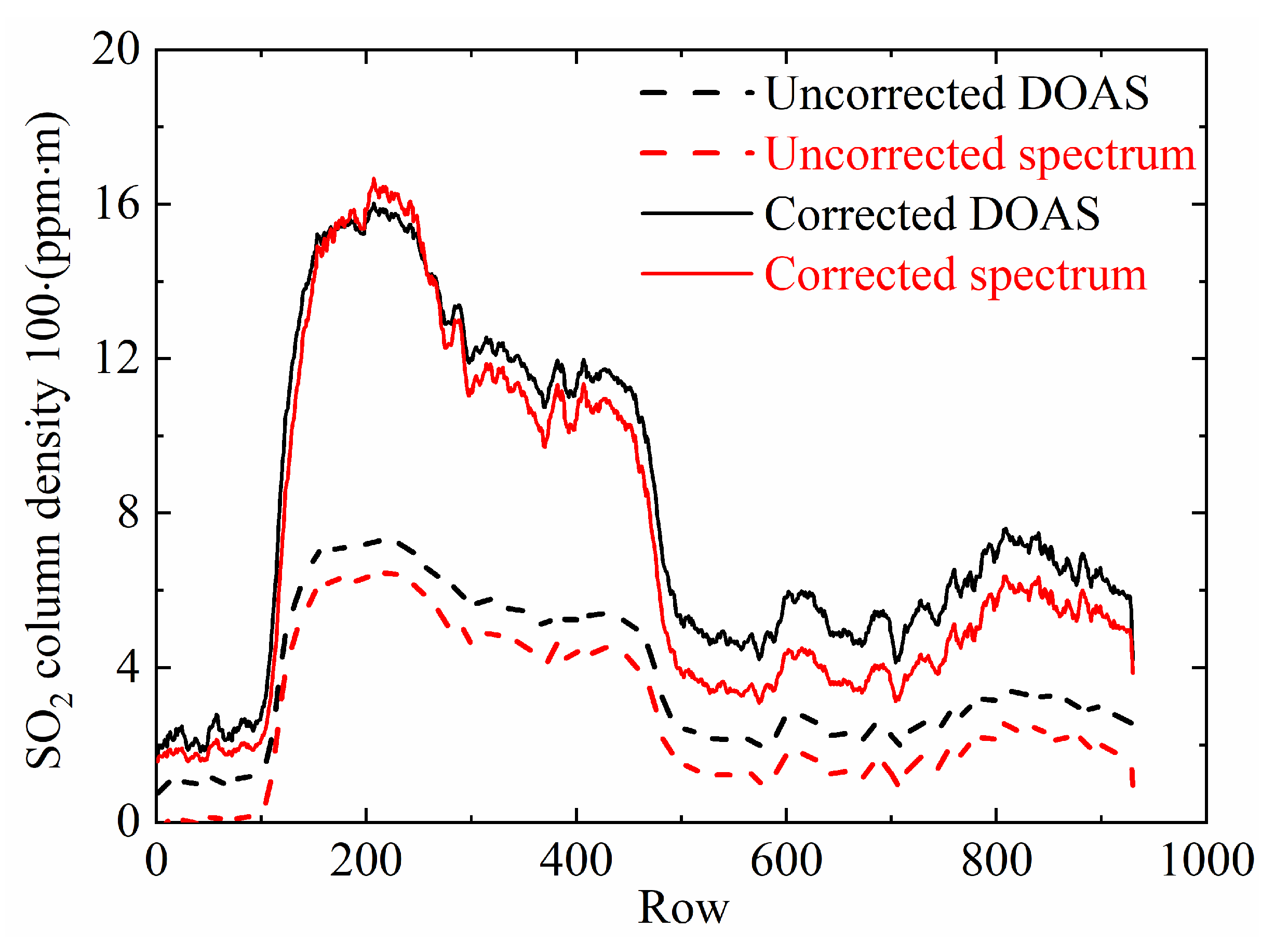
For a more intuitive expression of the difference with the inversion results retrieved by the two calibration methods, the column density values in the same column (200) of the column density images are selected and jointly presented in Figure 8. It is obvious that the inversion results are seriously underestimated without considering the light dilution effect. The result of the DOAS method is underestimated by about 2.2 times, while the underestimate for the spectral method is more obvious by about 2.5 times. Moreover, the column density curves retrieved by the two methods are more consistent under the condition of considering the light dilution effect with an average difference of about 10%. Furthermore, for areas with low particle concentration, their inversion results are in better agreement, with a difference of less than 4%. For values between the 500 and 930th row where aerosol optical thickness is relatively high, the SO2 column density retrieved by the spectral calibration method is slightly lower than that retrieved by DOAS. This is because the spectral calibration method takes the wavelength dependence of particle scattering into account and, therefore, is essentially free of the influence of particulate matter in the plume.
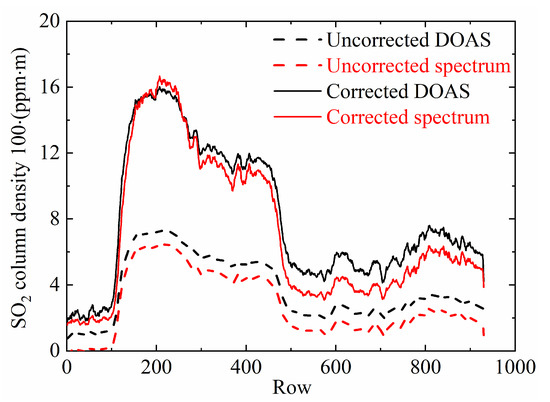
Figure 8.
SO2 column density curves in column 200 of Figure 7.
5.2. Speed Acquisition
The inversion-derived column density images provide an effective visualization of the spatial distribution and temporal evolution of SO2 plume within a two-dimensional domain. However, in practical engineering applications, there is often a greater focus on the variation in SO2 gas emissions over time. Therefore, the column density image of the SO2 plume needs to be converted to the SO2 emission rate with the following equation [33]:
where is the SO2 emission rate of the cross-section, is the focal length of the camera, is the position range of the plume cross-section, is the velocity component in the direction normal to the plume cross-section obtained by the optical flow method, is the distance from the camera to the plume, and is the integration step of the plume cross-section. From Equation (9), it can be seen that the gas velocity of SO2 is another important factor affecting the accurate inversion of SO2 emission rate. Note that the plume cross-section should be selected in the direction normal to the overall motion of the plume.
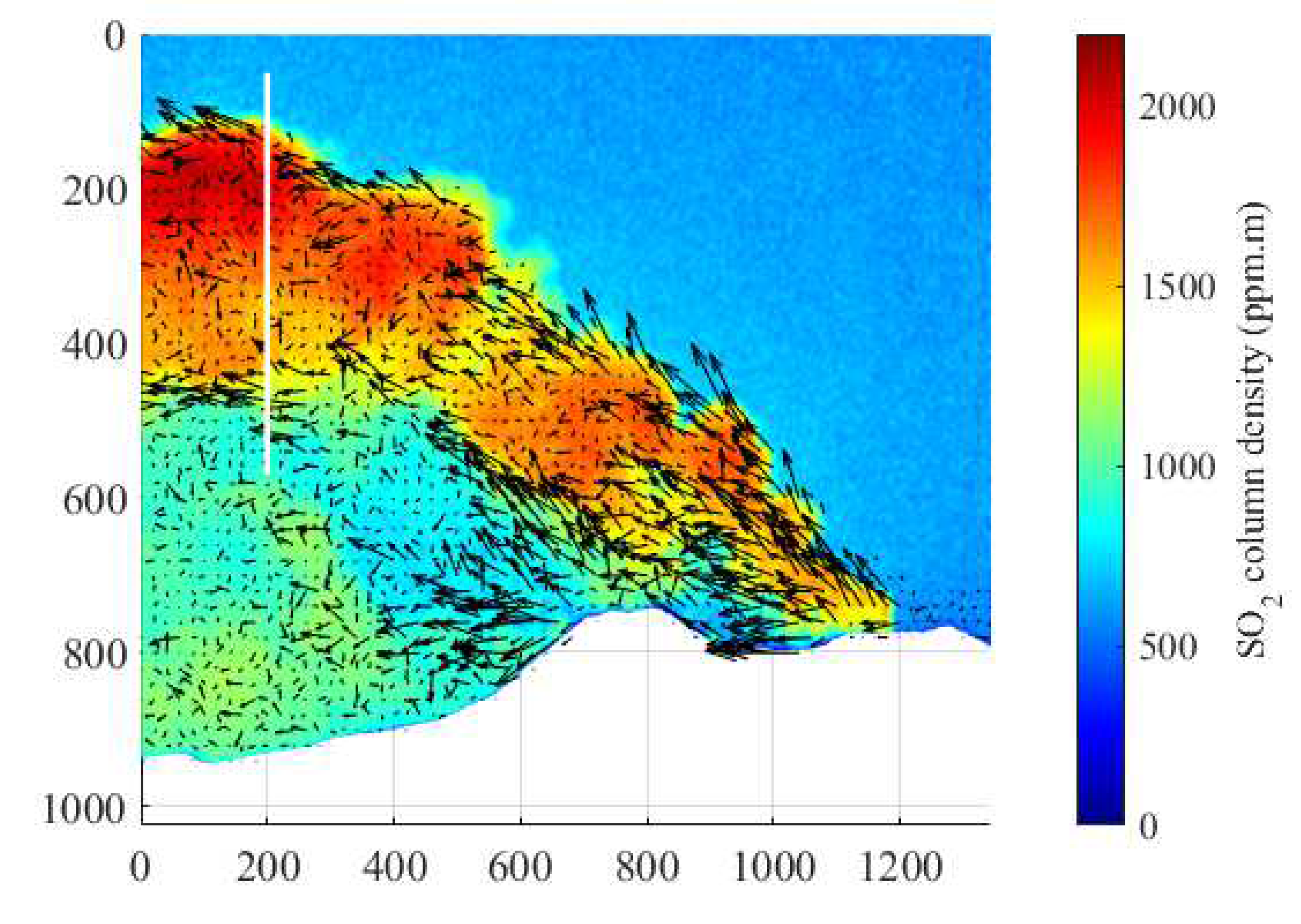
Among the various techniques available to obtain the velocity field of SO2 gas, the optical flow method has emerged as the leading algorithm for estimating gas diffusion motion owing to the notable advantages in computational speed and accuracy. The Farnebäck optical flow method is a pyramidal iterative approach that estimates motion by starting with coarse features and then gradually refining them until the optical flow of each pixel across the entire image is obtained [35]. The Farnebäck optical flow method was shown to be effective in terms of operational speed as well as computational accuracy in the study by Peters et al., 2015 [36], so the Farnebäck optical flow method was next used to estimate the velocity field of SO2 gas. Figure 9 shows the SO2 column density image at 07:07 on 18 September 2015, along with information on the plume velocity calculated using the Farnebäck optical flow method (as depicted by the black arrows). The optical flow method utilizes the OD acquired from the 310 nm band channel to estimate the displacement vector fields; each displacement vector field contains 20 × 20 pixels. The vector length of each display was amplified tenfold to enhance plume motion details.
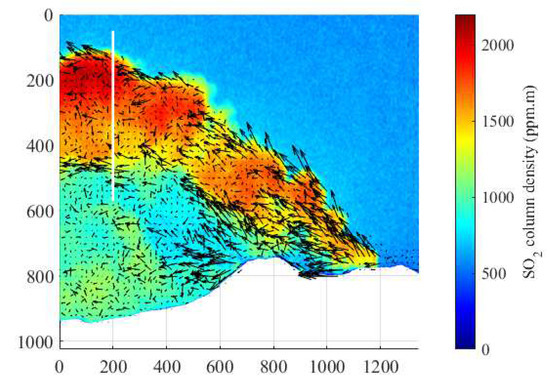
Figure 9.
SO2 column density image and the corresponding optical flow vector field for this column density distribution retrieved from the data at 07:07:18:40 on 16 September 2015, and the white line is the cross-section of the plume, whose two endpoints have the co-ordinates (200, 70) and (200, 570), respectively.
5.3. Emission Rate Inversion
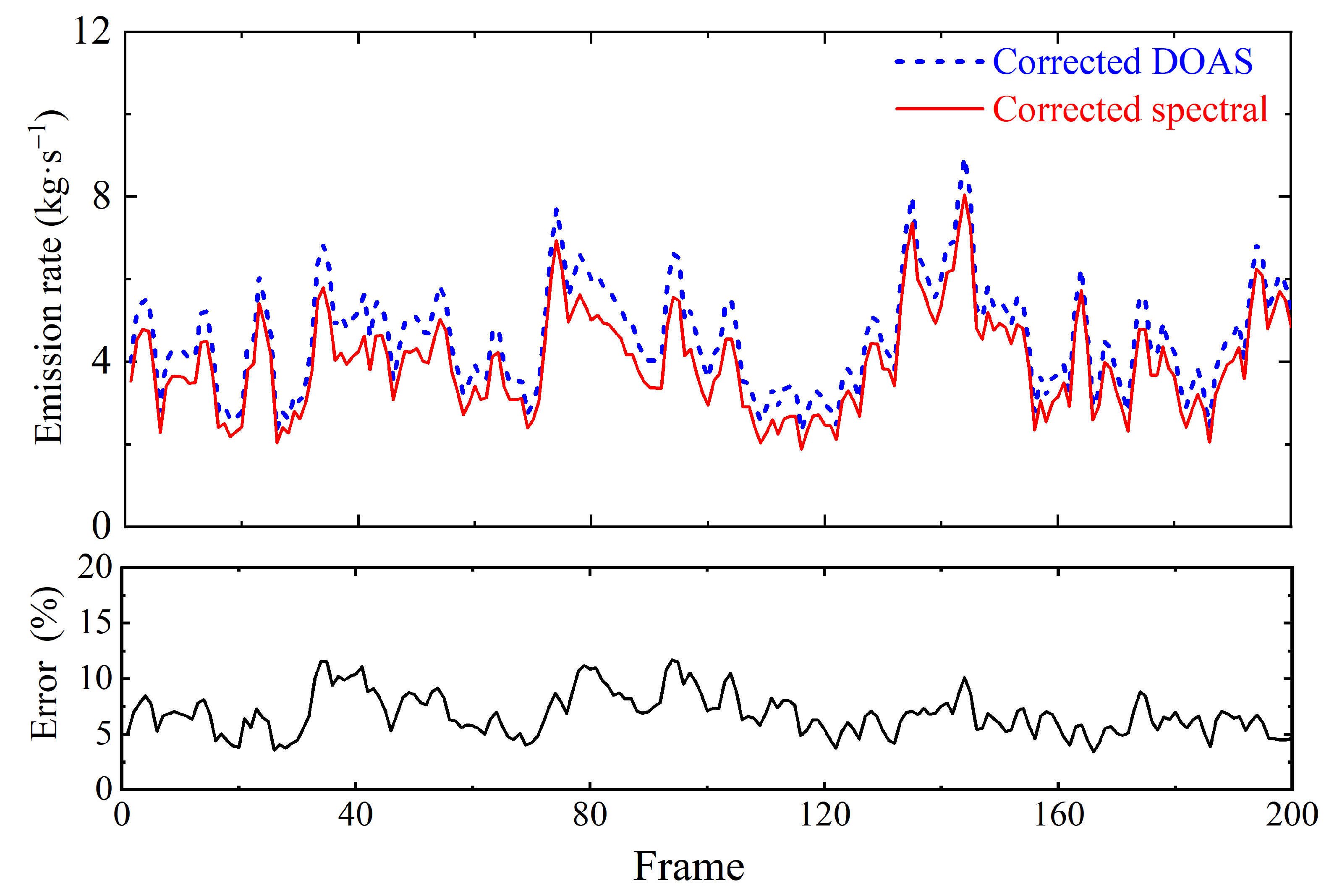
After obtaining the velocity field of SO2 gas, the SO2 emission rate can be determined by inverting Equation (9), combined with the SO2 column density image of Section 5.1 inversions, as shown in Figure 10. Specifically, , , . As depicted in the figure, the SO2 emission rates obtained through the spectral calibration method and the DOAS calibration method are consistent over time, with an error margin of no more than 15%, which provides strong evidence for the scientific validity of the spectral calibration method.
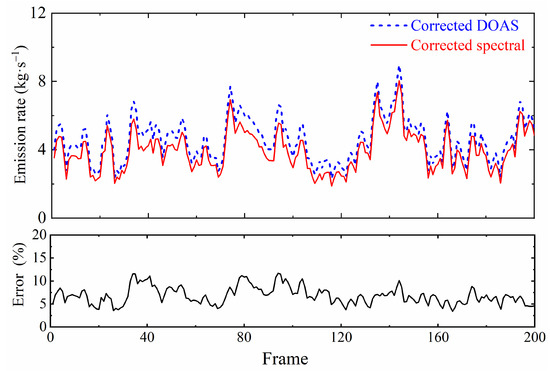
Figure 10.
The 16 September 2015 07:07:18:40 to 07:21:15:24 emission rate inversion results and errors from DOAS and spectral calibration after optical dilution correction.
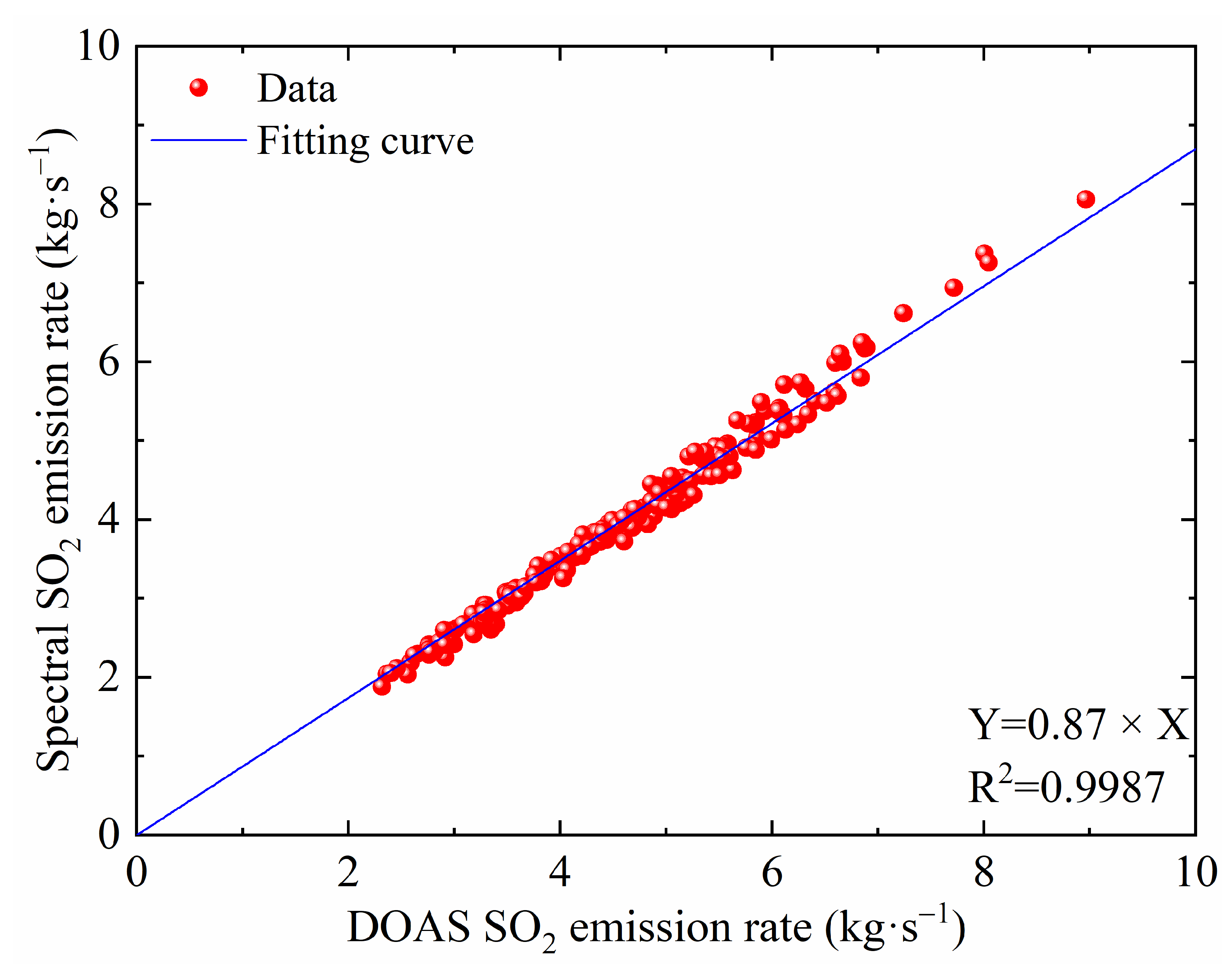
To further illustrate the differences between the two methods, a linear fit will be made to the inversion results of the SO2 emission rates of the two calibration methods. The resulting fitting equation is shown in Figure 11, which reveals that the equation for both methods is Y = 0.87 × X and the R-squared value is 0.9987, demonstrating the feasibility of using spectral calibration. Conversely, the DOAS calibration method produced a fitting coefficient of less than 1 when compared to the spectral calibration method, likely due to OD of the particles, which cannot be effectively corrected using the DOAS approach. In addition, the DOAS calibration method can directly obtain the spectral information, so it can more comprehensively consider the influence of radiation transmission on the measurement results and is, therefore, more effective in eliminating errors caused by the light dilution effect. However, this method suffers from the problem of difficult spatial matching, which leads to systematic errors. The spectral calibration method may be inferior to the DOAS calibration method in eliminating the light dilution effect, though it does not have the problem of systematic errors due to spatial matching. Therefore, some errors are inevitable for the inversion results obtained from these two methods.
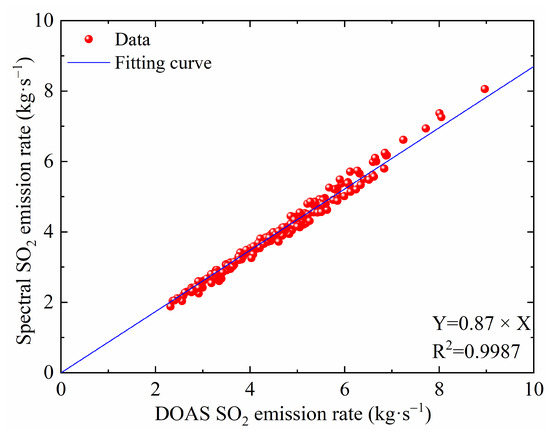
Figure 11.
Fitted curves of emission rates for DOAS and spectral calibration methods.
6. Discussion
In this paper, a spectral calibration method for nonlinear calibration is proposed, focusing on correcting the specific effects of light dilution and aerosol extinction and comparing it with the DOAS calibration method to verify the scientific validity of the spectral calibration method. The comparison of the results of the inversion of the two calibration methods is shown in Figure 10, and it can be seen that there is a relatively good consistency between the two but there is still an error of 13%. The main reasons are analyzed as follows: first, the DOAS calibration method uses a spectrometer to directly measure the SO2 column density within the plume, and the light dilution effect can be well taken into account by modeling multiple scattering. However, the DOAS calibration method requires matching the SO2 column density at a point in the plume measured by the spectrometer with the SO2 OD measured by the SO2 camera at the same spatial location, which usually has the problem of difficult matching and is prone to systematic errors. In contrast, the spectral calibration method is based on a single scattering model to correct for the light dilution effect. Although this effect is slightly underestimated, no difficulty is found in matching the FOV. Thus, it is conceived that the matching accuracy is better than that of the DOAS calibration method. However, there are some errors in the accuracy of the monitoring distance and extinction coefficient during the calculation, which will further have some influence on the spectral calibration method. Meanwhile, the spectral calibration method is based on the assumption that the SO2 OD is a quadratic function of the SO2 column density, which may be invalid when the concentration of carbon black particulate matter in the plume is particularly large [37]. Ultimately, under the combined influence of the above factors, there is a large error in the SO2 emission rate resulting from the inversion using the two calibration methods.
For the dual-channel UV imaging system, the intrinsic factors of the system and the monitoring conditions can also cause errors in the inversion results. When using the SO2 camera for experiments, other light from the atmosphere (especially short-wave ultraviolet and blue light) entering the optical path can cause interference with the quality of the images and, thus, affect the accuracy of the SO2 column density inversion. To better study the distribution and variation of SO2 column density in the smoke plume, filters must be placed to allow only specific wavelengths of light to enter the camera. However, filter placement can significantly affect the accuracy of SO2 inversion, especially at the edges of the image. When the filter is placed behind the lens, undesirable variations in maximum transmittance and central bandpass wavelength at the edge of the image can be greatly reduced. In the following sections, we analyze in detail the effect of differences in quantum efficiency between the two channels and the sensitivity of the off-axis system on SO2 inversion, using filter placement behind the lens as an example.
6.1. Quantum Efficiency
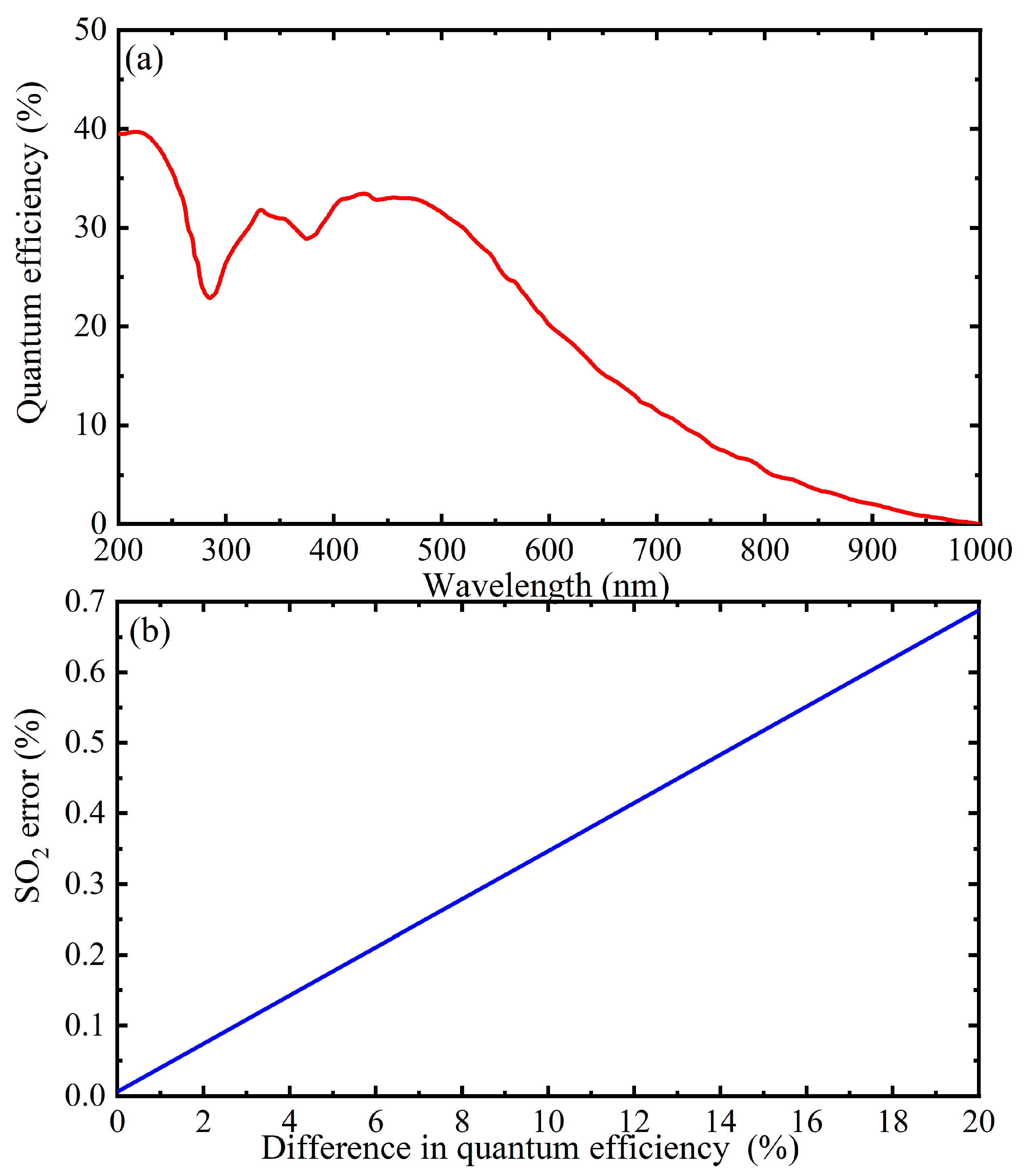
Quantum efficiency refers to the photoelectric conversion efficiency, which is the ratio of the number of photons received by the camera to the actual number of electrons produced. The higher the quantum efficiency, the more effectively the camera can capture smoke plume signals, thus improving the detection sensitivity and measurement accuracy of SO2. The dual-channel UV camera uses two channels with different wavelengths for measurement, which can eliminate some interfering factors in the atmosphere and improve the accuracy of SO2 column density inversion. However, the quantum efficiency of the two channels may not be the same, as shown in the spectral response curve of Figure 12a, where the quantum efficiency varies with wavelength. Therefore, the effect of the quantum efficiency of the two channels must be evaluated and corrected before conducting experiments. The central wavelengths of the filters used in this experiment were 310 and 330 nm, with bandwidths of 10 nm. Figure 12b shows the impact of the difference in quantum efficiency between the two channels on the SO2 inversion error under such conditions, with the error for SO2 inversion results not exceeding 0.7% despite the 20% difference in quantum efficiency between the two channels. In the experiment, the relative difference in the quantum efficiency of the camera used was about 4.5% for the two channels, with the error of the corresponding inversion results for SO2 not exceeding 0.2%, making it negligible.
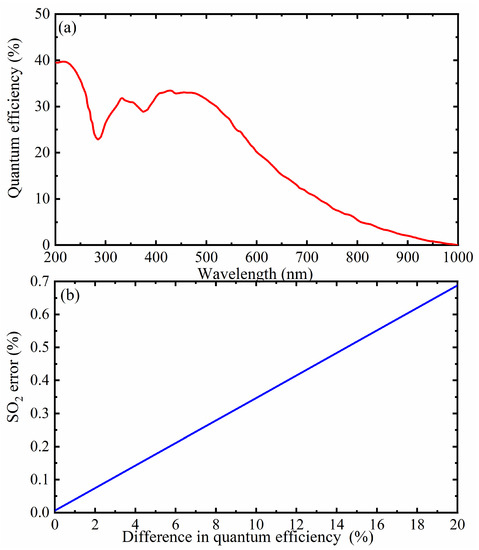
Figure 12.
(a) Spectral response curve; (b) effect of the difference in quantum efficiency on SO2 error.
6.2. Off-Axis System Sensitivity
Off-axis system sensitivity usually refers to the imaging quality sensitivity at a point off the optical axis in an optical system due to system errors. At the off-axis point, the light is no longer perpendicular to the optical axis, causing the angle of optical incidence on the filter to shift, thus changing the effective transmittance and central wavelength of the filter, which will affect the SO2 UV camera sensitivity.
Although, ideally, all light is incident vertically, this condition is not always satisfied in an optical imaging system. As a result, the effective transmittance of the filter is not consistent with the manufacturer’s specifications, and the effect of the angle of incidence of the light needs to be considered. The effective bandpass center can be expressed as [20]:
where is the air refractive index, is the filter refractive index, and is the angle of incidence. When the angle of incidence increases, the effective bandpass center decreases, i.e., it is shifted toward the short-wave direction.
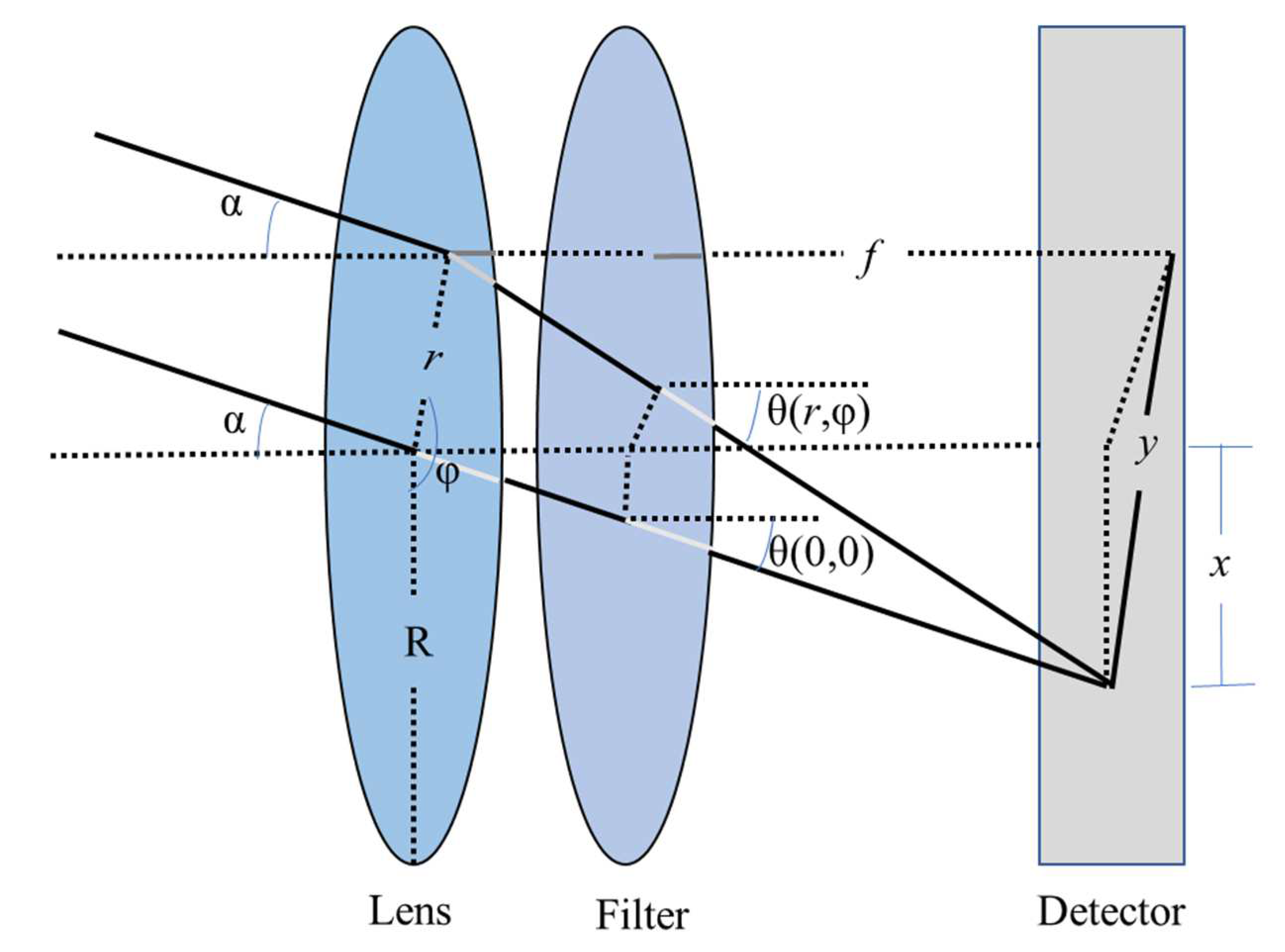
In the experiment, the filter is positioned behind the lens as shown in Figure 13. This practice converges the light passing through the lens on the filter to effectively reduce undesirable variations at the edges of the image. Nevertheless, the angle of incidence may still impact the central wavelength, effective transmission bandwidth, and transmittance of the filter, even when placed behind the lens. Therefore, a thorough examination of these effects is necessary to pinpoint potential error sources in the inversion of SO2.
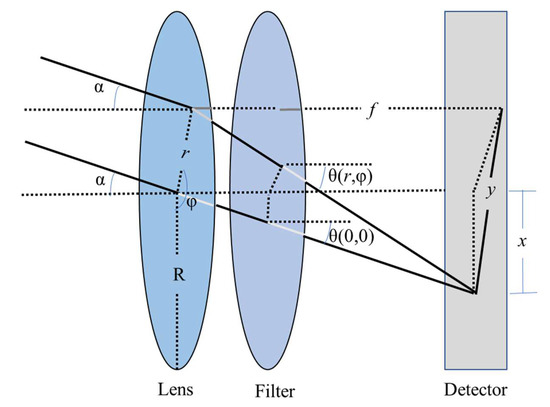
Figure 13.
Schematic diagram of the UV imaging system with the filter placed behind the lens.
When the filter is placed behind the lens, in order to specifically obtain the effective transmittance of the device, the angle of incidence can be expressed in terms of the position where the light intersects with the lens, using polar co-ordinates in the form of the filter mark and finding the angle of incidence ; at this point, is:
where r is the distance from the light shining on the filter to the center of the filter, is the direction relative to the x, is the viewing angle, and is the magnification.
The effective transmittance of the device is obtained by integrating the maximum transmittance of the filter , the Gaussian bell curve G over the effective aperture radius R, and all relative directions .
where is the normalization factor and is the nominal maximum transmittance.
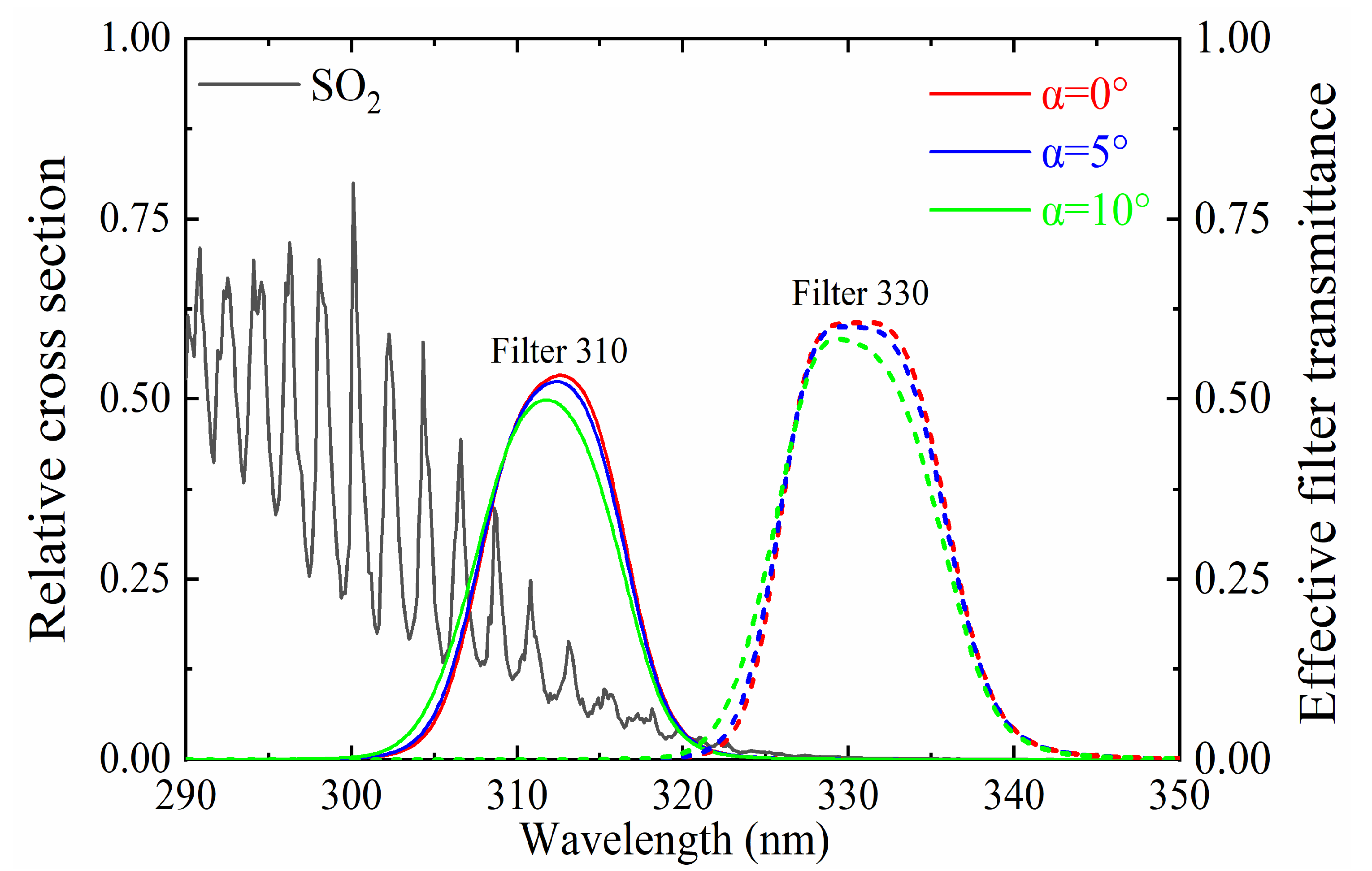
Figure 14 illustrates the relative absorption cross-section of SO2 in the presence of a filter placed behind the lens, along with the effective transmittance curves of the two channels at viewing angles of 0°, 5°, and 10°. As shown in the figure, the transmittance of the filter reaches its maximum value within its designated wavelength range, with a rapid decrease observed outside this range. Furthermore, the angle of incidence affects the transmittance of the filter. When the light is not incident vertically, the actual transmittance deviates from the standard curve provided by the manufacturer, and the effective bandpass center also shifts. At normal incidence, the transmittance of the effective bandpass center is highest and exerts minimal impact on the overall transmittance. However, as the angle of incidence varies, the effect of the effective bandpass center on transmittance increases, with effective bandpass center moving towards shorter wavelengths.
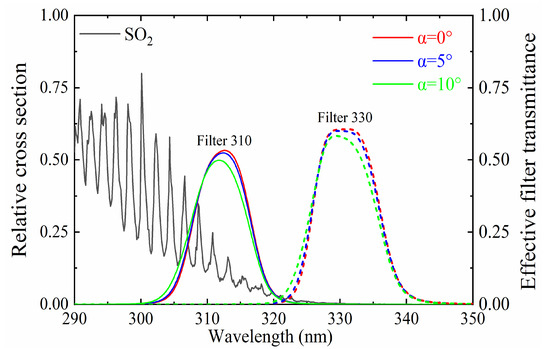
Figure 14.
SO2 relative absorption cross-section; effective transmittance curves at 0°, 5°, and 10° with the filter placed behind the lens.
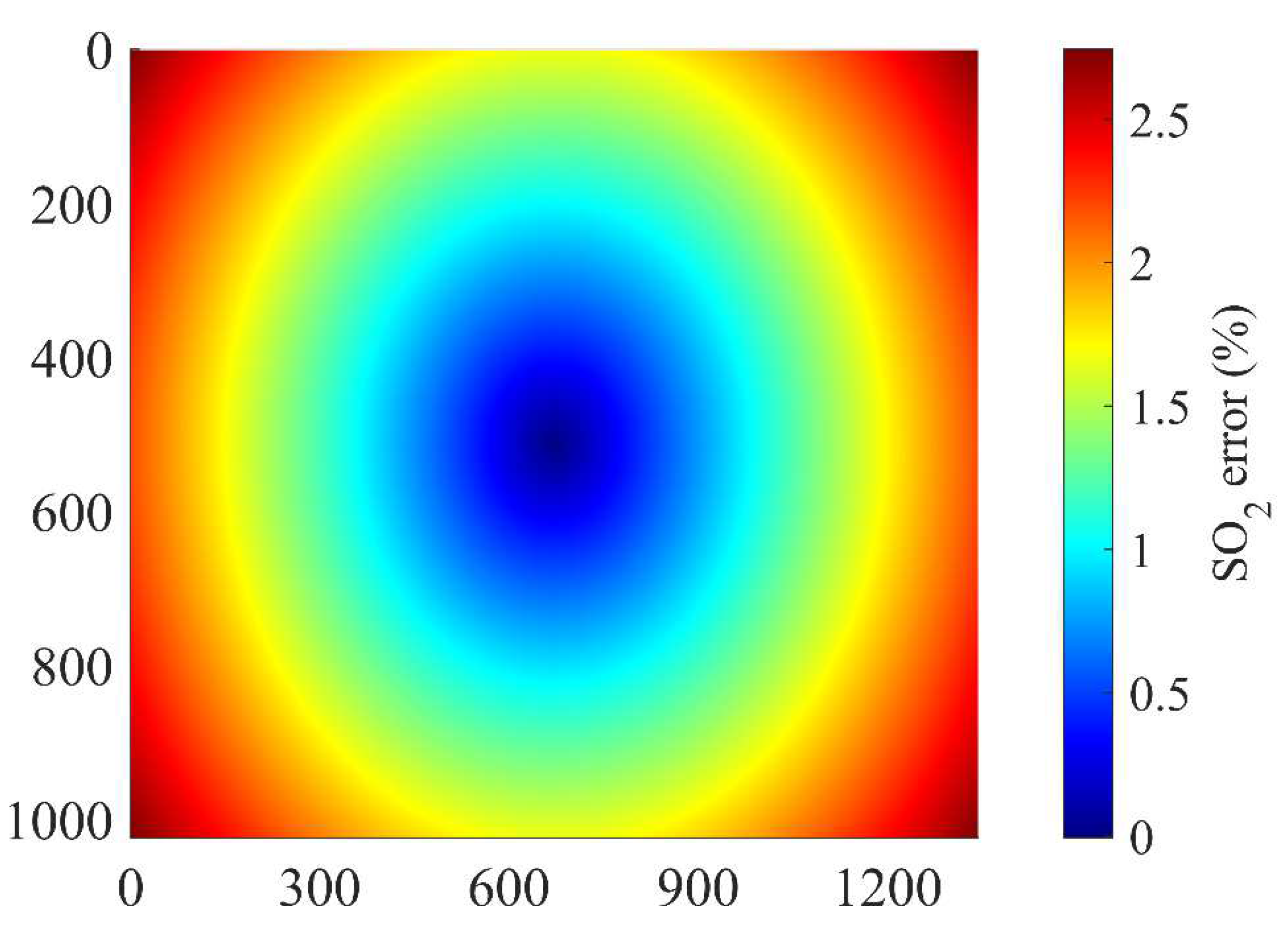
Variations in maximum transmittance and effective bandpass center can have a significant impact on the experimental outcomes. Increasing viewing angles lead to a gradual reduction in maximum transmittance, which, in turn, decreases the signal-to-noise ratio at the detector edge. Additionally, the effective bandpass center shifts towards shorter wavelengths, altering the system sensitivity to SO2 and ultimately influencing the inversion results. Given that both factors are influenced by variations in angle of incidence resulting from converging light through the lens, changes in viewing angle can serve as an indicator of SO2 sensitivity. With the filter placed behind the lens and the center wavelength of 310 and 330 nm, respectively, the SO2 error with the change in view angle is shown in Figure 15. The figure shows that the impact on SO2 inversion is minimal at the center of the camera’s sensing surface due to near-vertical incidence, but the error gradually increases with increasing viewing angles. However, even at the image edge, where the error reaches 3%, it remains within acceptable limits.
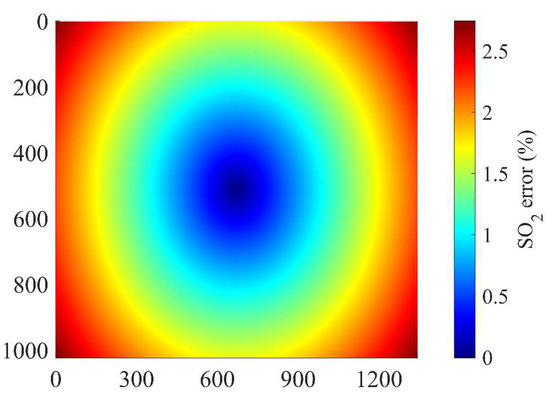
Figure 15.
SO2 inversion errors at different viewing angles.
7. Conclusions
This study introduces the dual-channel SO2 UV camera and its application to volcanoes, illustrates the working principle of obtaining SO2 column density images, analyzes the light dilution effect on SO2 column density inversion, and focuses on the physical mechanism and implementation method of the new spectral calibration method. Moreover, on the basis of the DOAS and the new spectral calibration methods, the SO2 column density images are retrieved. The comparative analysis demonstrates the great advantages of the new calibration method in ensuring accuracy and operability, especially for long-distance detection.
Then, after introducing the working principle of the dual-channel SO2 UV camera and the spectral characteristics of SO2 absorption cross-section and solar-radiation scattering in the atmosphere, the reasons for selecting the 310 and 330 nm bands are clarified. On the basis of the realistic radiative transfer, the SO2 OD of the Etna volcanic plume is obtained. By analyzing the principles of the DOAS calibration method, this study expounds the reasons why the calibration method gives misleading results in SO2 remote monitoring. On the premise of synthetically accounting for the influences on camera sensitivity and calibration curves due to the light dilution effect and wavelength dependence of particle scattering, a new spectral calibration method is proposed. This method takes into account the underestimate of the inversion result caused by the nonparaxial effect of the filters and can achieve personalized real-time calibration for each pixel of the camera systems. Furthermore, the reason why the calibration curve obtained by this new method presents nonlinear characteristics is also highlighted. A quadratic function relationship exists between the calibration coefficient and the particle OD. The instrument sensitivity towards SO2 decreases significantly with increase in particle OD. The comparison between the SO2 images retrieved by the two calibration curves suggests that the new calibration method is more rigorous and scientific than the DOAS method. Moreover, its superiority becomes more obvious for long-distance detection of optically thick plumes. In addition, compared with the DOAS calibration approach, the inversion error of the emission rate can be reduced by 14% if the spectral calibration is adopted due to the fact that the new method is essentially free of the influence of particulate matter in the plume.
Despite the major advantages of the new calibration method, its novelty necessarily means that many algorithmic and instrumental problems remain unresolved. For instance, aerosol scattering and absorption are difficult to accurately distinguish in practical settings, and the calibration errors caused by light-absorbing aerosols are extremely hard to predict or estimate. The general impact of aerosol absorption on camera sensitivity reduces the average penetration depth of solar radiation scattering that passes through the plume. In addition, the effects of atmospheric visibility and thick clouds will lead to a much larger uncertainty in SO2 column density inversion. Therefore, more sophisticated approaches must be proposed to confidently calibrate SO2 cameras with higher accuracy.
This study unequivocally shows that explicit treatment of radiative transfer plays a crucial role in improving calibration accuracy. The spectral calibration method proposed in this study solves the technical problem of accurate calibration of SO2 UV cameras and has been well applied in remote monitoring of volcanic eruptions. Hopefully, this calibration method will also show great application prospects in the remote sensing monitoring of industrial chimney and ship exhaust.
Author Contributions
Conceptualization, K.W., J.G. and W.H.; methodology, K.W. and W.H.; software, J.G. and Z.Z.; validation, J.G., Z.Z. and H.Z.; formal analysis, J.L.; investigation, H.Z.; resources, W.H.; data curation, F.L.; writing—original draft preparation, K.W., J.G. and W.H.; writing—review and editing, K.W.; visualization, J.L. and F.L.; supervision, Z.Z.; project administration, W.H.; funding acquisition, K.W. and W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 41975039 and 61705253, the National Key R&D Program of China, grant number 2017YFC0211900, the Natural Science Foundation of Shandong Province, grant number ZR2021QD088, the Youth Innovation Technology Project of Higher School in Shandong Province, grant number 2021KJ008, and the Graduate Innovation Foundation of Yantai University, grant number GGIFYTU2313.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Jonas Gliß of the Norwegian Air Research Institute for providing the original image data of the Etna volcanic plume collected by the SO2 UV camera.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, B.; Fu, A.; Yao, Z.; Qu, F.; Man, T. SO2 Column density retrieval algorithm using EMD and PCA with application in CEMS based on UV-DOAS. Optik 2018, 158, 273–282. [Google Scholar] [CrossRef]
- Anand, A.; Wei, P.; Gali, N.K.; Sun, L.; Yang, F.; Westerdahl, D.; Zhang, Q.; Deng, Z.; Wang, Y.; Liu, D.; et al. Protocol development for real-time ship fuel sulfur content determination using drone based plume sniffing microsensor system. Sci. Total Environ. 2020, 744, 140885. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.; Kinne, J.; Lautenbach, S.; Blaschke, T.; Lenz, D.; Resch, B. Greenwashing in the US metal industry? A novel approach combining SO2 column densitys from satellite data, a plant-level firm database and web text mining. Sci. Total Environ. 2022, 835, 155512. [Google Scholar] [CrossRef] [PubMed]
- Krotkov, N.; Realmuto, V.; Li, C.; Seftor, C.; Li, J.; Brentzel, K.; Stuefer, M.; Cable, J.; Dierking, C.; Delamere, J.; et al. Day–Night Monitoring of Volcanic SO2 and Ash Clouds for Aviation Avoidance at Northern Polar Latitudes. Remote Sens. 2021, 13, 4003. [Google Scholar] [CrossRef]
- Elias, T.; Kern, C.; Horton, K.A.; Sutton, A.J.; Garbeil, H. Measuring SO2 Emission Rates at Kīlauea Volcano, Hawaii, Using an Array of Upward-Looking UV Spectrometers, 2014–2017. Front. Earth Sci. 2018, 6, 214. [Google Scholar] [CrossRef]
- Costa, A.; Suzuki, Y.J.; Koyaguchi, T. Understanding the plume dynamics of explosive super-eruptions. Nat. Commun. 2018, 9, 654. [Google Scholar] [CrossRef]
- Lierenfeld, M.B.; Zajacz, Z.; Bachmann, O.; Ulmer, P. Sulfur diffusion in dacitic melt at various oxidation states: Implications for volcanic degassing. Geochim. Et Cosmochim. Acta 2018, 226, 50–68. [Google Scholar] [CrossRef]
- Shreve, T.; Grandin, R.; Boichu, M.; Garaebiti, E.; Moussallam, Y.; Ballu, V.; Delgado, F.; Leclerc, F.; Vallée, M.; Henriot, N.; et al. From prodigious volcanic degassing to caldera subsidence and quiescence at Ambrym (Vanuatu): The influence of regional tectonics. Sci. Rep. 2019, 9, 18868. [Google Scholar] [CrossRef]
- Szakács, A.; Pécskay, Z.; Gál, Á. Patterns and trends of time–space evolution of Neogene volcanism in the Carpathian–Pannonian region: A review. Acta. Geod. Geophys. 2018, 53, 347–367. [Google Scholar] [CrossRef]
- Roberts, T.; Dayma, G.; Oppenheimer, C. Reaction Rates Control High-Temperature Chemistry of Volcanic Gases in Air. Front. Earth Sci. 2019, 7, 154. [Google Scholar] [CrossRef]
- Liu, Y.; Pellikka, P.K.E.; Li, H.; Fang, X. Detection of the dispersion and residence of volcanic SO2 and sulfate aerosol from Nabro in 2011. Atmos. Environ. 2019, 197, 36–44. [Google Scholar] [CrossRef]
- Seyler, A.; Wittrock, F.; Kattner, L.; Mathieu-Üffing, B.; Peters, E.; Richter, A.; Schmolke, S.; Burrows, J. Monitoring shipping emissions in the German Bight using MAX-DOAS measurements. Atmos. Chem. Phys. 2017, 17, 10997–11023. [Google Scholar] [CrossRef]
- Huret, N.; Segonne, C.; Payan, S.; Salerno, G.; Catoire, V.; Ferrec, Y.; Roberts, T.; Fossi, A.P.; Rodriguez, D.; Croizé, L.; et al. Infrared Hyperspectral and Ultraviolet Remote Measurements of Volcanic Gas Plume at MT Etna during IMAGETNA Campaign. Remote Sens. 2019, 11, 1175. [Google Scholar] [CrossRef]
- Wood, K.; Thomas, H.; Watson, M.; Calway, A.; Richardson, T.; Stebel, K.; Naismith, A.; Berthoud, L.; Lucas, J. Measurement of three dimensional volcanic plume properties using multiple ground based infrared cameras. ISPRS J. Photogramm. Remote Sens. 2019, 154, 163–175. [Google Scholar] [CrossRef]
- Somekawa, T.; Ichikawa, Y.; Ogita, M.; Sugimoto, S.; Chosrowjan, H.; Taniguchi, S.; Asahi, I. Flash resonance Raman lidar for SO2 gas leak detection. Opt. Commun. 2022, 513, 128083. [Google Scholar] [CrossRef]
- Wu, K.; Xiong, Y.; Feng, Y.; Yu, Y.; Li, F. Development of a self-calibration method for real-time monitoring of SO2 ship emissions with UV cameras. Opt. Express 2021, 29, 1813–1823. [Google Scholar] [CrossRef]
- Bluth, G.J.S.; Shannon, J.M.; Watson, I.M.; Prata, A.J.; Realmuto, V.J. Development of an ultraviolet digital camera for volcanic SO2 imaging. J. Volcanol. Geoth. Res. 2007, 161, 47–56. [Google Scholar] [CrossRef]
- Mori, T.; Burton, M. The SO2 camera: A simple, fast and cheap method for ground-based imaging of SO2 in volcanic plumes. Geophys. Res. Lett. 2006, 33, L17315. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, Z.; Li, Y.; Zheng, Y.; Xie, M. Ship fuel sulfur content prediction based on convolutional neural network and ultraviolet camera images. Environ. Pollut. 2021, 273, 116501. [Google Scholar] [CrossRef]
- Kern, C.; Werner, C.; Elias, T.; Sutton, A.J.; Lübcke, P. Applying UV cameras for SO2 detection to distant or optically thick volcanic plumes. J. Volcanol. Geoth. Res. 2013, 262, 80–89. [Google Scholar] [CrossRef]
- Pering, T.D.; Liu, E.; Wood, K.; Wilkes, T.; Aiuppa, A.; Tamburello, G.; Bitetto, M.; Richardson, T.; McGonigle, A. Combined ground and aerial measurements resolve vent-specific gas fluxes from a multi-vent volcano. Nat. Commun. 2020, 11, 3039. [Google Scholar] [CrossRef] [PubMed]
- Thomas, H.E.; Prata, A.J. Computer vision for improved estimates of SO2 emission rates and plume dynamics. Int. J. Remote Sens. 2018, 39, 1285–1305. [Google Scholar] [CrossRef]
- Varnam, M.; Burton, M.; Esse, B.; Salerno, G.; Kazahaya, R.; Ibarra, M. Two Independent Light Dilution Corrections for the SO2 Camera Retrieve Comparable Emission Rates at Masaya Volcano, Nicaragua. Remote Sens. 2021, 13, 935. [Google Scholar] [CrossRef]
- Gliß, J.; Stebel, K.; Kylling, A.; Dinger, A.S.; Sihler, H.; Sudbø, A. Pyplis—A Python software toolbox for the analysis of SO2 camera images for emission rate retrievals from point sources. Geosciences 2017, 7, 134. [Google Scholar] [CrossRef]
- Gutmann, A.; Bobrowski, N.; Liotta, M.; Hoffmann, T. Bromine speciation in volcanic plumes: New in situ derivatization LC-MS method for the determination of gaseous hydrogen bromide by gas diffusion denuder sampling. Atmos. Meas. Tech. 2021, 14, 6395–6406. [Google Scholar] [CrossRef]
- Schiavo, B.; Stremme, W.; Grutter, M.; Campion, R.; Guarin, C.A.; Rivera, C.; Inguaggiato, S. Characterization of a UV camera system for SO2 measurements from Popocatépetl Volcano. J. Volcanol. Geoth. Res. 2021, 370, 82–94. [Google Scholar] [CrossRef]
- He, L.; Wu, H.; Li, J.; Li, B.; Sun, Y.; Jiang, P.; Wang, X.; Lin, G. Solid Particle Swarm Measurement in Jet Fuel Based on Mie Scattering Theory and Extinction Method. Sensors 2023, 23, 2837. [Google Scholar] [CrossRef]
- Mei, L.; Somesfalean, G.; Svanberg, S. Pathlength Determination for Gas in Scattering Media Absorption Spectroscopy. Sensors 2014, 14, 3871–3890. [Google Scholar] [CrossRef]
- Ilanko, T.; Pering, T.D.; Wilkes, T.; Woitischek, J.; D’Aleo, R.; Aiuppa, A.; McGonigle, A.; Edmonds, M.; Garaebiti, E. Ultraviolet Camera Measurements of Passive and Explosive (Strombolian) Sulphur Dioxide Emissions at Yasur Volcano, Vanuatu. Remote Sens. 2020, 12, 2703. [Google Scholar] [CrossRef]
- Prata, F. Measuring SO2 ship emissions with an ultraviolet imaging camera. Atmos. Meas. Tech. 2014, 7, 1213–1229. [Google Scholar] [CrossRef]
- Lübcke, P.; Bobrowski, N.; Illing, S.; Kern, C.; Nieves, J.; Vogel, L.; Zielcke, J.; Delgado Granados, H.; Platt, U. On the absolute calibration of SO2 cameras. Atmos. Meas. Tech. 2012, 5, 6183–6240. [Google Scholar] [CrossRef]
- Wu, K.; Feng, Y.; Xiong, Y.; Duan, W.; Yu, G.; Li, F. Real-time continuous calibration method for an ultraviolet camera. Opt. Lett. 2020, 45, 6851–6854. [Google Scholar] [CrossRef]
- Gliß, J.; Stebel, K.; Kylling, A.; Sudbø, A. Improved optical flow velocity analysis in SO2 camera images of volcanic plumes–implications for emission-rate retrievals investigated at Mt Etna, Italy and Guallatiri, Chile. Atmos. Meas. Tech. 2018, 11, 781–801. [Google Scholar] [CrossRef]
- Ostrikov, V.; Plakhotnikov, O.; Kirienko, A. Estimation of Spectral Resolution of Imaging Spectrometers from Fraunhofer Lines with the MODTRAN Atmospheric Model. Atmos. Ocean. Opt. 2019, 32, 622–627. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Application of Local Optical Flow Methods to High-Velocity Free-surface Flows: Validation and Application to Stepped Chutes. Exp. Therm. Fluid Sci. 2018, 90, 186–199. [Google Scholar] [CrossRef]
- Peters, N.; Hoffmann, A.; Barnie, T.; Herzog, M.; Oppenheimer, C. Use of motion estimation algorithms for improved flux measurements using SO2 cameras. J. Volcanol. Geoth. Res. 2015, 300, 58–69. [Google Scholar] [CrossRef]
- Shao, L.; Wang, S.; Tang, G.; Xu, C. Influence of Particle Mie Scattering on Differential Optical Absorption Spectroscopy. Acta Opt. Sin. 2009, 29, 594. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).