Analysis of the Results Determining the Positions and Velocities of Satellite Laser Ranging Stations during Earthquakes in 2010–2011
Abstract
:1. Introduction
2. Materials and Methods
2.1. Determining the Distance to Satellites
2.2. Position of the SLR Station
2.3. Velocity of the SLR Station
3. Network of the SLR Stations for the Period 2008–2013
4. Results
4.1. Selection of SLR Stations
- I.
- Number of normal points (N) of a given SLR station per one monthly arc of the orbit and covering the total observation of the LAGEOS-1 and LAGEOS-2 satellites for the entire observation period;
- II.
- Observation period (Δ) for the SLR station data that must be contained in the range of not less than 3–5 years due to increasing errors in determining the velocity of the SLR station for shorter periods;
- III.
- Stability of the determined coordinates (Equation (10)) in the absence of earthquakes is the best parameter to assess the accuracy of the observations of a given station.
- Geocentric X, Y, Z and topocentric N, E, U [21] station coordinates for the reference epoch 2005.0 taking into account the velocity in the ITRF 2008—detrended data;
- Geocentric X, Y, Z and topocentric N, E, U station coordinates for reference epoch of each arc (first day of each month)—trended data;
- Standard deviations of the determined station coordinates;
- Stability (RMS) of designated X, Y, Z and N, E, U coordinates (9, 10);
- Total standard deviation (3D) of the coordinates (σ);
- Position uncertainty, i.e., error bars (3σ) resulting from the T-Student distribution;
- Number of normal points for each arc, separately for LEGEOS-1 and LAGEOS-2 satellites;
- Range bias for each arc, separately for LEGEOS-1 and LAGEOS-2 satellites;
- Orbital RMS for each arc, separately for LEGEOS-1 and LAGEOS-2 satellites;
- The number of RMS normal points for each arc for all the core stations;
- Orbital RMS for each arc for all the core stations.
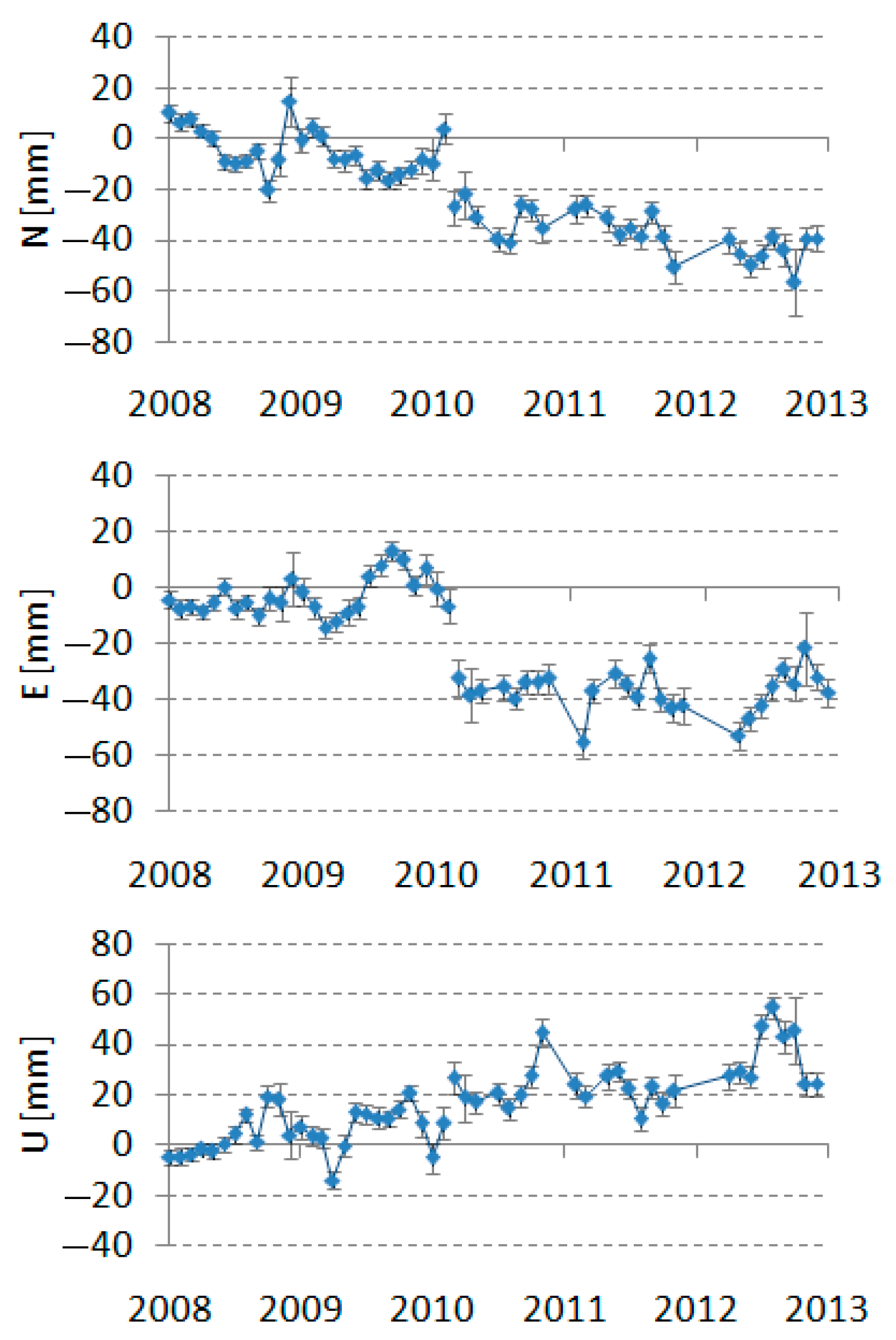
4.2. Station Position Changes
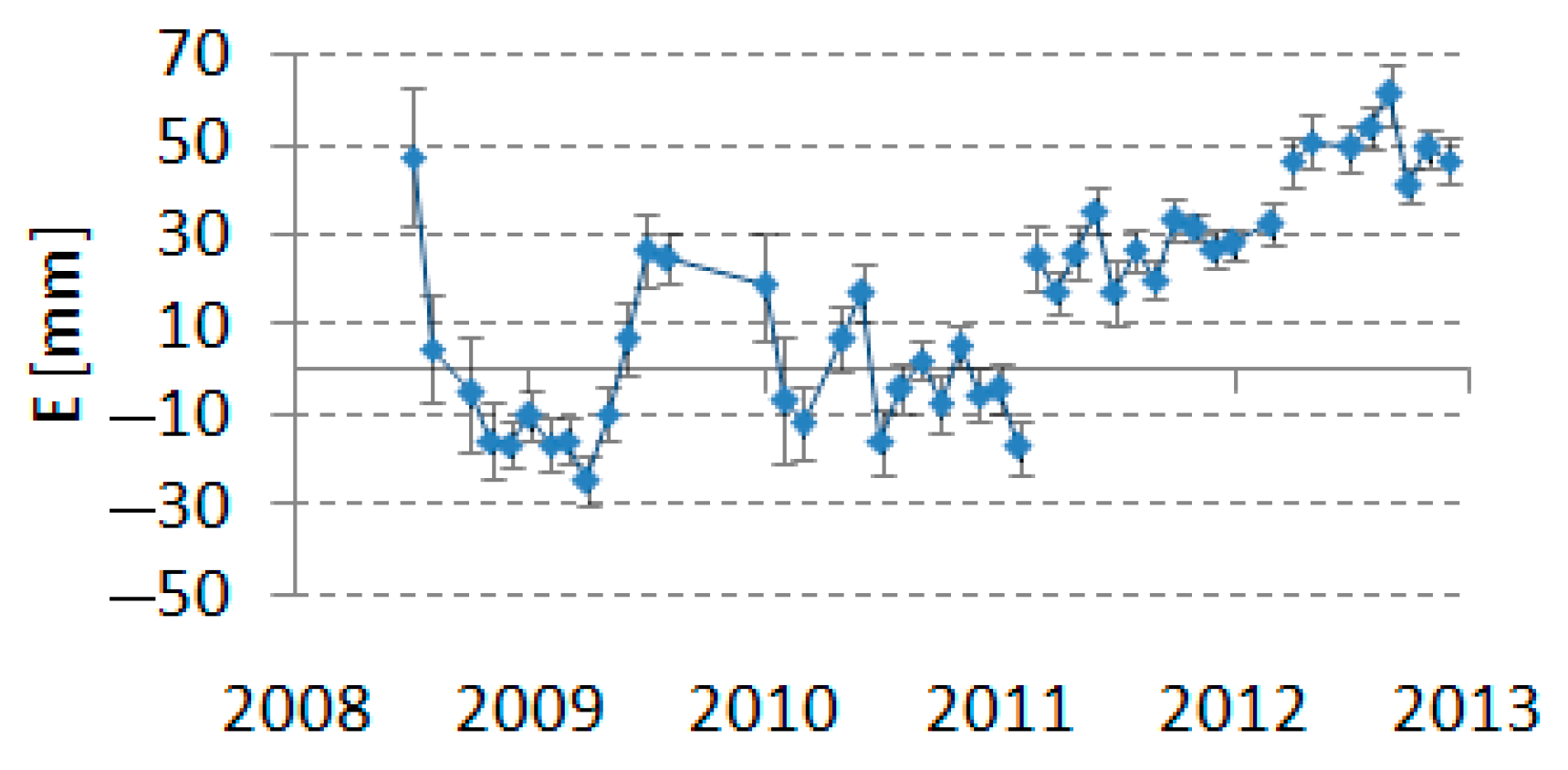
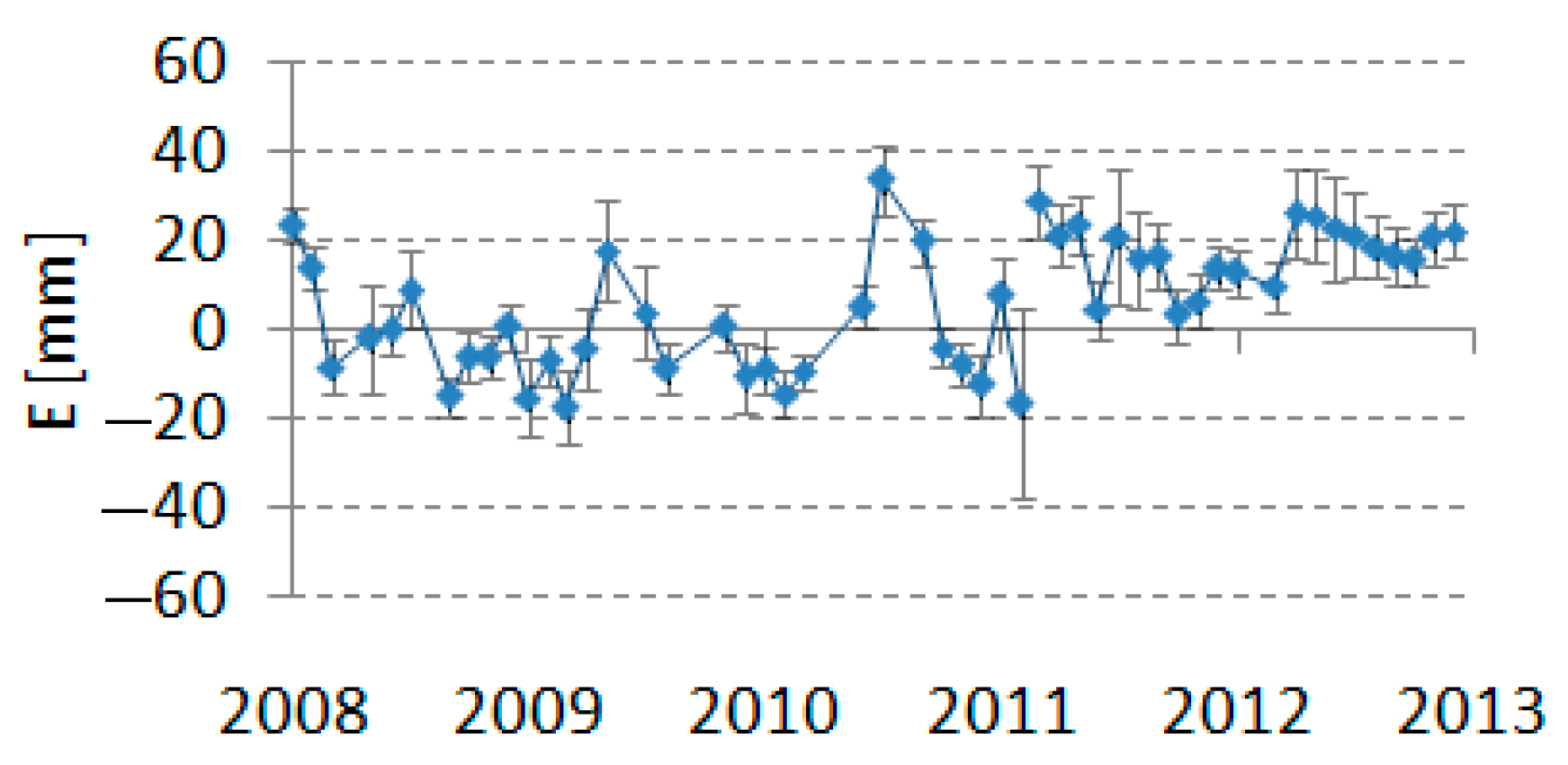
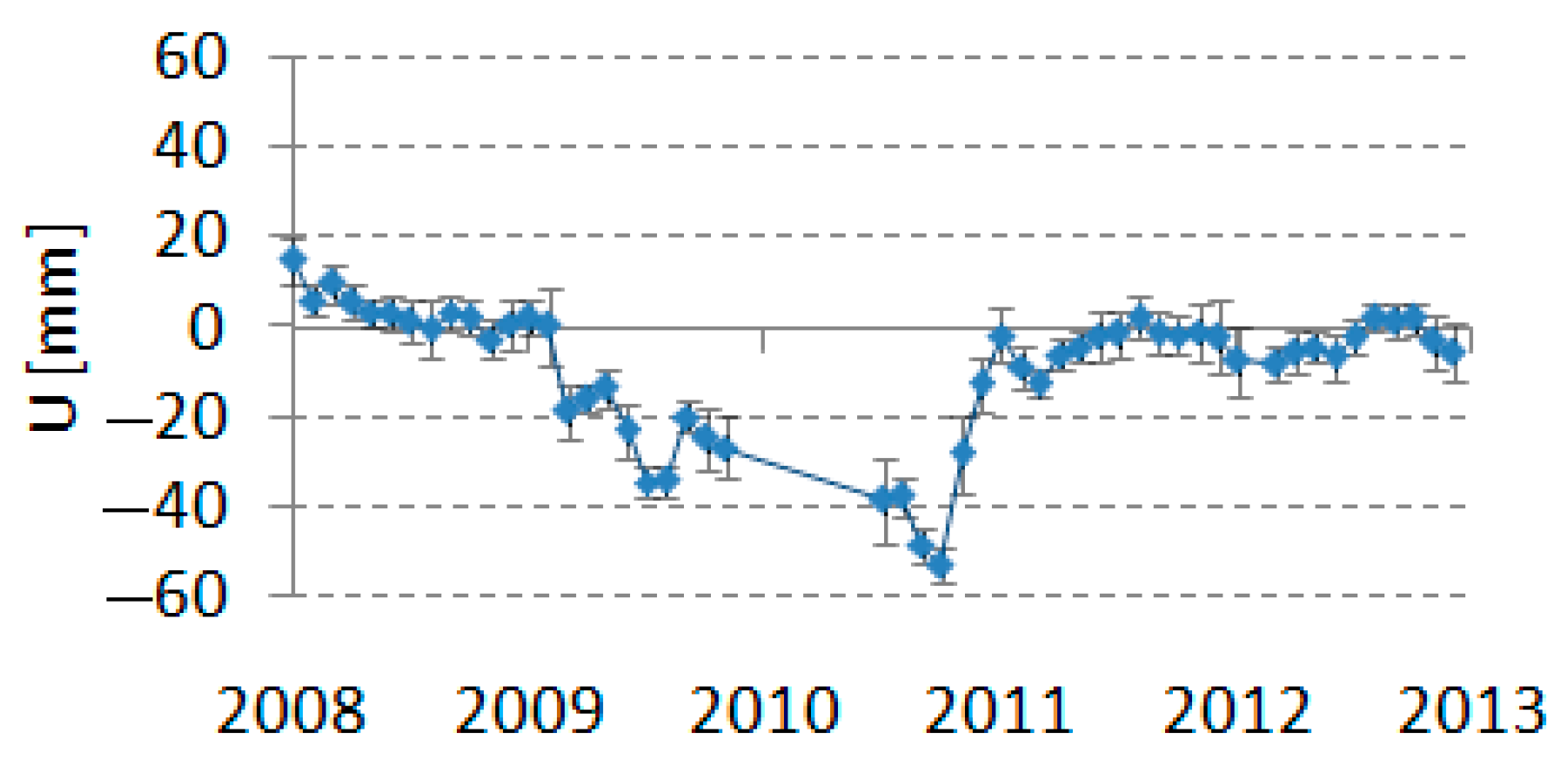
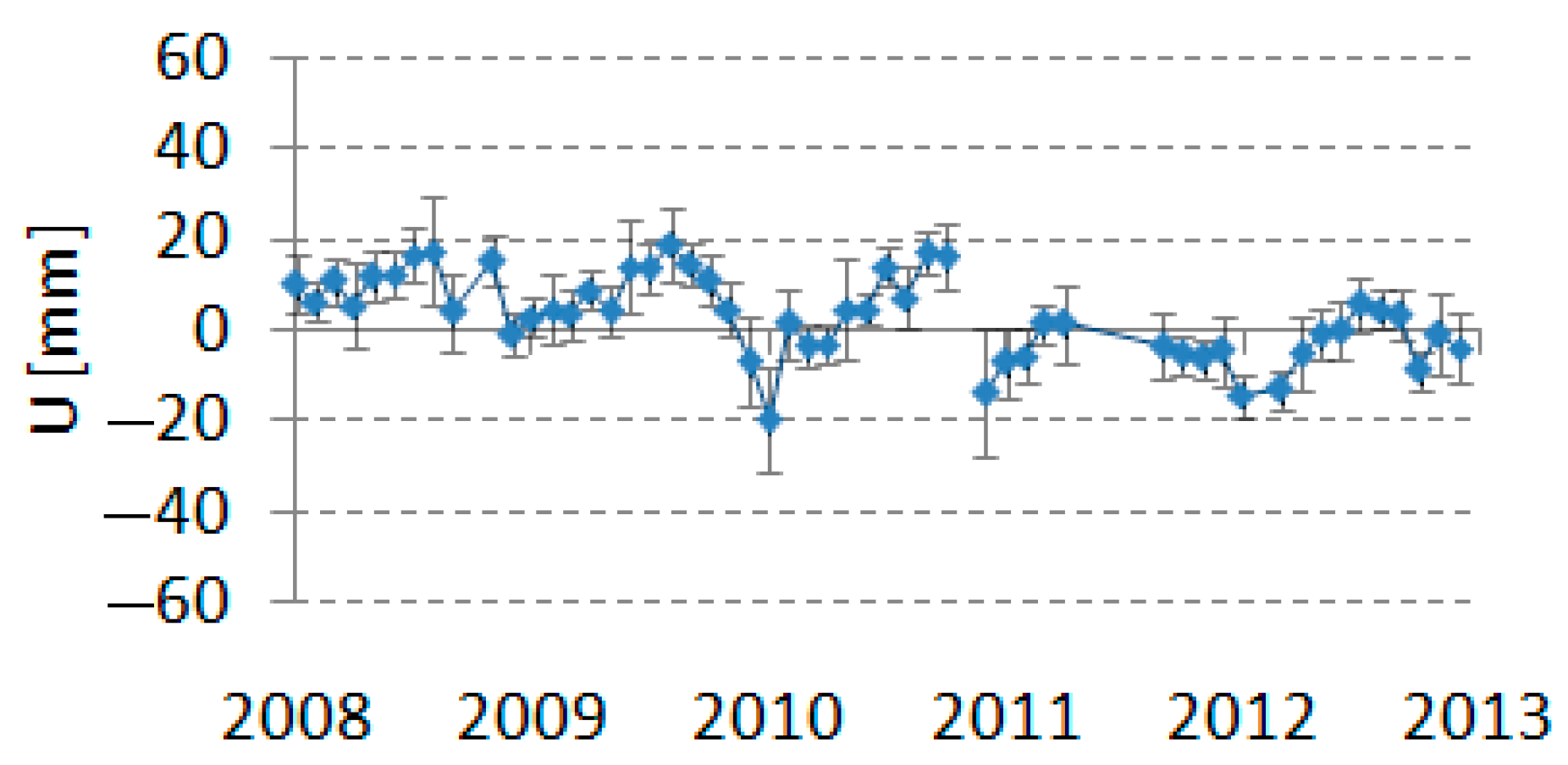
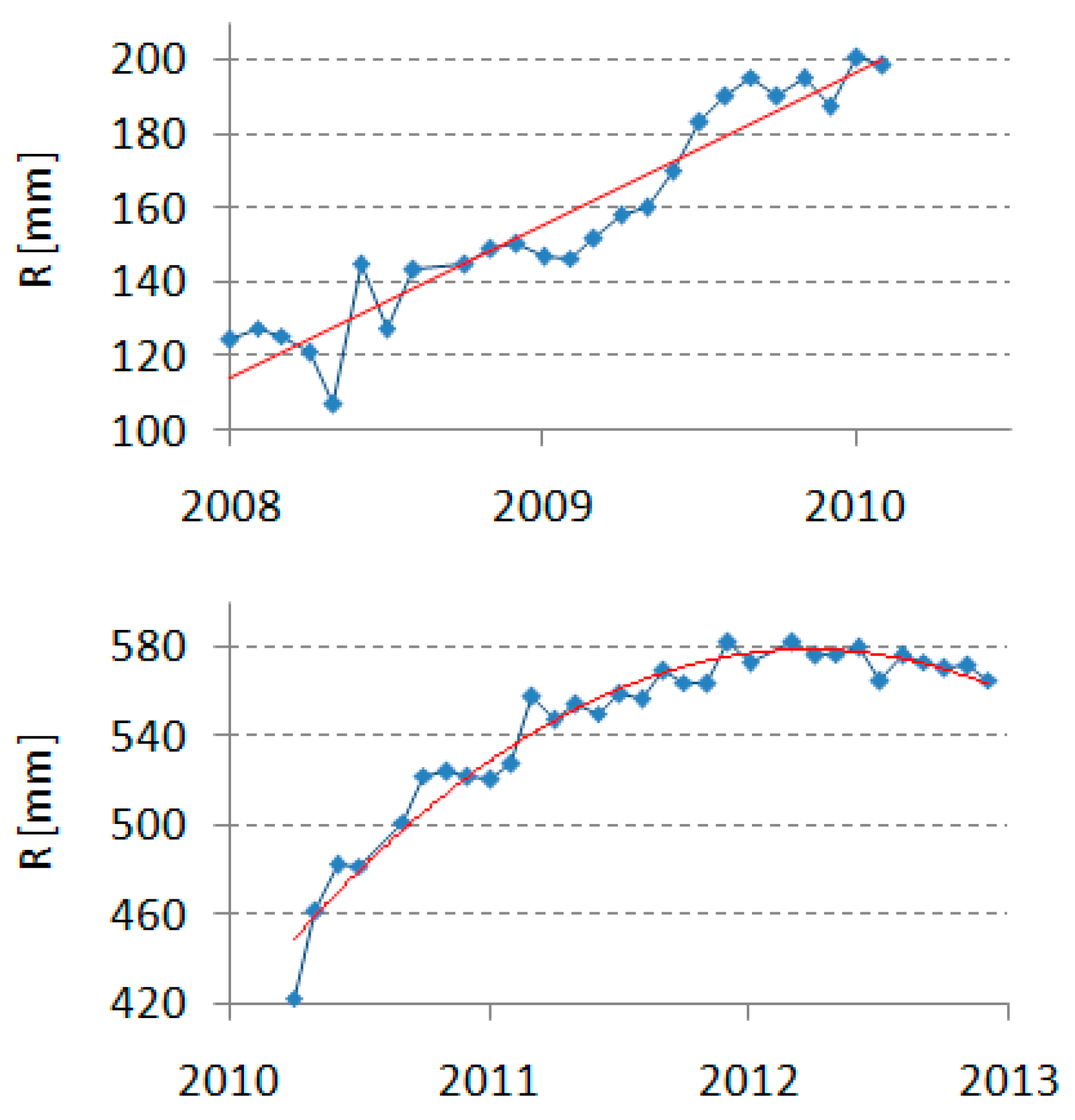
4.2.1. Earthquakes
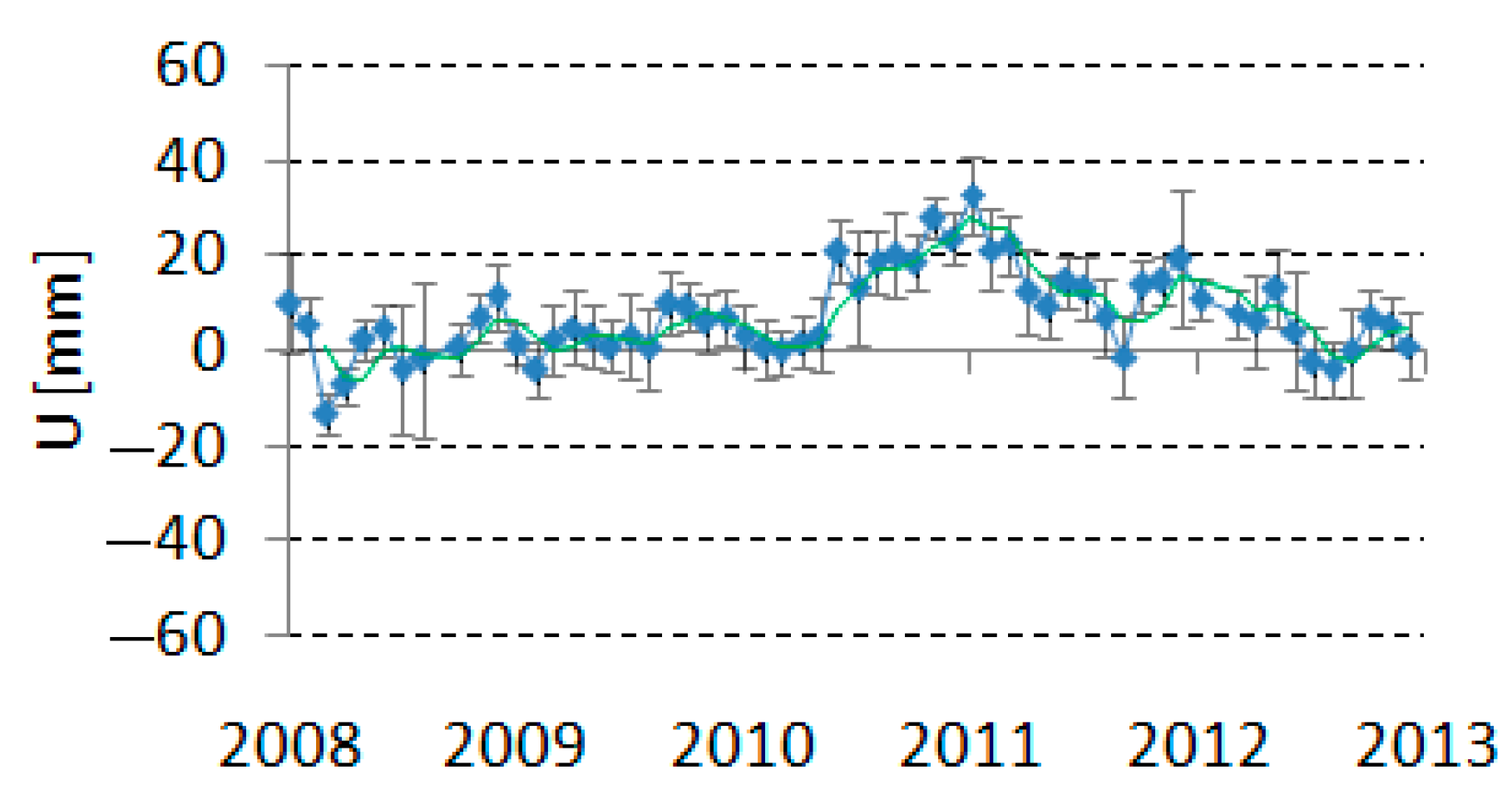
4.2.2. Other Systematic Shifts
4.2.3. Random Errors
4.3. Station Velocities
5. Discussion and Conclusions
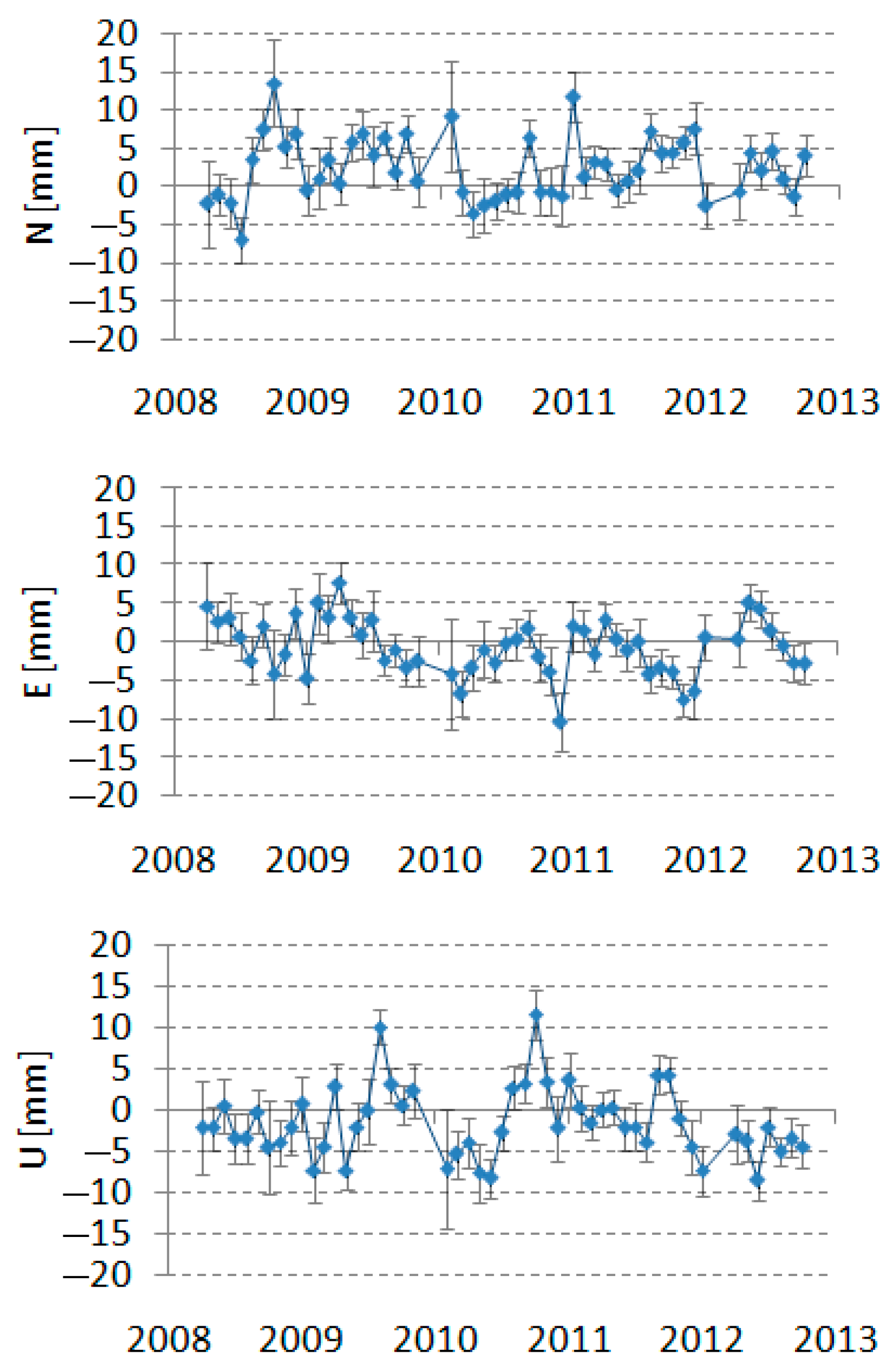
- It was found that the largest jump in the component N for the examined period of five years was recorded for the Koganei station (7308), amounting to 39.3 mm (July 2010), computed for the period before the earthquake. On the other hand, the smallest noticeable shift was 9.5 mm for the Yarragadee station (7090) (May 2009). It can therefore be concluded that the noticeable variability in the component N of the analyzed SLR stations oscillated between 9.5 mm and 39.3 mm;
- The largest jump in the component E for the analyzed period was recorded for the San Fernando station (7824), which was 55.0 mm (January 2008). The smallest observable change was recorded for the Zimmerwald station (7810) and it amounted to 12.3 mm (December 2010). It should therefore be concluded that the noticeable variation in component E of the positions of the tested SLR stations ranges from 12.3 mm to 55.0 mm;
- The largest visible jump for the vertical component U was 31.7 mm (May 2008) at the Hartebeesthoek station (7501), while the smallest visible jump was 9.4 mm (June 2009) at the Herstmonceux station (7840). Thus, the variability in the vertical component U for the analyzed SLR stations in the five-year period oscillated between 9.4 mm and 31.7 mm.
5.1. Changes in Position Caused by Earthquakes
5.2. Changes in Position Caused by Systematic Errors
5.3. Station Velocities
5.4. Accuracy
5.5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Station Number | Station Name | Period of Observation Monthyear | Time of Observations in Years (Δ) | Number of Monthly Arcs (N) | Mean Stability of Station Coordinates 3D [mm] (Sc) | Mean Standard Deviation of the Station Coordinates Determination [mm] (σ) |
|---|---|---|---|---|---|---|
| 1824 | Kyiv Ukraine | 0810–1210 | 4.1 | 17 | 28.2 | 4.5 |
| 1868 | Komsomolsk- na-Amure Russia | 0812–1212 | 4.1 | 7 | 35.1 | 11.2 |
| 1873 | Simeiz Crimea | 0801–1212 | 5.0 | 24 | 49.0 | 4.1 |
| 1879 | Altay Russia | 0810–1212 | 4.2 | 31 | 17.8 | 4.0 |
| 1884 | Riga Latvia | 0805–1111 | 3.4 | 25 | 25.7 | 4.7 |
| 1886 | Arkhyz Russia | 1103–1211 | 1.7 | 12 | 20.6 | 4.2 |
| 1887 | Baikonur Kazakhstan | 1204–1211 | 0.7 | 8 | 11.5 | 2.6 |
| 1888 | Svetloe St.Petersburg Russia | 1205 | - | 1 | - | 3.1 |
| 1889 | Zelenchukskya Russia | 1204–1210 | 0.6 | 6 | 13.7 | 5.0 |
| 1890 | Badary Russia | 1203–1210 | 0.7 | 7 | 12.6 | 4.1 |
| 1893 | Katzively Crimea | 0802–1212 | 4.9 | 51 | 18.8 | 4.1 |
| 7080 | McDonald Texsas-USA | 0801–1212 | 5.0 | 58 | 9.3 | 2.4 |
| 7090 | Yarragadee West Australia | 0801–1212 | 5.0 | 59 | 5.0 | 0.9 |
| 7105 | Greenbelt Maryland-USA | 0801–1212 | 5.0 | 52 | 5.9 | 1.7 |
| 7110 | Monument Peak California-USA | 0801–1212 | 5.0 | 56 | 12.8 | 1.8 |
| 7119 | Haleakala Hawaii-USA | 0801–1212 | 5.0 | 57 | 13.5 | 1.9 |
| 7124 | Tahiti French Polynesia | 0806–1211 | 4.5 | 35 | 12.0 | 2.8 |
| 7237 | Changchun China | 0801–1212 | 5.0 | 51 | 13.9 | 2.4 |
| 7249 | Beijing China | 0801–1210 | 4.8 | 26 | 20.9 | 3.6 |
| 7308 | Koganei Tokyo-Japan | 0801–1211 | 4.9 | 33 | 13.9 | 2.8 |
| 7328 | Koganei Tokyo-Japan | 1012–1102 | 0.2 | 3 | 4.5 | 3.6 |
| 7358 | Tanegashima Kiusiu-Japan | 0804–1104 | 3.1 | 18 | 17.4 | 4.1 |
| 7403 | Arequipa Peru | 0806–1211 | 4.5 | 23 | 13.2 | 2.8 |
| 7405B | Concepcion Chile | 0909–0911 | 0.2 | 3 | 3.3 | 2.6 |
| 7405IR | Concepcion Chile | 0801–1212 | 5.0 | 56 | 21.8 | 1.7 |
| 7406 | San Juan Argentina | 0801–1212 | 5.0 | 52 | 17.4 | 1.6 |
| 7501 | Hartebeesthoek Pretoria-South Africa | 0802–1212 | 4.9 | 46 | 13.1 | 2.1 |
| 7810 | Zimmerwald Switzerland | 0804–1210 | 4.6 | 51 | 4.0 | 1.0 |
| 7811 | Borowiec Poland | 0806–0909 | 1.2 | 7 | 12.2 | 7.5 |
| 7820 | Kunming Junan-China | 0804–0902 | 0.9 | 3 | 33.9 | 5.0 |
| 7821 | Shanghai China | 0805–1210 | 4.6 | 30 | 13.6 | 3.6 |
| 7822 | Tahiti French Polynesia | 1106–1109 | 0.3 | 4 | 8.1 | 2.7 |
| 7824 | San Fernando Spain | 0801–1210 | 4.8 | 41 | 15.3 | 3.4 |
| 7825 | Mount Stromlo Canberra- Australia | 0801–1212 | 5.0 | 58 | 6.3 | 1.6 |
| 7832 | Riyadh Saudi Arabia | 0801–1110 | 3.8 | 33 | 8.9 | 2.5 |
| 7838 | Simosato Honsiu-Japan | 0807–1212 | 4.5 | 46 | 19.2 | 2.2 |
| 7839 | Graz Austria | 0801–1212 | 5.0 | 59 | 4.5 | 1.6 |
| 7840 | Herstmonceux UK | 0801–1212 | 5.0 | 59 | 4.4 | 1.4 |
| 7841 | Potsdam Germany | 0801–1212 | 5.0 | 53 | 8.4 | 2.2 |
| 7845 | Grasse France | 0811–1212 | 4.1 | 47 | 6.3 | 1.7 |
| 7941 | Matera Italy | 0801–1212 | 5.0 | 55 | 5.5 | 1.2 |
| 8834 | Wettzell Germany | 0801–1212 | 5.0 | 52 | 9.8 | 1.6 |
| SLR Station | N [mm] | RMS for N [mm] | E [mm] | RMS for E [mm] | U [mm] | RMS for U [mm] | 3DRMS [mm] | 3Dσ [mm] |
|---|---|---|---|---|---|---|---|---|
| McDonald (7080) | 2.3 | 9.2 | −2.8 | 9.6 | 7.5 | 9.0 | 9.3 | 2.4 |
| Yarragadee (7090) | −1.1 | 4.4 | 2.1 | 3.9 | −1.9 | 6.4 | 5.0 | 0.9 |
| Greenbelt (7105) | 3.2 | 5.4 | −1.5 | 5.9 | 5.4 | 6.4 | 5.9 | 1.7 |
| Monument Peak before EQ (7110) | −6.1 | 10.0 | −1.0 | 11.2 | −6.3 | 15.1 | 12.3 | 2.2 |
| Monument Peak after EQ (7110) | −12.1 | 9.9 | −22.4 | 9.8 | −11.7 | 10.0 | 9.9 | 1.5 |
| Haleakala (7119) | −0.7 | 10.3 | 5.5 | 12.6 | 5.0 | 16.7 | 13.5 | 1.9 |
| Tahiti (7124) | −2.4 | 14.5 | 1.6 | 11.1 | −0.3 | 9.9 | 12.0 | 2.8 |
| Changchun before EQ (7237) | −3.2 | 10.8 | −1.4 | 12.8 | 22.3 | 13.8 | 12.5 | 2.3 |
| Changchun after EQ (7237) | −9.5 | 11.1 | 17.3 | 7.1 | 37.4 | 13.8 | 11.5 | 2.5 |
| Koganei before EQ (7308) | −8.5 | 15.8 | 4.6 | 10.1 | 0.2 | 15.0 | 13.9 | 2.8 |
| Koganei after EQ (7308) | 47.8 | 15.0 | 423.4 | 56.5 | −12.5 | 17.6 | 35.2 | 7.1 |
| Concepcion before EQ (7405IR) | −0.4 | 6.6 | −2.4 | 10.1 | −6.2 | 9.2 | 8.8 | 1.4 |
| Concepcion after EQ (7405IR) | −673.2 | 6.8 | −3221.1 | 56.7 | −50.7 | 10.3 | 33.5 | 30.3 |
| San Juan before EQ (7406) | −4.8 | 9.0 | −2.9 | 7.0 | 5.0 | 8.6 | 8.2 | 1.4 |
| San Juan after EQ (7406) | −37.2 | 8.6 | −37.1 | 7.4 | 27.0 | 11.1 | 9.2 | 1.8 |
| Hartebeesthoek (7501) | −3.2 | 9.0 | −3.2 | 12.9 | 3.0 | 11.4 | 11.2 | 2.1 |
| Zimmerwald (7810) | 2.4 | 4.1 | −0.6 | 3.6 | −1.5 | 4.3 | 4.0 | 1.0 |
| San Fernando (7824) | 8.6 | 11.8 | −2.1 | 14.4 | 6.0 | 18.8 | 15.3 | 3.4 |
| Mount Stromlo (7825) | −3.0 | 6.9 | 2.7 | 5.2 | 2.2 | 6.7 | 6.3 | 1.6 |
| Simosato before EQ (7838) | −36.4 | 14.1 | −1.0 | 16.7 | −49.6 | 21.1 | 17.5 | 2.5 |
| Simosato after EQ (7838) | −24.4 | 8.1 | 35.8 | 12.9 | −40.3 | 15.0 | 12.3 | 1.7 |
| Graz (7839) | 4.5 | 5.0 | 1.2 | 4.3 | 2.6 | 4.2 | 4.5 | 1.6 |
| Herstmonceux (7840) | 5.0 | 4.9 | −0.3 | 4.2 | −2.2 | 4.2 | 4.4 | 1.4 |
| Potsdam (7841) | 2.3 | 8.7 | 0.3 | 7.0 | 2.8 | 9.2 | 8.4 | 2.2 |
| Grasse (7845) | 1.8 | 5.9 | 3.0 | 5.6 | 28.8 | 7.3 | 6.3 | 1.7 |
| Matera (7941) | 4.6 | 5.7 | −2.0 | 4.2 | 0.7 | 6.5 | 5.5 | 1.2 |
| Wettzell (8834) | −3.5 | 5.6 | −2.7 | 6.0 | −8.8 | 14.9 | 9.8 | 1.6 |
| Nr | SLR Station | Component Velocities [mm/year] | Total Velocities [mm/year] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| VX | VY | VZ | VN | VE | VU | V3D (XYZ) | V3D (NEU) | V2D (NE) | Azimuth [deg.] | ||
| 1 | McDonald (7080) | −12.2 | −1.8 | −4.8 | −6.6 | −11.4 | 1.6 | 13.2 | 13.3 | 13.2 | 239.9 |
| 2 | Yarragadee (7090) | −46.5 | 7.5 | 49.8 | 56.7 | 38.9 | −0.9 | 68.6 | 68.8 | 68.8 | 34.5 |
| 3 | Greenbelt (7105) | −13.7 | −1.1 | 3.4 | 4.0 | −13.6 | 0.5 | 14.2 | 14.2 | 14.2 | 286.4 |
| 4 | Monument Peak (7110) | −37.3 | 29.8 | 11.3 | 15.1 | −46.6 | −2.3 | 49.1 | 49.0 | 49.0 | 288.0 |
| 5 | Haleakala (7119) | −14.9 | 62.2 | 33.0 | 35.1 | −62.9 | 1.0 | 72.0 | 72.0 | 72.0 | 299.2 |
| 6 | Tahiti (7124) | −42.5 | 52.8 | 32.8 | 34.4 | −67.1 | −0.4 | 75.3 | 75.4 | 75.4 | 297.1 |
| 7 | Changchun (7237) | −32.4 | −8.7 | −9.1 | −14.8 | 31.4 | 2.1 | 34.8 | 34.8 | 34.7 | 115.2 |
| 8 | Koganei (7308) to Feb. 2011 | −4.0 | 2.5 | −7.8 | −9.1 | 0.7 | −0.8 | 9.1 | 9.1 | 9.2 | 175.6 |
| 9 | Concepcion (7405IR) to Feb. 2010 | 42.1 | 10.1 | 15.4 | 16.4 | 38.5 | −4.7 | 46.0 | 42.1 | 41.8 | 66.9 |
| Concepcion (7405IR) from Apr. 2010 | −37.1 | −14.7 | 18.4 | 16.7 | −39.8 | −8.5 | 43.9 | 44.0 | 43.2 | 292.8 | |
| 10 | San Juan (7406) to Feb. 2010 | 17.9 | −4.6 | 6.1 | 10.9 | 14.9 | 6.0 | 19.5 | 19.4 | 18.5 | 53.8 |
| San Juan (7406) from Mar. 2010 | 13.5 | −6.7 | 5.6 | 10.7 | 10.2 | 6.6 | 16.1 | 16.2 | 14.8 | 43.6 | |
| 11 | Hartebeesthoek (7501) | 0.5 | 17.8 | 15.1 | 17.5 | 15.5 | 1.3 | 23.3 | 23.4 | 23.4 | 41.5 |
| 12 | Zimmerwald (7810) | −13.7 | 17.4 | 12.2 | 16.6 | 19.1 | 1.2 | 25.3 | 25.3 | 25.3 | 49.0 |
| 13 | San Fernando (7824) | −9.1 | 17.1 | 16.4 | 19.7 | 16.0 | 1.0 | 25.4 | 25.4 | 25.4 | 39.1 |
| 14 | Mount Stromlo (7825) | −35.8 | −1.4 | 45.8 | 54.9 | 19.6 | −2.1 | 58.1 | 58.3 | 58.3 | 19.6 |
| 15 | Simosato (7838) to Feb. 2011 | 7.0 | 6.5 | −6.5 | −5.2 | −9.6 | −4.1 | 11.6 | 11.7 | 10.9 | 118.4 |
| 16 | Graz (7839) | −16.6 | 17.8 | 11.0 | 15.7 | 21.6 | 0.4 | 26.7 | 26.7 | 26.7 | 54.0 |
| 17 | Herstmonceux (7840) | −13.7 | 16.8 | 10.2 | 17.0 | 16.9 | −0.6 | 24.0 | 24.0 | 24.0 | 44.8 |
| 18 | Potsdam (7841) | −18.8 | 13.4 | 7.3 | 16.6 | 17.4 | −3.5 | 24.2 | 24.3 | 24.0 | 46.3 |
| 19 | Grasse (7845) | −13.9 | 19.0 | 10.1 | 15.3 | 20.5 | −1.4 | 25.6 | 25.6 | 25.6 | 53.3 |
| 20 | Matera (7941) | −19.1 | 19.1 | 15.1 | 19.8 | 23.7 | 0.1 | 30.9 | 30.9 | 30.9 | 50.1 |
| 21 | Wettzell (8834) | −16.0 | 17.1 | 11.1 | 16.2 | 20.2 | 0.6 | 25.9 | 25.9 | 25.9 | 51.3 |
References
- CDDIS. SLR and GPS (and Plate Tectonic and Earthquakes), NASA. 2009. Available online: https://cddis.nasa.gov/docs/2009/HTS_0910.pdf (accessed on 10 February 2023).
- Altamimi, Z.; Collilieux, X.; Metivier, L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame. J. Geodesy 2011, 85, 457–473. [Google Scholar] [CrossRef] [Green Version]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Noll, C.E.; Pavlis, E.C.; Lemoine, F.G.; Combrink, L.; Degnan, J.D.; Kirchner, G.; Schreiber, U. The ILRS: Approaching 20 years and planning for the future. J. Geodesy 2019, 93, 2161–2180. [Google Scholar] [CrossRef]
- NASA. How Satellite Laser Ranging Got Its Start 50 Years Ago. 2014. Available online: https://www.nasa.gov/content/goddard/laser-ranging-50-years (accessed on 21 February 2023).
- ILRSa ASC Product and Information Server. Available online: http://geodesy.jcet.umbc.edu/ILRS_AWG_MONITORING/ (accessed on 15 March 2023).
- ILRSb Monthly/Quarterly Global Performance Report Card. Available online: https://ilrs.gsfc.nasa.gov/network/system_performance/global_report_cards/quarterly/ (accessed on 15 March 2023).
- Geoscience Hitotsubashi: Multi-Satellite Bias Analysis Report. Available online: https://geo.science.hit-u.ac.jp/slr/bias/ (accessed on 12 February 2023).
- Zimmerwald: ILRS Combined Range Bias Report. Available online: http://ftp.aiub.unibe.ch/slr/summary_report.txt (accessed on 19 February 2023).
- DGFI. DGFI-TUM ILRS Analysis Centre. 2023. Available online: https://www.dgfi.tum.de/en/international-services/ilrs/ (accessed on 23 March 2023).
- Torrence, M.H.; Klosko, S.M.; Christodoulidis, D.C. The construction and testing of normal point at Goddard Space Flight Center. In Proceedings of the 5th International Workshop on Laser Ranging Instrumentation, Herstmonceux, UK, 10 September 1984; pp. 506–516. Available online: https://ilrs.gsfc.nasa.gov/about/reports/workshop/lw05.html (accessed on 1 February 2023).
- Pavlis, D.E.; Luo, S.; Dahiroc, P.; McCarthy, J.J.; Lutchke, S.B. GEODYN II System Description; Hughes STX Contractor Report; Goddard Space Flight Center: Greenbelt, MD, USA, 1998.
- Schillak, S.; Lejba, P.; Michałek, P.; Suchodolski, T.; Smagło, A.; Zapaśnk, S. Analysis of the Results of the Borowiec SLR Station (7811) for the period 1993-2019 as an Example of the Quality Assessment of Satellite Laser Ranging Stations. Sensors 2022, 22, 616. [Google Scholar] [CrossRef] [PubMed]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An Earth Gravitational Model to Degree 2160:EGM2008. In Proceedings of the 2008 General Assembly of the European Geoscience Union, Vienna, Austria, 13 April 2008. [Google Scholar]
- McCarthy, D.D.; Petit, G. (Eds.) IERS Conventions (2003), IERS Technical Note No. 32; International Earth Rotation and Reference Systems Service: Frankfurt am Main, Germany; Bundesamt für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2004.
- Ray, R.D. A global Ocean Tide Model from TOPEX/POSEIDON Altimetry: GOT99.2; NASA/TMm1999-200478; Goddard Space Flight Center: Greenbelt, MD, USA, 1999; pp. 1–66.
- Standish, E.M.; Newhall, X.X.; Williams, J.G.; Folkner, W.F. JPL Planetary and Lunar Ephemerides DE403/LE403. JPL IOM 1995, 31, 10–127. [Google Scholar]
- Petit, G.; Luzum, B. (Eds.) IERS Conventions, IERS Technical Note No. 36; International Earth Rotation and Reference Systems Service: Frankfurt am Main, Germany; Bundesamt für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010.
- Mendes, V.B.; Prates, G.; Pavlis, E.C.; Pavlis, D.E.; Langley, R.B. Improved mapping functions for atmospheric refraction in SLR. Geophys. Res. Lett. 2002, 29, 53-1–53-4. [Google Scholar] [CrossRef] [Green Version]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, L14602. [Google Scholar] [CrossRef] [Green Version]
- Borkowski, K.M. Accurate algorithms to transform geocentric to geographic coordinates. Bull. Geod. 1989, 63, 50–56. [Google Scholar] [CrossRef]
- Schillak, S.; Szafranek, K.; Araszkiewicz, A.; Figurski, M.; Lejba, P.; Lehmann, M. Earthquakes Problem in ITRF Position and Velocity Determination from SLR and GNSS Data; IAG Scientific Assembly: Potsdam, Germany, 2013. [Google Scholar]
- Szafranek, K.; Schillak, S.; Araszkiewicz, A.; Figurski, M.; Lehmann, M.; Lejba, P. Comparison of long-term SLR and GNSS solutions from selected stations in the frame of GGOS realization. In EGU General Assembly Conference Abstracts; EGU General Assembly: Vienna, Austria, 2012; Volume 14. [Google Scholar]
- Degnan, J. Milimeter Accuracy Satellite Laser Ranging: A Review. Contrib. Space Geod. Geodyn. Technol. Geodyn. 1993, 25, 133–162. [Google Scholar]
- Drożdżewski, M.; Sośnica, K. Satellite laser ranging as a tool for the recovery of tropospheric gradients. Atmos. Res. 2018, 212, 33–42. [Google Scholar] [CrossRef]
- Drożdżewski, M.; Sośnica, K.; Zus, F.; Balidakis, K. Troposphere delay modeling with horizontal gradients for satellite laser ranging. J. Geodesy 2019, 93, 1853–1866. [Google Scholar] [CrossRef] [Green Version]
- Drożdżewski, M.; Sośnica, K. Tropospheric and range biases in Satellite Laser Ranging. J. Geodesy 2021, 95, 100–117. [Google Scholar] [CrossRef]




| Force models | |
| Earth gravity field | EGM2008 20 × 20 [14] |
| Earth tides | Convention IERS 2003 [15] |
| Ocean tides | GOT99.2 [16] |
| Third body gravity: moon, sun, and planets | DE403 [17] |
| Solar radiation pressure | Coefficient CR = 1.13 |
| Tide amplitudes—k2, k3, phase k2 | k2 = 0.3019, k3 = 0.093, phase k2 = 0.0 [18] |
| Earth albedo | [12] |
| Dynamic polar motion | [12] |
| Relativistic corrections | [12] |
| Constants | |
| Earth gravity parameter (GM) | 3.986004415 × 1014 m3/s2 |
| Light velocity | 29,792.458 km/s |
| Semimajor axis of the Earth | 6378.13630 km |
| Inverse of the Earth’s flattening | 298.25642 |
| Reference frame | |
| Inertial reference frame | J2000.0 |
| Coordinates reference system | true of date at 0 h of the first day of the each month |
| Stations coordinates | ITRF2008 [2] |
| Precession and nutation | IAU 2000 |
| Polar motion | C04 IERS |
| Tidal uplift | Love model h2 = 0.6078, l2 = 0.0847 [18] |
| Pole tide | [12] |
| Estimated parameters | |
| Satellite state vector | 6 parameters |
| Station geocentric coordinates | 3 parameters |
| Acceleration parameters | along-track, cross-track and radial at 5-days intervals |
| Measurement model | |
| Observations | 120 sec window of normal point, |
| data from EUROLAS Data Center | |
| Satellites | LAGEOS–1 and LAGEOS–2 |
| Center of mass correction | 25.1 cm |
| Cross—section area | 0.2827 m2 |
| Mass | 406.965 kg (LAGEOS-1), 405.380 kg (LAGOES-2) |
| Laser pulse wavelength | 532 nm, 864 nm (7405IR) |
| Tropospheric refraction | Model Mendes–Pavlis [19,20] |
| Editing criteria | |
| Normal points residual | 5σ per arc |
| Cut-off | elevation 10o |
| Station coordinates cut-off | <50 normal points per station per arc |
| Numerical integration | |
| Integration | Cowell method |
| Orbit integration step size | 120 s |
| Arc length | 1 month |
| Station Number | a | Δa | R2 | Sy | F | ƒ | |
|---|---|---|---|---|---|---|---|
| 7080 | −6.6 | 0.8 | 0.5 | 9.2 | 60.1 | 56 | N |
| −11.4 | 0.9 | 0.8 | 9.5 | 171.3 | 56 | E | |
| 7090 | 56.7 | 0.4 | 1.0 | 4.0 | 24,712.2 | 57 | N |
| 38.9 | 0.4 | 1.0 | 3.9 | 11,995.5 | 57 | E | |
| 7105 | 4.0 | 0.5 | 0.6 | 5.5 | 64.9 | 50 | N |
| −13.6 | 0.5 | 0.9 | 5.7 | 684.7 | 50 | E | |
| 7110 | 15.1 | 0.9 | 0.8 | 9.5 | 284.9 | 54 | N |
| −46.6 | 0.9 | 1.0 | 9.6 | 2717.9 | 54 | E | |
| 7119 | 35.1 | 0.9 | 1.0 | 10.2 | 1457.7 | 55 | N |
| −62.9 | 1.1 | 1.0 | 12.6 | 3025.7 | 55 | E | |
| 7124 | 34.4 | 1.7 | 0.9 | 14.7 | 390.8 | 33 | N |
| −67.1 | 1.3 | 1.0 | 11.1 | 2598.5 | 33 | E | |
| 7237 all period | −14.8 | 1.0 | 0.8 | 10.6 | 215.3 | 49 | N |
| 31.4 | 1.1 | 0.9 | 12.1 | 749.1 | 49 | E | |
| 7237 to Feb. 2011 | −14.8 | 2.1 | 0.6 | 10.7 | 52.0 | 28 | N |
| 25.4 | 2.5 | 0.8 | 13.0 | 103.4 | 28 | E | |
| 7308 all period | 7.6 | 2.9 | 0.2 | 23.0 | 7.0 | 31 | N |
| 104.6 | 13.4 | 0.7 | 107.1 | 61.3 | 31 | E | |
| 7308 to Feb. 2011 | −9.1 | 3.4 | 0.2 | 15.7 | 7.2 | 23 | N |
| 0.7 | 2.2 | 0.005 | 10.0 | 0.1 | 23 | E | |
| 7405IR all period | 11.4 | 0.7 | 0.7 | 7.8 | 254.2 | 54 | N |
| −199.6 | 14.9 | 0.8 | 162.2 | 180.1 | 54 | E | |
| 7406 all period | 6.2 | 0.8 | 0.6 | 8.2 | 65.3 | 50 | N |
| 0.5 | 1.2 | 0.003 | 12.4 | 0.2 | 50 | E | |
| 7501 | 17.5 | 0.9 | 0.9 | 9.0 | 392.8 | 44 | N |
| 15.7 | 1.2 | 0.8 | 12.4 | 165.3 | 44 | E | |
| 7810 | 16.6 | 0.4 | 1.0 | 4.1 | 1453.7 | 49 | N |
| 19.1 | 0.4 | 1.0 | 3.6 | 2589.0 | 49 | E | |
| 7824 | 19.7 | 1.3 | 0.9 | 11.3 | 244.6 | 39 | N |
| 16.0 | 1.6 | 0.7 | 14.5 | 97.9 | 39 | E | |
| 7825 | 54.9 | 0.6 | 1.0 | 6.5 | 8650.0 | 56 | N |
| 19.6 | 0.4 | 1.0 | 4.6 | 2210.7 | 56 | E | |
| 7838 all period | 0.2 | 1.4 | 0.0004 | 12.5 | 0.018 | 44 | N |
| 5.1 | 1.9 | 0.1 | 17.0 | 7.1 | 44 | E | |
| 7838 to Feb. 2011 | −5.2 | 3.4 | 0.1 | 14.3 | 2.3 | 24 | N |
| −9.6 | 4.1 | 0.2 | 16.9 | 5.6 | 24 | E | |
| 7839 | 15.7 | 0.5 | 1.0 | 5.0 | 1196.1 | 57 | N |
| 21.6 | 0.4 | 1.0 | 4.4 | 2960.7 | 57 | E | |
| 7840 | 17.0 | 0.4 | 1.0 | 4.9 | 1464.6 | 57 | N |
| 16.9 | 0.4 | 1.0 | 4.3 | 1930.0 | 57 | E | |
| 7841 | 16.6 | 0.8 | 0.9 | 8.5 | 433.7 | 51 | N |
| 17.4 | 0.6 | 0.9 | 6.5 | 825.1 | 51 | E | |
| 7845 | 15.3 | 0.7 | 0.9 | 5.8 | 466.6 | 45 | N |
| 20.5 | 0.7 | 1.0 | 5.7 | 867.3 | 45 | E | |
| 7941 | 19.8 | 0.5 | 1.0 | 5.6 | 1456.3 | 53 | N |
| 23.7 | 0.4 | 1.0 | 4.3 | 3551.9 | 53 | E | |
| 8834 | 16.2 | 0.5 | 1.0 | 5.7 | 988.8 | 50 | N |
| 20.2 | 0.5 | 1.0 | 6.1 | 1359.9 | 50 | E |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schillak, S.; Satarowska, A.; Sankowski, D.; Michałek, P. Analysis of the Results Determining the Positions and Velocities of Satellite Laser Ranging Stations during Earthquakes in 2010–2011. Remote Sens. 2023, 15, 3659. https://doi.org/10.3390/rs15143659
Schillak S, Satarowska A, Sankowski D, Michałek P. Analysis of the Results Determining the Positions and Velocities of Satellite Laser Ranging Stations during Earthquakes in 2010–2011. Remote Sensing. 2023; 15(14):3659. https://doi.org/10.3390/rs15143659
Chicago/Turabian StyleSchillak, Stanisław, Agnieszka Satarowska, Dominik Sankowski, and Piotr Michałek. 2023. "Analysis of the Results Determining the Positions and Velocities of Satellite Laser Ranging Stations during Earthquakes in 2010–2011" Remote Sensing 15, no. 14: 3659. https://doi.org/10.3390/rs15143659
APA StyleSchillak, S., Satarowska, A., Sankowski, D., & Michałek, P. (2023). Analysis of the Results Determining the Positions and Velocities of Satellite Laser Ranging Stations during Earthquakes in 2010–2011. Remote Sensing, 15(14), 3659. https://doi.org/10.3390/rs15143659








