Crown Information Extraction and Annual Growth Estimation of a Chinese Fir Plantation Based on Unmanned Aerial Vehicle–Light Detection and Ranging
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. UAV–LiDAR Data Collection
2.3. Field Data
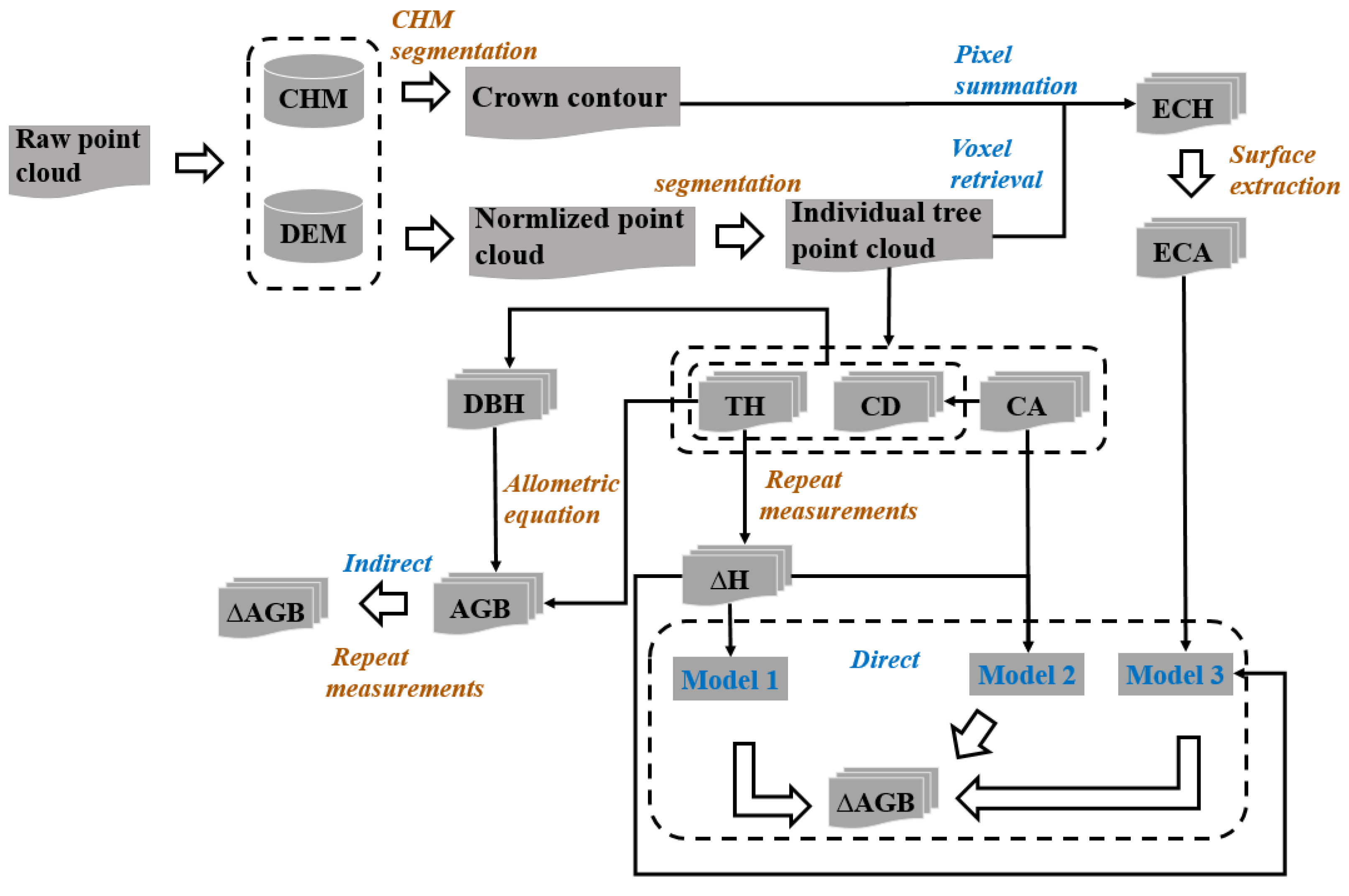
2.4. UAV–LiDAR Data Processing
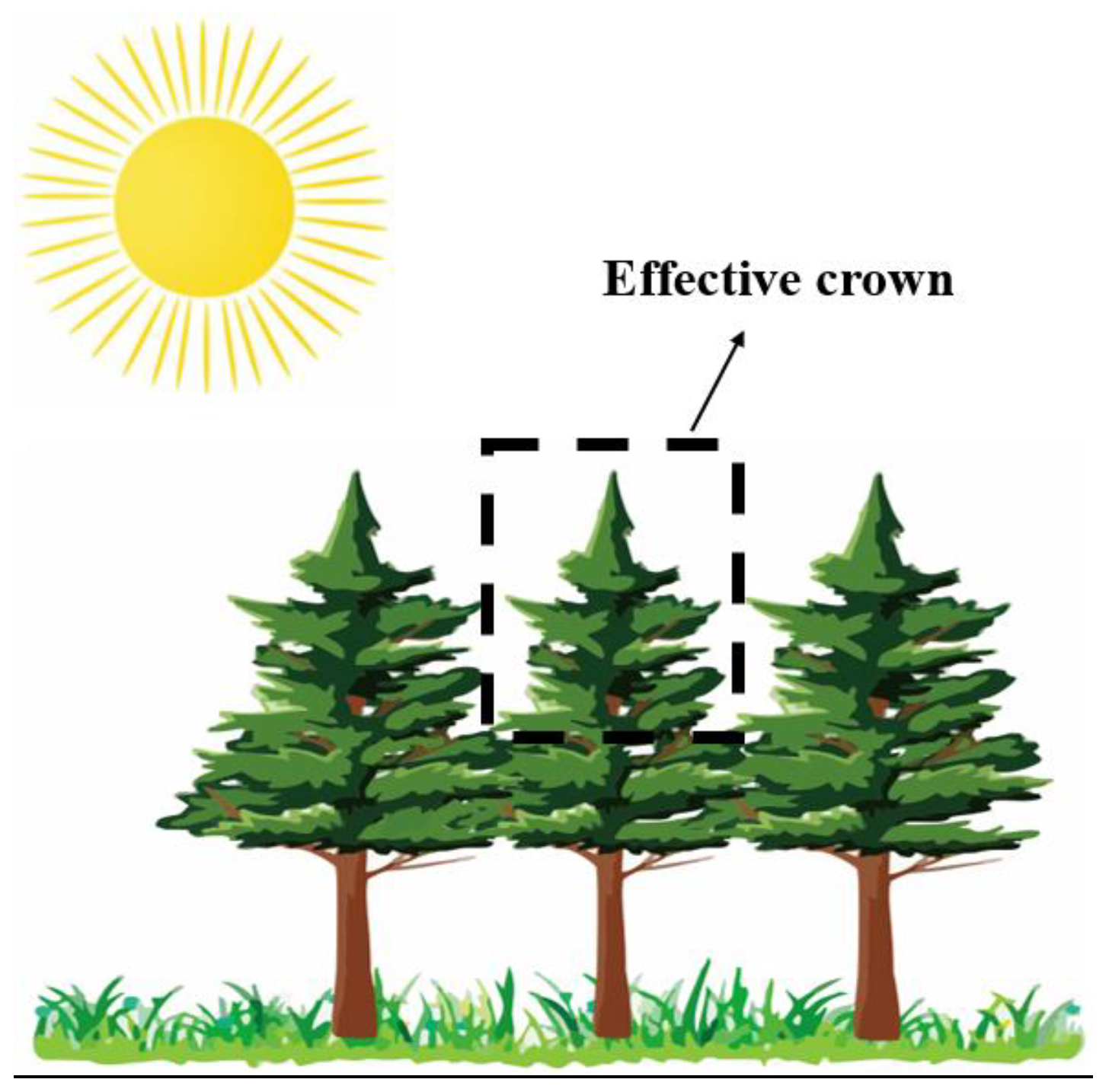
2.5. Effective Crown Area Extraction
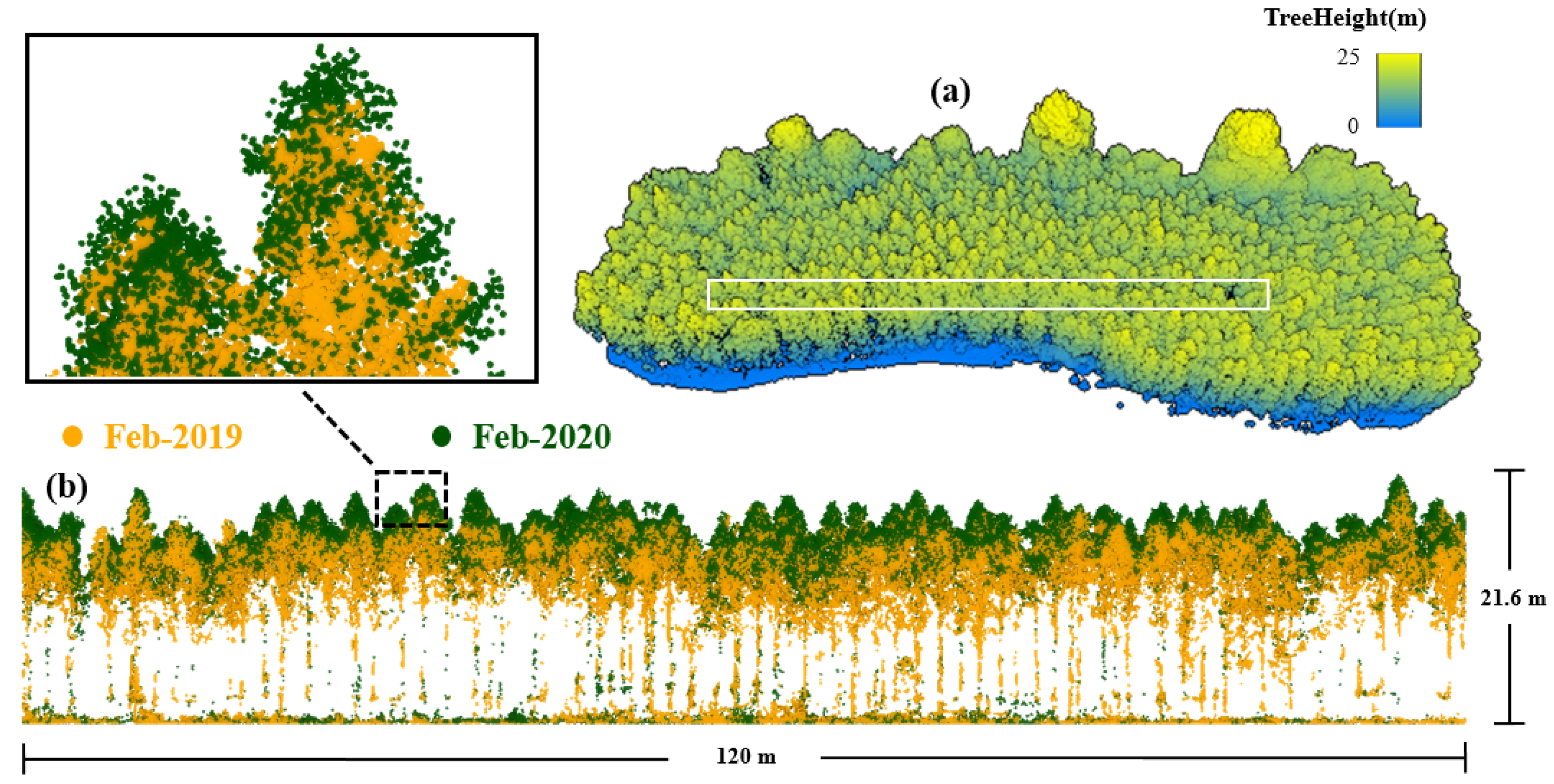
2.6. Biomass Dynamic Estimation
2.7. Precision Verification and Statistical Analysis
3. Results
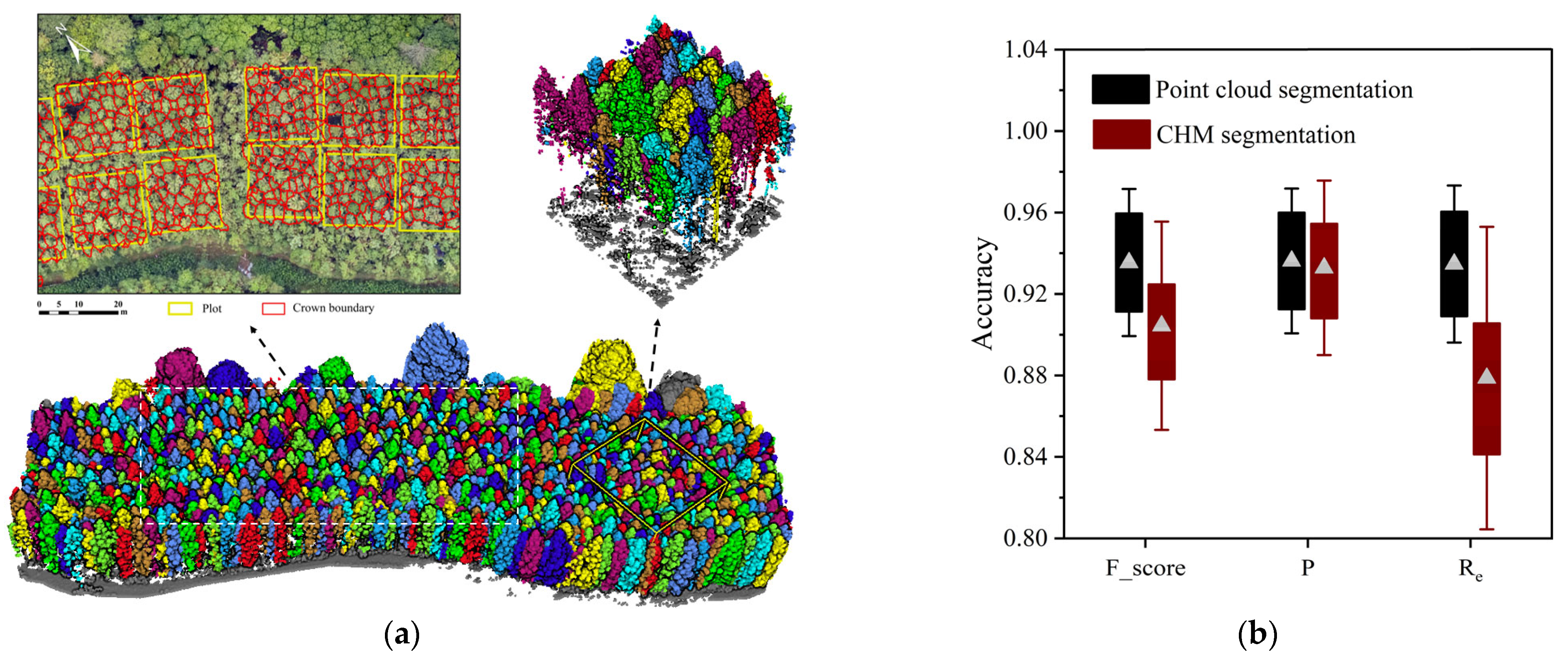
3.1. Verification of Individual tree Segmentation Accuracy
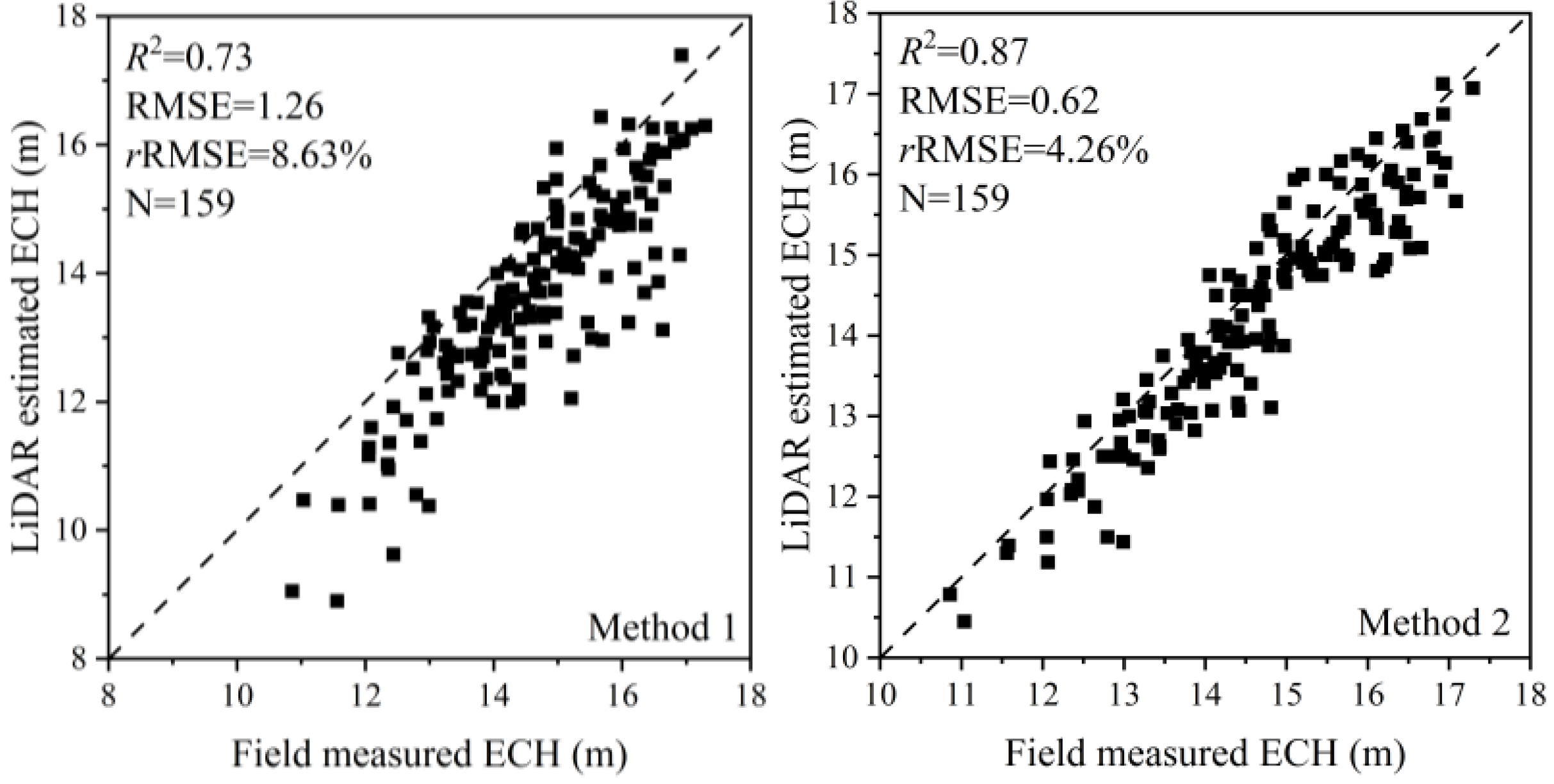
3.2. Validation of Effective Crown Height
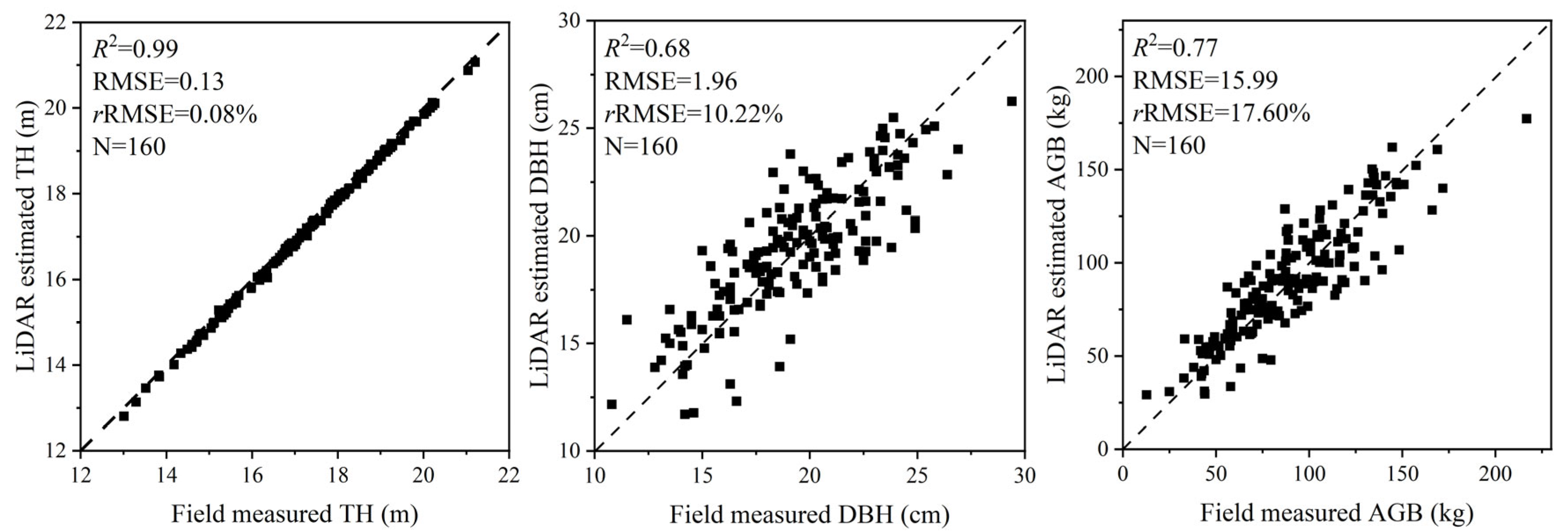
3.3. Verification of Structural Parameter Estimation
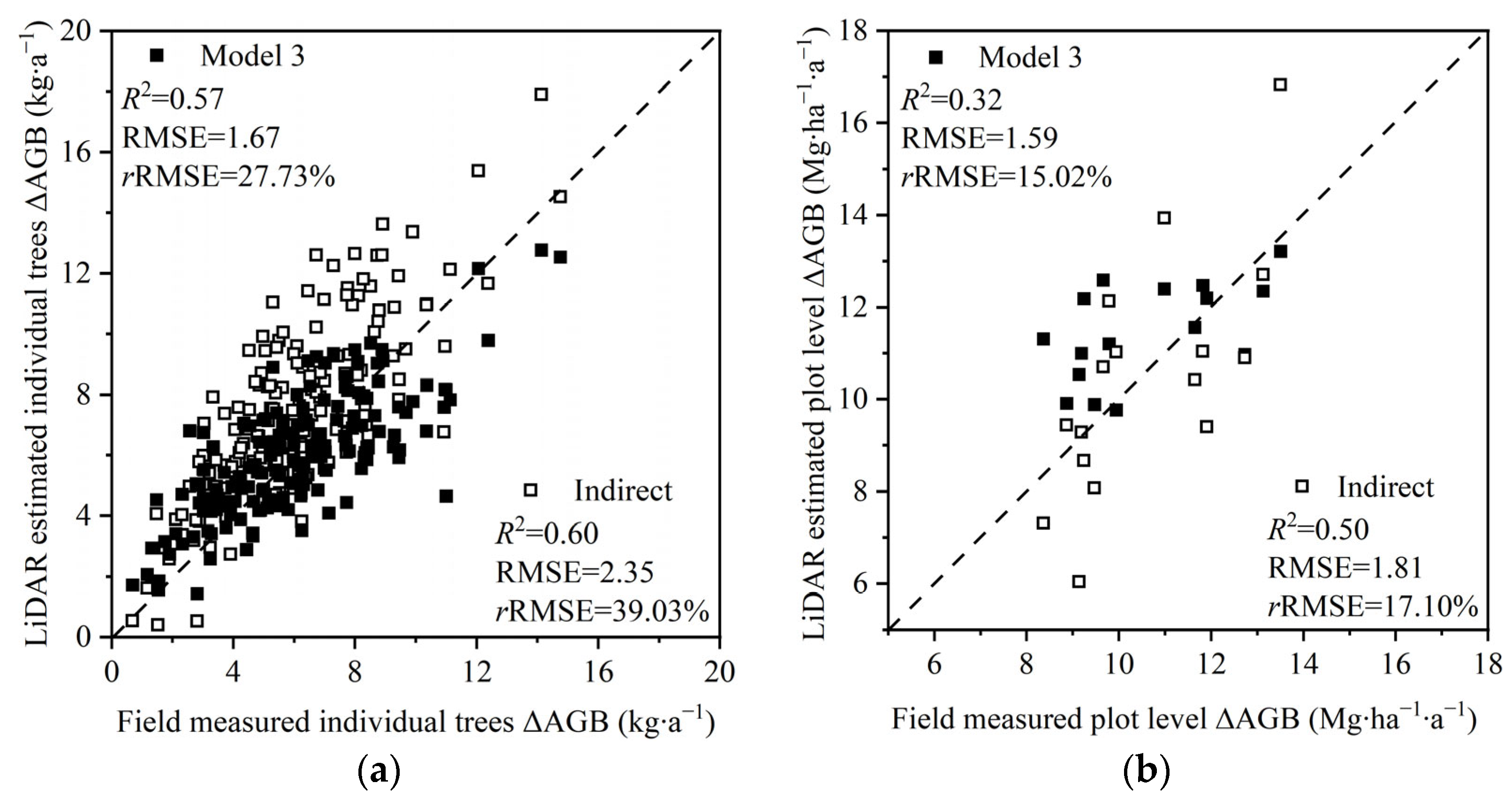
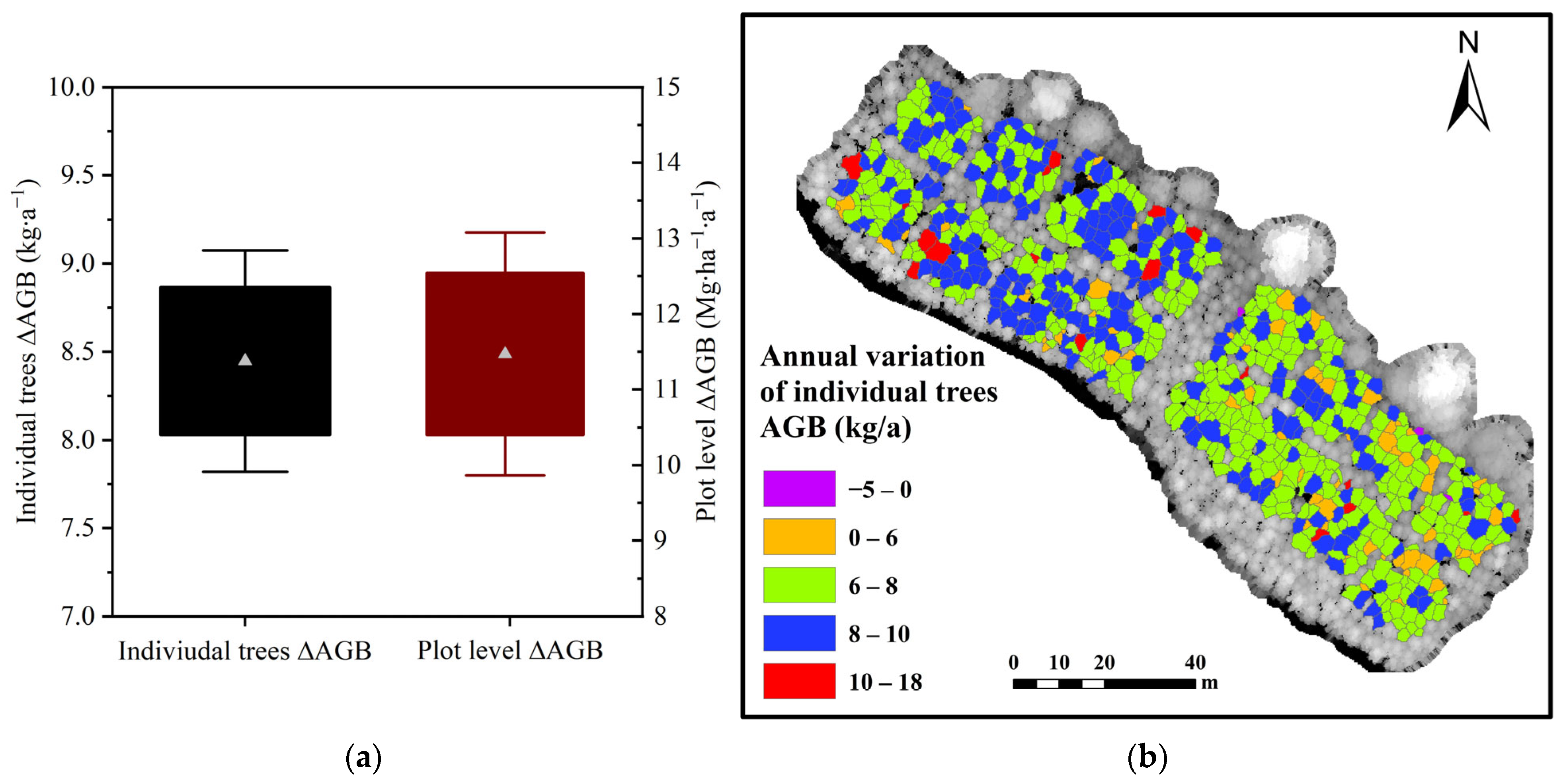
3.4. Analysis of Growth from Biomass Changes
4. Discussion
4.1. Effective Crown Extraction
4.2. Comparison of Forest Annual Growth Estimation by Direct and Indirect Methods
5. Conclusions
- (1)
- Compared with the canopy boundary height average method based on CHM segmentation, the voxel extraction method based on normalized point cloud segmentation can obtain a more accurate ECH. However, the accuracy of ECH extraction was influenced by the voxel size setting. Referring to the average tree crown radius, the horizontal plane of the voxel was set to 1 m × 1 m, and the optimal voxel height was determined to be 0.25 m.
- (2)
- The ECA was a crucial factor for accurately estimating the annual growth of Chinese fir plantations. Moreover, ECA exerts a more significant influence than CA on enhancing the fitting effect of the annual growth regression model.
- (3)
- The use of multi-temporal UAV–LiDAR allows for the reliable and efficient monitoring of AGB in Chinese fir plantations, including its annual changes. The regression model, which incorporates two variables: ECA and ∆TH, was superior to the indirect method for annual growth estimation. By assessing the AGB and its variation from individual plant to plot level, a reduction in relative error was observed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using lidar remote sensing at La Selva, Costa Rica. J. Geophys. Res. Biogeosci. 2010, 115, G00E09. [Google Scholar] [CrossRef]
- Houghton, R.A.; Goetz, S.J. New Satellites Help Quantify Carbon Sources and Sinks. Eos Trans. Am. Geophys. Union 2008, 89, 417–418. [Google Scholar] [CrossRef]
- Clark, D.A. Tropical forests and global warming: Slowing it down or speeding it up? Front. Ecol. Environ. 2004, 2, 73–80. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.N.; Cao, L. Estimating forest stand characteristics in a coastal plain forest plantation based on vertical structure profile parameters derived from ALS data. Natl. Remote Sens. Bull. 2018, 22, 872–888. (In Chinese) [Google Scholar] [CrossRef]
- Guo, Q.H.; Liu, J.; Tao, S.L.; Xue, B.L.; Li, L.; Xu, G.C.; Li, W.K.; Wu, F.F.; Li, Y.M.; Chen, L.H. Application status and Prospect of lidar in forest ecosystem monitoring and simulation. Chin. Sci. Bull. 2014, 56, 20. (In Chinese) [Google Scholar]
- Marinelli, D.; Paris, C.; Bruzzone, L. A Novel Approach to 3-D Change Detection in Multitemporal LiDAR Data Acquired in Forest Areas. Ieee Trans. Geosci. Remote Sens. 2018, 56, 3030–3046. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Gregoire, T.G.; Ståhl, G. Model-assisted estimation of change in forest biomass over an 11year period in a sample survey supported by airborne LiDAR: A case study with post-stratification to provide “activity data”. Remote Sens. Environ. 2013, 128, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Gregoire, T.G.; Næsset, E.; Øyen, B.-H. Detection of biomass change in a Norwegian mountain forest area using small footprint airborne laser scanner data. Stat. Methods Appl. 2012, 22, 113–129. [Google Scholar] [CrossRef]
- Økseter, R.; Bollandsås, O.M.; Gobakken, T.; Næsset, E. Modeling and predicting aboveground biomass change in young forest using multi-temporal airborne laser scanner data. Scand. J. For. Res. 2015, 30, 458–469. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Bollandsas, O.M. Indirect and direct estimation of forest biomass change using forest inventory and airborne laser scanning data. Remote Sens. Environ. 2015, 164, 36–42. [Google Scholar] [CrossRef]
- Kato, A.; Moskal, L.M.; Schiess, P.; Swanson, M.E.; Calhoun, D.; Stuetzle, W. Capturing tree crown formation through implicit surface reconstruction using airborne lidar data. Remote Sens. Environ. 2009, 113, 1148–1162. [Google Scholar] [CrossRef]
- Kajihara, M. Estimation of stem-volume increment by using sunny crown-surface area and stem-surface area. J. Jpn. Soc. 2008, 67, 501–505. [Google Scholar]
- Li, F.R.; Wang, Z.F. Studies on the effective crowndevelopment of larix olgensis (I)—Determination of the effective crown. J. Northeast For. Univ. 1996, 24, 1–8. (In Chinese) [Google Scholar]
- Mller, C.M. The influence of pruning on the growth of conifers. Forestry 1962, 33, 37–53. [Google Scholar] [CrossRef]
- Liu, Q.; Xie, L.; Dong, L.; Li, F. Dynamic simulation of the multilayer crown net photosynthetic rate and determination of the functional crown for larch (Larix olgensis) trees. New For. 2021, 52, 1011–1035. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, W.; Wang, Q.; Huang, X. Deriving individual-tree biomass from effective crown data generated by terrestrial laser scanning. Remote Sens. 2019, 11, 2793. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Liu, Z.; Jia, W.; Li, D. Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus koraiensis Plantations Based on Knot Analysis. Forests 2021, 12, 1778. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Nunes, M.; Ewers, R.; Turner, E.; Coomes, D. Mapping Aboveground Carbon in Oil Palm Plantations Using LiDAR: A Comparison of Tree-Centric versus Area-Based Approaches. Remote Sens. 2017, 9, 816. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating Individual Trees in a Savanna Woodland Using Small Footprint Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef] [Green Version]
- Ma, K.; Chen, Z.; Fu, L.; Tian, W.; Jiang, F.; Yi, J.; Du, Z.; Sun, H. Performance and Sensitivity of Individual Tree Segmentation Methods for UAV-LiDAR in Multiple Forest Types. Remote Sens. 2022, 14, 298. [Google Scholar] [CrossRef]
- Bai, D.X.; Liu, Q.; Dong, L.H.; Li, F.R. Determination and analysis of height to effective crown for planted Larix olgensis trees. J. Beijing For. Univ. 2019, 41, 76–87. (In Chinese) [Google Scholar]
- Zhang, X.; Duan, A.; Zhang, J. Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method. PLoS ONE 2013, 8, e79868. [Google Scholar] [CrossRef] [Green Version]
- Department Of Forest Resources Management S.F.A. The 7th National forest inventory and status of forest resources. For. Resour. Manag. 2010, 1, 1–8. (In Chinese) [Google Scholar]
- Qian, N.Z.; Ye, J.Z. Biomass of Chinese fir mixed family plantation in Yangkou forest farm. J. Nanjing For. Univ. Nat. Sci. 1992, 16, 6. (In Chinese) [Google Scholar]
- Bollandsås, O.M.; Næsset, E. Using delta values of multi-temporal first-return small footprint airborne laser scanner data to predict change of tree biomass in mountain spruce forests. Silvilaser 2010, 9, 411–417. [Google Scholar]
- Geng, L.; Li, M.Z.; Fan, W.Y.; Wang, B. Individual Tree Structure Parameters and Effective Crown of the Stand Extraction Base on Airborn LiDAR Data. Sci. Silvae Sin. 2018, 54, 11. (In Chinese) [Google Scholar]
- Zheng, G.; Ma, L.; Eitel, J.; Wei, H.; Magney, T.S.; Moskal, L.M.; Li, M. Retrieving directional gap fraction, extinction coefficient, and effective leaf area index by incorporating scan angle information from discrete aerial lidar data. IEEE Trans. Geosci. Remote Sens. 2016, 55, 577–590. [Google Scholar] [CrossRef]
- Wang, C.; Luo, S.; Xi, X.; Nie, S.; Ma, D.; Huang, Y. Influence of voxel size on forest canopy height estimates using full-waveform airborne lidar data. For. Ecosyst. 2020, 7, 12. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of multitemporal lidar for forest and carbon monitoring: Tree growth, biomass dynamics, and carbon flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J.; d’Oliveira, M.V.N.; Keller, M. Monitoring selective logging in western Amazonia with repeat lidar flights. Remote Sens. Environ. 2014, 151, 157–165. [Google Scholar] [CrossRef] [Green Version]



| Equation | R2 |
|---|---|
| y = ++ |
| Voxel Height (m) | R2 | RMSE (m) | Bais (m) | rRMSE | N |
|---|---|---|---|---|---|
| 1.00 | 0.86 | 0.89 | 0.72 | 6.09% | 159 |
| 0.50 | 0.85 | 0.73 | 0.47 | 4.97% | 159 |
| 0.25 | 0.87 | 0.62 | 0.36 | 4.26% | 159 |
| 0.10 | 0.87 | 0.58 | 0.29 | 3.98% | 156 |
| Model | Equation | R2 | N |
|---|---|---|---|
| 1 | 0.33 | 166 | |
| 2 | 0.57 | 166 | |
| 3 | 0.63 | 166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, J.; Zeng, H.; Cai, G.; Li, Y.; Chen, J.M.; Miao, G. Crown Information Extraction and Annual Growth Estimation of a Chinese Fir Plantation Based on Unmanned Aerial Vehicle–Light Detection and Ranging. Remote Sens. 2023, 15, 3869. https://doi.org/10.3390/rs15153869
Xiong J, Zeng H, Cai G, Li Y, Chen JM, Miao G. Crown Information Extraction and Annual Growth Estimation of a Chinese Fir Plantation Based on Unmanned Aerial Vehicle–Light Detection and Ranging. Remote Sensing. 2023; 15(15):3869. https://doi.org/10.3390/rs15153869
Chicago/Turabian StyleXiong, Jingfeng, Hongda Zeng, Guo Cai, Yunfei Li, Jing M. Chen, and Guofang Miao. 2023. "Crown Information Extraction and Annual Growth Estimation of a Chinese Fir Plantation Based on Unmanned Aerial Vehicle–Light Detection and Ranging" Remote Sensing 15, no. 15: 3869. https://doi.org/10.3390/rs15153869
APA StyleXiong, J., Zeng, H., Cai, G., Li, Y., Chen, J. M., & Miao, G. (2023). Crown Information Extraction and Annual Growth Estimation of a Chinese Fir Plantation Based on Unmanned Aerial Vehicle–Light Detection and Ranging. Remote Sensing, 15(15), 3869. https://doi.org/10.3390/rs15153869







