ICESat-2 for Coastal MSS Determination—Evaluation in the Norwegian Coastal Zone
Abstract
:1. Introduction
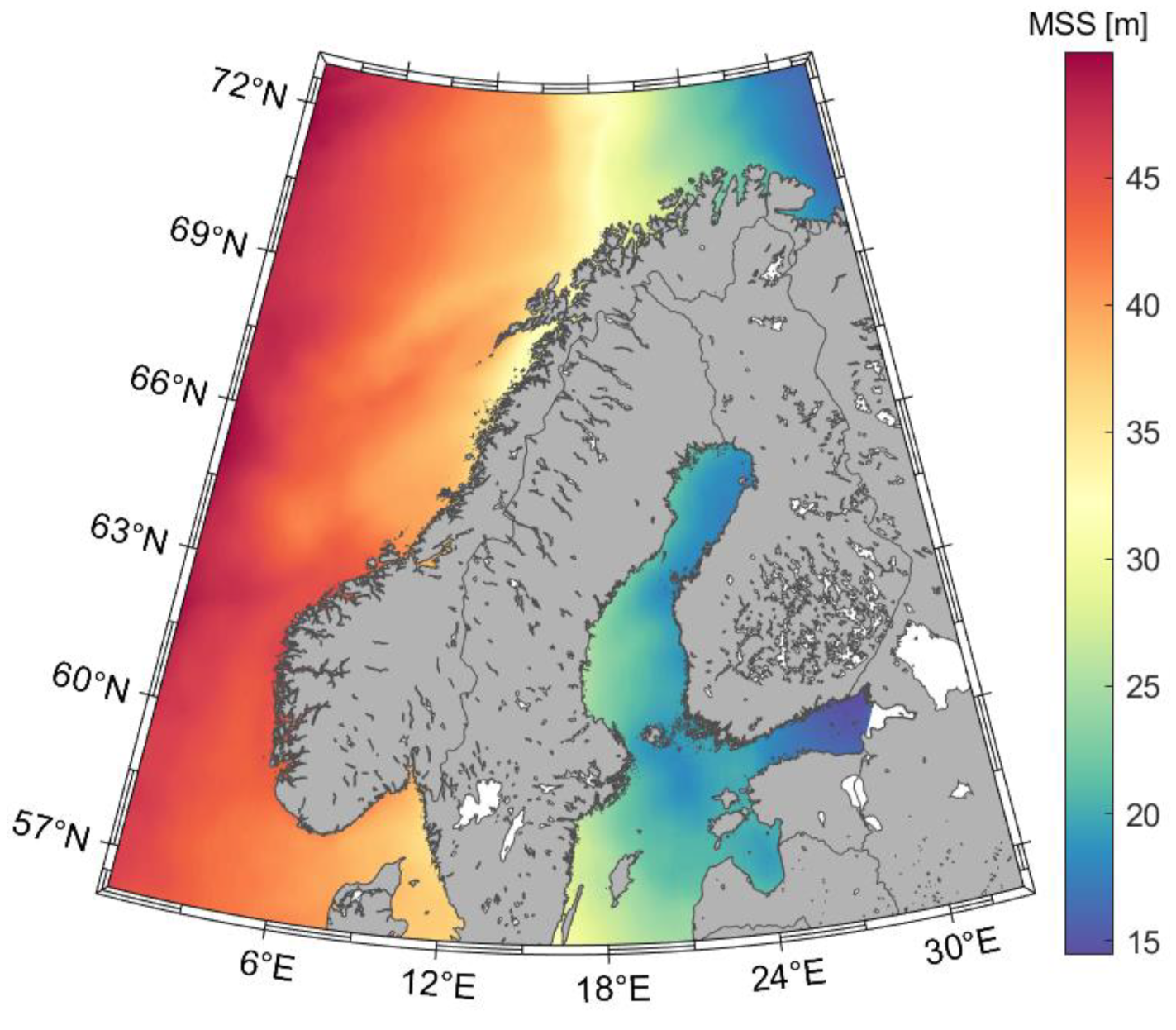
2. Metocean Conditions of the Study Area
3. Data and Methods
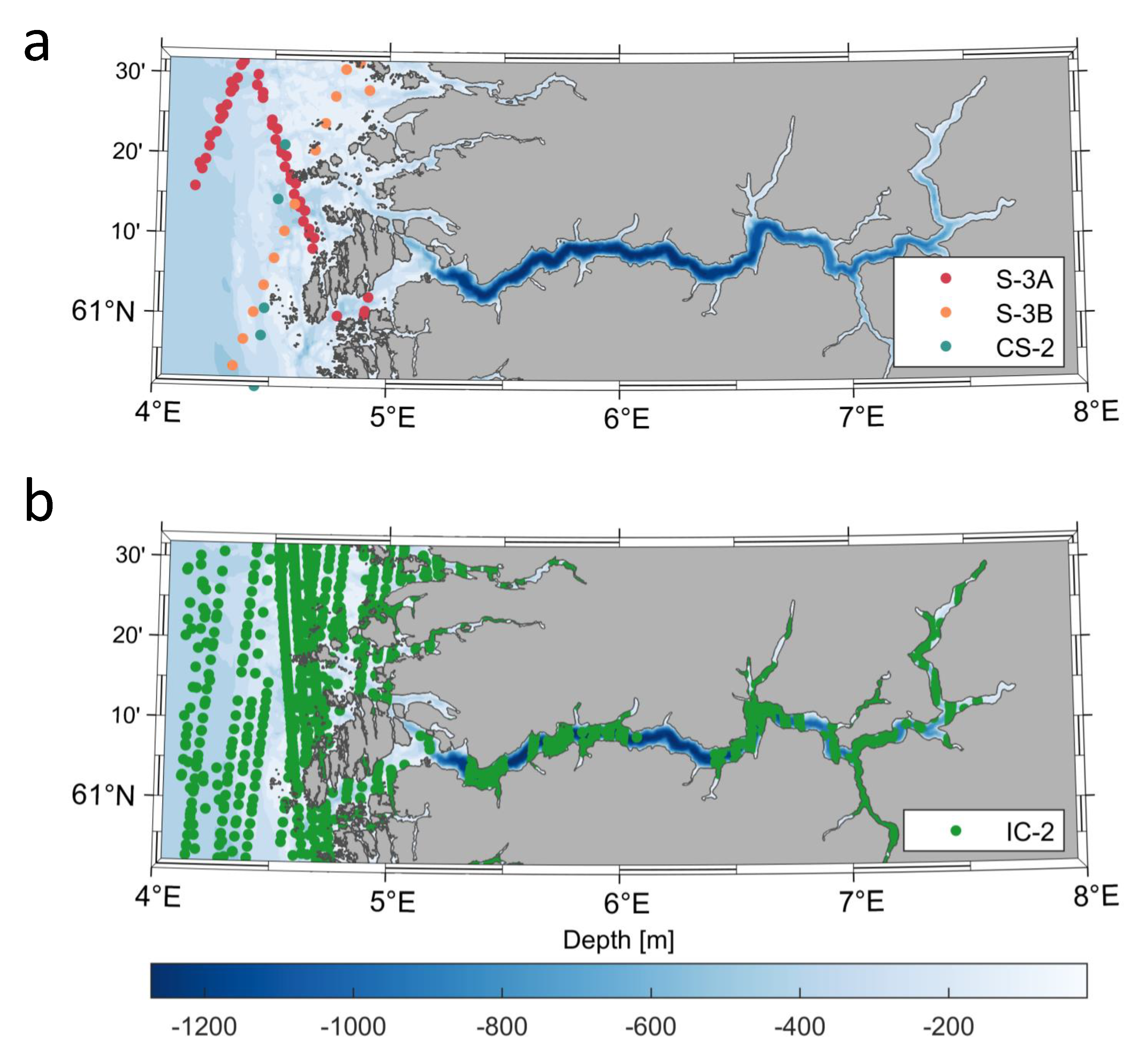
3.1. ICESat-2 ATL12 Data
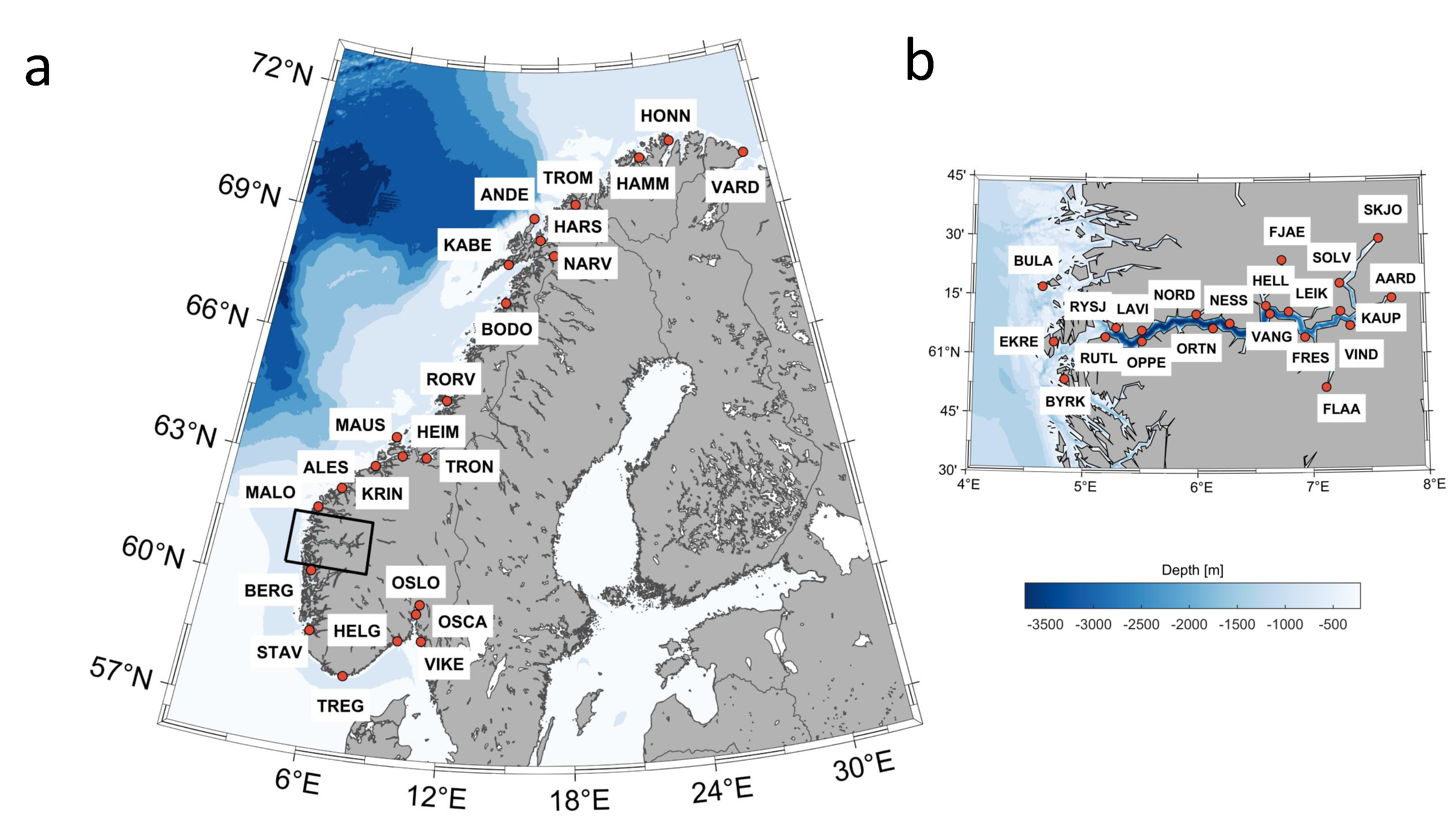
3.2. Tide Gauge Observations
3.3. Mean Sea Surface Models
3.4. MSS Determination from ICESat-2
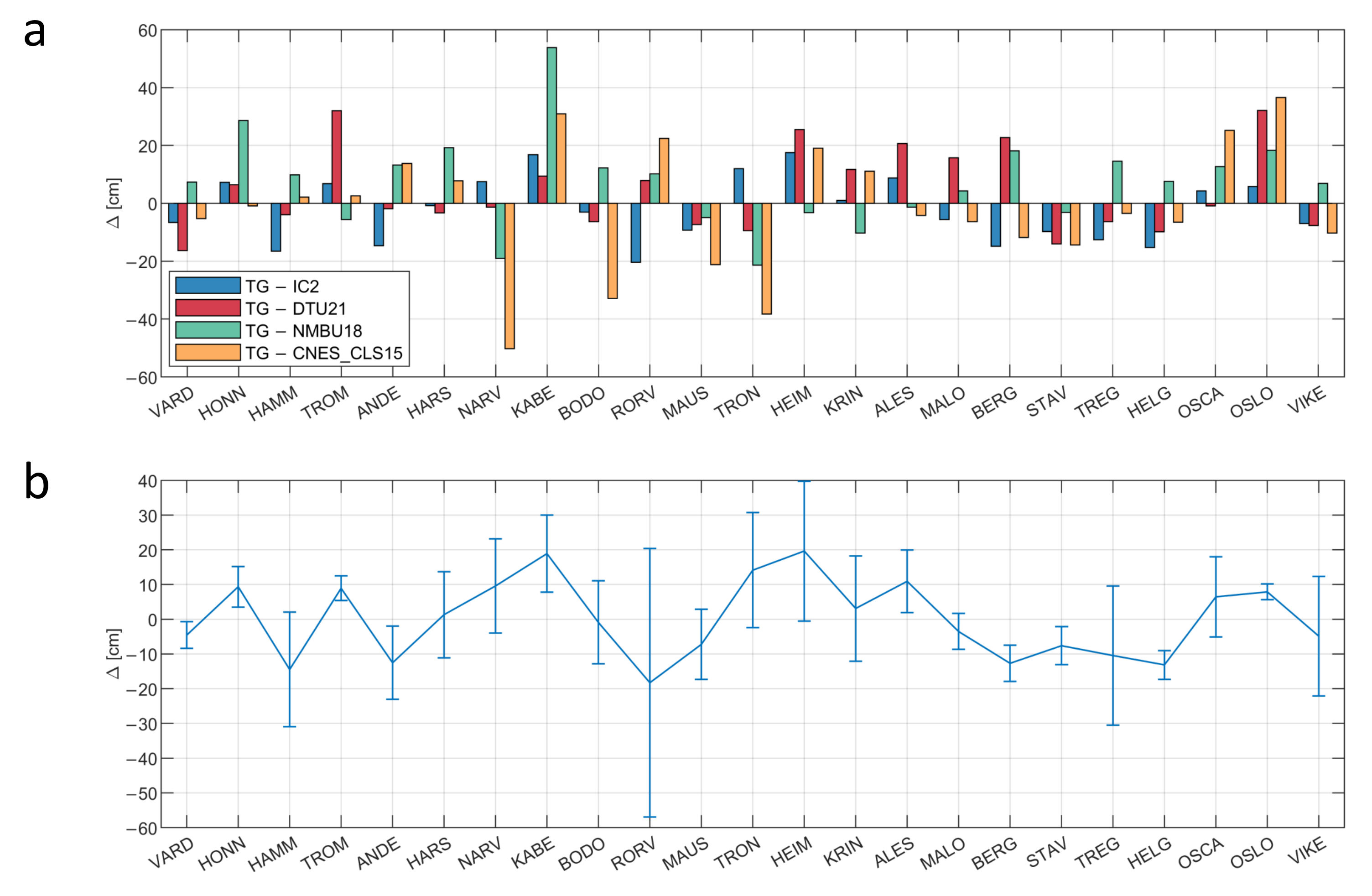
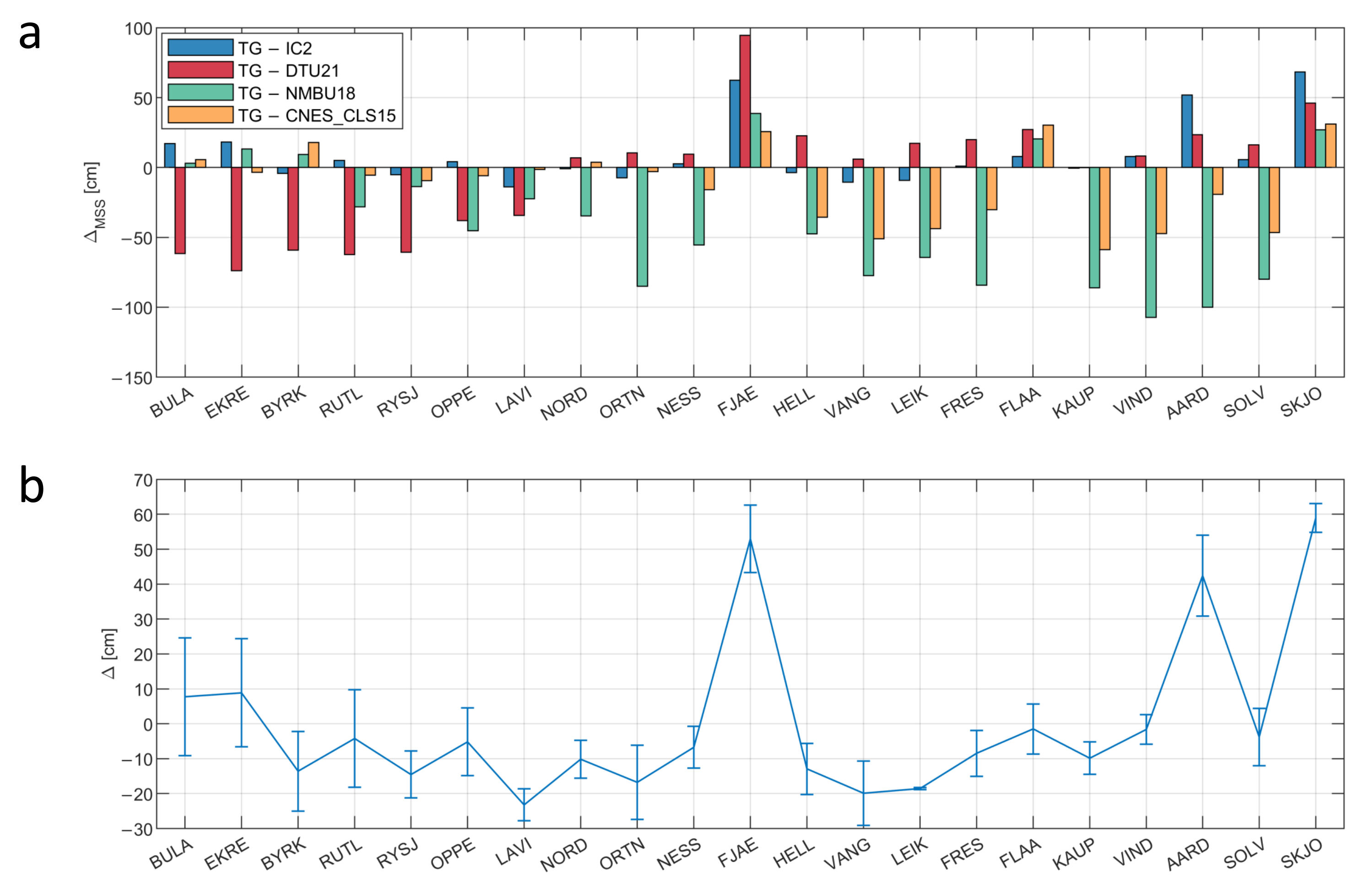
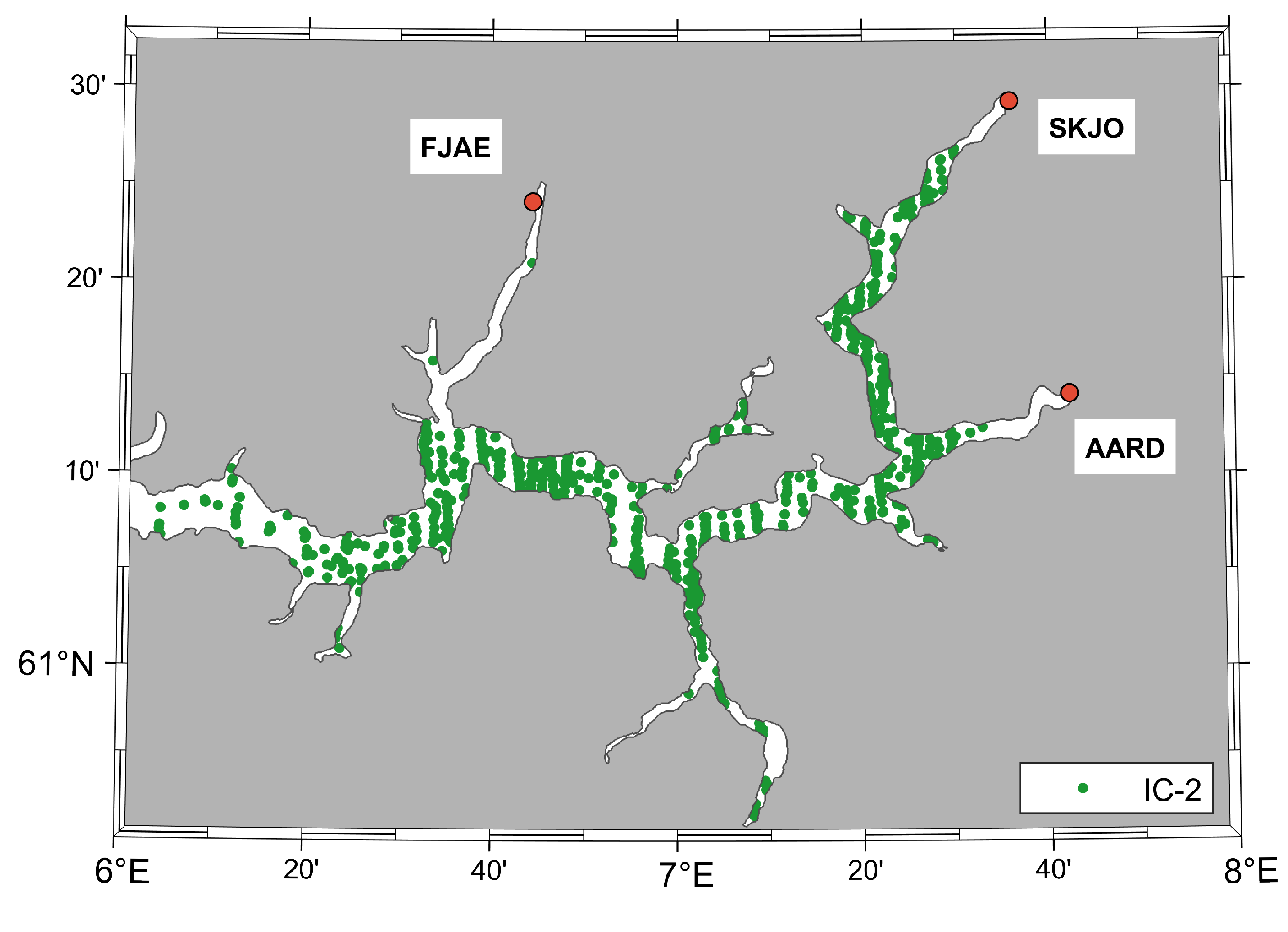
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. Ocean. 2009, 114, 1–12. [Google Scholar] [CrossRef]
- Andersen, O.B.; Scharroo, R. Range and Geophysical Corrections in Coastal Regions: Furthermore, Implications for Mean Sea Surface Determination. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 103–145. [Google Scholar] [CrossRef]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.L.; Picot, N.; Raynal, M.; Roinard, H. Satellite Altimetry Measurements of Sea Level in the Coastal Zone; Springer: Amsterdam, The Netherlands, 2019; Volume 40, pp. 1319–1349. [Google Scholar] [CrossRef]
- Vignudelli, S.; Scozzari, A.; Abileah, R.; Gómez-Enri, J.; Benveniste, J.; Cipollini, P. Water Surface Elevation in Coastal and Inland Waters Using Satellite Radar Altimetry; Elsevier Inc.: Amsterdam, The Netherlands, 2019; pp. 87–127. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- Bagnardi, M.; Kurtz, N.T.; Petty, A.A.; Kwok, R. Sea Surface Height Anomalies of the Arctic Ocean From ICESat-2: A First Examination and Comparisons With CryoSat-2. Geophys. Res. Lett. 2021, 48, 93155. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite—2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Morison, J.H.; Hancock, D.; Dickinson, S.; Robbins, J.; Roberts, L.; Kwok, R.; Palm, S.P.; Smith, B.; Jasinski, M.F.; the ICESat-2 Science Team. ATLAS/ICESat-2 L3A Ocean Surface Height, Version 4; National Snow and Ice Data Center: Boulder, CO, USA, 2021. [Google Scholar]
- Smith, B.; Fricker, H.A.; Holschuh, N.; Gardner, A.S.; Adusumilli, S.; Brunt, K.M.; Csatho, B.; Harbeck, K.; Huth, A.; Neumann, T.; et al. Land ice height-retrieval algorithm for NASA’s ICESat-2 photon-counting laser altimeter. Remote Sens. Environ. 2019, 233, 111352. [Google Scholar] [CrossRef]
- Neumann, T.A.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 5; National Snow and Ice Data Center: Boulder, CO, USA, 2021. [Google Scholar]
- NASA. Data Products|ICESat-2. Available online: https://icesat-2.gsfc.nasa.gov/science/data-products (accessed on 26 July 2023).
- Buzzanga, B.; Heijkoop, E.; Hamlington, B.D.; Nerem, R.S.; Gardner, A. An Assessment of Regional ICESat-2 Sea-Level Trends. Geophys. Res. Lett. 2021, 48, 1–9. [Google Scholar] [CrossRef]
- Klotz, B.W.; Neuenschwander, A.; Magruder, L.A. High-Resolution Ocean Wave and Wind Characteristics Determined by the ICESat-2 Land Surface Algorithm. Geophys. Res. Lett. 2020, 47, 1–10. [Google Scholar] [CrossRef]
- Morison, J.; Hancock, D.; Dickinson, S.; Robbins, J.; Roberts, L.; Kwok, R.; Palm, S.; Smith, B.; Jasinski, M.; Plant, B.; et al. Algorithm Theoretical Basis Document (ATBD) for Ocean Surface Height; Technical Report; Goddard Space Flight Center Greenbelt (NASA): Greenbelt, MD, USA, 2021. [Google Scholar]
- Gommenginger, C.; Thibaut, P.; Fenoglio-Marc, L.; Quartly, G.; Deng, X.; Gómez-Enri, J.; Challenor, P.; Gao, Y. Retracking Altimeter Waveforms Near the Coasts. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–101. [Google Scholar] [CrossRef]
- Jiang, L.; Schneider, R.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 Altimetry Applications over Rivers and Lakes. Water 2017, 9, 211. [Google Scholar] [CrossRef]
- Ophaug, V.; Breili, K.; Andersen, O.B. A coastal mean sea surface with associated errors in Norway based on new-generation altimetry. Adv. Space Res. 2021, 68, 1103–1115. [Google Scholar] [CrossRef]
- Idžanović, M.; Ophaug, V.; Andersen, O.B. Coastal sea level from CryoSat-2 SARIn altimetry in Norway. Adv. Space Res. 2018, 62, 1344–1357. [Google Scholar] [CrossRef]
- Mangini, F.; Chafik, L.; Bonaduce, A.; Bertino, L.; Nilsen, J.E.O. Sea-level variability and change along the Norwegian coast between 2003 and 2018 from satellite altimetry, tide gauges, and hydrography. Ocean Sci. 2022, 18, 331–359. [Google Scholar] [CrossRef]
- Breili, K. Dynamisk havtopografi fra Sentinel-3 og vannstandsmålere langs norskekysten. Kart Og Plan 2021, 114, 37–54. [Google Scholar] [CrossRef]
- GEBCO. GEBCO Gridded Bathymetry Data. 2021. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 1 March 2023).
- Grabbe, M.; Lalander, E.; Lundin, S.; Leijon, M. A review of the tidal current energy resource in Norway. Renew. Sustain. Energy Rev. 2009, 13, 1898–1909. [Google Scholar] [CrossRef]
- Ryrfors, T. Surface Circulation in the North-Eastern Skagerrak and the Spreading of Glomma Water along the Swedish Coast Surface Circulation in the North-Eastern Skagerrak and the Spreading of Glomma Water along the Swedish Coast. Master’s Thesis, 30 Credits UNIVERSITY OF GOTHENBURG Tomas Ryrfors Supervisor: Anders Stigebrandt. University of Gothenburg, Göteborg, Sweden, 2015. [Google Scholar] [CrossRef]
- Kartverket. What Does Storm-Surge Mean?|Kartverket.no. Available online: https://www.kartverket.no/en/at-sea/se-havniva/tides-and-water-level/what-does-storm-surge-mean (accessed on 28 July 2023).
- Naveira Garabato, A.C.; Oliver, K.I.; Watson, A.J.; Messias, M.J. Turbulent diapycnal mixing in the Nordic seas. J. Geophys. Res. Ocean. 2004, 109, 1–9. [Google Scholar] [CrossRef]
- Pugh, D.T. Tides, Surges and Mean Sea-Level (Reprinted with Corrections); Wiley Ltd.: Chichester, UK, 1996. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, 8916. [Google Scholar]
- Morison, J.; Dickinson, S.; Hancock, D.; Robbins, J.; Roberts, L. ICESat-2 ATL12 Ocean Surface Height and ATL19 Gridded Dynamic Ocean Topography. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Nilsson, B.; Andersen, O.B.; Ranndal, H.; Rasmussen, M.L. Consolidating ICESat-2 Ocean Wave Characteristics with CryoSat-2 during the CRYO2ICE Campaign. Remote Sens. 2022, 14, 1300. [Google Scholar] [CrossRef]
- Tomić, M.; Breili, K.; Gerlach, C.; Ophaug, V. Validation of conventional and retracked Sentinel-3 observations along the Norwegian coast. Unpublished Manuscript, Department of Geomatics, Faculty of Science and Technology (RealTek), Norwegian University of Life Sciences (NMBU).
- Andersen, O.B.; Rose, S.K.; Abulaitijiang, A.; Zhang, S.; Fleury, S. The DTU21 Global Mean Sea Surface and First Evaluation. Earth Syst. Sci. Data Discuss. 2023, 2023, 1–19. [Google Scholar] [CrossRef]
- Pujol, M.I.; Schaeffer, P.; Faugère, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the Improvement of Recent Mean Sea Surface Models: A New Approach for Identifying and Quantifying Their Errors. J. Geophys. Res. Ocean. 2018, 123, 5889–5911. [Google Scholar]
- Jekeli, C. Geometric Reference Systems in Geodesy; Division of Geodetic Science, School of Earth Sciences Ohio State University: Columbus, OH, USA, 2006; Volume 25. [Google Scholar]
- Veng, T.; Andersen, O.B. Consolidating sea level acceleration estimates from satellite altimetry. Adv. Space Res. 2021, 68, 496–503. [Google Scholar] [CrossRef]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer Science & Business Media: Berlin, Germany, 1999. [Google Scholar]
- Revhaug, I. Grovfeilsøk ved multippel testing med Students t-test og Fischer F-test. Kart Og Plan 2007, 67, 101–107. [Google Scholar]
- Cazenave, A.; Palanisamy, H.; Ablain, M. Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges? Adv. Space Res. 2018, 62, 1639–1653. [Google Scholar] [CrossRef]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1981; pp. 21–36. [Google Scholar]
- Ophaug, V.; Breili, K.; Gerlach, C. A comparative assessment of coastal mean dynamic topography in Norway by geodetic and ocean approaches. J. Geophys. Res. Ocean. 2015, 120, 7807–7826. [Google Scholar]

| Tide Gauge | ID | Var_obs_SL | Var_T | Var_SL | Var_IC-2 | ||
|---|---|---|---|---|---|---|---|
| Vardø | VARD (OS) | 31.104 | 70.375 | 63.4 | 60.7 | 2.7 | 2.3 |
| Honningsvåg | HONN (OS) | 25.973 | 70.980 | 46.7 | 44.1 | 2.7 | 5.0 |
| Hammerfest | HAMM (OS) | 23.683 | 70.665 | 48.9 | 46.1 | 2.8 | 3.4 |
| Tromsø | TROM (F) | 18.961 | 69.647 | 44.8 | 41.9 | 2.9 | 2.8 |
| Andenes | ANDE (OS) | 16.135 | 69.326 | 29.5 | 26.4 | 3.2 | 2.8 |
| Harstad | HARS (F) | 16.548 | 68.801 | 32.3 | 29.4 | 2.9 | 4.2 |
| Narvik | NARV (F) | 17.426 | 68.428 | 64.4 | 60.5 | 3.8 | 2.0 |
| Kabelvåg | KABE (OS) | 14.482 | 68.213 | 56.0 | 52.2 | 3.8 | 2.7 |
| Bodø | BODO (OS) | 14.391 | 67.288 | 49.5 | 45.8 | 3.7 | 2.5 |
| Rørvik | RORV (OS) | 11.230 | 64.859 | 40.8 | 37.3 | 3.5 | 2.2 |
| Mausund | MAUS (OS) | 8.665 | 63.869 | 35.4 | 32.4 | 3.0 | 3.4 |
| Heimsjø | HEIM (F) | 9.102 | 63.425 | 39.7 | 36.3 | 3.4 | 2.3 |
| Trondheim | TRON (F) | 10.392 | 63.436 | 54.3 | 51.3 | 3.0 | 3.8 |
| Kristiansund | KRIN (OS) | 7.734 | 63.114 | 31.2 | 27.7 | 3.6 | 2.5 |
| Ålesund | ALES (OS) | 6.152 | 62.469 | 26.7 | 23.1 | 3.6 | 1.5 |
| Måløy | MALO (OS) | 5.113 | 61.934 | 23.6 | 20.3 | 3.3 | 0.6 |
| Bergen | BERG (F) | 5.321 | 60.398 | 14.8 | 12.3 | 2.5 | 0.6 |
| Stavanger | STAV (OS) | 5.730 | 58.974 | 4.3 | 1.7 | 2.6 | 1.3 |
| Tregde | TREG (OS) | 7.555 | 58.006 | 2.7 | 0.6 | 2.1 | 1.6 |
| Helgeroa | HELG (OS) | 9.856 | 58.995 | 4.1 | 0.9 | 3.2 | 1.6 |
| Oscarsborg | OSCA (F) | 10.605 | 59.678 | 6.1 | 1.4 | 4.7 | 2.9 |
| Oslo | OSLO (F) | 10.735 | 59.909 | 6.6 | 1.5 | 0.5 | 1.1 |
| Viker | VIKE (O) | 10.950 | 59.036 | 5.1 | 1.0 | 4.1 | 2.1 |
| Tide Gauge | ID | Obs. Period | Var_obs_SL | Var_SL | Var_T | Var_IC-2 | ||
|---|---|---|---|---|---|---|---|---|
| Bulandet | BULA | 4.633 | 61.286 | Apr 2018–Jun 2019 | 17.6 | 15.2 | 2.4 | 2.9 |
| Ekrevika | EKRE | 4.738 | 61.052 | Apr 2018–Jun 2019 | 16.7 | 14.4 | 2.3 | 0.3 |
| Byrknes | BYRK | 4.840 | 60.894 | Apr 2018–Jun 2019 | 15.3 | 13.0 | 2.2 | 1.5 |
| Rutledal | RUTL | 5.190 | 61.075 | May 2018–Jun 2019 | 18.3 | 15.8 | 2.5 | 0 |
| Rysjedalsvika | RYSJ | 5.283 | 61.114 | May 2018–Jun 2019 | 18.1 | 17.7 | 2.3 | 1.0 |
| Oppedal | OPPE | 5.510 | 61.057 | May 2018–Jun 2019 | 18.2 | 15.8 | 2.4 | 1.1 |
| Lavik | LAVI | 5.508 | 61.104 | May 2018–Jun 2019 | 18.9 | 16.0 | 2.9 | 2.0 |
| Nordeide | NORD | 5.9859 | 61.172 | May 2018–Oct 2019 | 18.9 | 16.1 | 2.8 | 1.9 |
| Ortnevik | ORTN | 6.133 | 61.113 | May 2018–Jan 2019 | 18.8 | 16.4 | 2.4 | 1.5 |
| Nessane | NESS | 6.279 | 61.134 | May 2018–Jun 20199 | 18.8 | 16.5 | 2.3 | 1.8 |
| Fjærland | FJAE | 6.739 | 61.402 | Jun 2018–Jun 2019 | 19.5 | 17.0 | 2.4 | 2.1 |
| Hella | HELL | 6.597 | 61.208 | May 2018–May 2020 | 19.4 | 16.6 | 2.8 | 1.6 |
| Vangsnes | VANG | 6.633 | 61.174 | Jun 2018–Jun 2019 | 19.2 | 16.9 | 2.3 | 0.8 |
| Leikanger | LEIK | 6.800 | 61.183 | Jun 2018–Oct 2020 | 19.3 | 16.7 | 2.6 | 1.6 |
| Fresvik | FRES | 6.939 | 61.074 | May 2018–Jun 2019 | 18.6 | 17.1 | 1.5 | 1.1 |
| Flåm | FLAA | 7.120 | 60.861 | Jun 2018–Jun 2019 | 19.4 | 17.3 | 2.1 | 1.0 |
| Kaupanger | KAUP | 7.252 | 61.182 | Jun 2018–Oct 2020 | 19.5 | 16.9 | 2.6 | 1.1 |
| Vindedalen | VIND | 7.336 | 61.121 | Jun 2018–Jun 2019 | 19.6 | 17.2 | 2.4 | 2.0 |
| Årdalstangen | AARD | 7.703 | 61.235 | Jun 2018–May 2020 | 20.0 | 2.9 | 17.1 | 2.2 |
| Solvorn | SOLV | 7.249 | 61.301 | Jun 2018–Jun 2019 | 19.6 | 17.2 | 2.1 | 4.0 |
| Skjolden | SKJO | 7.600 | 61.488 | Jun 2018–May 2020 | 20.3 | 17.2 | 3.1 | 4.5 |
| MIN [cm] | MAX [cm] | MEAN [cm] | STD [cm] | |
|---|---|---|---|---|
| TG-IC2 | −20.4 | 17.5 | −2.1 | 11.1 |
| TG-DTU21 | −16.4 | 32.0 | 4.1 | 14.6 |
| TG-NMBU18 | −21.4 | 53.9 | 7.3 | 16.0 |
| TG-CNES_CLS15 | −50.3 | 36.6 | −1.5 | 21.6 |
| MIN [cm] | MAX [cm] | MEAN [cm] | STD [cm] | |
|---|---|---|---|---|
| TG-IC2 | −13.8 | 68.3 | 9.4 | 23.2 |
| TG-DTU21 | −73.8 | 94.5 | −3.9 | 42.9 |
| TG-NMBU18 | −107.3 | 38.8 | −39.0 | 45.2 |
| TG-CNES_CLS15 | −58.7 | 31.1 | −12.5 | 27.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomić, M.; Baltazar Andersen, O. ICESat-2 for Coastal MSS Determination—Evaluation in the Norwegian Coastal Zone. Remote Sens. 2023, 15, 3974. https://doi.org/10.3390/rs15163974
Tomić M, Baltazar Andersen O. ICESat-2 for Coastal MSS Determination—Evaluation in the Norwegian Coastal Zone. Remote Sensing. 2023; 15(16):3974. https://doi.org/10.3390/rs15163974
Chicago/Turabian StyleTomić, Matea, and Ole Baltazar Andersen. 2023. "ICESat-2 for Coastal MSS Determination—Evaluation in the Norwegian Coastal Zone" Remote Sensing 15, no. 16: 3974. https://doi.org/10.3390/rs15163974
APA StyleTomić, M., & Baltazar Andersen, O. (2023). ICESat-2 for Coastal MSS Determination—Evaluation in the Norwegian Coastal Zone. Remote Sensing, 15(16), 3974. https://doi.org/10.3390/rs15163974






