Enabling High-Resolution Micro-Vibration Detection Using Ground-Based Synthetic Aperture Radar: A Case Study for Pipeline Monitoring
Abstract
:1. Introduction
- Presenting a framework for resolving a scatterer’s cross-range location and vibrational displacement parameters from a GBSAR signal.
- Providing an in-depth analysis on the performance and limitations of the proposed framework.
- Investigating the applicability of the proposed framework for the high-resolution and accurate imaging of pipelines with micrometer vibrations.
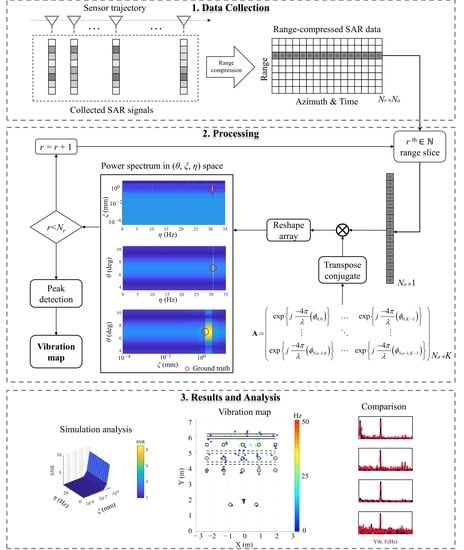
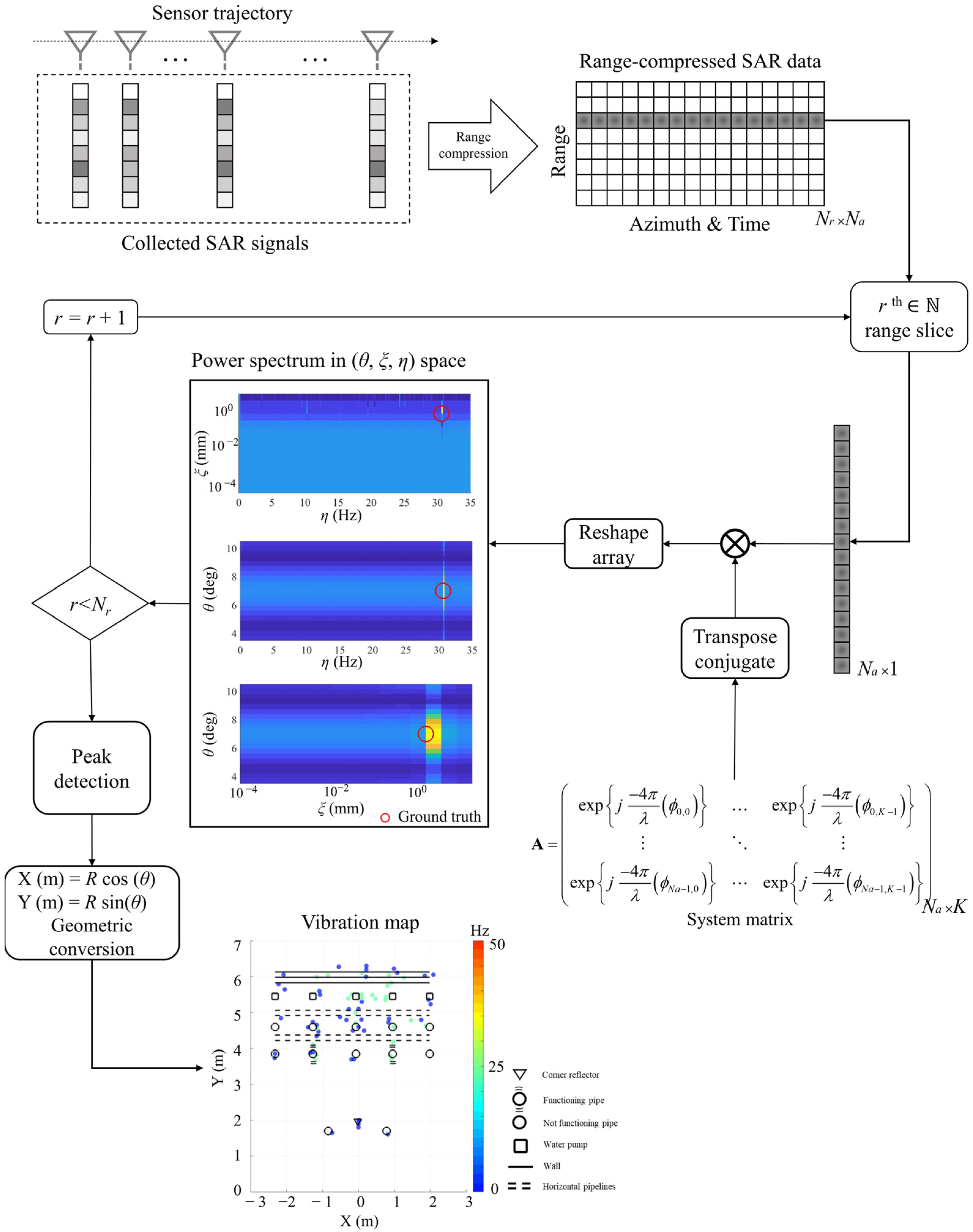
2. Materials and Methods
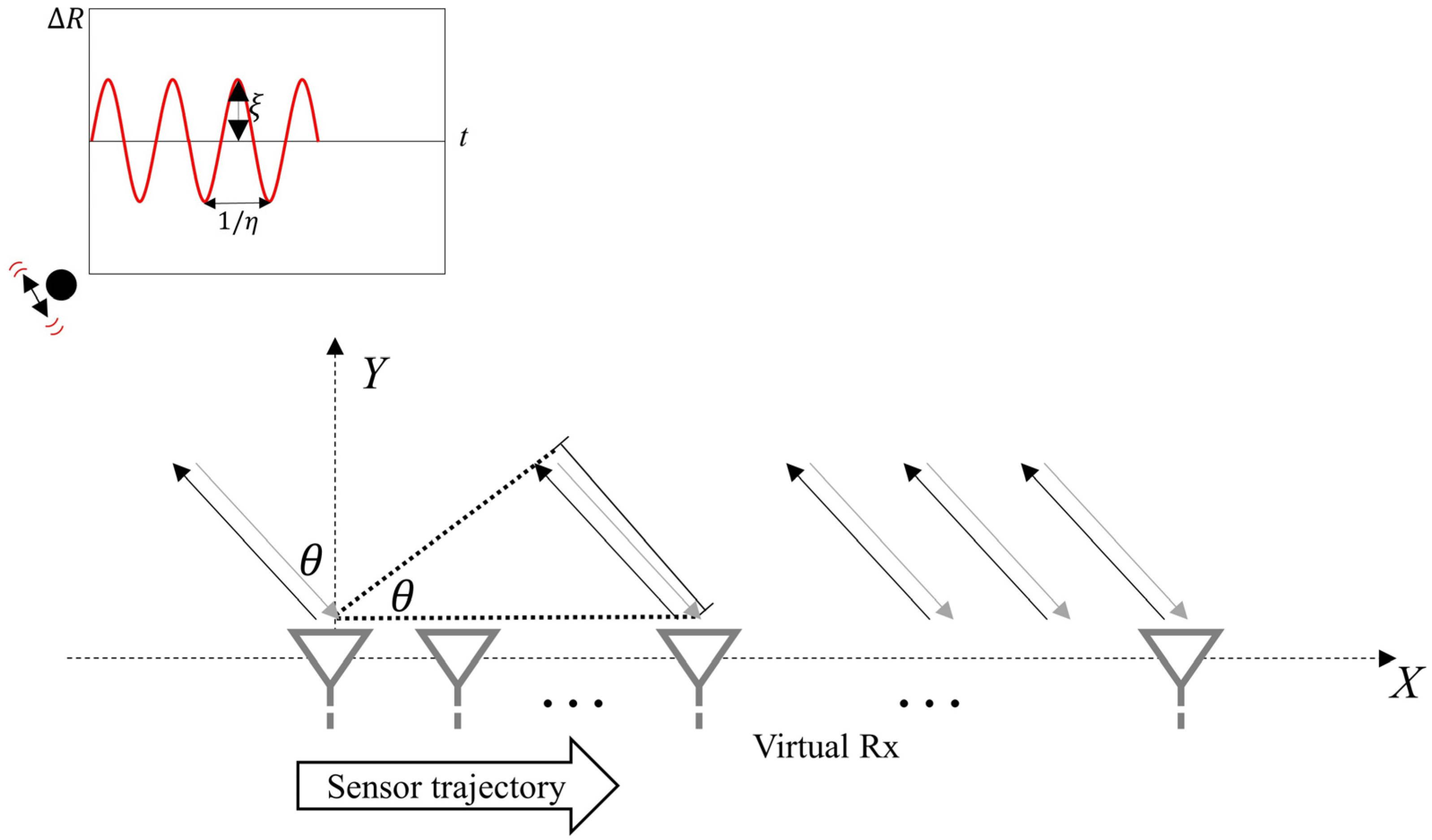
2.1. Problem Statement and Signal Model
2.2. Inversion Model
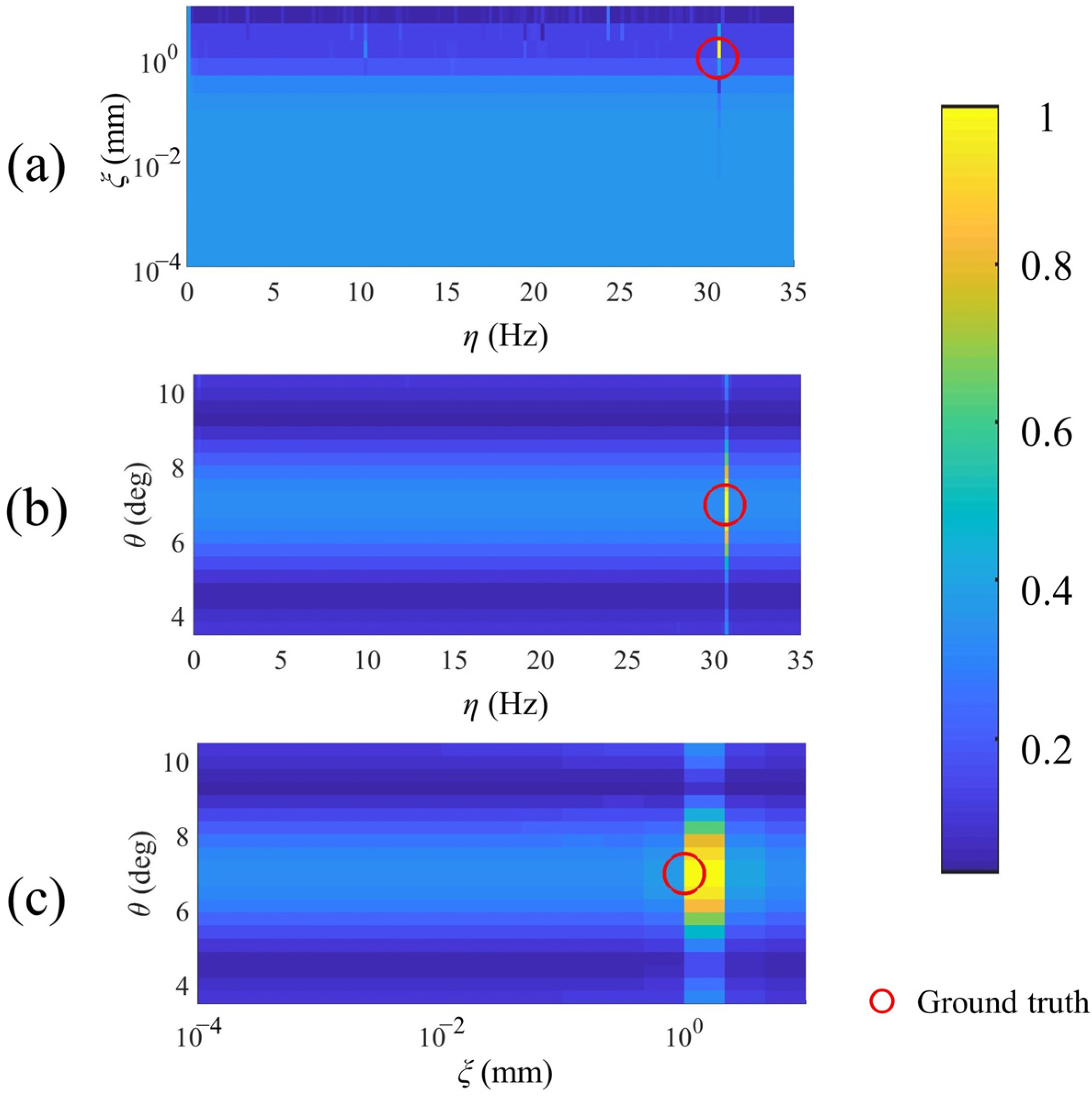
3. Experiments and Results
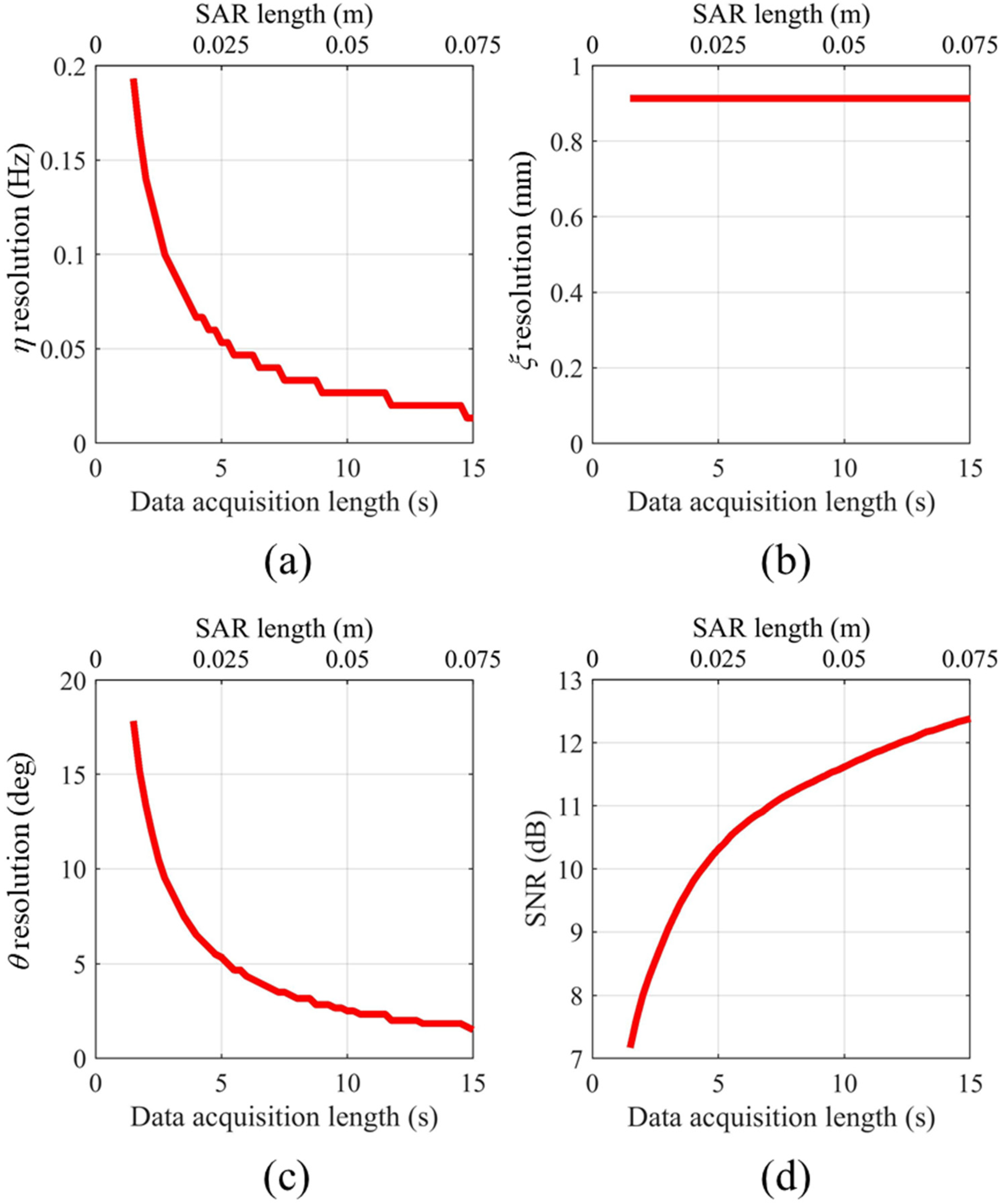
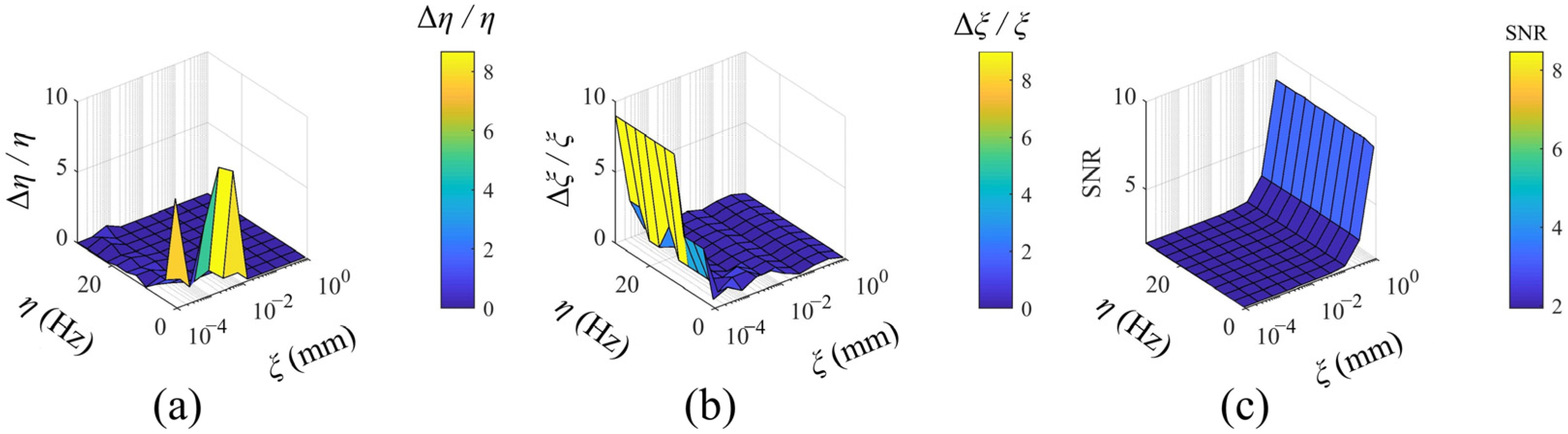
3.1. Simulations and Numerical Experiments
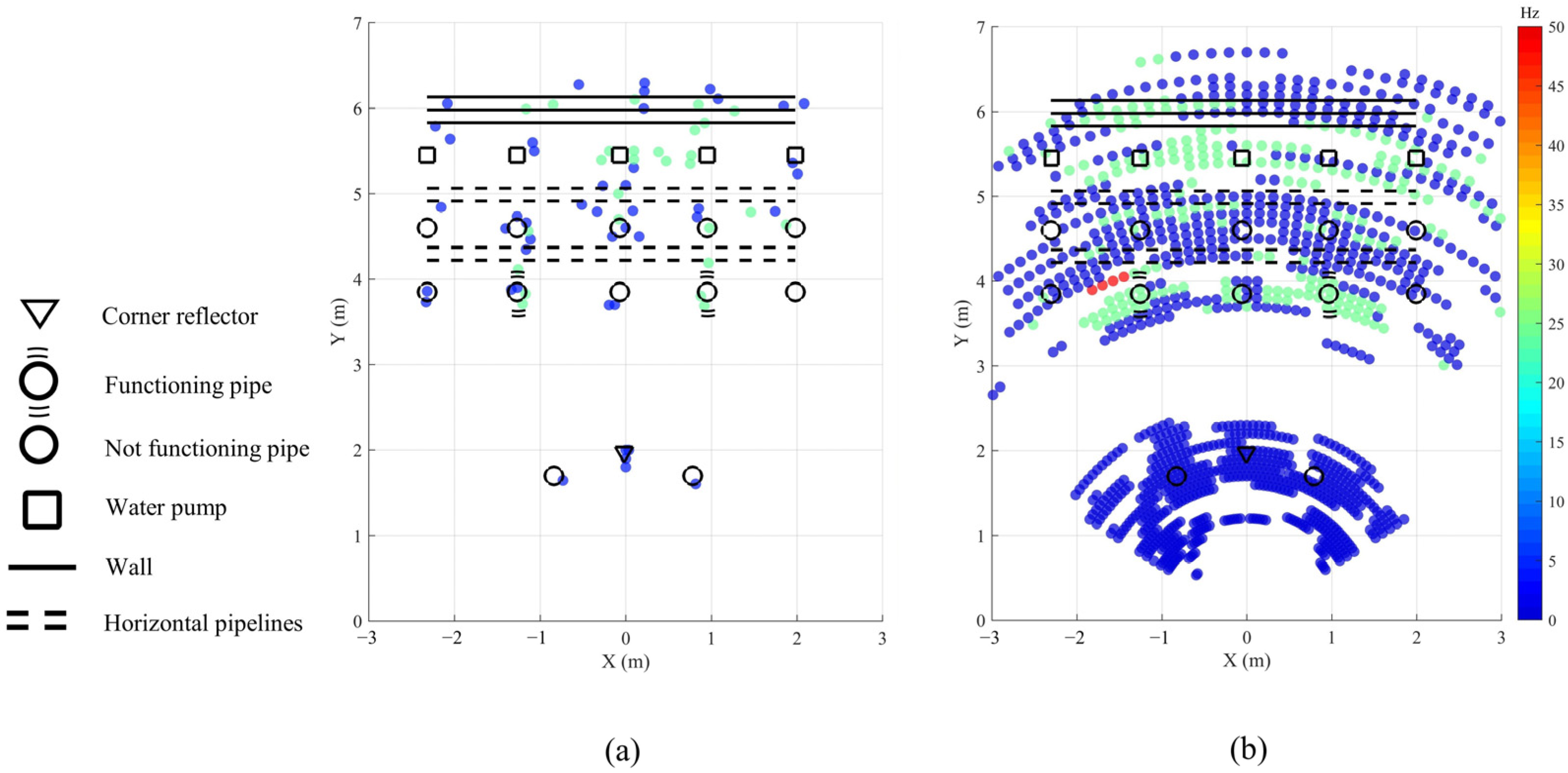
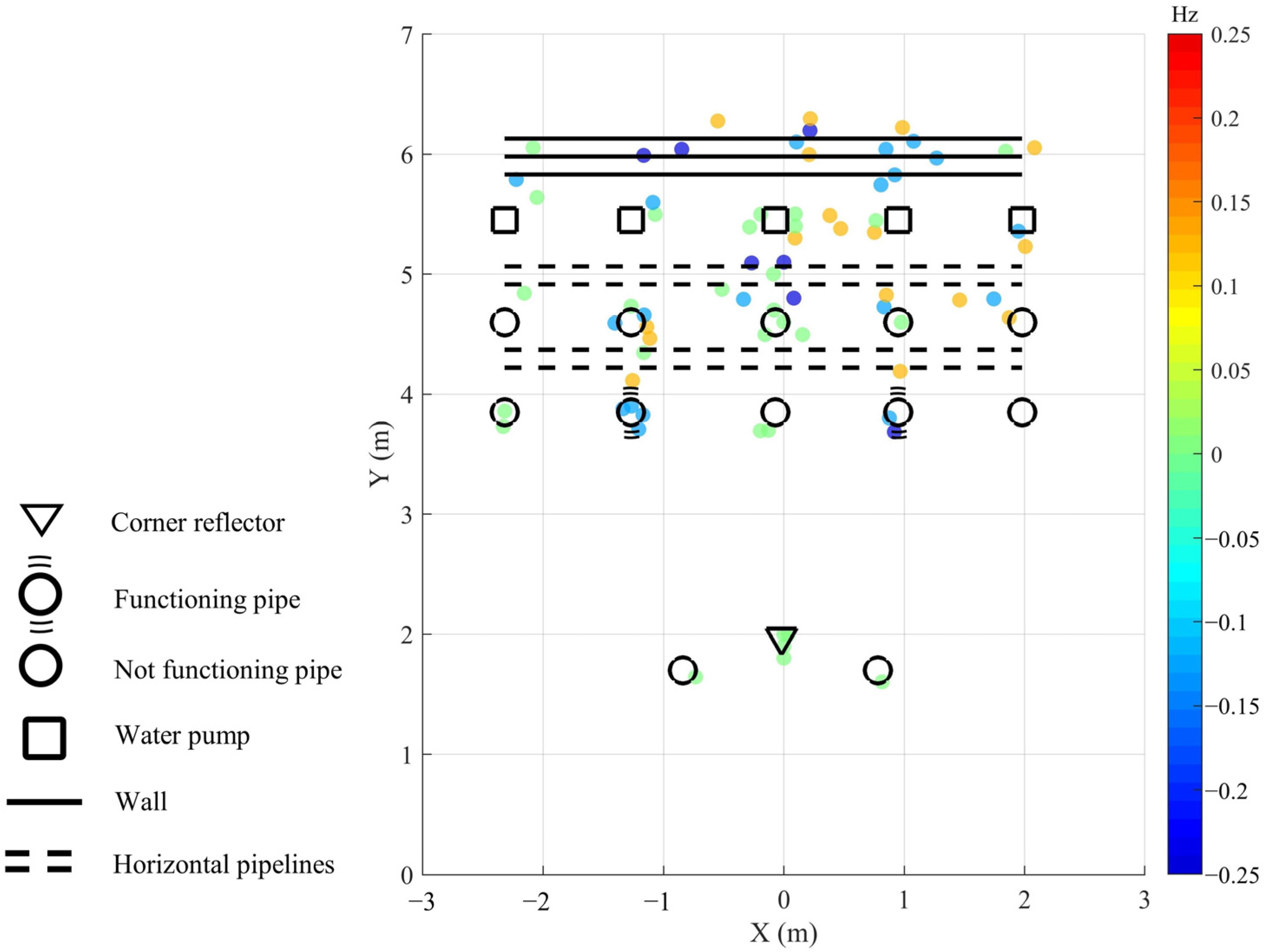
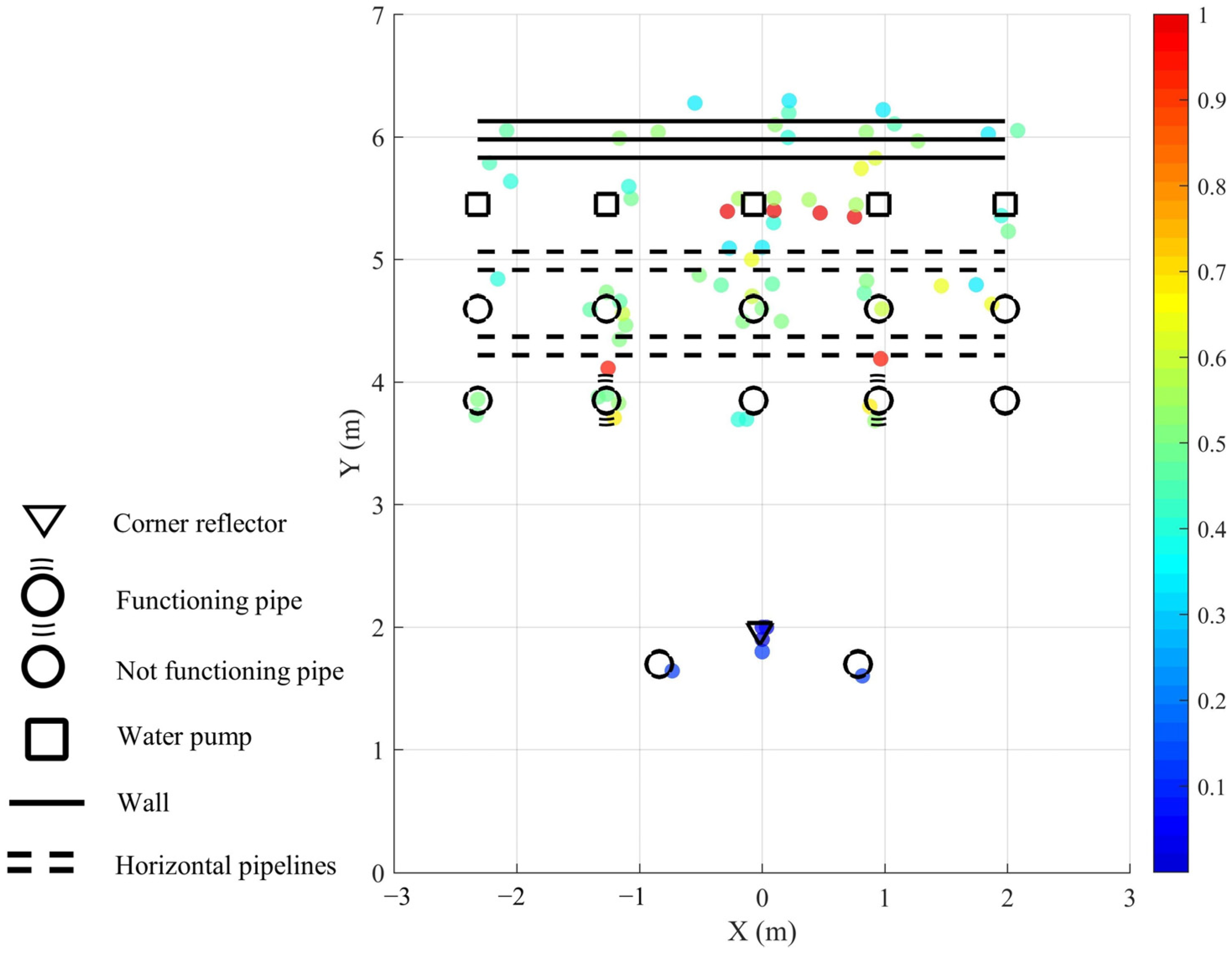
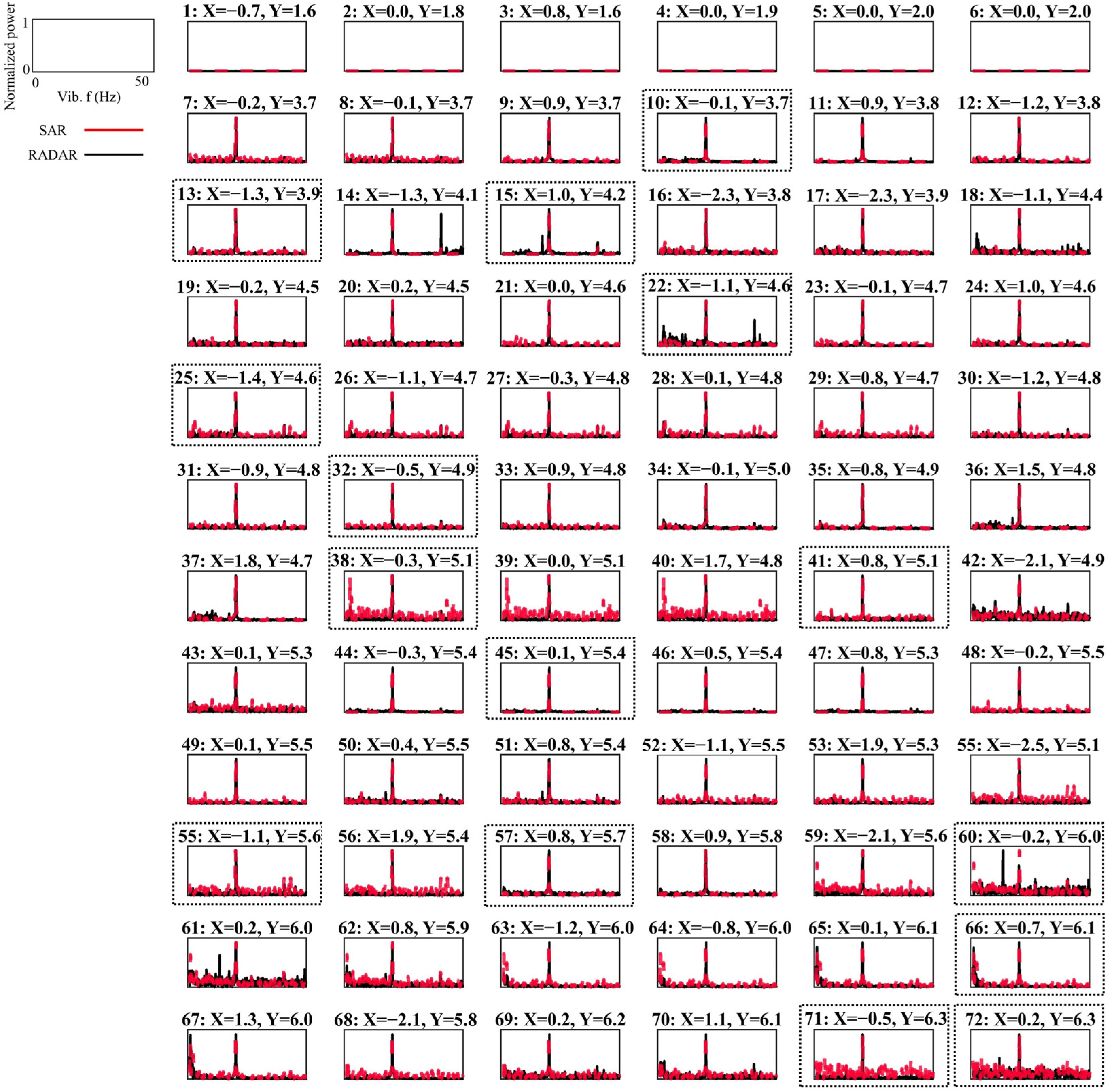
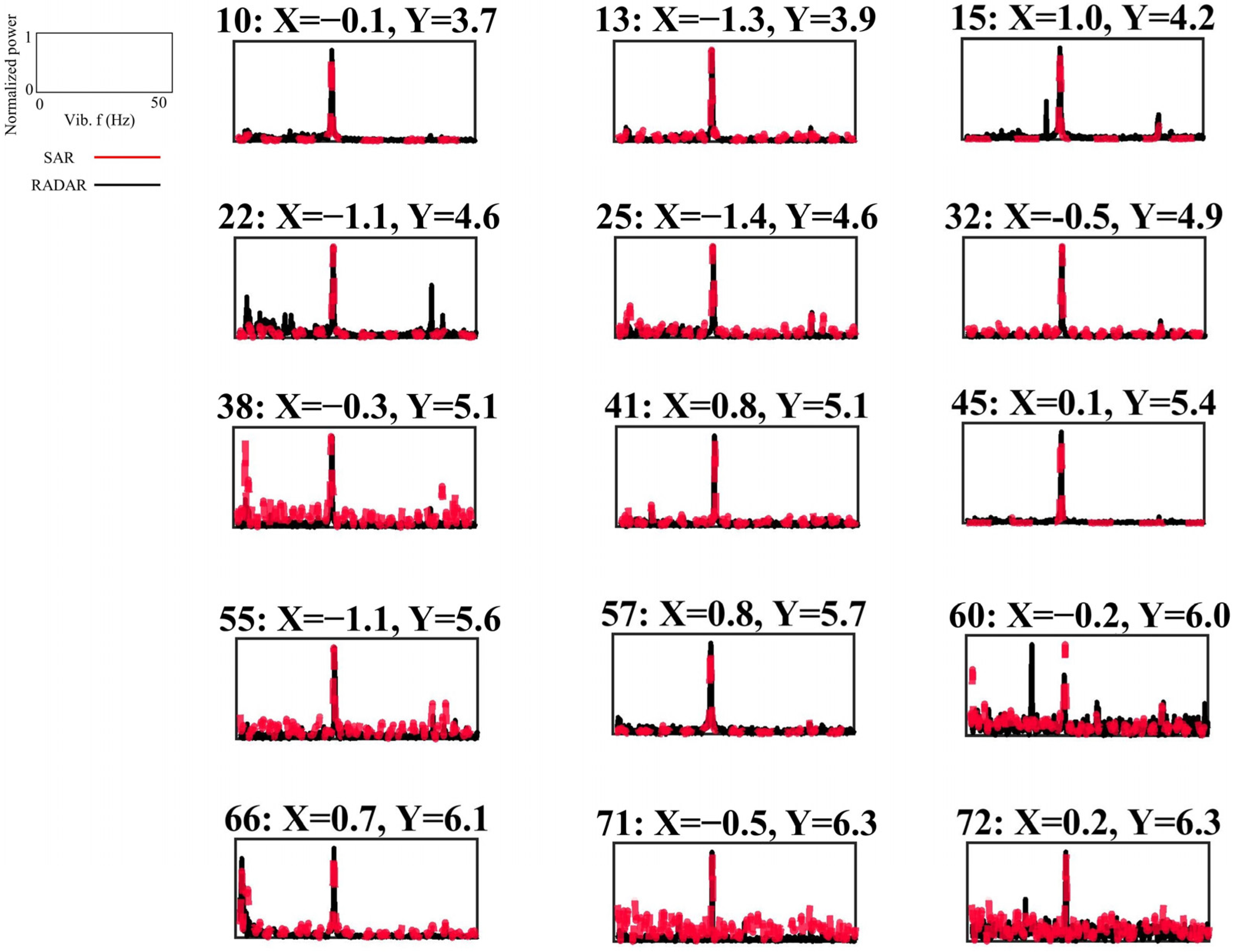
3.2. Real Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pieraccini, M. Monitoring of civil infrastructures by interferometric radar: A review. Sci. World J. 2013, 2013, 786961. [Google Scholar] [CrossRef]
- Michel, C.; Keller, S. Advancing Ground-Based Radar Processing for Bridge Infrastructure Monitoring. Sensors 2021, 21, 2172. [Google Scholar] [CrossRef]
- Alva, R.E.; Pujades, L.G.; González-Drigo, R.; Luzi, G.; Caselles, O.; Pinzón, L.A. Dynamic Monitoring of a Mid-Rise Building by Real-Aperture Radar Interferometer: Advantages and Limitations. Remote Sens. 2020, 12, 1025. [Google Scholar] [CrossRef] [Green Version]
- Luzi, G.; Crosetto, M.; Cuevas-González, M. A radar-based monitoring of the Collserola tower (Barcelona). Mech. Syst. Signal Process. 2014, 49, 234–248. [Google Scholar] [CrossRef] [Green Version]
- Baumann-Ouyang, A.; Butt, J.A.; Varga, M.; Wieser, A. MIMO-SAR Interferometric Measurements for Wind Turbine Tower Deformation Monitoring. Energies 2023, 16, 1518. [Google Scholar] [CrossRef]
- Chen, F.; Guo, H.; Tapete, D.; Cigna, F.; Piro, S.; Lasaponara, R.; Masini, N. The role of imaging radar in cultural heritage: From technologies to applications. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102907. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.; Falcone, P.; d’Aria, D.; Giunta, G. 3D vibration estimation from ground-based radar. Remote Sens. 2018, 10, 1670. [Google Scholar] [CrossRef] [Green Version]
- Sampath, S.; Bhattacharya, B.; Aryan, P.; Sohn, H. A real-time, non-contact method for in-line inspection of oil and gas pipelines using optical sensor array. Sensors 2019, 19, 3615. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Automatic leak detection in buried plastic pipes of water supply networks by means of vibration measurements. Shock Vib. 2015, 2015, 165304. [Google Scholar] [CrossRef] [Green Version]
- Lalam, N.; Lu, P.; Venketeswaran, A.; Buric, M.P. Pipeline Monitoring Using Highly Sensitive Vibration Sensor Based on Fiber Ring Cavity Laser. Sensors 2021, 21, 2078. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.A.; Karki, H.; Shukla, A.; Zhang, X. A smart robotic system for non-contact condition monitoring and fault detection in buried pipelines. In Proceedings of the Society of Petroleum Engineers-Abu Dhabi International Petroleum Exhibition and Conference 2018, ADIPEC 2018, Abu Dhabi, United Arab Emirates, 12–15 November 2018; OnePetro: Richardson, TX, USA, 2019. [Google Scholar]
- Bhadran, V.; Shukla, A.; Karki, H. Non-contact flaw detection and condition monitoring of subsurface metallic pipelines using magnetometric method. Mater. Today Proc. 2019, 28, 860–864. [Google Scholar] [CrossRef]
- Ghazali, M.H.; Hee, L.M.; Leong, M.S. Piping vibration due to pressure pulsations. Adv. Mater. Res. 2014, 845, 350–354. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef] [Green Version]
- Radman, A.; Akhoondzadeh, M.; Hosseiny, B. Integrating InSAR and deep-learning for modeling and predicting subsidence over the adjacent area of Lake Urmia, Iran. GIScience Remote Sens. 2021, 58, 1413–1433. [Google Scholar] [CrossRef]
- Reigber, A.; Scheiber, R.; Jager, M.; Prats-Iraola, P.; Hajnsek, I.; Jagdhuber, T.; Papathanassiou, K.P.; Nannini, M.; Aguilera, E.; Baumgartner, S.; et al. Very-High-Resolution Airborne Synthetic Aperture Radar Imaging: Signal Processing and Applications. Proc. IEEE 2013, 101, 759–783. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wang, Z.; Wang, Y.; Wu, J.; Wang, J.; Jia, Y.; Gui, G. Classification of high-spatial-resolution remote sensing scenes method using transfer learning and deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1986–1995. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Y.; Zhao, W.; Zhang, J. Radar-based multipoint displacement measurements of a 1200-m-long suspension bridge. ISPRS J. Photogramm. Remote Sens. 2020, 167, 71–84. [Google Scholar] [CrossRef]
- Akbari, V.; Lauknes, T.R.; Rouyet, L.; Negrel, J.; Eltoft, T. Validation of SAR iceberg detection with ground-based radar and GPS measurements. Int. Geosci. Remote Sens. Symp. 2018, 2018, 4623–4626. [Google Scholar] [CrossRef] [Green Version]
- Hosseiny, B.; Amini, J.; Safavi-Naeini, S. Simulation and Evaluation of an mm-Wave MIMO Ground-Based SAR Imaging System for Displacement Monitoring. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8213–8216. [Google Scholar]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef] [Green Version]
- Pieraccini, M.; Miccinesi, L. Ground-based radar interferometry: A bibliographic review. Remote Sens. 2019, 11, 1029. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-Based Differential Interferometry SAR: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 43–70. [Google Scholar] [CrossRef]
- Baumann-Ouyang, A.; Butt, J.A.; Salido-Monzú, D.; Wieser, A. MIMO-SAR Interferometric Measurements for Structural Monitoring: Accuracy and Limitations. Remote Sens. 2021, 13, 4290. [Google Scholar] [CrossRef]
- Ciattaglia, G.; De Santis, A.; Disha, D.; Spinsante, S.; Castellini, P.; Gambi, E. Performance Evaluation of Vibrational Measurements through mmWave Automotive Radars. Remote Sens. 2020, 13, 98. [Google Scholar] [CrossRef]
- Hosseiny, B.; Amini, J.; Aghababaei, H. Interferometric Processing of a Developed Mimo Gbsar for Displacement Monitoring. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, X-4/W1-2022, 301–306. [Google Scholar] [CrossRef]
- Baumann-Ouyang, A.; Butt, J.A.; Wieser, A. Estimating 3D displacement vectors from line-of-sight observations with application to MIMO-SAR. J. Appl. Geod. 2023, 17, 269–283. [Google Scholar] [CrossRef]
- Miccinesi, L.; Consumi, T.; Beni, A.; Pieraccini, M. W-band MIMO GB-SAR for Bridge Testing/Monitoring. Electronics 2021, 10, 2261. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Wang, J.; Wang, Y.; Li, Y.; Huang, X. Fast Displacement Estimation of Multiple Close Targets with MIMO Radar and MUSICAPES Method. Remote Sens. 2022, 14, 2005. [Google Scholar] [CrossRef]
- Hosseiny, B.; Amini, J.; Aghababaei, H. Structural displacement monitoring using ground-based synthetic aperture radar. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103144. [Google Scholar] [CrossRef]
- Xiong, Y.; Peng, Z.; Jiang, W.; He, Q.; Zhang, W.; Meng, G. An Effective Accuracy Evaluation Method for LFMCW Radar Displacement Monitoring with Phasor Statistical Analysis. IEEE Sens. J. 2019, 19, 12224–12234. [Google Scholar] [CrossRef]
- Artese, S.; Nico, G. TLS and GB-RAR Measurements of Vibration Frequencies and Oscillation Amplitudes of Tall Structures: An Application to Wind Towers. Appl. Sci. 2020, 10, 2237. [Google Scholar] [CrossRef] [Green Version]
- Rojhani, N.; Passafiume, M.; Lucarelli, M.; Collodi, G.; Cidronali, A. Assessment of Compressive Sensing 2 × 2 MIMO Antenna Design for Millimeter-Wave Radar Image Enhancement. Electronics 2020, 9, 624. [Google Scholar] [CrossRef] [Green Version]
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO radar and ground-based SAR imaging systems: Equivalent approaches for remote sensing. IEEE Trans. Geosci. Remote Sens. 2012, 51, 425–435. [Google Scholar] [CrossRef]
- Chen, C.-Y. Signal Processing Algorithms for MIMO Radar; California Institute of Technology: Pasadena, CA, USA, 2009; ISBN 1267438711. [Google Scholar]
- Fortuny-Guasch, J. A fast and accurate far-field pseudopolar format radar imaging algorithm. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1187–1196. [Google Scholar] [CrossRef]
- Zhang, W.; Li, G.; Wang, Z.; Wu, H. Non-contact monitoring of human heartbeat signals using mm-wave frequency-modulated continuous-wave radar under low signal-to-noise ratio conditions. IET Radar Sonar Navig. 2022, 16, 456–469. [Google Scholar] [CrossRef]
- Fornaro, G.; Lombardini, F.; Pauciullo, A.; Reale, D.; Viviani, F. Tomographic processing of interferometric SAR data: Developments, applications, and future research perspectives. IEEE Signal Process. Mag. 2014, 31, 41–50. [Google Scholar] [CrossRef]
- Lombardini, F. Differential tomography: A new framework for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 37–44. [Google Scholar] [CrossRef]
- Aghababaei, H. On the assessment of non-local multi-looking in detection of persistent scatterers using SAR tomography. Remote Sens. 2020, 12, 3195. [Google Scholar] [CrossRef]
- Rambour, C.; Budillon, A.; Johnsy, A.C.; Denis, L.; Tupin, F.; Schirinzi, G. From interferometric to tomographic SAR: A review of synthetic aperture radar tomography-processing techniques for scatterer unmixing in urban areas. IEEE Geosci. Remote Sens. Mag. 2020, 8, 6–29. [Google Scholar] [CrossRef]
- Aghababaee, H.; Ferraioli, G.; Schirinzi, G.; Pascazio, V. Regularization of SAR tomography for 3-D height reconstruction in urban areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 648–659. [Google Scholar] [CrossRef]


| Name | Value |
|---|---|
| Radar model | TI-AWR1642BOOST |
| Signal type | Linear FMCW |
| System’s operating frequency | 76–81 GHz |
| Carrier frequency (fc) | 77 GHz |
| Wavelength (λ) | 0.0039 m |
| Bandwidth (B) | 1.5 GHz |
| Range resolution | 0.1 m |
| Range samples | 512 |
| Sweep time | 60 μs |
| Maximum length of SAR | 0.15 m |
| Maximum cross-range resolution | 0.013 rad |
| SAR velocity | 0.005 m/s |
| Parameter | Value |
|---|---|
| Signal SNR | 5 dB |
| SAR length | 0.04 m |
| Signal repetition time | 8 ms |
| Total acquisition duration | 8 s |
| Target’s location | r = 5 m θ = 7 deg |
| Target’s vibration | ξ = 0.51 mm η = 24.2 deg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseiny, B.; Amini, J.; Aghababaei, H.; Ferraioli, G. Enabling High-Resolution Micro-Vibration Detection Using Ground-Based Synthetic Aperture Radar: A Case Study for Pipeline Monitoring. Remote Sens. 2023, 15, 3981. https://doi.org/10.3390/rs15163981
Hosseiny B, Amini J, Aghababaei H, Ferraioli G. Enabling High-Resolution Micro-Vibration Detection Using Ground-Based Synthetic Aperture Radar: A Case Study for Pipeline Monitoring. Remote Sensing. 2023; 15(16):3981. https://doi.org/10.3390/rs15163981
Chicago/Turabian StyleHosseiny, Benyamin, Jalal Amini, Hossein Aghababaei, and Giampaolo Ferraioli. 2023. "Enabling High-Resolution Micro-Vibration Detection Using Ground-Based Synthetic Aperture Radar: A Case Study for Pipeline Monitoring" Remote Sensing 15, no. 16: 3981. https://doi.org/10.3390/rs15163981
APA StyleHosseiny, B., Amini, J., Aghababaei, H., & Ferraioli, G. (2023). Enabling High-Resolution Micro-Vibration Detection Using Ground-Based Synthetic Aperture Radar: A Case Study for Pipeline Monitoring. Remote Sensing, 15(16), 3981. https://doi.org/10.3390/rs15163981