An Efficient BDS-3 Long-Range Undifferenced Network RTK Positioning Algorithm
Abstract
:1. Introduction
2. Long-Range URTK Algorithm
2.1. Reference Station Network Double-Difference Integer AR
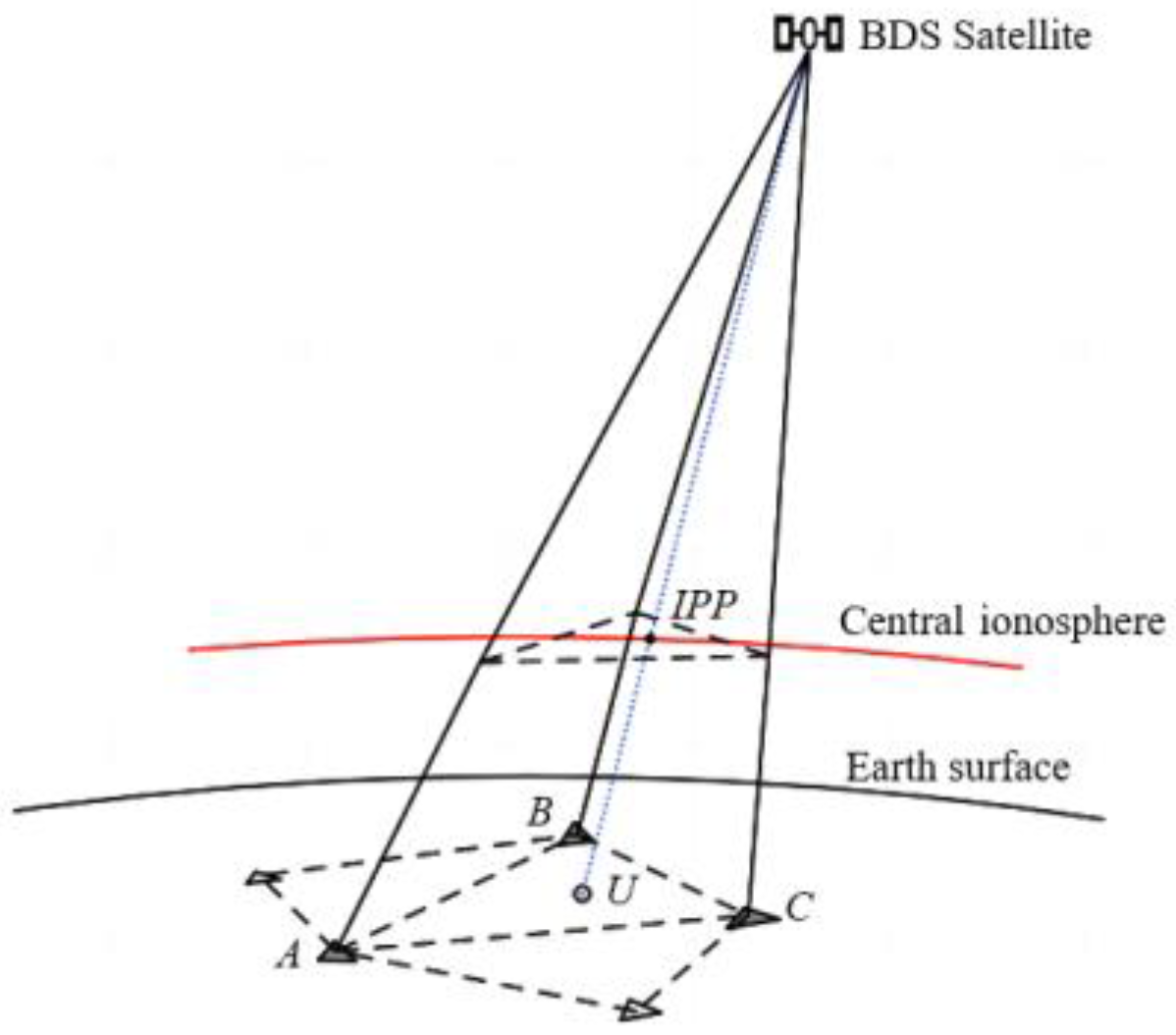
2.2. Undifferenced Error Correction Value Calculation
2.3. Phase Integer AR and Rover Station Positioning
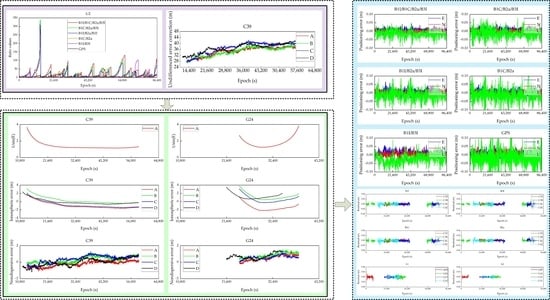
3. Experimental Results Analysis
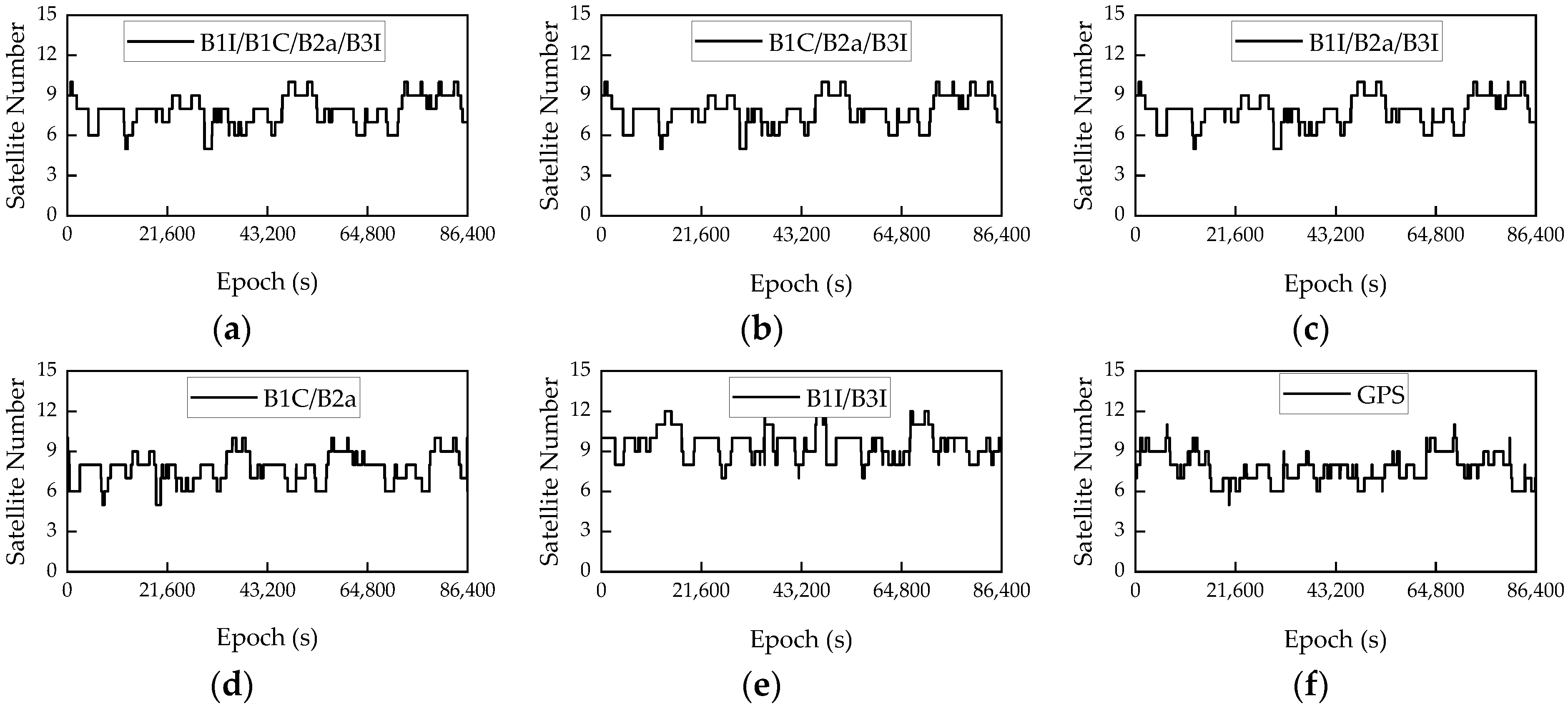
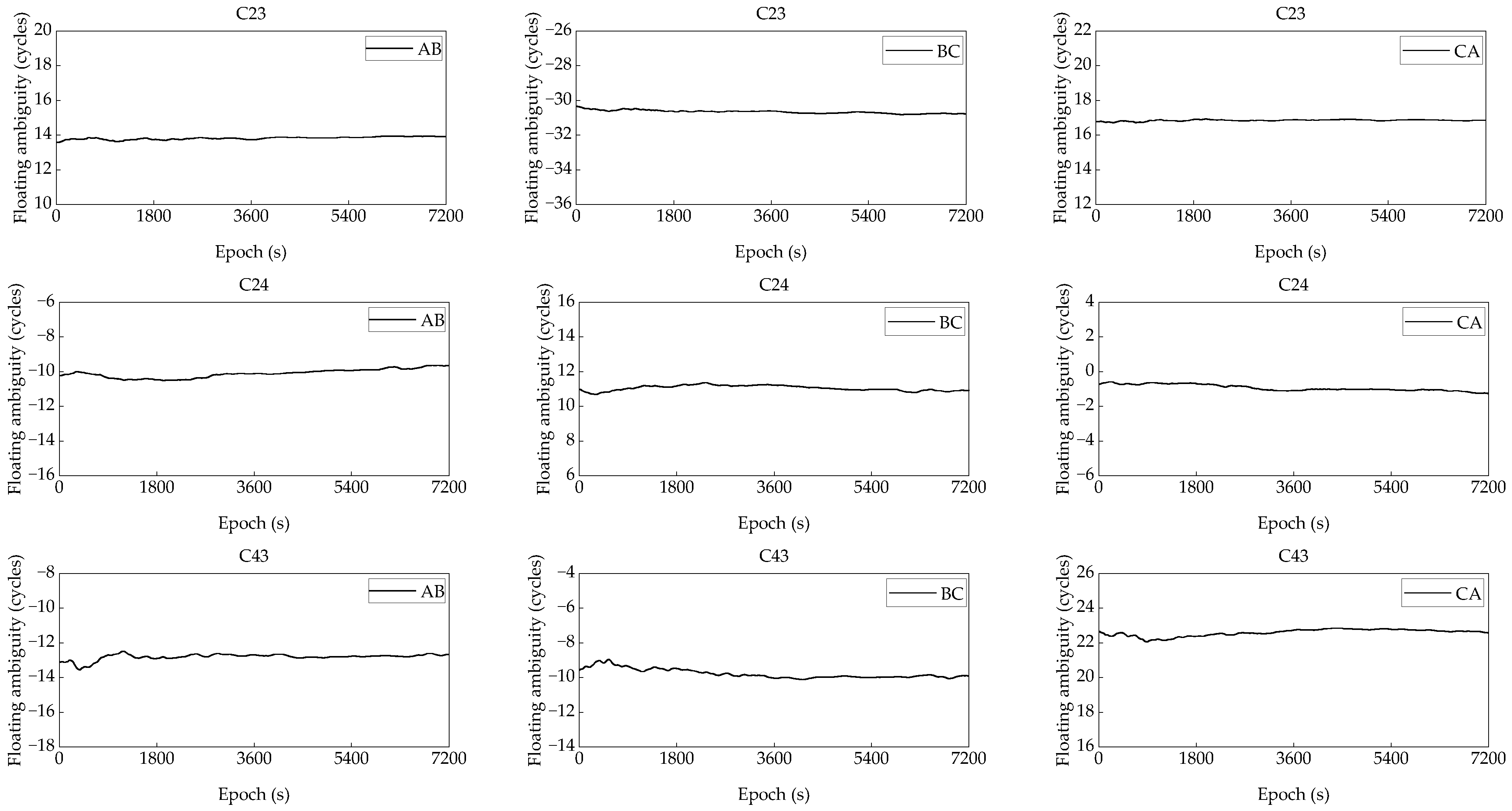
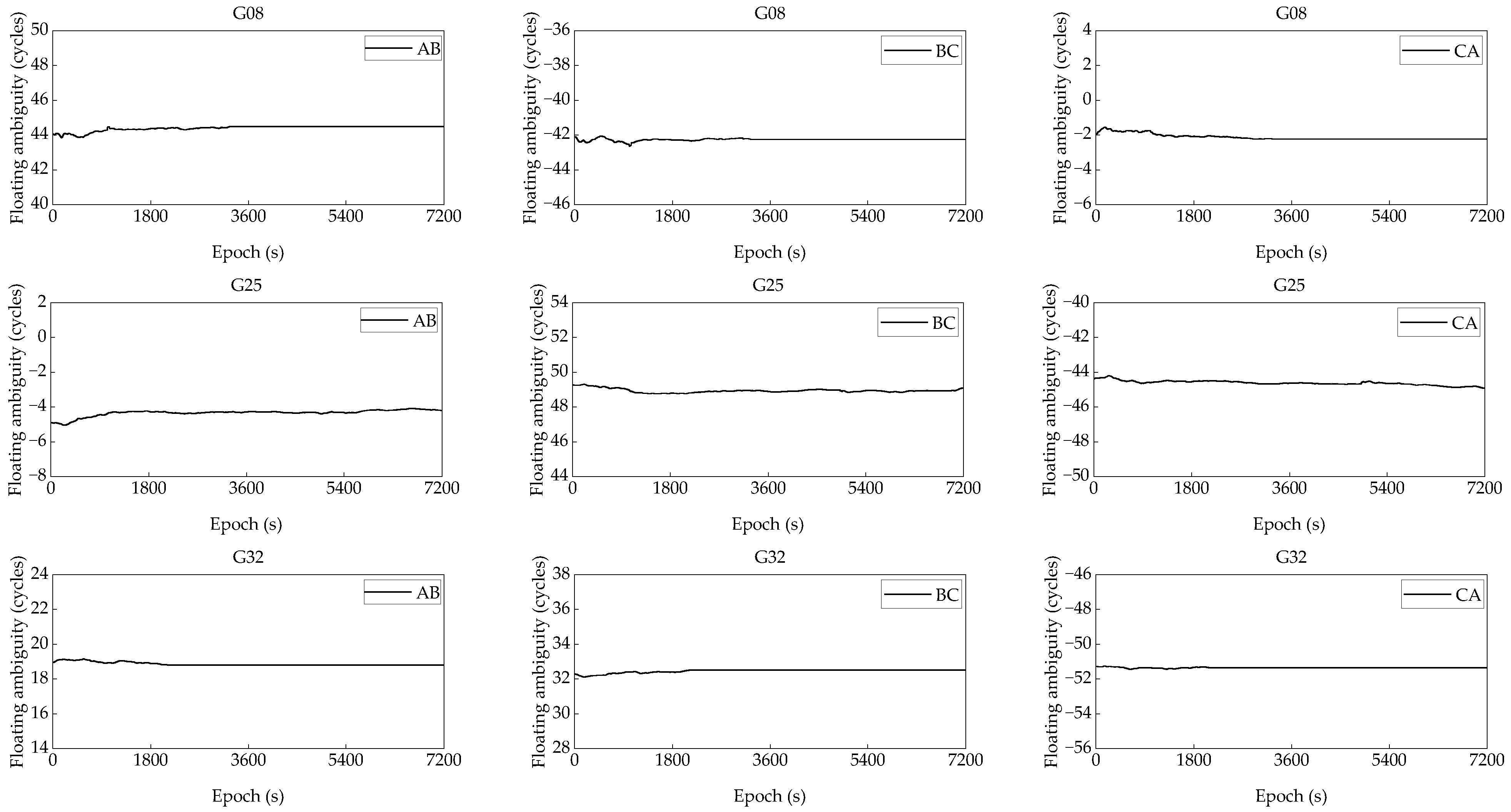
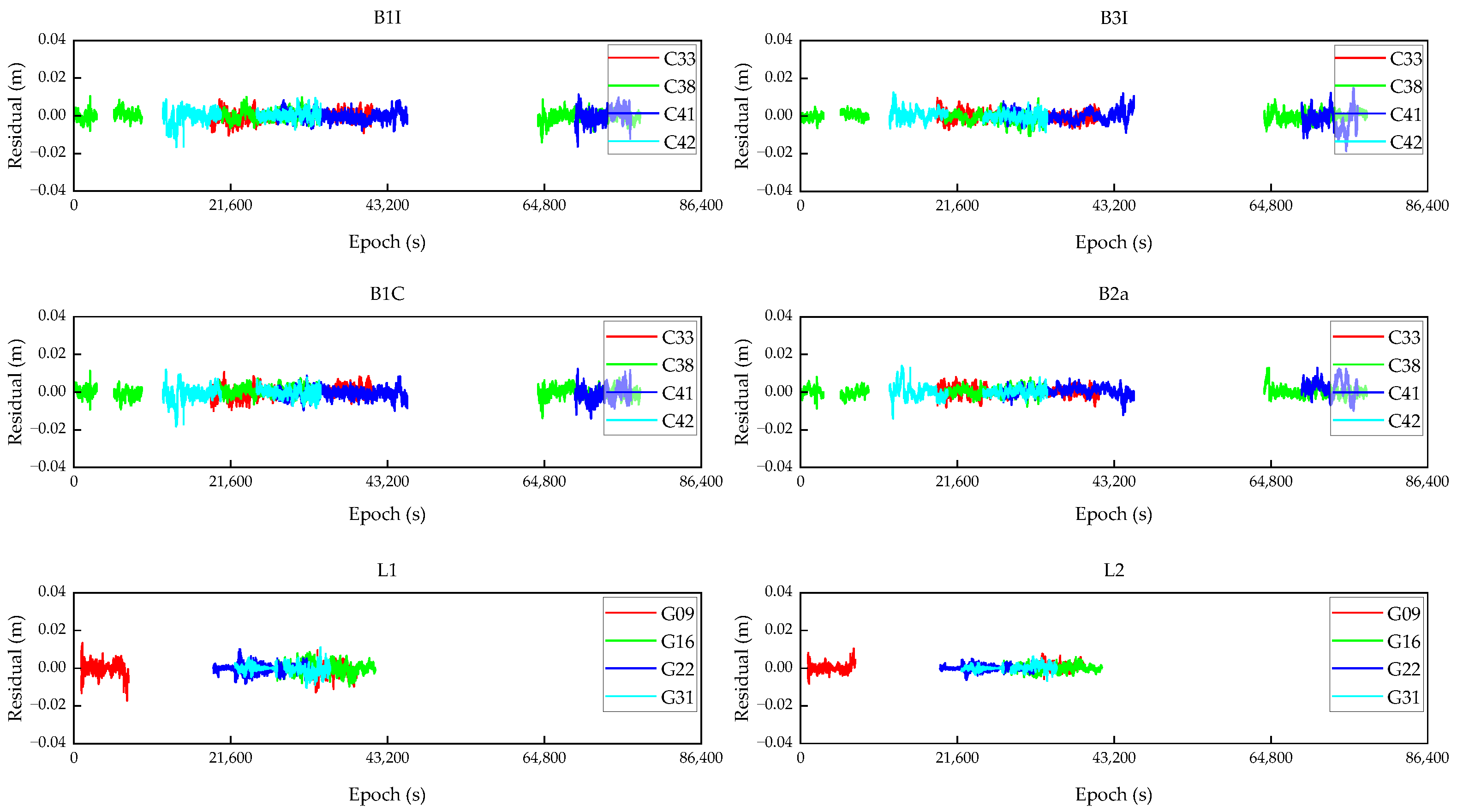
3.1. Reference Station AR
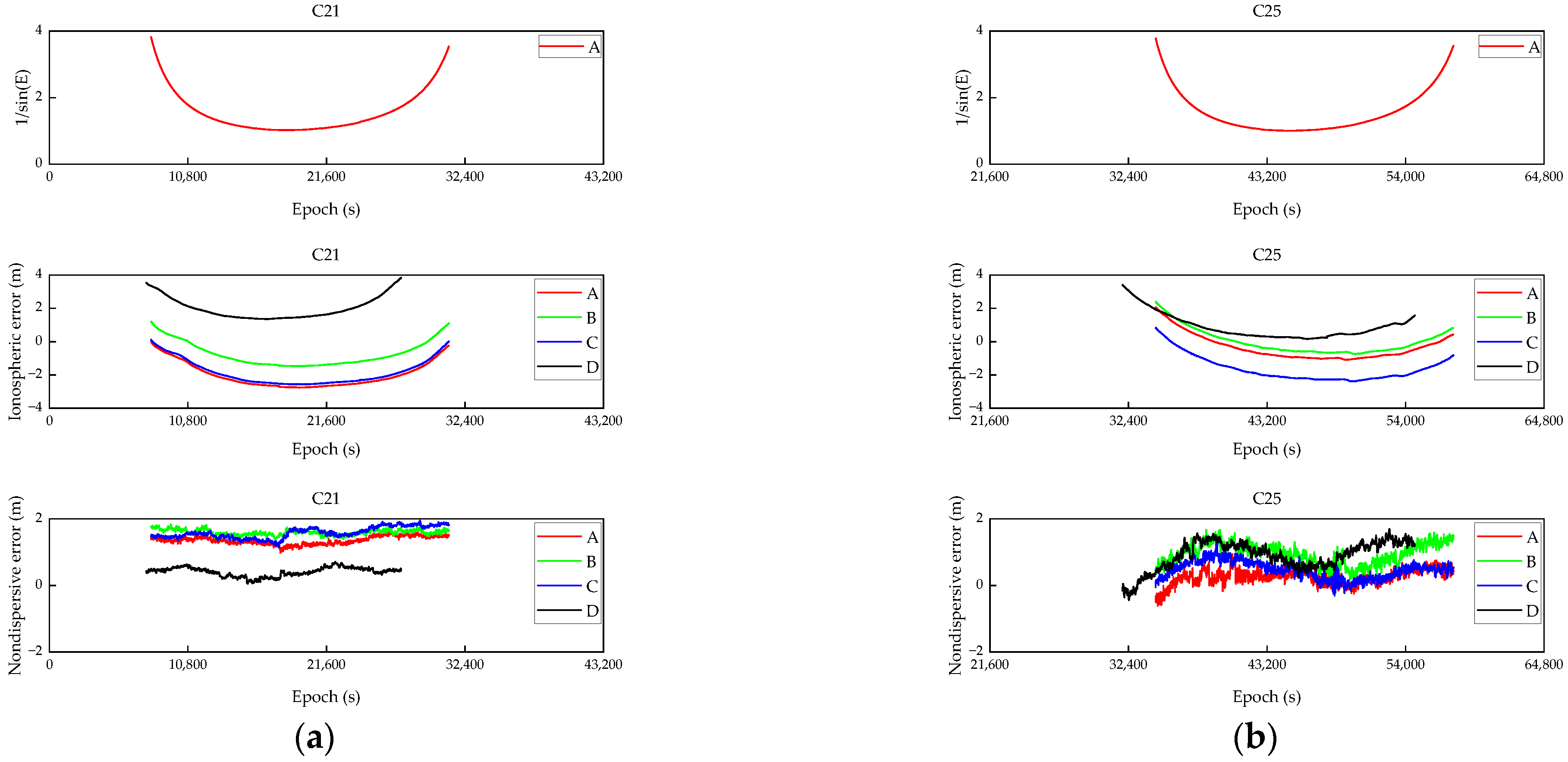
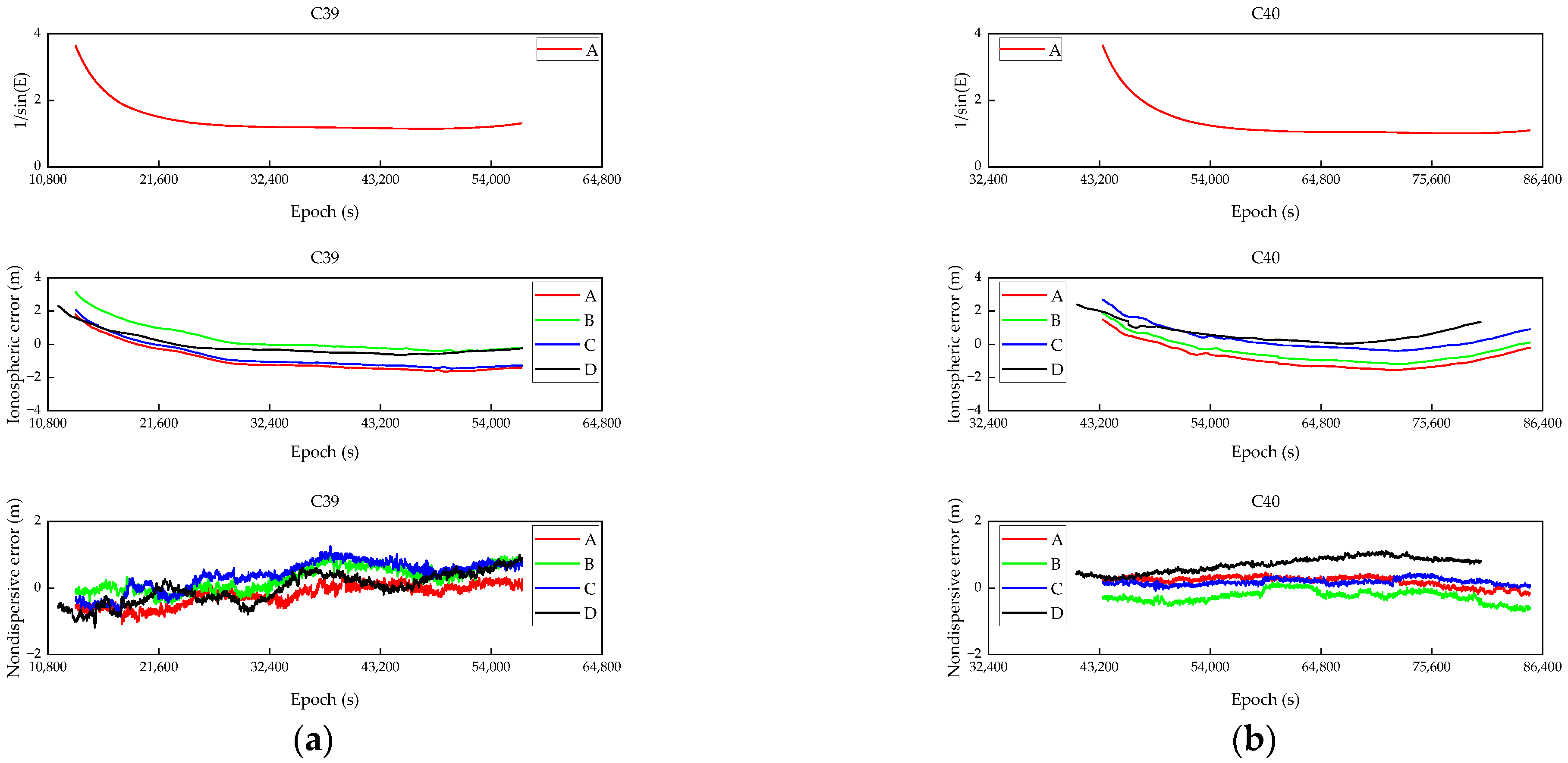
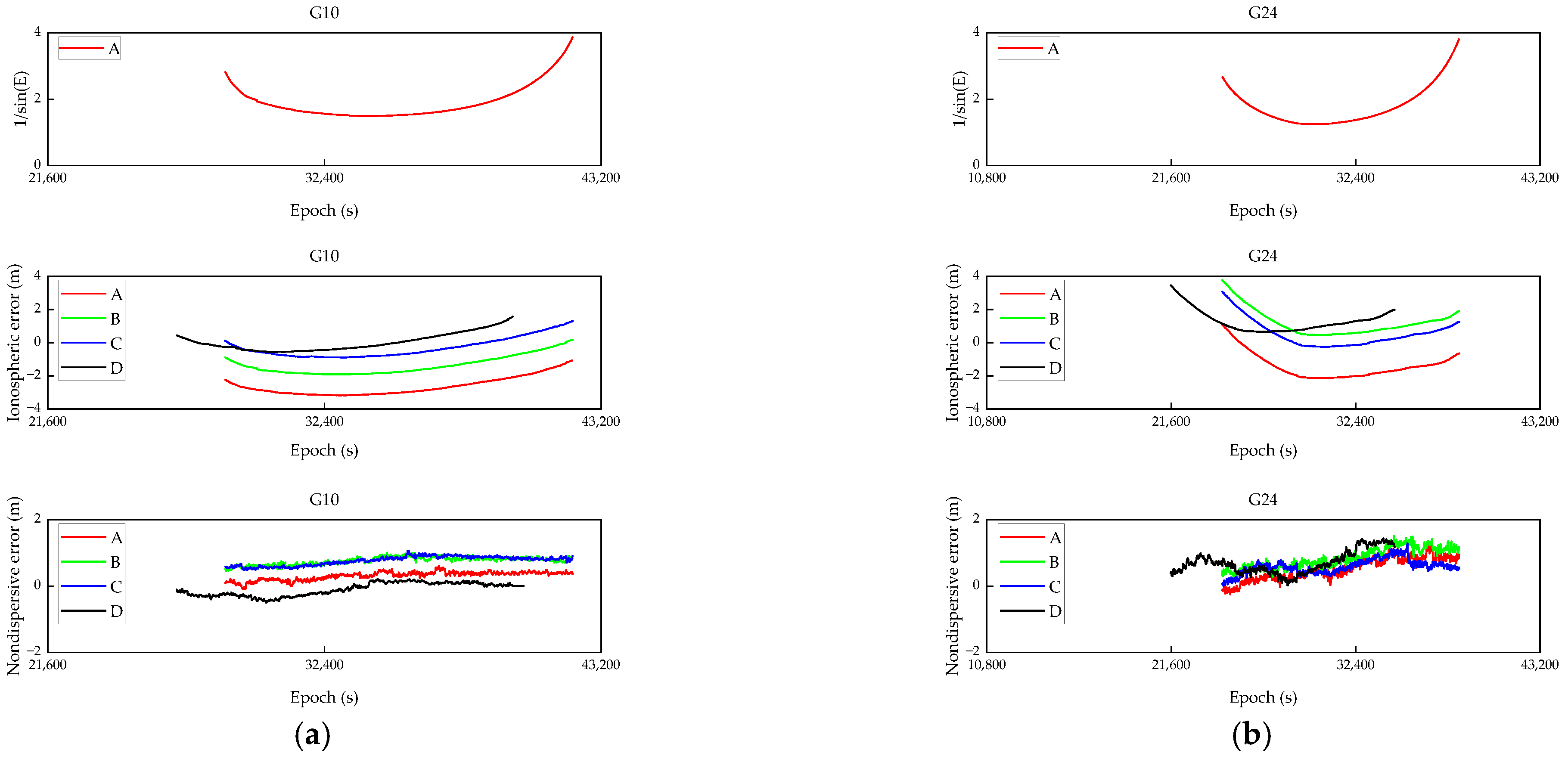
3.2. Undifferenced Error Correction Results
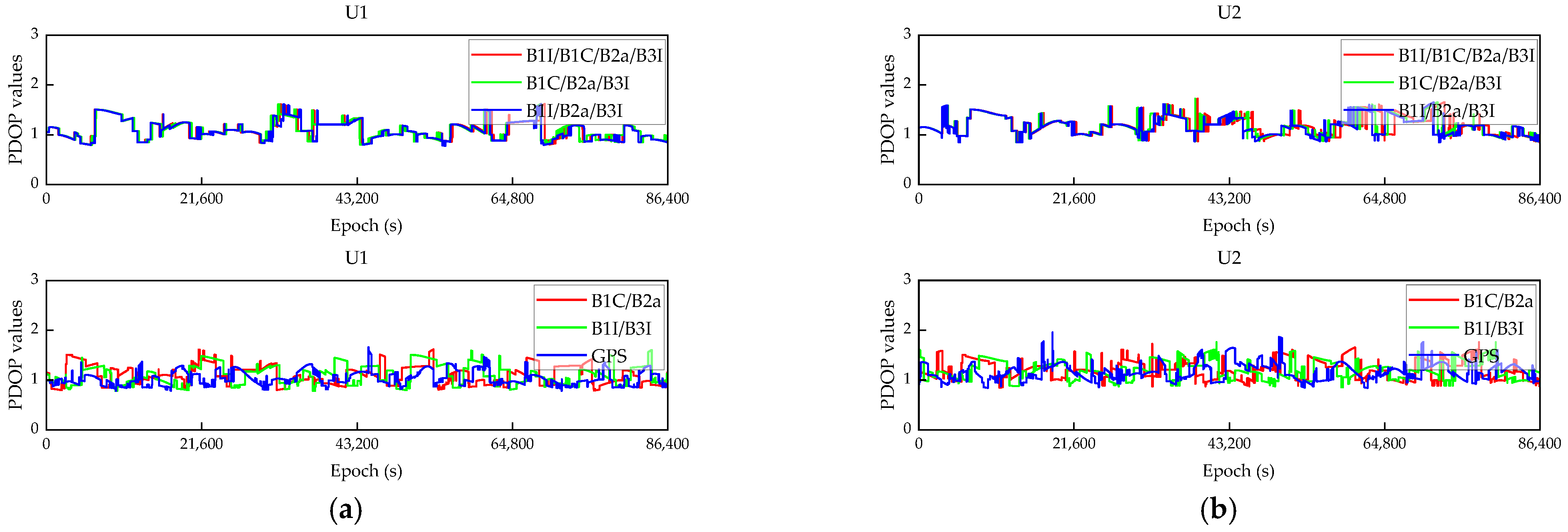
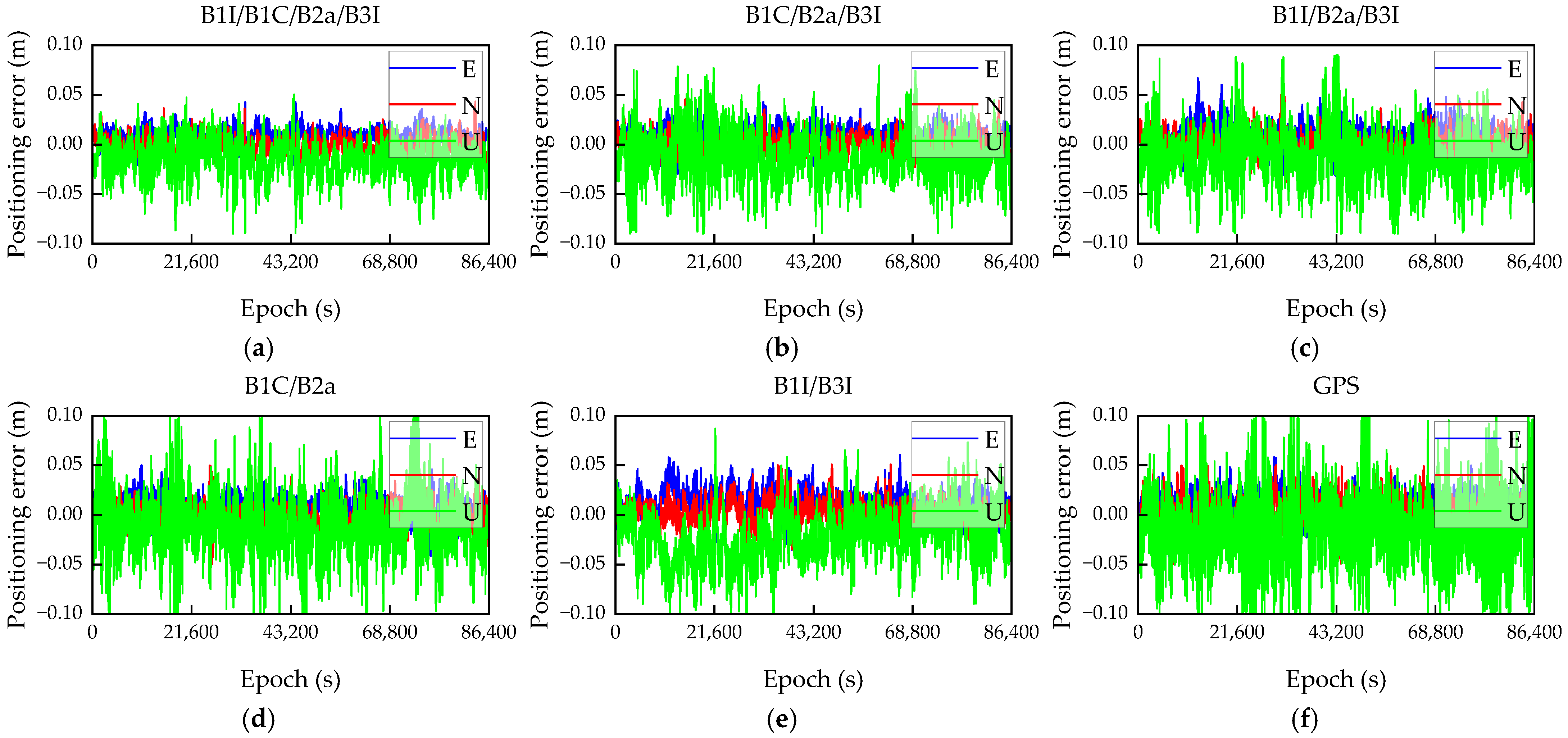
3.3. Positioning Accuracy
4. Discussion
- Realization of a multi-system multi-frequency long-range undifferenced network RTK method;
- Verification of the global performance of the BDS-3, using the observation data of different regions in the world;
- Studying positioning performance in a complex environment.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Yang, C.; Ren, X. PNT Intelligent Services. Acta Geod. Cartogr. Sin. 2021, 50, 1006–1012. (In Chinese) [Google Scholar]
- Cai, H.; Meng, Y.; Geng, C.; Gao, W.; Zhang, T.; Li, G.; Shao, B.; Xin, J.; Lu, H.; Mao, Y.; et al. BDS-3 performance assessment: PNT, SBAS, PPP, SMC and SAR. Acta Geod. Cartogr. Sin. 2021, 50, 427–435. (In Chinese) [Google Scholar]
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and Performance Evaluation of BeiDou Global Navigation Satellite System: Data Analysis Based on BDS-3 Demonstration System. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 Navigation Satellite System. NAVIGATION 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Sun, B. Basic Performance and Future Developments of BeiDou Global Navigation Satellite System. Satell. Navig. 2020, 1, 1. [Google Scholar] [CrossRef]
- Zhu, H.; Li, J.; Yu, Z.; Zhang, K.; Xu, A. The Algorithm of Multi-frequency Carrier Phase Integer Ambiguity Resolution with GPS/BDS Between Long Range Network RTK Reference Stations. Acta Geod. Cartogr. Sin. 2020, 49, 300–311. (In Chinese) [Google Scholar]
- Garrido, M.S.; Giménez, E.; Ramos, M.I.; Gil, A.J. A High Spatio-Temporal Methodology for Monitoring Dunes Morphology Based on Precise GPS-NRTK Profiles: Test-Case of Dune of Mónsul on the South-East Spanish Coastline. Aeolian Res. 2013, 8, 75–84. [Google Scholar] [CrossRef]
- Gümüş, K.; Selbesoğlu, M.O. Evaluation of NRTK GNSS Positioning Methods for Displacement Detection by a Newly Designed Displacement Monitoring System. Measurement 2019, 142, 131–137. [Google Scholar] [CrossRef]
- Dabove, P. The Usability of GNSS Mass-Market Receivers for Cadastral Surveys Considering RTK and NRTK Techniques. Geod. Geodyn. 2019, 10, 282–289. [Google Scholar] [CrossRef]
- Elsayed, H.; El-Mowafy, A.; Wang, K. Bounding of Correlated Double-Differenced GNSS Observation Errors Using NRTK for Precise Positioning of Autonomous Vehicles. Measurement 2023, 206, 112303. [Google Scholar] [CrossRef]
- Weng, D.; Ji, S.; Lu, Y.; Chen, W.; Li, Z. Improving DGNSS Performance through the Use of Network RTK Corrections. Remote Sens. 2021, 13, 1621. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Feng, Y.; Gao, W.; Yang, L. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK. J. Geod. 2014, 88, 99–112. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, H.; Bai, Z.; Qian, C.; Fan, C.; Zhou, P.; Shu, B. Fast Ambiguity Resolution for Long-Range Reference Station Networks with Ionospheric Model Constraint Method. GPS Solut. 2017, 21, 617–626. [Google Scholar] [CrossRef]
- Pan, S.G.; Meng, X.; Wang, S.L.; Nie, W.F.; Chen, W.R. Ambiguity Resolution with Double Troposphere Parameter Restriction for Long Range Reference Stations in NRTK System. Surv. Rev. 2015, 47, 429–437. [Google Scholar] [CrossRef]
- Tang, W.; Shen, M.; Deng, C.; Cui, J.; Yang, J. Network-Based Triple-Frequency Carrier Phase Ambiguity Resolution between Reference Stations Using BDS Data for Long Baselines. GPS Solut. 2018, 22, 73. [Google Scholar] [CrossRef]
- Zhang, M.; Lü, J.; Bai, Z.; Liu, H.; Fan, C. Improving the Initialization Speed for Long-Range NRTK in Network Solution Mode. Sci. China Technol. Sci. 2020, 63, 866–873. [Google Scholar] [CrossRef]
- Wang, S.; You, Z.; Sun, X. A Partial Carrier Phase Integer Ambiguity Fixing Algorithm for Combinatorial Optimization between Network RTK Reference Stations. Sensors 2022, 22, 165. [Google Scholar] [CrossRef]
- Zhu, H.; Lei, X.; Xu, A.; Li, J.; Gao, M. The Integer Ambiguity Resolution of BDS Triple-frequency Between Long Range Stations with GEO Satellite Constraints. Acta Geod. Cartogr. Sin. 2020, 49, 1222–1234. (In Chinese) [Google Scholar]
- Zhu, H.; Lei, X.; Li, J.; Gao, M.; Xu, A. The Algorithm of Integer Ambiguity Resolution with BDS Triple-frequency between Reference Stations at Single Epoch. Acta Geod. Cartogr. Sin. 2020, 49, 1388–1398. (In Chinese) [Google Scholar]
- Zou, X.; Ge, M.; Tang, W.; Shi, C.; Liu, J. URTK: Undifferenced Network RTK Positioning. GPS Solut. 2013, 17, 283–293. [Google Scholar] [CrossRef]
- Tu, R.; Liu, J.; Lu, C.; Zhang, R.; Zhang, P.; Lu, X. The Comparison and Analysis of BDS NRTK between DD and UD Models. NAVIGATION 2018, 65, 275–285. [Google Scholar] [CrossRef]
- Zhu, H.; Li, J.; Yu, Z.; Xu, A.; Gao, M. The Algorithm of Network RTK of Beidou Navigation Satellite System between Long Range. J. China Univ. Min. Technol. 2019, 48, 1143–1151. (In Chinese) [Google Scholar] [CrossRef]
- Zou, X.; Wang, Y.; Deng, C.; Tang, W.; Li, Z.; Cui, J.; Wang, C.; Shi, C. Instantaneous BDS + GPS Undifferenced NRTK Positioning with Dynamic Atmospheric Constraints. GPS Solut. 2017, 22, 17. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, Y.; Xu, A.; Li, J. A Network Real-time Kinematic Method for GPS and BDS Double Systems Between Long Range. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 252–261. (In Chinese) [Google Scholar] [CrossRef]
- Xu, Y.; Chen, W. Performance Analysis of GPS/BDS Dual/Triple-Frequency Network RTK in Urban Areas: A Case Study in Hong Kong. Sensors 2018, 18, 2437. [Google Scholar] [CrossRef]
- Liu, J.; Tu, R.; Han, J.; Zhang, R.; Fan, L.; Zhang, P.; Hong, J.; Lu, X. Initial Evaluation and Analysis of NRTK Positioning Performance with New BDS-3 Signals. Meas. Sci. Technol. 2020, 32, 014002. [Google Scholar] [CrossRef]
- Wang, P.; Liu, H.; Yang, Z.; Shu, B.; Xu, X.; Nie, G. Evaluation of Network RTK Positioning Performance Based on BDS-3 New Signal System. Remote Sens. 2022, 14, 2. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, C.; Wang, Z.; Zhao, Q.; Shang, R.; Peng, Z.; Liu, Q. Ambiguity Resolution for Long Baseline in a Network with BDS-3 Quad-F28requency Ionosphere-Weighted Model. Remote Sens. 2022, 14, 1654. [Google Scholar] [CrossRef]
- Ge, M.; Liu, J. The Estimation Methods for Tropospheric Delays in Global Positioning System. Acta Geod. Cartogr. Sin. 1996, 25, 46–52. (In Chinese) [Google Scholar]
- Zhu, H.; Li, J.; Tang, L.; Ge, M.; Xu, A. Improving the Stochastic Model of Ionospheric Delays for BDS Long-Range Real-Time Kinematic Positioning. Remote Sens. 2021, 13, 2739. [Google Scholar] [CrossRef]
- Li, J.; Zhu, H.; Xu, A.; Xu, Z. Estimating Ionospheric Power Spectral Density for Long-Range RTK Positioning Using Uncombined Observations. GPS Solut. 2023, 27, 109. [Google Scholar] [CrossRef]
- Tang, W.; Liu, W.; Zou, X.; Li, Z.; Chen, L.; Deng, C.; Shi, C. Improved Ambiguity Resolution for URTK with Dynamic Atmos phere Constraints. J. Geod. 2016, 90, 1359–1369. [Google Scholar] [CrossRef]
- Han, Y.; Ma, L.; Qiao, Q.; Yin, Z.; Shi, H.; Ai, G. Functions of Retired GEO Communication Satellites in Improving the PDOP Value of CAPS. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 423–433. [Google Scholar] [CrossRef]


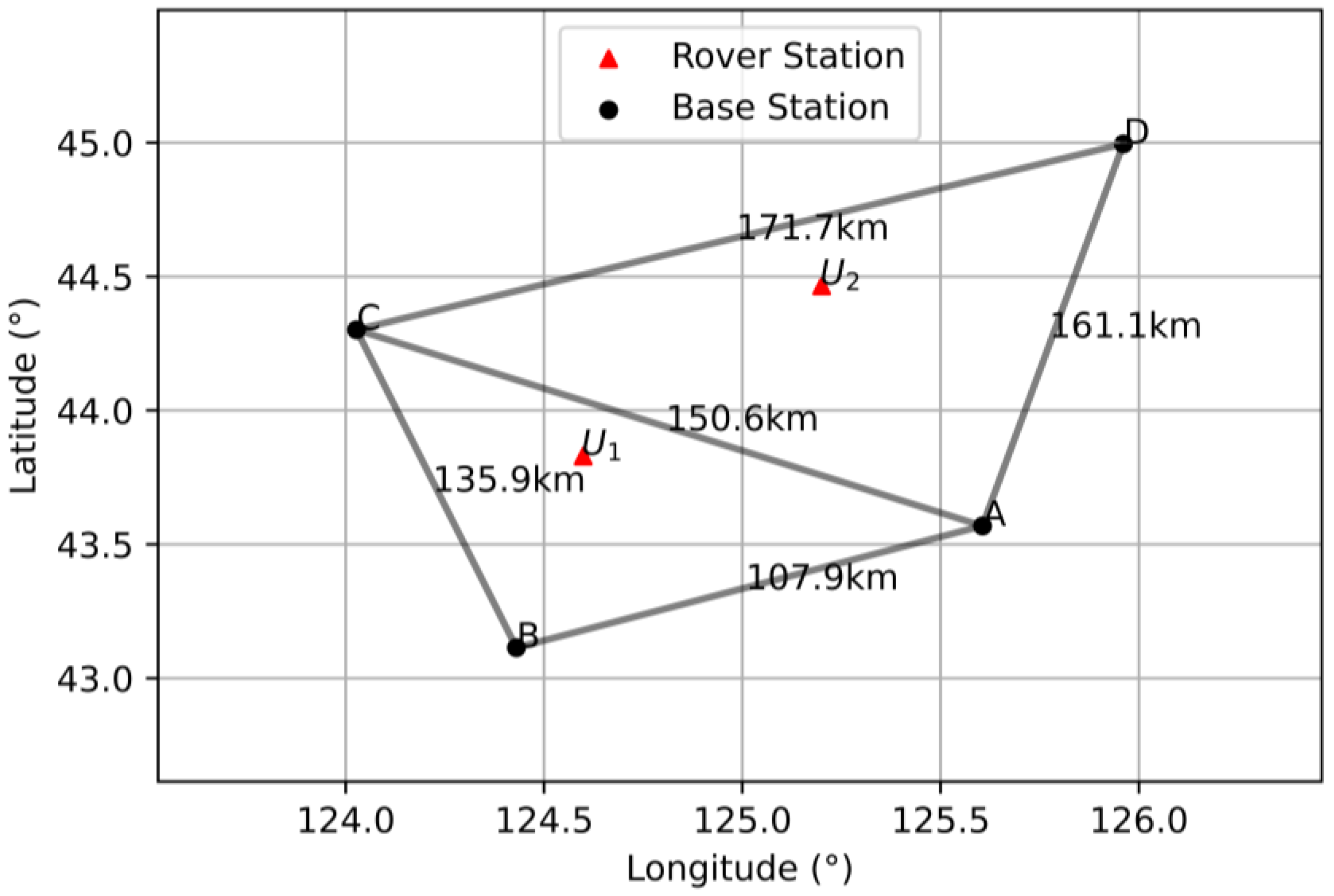




| Baseline | A-B | B-C | C-A | A-D | D-C | U1-U2 |
|---|---|---|---|---|---|---|
| Length (km) | 108 | 136 | 151 | 161 | 172 | 85 |
| Combined Model | Rover Station | Maximum Value | Minimum Value | Mean Value |
|---|---|---|---|---|
| B1I/B1C/B2a/B3I | U1 | 1.616 | 0.794 | 1.093 |
| U2 | 1.725 | 0.847 | 1.191 | |
| B1C/B2a | U1 | 1.616 | 0.787 | 1.102 |
| U2 | 1.761 | 0.847 | 1.209 | |
| B1I/B3I | U1 | 1.605 | 0.778 | 1.102 |
| U2 | 1.760 | 0.848 | 1.196 | |
| GPS | U1 | 1.658 | 0.783 | 1.030 |
| U2 | 1.958 | 0.841 | 1.158 |
| PRN | Reference Station Network | Number of Observations | Fixed Number | Unfixed Number | Fixed Success Rate (%) |
|---|---|---|---|---|---|
| C22 | 1 | 17,464 | 17,389 | 75 | 99.57 |
| 2 | 14,878 | 14,739 | 139 | 99.06 | |
| C27 | 1 | 18,035 | 17,851 | 184 | 98.97 |
| 2 | 18,035 | 18,035 | 0 | 100 | |
| C32 | 1 | 22,195 | 21,998 | 197 | 99.11 |
| 2 | 22,195 | 22,195 | 0 | 100 | |
| C35 | 1 | 8135 | 8135 | 0 | 100 |
| 2 | 8135 | 8135 | 0 | 100 | |
| C45 | 1 | 20,823 | 20,823 | 0 | 100 |
| 2 | 20,823 | 20,586 | 237 | 98.86 |
| PRN | Reference Station Network | Number of Observations | Fixed Number | Unfixed Number | Fixed Success Rate (%) |
|---|---|---|---|---|---|
| C22 | 1 | 17,464 | 17,385 | 79 | 99.54 |
| 2 | 14,878 | 14,863 | 15 | 99.89 | |
| C27 | 1 | 18,035 | 17,856 | 179 | 99.01 |
| 2 | 18,035 | 18,035 | 0 | 100 | |
| C32 | 1 | 22,195 | 22,120 | 75 | 99.66 |
| 2 | 22,195 | 22,195 | 0 | 100 | |
| C35 | 1 | 8135 | 8135 | 0 | 100 |
| 2 | 8135 | 8135 | 0 | 100 | |
| C45 | 1 | 20,823 | 20,738 | 85 | 99.59 |
| 2 | 20,823 | 20,573 | 250 | 98.79 |
| PRN | Reference Station Network | Number of Observations | Fixed Number | Unfixed Number | Fixed Success Rate (%) |
|---|---|---|---|---|---|
| C22 | 1 | 17,464 | 17,123 | 341 | 98.04 |
| 2 | 14,878 | 14,464 | 414 | 97.21 | |
| C27 | 1 | 18,035 | 17,752 | 283 | 98.43 |
| 2 | 18,035 | 17,519 | 516 | 97.13 | |
| C32 | 1 | 22,195 | 21,876 | 319 | 98.56 |
| 2 | 22,195 | 21,952 | 243 | 98.90 | |
| C35 | 1 | 8135 | 8135 | 0 | 100 |
| 2 | 8135 | 8135 | 0 | 100 | |
| C45 | 1 | 20,823 | 20,443 | 380 | 98.17 |
| 2 | 20,823 | 20,298 | 525 | 97.47 |
| PRN | Reference Station Network | Number of Observations | Fixed Number | Unfixed Number | Fixed Success Rate (%) |
|---|---|---|---|---|---|
| G06 | 1 | 18,413 | 18,234 | 179 | 99.02 |
| 2 | 16,675 | 16,299 | 376 | 97.74 | |
| G13 | 1 | 15,248 | 15,186 | 62 | 99.59 |
| 2 | 14,808 | 14,702 | 106 | 99.28 | |
| G20 | 1 | 20,926 | 20,877 | 49 | 99.76 |
| 2 | 19,084 | 18,551 | 533 | 97.20 | |
| G21 | 1 | 14,860 | 14,060 | 254 | 98.29 |
| 2 | 14,860 | 14,534 | 326 | 97.80 | |
| G29 | 1 | 24,459 | 24,155 | 304 | 98.75 |
| 2 | 24,459 | 23,885 | 574 | 97.65 |
| Combined Model | Rover Station U1 | Rover Station U2 |
|---|---|---|
| B1I/B1C/B2a/B3I | 124 | 164 |
| B1C/B2a/B3I | 122 | 113 |
| B1I/B2a/B3I | 128 | 171 |
| B1C/B2a | 178 | 117 |
| B1I/B3I | 359 | 400 |
| GPS | 286 | 338 |
| Combined Model | Rover Station | E | N | U |
|---|---|---|---|---|
| B1I/B1C/B2a/B3I | U1 | 0.0085 | 0.0075 | 0.0181 |
| U2 | 0.0108 | 0.0079 | 0.0227 | |
| B1C/B2a/B3I | U1 | 0.0087 | 0.0081 | 0.0206 |
| U2 | 0.0110 | 0.0089 | 0.0252 | |
| B1I/B2a/B3I | U1 | 0.0096 | 0.0094 | 0.0243 |
| U2 | 0.0130 | 0.0103 | 0.0261 | |
| B1C/B2a | U1 | 0.0098 | 0.0087 | 0.0249 |
| U2 | 0.0122 | 0.0101 | 0.0292 | |
| B1I/B3I | U1 | 0.0103 | 0.0099 | 0.0169 |
| U2 | 0.0174 | 0.0122 | 0.0330 | |
| GPS | U1 | 0.0108 | 0.0126 | 0.0285 |
| U2 | 0.0136 | 0.0138 | 0.0332 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Zhang, J.; Li, J.; Xu, A. An Efficient BDS-3 Long-Range Undifferenced Network RTK Positioning Algorithm. Remote Sens. 2023, 15, 4060. https://doi.org/10.3390/rs15164060
Zhu H, Zhang J, Li J, Xu A. An Efficient BDS-3 Long-Range Undifferenced Network RTK Positioning Algorithm. Remote Sensing. 2023; 15(16):4060. https://doi.org/10.3390/rs15164060
Chicago/Turabian StyleZhu, Huizhong, Jie Zhang, Jun Li, and Aigong Xu. 2023. "An Efficient BDS-3 Long-Range Undifferenced Network RTK Positioning Algorithm" Remote Sensing 15, no. 16: 4060. https://doi.org/10.3390/rs15164060
APA StyleZhu, H., Zhang, J., Li, J., & Xu, A. (2023). An Efficient BDS-3 Long-Range Undifferenced Network RTK Positioning Algorithm. Remote Sensing, 15(16), 4060. https://doi.org/10.3390/rs15164060