Evaluation of HY-2C and CFOSAT Satellite Retrieval Offshore Wind Energy Using Weather Research and Forecasting (WRF) Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. GFS, GDAS Reanalysis Dataset
2.1.2. ERA5 Hourly Data on Single Levels
2.1.3. HY-2C and CFOSAT Satellite-Borne Scatterometers Dataset
2.1.4. Measured Wind Speed
2.2. Methodology
2.2.1. WRF Model
2.2.2. Assessment of Model Performance
2.2.3. Sensitivity Experiments
Different Boundary Layer and Near-Ground Parameterization Schemes (Sensitivity Experiment A)
Different Initial Fields
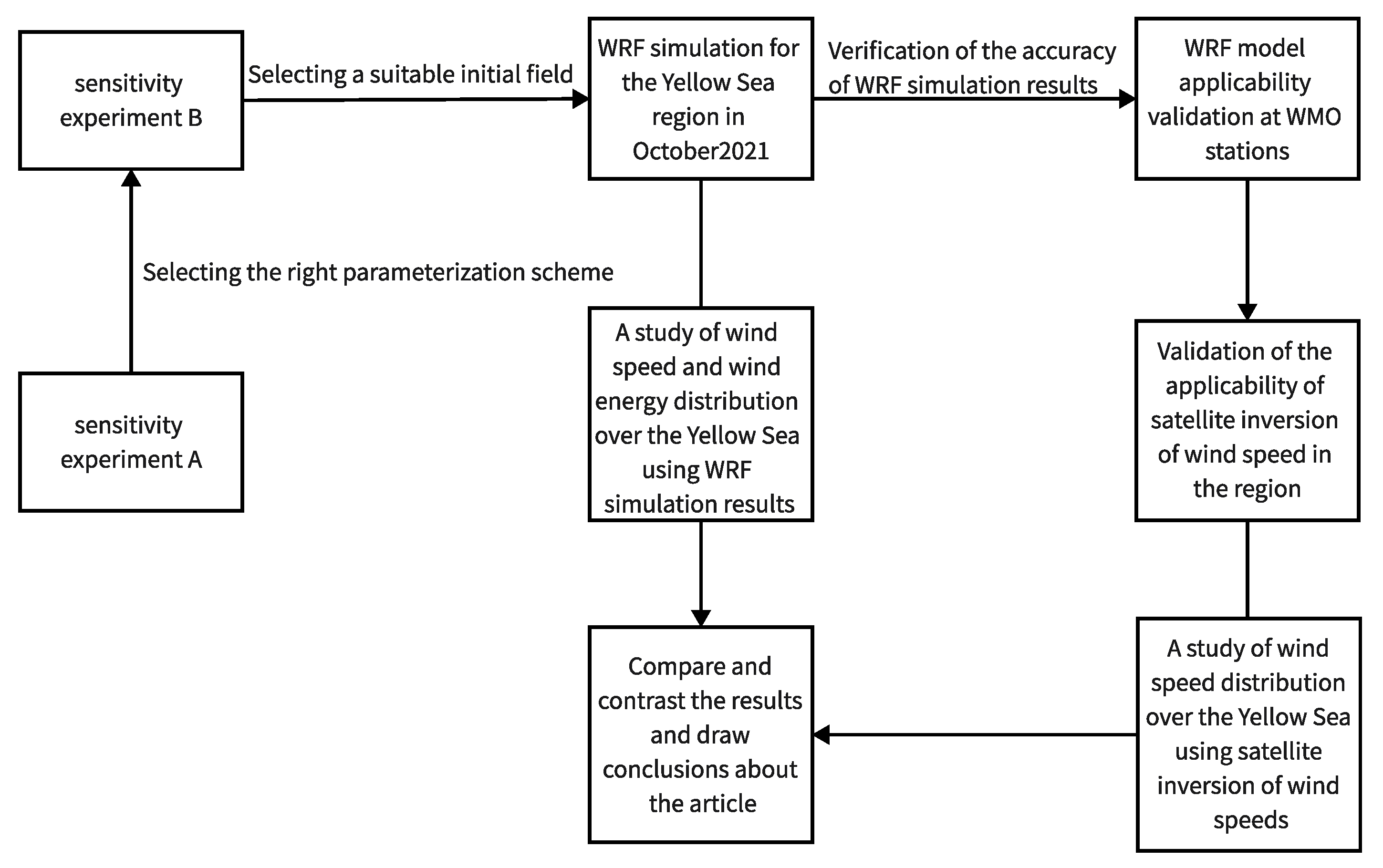
2.2.4. WRF Simulation for the Yellow Sea Region in October 2021
2.2.5. Dataset Validation
2.2.6. Wind Energy Calculation
3. Results
3.1. WRF Simulation of Wind Speeds in the East China Sea
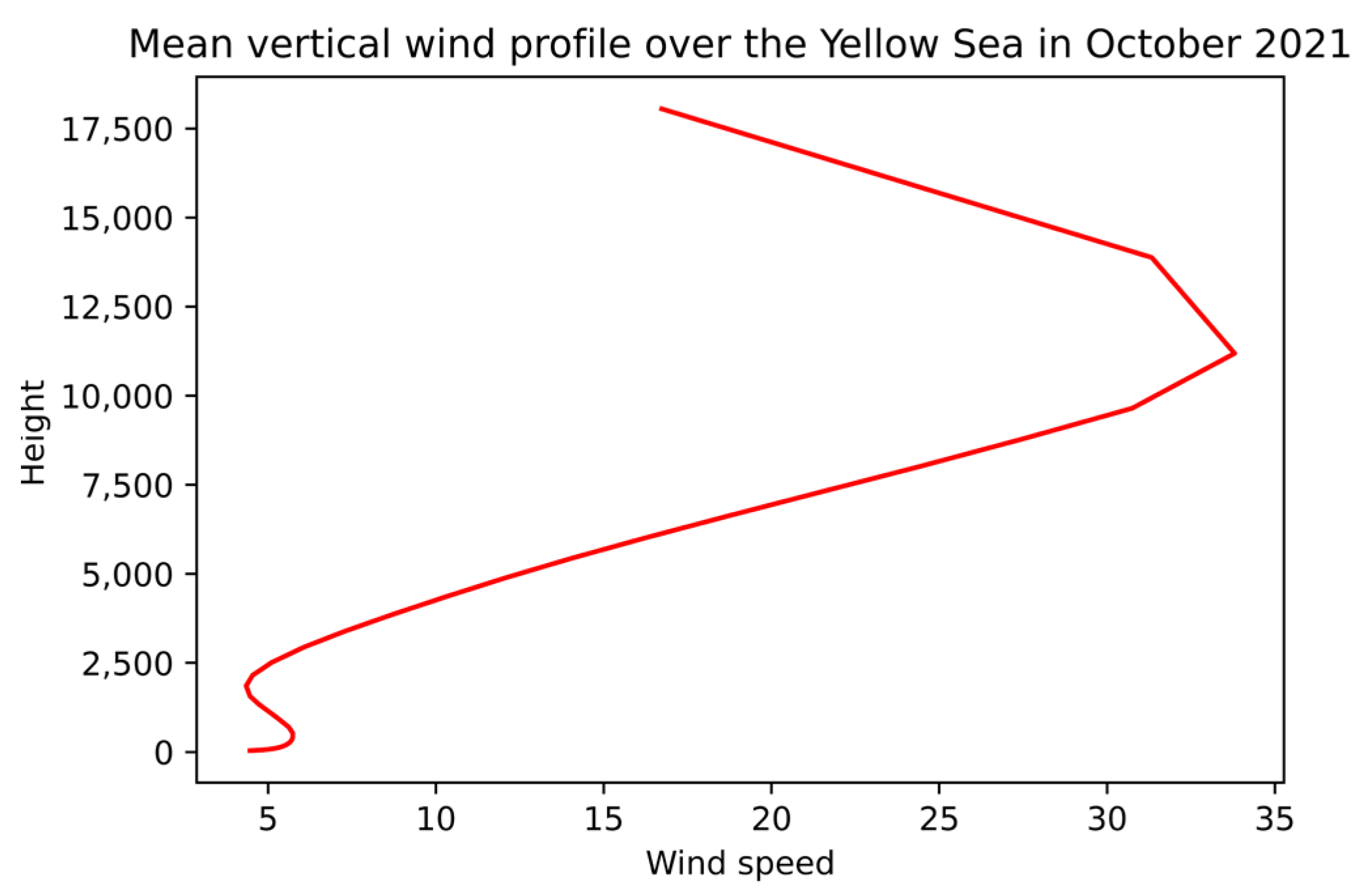
3.1.1. WRF Simulation of the Vertical Distribution of Wind Speeds over the East China Sea
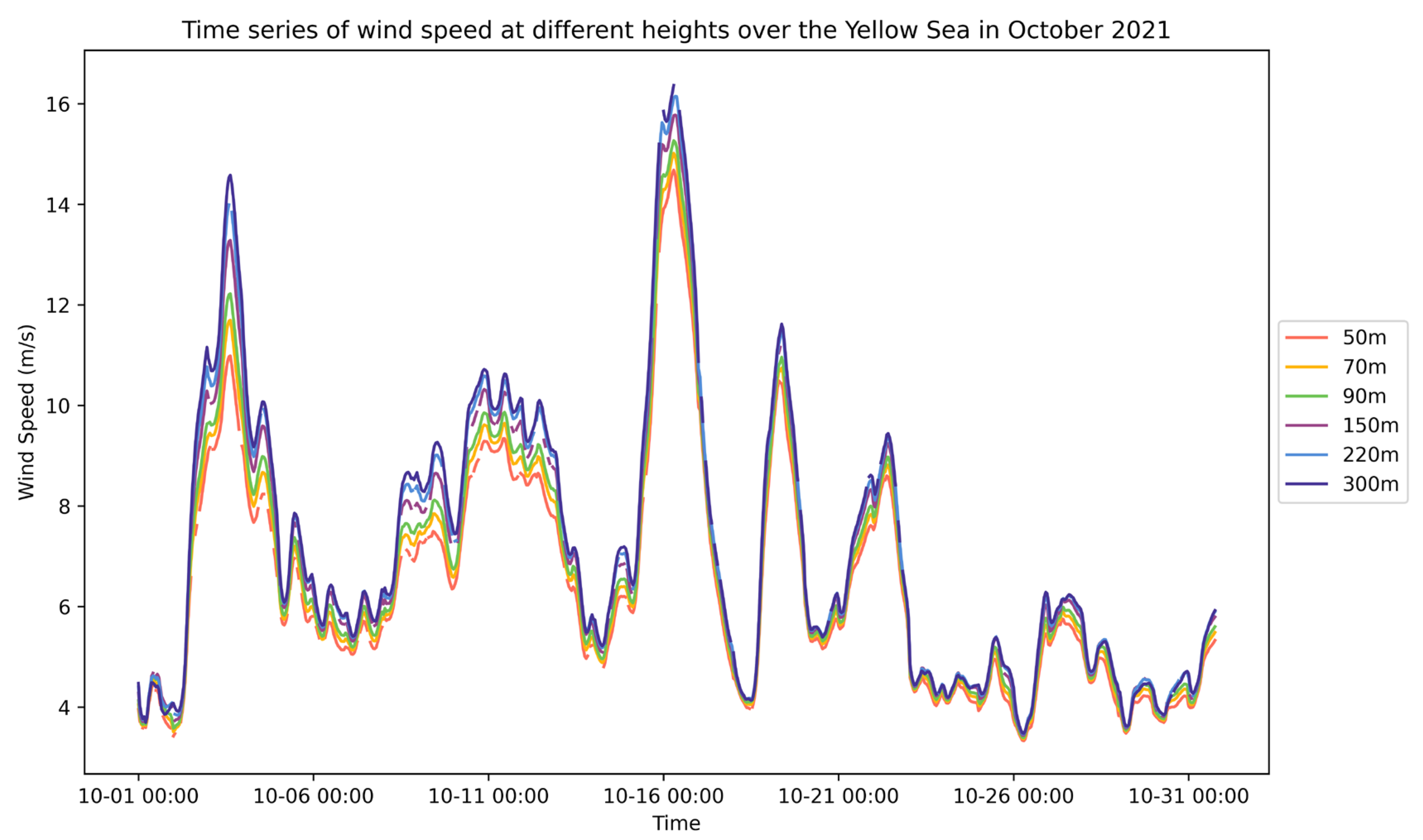
3.1.2. Time-Series Distribution of Wind Speeds over the East China Sea Simulated Using WRF
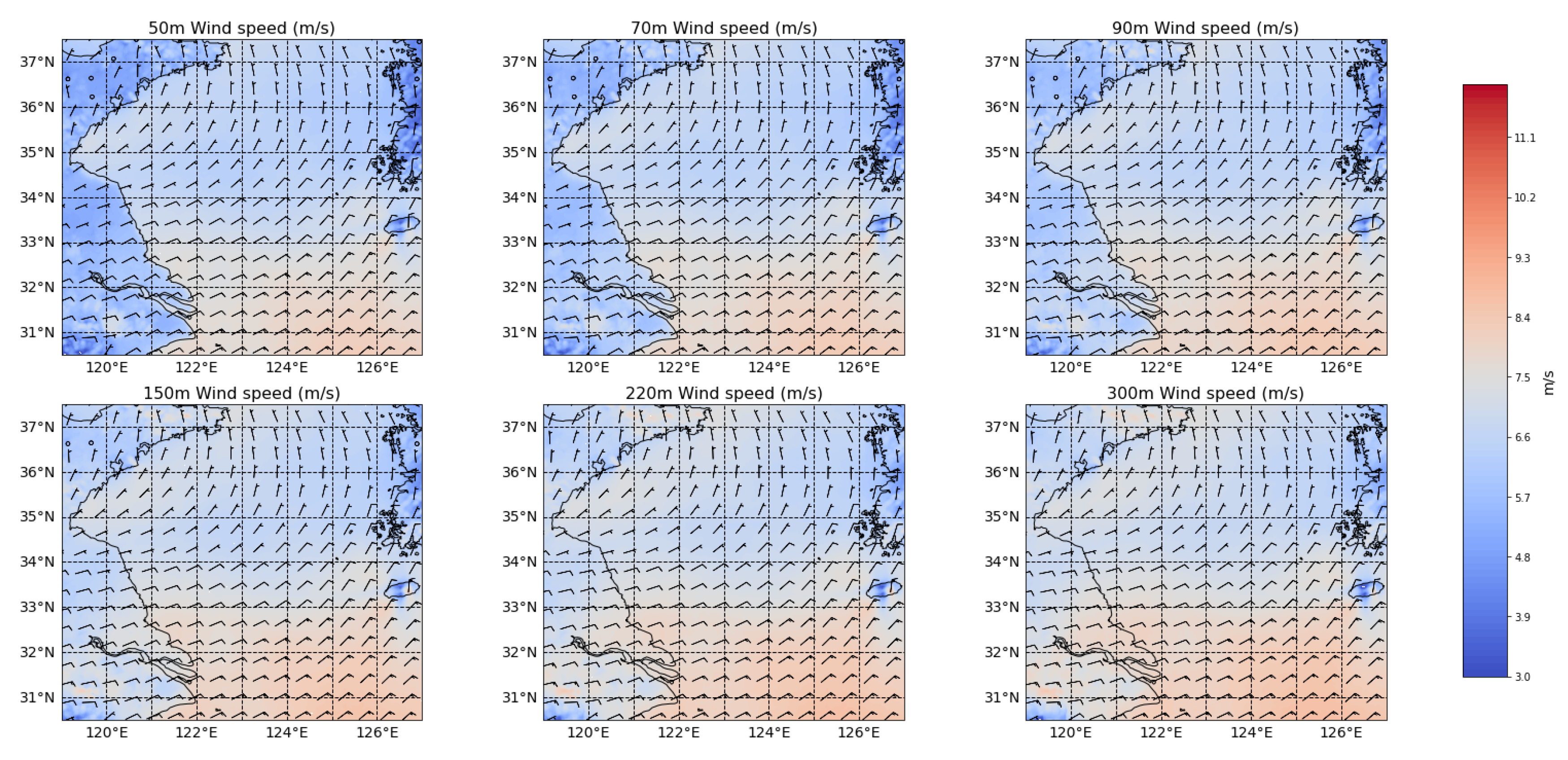
3.1.3. Horizontal Distribution of Wind Speeds at Each Height in the Yellow Sea Simulated by WRF
3.2. WRF Simulates the Horizontal Distribution of Wind Energy in the Yellow Sea
3.3. Satellite Inversion 10 m Wind Field
3.3.1. HY-2C, CFOSAT Inversion 10 m Wind Field Distribution
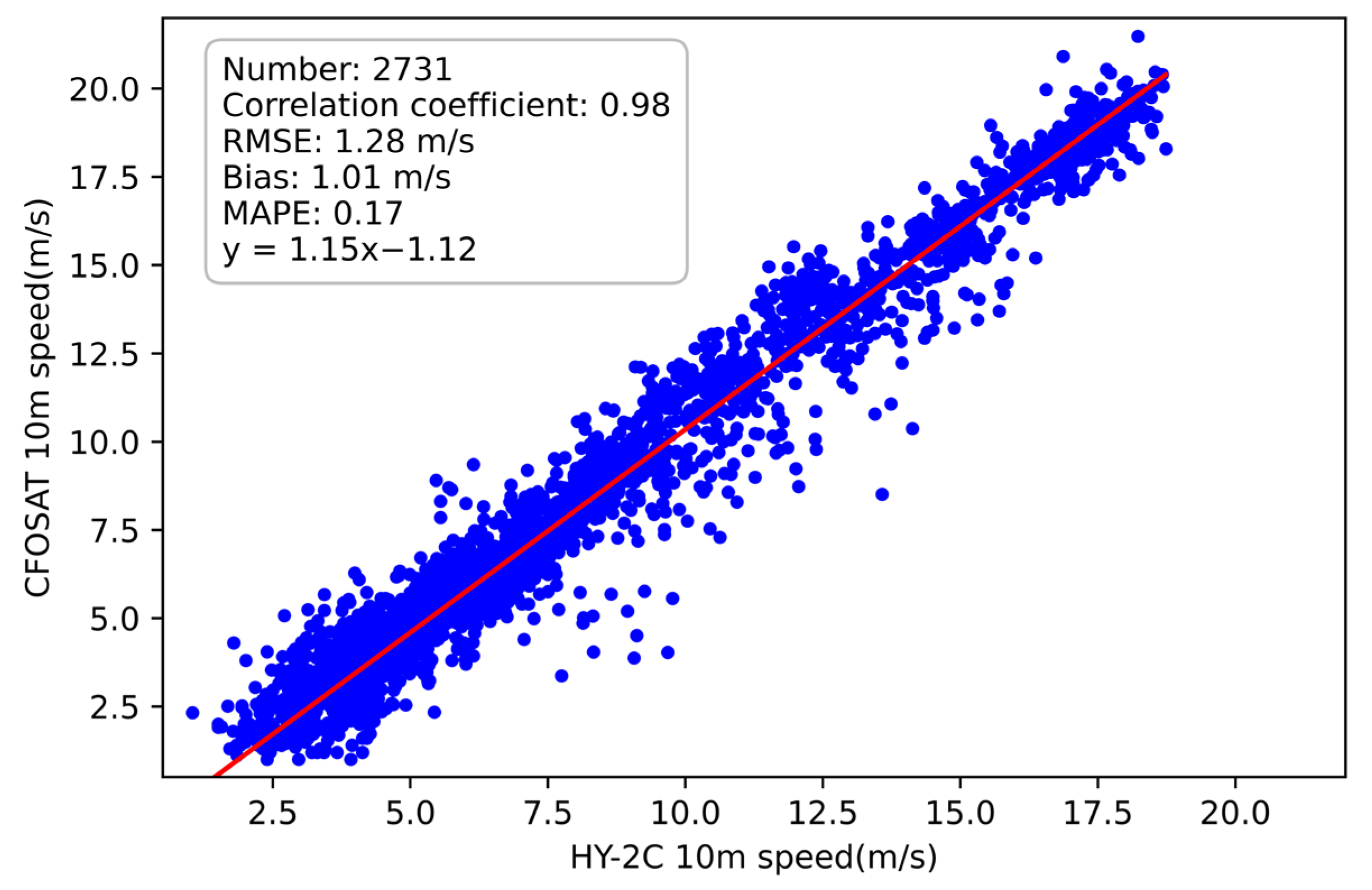
3.3.2. Comparison of HY-2C and CFOSAT Inversion 10 m Wind Field
3.4. Relationship between Satellite Inversion Wind Field and Wind Energy Density over the Yellow Sea
4. Discussion
4.1. Comparison of HY-2C and CFOSAT Inversion Data with ERA5
4.2. The Limitations of This Study and Future Research Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, F.; Sun, F.; Liu, W.; Wang, T.; Wang, H.; Wang, X.; Lim, W.H. On wind speed pattern and energy potential in China. Appl. Energy 2019, 236, 867–876. [Google Scholar] [CrossRef]
- Shu, Z.R.; Jesson, M. Estimation of Weibull parameters for wind energy analysis across the UK. J. Renew. Sustain. Energy 2021, 13, 023303. [Google Scholar] [CrossRef]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar] [CrossRef]
- Bagci, K.; Arslan, T.; Celik, H.E. Inverted Kumarswamy distribution for modeling the wind speed data: Lake Van, Turkey. Renew. Sustain. Energy Rev. 2020, 135, 110110. [Google Scholar] [CrossRef]
- He, J.Y.; Chan, P.W.; Li, Q.S.; Lee, C.W. Characterizing coastal wind energy resources based on sodar and microwave radiometer observations. Renew. Sustain. Energy Rev. 2022, 163, 112498. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, R. Research on wind energy resource assessment technology and methods. Acta Meteor. Sin. 2007, 5, 708–717. (In Chinese) [Google Scholar]
- Zhou, J. Wind Farm Regional Wind Energy Resource Assessment. In Proceedings of the 6th Symposium on Energy Conservation and Emission Reduction in Power Industry, Yixing, China, 28–30 June 2011; pp. 182–184. [Google Scholar]
- Archer, C.L.; Jacobson, M.Z. Evaluation of global wind power. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- He, X.; Zhou, R.; Zhu, R. Research on classification methods for numerical simulation evaluation of wind energy resources. Acta Meteor. Sin. 2015, 73, 975–984. (In Chinese) [Google Scholar]
- Du, M.; Yi, K. Research on applicability of different physical parameterization scheme combinations in WRF model to offshore wind energy resource assessment in China. Mar. Forecast. 2023, 40, 65–78. [Google Scholar]
- Li, J. Research on the Application of Dynamic Downscaling and System Integration Technology to Fine Wind Field Forecast. Master’s Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2017. [Google Scholar]
- Tang, J.; Gao, H. A statistical downscaling method for wind energy change in China in the 21st century under the IPC-A2 scenario. Acta Energiae Solaris Sin. 2009, 30, 655–666. [Google Scholar]
- Storm, B.; Dudhia, J.; Basu, S.; Swift, A.; Giammanco, I. Evaluation of the Weather Research and Forecasting Model on Forecasting Low-level Jets: Implications for Wind Energy. Wind. Energy 2009, 12, 81–90. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.Y. Intercomparison of Planetary Boundary-Layer Parametrizations in the WRF Model for a Single Day from CASES-99. Bound. Layer Meteorol. 2011, 139, 261–281. [Google Scholar] [CrossRef]
- Deppe, A.J.; Gallus, W.A., Jr.; Takle, E.S. A WRF ensemble for improved wind speed forecasts at turbine height. Weather Forecast. 2013, 28, 212–228. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Pena, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind Energy 2013, 17, 39–55. [Google Scholar] [CrossRef]
- Zuo, H.; Sun, Y. Comparative analysis of the effect of three downscaling schemes of WRF model in wind power forecast service. Power Syst. Clean Energy 2013, 29, 105–108. [Google Scholar]
- Chao, Z. Statistical downscaling of temperature data in western China. Arid. Zone Res. 2011, 28, 879–884. [Google Scholar] [CrossRef]
- Ma, J.; Liu, Z. Research on fine evaluation of wind resources based on WRF-Windsim microscale coupling technology. Ningxia Electr. Power 2023, 1, 1–5. [Google Scholar]
- Zhang, H.; Li, Y. Study on disturbance construction method of initial value for regional ensemble forecasting based on dynamic downscaling. Meteorol. Mon. 2017, 43, 1461–1472. [Google Scholar]
- Ramos, D.N.D.S.; Lyra, R.F.D.F.; Silva, R.S.d., Jr. Previsão do vento utilizando o modelo atmosférico WRF para o estado de Alagoas. Rev. Bras. Meteorol. 2013, 28, 163–172. [Google Scholar] [CrossRef]
- Tuchtenhagen, P.; Basso, J.; Yamasaki, Y. Wind power assessment over Brazil in 2011. Ciência Nat. 2014, 36, 390–401. [Google Scholar] [CrossRef]
- Krogsaeter, O.; Reuder, J. Validation of boundary layer parameterization schemes in the Weather Research and Forecasting (WRF) model under the aspect of offshore wind energy applications—Part II: Boundary layer height and atmospheric stability. Wind. Energy 2015, 18, 1291–1302. [Google Scholar] [CrossRef]
- García-Díez, M.; Fernández, J.; Fita, L.; Yagüe, C. Seasonal dependence of WRF model biases and sensitivity to PBL schemes over Europe. Q. J. R. Meteorol. Soc. 2013, 139, 501–514. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z. Research on wind field simulation of complex terrain based on NWP/CFD nesting. Acta Energiae Solaris Sin. 2021, 42, 205–210. [Google Scholar] [CrossRef]
- Amjad, M.; Zafar, Q.; Khan, F.; Sheikh, M.M. Evaluation of weather research and forecasting model for the assessment of wind resource over Gharo, Pakistan. Int. J. Climatol. 2015, 35, 1821–1832. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note, NCAR/TN-468+STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Liu, W. Wind Energy and Wind Power Technology; Chemical Industry Press: Beijing, China, 2006. [Google Scholar]
- Shikhovtsev, A.Y.; Kovadlo, P.G.; Lezhenin, A.A.; Korobov, O.A.; Kiselev, A.V.; Russkikh, I.V.; Kolobov, D.Y.; Shikhovtsev, M.Y. Influence of Atmospheric Flow Structure on Optical Turbulence Characteristics. Appl. Sci. 2023, 13, 1282. [Google Scholar] [CrossRef]
- Ma, H.; Cao, X.; Ma, X.; Su, H.; Jing, Y.; Zhu, K. Improving the Wind Power Density Forecast in the Middle- and High-Latitude Regions of China by Selecting the Relatively Optimal Planetary Boundary Layer Schemes. Atmosphere 2022, 13, 2034. [Google Scholar] [CrossRef]
- Salvao, N.; Guedes Soares, C. Wind resource assessment offshore the Atlantic Iberian coast with the WRF model. Energy 2018, 145, 276–287. [Google Scholar] [CrossRef]
- Giannakopoulou, E.M.; Nhili, R. WRF Model Methodology for Offshore Wind Energy Applications. Adv. Meteorol. 2014, 2014, 68–79. [Google Scholar] [CrossRef]
- China National Energy Administration. Available online: http://www.nea.gov.cn/ (accessed on 13 July 2023).
- Summary of Replies to Proposal No. 01612 (No. 103 in the Category of Economic Development) of the Fifth Session of the 13th National Committee of the Chinese People’s Political Consultative Conference. Available online: http://zfxxgk.nea.gov.cn/2022-08/23/c_1310665817.htm (accessed on 13 July 2023).
- Juan, Y.H.; Wen, C.Y.; Chen, W.Y.; Yang, A.S. Numerical assessments of wind power potential and installation arrangements in realistic highly urbanized areas. Renew. Sustain. Energy Rev. 2021, 135, 110165. [Google Scholar] [CrossRef]
- Christiansen, M.B.; Koch, W.; Horstmann, J.; Hasager, C.B.; Nielsen, M. Wind resource assessment from C-band SAR. Remote Sens. Environ. 2006, 105, 68–81. [Google Scholar] [CrossRef]
- Hasager, C.B.; Mouche, A.; Badger, M.; Bing?L, F.; Karagali, I.; Driesenaar, T.; Stoffelen, A.; Pe?A, A.; Longépé, N. Offshore wind climatology based on synergetic use of Envisat ASAR, ASCAT and QuikSCAT. Remote Sens. Environ. 2015, 156, 247–263. [Google Scholar] [CrossRef]
- Mou, X.; Lin, W.; He, Y. Towards a Consistent Wind Data Record for the CFOSAT Scatterometer. Remote Sens. 2023, 15, 2081. [Google Scholar] [CrossRef]
- Liu, S.; Lin, W.; Portabella, M.; Wang, Z. Characterization of Tropical Cyclone Intensity Using the HY-2B Scatterometer Wind Data. Remote Sens. 2022, 14, 1035. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, J.; Zhang, Y.; Stoffelen, A.; Lin, W.; He, Y.; Feng, Q.; Zhang, Y.; Mu, B.; Lin, M. Intercalibration of Backscatter Measurements among Ku-Band Scatterometers Onboard the Chinese HY-2 Satellite Constellation. Remote Sens. 2021, 13, 4783. [Google Scholar] [CrossRef]
- Research Data Archive. NCAR RDA Dataset Ds083.2. Available online: http://rda.ucar.edu/datasets/ds083.2/ (accessed on 19 June 2023).
- Research Data Archive. NCAR RDA Dataset Ds083.3. Available online: http://rda.ucar.edu/datasets/ds083.3/ (accessed on 19 June 2023).
- Copernicus Climate Data Store. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 6 August 2023).
- OSDDS.NSOAS.ORG.CN. Available online: http://osdds.nsoas.org.cn/ (accessed on 20 June 2023).
- Haversine Formula Introduction. Available online: http://blog.csdn.net/gaocuisheng/article/details/126060795 (accessed on 17 June 2023).





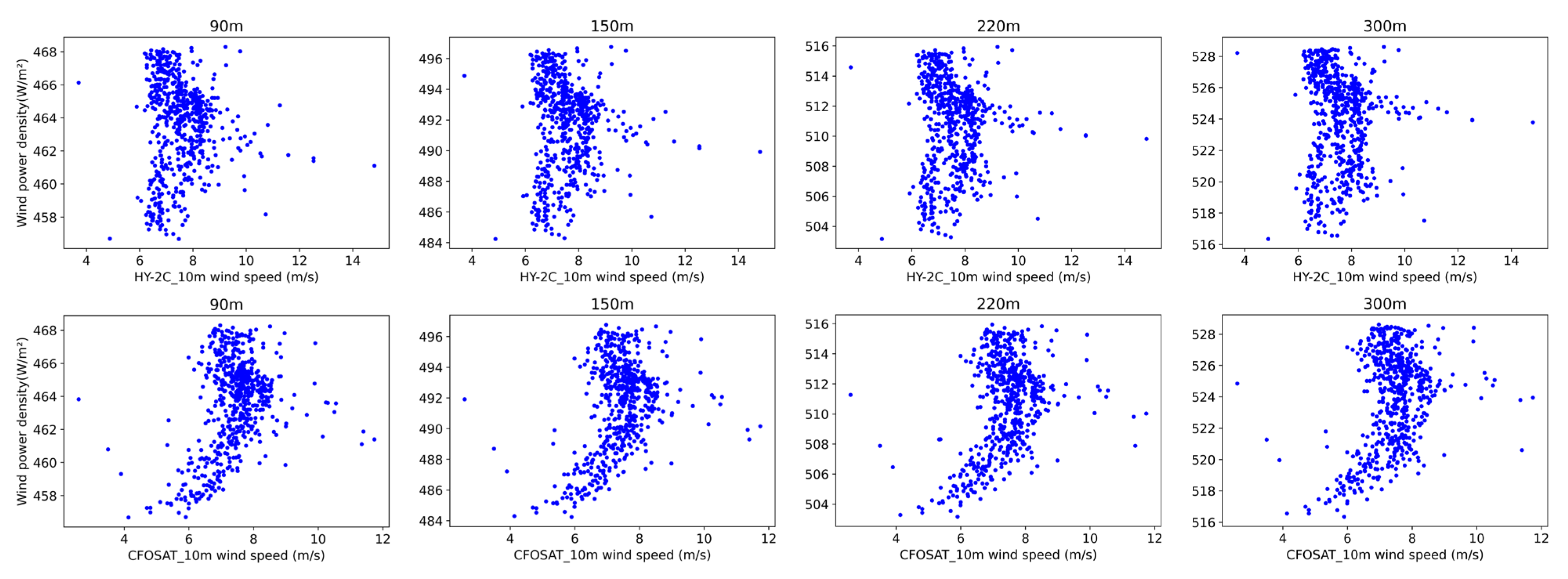

| Data | HY-2C | CFOSAT |
|---|---|---|
| 10 Oct | 10_10_10:28:44 | 10_10_10:19:50 |
| 16 Oct | 10_16_08:45:15 | 10_16_09:56:42 |
| 18 Oct | 10_18_23:13:03 | 10_18_23:07:33 |
| 24 Oct | 10_24_21:29:38 | 10_24_22:14:48 |
| 25 Oct | 10_25_21:47:04 | 10_25_22:00:09 |
| Number | Boundary Layer Scheme | Near-Surface Scheme | Correlation Coefficient | RMSE (m/s) | Bias (m/s) | MAPE |
|---|---|---|---|---|---|---|
| exp1 | YSU | MM5 | 0.92 | 1.95 | 1.57 | 0.21 |
| exp2 | MRF | MM5 | 0.92 | 1.61 | 1.21 | 0.18 |
| exp3 | MYJ | MO | 0.89 | 2.13 | 1.73 | 0.23 |
| exp4 | BL | MM5 | 0.70 | 3.15 | 2.52 | 0.38 |
| exp5 | MYNN3 | MYNN | 0.70 | 3.55 | 2.86 | 0.45 |
| exp6 | MYNN2.5 | MYNN | 0.11 | 3.38 | 2.61 | 0.40 |
| exp7 | QNSE | QNSE | 0.59 | 5.68 | 5.00 | 0.72 |
| Number | Initial Field | Correlation Coefficient | RMSE (m/s) | Bias (m/s) | MAPE (m/s) |
|---|---|---|---|---|---|
| exp1 | GDAS | 0.93 | 1.57 | 1.24 | 0.17 |
| exp2 | GFS | 0.92 | 1.61 | 1.21 | 0.18 |
| RMSE (m/s) | Bias (m/s) | MAPE | WDAR (%) | |
|---|---|---|---|---|
| 54953 | 2.73 | 2.13 | 0.15 | 78.57 |
| 58264 | 1.63 | 1.35 | 0.18 | 89.28 |
| 58265 | 2.69 | 1.96 | 0.18 | 96.43 |
| RMSE | Bias | MAPE | |
|---|---|---|---|
| HY-2C | 1.19 | 0.95 | 0.06 |
| CFOSAT | 1.25 | 0.97 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wan, B.; Duan, Z.; He, Y.; Yu, Y.; Chen, H. Evaluation of HY-2C and CFOSAT Satellite Retrieval Offshore Wind Energy Using Weather Research and Forecasting (WRF) Simulations. Remote Sens. 2023, 15, 4172. https://doi.org/10.3390/rs15174172
Li Z, Wan B, Duan Z, He Y, Yu Y, Chen H. Evaluation of HY-2C and CFOSAT Satellite Retrieval Offshore Wind Energy Using Weather Research and Forecasting (WRF) Simulations. Remote Sensing. 2023; 15(17):4172. https://doi.org/10.3390/rs15174172
Chicago/Turabian StyleLi, Zheng, Bingcheng Wan, Zexia Duan, Yuanhong He, Yingxin Yu, and Huansang Chen. 2023. "Evaluation of HY-2C and CFOSAT Satellite Retrieval Offshore Wind Energy Using Weather Research and Forecasting (WRF) Simulations" Remote Sensing 15, no. 17: 4172. https://doi.org/10.3390/rs15174172
APA StyleLi, Z., Wan, B., Duan, Z., He, Y., Yu, Y., & Chen, H. (2023). Evaluation of HY-2C and CFOSAT Satellite Retrieval Offshore Wind Energy Using Weather Research and Forecasting (WRF) Simulations. Remote Sensing, 15(17), 4172. https://doi.org/10.3390/rs15174172





