Combining Chlorophyll Fluorescence and Vegetation Reflectance Indices to Estimate Non-Photochemical Quenching (NPQ) of Rice at the Leaf Scale
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site and Design
2.2. Data Processing
2.2.1. Data Acquisition and Calculation
2.2.2. Data Selection and Modeling
2.3. Statistical Analysis
3. Results
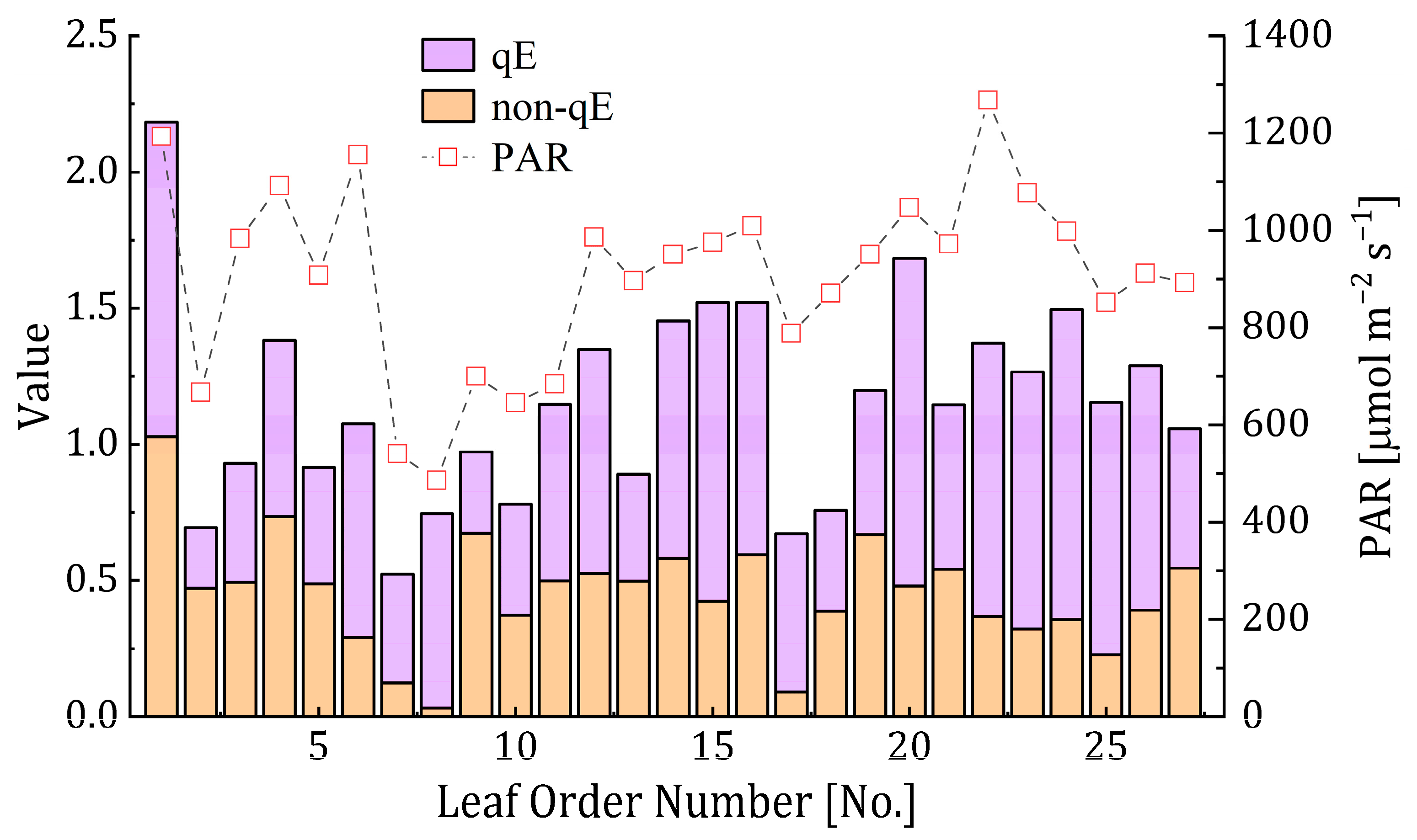
3.1. Relationship between NPQ, qE and Non-qE
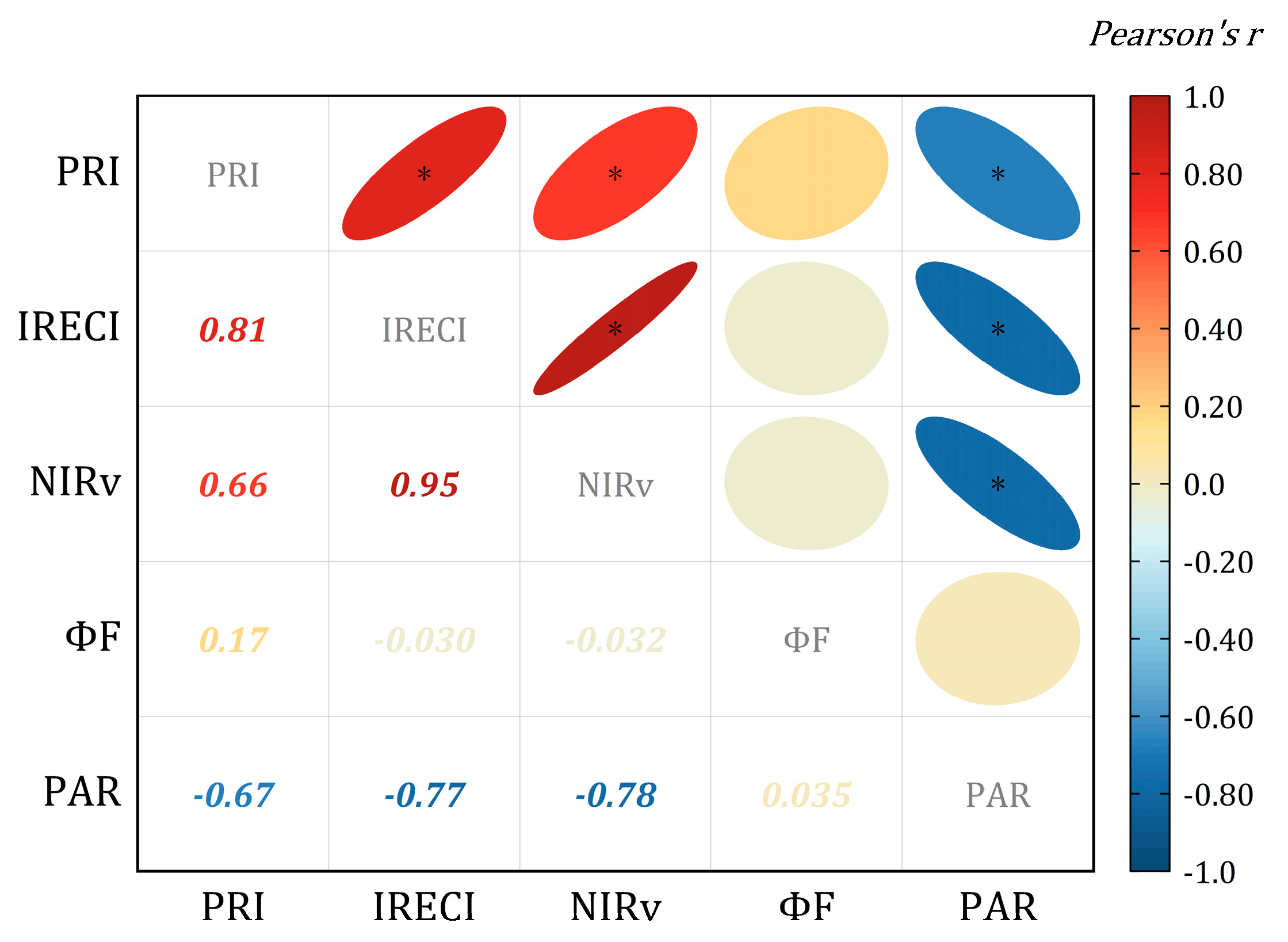
3.2. Relationship between NPQ and Leaf Observation Parameters
3.3. Modeling NPQ with Vegetation Reflectance Indices, ΦF and PAR
4. Discussion
4.1. Role of Leaf Parameters in Estimating NPQ
4.2. Performance of Multi-Parameter NPQ Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farquhar, G.D.; von Caemmerer, S.V.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef]
- Barber, J. Photosynthetic energy conversion: Natural and artificial. Chem. Soc. Rev. 2009, 38, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Bambach, N.; Gilbert, M.E. A dynamic model of RuBP-regeneration limited photosynthesis accounting for photoinhibition, heat and water stress. Agric. For. Meteorol. 2020, 285, 107911. [Google Scholar] [CrossRef]
- Powles, S.B. Photoinhibition of photosynthesis induced by visible light. Annu. Rev. Plant Physiol. 1984, 35, 15–44. [Google Scholar] [CrossRef]
- Yamori, W.; Makino, A.; Shikanai, T. A physiological role of cyclic electron transport around photosystem I in sustaining photosynthesis under fluctuating light in rice. Sci Rep. 2016, 6, 20147. [Google Scholar] [CrossRef]
- Horton, P.; Ruban, A.V.; Walters, R.G. Regulation of light harvesting in green plants. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1996, 47, 655–684. [Google Scholar] [CrossRef]
- Demmig-Adams, B.; Koh, S.; Cohu, C.M.; Muller, O.; Stewart, J.J.; Adams, W.W. Non-Photochemical Fluorescence Quenching in Contrasting Plant Species and Environments. In Non-Photochemical Quenching and Energy Dissipation in Plants, Algae and Cyanobacteria; Demmig-Adams, B., Garab, G., Adams, W., III, Govindjee, Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 531–552. [Google Scholar]
- Murchie, E.H.; Ruban, A.V. Dynamic non-photochemical quenching in plants: From molecular mechanism to productivity. Plant J. 2020, 101, 885–896. [Google Scholar] [CrossRef]
- Nicol, L.; Nawrocki, W.J.; Croce, R. Disentangling the sites of non-photochemical quenching in vascular plants. Nat. Plants 2019, 5, 1177–1183. [Google Scholar] [CrossRef]
- Wraight, C.A.; Crofts, A.R. Energy-Dependent Quenching of Chlorophyll a Fluorescence in Isolated Chloroplasts. Eur. J. Biochem. 1970, 17, 319–327. [Google Scholar] [CrossRef]
- Allen, J.F.; Bennett, J.; Steinback, K.E.; Arntzen, C.J. Chloroplast protein phosphorylation couples plastoquinone redox state to distribution of excitation energy between photosystems. Nature 1981, 291, 25–29. [Google Scholar] [CrossRef]
- Krause, G.H.; Weis, E. Chlorophyll fluorescence and photosynthesis: The basics. Annu. Rev. Plant Biol. 1991, 42, 313–349. [Google Scholar] [CrossRef]
- Nilkens, M.; Kress, E.; Lambrev, P.; Miloslavina, Y.; Müller, M.; Holzwarth, A.R.; Jahns, P. Identification of a slowly inducible zeaxanthin-dependent component of non-photochemical quenching of chlorophyll fluorescence generated under steady-state conditions in Arabidopsis. Biochim. Et Biophys. Acta (BBA)-Bioenerg. 2010, 1797, 466–475. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A. A high-resolution portrait of the annual dynamics of photochemical and non-photochemical quenching in needles of Pinus sylvestris. Physiol. Plant. 2011, 143, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Ruban, A.V. Nonphotochemical Chlorophyll Fluorescence Quenching: Mechanism and Effectiveness in Protecting Plants from Photodamage. Plant Physiol. 2016, 170, 1903–1916. [Google Scholar] [CrossRef]
- Ahn, T.K.; Avenson, T.J.; Peers, G.; Li, Z.; Dall Osto, L.; Bassi, R.; Niyogi, K.K.; Fleming, G.R. Investigating energy partitioning during photosynthesis using an expanded quantum yield convention. Chem. Phys. 2009, 357, 151–158. [Google Scholar] [CrossRef]
- Guadagno, C.R.; Virzo De Santo, A.; D’Ambrosio, N. A revised energy partitioning approach to assess the yields of non-photochemical quenching components. Biochim. Et Biophys. Acta (BBA)-Bioenerg. 2010, 1797, 525–530. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, U.; Schliwa, U. A solid-state, portable instrument for measurement of chlorophyll luminescence induction in plants. Photosynth. Res. 1987, 11, 173–182. [Google Scholar] [CrossRef] [PubMed]
- White, S.; Anandraj, A.; Bux, F. PAM fluorometry as a tool to assess microalgal nutrient stress and monitor cellular neutral lipids. Bioresour. Technol. 2011, 102, 1675–1682. [Google Scholar] [CrossRef]
- Alonso, L.; Van Wittenberghe, S.; Amorós-López, J.; Vila-Francés, J.; Gómez-Chova, L.; Moreno, J. Diurnal cycle relationships between passive fluorescence, PRI and NPQ of vegetation in a controlled stress experiment. Remote Sens. 2017, 9, 770. [Google Scholar] [CrossRef]
- Flexas, J.; Escalona, J.M.; Evain, S.; Gulías, J.; Moya, I.; Osmond, C.B.; Medrano, H. Steady-state chlorophyll fluorescence (Fs) measurements as a tool to follow variations of net CO2 assimilation and stomatal conductance during water-stress in C3 plants. Physiol. Plant. 2002, 114, 231–240. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; Tol, C.; Flexas, J.; Pfündel, E.; Moreno, J.; Frankenberg, C.; Berry, J. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Chou, S.; Chen, J.M.; Yu, H.; Chen, B.; Zhang, X.; Croft, H.; Khalid, S.; Li, M.; Shi, Q. Canopy-Level Photochemical Reflectance Index from Hyperspectral Remote Sensing and Leaf-Level Non-Photochemical Quenching as Early Indicators of Water Stress in Maize. Remote Sens. 2017, 9, 794. [Google Scholar] [CrossRef]
- D’Odorico, P.; Schönbeck, L.; Vitali, V.; Meusburger, K.; Schaub, M.; Ginzler, C.; Zweifel, R.; Velasco, V.M.E.; Gisler, J.; Gessler, A.; et al. Drone-based physiological index reveals long-term acclimation and drought stress responses in trees. Plant Cell Environ. 2021, 44, 3552–3570. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, J.M.; Ju, W. Photochemical reflectance index (PRI) can be used to improve the relationship between gross primary productivity (GPP) and sun-induced chlorophyll fluorescence (SIF). Remote Sens. Environ. 2020, 246, 111888. [Google Scholar] [CrossRef]
- Wong, C.Y.S.; Gamon, J.A. Three causes of variation in the photochemical reflectance index (PRI) in evergreen conifers. New Phytol. 2015, 206, 187–195. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gamon, J.A.; Solovchenko, A. Multiple drivers of seasonal change in PRI: Implications for photosynthesis 1. Leaf level. Remote Sens. Environ. 2017, 191, 110–116. [Google Scholar] [CrossRef]
- Yang, P. Exploring the interrelated effects of soil background, canopy structure and sun-observer geometry on canopy photochemical reflectance index. Remote Sens. Environ. 2022, 279, 113133. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Chemura, A.; Mutanga, O.; Odindi, J.; Kutywayo, D. Mapping spatial variability of foliar nitrogen in coffee (Coffea arabica L.) plantations with multispectral Sentinel-2 MSI data. Isprs-J. Photogramm. Remote Sens. 2018, 138, 1–11. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. Isprs-J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, M.; Hao, D.; Damm, A.; Badgley, G.; Rascher, U.; Johnson, J.E.; Dechant, B.; Siegmann, B.; Ryu, Y.; et al. Combining near-infrared radiance of vegetation and fluorescence spectroscopy to detect effects of abiotic changes and stresses. Remote Sens. Environ. 2022, 270, 112856. [Google Scholar] [CrossRef]
- Maleki, M.; Arriga, N.; Roland, M.; Wieneke, S.; Barrios, J.M.; Van Hoolst, R.; Peñuelas, J.; Janssens, I.A.; Balzarolo, M. Soil water depletion induces discrepancies between in situ measured vegetation indices and photosynthesis in a temperate heathland. Agric. For. Meteorol. 2022, 324, 109110. [Google Scholar] [CrossRef]
- Zeng, Y.; Badgley, G.; Dechant, B.; Ryu, Y.; Chen, M.; Berry, J.A. A practical approach for estimating the escape ratio of near-infrared solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2019, 232, 111209. [Google Scholar] [CrossRef]
- Badgley, G.; Anderegg, L.D.L.; Berry, J.A.; Field, C.B. Terrestrial gross primary production: Using NIRV to scale from site to globe. Glob. Change Biol. 2019, 25, 3731–3740. [Google Scholar] [CrossRef]
- Atherton, J.; Nichol, C.J.; Porcar-Castell, A. Using spectral chlorophyll fluorescence and the photochemical reflectance index to predict physiological dynamics. Remote Sens. Environ. 2016, 176, 17–30. [Google Scholar] [CrossRef]
- Mohammed, G.H.; Colombo, R.; Middleton, E.M.; Rascher, U.; van der Tol, C.; Nedbal, L.; Goulas, Y.; Pérez-Priego, O.; Damm, A.; Meroni, M.; et al. Remote sensing of solar-induced chlorophyll fluorescence (SIF) in vegetation: 50 years of progress. Remote Sens. Environ. 2019, 231, 111177. [Google Scholar] [CrossRef]
- Maguire, A.J.; Eitel, J.U.H.; Griffin, K.L.; Magney, T.S.; Long, R.A.; Vierling, L.A.; Schmiege, S.C.; Jennewein, J.S.; Weygint, W.A.; Boelman, N.T.; et al. On the Functional Relationship Between Fluorescence and Photochemical Yields in Complex Evergreen Needleleaf Canopies. Geophys. Res. Lett. 2020, 47, e2020G–e87858G. [Google Scholar] [CrossRef]
- Magney, T.S.; Barnes, M.L.; Yang, X. On the Covariation of Chlorophyll Fluorescence and Photosynthesis Across Scales. Geophys. Res. Lett. 2020, 47, e2020G–e91098G. [Google Scholar] [CrossRef]
- Liu, B.; Cui, Y.; Tan, J.; Luo, Y.; Xiang, Z. CO2 fluxes over two paddy fields with different management practices in Southern China. Agric. For. Meteorol. 2021, 310, 108650. [Google Scholar] [CrossRef]
- Xu, S.; Atherton, J.; Riikonen, A.; Zhang, C.; Oivukkamäki, J.; MacArthur, A.; Honkavaara, E.; Hakala, T.; Koivumäki, N.; Liu, Z.; et al. Structural and photosynthetic dynamics mediate the response of SIF to water stress in a potato crop. Remote Sens. Environ. 2021, 263, 112555. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.; Baker, N.R. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Et Biophys. Acta (BBA)-Gen. Subj. 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Mueller-moule, P.; Li, X.; Niyogi, K. Non-Photochemical Quenching. A Response to Excess Light Energy. Plant Physiol. 2001, 125, 1558–1566. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.R. Chlorophyll Fluorescence: A Probe of Photosynthesis In Vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; van der Tol, C.; Campbell, P.K.E.; Middleton, E.M. Fluorescence Correction Vegetation Index (FCVI): A physically based reflectance index to separate physiological and non-physiological information in far-red sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2020, 240, 111676. [Google Scholar] [CrossRef]
- Cendrero-Mateo, M.P.; Moran, M.S.; Papuga, S.A.; Thorp, K.R.; Alonso, L.; Moreno, J.; Ponce-Campos, G.; Rascher, U.; Wang, G. Plant chlorophyll fluorescence: Active and passive measurements at canopy and leaf scales with different nitrogen treatments. J. Exp. Bot. 2016, 67, 275–286. [Google Scholar] [CrossRef]
- Gamon, J.A.; Penuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Ruban, A.V.; Johnson, M.P.; Duffy, C.D. The photoprotective molecular switch in the photosystem II antenna. Biochim. Et Biophys. Acta (BBA)-Bioenerg. 2012, 1817, 167–181. [Google Scholar] [CrossRef]
- Gamon, J.A.; Berry, J.A. Facultative and constitutive pigment effects on the Photochemical Reflectance Index (PRI) in sun and shade conifer needles. Isr. J. Plant Sci. 2012, 60, 85–95. [Google Scholar] [CrossRef]
- Sukhova, E.; Sukhov, V. Analysis of Light-Induced Changes in the Photochemical Reflectance Index (PRI) in Leaves of Pea, Wheat, and Pumpkin Using Pulses of Green-Yellow Measuring Light. Remote Sens. 2019, 11, 810. [Google Scholar] [CrossRef]
- Wong, C.Y.; D Odorico, P.; Arain, M.A.; Ensminger, I. Tracking the phenology of photosynthesis using carotenoid-sensitive and near-infrared reflectance vegetation indices in a temperate evergreen and mixed deciduous forest. New Phytol. 2020, 226, 1682–1695. [Google Scholar] [CrossRef] [PubMed]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Ayu Purnamasari, R.; Noguchi, R.; Ahamed, T. Land suitability assessments for yield prediction of cassava using geospatial fuzzy expert systems and remote sensing. Comput. Electron. Agric. 2019, 166, 105018. [Google Scholar] [CrossRef]
- Nauš, J.; Prokopová, J.; Řebíček, J.; Špundová, M. SPAD chlorophyll meter reading can be pronouncedly affected by chloroplast movement. Photosynth. Res. 2010, 105, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Peguero-Pina, J.J.; Pelegrín, E.; Morales, F. Three pools of zeaxanthin in Quercus coccifera leaves during light transitions with different roles in rapidly reversible photoprotective energy dissipation and photoprotection. J. Exp. Bot. 2013, 64, 1649–1661. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. Isprs-J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Schreiber, U. Chlorophyll fluorescence: New Instruments for Special Applications. In Photosynthesis: Mechanisms and Effects: Volume I–V: Proceedings of the XIth International Congress on Photosynthesis, Budapest, Hungary, 17–22 August 1998; Garab, G., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 4253–4258. [Google Scholar]






| Abbreviation | Description |
|---|---|
| Instantaneous steady-state fluorescence measured under ambient light at any point in time. | |
| Maximum fluorescence measured upon a saturating light pulse after adequate dark adaptation. Usually, at 23:00 local time in this study. | |
| Maximum fluorescence measured upon a saturating light pulse under ambient light at any point in time. | |
| Maximum fluorescence measured upon a saturating light pulse after 10 min dark adaptation. |
| ID | Number of Parameters | Parameter(s) Used in the Model |
|---|---|---|
| 1 | 1 | PRI |
| 2 | IRECI | |
| 3 | NIRv | |
| 4 | PAR | |
| 5 | ΦF | |
| 6 | 2 | IRECI, NIRv |
| 7 | PRI, IRECI | |
| 8 | PRI, NIRv | |
| 9 | PAR, PRI | |
| 10 | PAR, IRECI | |
| 11 | PAR, NIRv | |
| 12 | ΦF, PRI | |
| 13 | ΦF, IRECI | |
| 14 | ΦF, NIRv | |
| 15 | ΦF, PAR | |
| 16 | 3 | PRI, IRECI, NIRv |
| 17 | PAR, PRI, IRECI | |
| 18 | PAR, PRI, NIRv | |
| 19 | PAR, IRECI, NIRv | |
| 20 | ΦF, IRECI, NIRv | |
| 21 | ΦF, PRI, IRECI | |
| 22 | ΦF, PRI, NIRv | |
| 23 | ΦF, PAR, PRI | |
| 24 | ΦF, PAR, IRECI | |
| 25 | ΦF, PAR, NIRv | |
| 26 | 4 | PAR, PRI, IRECI, NIRv |
| 27 | ΦF, PRI, IRECI, NIRv | |
| 28 | ΦF, PAR, IRECI, NIRv | |
| 29 | ΦF, PAR, PRI, IRECI | |
| 30 | ΦF, PAR, PRI, NIRv | |
| 31 | 5 | ΦF, PAR, PRI, IRECI, NIRv |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Liu, Z.; Wang, J.; Yang, P.; Zhang, R.; Zhang, X.; Zheng, P. Combining Chlorophyll Fluorescence and Vegetation Reflectance Indices to Estimate Non-Photochemical Quenching (NPQ) of Rice at the Leaf Scale. Remote Sens. 2023, 15, 4222. https://doi.org/10.3390/rs15174222
Jiang H, Liu Z, Wang J, Yang P, Zhang R, Zhang X, Zheng P. Combining Chlorophyll Fluorescence and Vegetation Reflectance Indices to Estimate Non-Photochemical Quenching (NPQ) of Rice at the Leaf Scale. Remote Sensing. 2023; 15(17):4222. https://doi.org/10.3390/rs15174222
Chicago/Turabian StyleJiang, Hao, Zhigang Liu, Jin Wang, Peiqi Yang, Runfei Zhang, Xiuping Zhang, and Pu Zheng. 2023. "Combining Chlorophyll Fluorescence and Vegetation Reflectance Indices to Estimate Non-Photochemical Quenching (NPQ) of Rice at the Leaf Scale" Remote Sensing 15, no. 17: 4222. https://doi.org/10.3390/rs15174222
APA StyleJiang, H., Liu, Z., Wang, J., Yang, P., Zhang, R., Zhang, X., & Zheng, P. (2023). Combining Chlorophyll Fluorescence and Vegetation Reflectance Indices to Estimate Non-Photochemical Quenching (NPQ) of Rice at the Leaf Scale. Remote Sensing, 15(17), 4222. https://doi.org/10.3390/rs15174222






