An Integrated Framework for Remote Sensing Assessment of the Trophic State of Large Lakes
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Data Collection
2.2.1. Field Measurements
2.2.2. Remote Sensing Data
2.2.3. Meteorological Data
3. Methods
3.1. An Integrated Framework for TSI Inversion
- Step 1: Data collection and collation, and identification of the main driving factors of TSI. Complex environmental factors were used to compensate for the uncertainty of remote sensing inversion.
- Step 2: Quantification of the degree of influence of driving factors on TSI. Key environmental factors were selected as the optional input variables for the model.
- Step 3: Data preprocessing, outlier cleaning, etc., to obtain the data set.
- Step 4: Construction and optimization of the TSI inversion model.
- Step 5: Model accuracy assessment and temporal and spatial distribution mapping.
3.2. Data Preprocessing
3.2.1. Region of Interest Extraction
3.2.2. Preprocessing of Remote Sensing Images
3.2.3. Spectral Curve Outlier Removal
3.2.4. TSI Outlier Removal
3.3. TSI Inversion Model Based on Backpropagation Neural Network
3.4. Optimization of Model Parameters Based on Sparrow Search Algorithm
3.5. Model Accuracy Assessment
4. Results
4.1. Selection of Key Factors Driving Eutrophication
4.2. Trophic State of Water
4.3. Performance Comparison of the TSI Model with Environmental Factors
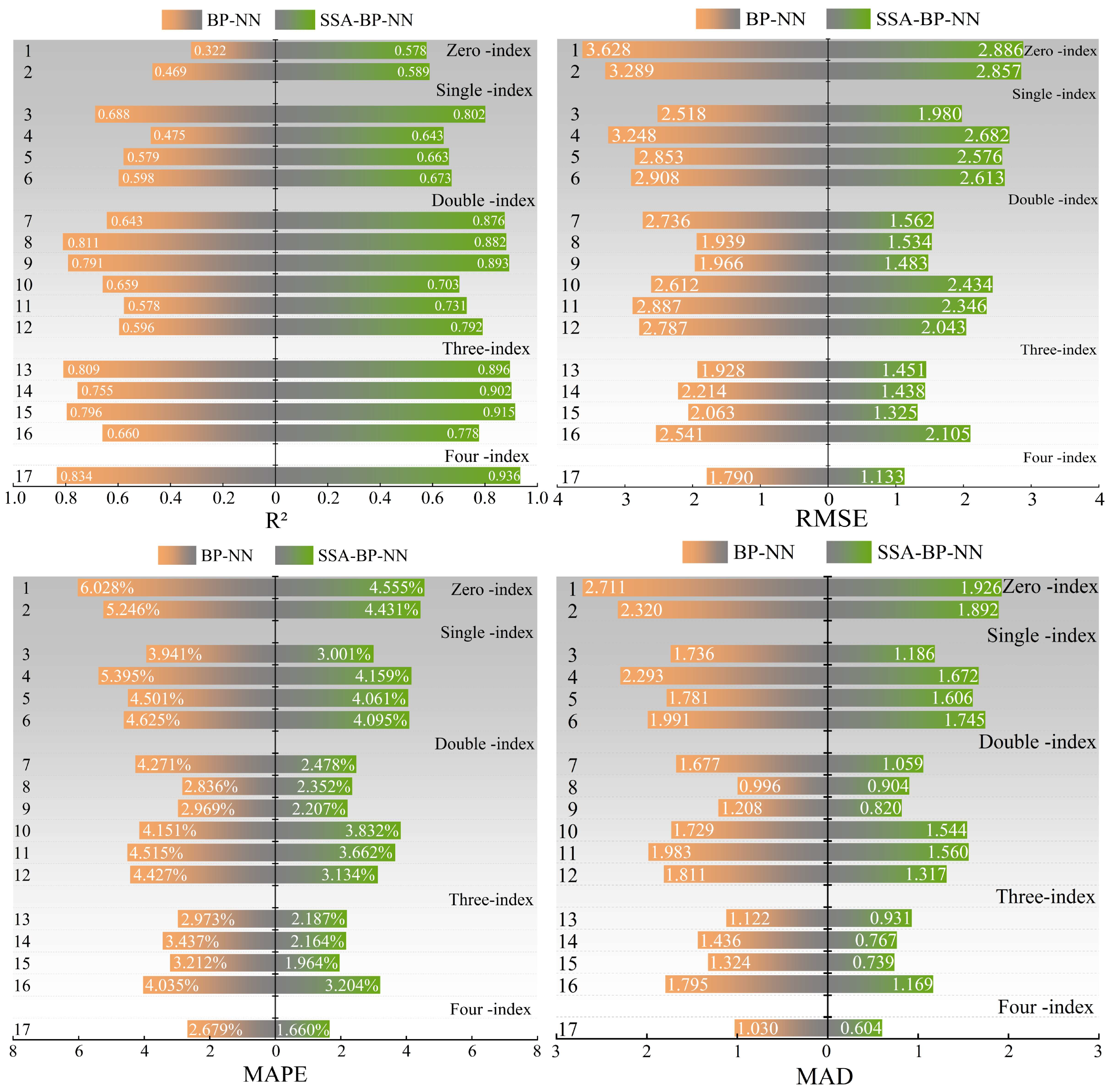
4.3.1. Performance Comparison of TSI Model Based on BP-NN
4.3.2. Performance Comparison of the TSI Model Based on SSA-BP-NN
4.4. Temporal and Spatial Distribution of Trophic State
5. Discussion
5.1. Construction and Assessment of the TSI Inversion Framework
5.2. Selection of the Input Variables
5.3. Limitations and Future Perspectives
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mortsch, L.D.; Quinn, F.H. Climate Change Scenarios for Great Lakes Basin Ecosystem Studies. Limnol. Oceanogr. 1996, 41, 903–911. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, S.; Liu, J.; Liu, C.; Hao, F.; Wang, Z.; Zhang, H.; Song, J.; Mitrovic, S.M.; Lim, R.P. Linking Fish Tolerance to Water Quality Criteria for the Assessment of Environmental Flows: A Practical Method for Streamflow Regulation and Pollution Control. Water Res. 2018, 141, 96–108. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, J.; Zhang, B.; Spyrakos, E.; Tyler, A.N.; Shen, Q.; Zhang, F.; Kuster, T.; Lehmann, M.K.; Wu, Y.; et al. Trophic State Assessment of Global Inland Waters Using a MODIS-Derived Forel-Ule Index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef]
- Bricker, S.B.; Longstaff, B.; Dennison, W.; Jones, A.; Boicourt, K.; Wicks, C.; Woerner, J. Effects of Nutrient Enrichment in the Nation’s Estuaries: A Decade of Change. Harmful Algae 2008, 8, 21–32. [Google Scholar] [CrossRef]
- Mentzafou, A.; Panagopoulos, Y.; Dimitriou, E. Designing the National Network for Automatic Monitoring of Water Quality Parameters in Greece. Water 2019, 11, 1310. [Google Scholar] [CrossRef]
- Yamaguchi, N.; Fujii, Y. Rapid On-Site Monitoring of Bacteria in Freshwater Environments Using a Portable Microfluidic Counting System. Biol. Pharm. Bull. 2020, 43, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Dodds, W.K. Trophic State, Eutrophication and Nutrient Criteria in Streams. Trends Ecol. Evol. 2007, 22, 669–676. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Song, K.; Liu, M.; Zhou, Y.; Zhang, Y.; Li, Y.; Zhu, G.; Qin, B. A Semi-Analytical Approach for Remote Sensing of Trophic State in Inland Waters: Bio-Optical Mechanism and Application. Remote Sens. Environ. 2019, 232, 111349. [Google Scholar] [CrossRef]
- He, Y.; Gong, Z.; Zheng, Y.; Zhang, Y. Inland Reservoir Water Quality Inversion and Eutrophication Evaluation Using BP Neural Network and Remote Sensing Imagery: A Case Study of Dashahe Reservoir. Water 2021, 13, 2844. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Schaeffer, K.G.; Keith, D.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to Adopting Satellite Remote Sensing for Water Quality Management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Arabi, B.; Salama, M.S.; Pitarch, J.; Verhoef, W. Integration of In-Situ and Multi-Sensor Satellite Observations for Long-Term Water Quality Monitoring in Coastal Areas. Remote Sens. Environ. 2020, 239, 111632. [Google Scholar] [CrossRef]
- Gohin, F.; Van Der Zande, D.; Tilstone, G.; Eleveld, M.A.; Lefebvre, A.; Andrieux-Loyer, F.; Blauw, A.N.; Bryère, P.; Devreker, D.; Garnesson, P.; et al. Twenty Years of Satellite and in Situ Observations of Surface Chlorophyll-a from the Northern Bay of Biscay to the Eastern English Channel. Is the Water Quality Improving? Remote Sens. Environ. 2019, 233, 111343. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Wu, Y.; Wang, Q.; Huang, Z.; Wang, C. Urban River Water Quality Monitoring Based on Self-Optimizing Machine Learning Method Using Multi-Source Remote Sensing Data. Ecol. Indic. 2023, 146, 109750. [Google Scholar] [CrossRef]
- Sheela, A.M.; Letha, J.; Joseph, S.; Ramachandran, K.K.; Sanalkumar, S.P. Trophic State Index of a Lake System Using IRS (P6-LISS III) Satellite Imagery. Environ. Monit. Assess. 2011, 177, 575–592. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, F.; Alcântara, E.; Rodrigues, T.; Imai, N.; Barbosa, C.; Rotta, L. Estimation of Chlorophyll-a Concentration and the Trophic State of the Barra Bonita Hydroelectric Reservoir Using OLI/Landsat-8 Images. Int. J. Environ. Res. Public Health 2015, 12, 10391–10417. [Google Scholar] [CrossRef] [PubMed]
- Novo, E.M.L.D.M.; Londe, L.D.R.; Barbosa, C.C.F.; Araujo, C.A.S.D.; Rennó, C.D. Proposal for a Remote Sensing Trophic State Index Based upon Thematic Mapper/Landsat Images. Rev. Ambiente Água 2013, 8, 65–82. [Google Scholar] [CrossRef]
- Breitburg, D.; Levin, L.A.; Oschlies, A.; Grégoire, M.; Chavez, F.P.; Conley, D.J.; Garçon, V.; Gilbert, D.; Gutiérrez, D.; Isensee, K.; et al. Declining Oxygen in the Global Ocean and Coastal Waters. Science 2018, 359, eaam7240. [Google Scholar] [CrossRef] [PubMed]
- Tian, S.; Guo, H.; Xu, W.; Zhu, X.; Wang, B.; Zeng, Q.; Mai, Y.; Huang, J.J. Remote Sensing Retrieval of Inland Water Quality Parameters Using Sentinel-2 and Multiple Machine Learning Algorithms. Environ. Sci. Pollut. Res. 2022, 30, 18617–18630. [Google Scholar] [CrossRef]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication Changes in Fifty Large Lakes on the Yangtze Plain of China Derived from MERIS and OLCI Observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
- Cheng, K.H.; Chan, S.N.; Lee, J.H.W. Remote Sensing of Coastal Algal Blooms Using Unmanned Aerial Vehicles (UAVs). Mar. Pollut. Bull. 2020, 152, 110889. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Hall, B.; Li, L. Hyperspectral Remote Sensing of Total Phosphorus (TP) in Three Central Indiana Water Supply Reservoirs. Water Air Soil Pollut. 2012, 223, 1481–1502. [Google Scholar] [CrossRef]
- Carlson, R.E. A Trophic State Index for Lakes1: Trophic State Index. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Zhu, S.; Mao, J. A Machine Learning Approach for Estimating the Trophic State of Urban Waters Based on Remote Sensing and Environmental Factors. Remote Sens. 2021, 13, 2498. [Google Scholar] [CrossRef]
- Li, S.; Chen, F.; Song, K.; Liu, G.; Tao, H.; Xu, S.; Wang, X.; Wang, Q.; Mu, G. Mapping the Trophic State Index of Eastern Lakes in China Using an Empirical Model and Sentinel-2 Imagery Data. J. Hydrol. 2022, 608, 127613. [Google Scholar] [CrossRef]
- Qin, B.; Yang, G.; Ma, J.; Wu, T.; Li, W.; Liu, L.; Deng, J.; Zhou, J. Spatiotemporal Changes of Cyanobacterial Bloom in Large Shallow Eutrophic Lake Taihu, China. Front. Microbiol. 2018, 9, 451. [Google Scholar] [CrossRef]
- Izmailova, A.V.; Rumyantsev, V.A. Trophic Status of the Largest Freshwater Lakes in the World. Lakes Reserv. Res. Manag. 2016, 21, 20–30. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Ma, R.; Cao, Z. Remote Sensing Estimation of Lake Total Phosphorus Concentration Based on MODIS: A Case Study of Lake Hongze. Remote Sens. 2019, 11, 2068. [Google Scholar] [CrossRef]
- Cai, Y.; Ke, C.-Q.; Shen, X. Variations in Water Level, Area and Volume of Hongze Lake, China from 2003 to 2018. J. Great Lakes Res. 2020, 46, 1511–1520. [Google Scholar] [CrossRef]
- Yao, M.; Mao, X.; Sun, R. Spatio-temporal Variation of Water Quality in Hongze Lake from 2010 to 2020. Water Resour. Prot. 2022, 38, 174–180. [Google Scholar]
- Zhao, Y.; Yu, T.; Hu, B.; Zhang, Z.; Liu, Y.; Liu, X.; Liu, H.; Liu, J.; Wang, X.; Song, S. Retrieval of Water Quality Parameters Based on Near-Surface Remote Sensing and Machine Learning Algorithm. Remote Sens. 2022, 14, 5305. [Google Scholar] [CrossRef]
- Johansen, R.; Beck, R.; Nowosad, J.; Nietch, C.; Xu, M.; Shu, S.; Yang, B.; Liu, H.; Emery, E.; Reif, M.; et al. Evaluating the Portability of Satellite Derived Chlorophyll-a Algorithms for Temperate Inland Lakes Using Airborne Hyperspectral Imagery and Dense Surface Observations. Harmful Algae 2018, 76, 35–46. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote Sensing of Black Lakes and Using 810 Nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Mcfeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Yue, H.; Liu, Y.; Wang, H.; Zhang, W. Analysis of Dynamic Change of Hongjiannao Lake Based on MNDWI. IOP Conf. Ser. Earth Environ. Sci. 2017, 57, 012005. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A New Technique for Surface Water Mapping Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Koda, S.; Zeggada, A.; Melgani, F.; Nishii, R. Spatial and Structured SVM for Multilabel Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5948–5960. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Li, L.; Lu, H. Absorption Characteristics of Optically Complex Inland Waters: Implications for Water Optical classification: Water optical classification. J. Geophys. Res. Biogeosci. 2013, 118, 860–874. [Google Scholar] [CrossRef]
- Baban, S.M.J. Trophic Classification and Ecosystem Checking of Lakes Using Remotely Sensed Information. Hydrol. Sci. J. 1996, 41, 939–957. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E.; Han, W.S.; Kim, K.; Choung, S.; Chung, I.M. Identifying Outliers of Non-Gaussian Groundwater State Data Based on Ensemble Estimation for Long-Term Trends. J. Hydrol. 2017, 548, 135–144. [Google Scholar] [CrossRef]
- Awad, M. Sea Water Chlorophyll-a Estimation Using Hyperspectral Images and Supervised Artificial Neural Network. Ecol. Inform. 2014, 24, 60–68. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Yan, S.; Liu, W.; Li, X.; Yang, P.; Wu, F.; Yan, Z. Comparative Study and Improvement Analysis of Sparrow Search Algorithm. Wirel. Commun. Mobile Comput. 2022, 2022, 4882521. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, Y.; Guo, B.; Luo, X.; Peng, Q.; Jin, Z. A Hybrid Sparrow Search Algorithm of the Hyperparameter Optimization in Deep Learning. Mathematics 2022, 10, 3019. [Google Scholar] [CrossRef]
- Pu, M.; Xu, J.; Hu, K.; Peng, K.; Gong, Z.; Cai, Y.; Xiang, X. Community Structure and Driving Factors of Zooplankton in the Littoral Zone of Lake Hongze. J. Lake Sci. 2023, 35, 610–623. [Google Scholar]
- Chen, Q.; Huang, M.; Tang, X. Eutrophication Assessment of Seasonal Urban Lakes in China Yangtze River Basin Using Landsat 8-Derived Forel-Ule Index: A Six-Year (2013–2018) Observation. Sci. Total Environ. 2020, 745, 135392. [Google Scholar] [CrossRef]
- Tang, H.; Gao, M.; Yuan, S.; Zhang, H.; Xiao, Y.; Zhang, F.; Zhang, K. Impact of the Yellow River Capture on the Paleoenvironmental Changes of Hongze Lake, China. Int. J. Sediment Res. 2023, 38, 503–515. [Google Scholar] [CrossRef]
- Ren, Y.; Pei, H.; Hu, W.; Tian, C.; Hao, D.; Wei, J.; Feng, Y. Spatiotemporal Distribution Pattern of Cyanobacteria Community and Its Relationship with the Environmental Factors in Hongze Lake, China. Environ. Monit. Assess. 2014, 186, 6919–6933. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Bouchard, R.W.; Finlay, J.C.; Griffin, C.G.; Olmanson, L.G.; Anderson, J.P.; Arnold, W.A.; Hozalski, R. Color, Chlorophyll a, and Suspended Solids Effects on Secchi Depth in Lakes: Implications for Trophic State Assessment. Ecol. Appl. 2019, 29, e01871. [Google Scholar] [CrossRef]
- Watanabe, F.S.Y.; Miyoshi, G.T.; Rodrigues, T.W.P.; Bernardo, N.M.R.; Rotta, L.H.S.; Alcântara, E.; Imai, N.N. Inland Water’s Trophic Status Classification Based on Machine Learning and Remote Sensing Data. Remote Sens. Appl. Soc. Environ. 2020, 19, 100326. [Google Scholar] [CrossRef]
















| No. | Band Combination | Correlation | No. | Band Combination | Correlation |
|---|---|---|---|---|---|
| 1 | (B11 − B8)/(B11 + B8) | −0.317 * | 7 | B12/B11 | 0.311 * |
| 2 | (B8A − B8)/(B8A + B8) | −0.369 ** | 8 | (B8A − B6)/(B8A + B6) | −0.352 ** |
| 3 | (1.5B11 − (B8 + B3)/2)/(1.5B11 + (B8 + B3)/2) | −0.308 * | 9 | (B8A − B7)/(B8A + B7) | −0.380 ** |
| 4 | B4/B1 | 0.305 | 10 | B9/B3 | −0.305 |
| 5 | B8A/B5 | −0.291 | 11 | B9/B4 | −0.306 |
| 6 | B9/B5 | −0.335 * | 12 | (B9 + B11)/(B3 + B4) | −0.300 |
| Trophic State Index Grading Range | Degree of Water Eutrophication |
|---|---|
| TSI < 30 | Oligotrophic |
| 30 ≤ TSI ≤ 50 | Mesotrophic |
| 50 < TSI ≤ 60 | Light eutrophic |
| 60 < TSI ≤ 70 | Middle eutrophic |
| TSI > 70 | Hyper eutrophic |
| Group | Input Variables |
|---|---|
| Zero-Index | No.1.Band reflectance, No.2.RS |
| Single-Index | No.3.pH&RS, No.4.T&RS, No.5.AWS&RS, No.6.SC&RS |
| Double-Index | No.7.pH&T&RS, No.8.pH&AWS&RS, No.9.pH&SC&RS, No.10.T&AWS&RS, No.11.T&SC&RS, No.12.AWS&SC&RS |
| Three-Index | No.13.pH&T&AWS&RS, No.14.pH&T&SC&RS, No.15.pH&AWS&SC&RS, No.16.T&AWS&SC&RS |
| Four-Index | No.17.pH&T&AWS&SC&RS |
| No. | Hidden Layer Size | R2 | RMSE | MAPE | MAD |
|---|---|---|---|---|---|
| 1 | 5 | 0.802 | 2.017 | 3.067 | 1.265 |
| 2 | 6 | 0.808 | 1.960 | 2.986 | 1.168 |
| 3 | 7 | 0.857 | 1.672 | 2.558 | 1.082 |
| 4 | 8 | 0.875 | 1.584 | 2.430 | 0.997 |
| 5 | 9 | 0.868 | 1.619 | 2.492 | 1.029 |
| 6 | 10 | 0.918 | 1.280 | 1.954 | 0.798 |
| 7 | 11 | 0.936 | 1.133 | 1.660 | 0.604 |
| 8 | 12 | 0.931 | 1.168 | 1.650 | 0.599 |
| 9 | 13 | 0.870 | 1.601 | 2.351 | 0.908 |
| 10 | 14 | 0.818 | 1.907 | 3.043 | 1.186 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, D.; Mao, J.; Li, W.; Zhu, S.; Gao, H. An Integrated Framework for Remote Sensing Assessment of the Trophic State of Large Lakes. Remote Sens. 2023, 15, 4238. https://doi.org/10.3390/rs15174238
Meng D, Mao J, Li W, Zhu S, Gao H. An Integrated Framework for Remote Sensing Assessment of the Trophic State of Large Lakes. Remote Sensing. 2023; 15(17):4238. https://doi.org/10.3390/rs15174238
Chicago/Turabian StyleMeng, Dinghua, Jingqiao Mao, Weifeng Li, Shijie Zhu, and Huan Gao. 2023. "An Integrated Framework for Remote Sensing Assessment of the Trophic State of Large Lakes" Remote Sensing 15, no. 17: 4238. https://doi.org/10.3390/rs15174238
APA StyleMeng, D., Mao, J., Li, W., Zhu, S., & Gao, H. (2023). An Integrated Framework for Remote Sensing Assessment of the Trophic State of Large Lakes. Remote Sensing, 15(17), 4238. https://doi.org/10.3390/rs15174238











