Integration and Detection of a Moving Target with Multiple Beams Based on Multi-Scale Sliding Windowed Phase Difference and Spatial Projection
Abstract
:1. Introduction
- (1)
- The proposed MBPCF can accurately compensate for the beam migration;
- (2)
- The time information (the time when the moving target enters the beam and the time when it leaves the beam) can be accurately estimated by the proposed MSWPD. In this process, the RM and DFM are all eliminated, and coherent integration within the beam is realized;
- (3)
- Using the SP algorithm, multi-beam joint integration can be realized.
2. Geometric and Signal Models for Moving Targets with Multiple Beam
2.1. Geometric and Signal Models
2.2. Signal Characteristics
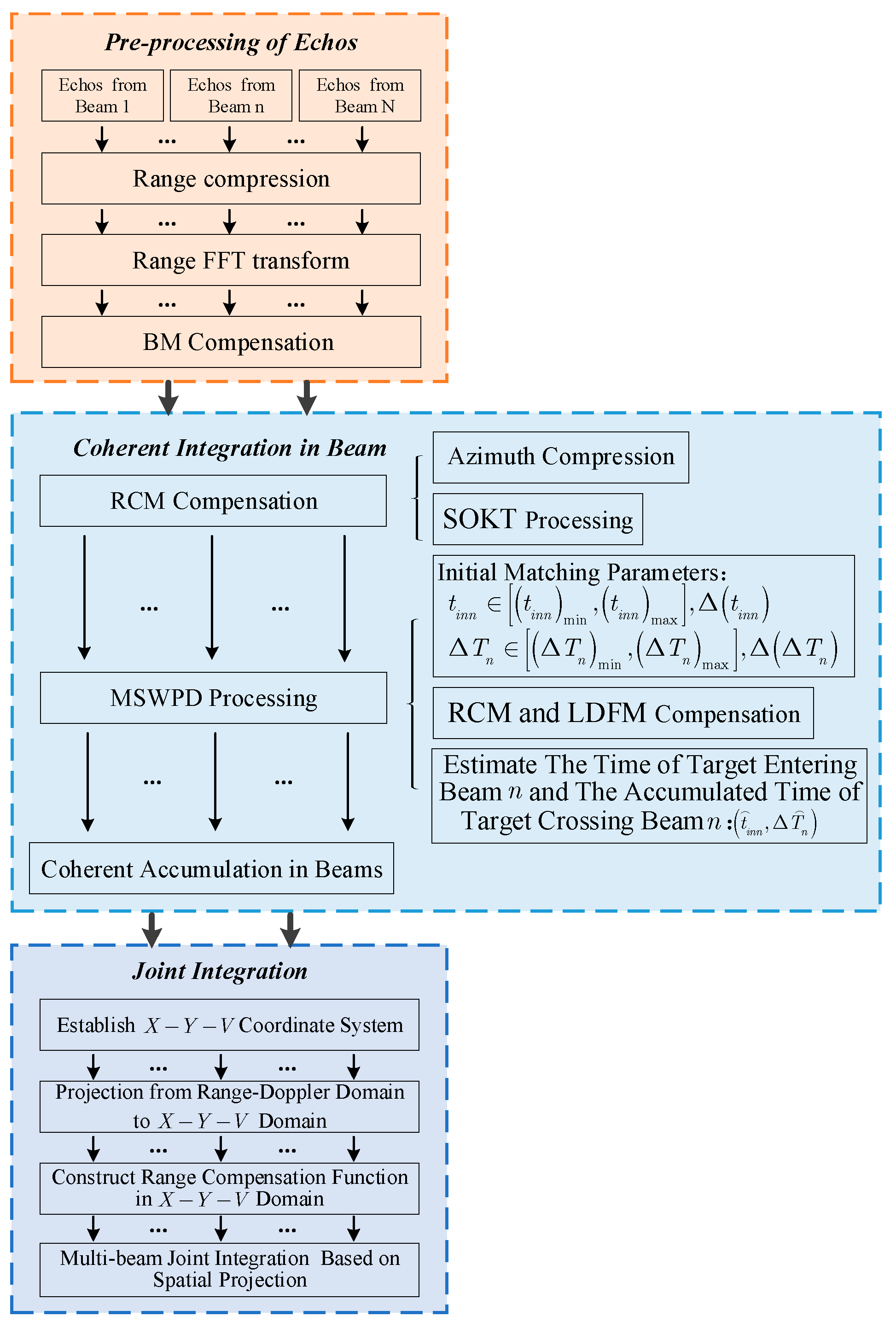
3. Propose Method Description
3.1. Beam Migration Compensation
3.2. Fine Focusing on Moving Target
3.2.1. Coherent Integration within the Beam
3.2.2. Joint Integration among Different Beams Based on Spatial Projection
4. Some Discussions for the Proposed Approach in Applications
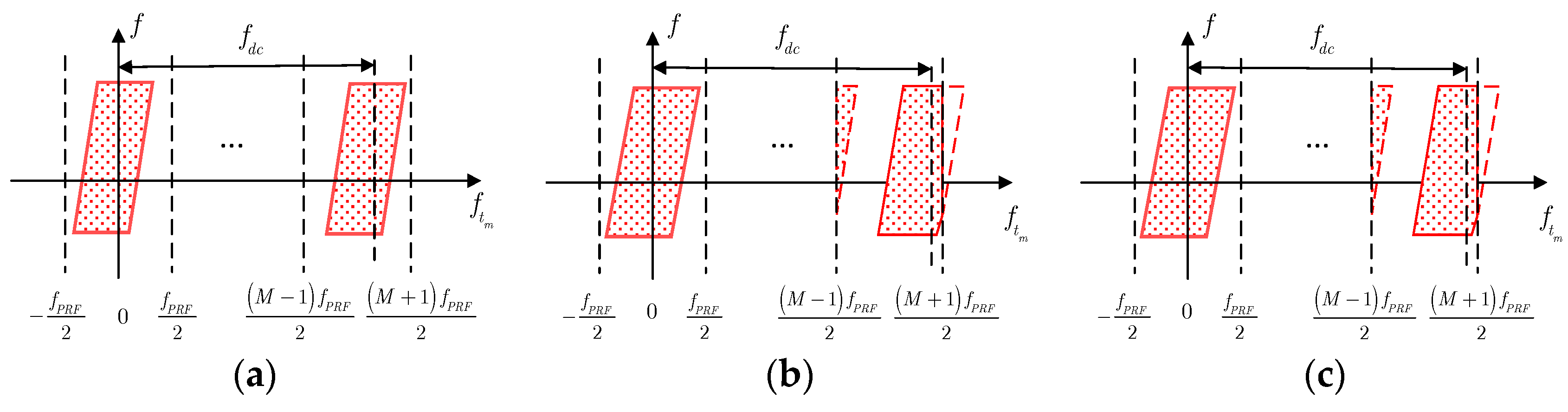
4.1. The Analysis of Azimuth Doppler–Spectrum Bandwidth
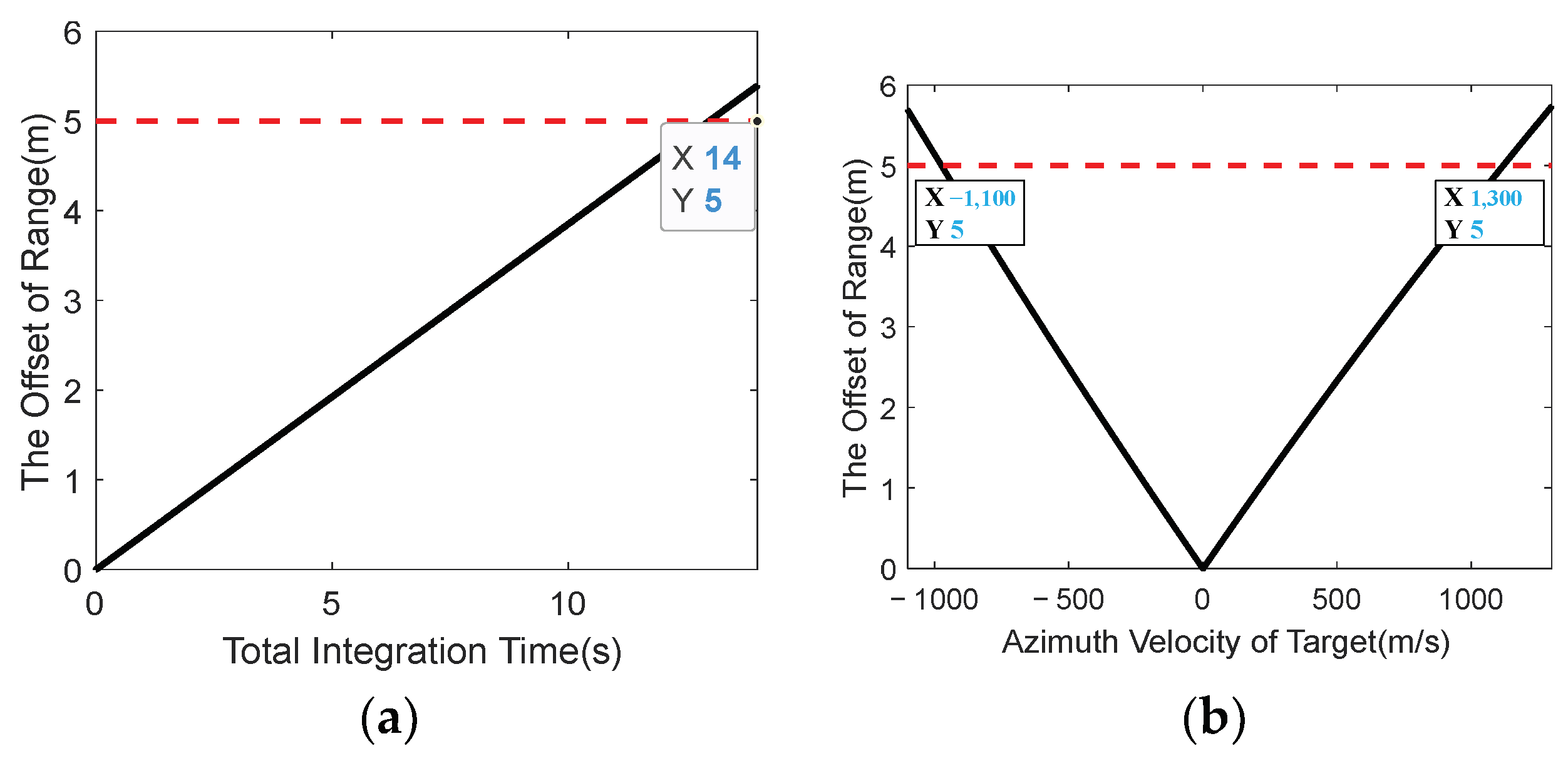
4.2. The Analysis of the Lag Variable in MSWPD Operation
4.3. The Analysis of Computational Complexity
4.4. Multi-Target Detection Analysis
5. Simulation and Experimental Results
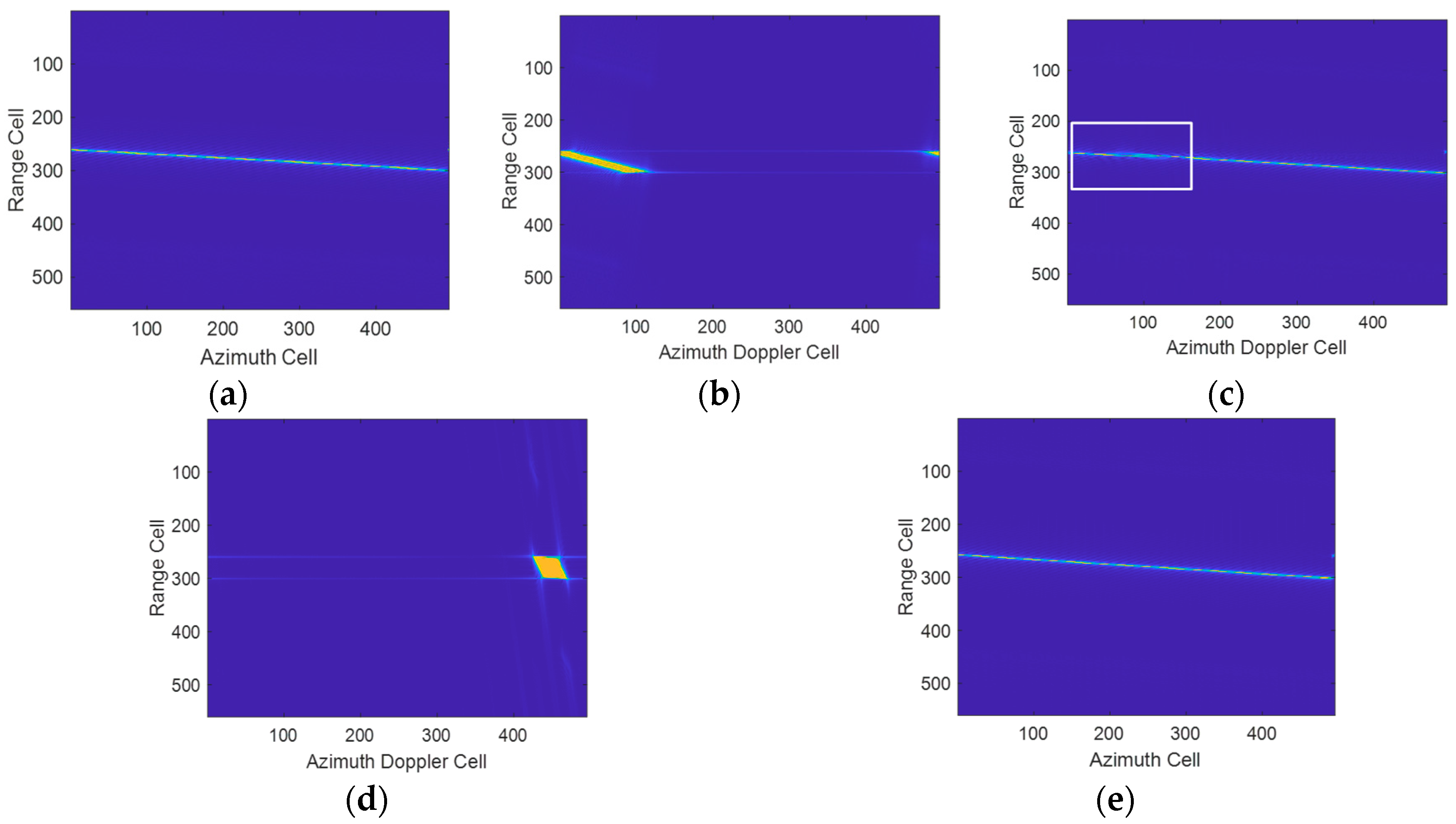
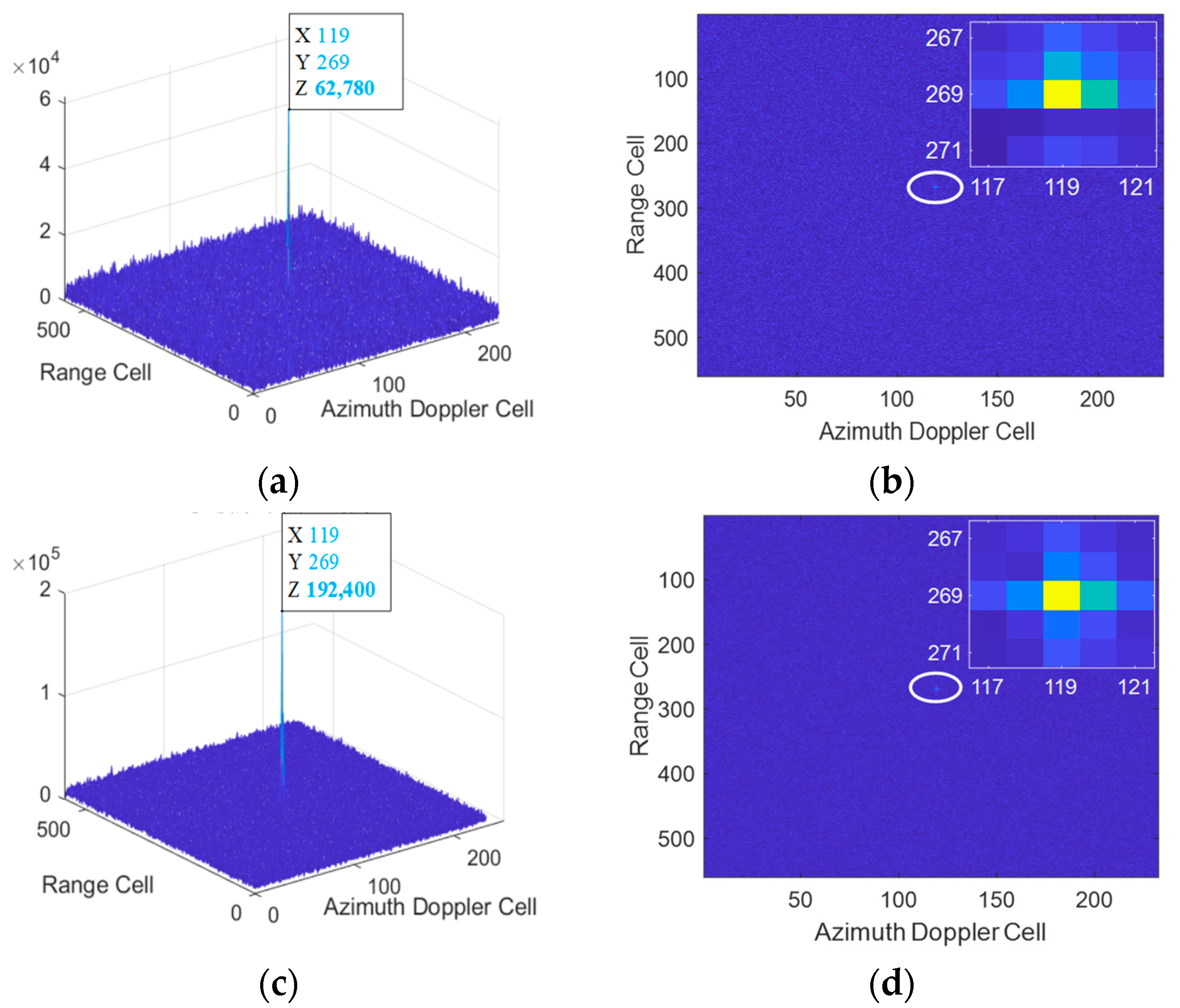
5.1. Validation of the Proposed Method
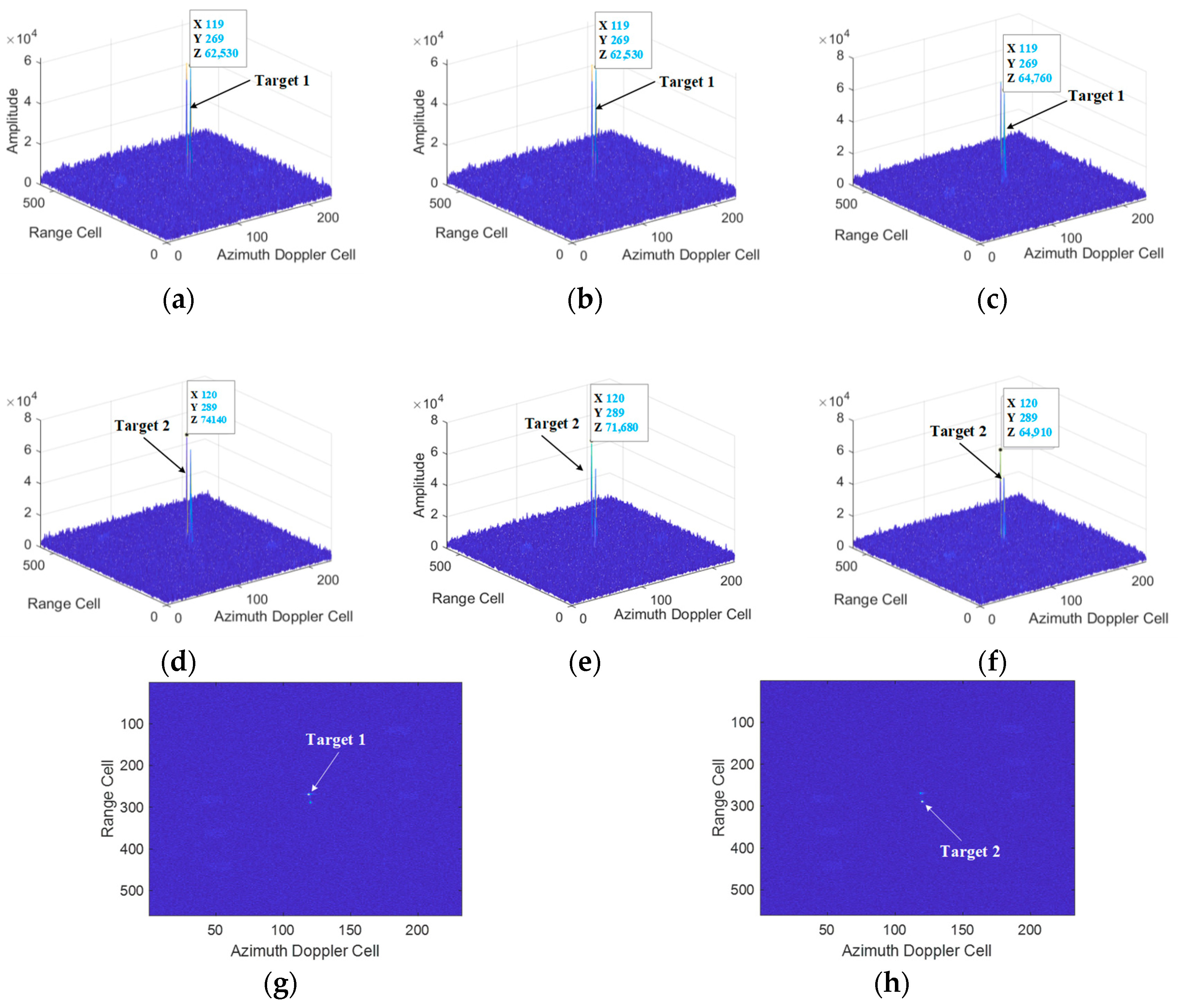
5.2. Multi-Target Simulation Experimental Results
5.3. Comparisons with the Existing Methods
6. The Results of Synthesized Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Chen, X.; Guan, J.; Huang, Y.; Liu, N.; He, Y. Radon-Linear canonical ambiguity function-based detection and estimation method for marine target with micromotion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2225–2240. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.; Zheng, J. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 2017, 55, 320–335. [Google Scholar] [CrossRef]
- Zuo, L.; Li, M.; Zhang, X.; Wang, Y.; Wu, Y. An efficient method for detecting slow-moving weak targets in sea clutter based on time-frequency iteration decomposition. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3639–3672. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, R.; Yang, T.; Liu, X.; Liu, H.; Su, T.; Wan, L. An efficient strategy for accurate detection and localization of UAV swarms. IEEE Internet Things J. 2021, 8, 15372–15381. [Google Scholar] [CrossRef]
- Noviello, C.; Fornaro, G.; Martorella, M. Focused SAR estimation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3460–3470. [Google Scholar] [CrossRef]
- Mu, H.; Zhang, Y.; Jiang, Y.; Ding, C. CV-GMTINet: GMTI using a deep complex-valued convolutional neural network for multichannel SAR-GMI system. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5201115. [Google Scholar] [CrossRef]
- Yuan, H.; Li, H.; Zhang, Y.; Wang, Y.; Liu, Z.; Wei, C.; Yao, C. High-resolution refocusing for defocused ISAR images by complex-valued Pix2pixHD network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4027205. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, H.; Li, H.; Wei, C.; Yao, C. Complex-valued graph neural network on space target classification for defocused ISAR images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4512905. [Google Scholar] [CrossRef]
- Yu, L.; Chen, C.; Wang, J.; Wang, P.; Men, Z. Refocusing high-resolution SAR images of complex moving vessels using co-evolutionary particle swarm optimization. Remote Sens. 2020, 12, 3302. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Yi, W.; Cui, G.; Kong, L. A coherent detection and velocity estimation algorithm for the high-speed target based on the modified location rotation transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2346–2361. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, T.; Liu, H.; Su, T. Efficient data transmission strategy for IIoTs with arbitrary geometrical array. IEEE Trans. Ind. Inform. 2021, 17, 3460–3468. [Google Scholar] [CrossRef]
- Xing, M.; Su, J.; Wang, G.; Bao, Z. New parameter estimation and detection algorithm for high speed small target. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 214–224. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, S.; Liu, W.; Zheng, J.; Liu, H.; Li, J. Tunable adaptive detection in colocated MIMO radar. IEEE Trans. Signal Process. 2018, 66, 1080–1092. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.; Xia, X. Focus-before-detection radar signal processing: Part I—Challenges and methods. IEEE Trans. Aerosp. Electron. Syst. 2017, 32, 48–59. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Zhang, J.; Li, S. Efficient angular chirp-Fourier transform and its application to high-speed target detection. Signal Process. 2019, 164, 234–248. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Li, S.; Zhao, Y. Radar highspeed small target detection based on keystone transform and linear canonical transform. Signal Process. 2018, 82, 203–215. [Google Scholar] [CrossRef]
- Arii, M. Efficient motion compensation of a moving object on SAR imagery based on velocity correlation function. IEEE Trans. Geosci. Remote Sens. 2014, 52, 936–946. [Google Scholar] [CrossRef]
- Zaugg, E.; Long, D. Theory and application of motion compensation for LFM-CW SAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2990–2998. [Google Scholar] [CrossRef]
- Hough, P. Method and Means for Recognizing Complex Patterns. U.S. Patent No. 3,069,654, 18 December 1962. [Google Scholar]
- Cai, L.; Rotation, S. Scale and translation invariant image watermarking using Radon transform and Fourier transform. In Proceedings of the IEEE 6th Circuits and Systems Symposium on Emerging Technologies: Frontiers of Mobile and Wireless Communication (IEEE Cat. No.04EX710), Shanghai, China, 31 May–2 June 2004; Volume 1, p. 281. [Google Scholar]
- Ye, Q.; Huang, R.; He, X.; Zhang, C. A SR-based radon transform to extract weak lines from noise images. In Proceedings of the ICIP 2003 International Conference on Image Processing (Cat. No.03CH37429), Barcelona, Spain, 14–17 September 2003; Volume 1, p. 1. [Google Scholar]
- Mohanty, N. Computer tracking of moving point targets in space. IEEE Trans. Pattern Anal. Mach. Intell. 1981, 3, 606–611. [Google Scholar] [CrossRef]
- Reed, I.; Gagliardi, R.; Shao, H. Application of three dimensional filtering to moving target detection. IEEE Trans. Aerosp. Electron. Syst. 1983, 19, 898–905. [Google Scholar] [CrossRef]
- Larson, R.; Peschon, J. A dynamic programming approach to trajectory estimation. IEEE Trans. Autom. Control 1966, 3, 537–540. [Google Scholar] [CrossRef]
- Carlson, B.; Evans, E.; Wilson, S. Search radar detection and track with the Hough transform. I. System concept. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 102–108. [Google Scholar] [CrossRef]
- Carlson, B.; Evans, E.; Wilson, S. Search radar detection and track with the Hough transform. II. Detection statistics. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 109–115. [Google Scholar] [CrossRef]
- Perry, R.; Dipietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–199. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.T.; Ma, J. Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform. IEEE Trans. Signal Process. 2016, 64, 4013–4026. [Google Scholar] [CrossRef]
- Kirkland, D. Imaging moving targets using the second-order keystone transform. IET Radar Sonar Navig. 2011, 5, 902–910. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.; Peng, Y. Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging. IEEE Trans. Geosci. Remote Sens. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.; Wu, Y.; Bao, Z. Robust ground moving-target imaging using deramp–keystone processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Liu, N.; Zhou, W.; He, Y. Detection of a low observable sea-surface target with micromotion via the Radon-linear canonical transform. IEEE Trans. Geosci. Remote Sens. Lett. 2014, 11, 1225–1229. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Coherent integration for maneuvering target detection based on Radon-Lv’s distribution. IEEE Trans. Signal Process. Lett. 2015, 22, 1467–1471. [Google Scholar] [CrossRef]
- Oveis, A.; Sebt, M.; Ali, M. Coherent method for ground-moving target indication and velocity estimation using Hough transform. IET Radar Sonar Navig. 2017, 11, 646–655. [Google Scholar] [CrossRef]
- Zheng, B.; Su, T.; Zhu, W.; He, X.; Liu, Q.H. Radar high-speed target detection based on the scaled inverse Fourier transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1108–1119. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Liu, H.; Liao, G.; Liu, Z.; Liu, Q. Radar high-speed target detection based on the frequency-domain deramp-keystone transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 285–294. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. A fast maneuvering target motion parameters estimation algorithm based on ACCF. IEEE Trans. Signal Process. Lett. 2015, 22, 270–274. [Google Scholar] [CrossRef]
- Almeida, L. The fractional Fourier transform and time-frequency representations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.; Xia, X. Radon-Fourier transform for radar target detection (I): Generalized Doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.; Xia, X. Radon-Fourier transform for radar target detection (II): Blind speed sidelobe suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.; Xia, X. Radon-Fourier transform for radar target detection (III): Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering target detection via radon-fractional Fourier transform-based long-time coherent integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.; Peng, S.; Yu, J.; Peng, Y.; Qian, L. Radar maneuvering target motion estimation based on generalized Radon-Fourier transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- Porat, B.; Friedlander, B. Asymptotic statistical analysis of the high-order ambiguity function for parameter estimation of polynomial-phase signals. IEEE Trans. Inf. Theory 1996, 42, 995–1001. [Google Scholar] [CrossRef]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s distribution: Principle, implementation, properties, and performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Zhang, X. A fast SAR imaging method for ground moving target using a second-order WVD transform. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1940–1956. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Su, J.; Liu, H.; Zhang, X.; Liao, G. Performances analysis of coherently integrated CPF for LFM signal under low SNR and its application to ground moving target imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6402–6419. [Google Scholar] [CrossRef]
- Rao, X. Research on Techniques of Long Time Coherent Integration Detection for Air Weak Moving Target. Doctoral Thesis, Xidian University, Xi’an, China, 2015. [Google Scholar]
- Zhan, M.; Huang, P.; Zhu, S.; Liu, X.; Liao, G.; Sheng, J.; Li, S. A modified keystone transform matched filtering method for space-moving target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5105916. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.; Liu, X.; Liao, G. Refocusing and motion parameter estimation for ground moving targets based on improved axis rotation-time reversal transform. IEEE Trans. Comput. Imaging 2018, 4, 479–494. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Zhang, X. An approach for refocusing of ground moving target without motion parameter estimation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 336–350. [Google Scholar] [CrossRef]
- Tian, J.; Cui, W.; Xia, X.; Wu, S. Parameter estimation of ground moving targets based on SKT-DLVT processing. IEEE Trans. Comput. Imaging 2016, 2, 13–26. [Google Scholar] [CrossRef]
- Wan, J.; Zhou, Y.; Zhang, L.; Chen, Z. Ground moving target focusing and motion parameter estimation method via MSOKT for synthetic aperture radar. IET Signal Process. 2019, 13, 528–537. [Google Scholar] [CrossRef]
- Zhu, S.; Liao, G.; Qu, Y.; Zhou, Z. Ground moving targets imaging algorithm for synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2011, 49, 462–477. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for SAR ground moving-target imaging. IEEE Trans. Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Approach for single channel SAR ground moving target imaging and motion parameter estimation. IET Radar Sonar Navig. 2007, 1, 59–66. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Liu, H.; Liao, G. A robust translational motion compensation method for ISAR imaging based on keystone transform and fractional Fourier transform under low SNR environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Xin, Z.; Liao, G.; Yang, Z.; Huang, P. A fast ground moving target focusing method based on first-order discrete polynomial-phase transform. Digit. Signal Process. 2017, 60, 287–295. [Google Scholar] [CrossRef]
- Richards, M. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York City, NY, USA, 2014. [Google Scholar]
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]









| Methods | Computational Complexity |
|---|---|
| The proposed method | |
| ACCF | |
| MTD |
| Parameter Name | Parameter Value |
|---|---|
| Carrier Frequency | |
| Range Bandwidth | |
| Average Power | |
| System Loss | |
| Noise Temperature | |
| Noise Coefficient | |
| Pulse Repetition Frequency | |
| Half-Power Beam-Width | |
| Gap-Width of Beam | |
| Azimuth Angle of Antenna | |
| Pitch Angle of Antenna | |
| Total Integration Time |
| Parameter Name | Parameter Value |
|---|---|
| Radar Platform Speed | |
| Radar Platform Height | |
| The Number of Beams |
| Parameter Name | Parameter Value |
|---|---|
| Range Velocity | |
| Azimuth velocity | |
| Range Position | |
| Azimuth Position | |
| Time of Entering First Beam | |
| Time of Leaving Last Beam |
| Range Velocity | Azimuth Velocity | |
|---|---|---|
| Target 1 | ||
| Target 2 |
| Parameter Name | Parameter Value |
|---|---|
| Carrier Frequency | |
| Range Bandwidth | |
| Pulse Repetition Frequency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Li, D.; Wan, J.; Kang, X.; Liu, Q.; Chen, Z.; Yang, X. Integration and Detection of a Moving Target with Multiple Beams Based on Multi-Scale Sliding Windowed Phase Difference and Spatial Projection. Remote Sens. 2023, 15, 4429. https://doi.org/10.3390/rs15184429
Hu R, Li D, Wan J, Kang X, Liu Q, Chen Z, Yang X. Integration and Detection of a Moving Target with Multiple Beams Based on Multi-Scale Sliding Windowed Phase Difference and Spatial Projection. Remote Sensing. 2023; 15(18):4429. https://doi.org/10.3390/rs15184429
Chicago/Turabian StyleHu, Rensu, Dong Li, Jun Wan, Xiaohua Kang, Qinghua Liu, Zhanye Chen, and Xiaopeng Yang. 2023. "Integration and Detection of a Moving Target with Multiple Beams Based on Multi-Scale Sliding Windowed Phase Difference and Spatial Projection" Remote Sensing 15, no. 18: 4429. https://doi.org/10.3390/rs15184429
APA StyleHu, R., Li, D., Wan, J., Kang, X., Liu, Q., Chen, Z., & Yang, X. (2023). Integration and Detection of a Moving Target with Multiple Beams Based on Multi-Scale Sliding Windowed Phase Difference and Spatial Projection. Remote Sensing, 15(18), 4429. https://doi.org/10.3390/rs15184429







