Pore and Microfracture Characterization in Tight Gas Sandstone Reservoirs with a New Rock-Physics-Based Seismic Attribute
Abstract
:1. Introduction
2. Methods
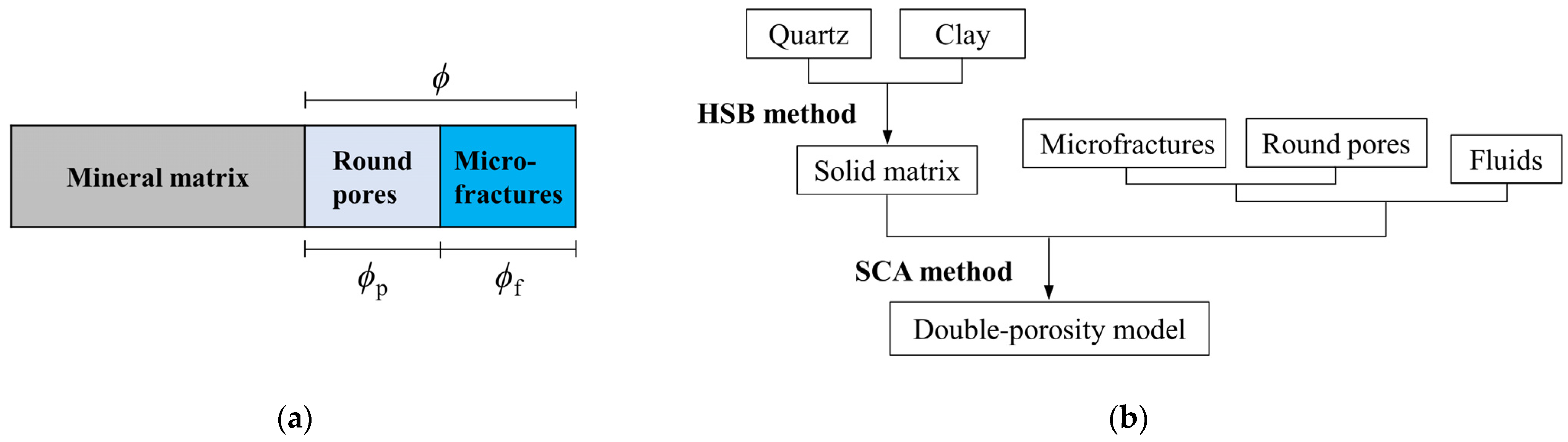
2.1. Rock Physics Model of Tight Gas Sandstones
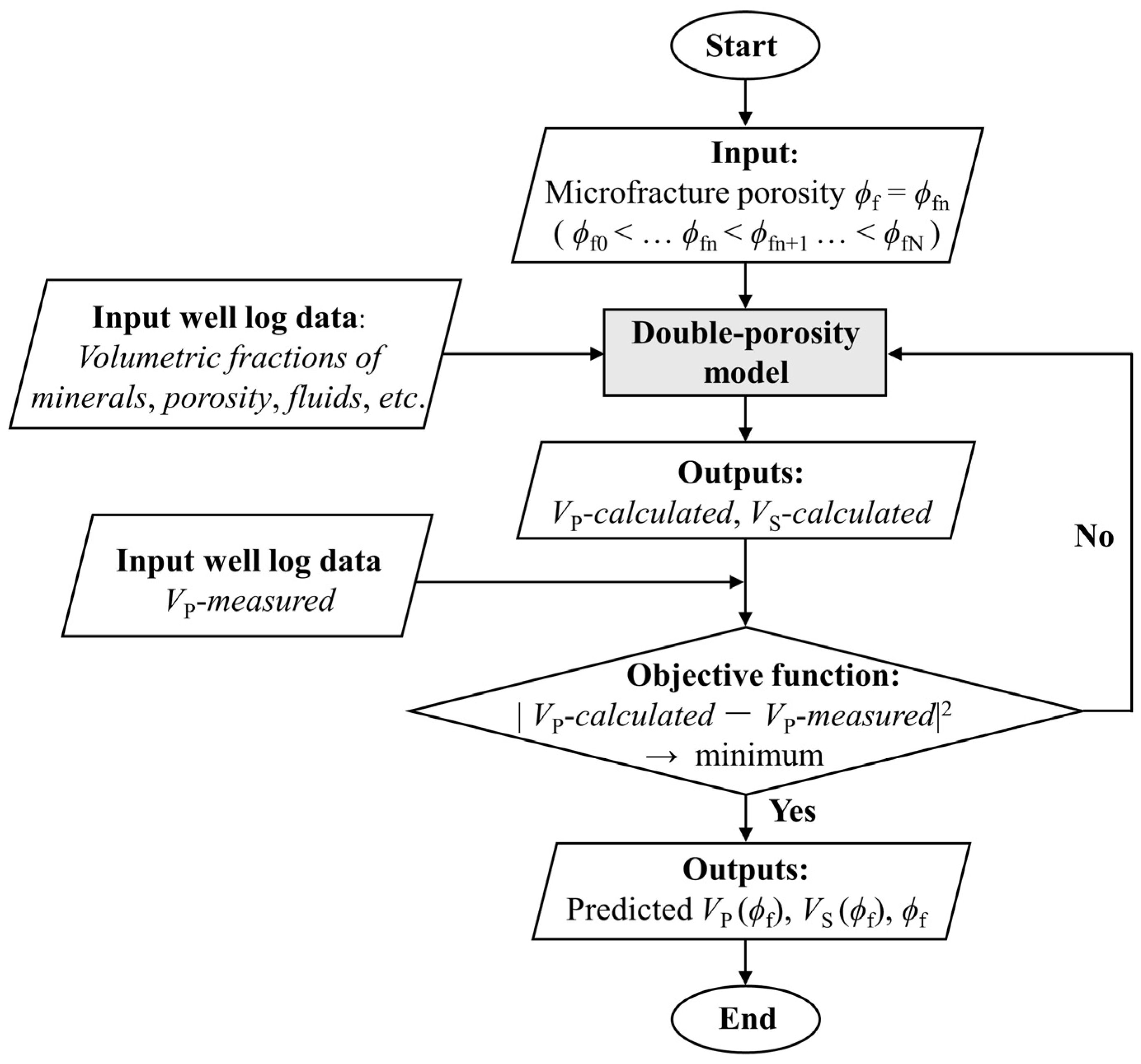
2.2. Estimation of Microfracture Porosity Based on the Double-Porosity Model via Well-Log Data
2.3. Pore–Microfracture Indicator (PMI) Defined Using Elastic Properties
3. Results
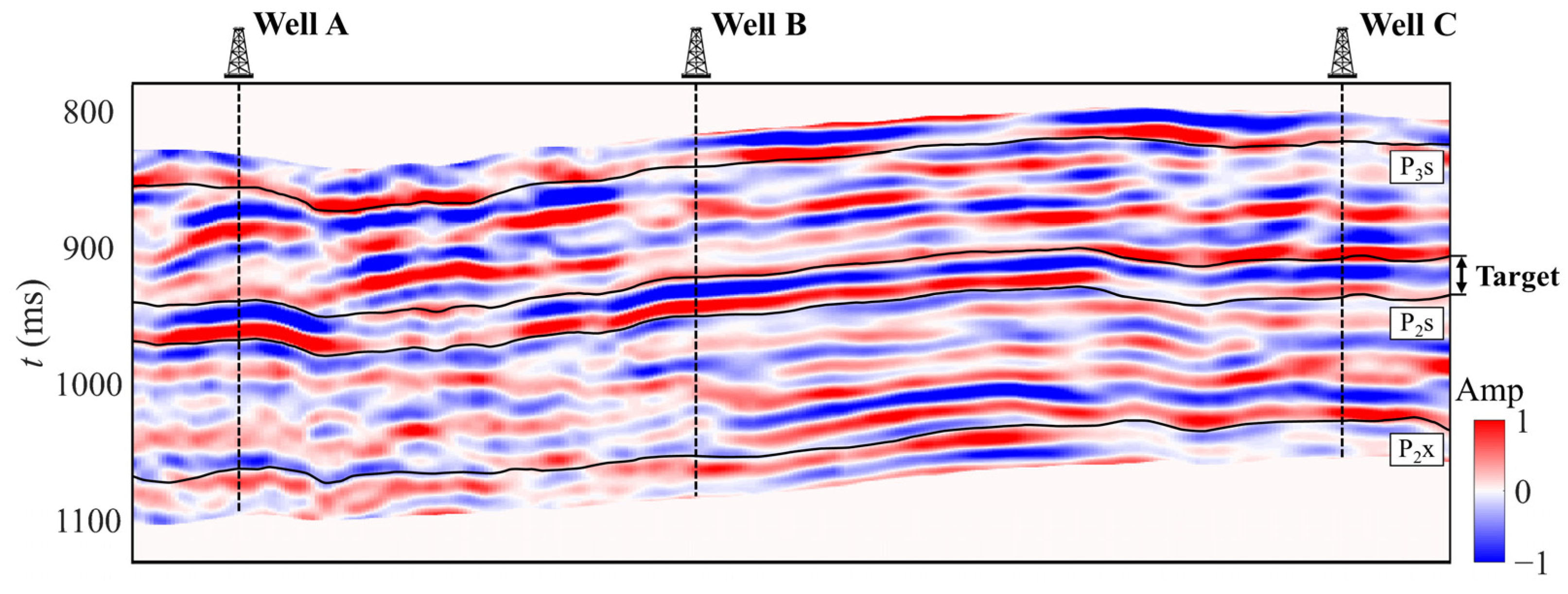
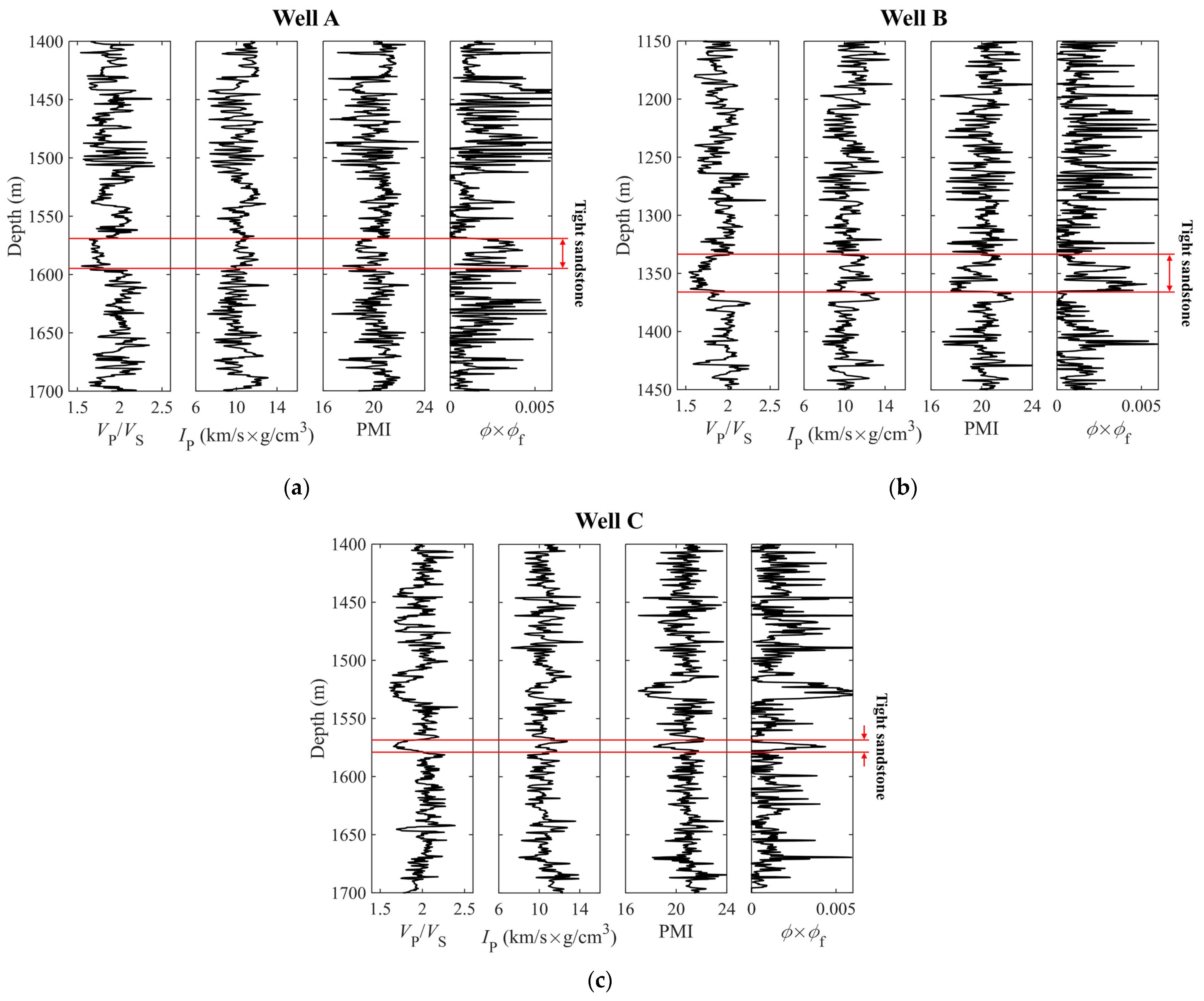
3.1. Study Area and Datasets
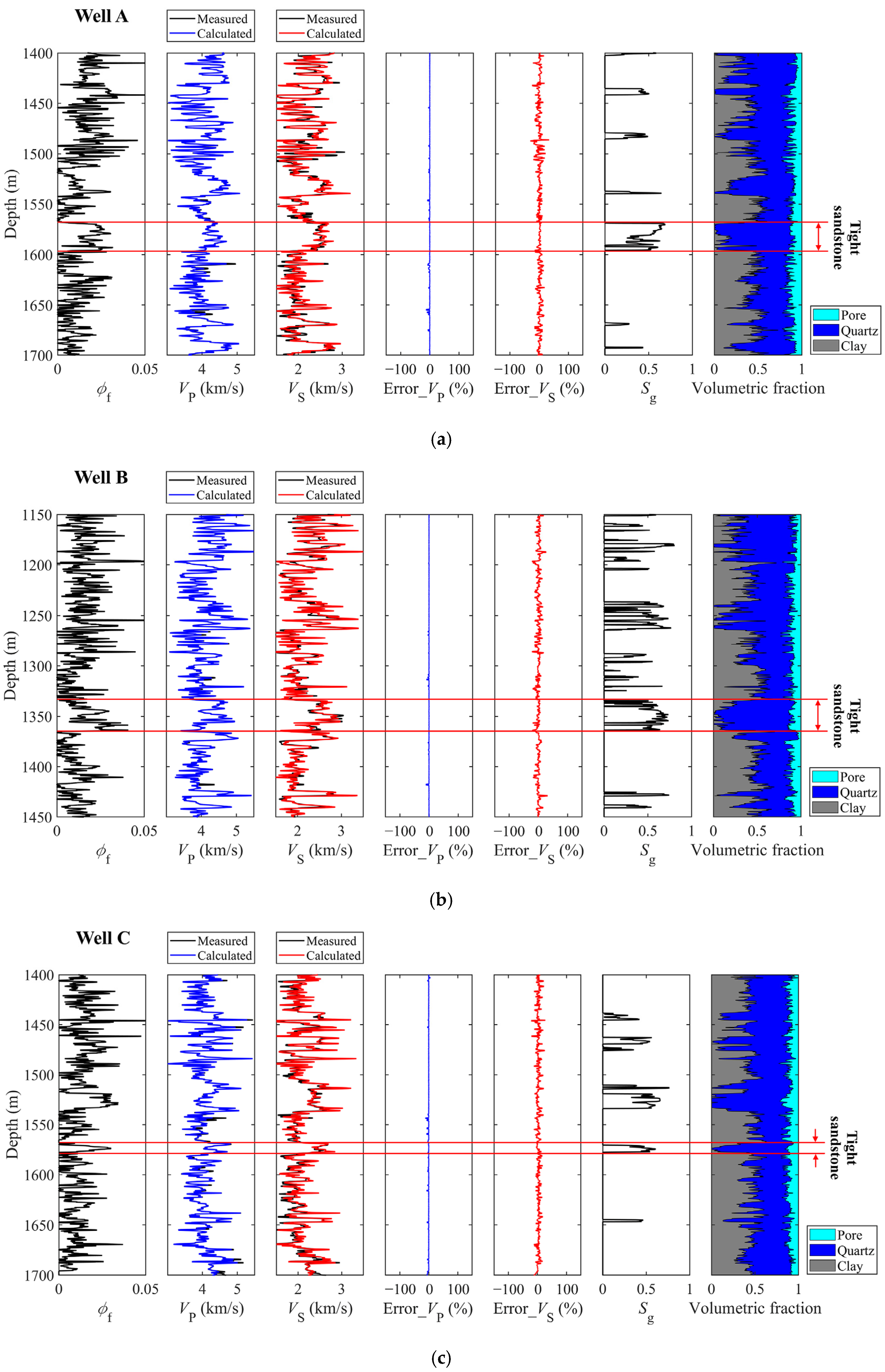
3.2. Prediction of the Microfracture Porosity in Tight Sandstones Using Well-Log Data
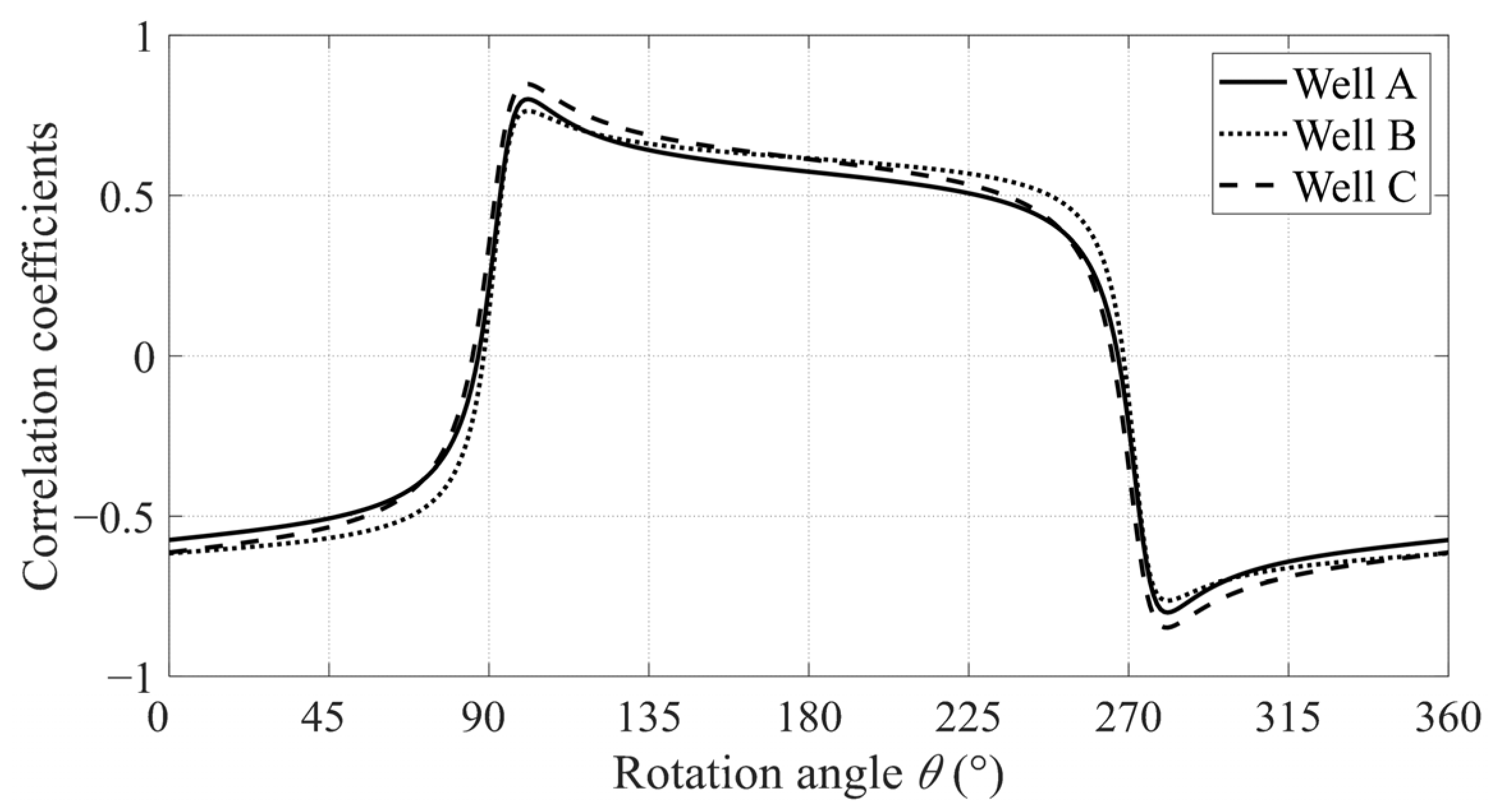
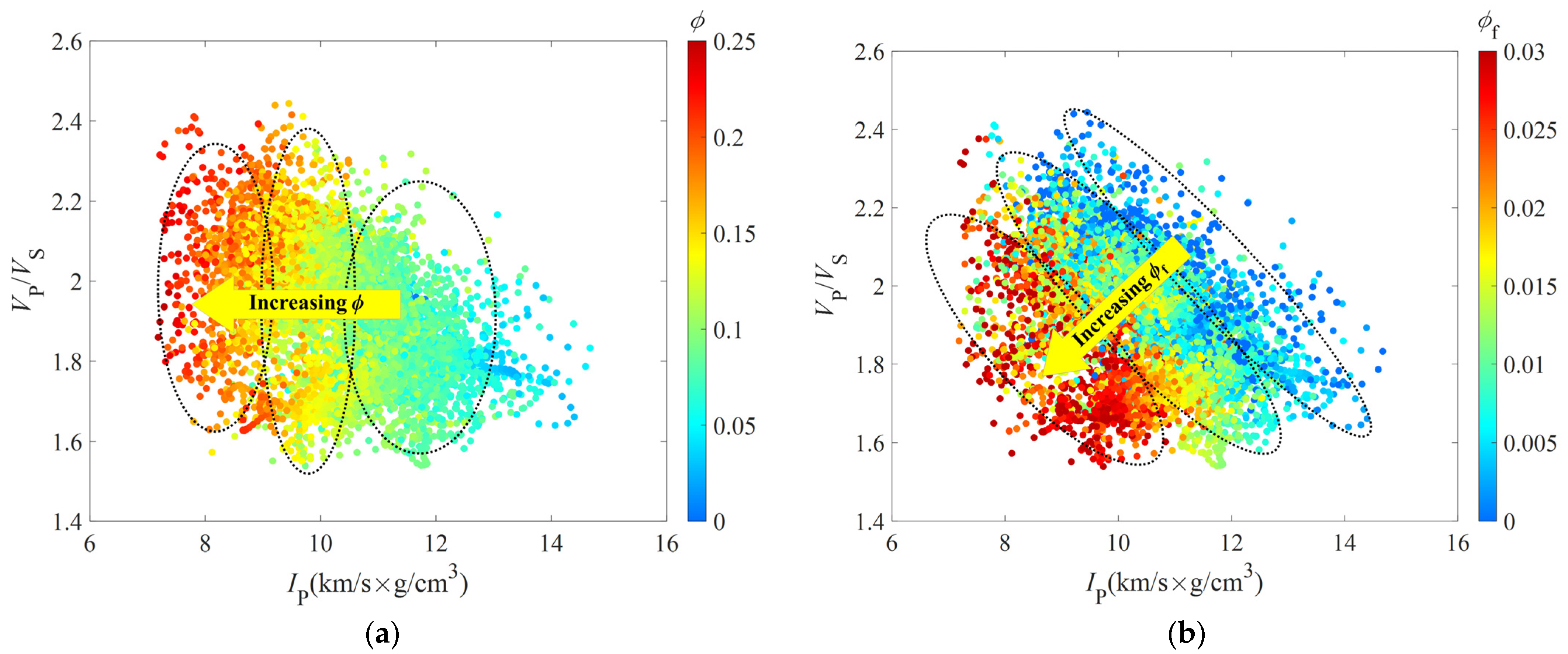
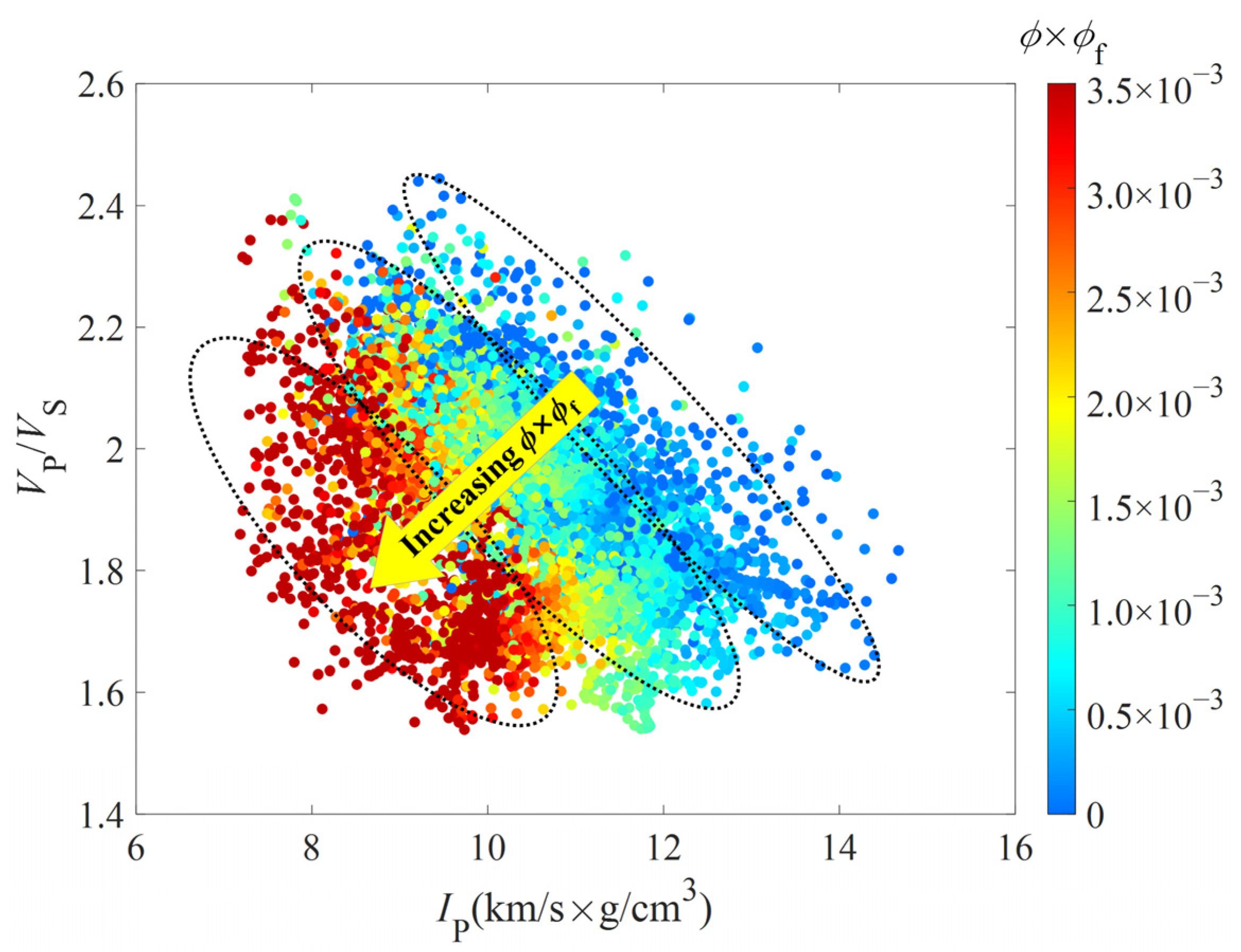
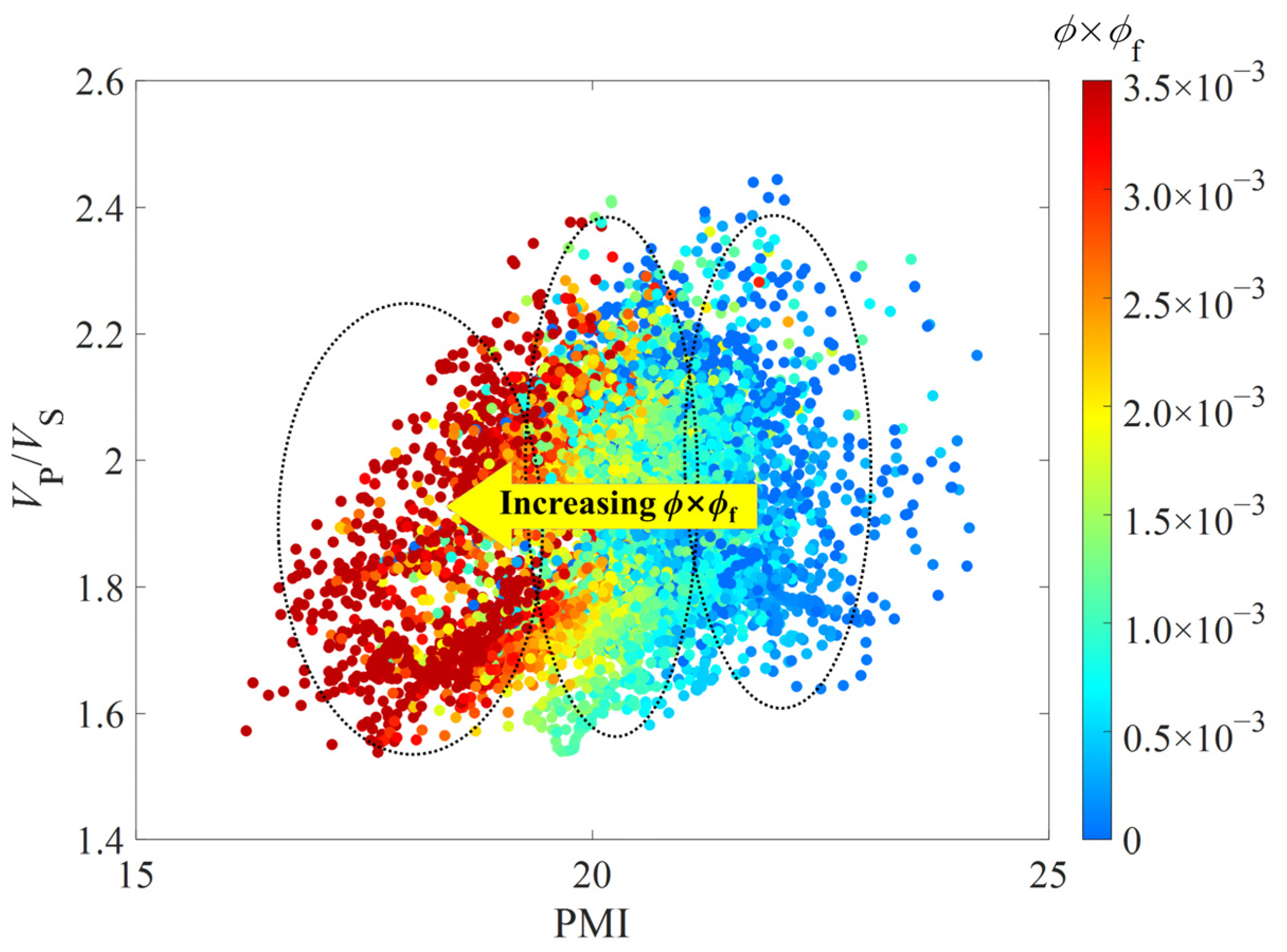
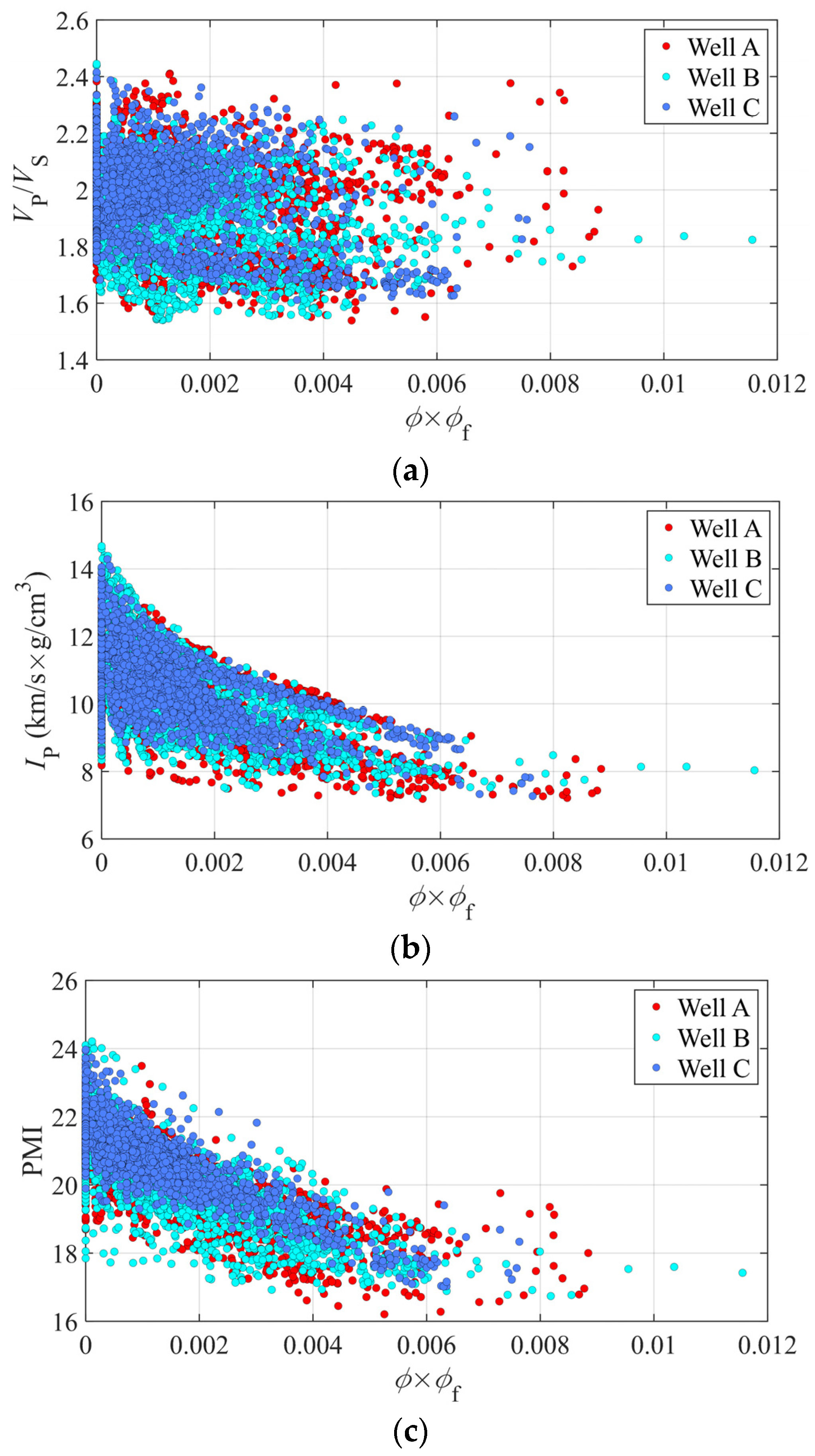
3.3. Calculation of the PMI for Pore and Microfracture Evaluation in Tight Gas Sandstones
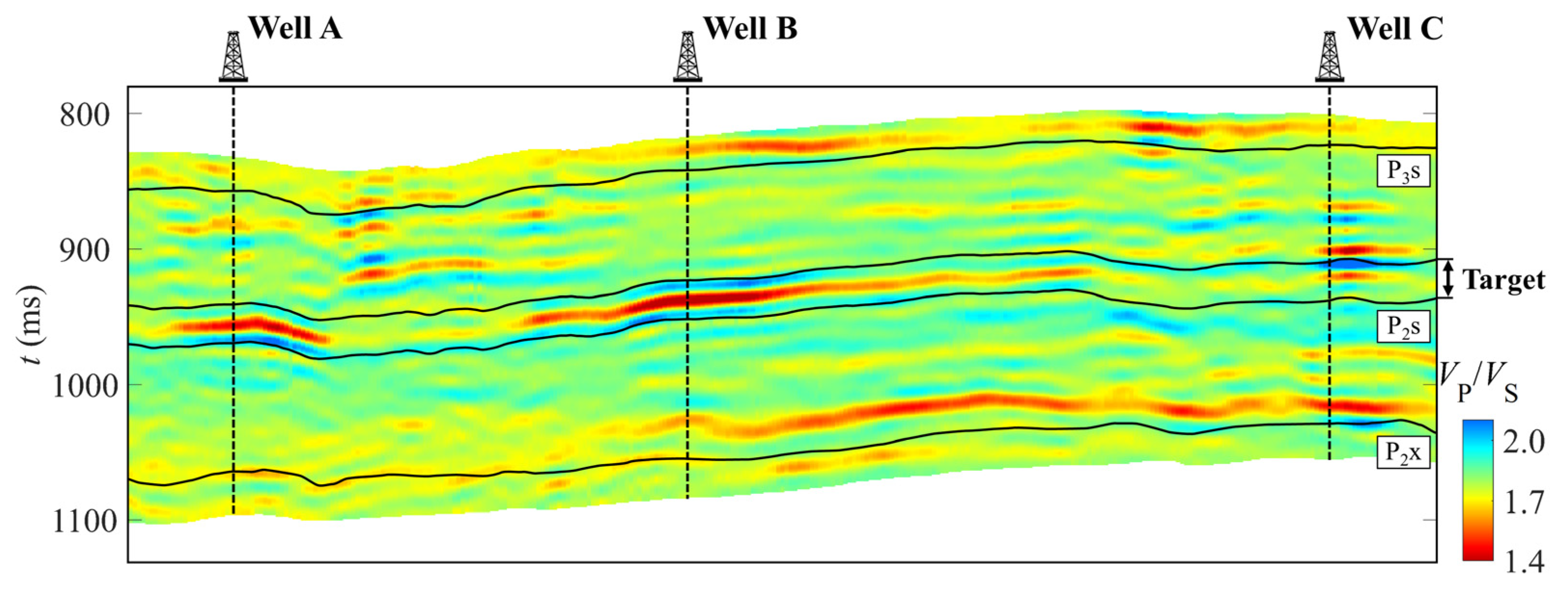
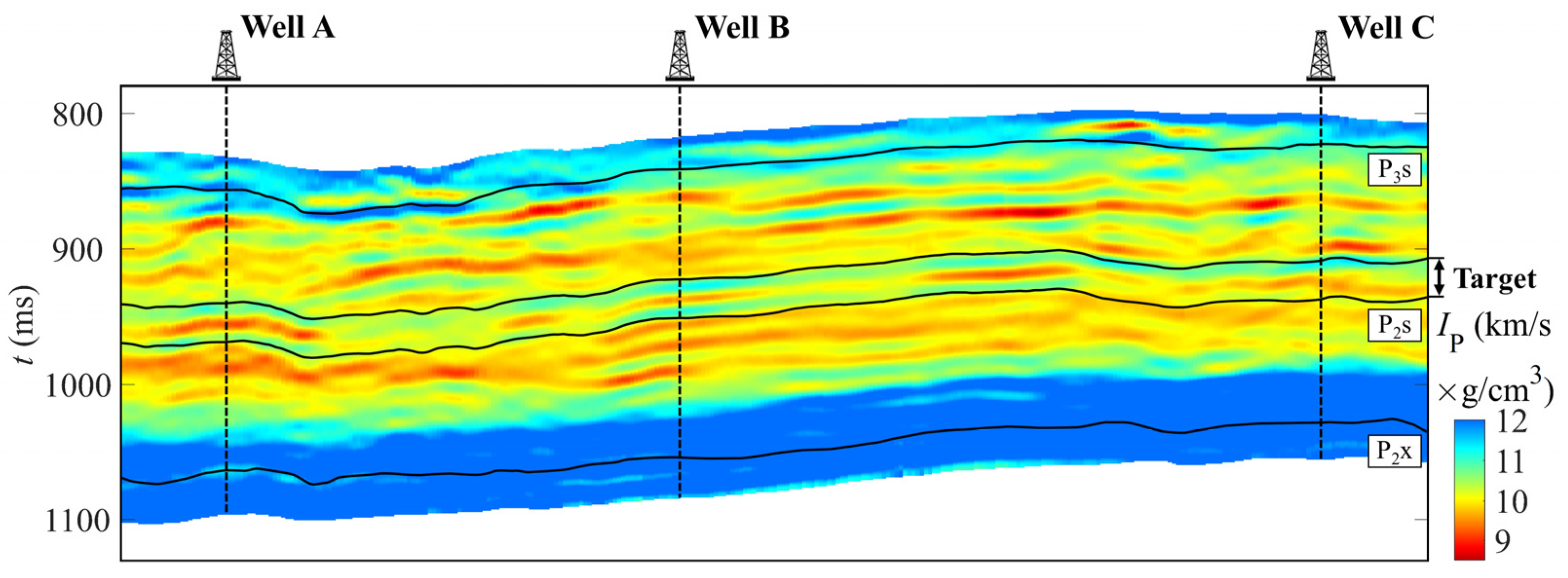
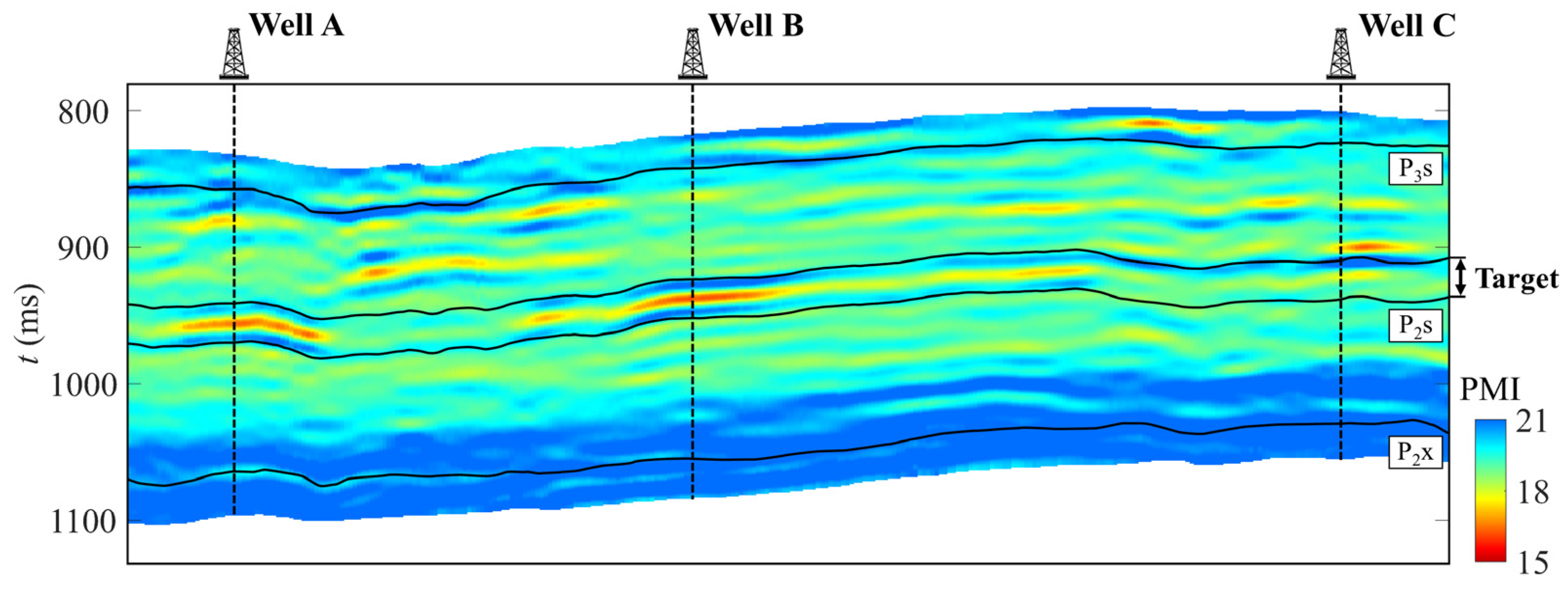
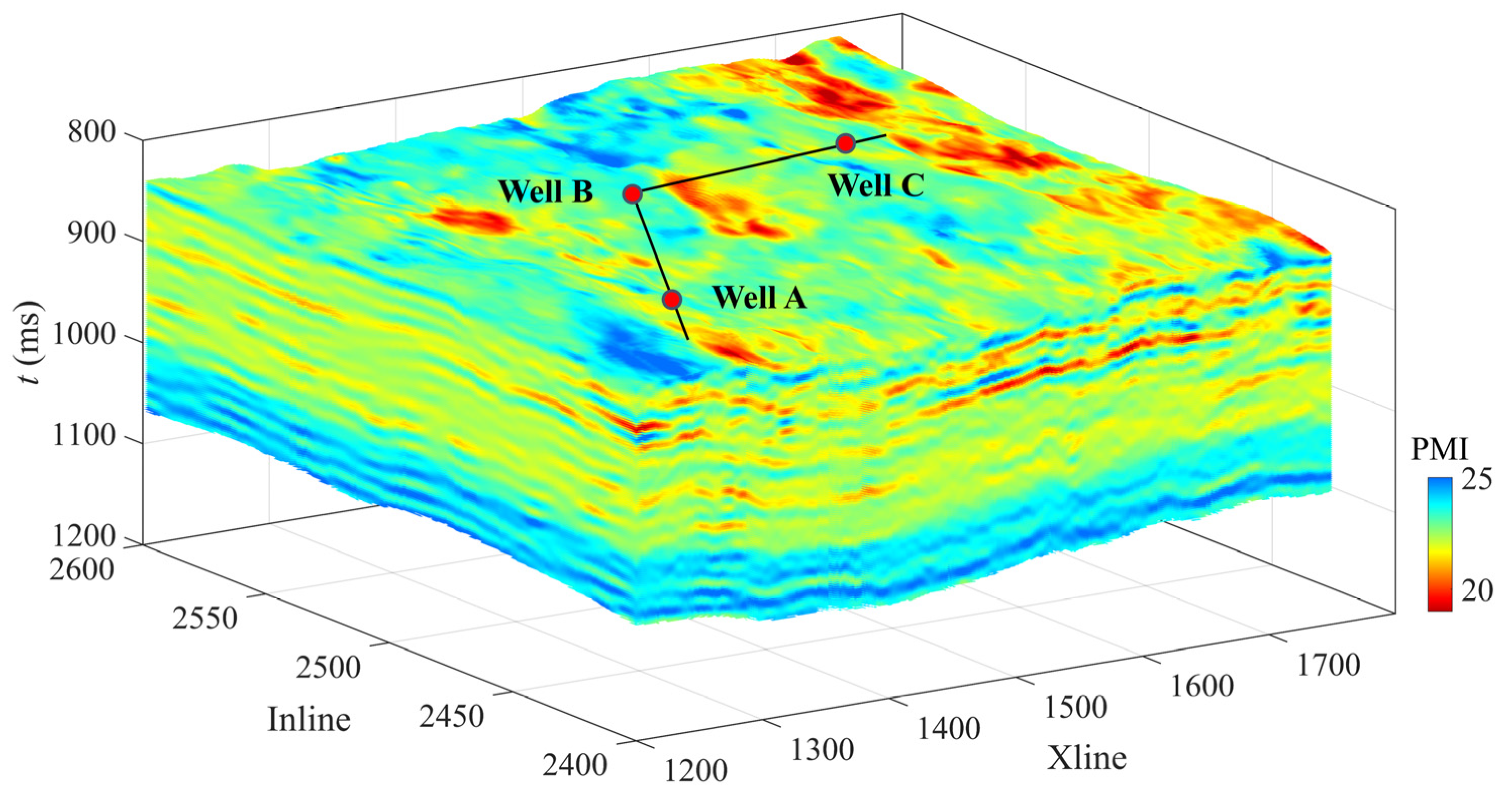
3.4. Estimation of the PMI Using Seismic Data
4. Discussions
4.1. Construction of the PMI for Pore and Microfracture Characterization in Tight Sandstones
4.2. Applicability of the Double-Porosity Model for Tight Sandstones
4.3. Potential Applications of the PMI
5. Conclusions
- The rock-physics-based PMI is an estimation of the factor ϕ × ϕf, representing the comprehensive effect of pores and microfractures. Therefore, the proposed PMI provides essential information in predicting high-quality tight gas sandstone reservoirs.
- The double-porosity model exhibits an effective tool for describing complex pore structures in tight sandstones in the study area. The modeling results of elastic wave velocities using well-log data confirmed the applicability of the double-porosity model. The computed microfracture porosity is a significant factor in defining the factor ϕ × ϕf and subsequently introducing PMI.
- The proposed PMI evaluates pore features and could be further employed to comprehensively characterize tight gas sandstones by incorporating other reservoir properties estimated with seismic methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.L.; Tang, D.Z.; Qin, Y.; Xu, H.; Lv, Y.M.; Tao, S.; Li, S. Evaluation of fracture system for coal macrolithotypes in the Hancheng Block, eastern margin of the Ordos Basin, China. J. Petrol. Sci. Eng. 2017, 159, 799–809. [Google Scholar] [CrossRef]
- Yin, S.; Han, C.; Wu, Z.H.; Li, Q.M. Developmental characteristics, influencing factors and prediction of fractures for a tight gas sandstone in a gentle structural area of the Ordos Basin, China. J. Petrol. Sci. Eng. 2019, 72, 103032. [Google Scholar] [CrossRef]
- Zeng, L.B.; Gong, L.; Guan, C.; Zhang, B.J.; Wang, Q.Q.; Zeng, Q.; Lyu, W.Y. Natural fractures and their contribution to tight gas conglomerate reservoirs: A case study in the northwestern Sichuan Basin, China. J. Petrol. Sci. Eng. 2022, 210, 110028. [Google Scholar] [CrossRef]
- Pan, X.P.; Zhang, G.Z. Amplitude variation with incident angle and azimuth inversion for Young’s impedance, Poisson’s ratio and fracture weaknesses in shale gas reservoirs. Geophys. Prosp. 2019, 67, 1898–1911. [Google Scholar] [CrossRef]
- Pan, X.P.; Zhang, P.F.; Zhang, G.Z.; Guo, Z.W.; Liu, J.X. Seismic characterization of fractured reservoirs with elastic impedance difference versus angle and azimuth: A low-frequency poroelasticity perspective. Geophysics 2021, 86, M123–M139. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Yang, R.; Zhou, Y.; Li, L.; Du, B.Y. Seismic fracture characterization in tight sand reservoirs: A case study of the Xujiahe Formation, Sichuan Basin, China. J. Appl. Geophys. 2022, 203, 104690. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Nie, N.F.; Liu, C. Fracture characterization based on improved seismic amplitude variation with azimuth inversion in tight gas sandstones, Ordos Basin, China. Mar. Pet. Geol. 2022, 146, 105941. [Google Scholar] [CrossRef]
- Smith, T.M.; Sayers, C.M.; Sondergeld, C.H. Rock properties in low-porosity/low-permeability sandstones. Lead Edge 2009, 28, 48–59. [Google Scholar] [CrossRef]
- Ruiz, F.; Cheng, A. A rock physics model for tight gas sand. Lead Edge 2010, 29, 1484–1489. [Google Scholar] [CrossRef]
- Sun, W.; Ba, J.; Carcione, J.M. Theory of wave propagation in partially saturated double-porosity rocks: A triple-layer patchy model. Geophys. J. Int. 2016, 205, 22–37. [Google Scholar] [CrossRef]
- Ba, J.; Xu, W.; Fu, L.; Carcione, J.M.; Zhang, L. Rock anelasticity due to patchy saturation and fabric heterogeneity: A double double-porosity model of wave propagation. J. Geophys. Res. Solid Earth 2017, 122, 1949–1976. [Google Scholar] [CrossRef]
- Zhang, J.J.; Yin, X.Y.; Zhang, G.Z. Rock physics modelling of porous rocks with multiple pore types a multiple-porosity variable critical porosity model. Geophys. Prosp. 2020, 68, 955–967. [Google Scholar] [CrossRef]
- Wang, D.X. A study on the rock physics model of gas reservoir in tight sandstone. Chin. J. Geophys. 2017, 60, 64–83. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, J.; Tand, G.; Zhao, L.; Ma, X.; Wang, S. Pressure and fluid effect on frequency-dependent elastic moduli in fully saturated tight sandstone. J. Geophys. Res. Solid Earth 2017, 122, 8925–8942. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Qin, X.Y.; Zhang, Y.M.; Niu, C.; Wang, D.; Ling, Y. Numerical investigation of the effect of heterogeneous pore structures on elastic properties of tight gas sandstones. Front. Earth Sci. 2021, 9, 641637. [Google Scholar] [CrossRef]
- Lu, M.H.; Cao, H.; Sun, W.T.; Yan, X.F.; Yang, Z.F.; Xu, Y.P.; Wang, Z.L.; Ouyang, M. Quantitative prediction of seismic rock physics of hybrid tight oil reservoirs of the Permain Lucaogou Formation, Junggar Basin, Northwest China. J. Asian Earth Sci. 2019, 178, 216–223. [Google Scholar] [CrossRef]
- Pang, M.Q.; Ba, J.; Fu, L.Y.; Carcione, J.M.; Markus, U.I.; Zhang, L. Estimation of microfracture porosity in deep carbonate reservoirs based on 3D rock-physics templates. Interpretation 2020, 8, SP43–SP52. [Google Scholar] [CrossRef]
- Giao, P.H.; Trang, P.H.; Hien, D.H.; Ngoc, P.Q. Construction and application of an adapted rock physics template (ARPT) for characterizing a deep and strongly cemented gas sand in the Nam Con Son Basin, Vietnam. J. Nat. Gas Sci. Eng. 2021, 94, 104117. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Lv, X.Y.; Liu, C.; Liu, X.W.; Liu, Y.W. Shale gas characterisation for hydrocarbon accumulation and brittleness by integrating a rock-physics-based framework with effective reservoir parameters. J. Nat. Gas Sci. Eng. 2022, 100, 104498. [Google Scholar] [CrossRef]
- Zhou, H.T.; Li, D.Y.; Liu, X.T.; Du, Y.S.; Gong, W. Sweet spot prediction in tight sandstone reservoir based on well-bore rock physical simulation. Pet. Sci. 2019, 16, 1285–1300. [Google Scholar] [CrossRef]
- Tan, W.H.; Ba, J.; Müller, T.; Fang, G.; Zhao, H.B. Rock Physics Model of Tight Oil Siltstone for seismic prediction of brittleness. Geophys. Prosp. 2020, 68, 1554–1574. [Google Scholar] [CrossRef]
- Cheng, W.; Ba, J.; Carcione, J.M.; Pang, M.Q.; Wu, C.F. Estimation of the Pore Microstructure of Tight-Gas Sandstone Reservoirs with Seismic Data. Front. Earth Sci. 2021, 9, 646372. [Google Scholar] [CrossRef]
- Ruan, C.; Ba, J.; Carcione, J.M.; Chen, T.; He, R. Microcrack Porosity Estimation Based on Rock Physics Templates A Case Study in Sichuan Basin, China. Energies 2021, 14, 7225. [Google Scholar] [CrossRef]
- Zhang, T.T.; Sun, Y.F. Two-parameter prestack seismic inversion of porosity and pore-structure parameter of fractured carbonate reservoirs Part 1—Methods. Interpretation 2018, 6, SM1–SM8. [Google Scholar] [CrossRef]
- Zhang, T.T.; Zhang, R.F.; Tia, J.Z.; Lu, L.F.; Qin, F.Q.; Zhao, X.Z.; Sun, Y.F. Two-parameter prestack seismic inversion of porosity and pore-structure parameter of fractured carbonate reservoirs Part 2—Applications. Interpretation 2018, 6, SM9–SM17. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Berryman, J.G. Long-wavelength propagation in composite elastic media II. Ellipsoidal inclusions. J. Acoust. Soc. Am. 1980, 68, 1820–1831. [Google Scholar] [CrossRef]
- Quakenbush, M.; Shang, B.; Tuttle, C. Poisson impedance. Lead Edge 2006, 25, 128–138. [Google Scholar] [CrossRef]
- Tian, L.X.; Zhou, D.H.; Lin, G.K.; Jiang, L.C. Reservoir prediction using Poisson impedance in Qinhuangdao, Bohai Sea. In SEG Technical Program Expanded Abstracts 2010; Society of Exploration Geophysicists: Houston, TX, USA, 2010; pp. 2261–2264. [Google Scholar] [CrossRef]
- Ming, J.; Qin, D.H. An effeictive method of fluid discrimination using Poisson impedance and multi-attribute inversion. In SEG Technical Program Expanded Abstracts 2016; Society of Exploration Geophysicists: Houston, TX, USA, 2016; pp. 2901–2905. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Whitcombe, D.N.; Connolly, P.A.; Reagan, R.L.; Redshaw, T.C. Extended elastic impedance for fluid and lithology prediction. Geophysics 2002, 67, 63. [Google Scholar] [CrossRef]
- Liu, Q.; Yin, X.Y.; Li, C. Fluid discrimination based on rock physics templates. J. Geophys. Eng. 2015, 12, 830–838. [Google Scholar] [CrossRef] [Green Version]
- Jiang, R.; Liu, C.L.; Zhang, J.; Zeng, Q.C.; He, P.; Huang, J.Q.; Du, B.Y.; He, W.W.; Hao, T.; Zhang, J.X. Quantitative Reservoir Characterization of Tight Sandstone Using Extended Elastic Impedance. Nat. Resour. Res. 2020, 30, 395–409. [Google Scholar] [CrossRef]




| Properties | Clay | Quartz | Water | Gas |
|---|---|---|---|---|
| K (GPa) | 21.00 | 36.60 | 2.25 | 0.012 |
| μ (GPa) | 7.00 | 45.00 | 0.00 | 0.000 |
| ρ (g/cm3) | 2.60 | 2.65 | 1.04 | 0.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Qin, X.; Liu, C. Pore and Microfracture Characterization in Tight Gas Sandstone Reservoirs with a New Rock-Physics-Based Seismic Attribute. Remote Sens. 2023, 15, 289. https://doi.org/10.3390/rs15020289
Guo Z, Qin X, Liu C. Pore and Microfracture Characterization in Tight Gas Sandstone Reservoirs with a New Rock-Physics-Based Seismic Attribute. Remote Sensing. 2023; 15(2):289. https://doi.org/10.3390/rs15020289
Chicago/Turabian StyleGuo, Zhiqi, Xiaoying Qin, and Cai Liu. 2023. "Pore and Microfracture Characterization in Tight Gas Sandstone Reservoirs with a New Rock-Physics-Based Seismic Attribute" Remote Sensing 15, no. 2: 289. https://doi.org/10.3390/rs15020289
APA StyleGuo, Z., Qin, X., & Liu, C. (2023). Pore and Microfracture Characterization in Tight Gas Sandstone Reservoirs with a New Rock-Physics-Based Seismic Attribute. Remote Sensing, 15(2), 289. https://doi.org/10.3390/rs15020289






