Sparse Inversion for the Iterative Marchenko Scheme of Irregularly Sampled Data
Abstract
:1. Introduction
2. Methods
2.1. Discrete Representations for the Marchenko Method
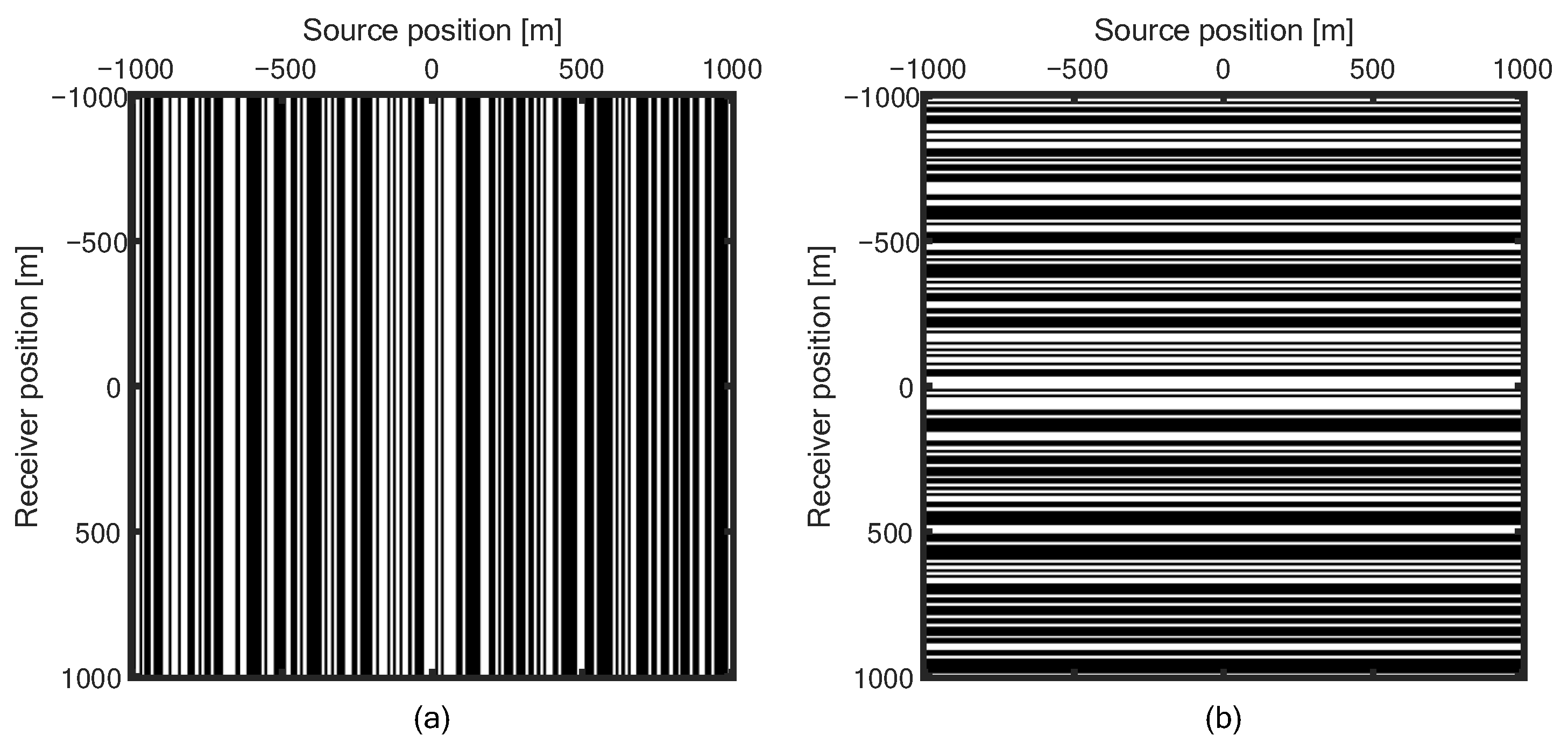
2.2. The Standard Marchenko Method with Irregular Sampling
2.3. Sparse Reconstruction of Focusing Functions
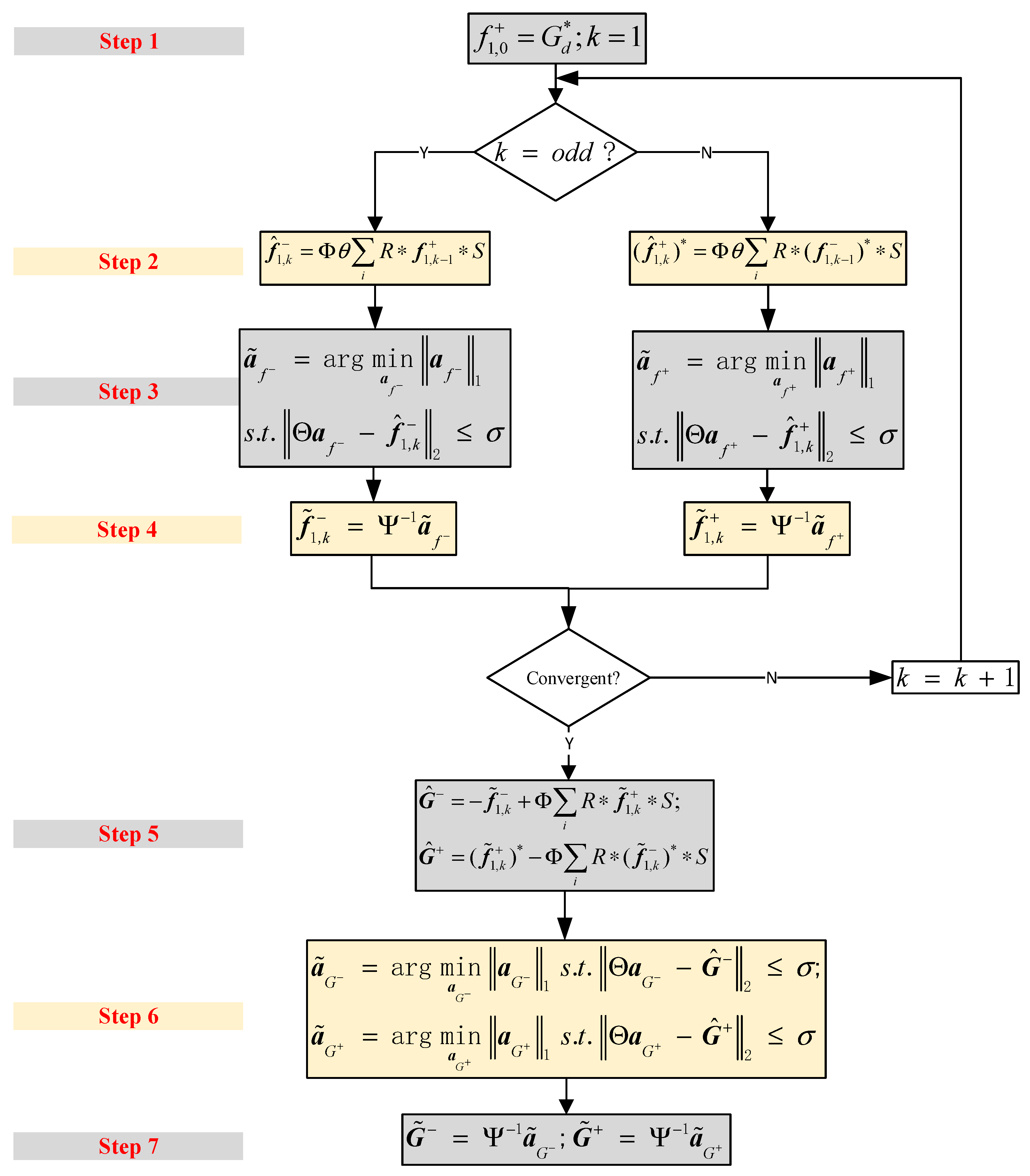
2.4. Sparse Inversion in Iterative Marchenko Scheme
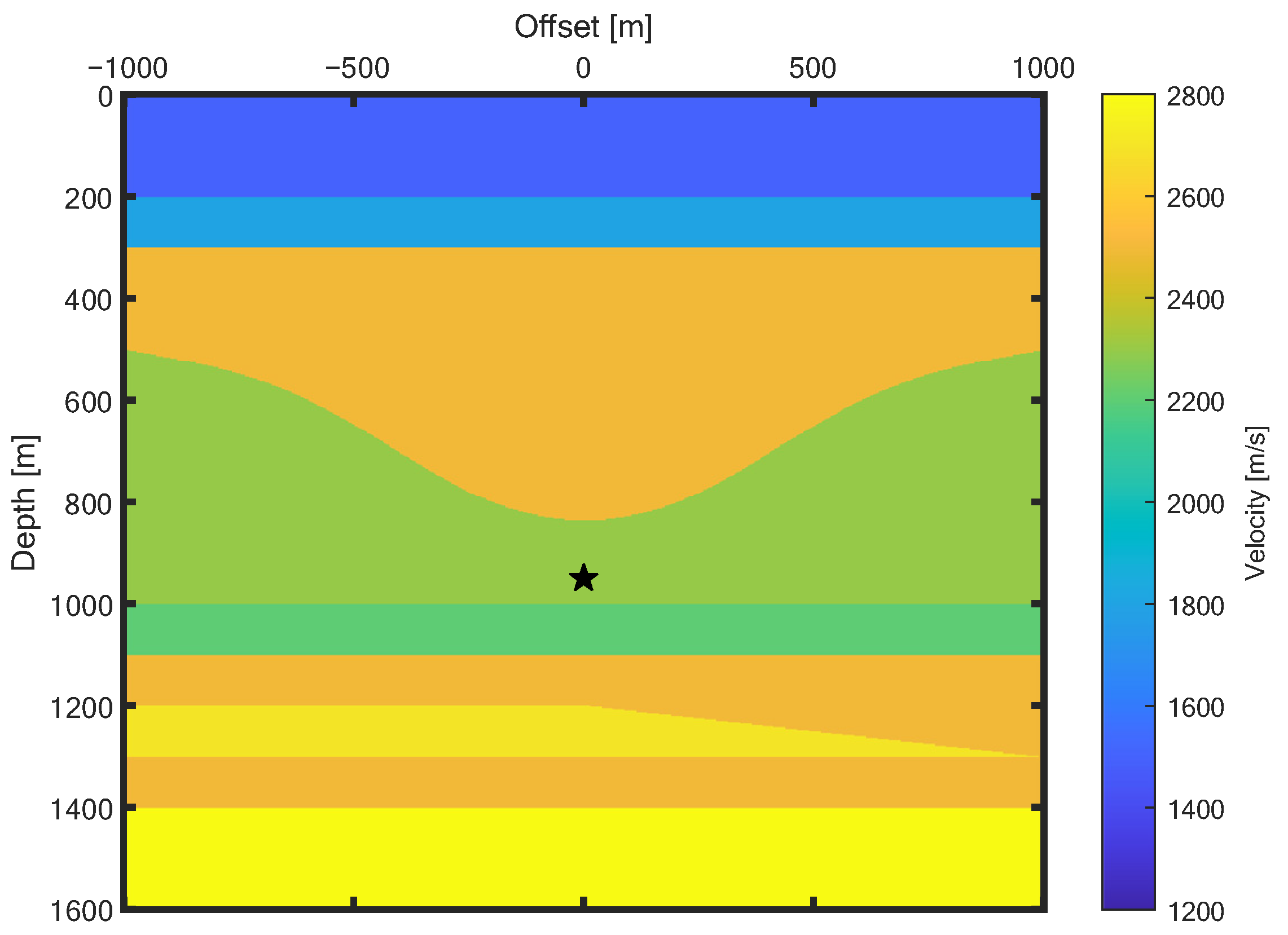
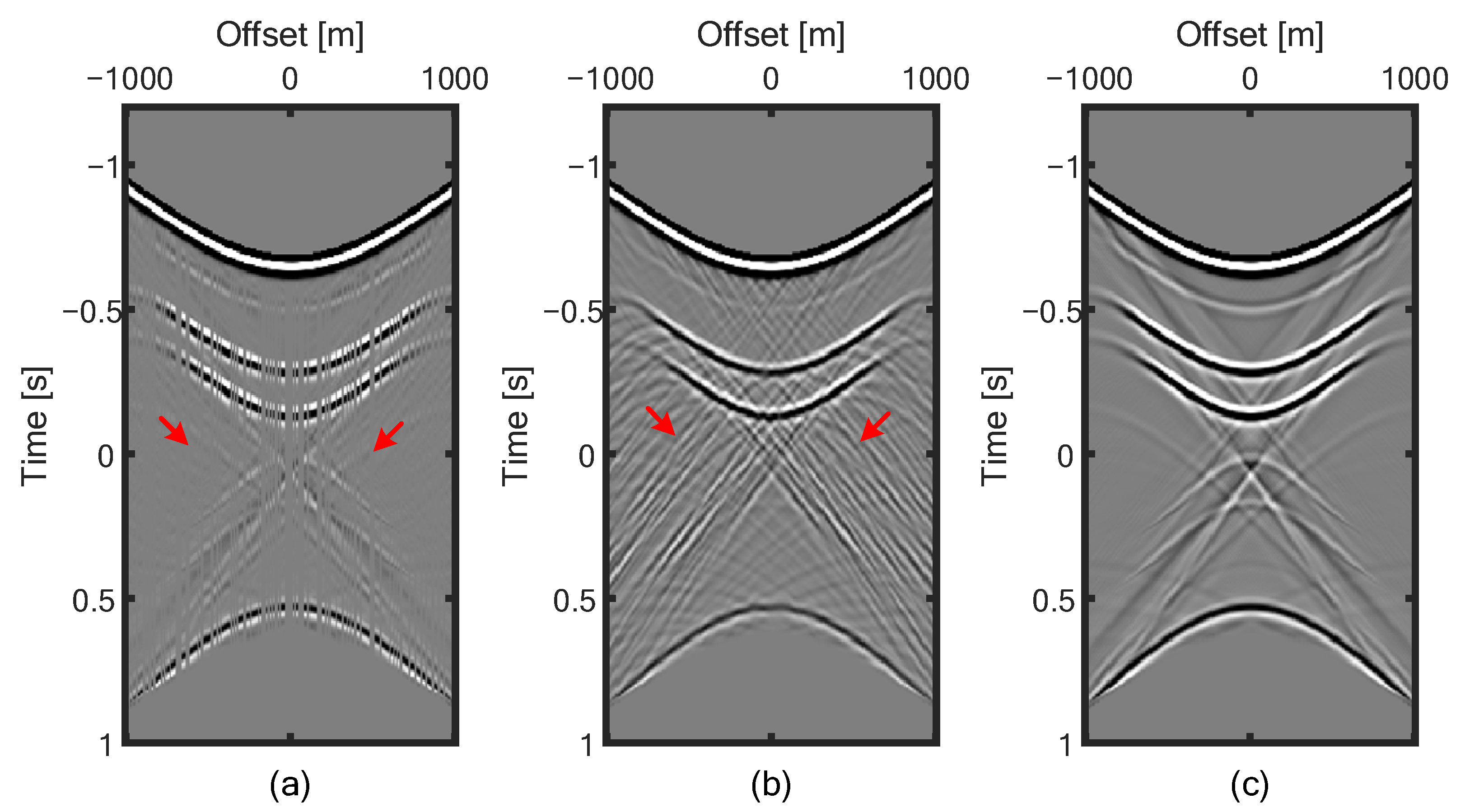
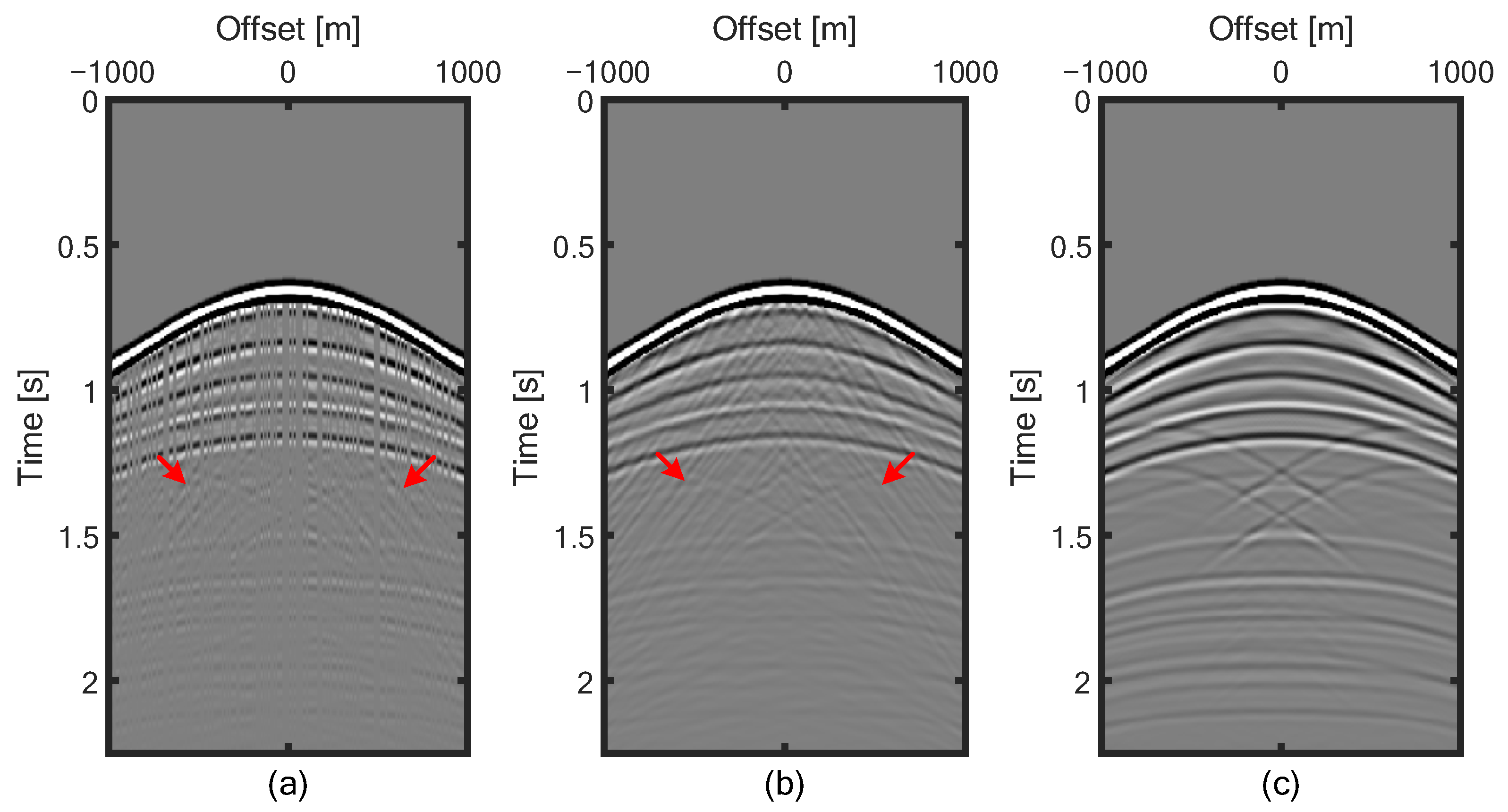
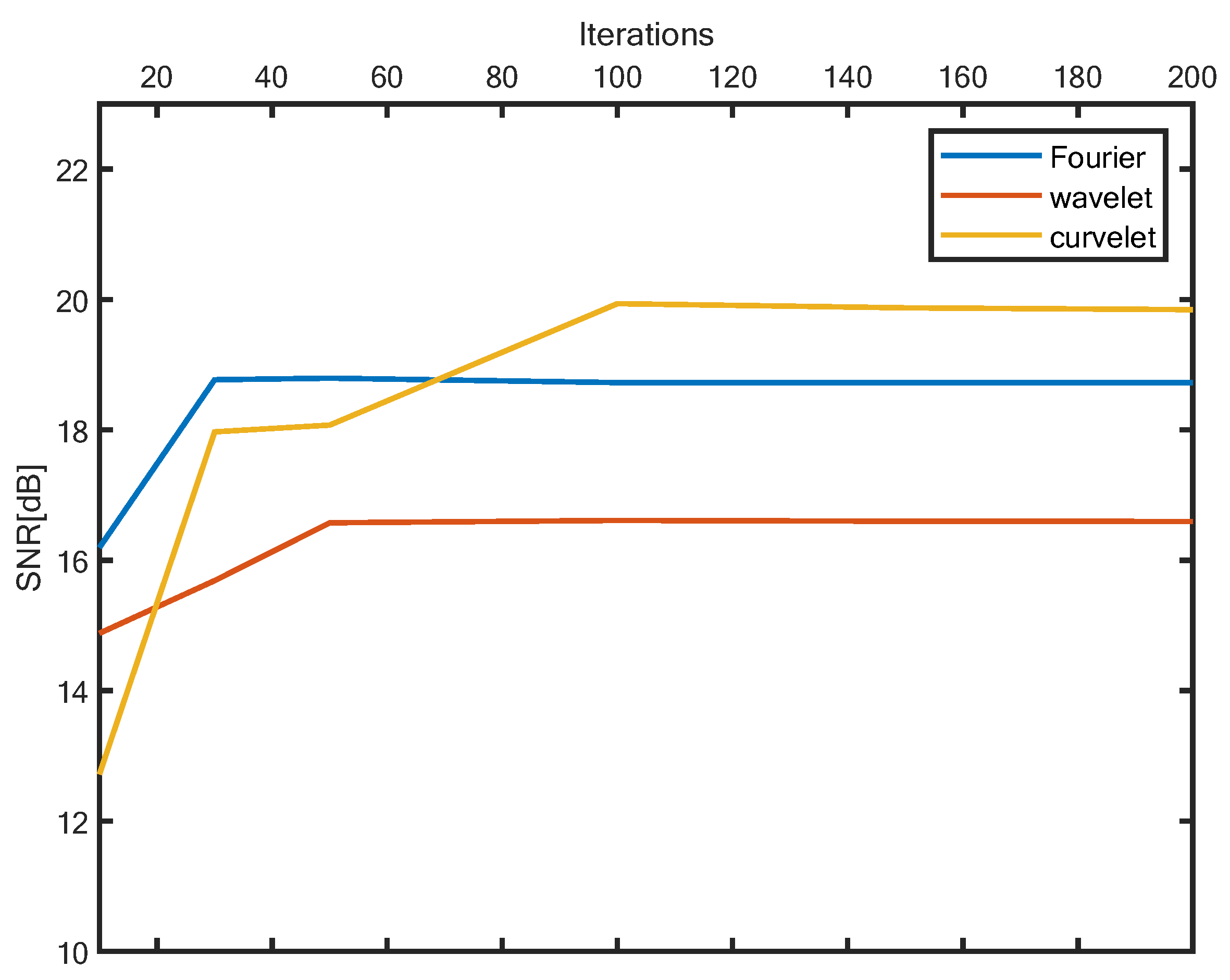
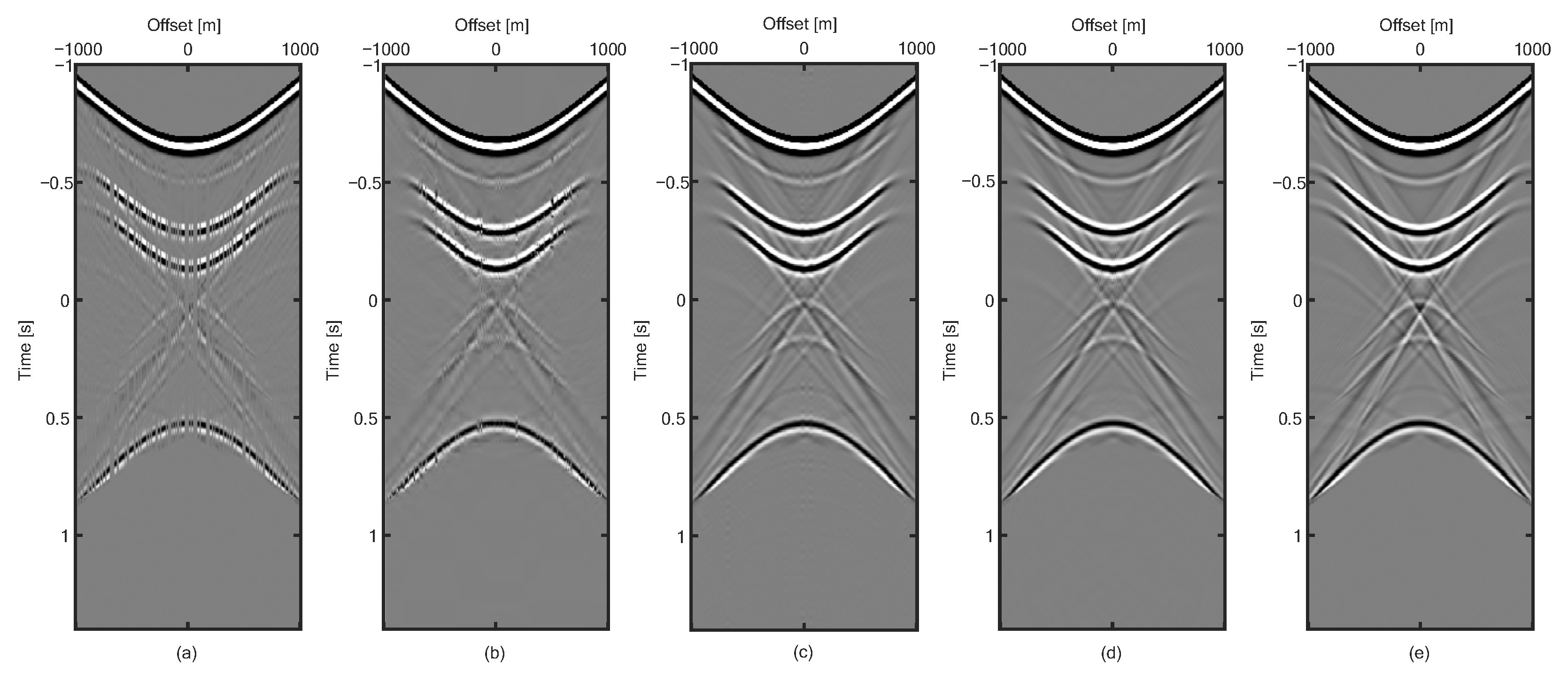
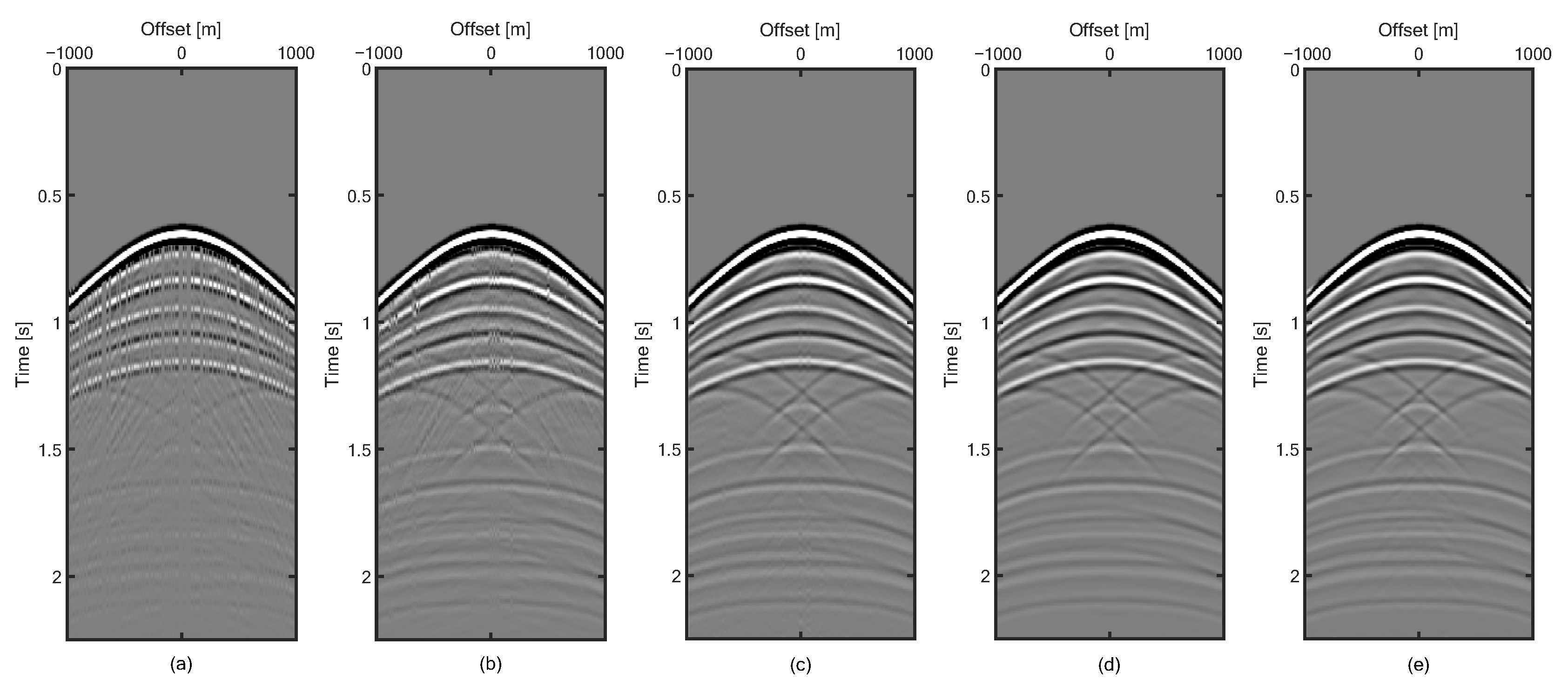
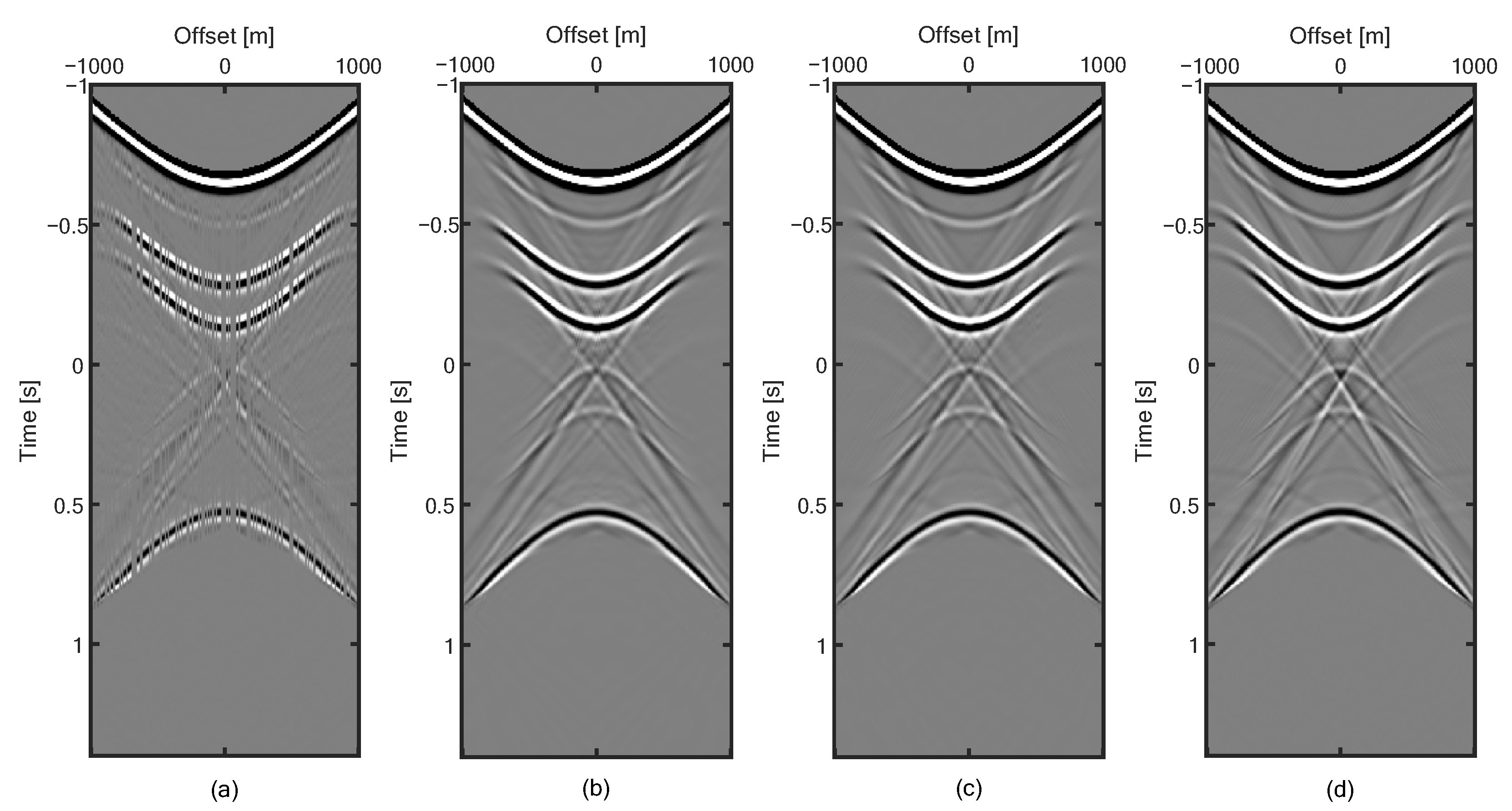
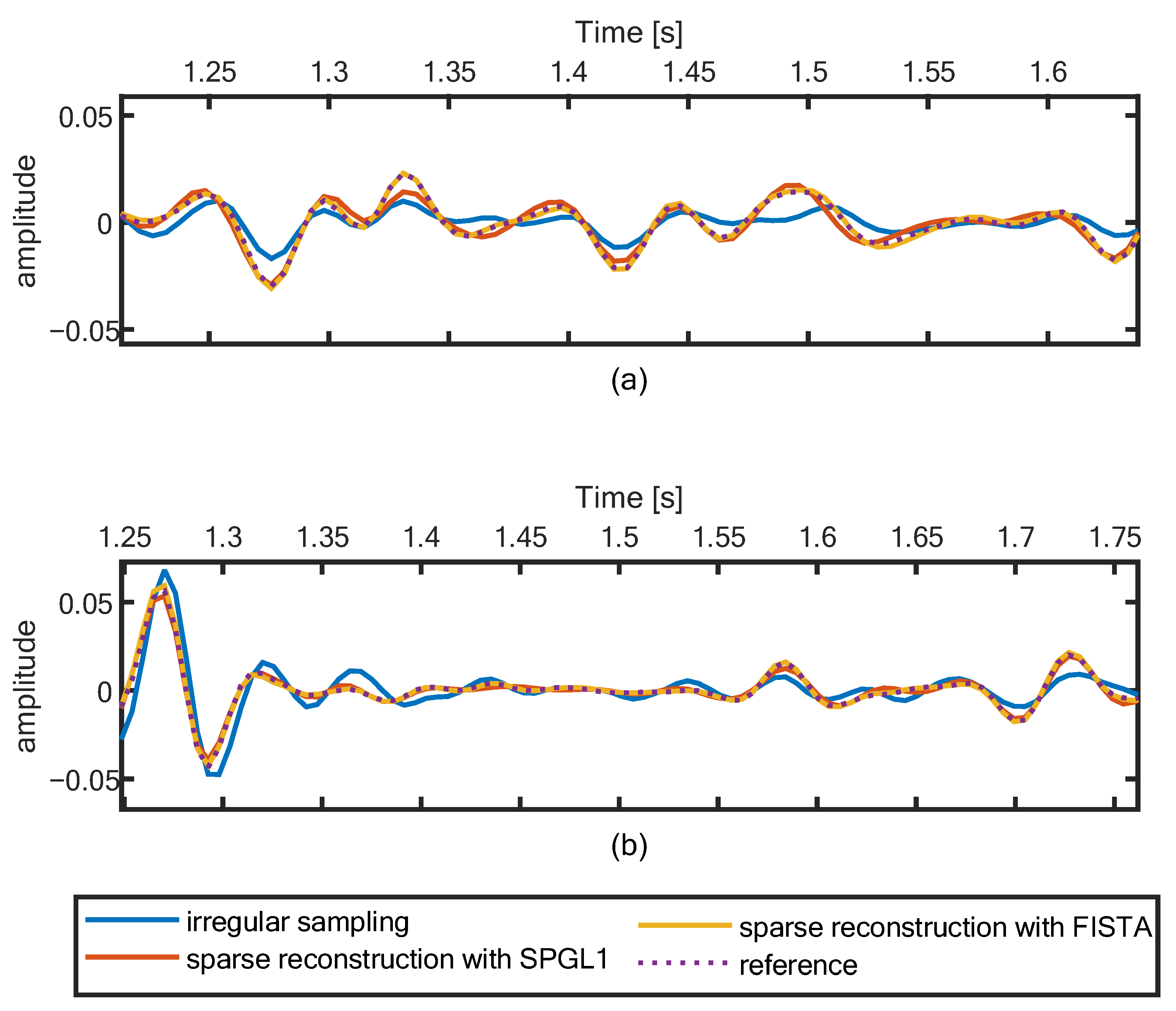
3. Numeral Examples
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Slob, E.; Wapenaar, K.; Broggini, F.; Snieder, R. Seismic reflector imaging using internal multiples with Marchenko-type equations. Geophysics 2014, 79, S63–S76. [Google Scholar] [CrossRef] [Green Version]
- Wapenaar, K.; Thorbecke, J.; Van Der Neut, J.; Broggini, F.; Slob, E.; Snieder, R. Marchenko imaging. Geophysics 2014, 79, WA39–WA57. [Google Scholar] [CrossRef] [Green Version]
- Wapenaar, K.; Brackenhoff, J.; Dukalski, M.; Meles, G.; Reinicke, C.; Slob, E.; Staring, M.; Thorbecke, J.; van der Neut, J.; Zhang, L. Marchenko redatuming, imaging, and multiple elimination and their mutual relations. Geophysics 2021, 86, WC117–WC140. [Google Scholar] [CrossRef]
- Lomas, A. Subsurface Seismic Imaging in the Presence of Multiply Scattered Waves. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2019. [Google Scholar]
- Marchenko, V.A. On reconstruction of the potential energy from phases of the scattered waves. Dokl. Akad. Nauk. SSSR 1955, 104, 695–698. [Google Scholar]
- Agranovich, Z.S.; Marchenko, V.A. The Inverse Problem of Scattering Theory; Gordon and Breach: New York, NY, USA, 1963. [Google Scholar]
- Burridge, R. The Gelfand-Levitan, the Marchenko, and the Gopinath-Sondhi integral equations of inverse scattering theory, regarded in the context of inverse impulse-response problems. Wave Motion 1980, 2, 305–323. [Google Scholar] [CrossRef]
- Marchenko, V.A. Nonlinear Equations and Operator Algebras; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Marchenko, V.; Slavin, V. Inverse Problems in the Theory of Small Oscillations; American Mathematical Society: Providence, RI, USA, 2018. [Google Scholar]
- Chadan, K.; Sabatier, P.C. Inverse Problems in Quantum Scattering Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Broggini, F.; Snieder, R. Connection of scattering principles: A visual and mathematical tour. Eur. J. Phys. 2012, 33, 593. [Google Scholar] [CrossRef]
- Bakulin, A.; Calvert, R. The virtual source method: Theory and case study. Geophysics 2006, 71, SI139–SI150. [Google Scholar] [CrossRef]
- Curtis, A.; Gerstoft, P.; Sato, H.; Snieder, R.; Wapenaar, K. Seismic interferometry—Turning noise into signal. Lead. Edge 2006, 25, 1082–1092. [Google Scholar] [CrossRef]
- Snieder, R.; Wapenaar, K.; Larner, K. Spurious multiples in seismic interferometry of primaries. Geophysics 2006, 71, SI111–SI124. [Google Scholar] [CrossRef] [Green Version]
- Wapenaar, K.; Broggini, F.; Slob, E.; Snieder, R. Three-dimensional single-sided Marchenko inverse scattering, data-driven focusing, Green’s function retrieval, and their mutual relations. Phys. Rev. Lett. 2013, 110, 084301. [Google Scholar] [CrossRef] [Green Version]
- Wapenaar, K.; Slob, E. On the Marchenko equation for multicomponent single-sided reflection data. Geophys. J. Int. 2014, 199, 1367–1371. [Google Scholar] [CrossRef]
- Reinicke Urruticoechea, C. Elastodynamic Marchenko Inverse Scattering: A Multiple-Elimination Strategy for Imaging of Elastodynamic Seismic Reflection Data. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
- Singh, S.; Snieder, R.; Behura, J.; van der Neut, J.; Wapenaar, K.; Slob, E. Marchenko imaging: Imaging with primaries, internal multiples, and free-surface multiples. Geophysics 2015, 80, S165–S174. [Google Scholar] [CrossRef] [Green Version]
- Slob, E. Green’s function retrieval and Marchenko imaging in a dissipative acoustic medium. Phys. Rev. Lett. 2016, 116, 164301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Behura, J.; Wapenaar, K.; Snieder, R. Autofocus imaging: Image reconstruction based on inverse scattering theory. Geophysics 2014, 79, A19–A26. [Google Scholar] [CrossRef] [Green Version]
- Van der Neut, J.; Wapenaar, K.; Thorbecke, J.; Slob, E.; Vasconcelos, I. An illustration of adaptive Marchenko imaging. Lead. Edge 2015, 34, 818–822. [Google Scholar] [CrossRef] [Green Version]
- Meles, G.A.; Wapenaar, K.; Curtis, A. Reconstructing the primary reflections in seismic data by Marchenko redatuming and convolutional interferometry. Geophysics 2016, 81, Q15–Q26. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Slob, E. Free-surface and internal multiple elimination in one step without adaptive subtractionMultiple elimination. Geophysics 2019, 84, A7–A11. [Google Scholar] [CrossRef]
- Zhang, L.; Thorbecke, J.; Wapenaar, K.; Slob, E. Transmission compensated primary reflection retrieval in the data domain and consequences for imaging. Geophysics 2019, 84, Q27–Q36. [Google Scholar] [CrossRef] [Green Version]
- Ravasi, M. Rayleigh-Marchenko redatuming for target-oriented, true-amplitude imaging. Geophysics 2017, 82, S439–S452. [Google Scholar] [CrossRef]
- Peng, H.; Vasconcelos, I. A study of acquisition-related sub-sampling and aperture effects on Marchenko focusing and redatuming. In Proceedings of the SEG International Exposition and Annual Meeting, San Antonio, TX, USA, 15–20 September 2019. [Google Scholar]
- Wapenaar, K.; van IJsseldijk, J. Discrete representations for Marchenko imaging of imperfectly sampled data. Geophysics 2020, 85, A1–A5. [Google Scholar] [CrossRef] [Green Version]
- Van Ijsseldijk, J.; Wapenaar, K. Adaptation of the iterative Marchenko scheme for imperfectly sampled data. Geophys. J. Int. 2021, 224, 326–336. [Google Scholar] [CrossRef]
- Haindl, C.; Ravasi, M.; Broggini, F. Handling gaps in acquisition geometries—Improving Marchenko-based imaging using sparsity-promoting inversion and joint inversion of time-lapse data. Geophysics 2021, 86, S143–S154. [Google Scholar] [CrossRef]
- Hennenfent, G.; Herrmann, F.J. Simply denoise: Wavefield reconstruction via jittered undersampling. Geophysics 2008, 73, V19–V28. [Google Scholar] [CrossRef] [Green Version]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Thorbecke, J.; Slob, E.; Brackenhoff, J.; van der Neut, J.; Wapenaar, K. Implementation of the Marchenko method. Geophysics 2017, 82, WB29–WB45. [Google Scholar] [CrossRef] [Green Version]
- Van den Berg, E.; Friedlander, M.P. SPGL1: A Solver for Large-Scale Sparse Reconstruction. 2007. Available online: https://friedlander.io/spgl1 (accessed on 28 November 2022).
- Van den Berg, E.; Friedlander, M.P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–912. [Google Scholar] [CrossRef] [Green Version]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Haindl, C.M.; Broggini, F.; Ravasi, M.; van Manen, D.J. Using sparsity to improve the accuracy of Marchenko imaging given imperfect acquisition geometries. In Proceedings of the 80th EAGE Conference and Exhibition, Copenhagen, Denmark, 10 June–15 July 2018; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2018; Volume 2018, pp. 1–5. [Google Scholar]
- Zhang, M. Compressive Sensing Acquisition with Application to Marchenko Imaging. Pure Appl. Geophys. 2022, 179, 2382–2404. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Han, L. Sparse Inversion for the Iterative Marchenko Scheme of Irregularly Sampled Data. Remote Sens. 2023, 15, 322. https://doi.org/10.3390/rs15020322
Zeng J, Han L. Sparse Inversion for the Iterative Marchenko Scheme of Irregularly Sampled Data. Remote Sensing. 2023; 15(2):322. https://doi.org/10.3390/rs15020322
Chicago/Turabian StyleZeng, Jingwen, and Liguo Han. 2023. "Sparse Inversion for the Iterative Marchenko Scheme of Irregularly Sampled Data" Remote Sensing 15, no. 2: 322. https://doi.org/10.3390/rs15020322
APA StyleZeng, J., & Han, L. (2023). Sparse Inversion for the Iterative Marchenko Scheme of Irregularly Sampled Data. Remote Sensing, 15(2), 322. https://doi.org/10.3390/rs15020322




