Entity Embeddings in Remote Sensing: Application to Deformation Monitoring for Infrastructure
Abstract
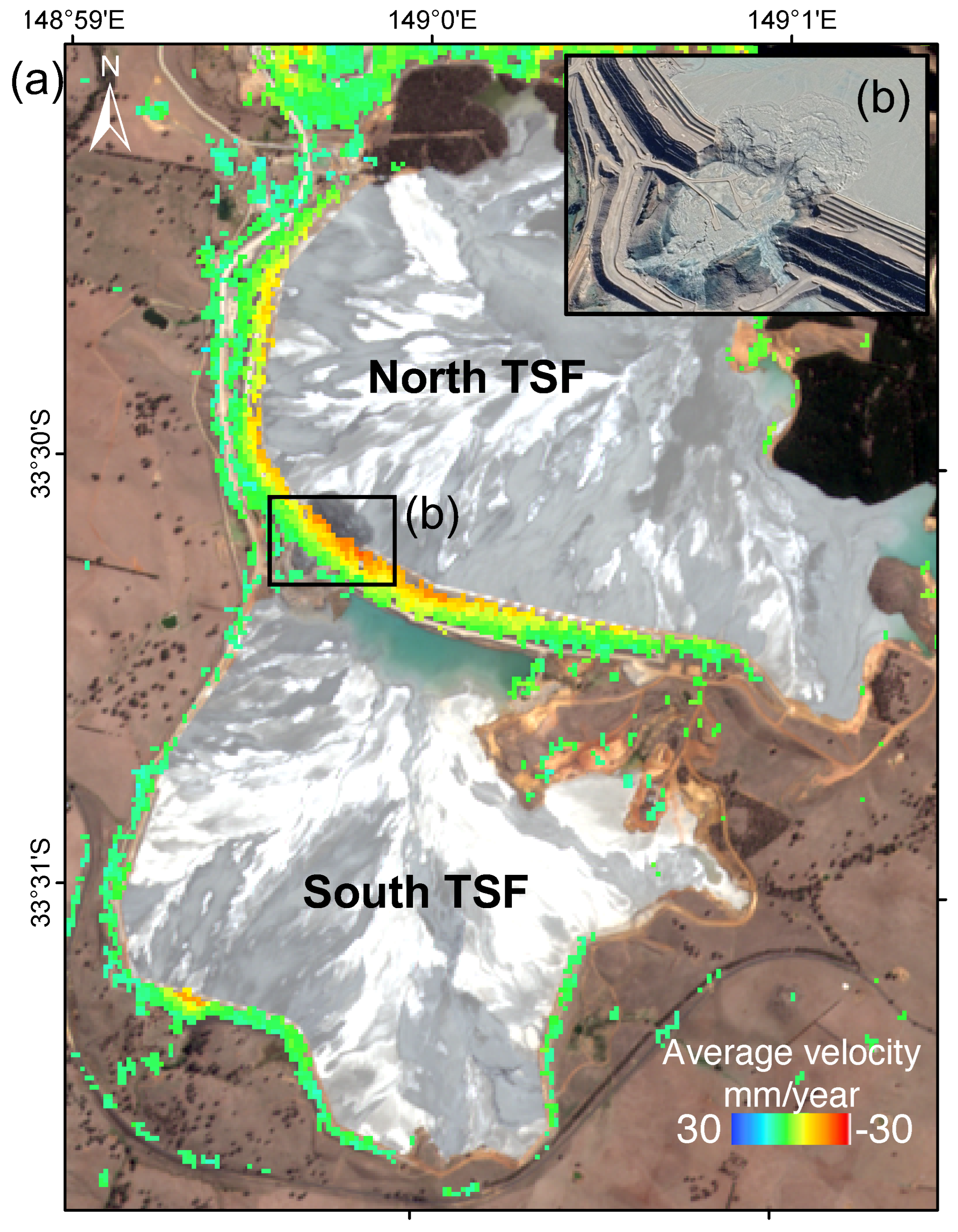
:1. Introduction
2. Data and Software
3. Methods
3.1. Entity Embedding
3.2. Fully Connected DL Architecture
3.3. Gaussian Process Regression
3.4. Defining Anomalous Deformation Behaviour
4. Results and Discussion
4.1. Prediction Performance of EE-DL Model
4.2. Prediction Performance of GPR
4.3. Comparison of EE-DL, GPR, and RF
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hund, K.; La Porta, D.; Fabregas, T.; Laing, T.; Dexhage, J. Minerals for Climate Action: The Mineral Intensity of the Clean Energy Transition. Climate-Smart Mining Facility; World Bank: Washington, DC, USA, 2020. [Google Scholar]
- Rossi, C.; Bateson, L.; Bayaraa, M.; Butcher, A.; Ford, J.; Hughes, A. Framework for remote sensing and modelling of lithium-brine deposit formation. Remote Sens. 2022, 14, 1383. [Google Scholar] [CrossRef]
- WMTF. 2020. Available online: https://worldminetailingsfailures.org/estimate-of-world-tailings-portfolio-2020/ (accessed on 13 July 2023).
- Robertson, P.; de Melo, L.; Williams, D.J.; Wilson, G.W. Report of the Expert Panel on the Technical Causes of the Failure of Feijão Dam I. 2020. Available online: http://www.b1technicalinvestigation.com/ (accessed on 13 July 2023).
- Torres-Cruz, L.A.; O’Donovan, C. Public remotely sensed data raise concerns about history of failed Jagersfontein dam. Sci. Rep. 2023, 13, 4953. [Google Scholar] [CrossRef] [PubMed]
- Bowker, L.N.; Chambers, D.M. The risk, public liability, & economics of tailings storage facility failures. Earthwork Act 2015, 24, 1–56. [Google Scholar]
- Crosetto, M.; Solari, L.; Mróz, M.; Balasis-Levinsen, J.; Casagli, N.; Frei, M.; Oyen, A.; Moldestad, D.A.; Bateson, L.; Guerrieri, L.; et al. The evolution of wide-area DInSAR: From regional and national services to the European Ground Motion Service. Remote Sens. 2020, 12, 2043. [Google Scholar] [CrossRef]
- Siegmund, R.; Brcic, R.; Kotzerke, P.; Eineder, M. The European Ground Motion Service EGMS—Processing Central Europe with First Results on Quality and Point Densities. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 5105–5108. [Google Scholar] [CrossRef]
- Even, M.; Schulz, K. InSAR deformation analysis with distributed scatterers: A review complemented by new advances. Remote Sens. 2018, 10, 744. [Google Scholar] [CrossRef]
- Selvakumaran, S.; Plank, S.; Geiß, C.; Rossi, C.; Middleton, C. Remote monitoring to predict bridge scour failure using Interferometric Synthetic Aperture Radar (InSAR) stacking techniques. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 463–470. [Google Scholar] [CrossRef]
- Selvakumaran, S.; Rossi, C.; Marinoni, A.; Webb, G.; Bennetts, J.; Barton, E.; Plank, S.; Middleton, C. Combined InSAR and Terrestrial Structural Monitoring of Bridges. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7141–7153. [Google Scholar] [CrossRef]
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perissin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space geodetic monitoring of engineered structures: The ongoing destabilization of the Mosul dam, Iraq. Sci. Rep. 2016, 6, 37408. [Google Scholar] [CrossRef]
- Macchiarulo, V.; Milillo, P.; DeJong, M.J.; Gonzalez Marti, J.; Sanchez, J.; Giardina, G. Integrated InSAR monitoring and structural assessment of tunnelling-induced building deformations. Struct. Control Health Monit. 2021, 28, e2781. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Satellite InSAR survey of structurally-controlled land subsidence due to groundwater exploitation in the Aguascalientes Valley, Mexico. Remote Sens. Environ. 2021, 254, 112254. [Google Scholar] [CrossRef]
- Grebby, S.; Sowter, A.; Gluyas, J.; Toll, D.; Gee, D.; Athab, A.; Girindran, R. Advanced analysis of satellite data reveals ground deformation precursors to the Brumadinho Tailings Dam collapse. Commun. Earth Environ. 2021, 2, 2. [Google Scholar] [CrossRef]
- Thomas, A.; Edwards, S.; Engels, J.; McCormack, H.; Hopkins, V.; Holley, R. Earth observation data and satellite InSAR for the remote monitoring of tailings storage facilities: A case study of Cadia Mine, Australia. In Proceedings of the 22nd International Conference on Paste, Thickened and Filtered Tailings. , Cape Town, South Africa, 8–10 May 2019; Australian Centre for Geomechanics: Perth, Australia, 2019; pp. 183–195. [Google Scholar]
- Carlà, T.; Intrieri, E.; Raspini, F.; Bardi, F.; Farina, P.; Ferretti, A.; Colombo, D.; Novali, F.; Casagli, N. Perspectives on the prediction of catastrophic slope failures from satellite InSAR. Sci. Rep. 2019, 9, 14137. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.; Sato, S.; Morin, R.; McParland, M.A. Comparison of Sentinel-1 and RADARSAT-2 Data for Monitoring of Tailings Storage Facilities. In Proceedings of the EUSAR 2021—13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Bayaraa, M.; Sheil, B.; Rossi, C. InSAR and numerical modelling for tailings dam monitoring—The Cadia failure case study. Géotechnique, 2022; ahead of print. [Google Scholar]
- Holden, D.; Donegan, S.; Pon, A. Brumadinho Dam InSAR study: Analysis of TerraSAR-X, COSMO-SkyMed and Sentinel-1 images preceding the collapse. In Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Perth, Western Australia, 12–14 May 2020; Australian Centre for Geomechanics: Perth, Australia, 2020; pp. 293–306. [Google Scholar]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Bull, D. A deep learning approach to detecting volcano deformation from satellite imagery using synthetic datasets. Remote Sens. Environ. 2019, 230, 111179. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Kelevitz, K.; Sadeghi, Z.; Wright, T.; Thompson, J.; Achim, A.M.; Bull, D. Detecting Ground Deformation in the Built Environment using Sparse Satellite InSAR data with a Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2940–2950. [Google Scholar] [CrossRef]
- Ma, P.; Zhang, F.; Lin, H. Prediction of InSAR time-series deformation using deep convolutional neural networks. Remote Sens. Lett. 2020, 11, 137–145. [Google Scholar] [CrossRef]
- Chen, Y.; Bruzzone, L.; Jiang, L.; Sun, Q. ARU-Net: Reduction of Atmospheric Phase Screen in SAR Interferometry Using Attention-Based Deep Residual U-Net. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5780–5793. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, Z.; Zheng, Y.; Ma, P. Recurrent neural networks for atmospheric noise removal from InSAR time series with missing values. ISPRS J. Photogramm. Remote Sens. 2021, 180, 227–237. [Google Scholar] [CrossRef]
- Brengman, C.M.; Barnhart, W.D. Identification of Surface Deformation in InSAR Using Machine Learning. Geochem. Geophys. Geosyst. 2021, 22, e2020GC009204. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Jolivet, R.; Dalaison, M.; Johnson, P.A.; Hulbert, C. Autonomous extraction of millimeter-scale deformation in InSAR time series using deep learning. Nat. Commun. 2021, 12, 6480. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Hill, P.; Bull, D. Application of Machine Learning to Classification of Volcanic Deformation in Routinely Generated InSAR Data. J. Geophys. Res. Solid Earth 2018, 123, 6592–6606. [Google Scholar] [CrossRef]
- De Brébisson, A.; Simon, É.; Auvolat, A.; Vincent, P.; Bengio, Y. Artificial neural networks applied to taxi destination prediction. arXiv 2015, arXiv:1508.00021. [Google Scholar]
- Guo, C.; Berkhahn, F. Entity embeddings of categorical variables. arXiv 2016, arXiv:1604.06737. [Google Scholar]
- Howard, J.; Gugger, S. Deep Learning for Coders with Fastai and PyTorch; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Girdhar, R.; El-Nouby, A.; Liu, Z.; Singh, M.; Alwala, K.V.; Joulin, A.; Misra, I. Imagebind: One embedding space to bind them all. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 15180–15190. [Google Scholar]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2015, 115, 78–89. [Google Scholar] [CrossRef]
- Lanari, R.; Casu, F.; Manzo, M.; Zeni, G.; Berardino, P.; Manunta, M.; Pepe, A. An overview of the small baseline subset algorithm: A DInSAR technique for surface deformation analysis. In Deformation and Gravity Change: Indicators of Isostasy, Tectonics, Volcanism, and Climate Change; Birkhäuser: Basel, Switzerland, 2007; pp. 637–661. [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Sowter, A.; Bateson, L.; Strange, P.; Ambrose, K.; Syafiudin, M.F. DInSAR estimation of land motion using intermittent coherence with application to the South Derbyshire and Leicestershire coalfields. Remote Sens. Lett. 2013, 4, 979–987. [Google Scholar] [CrossRef]
- Howard, J.; Gugger, S. Fastai: A layered API for deep learning. Information 2020, 11, 108. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Gardner, J.; Pleiss, G.; Weinberger, K.Q.; Bindel, D.; Wilson, A.G. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Introducing TensorFlow Feature Columns. 2017. Available online: https://developers.googleblog.com/2017/11/introducing-tensorflow-feature-columns.html (accessed on 13 July 2023).
- NN-SVG Tool. Available online: http://alexlenail.me/NN-SVG/index.html (accessed on 13 July 2023).
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of tricks for image classification with convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 558–567. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Santurkar, S.; Tsipras, D.; Ilyas, A.; Madry, A. How does batch normalization help optimization? arXiv 2018, arXiv:1805.11604. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- McHutchon, A.; Rasmussen, C. Gaussian process training with input noise. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Volume 24. [Google Scholar]
- Bonì, R.; Herrera, G.; Meisina, C.; Notti, D.; Béjar-Pizarro, M.; Zucca, F.; González, P.J.; Palano, M.; Tomás, R.; Fernández, J.; et al. Application of multi-sensor advanced DInSAR analysis to severe land subsidence recognition: Alto Guadalentín Basin (Spain). Proc. Int. Assoc. Hydrol. Sci. 2015, 372, 45–48. [Google Scholar] [CrossRef]
- Cigna, F.; Osmanoğlu, B.; Cabral-Cano, E.; Dixon, T.H.; Ávila-Olivera, J.A.; Garduño-Monroy, V.H.; DeMets, C.; Wdowinski, S. Monitoring land subsidence and its induced geological hazard with Synthetic Aperture Radar Interferometry: A case study in Morelia, Mexico. Remote Sens. Environ. 2012, 117, 146–161. [Google Scholar] [CrossRef]











| Random Forest | |
|---|---|
| n_estimators | 40 |
| max_samples | 200,000 |
| min_samples_leaf | 5 |
| max_features | 0.5 |
| Entity | Cardinality | Embedding Size |
|---|---|---|
| Coherence | 1016 | 77 |
| Longitude | 248 | 35 |
| Latitude | 205 | 32 |
| Day | 30 | 11 |
| Month | 12 | 6 |
| Year | 4 | 3 |
| Start | End | Total Dates | Steps | |
|---|---|---|---|---|
| Run-A | 2015-12-02 | 2016-08-10 | 21 | 1 |
| Run-B | 2015-12-02 | 2017-01-25 | 35 | 1 |
| Run-C | 2015-12-02 | 2017-01-25 | 35 | 4 |
| Run-D | 2015-12-02 | 2017-10-04 | 56 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayaraa, M.; Rossi, C.; Kalaitzis, F.; Sheil, B. Entity Embeddings in Remote Sensing: Application to Deformation Monitoring for Infrastructure. Remote Sens. 2023, 15, 4910. https://doi.org/10.3390/rs15204910
Bayaraa M, Rossi C, Kalaitzis F, Sheil B. Entity Embeddings in Remote Sensing: Application to Deformation Monitoring for Infrastructure. Remote Sensing. 2023; 15(20):4910. https://doi.org/10.3390/rs15204910
Chicago/Turabian StyleBayaraa, Maral, Cristian Rossi, Freddie Kalaitzis, and Brian Sheil. 2023. "Entity Embeddings in Remote Sensing: Application to Deformation Monitoring for Infrastructure" Remote Sensing 15, no. 20: 4910. https://doi.org/10.3390/rs15204910
APA StyleBayaraa, M., Rossi, C., Kalaitzis, F., & Sheil, B. (2023). Entity Embeddings in Remote Sensing: Application to Deformation Monitoring for Infrastructure. Remote Sensing, 15(20), 4910. https://doi.org/10.3390/rs15204910






