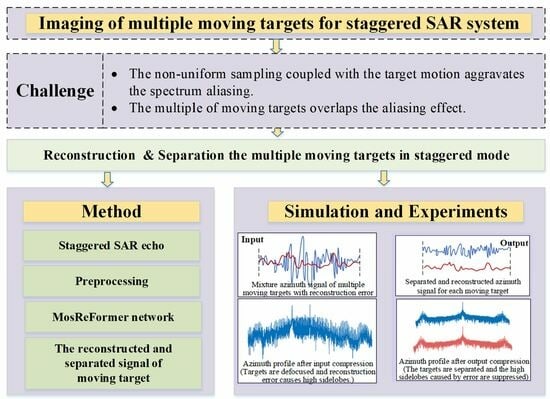
MosReformer: Reconstruction and Separation of Multiple Moving Targets for Staggered SAR Imaging
Abstract
:1. Introduction
- The impact of staggered SAR imaging on moving targets is accessed through temporal and spectral analyses. It becomes evident that the coupling of non-uniform sampling and the target motion result in reconstruction errors and spectrum aliasing, degrading the image quality. These issues need to be addressed effectively.
- We propose a Transformer-based method to image the multiple moving targets in the staggered SAR system. The reconstruction and the separation of the multiple moving targets are solved with a dual-path Transformer. To the best of our knowledge, this is the first article investigating deep learning methods in staggered SAR imaging, and also the first article employing deep learning to address the separation of multiple moving targets within an SAR system.
- The proposed MosReFormer network is designed by adopting a gated single-head Transformer architecture using convolution-augmented joint self-attentions, which can mitigate the reconstruction errors and separate the multiple moving targets simultaneously. The convolutional module provides great potential to mitigate the reconstruction error. The joint local and global self-attention is effective for dealing with the elemental interactions of long-azimuth samplings.
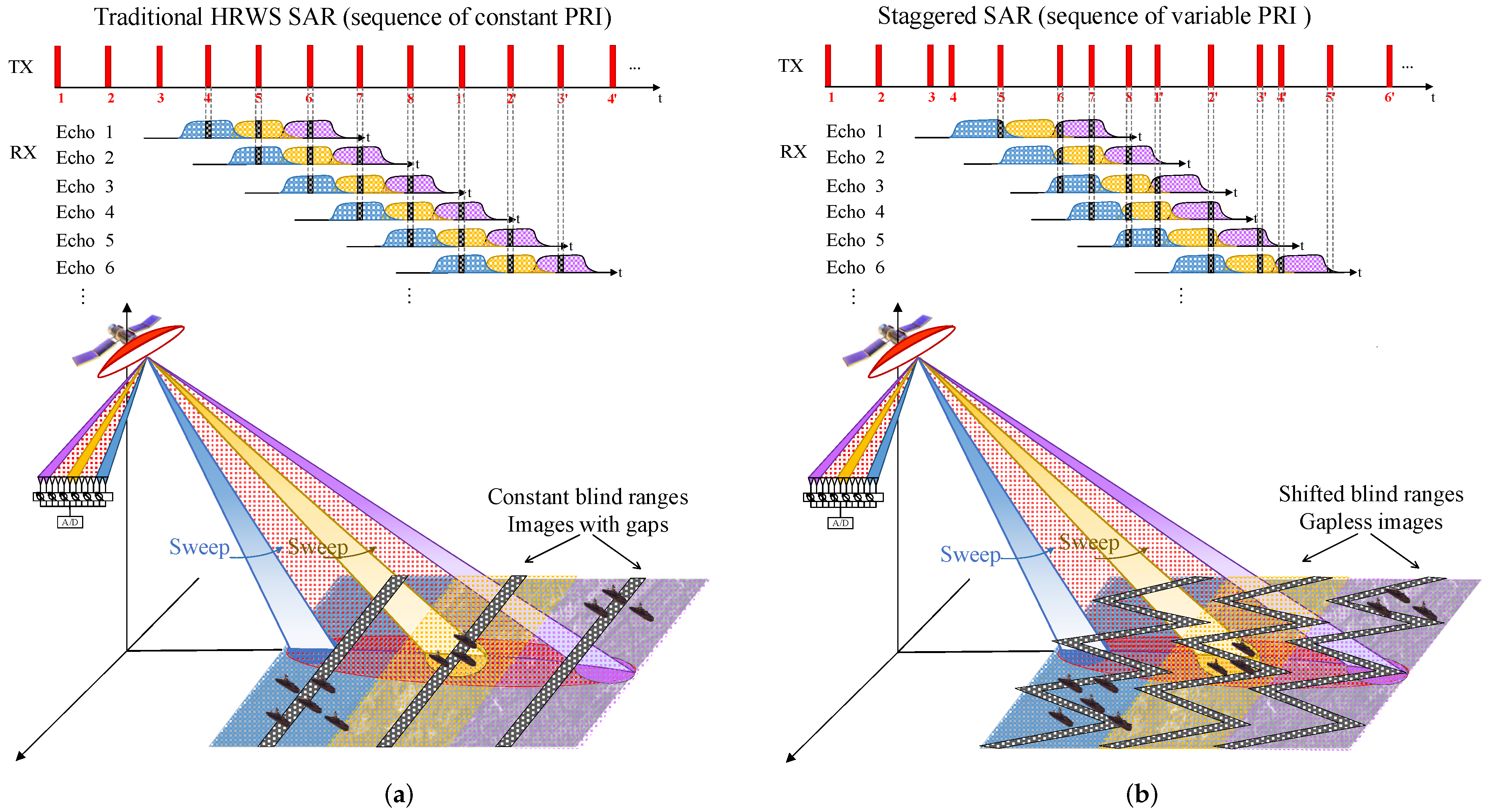
2. The Signal Model of Moving Targets in Staggered SAR system
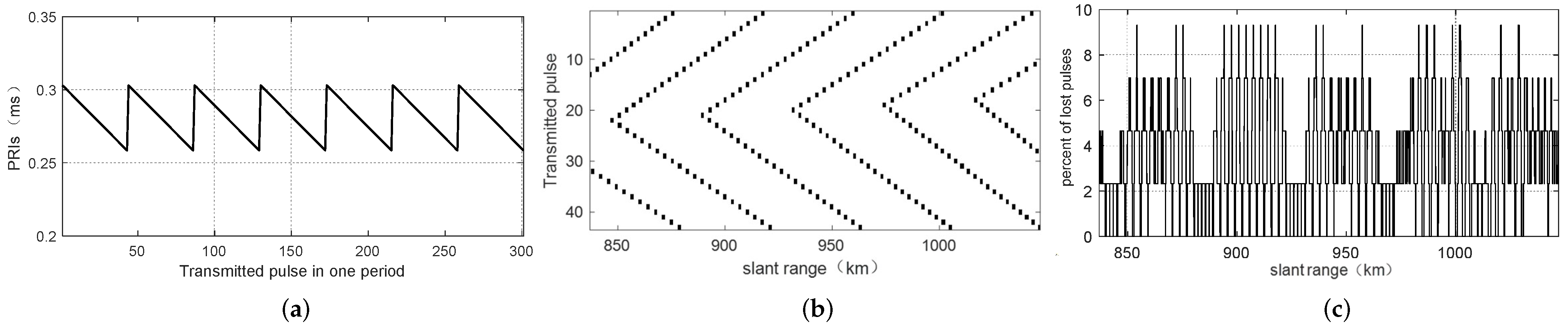
3. The Impact of Staggered SAR Imaging on Moving Targets
3.1. Temporal Analysis
Spectral Analysis
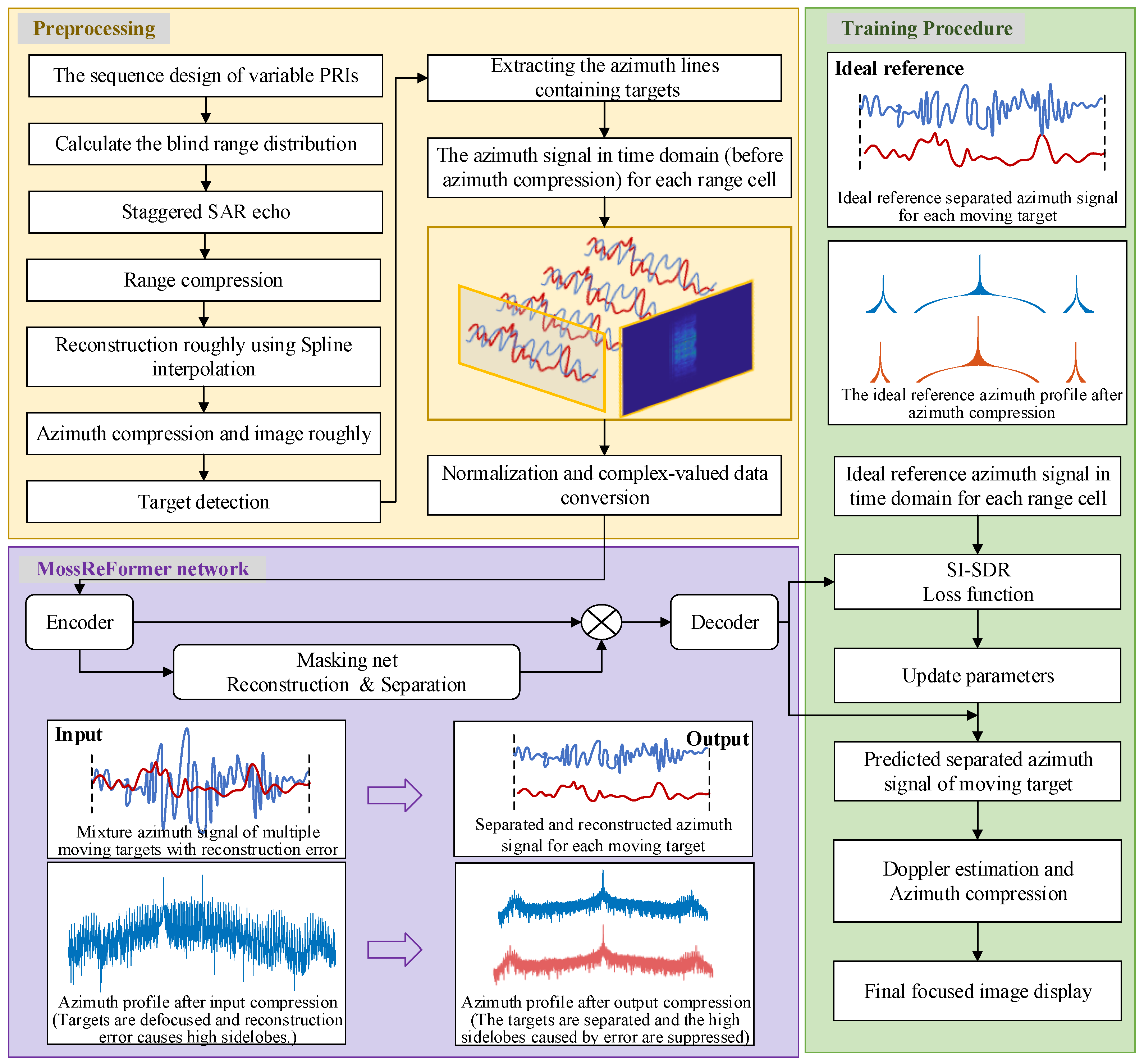
4. The Staggered SAR Imaging of Multiple Moving Targets Based on the Proposed MosReFormer Network
4.1. Task Description
4.2. Preprocessing
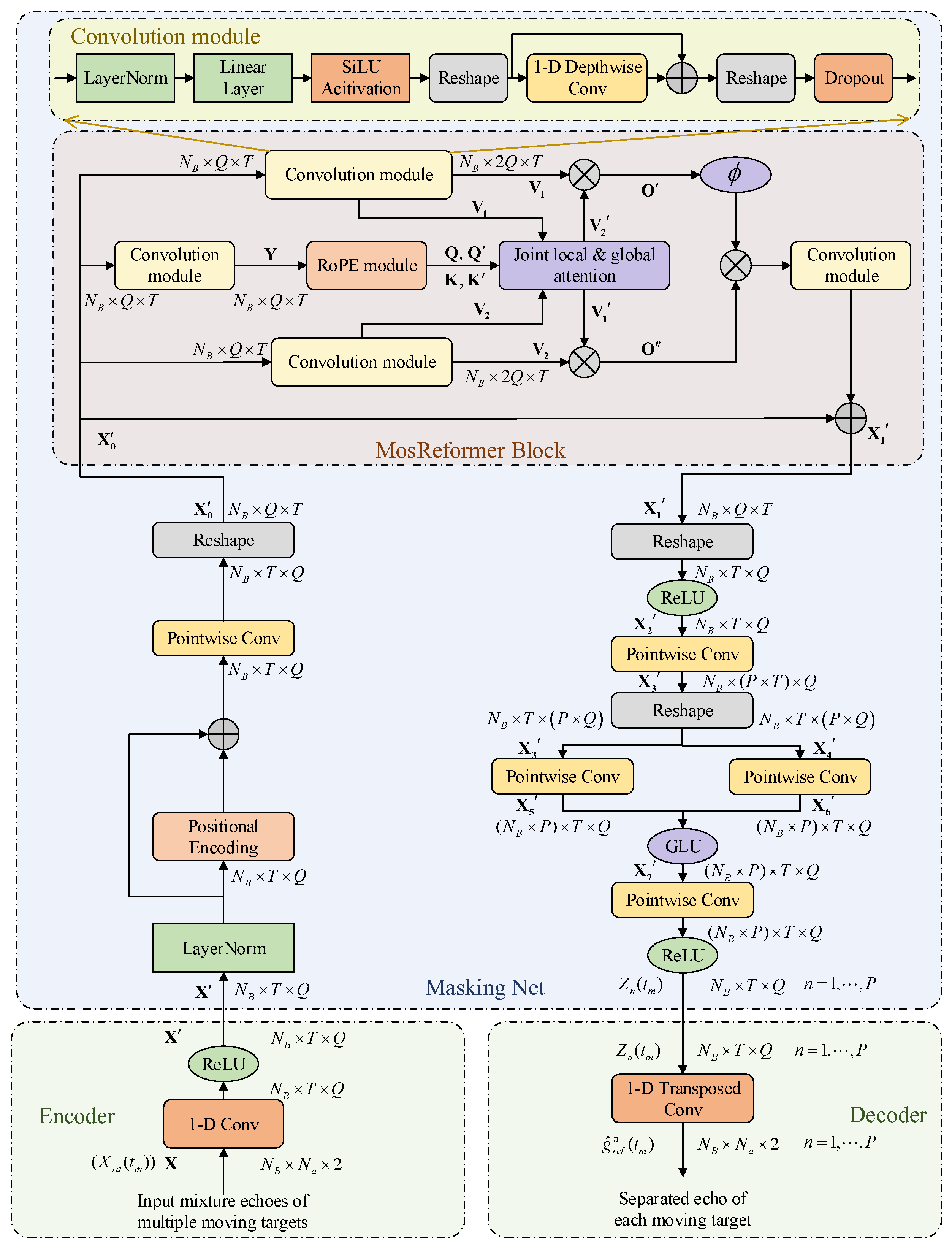
4.3. Architecture of MosReFormer Network
4.3.1. Encoder
4.3.2. Estimating the Reconstruction and Separation Masks
4.3.3. Decoder
4.3.4. MosReformer Operation
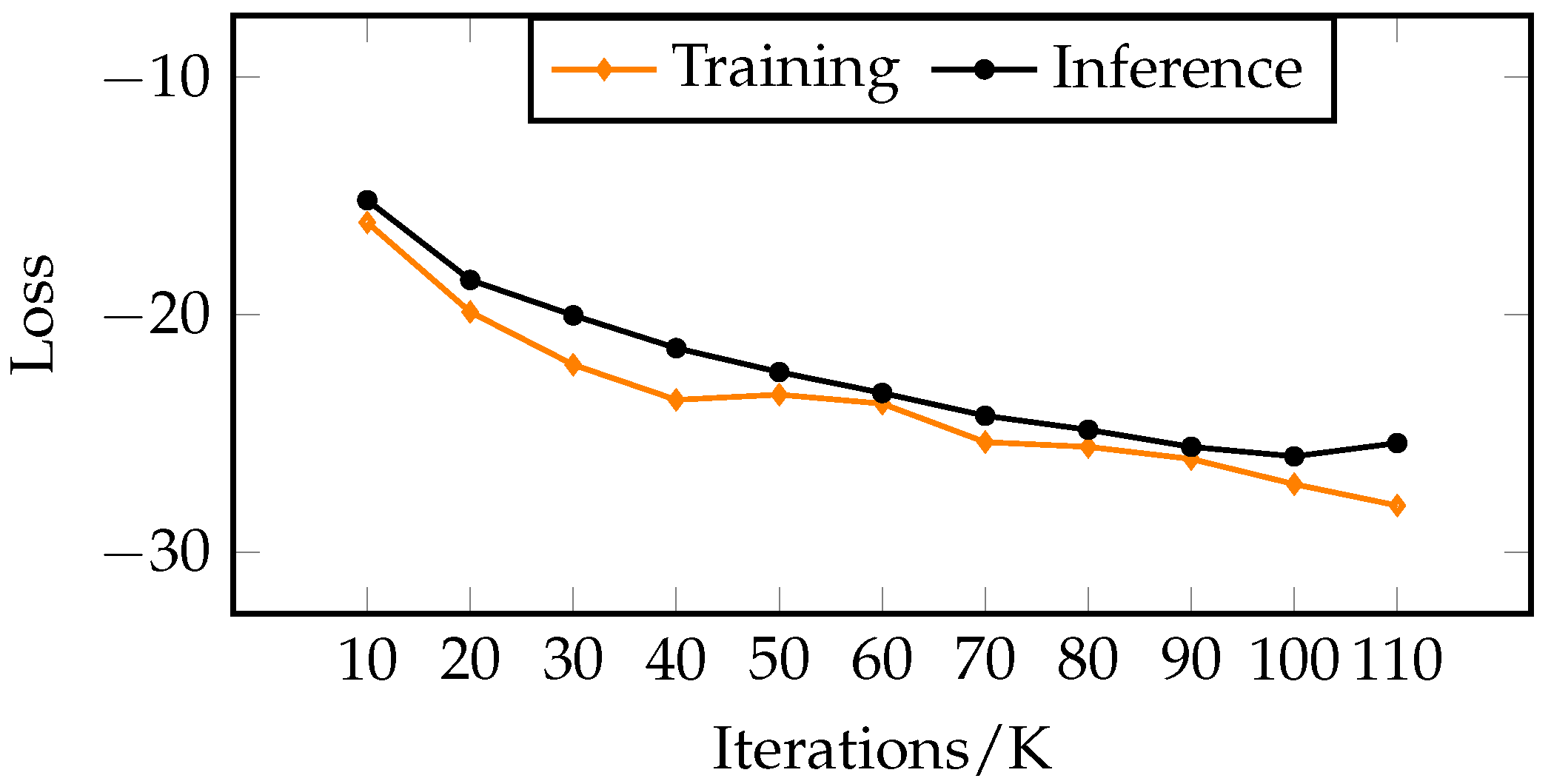
4.4. SI-SDR Loss Function
5. Experimental Results and Analysis
5.1. Dataset and Experimental Configuration
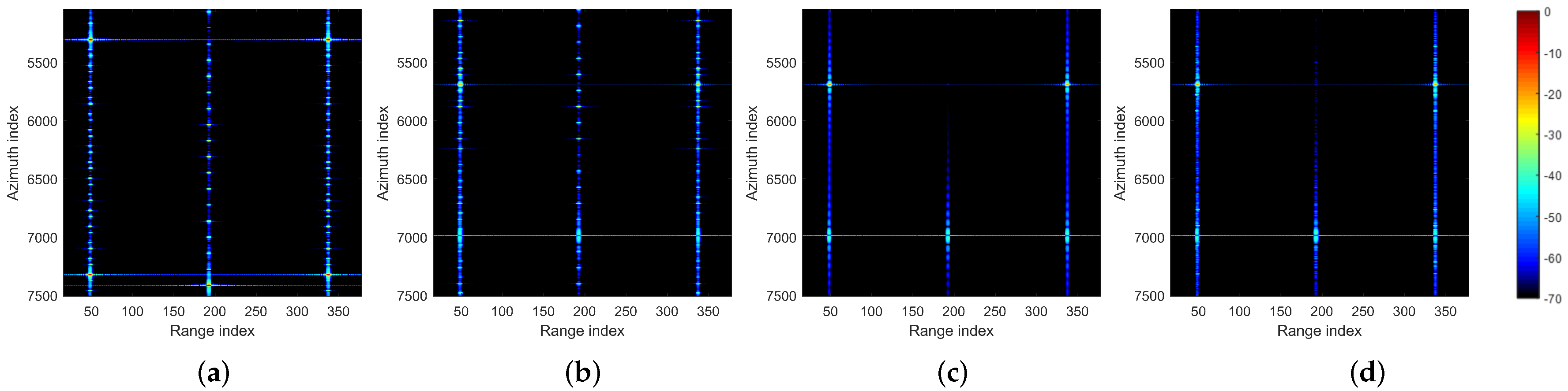
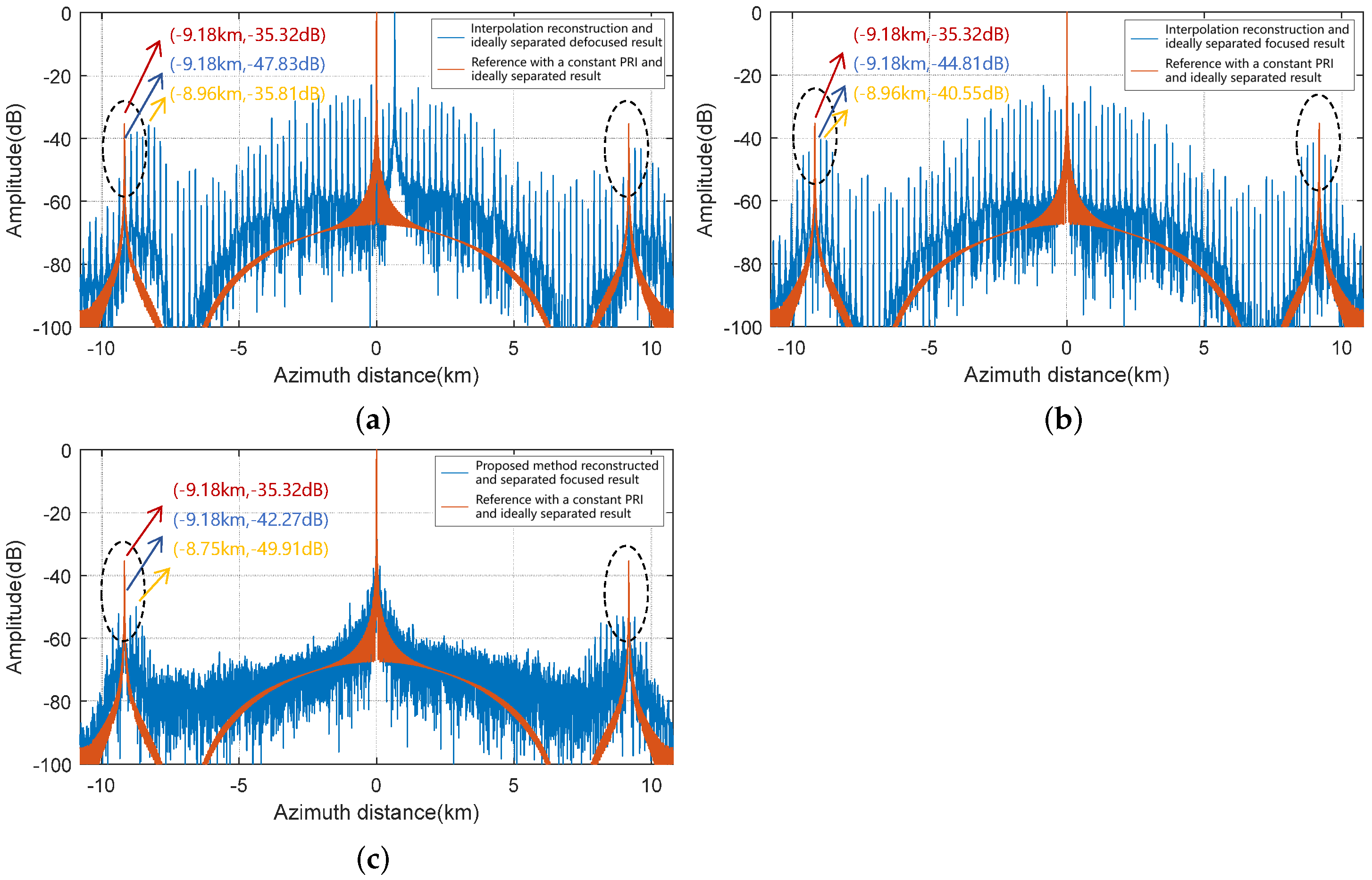
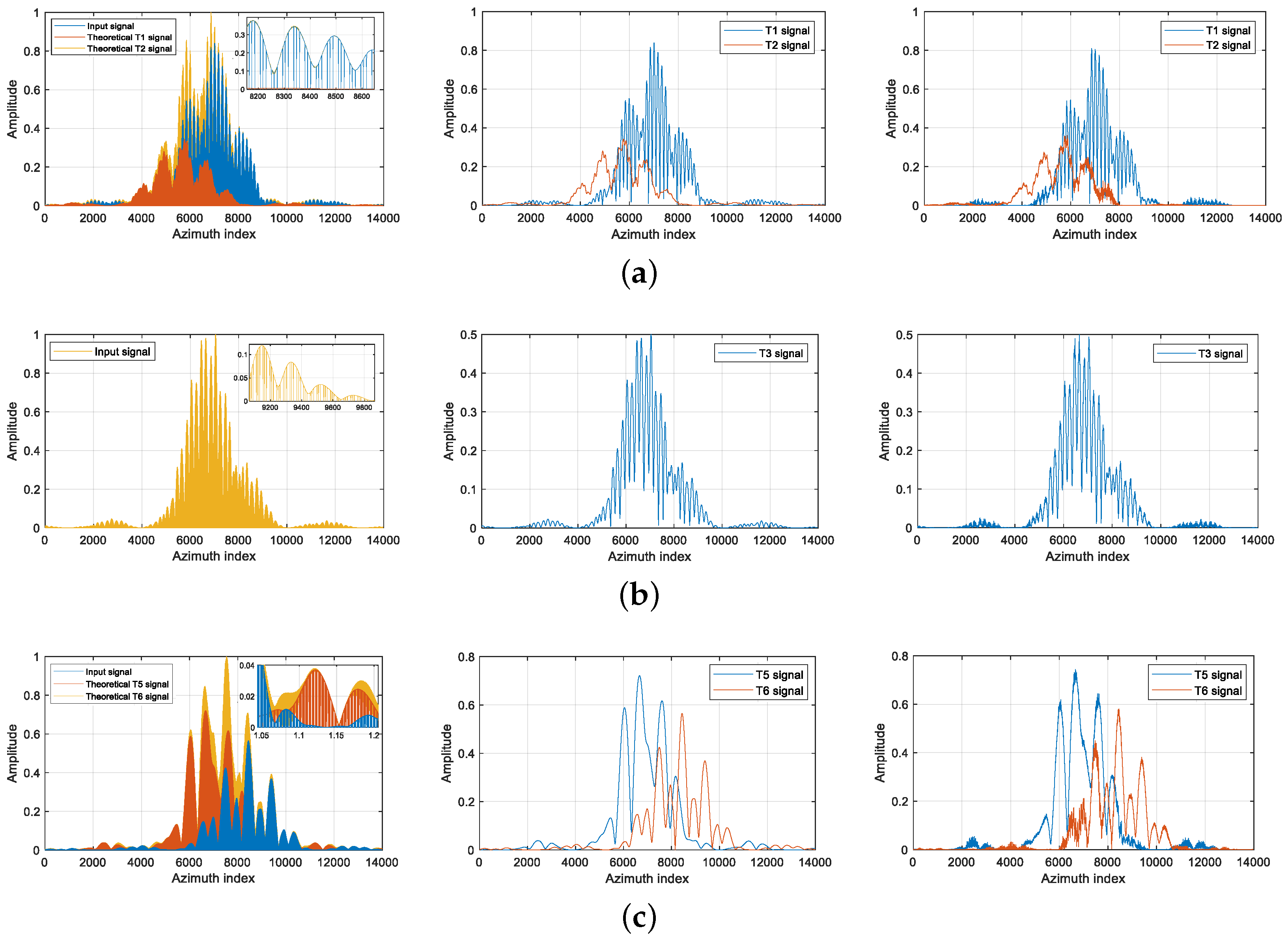
5.2. Results and Analysis of Multiple Moving Point Targets
5.3. Results and Analysis of Simulated SAR Data
5.4. Experiment on Spaceborne SAR Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhan, X.; Zhang, X.; Zhang, W.; Xu, Y.; Shi, J.; Wei, S.; Zeng, T. Target-Oriented High-Resolution and Wide-Swath Imaging with an Adaptive Receiving Processing Decision Feedback Framework. Appl. Sci. 2022, 12, 8922. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, F.; Tian, Y.; Chen, L.; Wang, R.; Wu, Y. High-Resolution and Wide-Swath 3D Imaging for Urban Areas Based on Distributed Spaceborne SAR. Remote Sens. 2023, 15, 3938. [Google Scholar] [CrossRef]
- Jin, T.; Qiu, X.; Hu, D.; Ding, C. An ML-Based Radial Velocity Estimation Algorithm for Moving Targets in Spaceborne High-Resolution and Wide-Swath SAR Systems. Remote Sens. 2017, 9, 404. [Google Scholar] [CrossRef]
- Chen, Y.; Li, G.; Zhang, Q.; Sun, J. Refocusing of Moving Targets in SAR Images via Parametric Sparse Representation. Remote Sens. 2017, 9, 795. [Google Scholar] [CrossRef]
- Shen, W.; Lin, Y.; Yu, L.; Xue, F.; Hong, W. Single Channel Circular SAR Moving Target Detection Based on Logarithm Background Subtraction Algorithm. Remote Sens. 2018, 10, 742. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.G.; Peng, Y.N. Doppler Keystone Transform: An Approach Suitable for Parallel Implementation of SAR Moving Target Imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Jungang, Y.; Xiaotao, H.; Tian, J.; Thompson, J.; Zhimin, Z. New Approach for SAR Imaging of Ground Moving Targets Based on a Keystone Transform. IEEE Geosci. Remote Sens. Lett. 2011, 8, 829–833. [Google Scholar] [CrossRef]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming for HRWS-SAR imaging: System design, performance and optimization strategies. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1836–1839. [Google Scholar]
- Yang, T.; Lv, X.; Wang, Y.; Qian, J. Study on a Novel Multiple Elevation Beam Technique for HRWS SAR System. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 5030–5039. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. MIMO SAR processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5034–5055. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.-D.; Xia, X.-G.; Guo, R.; Liu, Y.-Y.; Bao, Z. Robust Clutter Suppression and Moving Target Imaging Approach for Multichannel in Azimuth High-Resolution and Wide-Swath Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 687–709. [Google Scholar] [CrossRef]
- Li, X.; Xing, M.; Xia, X.G.; Sun, G.C.; Liang, Y.; Bao, Z. Simultaneous Stationary Scene Imaging and Ground Moving Target Indication for High-Resolution Wide-Swath SAR System. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4224–4239. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. Simultaneous High-Resolution Wide-Swath SAR Imaging and Ground Moving Target Indication: Processing Approaches and System Concepts. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 5015–5029. [Google Scholar] [CrossRef]
- Grafmüller, B.; Schaefer, C. Hochauflösende Synthetik-Apertur-Radar Vorrichtung und Antenne für eine Hochauflösende Synthetik Apertur Radar Vorrichtung. DE102005062031A1, 23 December 2005. [Google Scholar]
- Villano, M.; Krieger, G.; Moreira, A. Staggered-SAR: A New Concept for High-Resolution Wide-Swath Imaging. In Proceedings of the IEEE GOLD Remote Sensing Conference, Rome, Italy, 4–5 June 2012; pp. 1–3. [Google Scholar]
- Huber, S.; de Almeida, F.Q.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A. Tandem-L: A Technical Perspective on Future Spaceborne SAR Sensors for Earth Observation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4792–4807. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the earth’s surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Pinheiro, M.; Prats, P.; Villano, M.; Rodriguez-Cassola, M.; Rosen, P.A.; Hawkins, B.; Agram, P. Processing and performance analysis of NASA ISRO SAR (NISAR) staggered data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8374–8377. [Google Scholar]
- Kim, J.H.; Younis, M.; Prats-Iraola, P.; Gabele, M.; Krieger, G. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression. IEEE Trans. Geosci. Remote Sens. 2013, 51, 579–590. [Google Scholar] [CrossRef]
- Villano, M.; Moreira, A.; Krieger, G. Staggered-SAR for high-resolution wide-swath imaging. In Proceedings of the IET International Conference on Radar Systems (Radar 2012), Glasgow, UK, 22–25 October2012; pp. 1–6. [Google Scholar]
- Gebert, N.; Krieger, G. Ultra-Wide Swath SAR Imaging with Continuous PRF Variation. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Villano, M.; Krieger, G.; Moreira, A. Staggered SAR: High-resolution wide-swath imaging by continuous PRI variation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4462–4479. [Google Scholar] [CrossRef]
- Luo, X.; Wang, R.; Xu, W.; Deng, Y.; Guo, L. Modification of multichannel reconstruction algorithm on the SAR with linear variation of PRI. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 3050–3059. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Deng, Y.; Wang, W.; Li, N. SAR signal recovery and reconstruction in staggered mode with low oversampling factors. IEEE Geosci. Remote Sens. Lett. 2018, 15, 704–708. [Google Scholar] [CrossRef]
- Liao, X.; Jin, C.; Liu, Z. Compressed Sensing Imaging for Staggered SAR with Low Oversampling Ratio. In Proceedings of the EUSAR 2021; 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; pp. 1–4. [Google Scholar]
- Zhang, Y.; Qi, X.; Jiang, Y.; Li, H.; Liu, Z. Image Reconstruction for Low-Oversampled Staggered SAR Based on Sparsity Bayesian Learning in the Presence of a Nonlinear PRI Variation Strategy. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–24. [Google Scholar] [CrossRef]
- Zhou, Z.; Deng, Y.; Wang, W.; Jia, X.; Wang, R. Linear Bayesian approaches for low-oversampled stepwise staggered SAR data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5206123. [Google Scholar] [CrossRef]
- Ustalli, N.; Villano, M. High-Resolution Wide-Swath Ambiguous Synthetic Aperture Radar Modes for Ship Monitoring. Remote Sens. 2022, 14, 3102. [Google Scholar] [CrossRef]
- Oveis, A.H.; Giusti, E.; Ghio, S.; Martorella, M. A Survey on the Applications of Convolutional Neural Networks for Synthetic Aperture Radar: Recent Advances. IEEE Trans. Aerosp. Electron. Syst. Mag. 2022, 37, 18–42. [Google Scholar] [CrossRef]
- Chen, V.C.; Liu, B. Hybrid SAR/ISAR for distributed ISAR imaging of moving targets. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 658–663. [Google Scholar] [CrossRef]
- Wu, D.; Yaghoobi, M.; Davies, M.E. Sparsity-Driven GMTI Processing Framework with Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1434–1447. [Google Scholar] [CrossRef]
- Jao, J.K.; Yegulalp, A. Multichannel Synthetic Aperture Radar Signatures and Imaging of a Moving Target. Inv. Probl. 2013, 29, 054009. [Google Scholar] [CrossRef]
- Martorella, M.; Berizzi, F.; Giusti, E. Refocussing of moving targets in SAR images based on inversion mapping and ISAR processing. In Proceedings of the 2011 IEEE RadarCon (RADAR), Kansas City, MO, USA, 23–27 May 2011; pp. 68–72. [Google Scholar]
- Martorella, M.; Pastina, D.; Berizzi, F.; Lombardo, P. Spaceborne Radar Imaging of Maritime Moving Targets With the Cosmo-SkyMed SAR System. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2797–2810. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, Y.; Zhang, H. A Hybrid SAR/ISAR Approach for Refocusing Maritime Moving Targets with the GF-3 SAR Satellite. Sensors 2020, 20, 2037. [Google Scholar] [CrossRef]
- Jiang, H.; Peng, M.; Zhong, Y.; Xie, H.; Hao, Z.; Lin, J.; Ma, X.; Hu, X. A Survey on Deep Learning-Based Change Detection from High-Resolution Remote Sensing Images. Remote Sens. 2022, 14, 1552. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Z.; Zhang, C. SAR ship detection based on resnet and transfer learning. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1188–1191. [Google Scholar]
- Mu, H.; Zhang, Y.; Jiang, Y.; Ding, C. CV-GMTINet: GMTI Using a Deep Complex-Valued Convolutional Neural Network for Multichannel SAR-GMTI System. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5201115. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, H.; Xiao, T. SAR imaging of multiple maritime moving targets based on sparsity Bayesian learning. IET Radar Sonar Navigat. 2020, 14, 1717–1725. [Google Scholar] [CrossRef]
- Zhao, S.; Ma, B. MossFormer: Pushing the Performance Limit of Monaural Speech Separation Using Gated Single-Head Transformer with Convolution-Augmented Joint Self-Attentions. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Dauphin, Y.N.; Fan, A.; Auli, M.; Grangier, D. Language modeling with gated convolutional networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 933–941. [Google Scholar]
- Su, J.; Lu, Y.; Pan, S.; Zhang, C.; Zhang, W. Roformer: Enhanced transformer with rotary position embedding. arXiv 2020, arXiv:2104.09864. [Google Scholar]
- Le Roux, J.; Wisdom, S.; Erdogan, H.; Hershey, J.R. SDR–half-baked or well done? In Proceedings of the 44th International Conference on Acoustics, Speech, and Signal Processing, Brighton, UK, 12–17 May 2019; pp. 626–630. [Google Scholar]
- Luo, Y.; Mesgarani, N. Conv-TasNet: Surpassing Ideal Time-Frequency Magnitude Masking for Speech Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 27, 1256–1266. [Google Scholar] [CrossRef] [PubMed]
- Villano, M. Staggered Synthetic Aperture Radar. Ph.D. Thesis, Deutsches Zentrum für Luft-und Raumfahrt, DLR. Oberpfaffenhofen, Bavaria, Germany, 2016. [Google Scholar]
- Martorella, M.; Giusti, E.; Berizzi, F.; Bacci, A.; Mese, E.D. ISAR based technique for refocusing non-copperative targets in SAR images. IET Radar Sonar Navigat. 2012, 6, 332–340. [Google Scholar] [CrossRef]
- Brink, A.D. Minimum spatial entropy threshold selection. IEE Proc. Vis. Image Signal Process. 1995, 142, 128–132. [Google Scholar] [CrossRef]








| Parameter | Notation | Value |
|---|---|---|
| Carrier frequency | 9.6 GHz | |
| Orbit height | 760 km | |
| Off-nadir angle | 23.3°–40.5° | |
| Ground range coverage | 333–668 km | |
| Incidence angle | 26.3°–46.6° | |
| Range bandwidth | 180 MHz | |
| Transmitted pulse duration | 5 us | |
| Processed Doppler band | 2010 Hz | |
| Minimum PRF | 3300 Hz | |
| Maximum PRF | 3860 Hz | |
| The number of variable PRIs | M | 43 |
| Setting Up | Value | Hyper-Parameters | Value |
|---|---|---|---|
| Batch Size | 10 | No.MosReFormer Blocks | 24 |
| Learning Rate | 0.001 | Encoder Output Dimension (Q) | 512 |
| Learning Rate Schedule | linear | Encoder Kernel Size ()/Stride | 16/8 |
| Warmup | 3000 | Depthwise Conv Kernel Size () | 17 |
| Normalization | Chunk Size (P) | 256 | |
| Gradient Clipping | 2 | Attention Dimension (d) | 128 |
| Dropout | 0.1 | Gating Activation Function | Sigmoid |
| Performance/Methods | DIRIS | IRIS | Ideal Reference | MosReFormer-Based Method |
|---|---|---|---|---|
| ISLR | −13.34 | −13.25 | −18.45 | −18.02 |
| PSLR | −23.09 | −23.40 | −35.38 | −37.08 |
| Entropy | 5.49 | 4.69 | 4.37 | 4.39 |
| Entropy | DIRIS | IRIS | RID | Ideal Reference | MosReFormer-Based Method |
|---|---|---|---|---|---|
| Target1 | 7.04 | 6.36 | 6.55 | 6.24 | 6.25 |
| Target2 | 7.43 | 6.35 | 7.01 | 6.31 | 6.32 |
| Target3 | 7.48 | 6.31 | 6.92 | 6.28 | 6.28 |
| Target4 | 6.72 | 6.05 | 6.33 | 6.01 | 6.02 |
| Target5 | 7.22 | 6.33 | 7.20 | 6.30 | 6.31 |
| All scene | 9.11 | 8.19 | 8.82 | 7.86 | 7.88 |
| Performance | DIRIS | IRIS | RID | Ideal Reference | MosReFormer-Based Method |
|---|---|---|---|---|---|
| Entropy | 7.58 | 7.26 | 7.31 | 6.96 | 6.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, X.; Zhang, Y.; Jiang, Y.; Liu, Z.; Yang, C. MosReformer: Reconstruction and Separation of Multiple Moving Targets for Staggered SAR Imaging. Remote Sens. 2023, 15, 4911. https://doi.org/10.3390/rs15204911
Qi X, Zhang Y, Jiang Y, Liu Z, Yang C. MosReformer: Reconstruction and Separation of Multiple Moving Targets for Staggered SAR Imaging. Remote Sensing. 2023; 15(20):4911. https://doi.org/10.3390/rs15204911
Chicago/Turabian StyleQi, Xin, Yun Zhang, Yicheng Jiang, Zitao Liu, and Chang Yang. 2023. "MosReformer: Reconstruction and Separation of Multiple Moving Targets for Staggered SAR Imaging" Remote Sensing 15, no. 20: 4911. https://doi.org/10.3390/rs15204911
APA StyleQi, X., Zhang, Y., Jiang, Y., Liu, Z., & Yang, C. (2023). MosReformer: Reconstruction and Separation of Multiple Moving Targets for Staggered SAR Imaging. Remote Sensing, 15(20), 4911. https://doi.org/10.3390/rs15204911