Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China
Abstract
:1. Introduction
1.1. Heuristic Methods
1.2. Deterministic Methods
1.3. Statistical Methods
1.4. Models Used in This Study
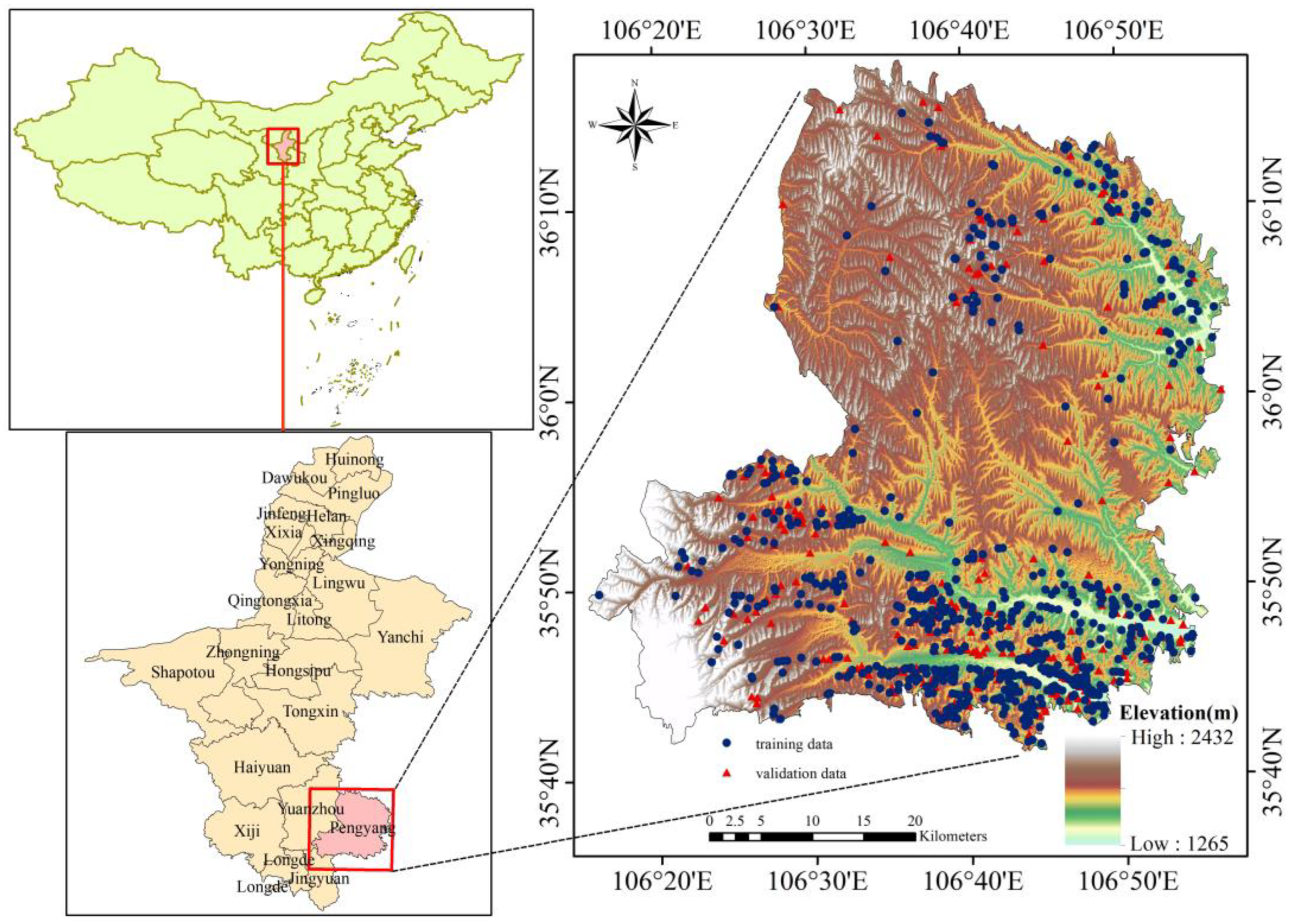
2. Description of Study Area
2.1. Geographic Location
2.2. Climate
2.3. Topography
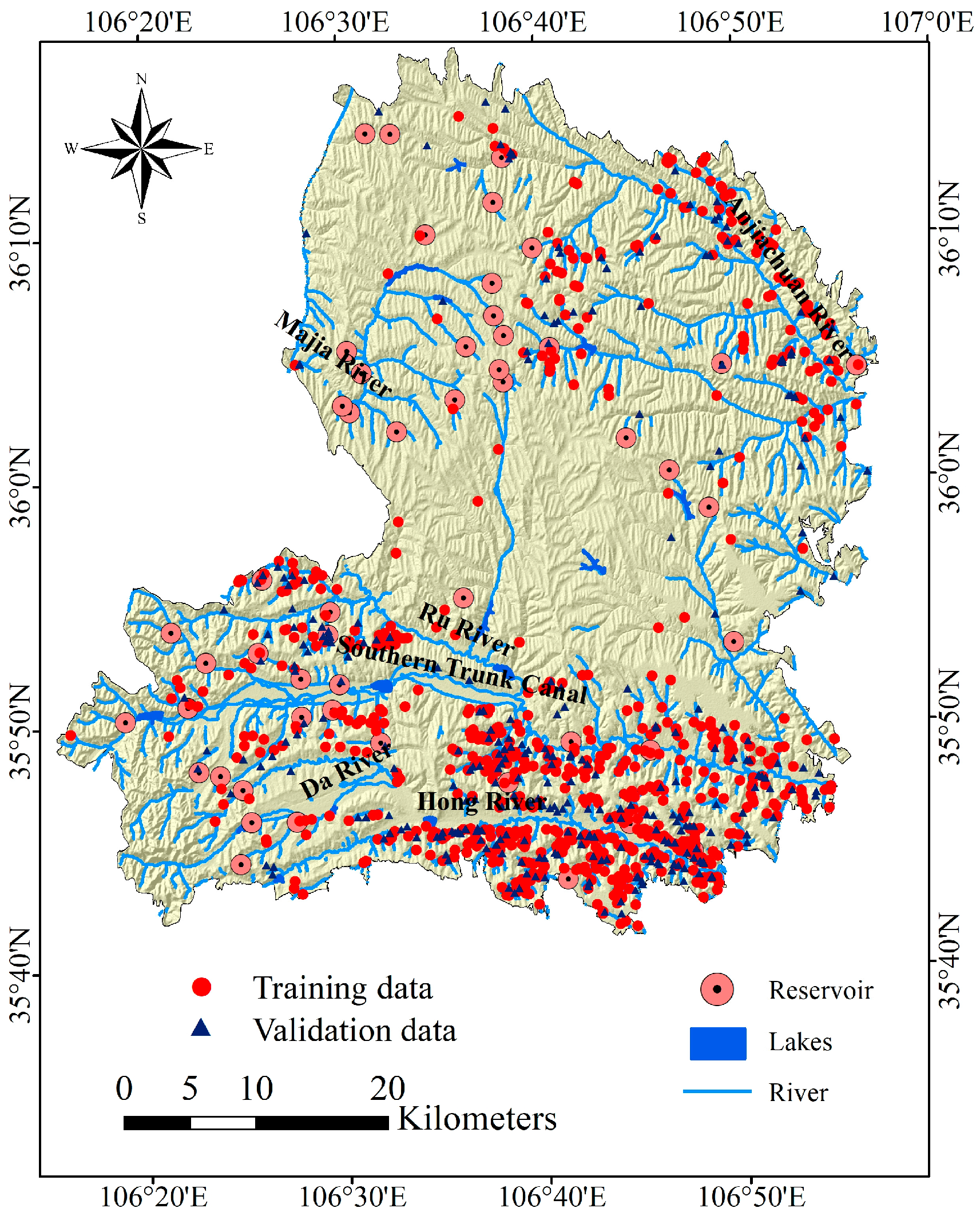
2.4. River System
3. Methodology
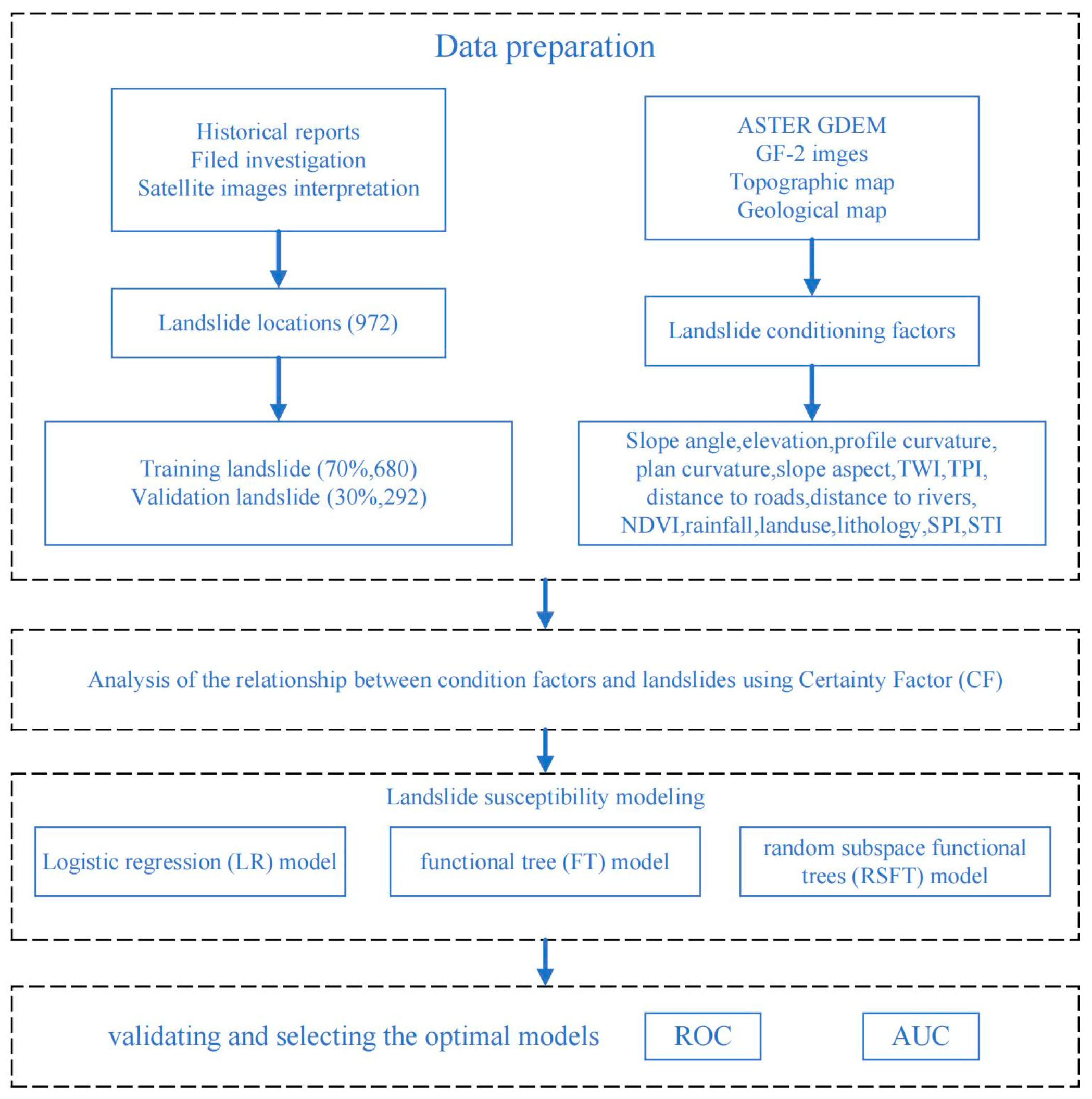
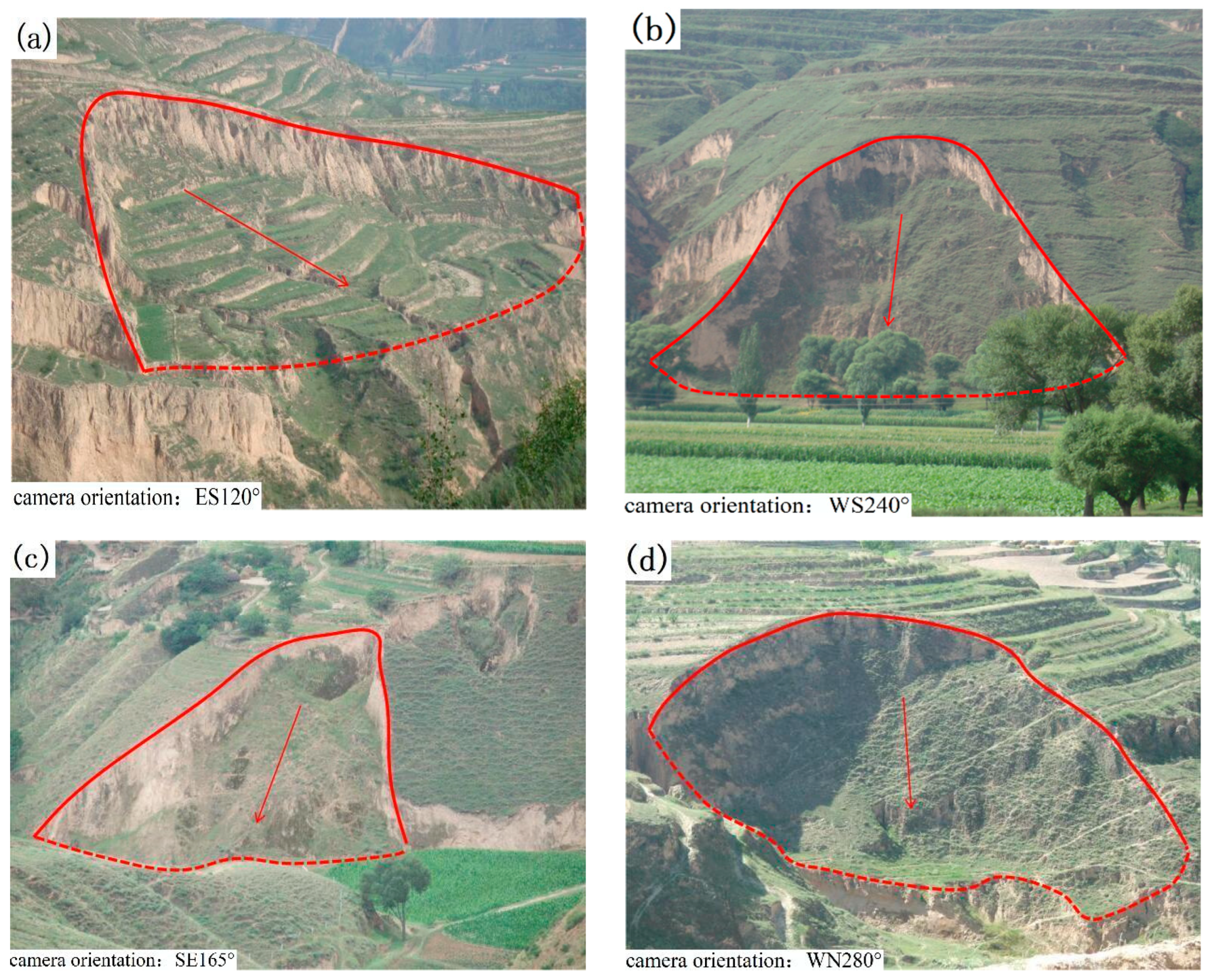
3.1. Preparation of Spatial Database
3.2. Spatial Prediction Modeling of Landslides
3.2.1. Certainty Factor (CF)
3.2.2. Logistic Regression (LR)
3.2.3. Functional Trees (FTs)
3.2.4. Random Subspace Functional Trees (RSFTs)
4. Results
4.1. Correlation between Landslides and Conditioning Factors
4.2. Multicollinearity Analysis of Landslide Conditioning Factors
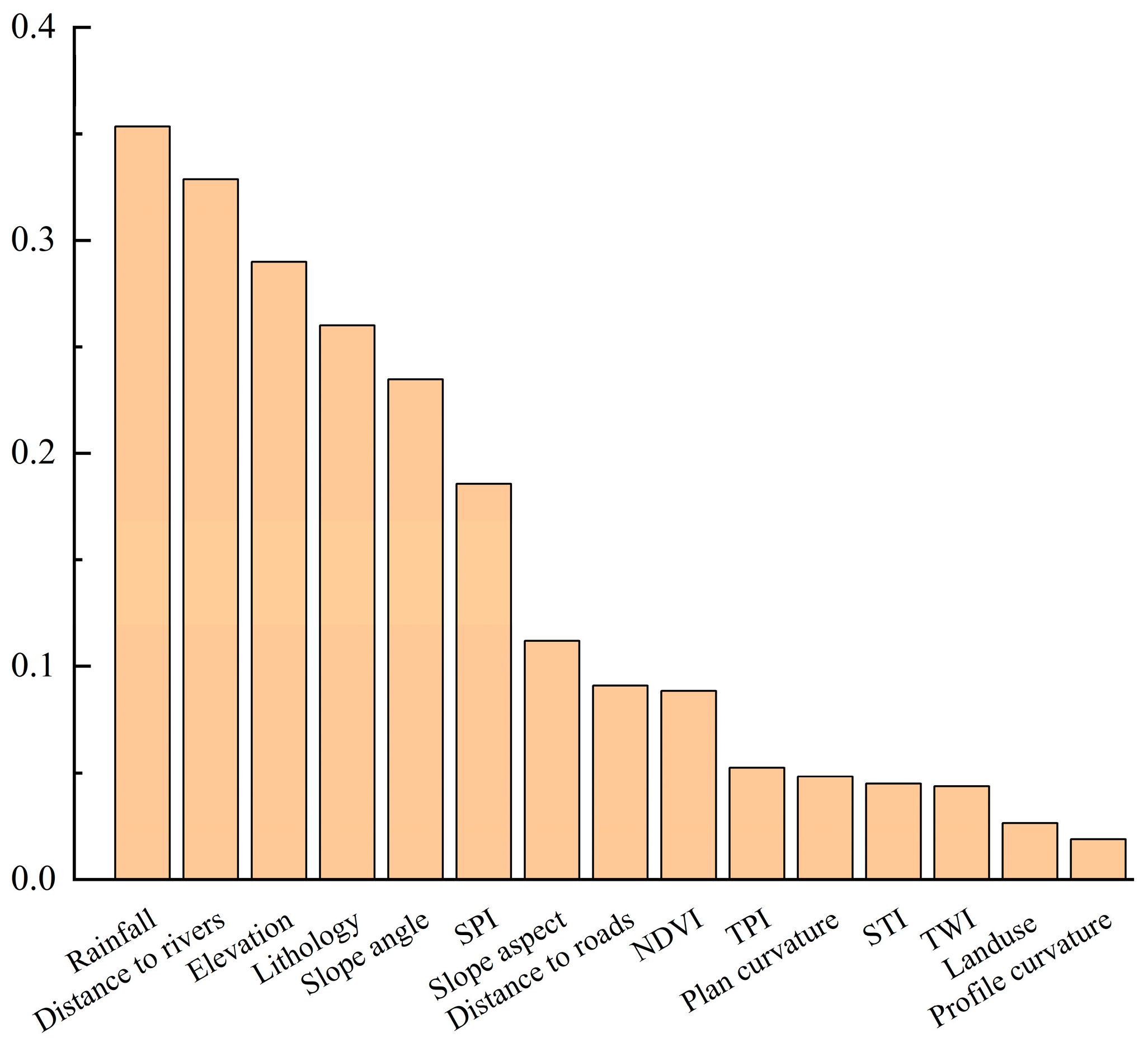
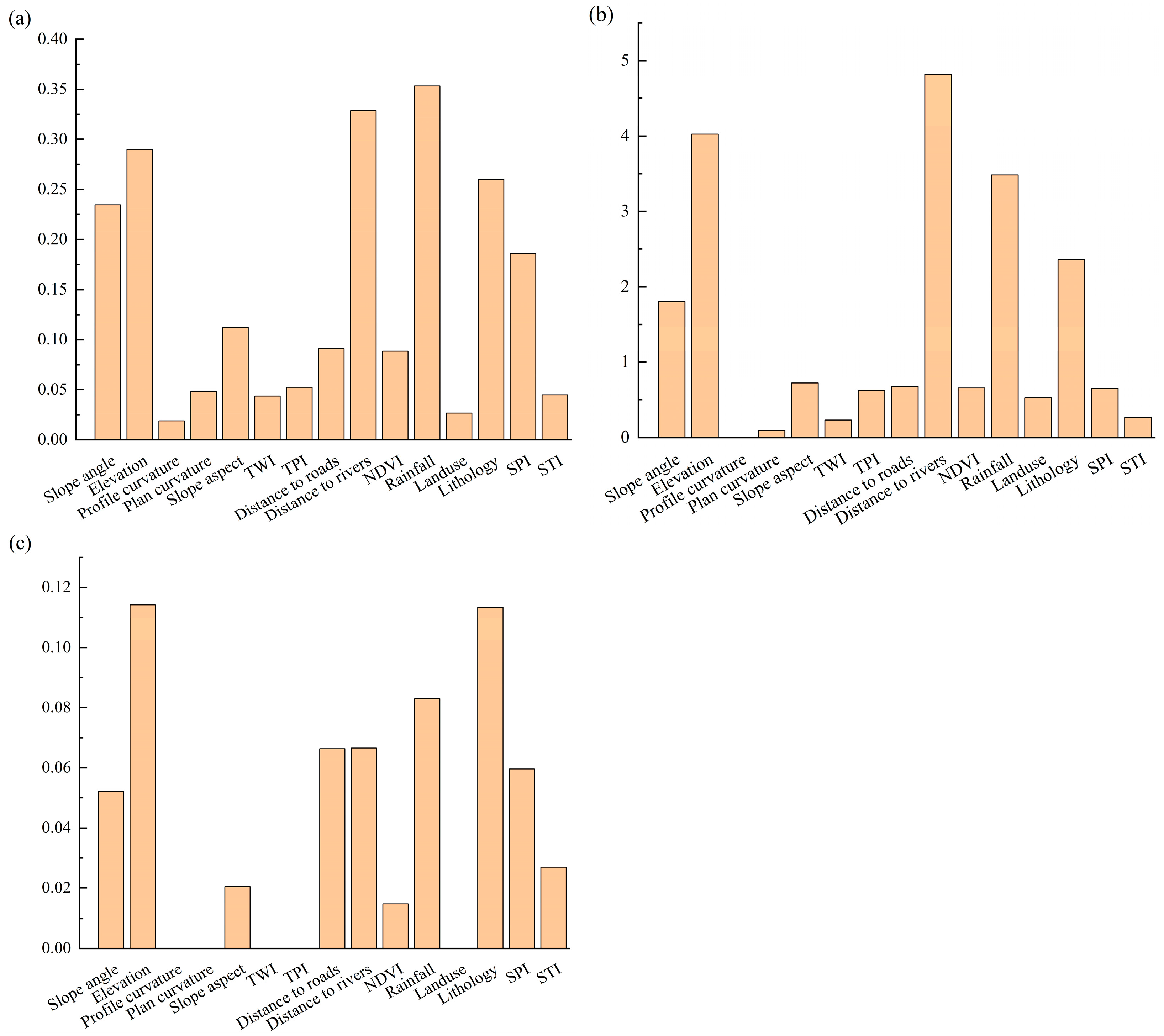
4.3. Contribution of Conditioning Factors
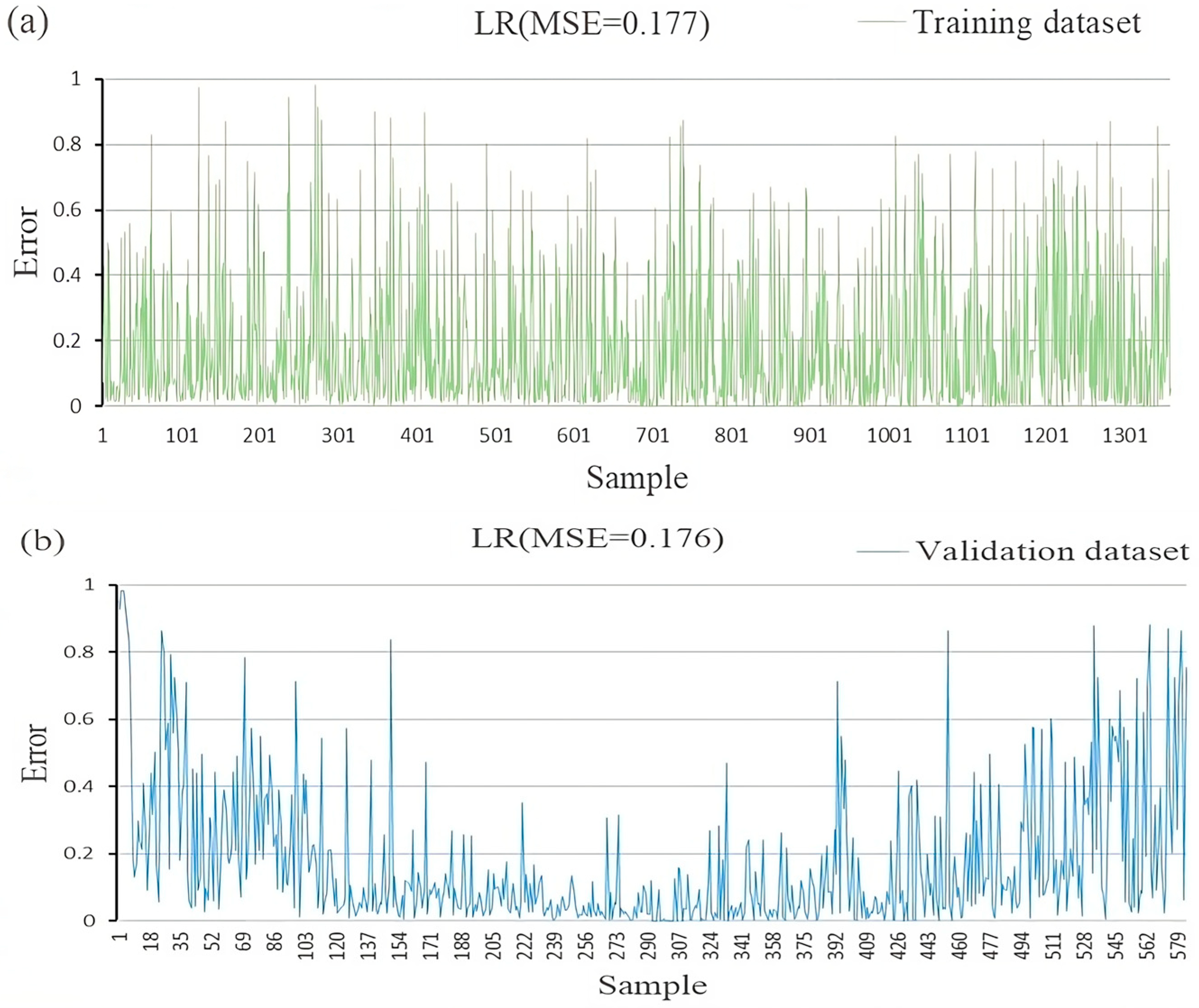
4.4. Application of LR Model
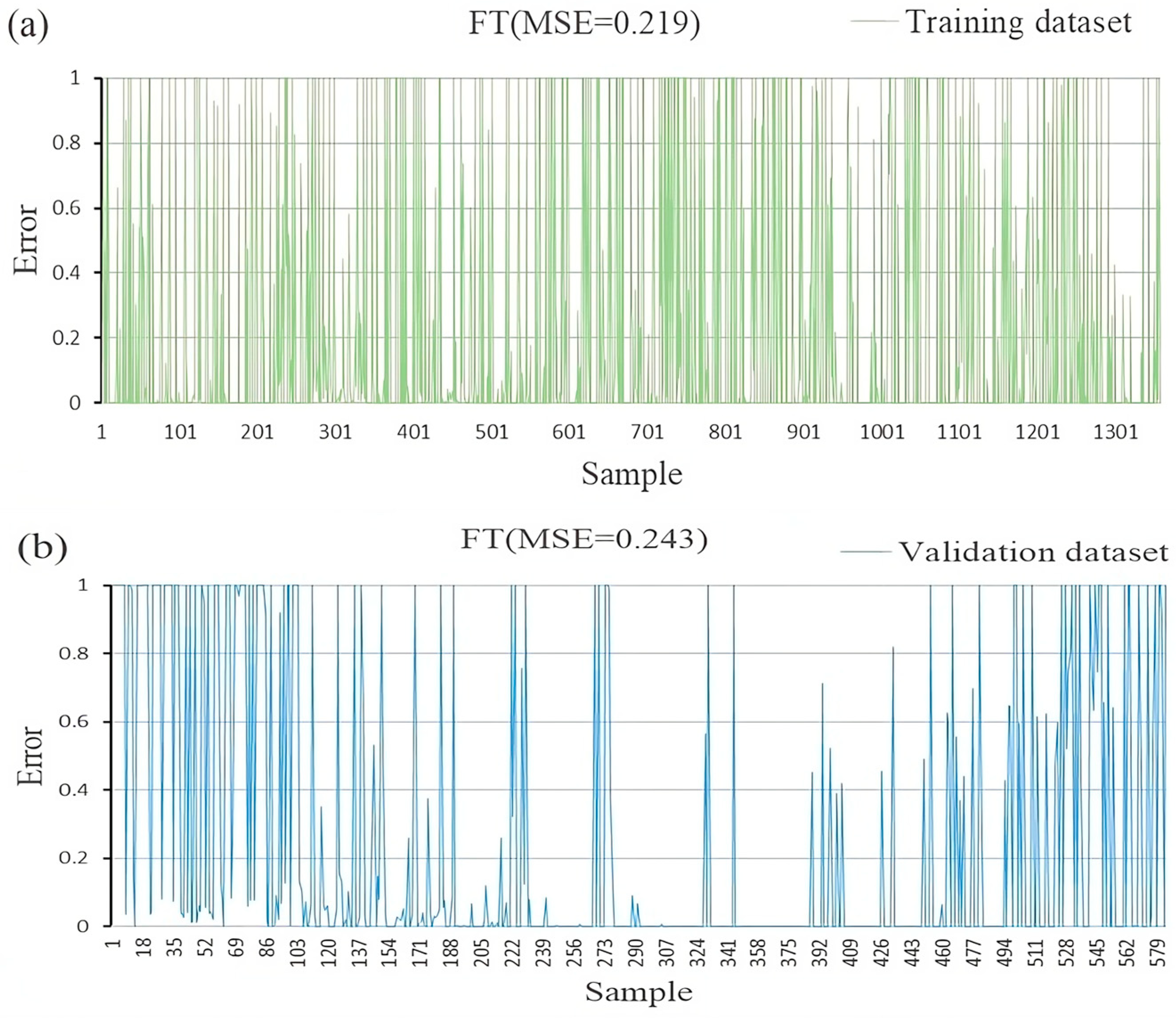
4.5. Application of FT Model
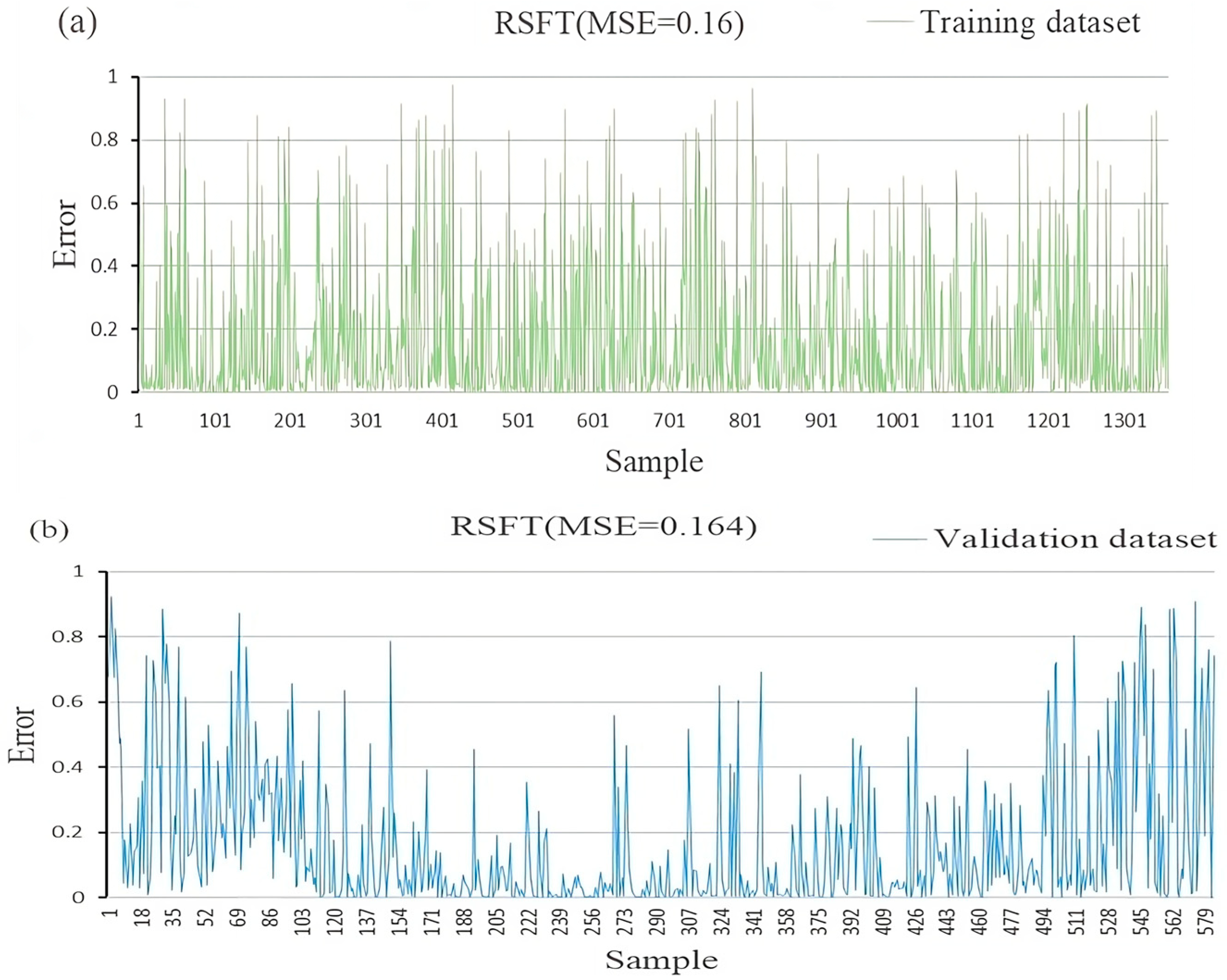
4.6. Application of RSFT Model
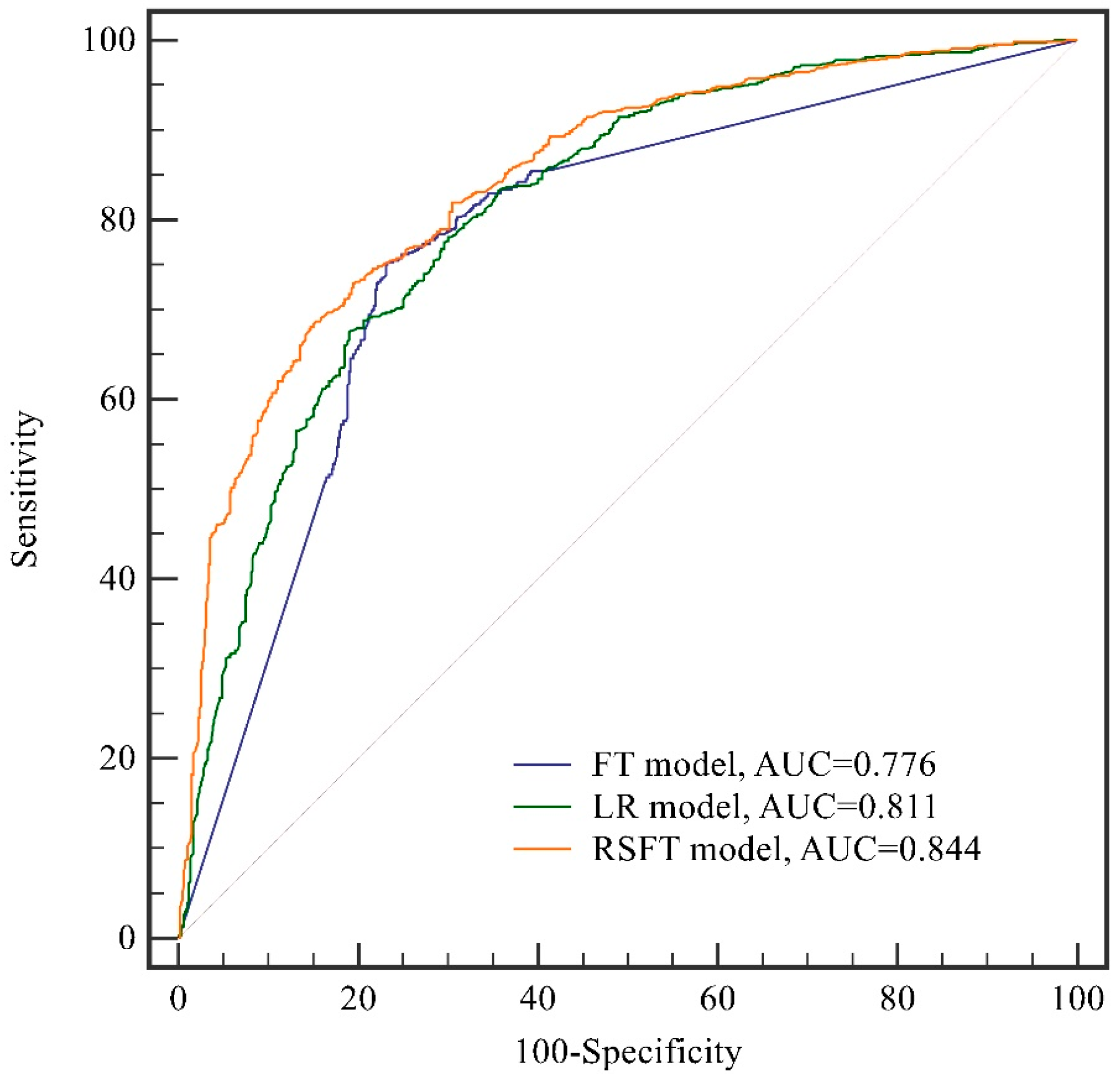
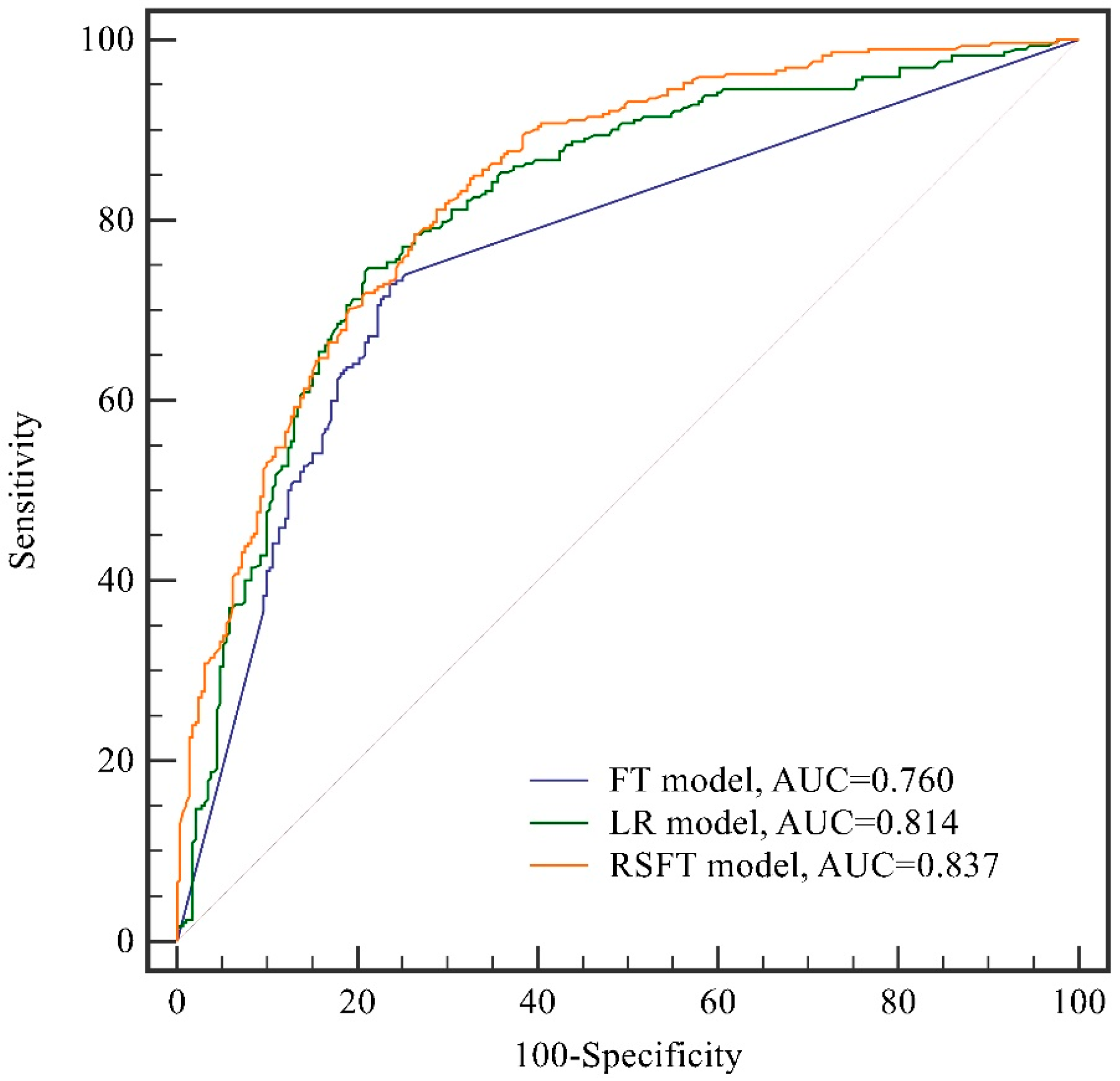
4.7. Validation and Comparison of Different Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive Bayes and RBFNetwork models for the Long County area (China). Bull. Eng. Geol. Environ. 2018, 78, 247–266. [Google Scholar] [CrossRef]
- Merghadi, A.; Abderrahmane, B.; Tien Bui, D. Landslide Susceptibility Assessment at Mila Basin (Algeria): A Comparative Assessment of Prediction Capability of Advanced Machine Learning Methods. ISPRS Int. J. Geo-Inf. 2018, 7, 268. [Google Scholar] [CrossRef]
- Peng, T.; Chen, Y.; Chen, W. Landslide Susceptibility Modeling Using Remote Sensing Data and Random SubSpace-Based Functional Tree Classifier. Remote Sens. 2022, 14, 4803. [Google Scholar] [CrossRef]
- Hong, H.; Chen, W.; Xu, C.; Youssef, A.M.; Pradhan, B.; Tien Bui, D. Rainfall-induced landslide susceptibility assessment at the Chongren area (China) using frequency ratio, certainty factor, and index of entropy. Geocarto Int. 2016, 6, 59. [Google Scholar] [CrossRef]
- Xiao, T.; Yin, K.; Yao, T.; Liu, S. Spatial prediction of landslide susceptibility using GIS-based statistical and machine learning models in Wanzhou County, Three Gorges Reservoir, China. Acta Geochim. 2019, 38, 654–669. [Google Scholar] [CrossRef]
- Clerici, A.; Perego, S.; Tellini, C.; Vescovi, P. A GIS-based automated procedure for landslide susceptibility mapping by the Conditional Analysis method: The Baganza valley case study (Italian Northern Apennines). Environ. Geol. 2006, 50, 941–961. [Google Scholar] [CrossRef]
- Pradhan, B. Manifestation of an advanced fuzzy logic model coupled with Geo-information techniques to landslide susceptibility mapping and their comparison with logistic regression modelling. Environ. Ecol. Stat. 2010, 18, 471–493. [Google Scholar] [CrossRef]
- Abedini, M.; Tulabi, S. Assessing LNRF, FR, and AHP models in landslide susceptibility mapping index: A comparative study of Nojian watershed in Lorestan province, Iran. Environ. Earth Sci. 2018, 77, 405. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H.; Ugawa, N. Landslide susceptibility mapping using GIS-based weighted linear combination, the case in Tsugawa area of Agano River, Niigata Prefecture, Japan. Landslides 2004, 1, 73–81. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Rajamanickam, G.V. Landslide Hazard and Risk Mapping Using the Weighted Linear Combination Model Applied to the Tevankarai Stream Watershed, Kodaikkanal, India. Hum. Ecol. Risk Assess. Int. J. 2014, 21, 1445–1461. [Google Scholar] [CrossRef]
- Tangestani, M.H. Landslide susceptibility mapping using the fuzzy gamma approach in a GIS, Kakan catchment area, southwest Iran. Aust. J. Earth Sci. 2004, 51, 439–450. [Google Scholar] [CrossRef]
- Park, H.J.; Lee, J.H.; Woo, I. Assessment of rainfall-induced shallow landslide susceptibility using a GIS-based probabilistic approach. Eng. Geol. 2013, 161, 1–15. [Google Scholar] [CrossRef]
- Ciurleo, M.; Cascini, L.; Calvello, M. A comparison of statistical and deterministic methods for shallow landslide susceptibility zoning in clayey soils. Eng. Geol. 2017, 223, 71–81. [Google Scholar] [CrossRef]
- Salciarini, D.; Godt, J.W.; Savage, W.Z.; Conversini, P.; Baum, R.L.; Michael, J.A. Modeling regional initiation of rainfall-induced shallow landslides in the eastern Umbria Region of central Italy. Landslides 2006, 3, 181–194. [Google Scholar] [CrossRef]
- Chen, W.; Fan, L.; Li, C.; Pham, B.T. Spatial Prediction of Landslides Using Hybrid Integration of Artificial Intelligence Algorithms with Frequency Ratio and Index of Entropy in Nanzheng County, China. Appl. Sci. 2019, 10, 29. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2006, 4, 33–41. [Google Scholar] [CrossRef]
- Mondal, S.; Maiti, R. Integrating the Analytical Hierarchy Process (AHP) and the frequency ratio (FR) model in landslide susceptibility mapping of Shiv-khola watershed, Darjeeling Himalaya. Int. J. Disaster Risk Sci. 2014, 4, 200–212. [Google Scholar] [CrossRef]
- Silalahi, F.E.S.; Pamela; Arifianti, Y.; Hidayat, F. Landslide susceptibility assessment using frequency ratio model in Bogor, West Java, Indonesia. Geosci. Lett. 2019, 6, 10. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y. Landslide susceptibility zonation using GIS and evidential belief function model. Arab. J. Geosci. 2016, 9, 697. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, S.; Ke, Y.; Yang, Z.; Zhao, H. Landslide susceptibility assessment using different slope units based on the evidential belief function model. Geocarto Int. 2019, 35, 1641–1664. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, F.; Chen, H.; Wu, Y.; Li, T.; Li, W.; Wang, Q.; Liu, P. GIS-based landslide susceptibility analysis using frequency ratio and evidential belief function models. Environ. Earth Sci. 2016, 75, 948. [Google Scholar] [CrossRef]
- Farooq, S.; Akram, M.S. Landslide susceptibility mapping using information value method in Jhelum Valley of the Himalayas. Arab. J. Geosci. 2021, 14, 824. [Google Scholar] [CrossRef]
- Alsabhan, A.H.; Singh, K.; Sharma, A.; Alam, S.; Pandey, D.D.; Rahman, S.A.S.; Khursheed, A.; Munshi, F.M. Landslide susceptibility assessment in the Himalayan range based along Kasauli–Parwanoo road corridor using weight of evidence, information value, and frequency ratio. J. King Saud Univ. Sci. 2022, 34, 101759. [Google Scholar] [CrossRef]
- Wubalem, A.; Meten, M. Landslide susceptibility mapping using information value and logistic regression models in Goncha Siso Eneses area, northwestern Ethiopia. SN Appl. Sci. 2020, 2, 807. [Google Scholar] [CrossRef]
- Bopche, L.; Rege, P.P. Landslide Susceptibility Mapping: An Integrated Approach using Geographic Information Value, Remote Sensing, and Weight of Evidence Method. Geotech. Geol. Eng. 2022, 40, 2935–2947. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Dai, F.; Xiao, J.; Tan, X.; Yuan, R. Landslide hazard mapping using GIS and weight of evidence model in Qingshui River watershed of 2008 Wenchuan earthquake struck region. J. Earth Sci. 2012, 23, 97–120. [Google Scholar] [CrossRef]
- Chen, W.; Sun, Z.; Han, J. Landslide Susceptibility Modeling Using Integrated Ensemble Weights of Evidence with Logistic Regression and Random Forest Models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2017, 9, 49–69. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C. Comparison and evaluation of landslide susceptibility maps obtained from weight of evidence, logistic regression, and artificial neural network models. Nat. Hazards 2018, 93, 249–274. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Zandi, D.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Al-Ansari, N.; Singh, S.K.; Dou, J.; Nguyen, H. Comparison of Support Vector Machine, Bayesian Logistic Regression, and Alternating Decision Tree Algorithms for Shallow Landslide Susceptibility Mapping along a Mountainous Road in the West of Iran. Appl. Sci. 2020, 10, 5047. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.; Panahi, M.; Hong, H.; et al. Landslide Detection and Susceptibility Mapping by AIRSAR Data Using Support Vector Machine and Index of Entropy Models in Cameron Highlands, Malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Sok, H.K.; Ooi, M.P.-L.; Kuang, Y.C. Sparse alternating decision tree. Pattern Recognit. Lett. 2015, 60, 57–64. [Google Scholar] [CrossRef]
- Sok, H.K.; Ooi, M.P.-L.; Kuang, Y.C.; Demidenko, S. Multivariate alternating decision trees. Pattern Recognit. 2016, 50, 195–209. [Google Scholar] [CrossRef]
- Lee, M.S.; Oh, S. Alternating decision tree algorithm for assessing protein interaction reliability. Vietnam J. Comput. Sci. 2014, 1, 169–178. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve Bayes tree classifiers for a landslide susceptibility assessment in Langao County, China. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. GIS-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, Naïve-Bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- Feng, X.; Li, S.; Yuan, C.; Zeng, P.; Sun, Y. Prediction of Slope Stability using Naive Bayes Classifier. KSCE J. Civ. Eng. 2018, 22, 941–950. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Pourghasemi, H.R.; Indra, P.; Dholakia, M.B. Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2015, 128, 255–273. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. Efficient approximate leave-one-out cross-validation for kernel logistic regression. Mach. Learn. 2008, 71, 243–264. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2018, 78, 4397–4419. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide Susceptibility Modeling Based on GIS and Novel Bagging-Based Kernel Logistic Regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Hu, X.; Huang, C.; Mei, H.; Zhang, H. Landslide susceptibility mapping using an ensemble model of Bagging scheme and random subspace–based naïve Bayes tree in Zigui County of the Three Gorges Reservoir Area, China. Bull. Eng. Geol. Environ. 2021, 80, 5315–5329. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2015, 13, 361–378. [Google Scholar] [CrossRef]
- Hai, L.; Mu, C.; Xu, Q.; Sun, Y.; Fan, H.; Xie, X.; Wei, X.; Mei, C.; Yu, H.; Manger, W.; et al. The Sequence Stratigraphic Division and Depositional Environment of the Jurassic Yan’an Formation in the Pengyang Area, Southwestern Margin of the Ordos Basin, China. Energies 2022, 15, 5310. [Google Scholar] [CrossRef]
- Mao, Z.; Shi, S.; Li, H.; Zhong, J.; Sun, J. Landslide susceptibility assessment using triangular fuzzy number-analytic hierarchy processing (TFN-AHP), contributing weight (CW) and random forest weighted frequency ratio (RF weighted FR) at the Pengyang county, Northwest China. Environ. Earth Sci. 2022, 81, 86. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Hoang, N.-D.; Thanh, N.Q.; Nguyen, D.B.; Van Liem, N.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2016, 14, 447–458. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S.; et al. Spatial Prediction of Landslide Susceptibility Using GIS-Based Data Mining Techniques of ANFIS with Whale Optimization Algorithm (WOA) and Grey Wolf Optimizer (GWO). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X.; Peng, J.; Panahi, M.; Lee, S. Landslide susceptibility modeling based on ANFIS with teaching-learning-based optimization and Satin bowerbird optimizer. Geosci. Front. 2021, 12, 93–107. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Asl, D.T.; Ahmad, B.B.; Quoc, N.K.; Lee, S. Landslide Susceptibility Assessment by Novel Hybrid Machine Learning Algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef]
- Lee, S.; Lee, M.-J.; Jung, H.-S.; Lee, S. Landslide susceptibility mapping using Naïve Bayes and Bayesian network models in Umyeonsan, Korea. Geocarto Int. 2019, 35, 1665–1679. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Pham, H.V.; Le, H.Q.; Prakash, I.; Dholakia, M.B. Landslide Hazard Assessment Using Random SubSpace Fuzzy Rules Based Classifier Ensemble and Probability Analysis of Rainfall Data: A Case Study at Mu Cang Chai District, Yen Bai Province (Viet Nam). J. Indian Soc. Remote Sens. 2016, 45, 673–683. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2013, 73, 209–263. [Google Scholar] [CrossRef]
- Zhu, A.X.; Wang, R.; Qiao, J.; Qin, C.-Z.; Chen, Y.; Liu, J.; Du, F.; Lin, Y.; Zhu, T. An expert knowledge-based approach to landslide susceptibility mapping using GIS and fuzzy logic. Geomorphology 2014, 214, 128–138. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.T. Evaluation of a combined spatial multi-criteria evaluation model and deterministic model for landslide susceptibility mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Chatterjee, D.; Murali Krishna, A. Effect of Slope Angle on the Stability of a Slope Under Rainfall Infiltration. Indian Geotech. J. 2019, 49, 708–717. [Google Scholar] [CrossRef]
- Katz, O.; Morgan, J.K.; Aharonov, E.; Dugan, B. Controls on the size and geometry of landslides: Insights from discrete element numerical simulations. Geomorphology 2014, 220, 104–113. [Google Scholar] [CrossRef]
- Tran, T.-H.; Dam, N.D.; Jalal, F.E.; Al-Ansari, N.; Ho, L.S.; Phong, T.V.; Iqbal, M.; Le, H.V.; Nguyen, H.B.T.; Prakash, I.; et al. GIS-Based Soft Computing Models for Landslide Susceptibility Mapping: A Case Study of Pithoragarh District, Uttarakhand State, India. Math. Probl. Eng. 2021, 2021, 9914650. [Google Scholar] [CrossRef]
- Wang, L.-J.; Sawada, K.; Moriguchi, S. Landslide-susceptibility analysis using light detection and ranging-derived digital elevation models and logistic regression models: A case study in Mizunami City, Japan. J. Appl. Remote Sens. 2013, 7, 3561. [Google Scholar] [CrossRef]
- Correa-Muñoz, N.A.; Murillo-Feo, C.A.; Martínez-Martínez, L.J. The potential of PALSAR RTC elevation data for landform semi-automatic detection and landslide susceptibility modeling. Eur. J. Remote Sens. 2018, 52, 148–159. [Google Scholar] [CrossRef]
- Zhou, G.; Yan, H.; Chen, K.; Zhang, R. Spatial analysis for susceptibility of second-time karst sinkholes: A case study of Jili Village in Guangxi, China. Comput. Geosci. 2016, 89, 144–160. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Loupasakis, C.; Wang, Y. Introducing a novel multi-layer perceptron network based on stochastic gradient descent optimized by a meta-heuristic algorithm for landslide susceptibility mapping. Sci. Total Environ. 2020, 742, 140549. [Google Scholar] [CrossRef]
- Nseka, D.; Kakembo, V.; Bamutaze, Y.; Mugagga, F. Analysis of topographic parameters underpinning landslide occurrence in Kigezi highlands of southwestern Uganda. Nat. Hazards 2019, 99, 973–989. [Google Scholar] [CrossRef]
- Wang, G.; Lei, X.; Chen, W.; Shahabi, H.; Shirzadi, A. Hybrid Computational Intelligence Methods for Landslide Susceptibility Mapping. Symmetry 2020, 12, 325. [Google Scholar] [CrossRef]
- Abdollahi, S.; Pourghasemi, H.R.; Ghanbarian, G.A.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2018, 78, 4017–4034. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Z. Quantitative Assessment of Landslide Susceptibility Comparing Statistical Index, Index of Entropy, and Weights of Evidence in the Shangnan Area, China. Entropy 2018, 20, 868. [Google Scholar] [CrossRef] [PubMed]
- Glass, R.J.; Nicholl, M.J.; Yarrington, L. A modified invasion percolation model for low-capillary number immiscible displacements in horizontal rough-walled fractures: Influence of local in-plane curvature. Water Resour. Res. 1998, 34, 3215–3234. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater Spring Potential Mapping Using Artificial Intelligence Approach Based on Kernel Logistic Regression, Random Forest, and Alternating Decision Tree Models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Geertsema, M.; Omidvar, E.; Clague, J.; Thai Pham, B.; Dou, J.; Talebpour Asl, D.; Bin Ahmad, B.; et al. New Ensemble Models for Shallow Landslide Susceptibility Modeling in a Semi-Arid Watershed. Forests 2019, 10, 743. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. GIS-based landslide susceptibility assessment using optimized hybrid machine learning methods. Catena 2021, 196, 104833. [Google Scholar] [CrossRef]
- Rosi, A.; Tofani, V.; Tanteri, L.; Tacconi Stefanelli, C.; Agostini, A.; Catani, F.; Casagli, N. The new landslide inventory of Tuscany (Italy) updated with PS-InSAR: Geomorphological features and landslide distribution. Landslides 2017, 15, 5–19. [Google Scholar] [CrossRef]
- Hu, S.; Ma, J.; Shugart, H.H.; Yan, X. Evaluating the impacts of slope aspect on forest dynamic succession in Northwest China based on FAREAST model. Environ. Res. Lett. 2018, 13, 034027. [Google Scholar] [CrossRef]
- Nattino, G.; Pennell, M.L.; Lemeshow, S. Rejoinder to “Assessing the goodness of fit of logistic regression models in large samples: A modification of the Hosmer-Lemeshow test”. Biometrics 2020, 76, 575–577. [Google Scholar] [CrossRef]
- Shano, L.; Raghuvanshi, T.K.; Meten, M. Landslide Hazard Zonation using Logistic Regression Model: The Case of Shafe and Baso Catchments, Gamo Highland, Southern Ethiopia. Geotech. Geol. Eng. 2021, 40, 83–101. [Google Scholar] [CrossRef]
- Qiu, H.; Regmi, A.D.; Cui, P.; Hu, S.; Wang, Y.; He, Y. Slope aspect effects of loess slides and its spatial differentiation in different geomorphologic types. Arab. J. Geosci. 2017, 10, 344. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Meng, T.; Liu, Y. Susceptibility mapping of damming landslide based on slope unit using frequency ratio model. Arab. J. Geosci. 2020, 13, 790. [Google Scholar] [CrossRef]
- El Jazouli, A.; Barakat, A.; Khellouk, R. GIS-multicriteria evaluation using AHP for landslide susceptibility mapping in Oum Er Rbia high basin (Morocco). Geoenviron. Disasters 2019, 6, 3. [Google Scholar] [CrossRef]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P.; et al. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, C.-W. Assessment of Landslide Susceptibility Using Statistical- and Artificial Intelligence-based FR–RF Integrated Model and Multiresolution DEMs. Remote Sens. 2019, 11, 999. [Google Scholar] [CrossRef]
- Raja, N.B.; Çiçek, I.; Türkoğlu, N.; Aydin, O.; Kawasaki, A. Landslide susceptibility mapping of the Sera River Basin using logistic regression model. Nat. Hazards 2016, 85, 1323–1346. [Google Scholar] [CrossRef]
- Ahmed, M.F.; Rogers, J.D.; Ismail, E.H. A regional level preliminary landslide susceptibility study of the upper Indus river basin. Eur. J. Remote Sens. 2017, 47, 343–373. [Google Scholar] [CrossRef]
- Sudarman, I.G.; Ahmad, A. Mapping of landslide-prone areas in the Lisu river basin Barru Regency based on binary logistic regression. IOP Conf. Ser. Earth Environ. Sci. 2021, 807, 022081. [Google Scholar] [CrossRef]
- Jin, G.; Wang, Y.; Wu, W.; Guo, T.; Xu, J. Distribution features of landslides in the Yalong River Basin, Southwest China. Environ. Earth Sci. 2021, 80, 285. [Google Scholar] [CrossRef]
- Mandal, S.; Mandal, K. Modeling and mapping landslide susceptibility zones using GIS based multivariate binary logistic regression (LR) model in the Rorachu river basin of eastern Sikkim Himalaya, India. Model. Earth Syst. Environ. 2018, 4, 69–88. [Google Scholar] [CrossRef]
- Dahigamuwa, T.; Yu, Q.; Gunaratne, M. Feasibility Study of Land Cover Classification Based on Normalized Difference Vegetation Index for Landslide Risk Assessment. Geosciences 2016, 6, 45. [Google Scholar] [CrossRef]
- Sahana, M.; Pham, B.T.; Shukla, M.; Costache, R.; Thu, D.X.; Chakrabortty, R.; Satyam, N.; Nguyen, H.D.; Phong, T.V.; Le, H.V.; et al. Rainfall induced landslide susceptibility mapping using novel hybrid soft computing methods based on multi-layer perceptron neural network classifier. Geocarto Int. 2020, 37, 2747–2771. [Google Scholar] [CrossRef]
- Medina, V.; Hürlimann, M.; Guo, Z.; Lloret, A.; Vaunat, J. Fast physically-based model for rainfall-induced landslide susceptibility assessment at regional scale. Catena 2021, 201, 105213. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Lee, S.-R.; Kim, Y.-T. A shallow slide prediction model combining rainfall threshold warnings and shallow slide susceptibility in Busan, Korea. Landslides 2018, 16, 647–659. [Google Scholar] [CrossRef]
- Zorgati, A.; Gallala, W.; Haddji, R.; Biswajeet, P.; Gaied, M. Essghaier Effects of clay properties in the landslides Genesis in flysch massif: Case study of Aïn Draham, North western Tunisia. Afr. Earth Sci. 2018, 12, 5. [Google Scholar] [CrossRef]
- López, P.; Qüense, J.; Henríquez, C.; Martínez, C. Applicability of spatial prediction models for landslide susceptibility in land-use zoning instruments: A guideline in a coastal settlement in South-Central Chile. Geocarto Int. 2021, 37, 6474–6493. [Google Scholar] [CrossRef]
- Meneses, B.M.; Pereira, S.; Reis, E. Effects of different land use and land cover data on the landslide susceptibility zonation of road networks. Nat. Hazards Earth Syst. Sci. 2019, 19, 471–487. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Chakrabortty, R.; Malik, S.; Das, B.; Roy, P.; Sen, K. Spatial prediction of landslide susceptibility using projected storm rainfall and land use in Himalayan region. Bull. Eng. Geol. Environ. 2021, 80, 5237–5258. [Google Scholar] [CrossRef]
- Tavoularis, N.; Papathanassiou, G.; Ganas, A.; Argyrakis, P. Development of the Landslide Susceptibility Map of Attica Region, Greece, Based on the Method of Rock Engineering System. Land 2021, 10, 148. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, K.; Song, Y.; Jiang, W.; Zhou, J. Study on landslide susceptibility mapping based on rock-soil characteristic factors. Sci. Rep. 2021, 11, 15476. [Google Scholar] [CrossRef]
- Zhao, B.; Zhu, J.; Hu, Y.; Liu, Q.; Liu, Y.; Loupasakis, C. Mapping Landslide Sensitivity Based on Machine Learning: A Case Study in Ankang City, Shaanxi Province, China. Geofluids 2022, 2022, 2058442. [Google Scholar] [CrossRef]
- Moayedi, H.; Dehrashid, A.A. A new combined approach of neural-metaheuristic algorithms for predicting and appraisal of landslide susceptibility mapping. Environ. Sci. Pollut. Res. 2023, 30, 82964–82989. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Sarkar, A.; Kundu, P.; Paul, S.; Chandra Sarkar, B. An ensemble of evidence belief function (EBF) with frequency ratio (FR) using geospatial data for landslide prediction in Darjeeling Himalayan region of India. Quat. Sci. Adv. 2023, 11, 100092. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Dehrashid, A.A.; Zhang, B.; Chen, Z.; Le, B.N.; Moayedi, H. A novel swarm intelligence: Cuckoo optimization algorithm (COA) and SailFish optimizer (SFO) in landslide susceptibility assessment. Stoch. Environ. Res. Risk Assess. 2023, 37, 1717–1743. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2012, 65, 135–165. [Google Scholar] [CrossRef]
- Fan, W.; Wei, X.; Cao, Y.; Zheng, B. Landslide susceptibility assessment using the certainty factor and analytic hierarchy process. J. Mt. Sci. 2017, 14, 906–925. [Google Scholar] [CrossRef]
- Jennifer, J.J.; Saravanan, S.; Abijith, D. Application of Frequency Ratio and Logistic Regression Model in the Assessment of Landslide Susceptibility Mapping for Nilgiris District, Tamilnadu, India. Indian Geotech. J. 2021, 51, 773–787. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Sridhar, V. Landslide Susceptibility Analysis: A Logistic Regression Model Case Study in Coonoor, India. Hydrology 2021, 8, 41. [Google Scholar] [CrossRef]
- Huangfu, W.; Wu, W.; Zhou, X.; Lin, Z.; Zhang, G.; Chen, R.; Song, Y.; Lang, T.; Qin, Y.; Ou, P.; et al. Landslide Geo-Hazard Risk Mapping Using Logistic Regression Modeling in Guixi, Jiangxi, China. Sustainability 2021, 13, 4830. [Google Scholar] [CrossRef]
- Tang, R.-X.; Yan, E.C.; Wen, T.; Yin, X.-M.; Tang, W. Comparison of Logistic Regression, Information Value, and Comprehensive Evaluating Model for Landslide Susceptibility Mapping. Sustainability 2021, 13, 3803. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Han, J.; Li, X.; Zhang, H.; Wang, H. Assessment of Landslide Susceptibility Using Integrated Ensemble Fractal Dimension with Kernel Logistic Regression Model. Entropy 2019, 21, 218. [Google Scholar] [CrossRef] [PubMed]
- Gu, T.; Li, J.; Wang, M.; Duan, P. Landslide susceptibility assessment in Zhenxiong County of China based on geographically weighted logistic regression model. Geocarto Int. 2021, 37, 4952–4973. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Chen, W.; Roy, J.; Pradhan, B.; Bui, D.T. Flash flood susceptibility modelling using functional tree and hybrid ensemble techniques. J. Hydrol. 2020, 587, 125007. [Google Scholar] [CrossRef]
- Mosavi, A.; Shirzadi, A.; Choubin, B.; Taromideh, F.; Hosseini, F.S.; Borji, M.; Shahabi, H.; Salvati, A.; Dineva, A.A. Towards an Ensemble Machine Learning Model of Random Subspace Based Functional Tree Classifier for Snow Avalanche Susceptibility Mapping. IEEE Access 2020, 8, 145968–145983. [Google Scholar] [CrossRef]
- Zhang, T.; Fu, Q.; Wang, H.; Liu, F.; Wang, H.; Han, L. Bagging-based machine learning algorithms for landslide susceptibility modeling. Nat. Hazards 2021, 110, 823–846. [Google Scholar] [CrossRef]
- Phong, T.V.; Pham, B.T.; Trinh, P.T.; Ly, H.B.; Vu, Q.H.; Ho, L.S.; Le, H.V.; Phong, L.H.; Avand, M.; Prakash, I. Groundwater Potential Mapping Using GIS-Based Hybrid Artificial Intelligence Methods. Ground Water 2021, 59, 745–760. [Google Scholar] [CrossRef]
- Tien Bui, D.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar] [CrossRef]
- Kotsiantis, S. Combining bagging, boosting, rotation forest and random subspace methods. Artif. Intell. Rev. 2010, 35, 223–240. [Google Scholar] [CrossRef]
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. The Use of Geographically Weighted Regression for Spatial Prediction: An Evaluation of Models Using Simulated Data Sets. Math. Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]
- Wang, X.; Tang, X. Random Sampling for Subspace Face Recognition. Int. J. Comput. Vis. 2006, 70, 91–104. [Google Scholar] [CrossRef]
- Vinayagam, A.; Othman, M.L.; Veerasamy, V.; Saravan Balaji, S.; Ramaiyan, K.; Radhakrishnan, P.; Raman, M.D.; Abdul Wahab, N.I. A random subspace ensemble classification model for discrimination of power quality events in solar PV microgrid power network. PLoS ONE 2022, 17, e0262570. [Google Scholar] [CrossRef] [PubMed]
- Nhu, V.-H.; Thi Ngo, P.-T.; Pham, T.D.; Dou, J.; Song, X.; Hoang, N.-D.; Tran, D.A.; Cao, D.P.; Aydilek, İ.B.; Amiri, M.; et al. A New Hybrid Firefly–PSO Optimized Random Subspace Tree Intelligence for Torrential Rainfall-Induced Flash Flood Susceptible Mapping. Remote Sens. 2020, 12, 2688. [Google Scholar] [CrossRef]
- Chen, X.; Powell, A.M. Randomized Subspace Actions and Fusion Frames. Constr. Approx. 2015, 43, 103–134. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, W.; Zheng, H. Combining the wisdom of crowds and technical analysis for financial market prediction using deep random subspace ensembles. Neurocomputing 2018, 299, 51–61. [Google Scholar] [CrossRef]
- Luo, X.; Lin, F.; Chen, Y.; Zhu, S.; Xu, Z.; Huo, Z.; Yu, M.; Peng, J. Coupling logistic model tree and random subspace to predict the landslide susceptibility areas with considering the uncertainty of environmental features. Sci. Rep. 2019, 9, 15369. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Liu, C.; Scaioni, M.; Sun, W.; Chen, Y.; Yao, D.; Chen, S.; Hong, Y.; Zhang, K.; Cheng, G. Spatio-temporal analysis and simulation on shallow rainfall-induced landslides in China using landslide susceptibility dynamics and rainfall I-D thresholds. Sci. China Earth Sci. 2017, 60, 720–732. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. GIS-Based Evaluation of Landslide Susceptibility Models Using Certainty Factors and Functional Trees-Based Ensemble Techniques. Appl. Sci. 2019, 10, 16. [Google Scholar] [CrossRef]
- Gao, J.; Shi, X.; Li, L.; Zhou, Z.; Wang, J. Assessment of Landslide Susceptibility Using Different Machine Learning Methods in Longnan City, China. Sustainability 2022, 14, 16716. [Google Scholar] [CrossRef]
- Razavi-Termeh, S.V.; Shirani, K.; Pasandi, M. Mapping of landslide susceptibility using the combination of neuro-fuzzy inference system (ANFIS), ant colony (ANFIS-ACOR), and differential evolution (ANFIS-DE) models. Bull. Eng. Geol. Environ. 2021, 80, 2045–2067. [Google Scholar] [CrossRef]
- Liu, Z.; Gilbert, G.; Cepeda, J.M.; Lysdahl, A.O.K.; Piciullo, L.; Hefre, H.; Lacasse, S. Modelling of shallow landslides with machine learning algorithms. Geosci. Front. 2021, 12, 385–393. [Google Scholar] [CrossRef]



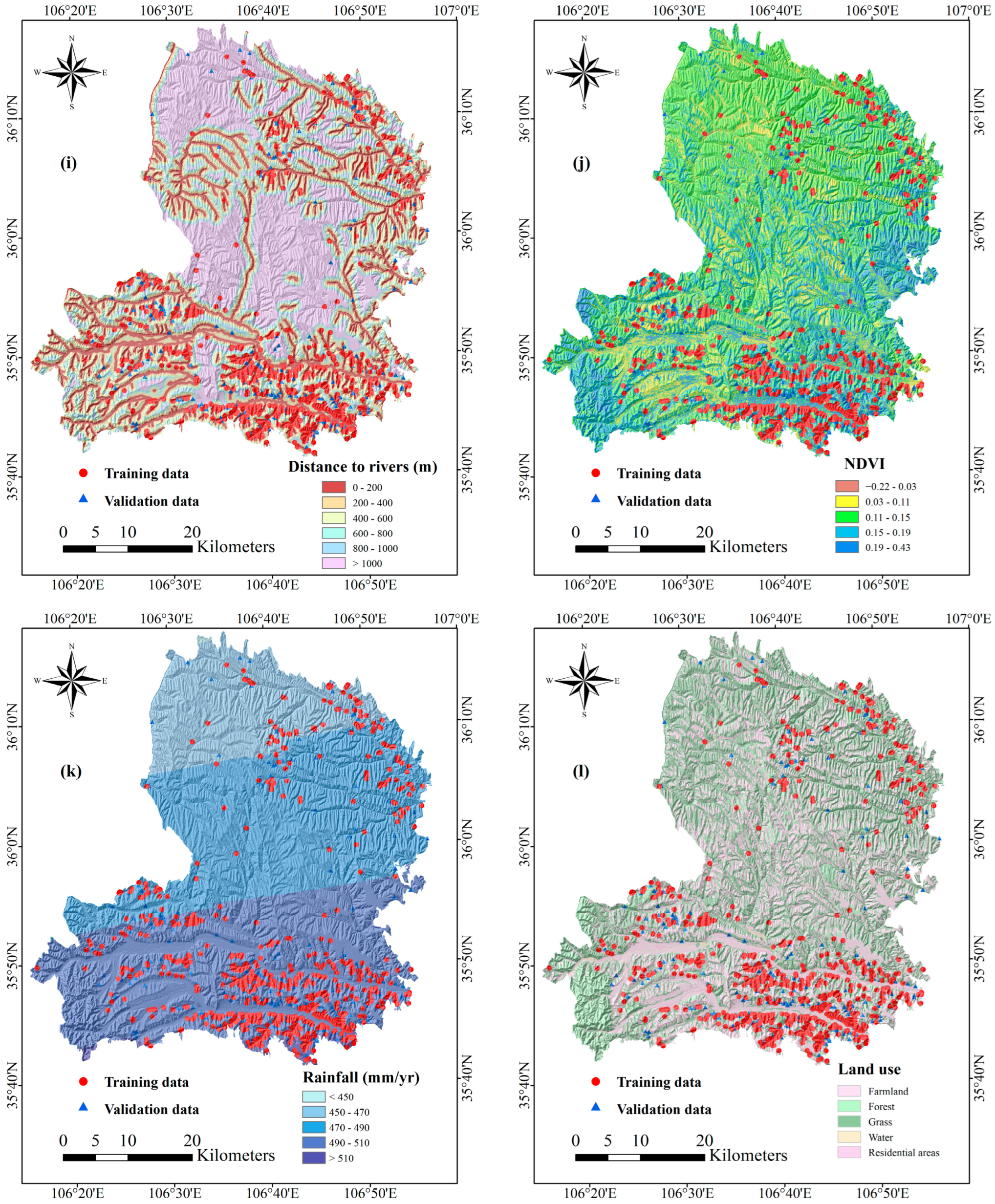

| Conditioning Factors | Class | Pixels | Landslides Pixels | CF | |
|---|---|---|---|---|---|
| Slope angle (°) | 0–10 | 1,233,976 | 9539 | 0.0077 | −0.472 |
| 10–20 | 1,884,829 | 31,370 | 0.0166 | 0.128 | |
| 20–30 | 808,346 | 16,669 | 0.0206 | 0.299 | |
| 30–40 | 121,503 | 1454 | 0.0120 | −0.180 | |
| 40–50 | 6305 | 0 | 0.0000 | −0.98 | |
| 50–60 | 221 | 0 | 0.0000 | −1 | |
| >60 | 8 | 0 | 0.0000 | −1 | |
| Elevation (m) | <1300 | 6481 | 1 | 0.0002 | −0.985 |
| 1300–1500 | 666,680 | 16,643 | 0.0250 | 0.423 | |
| 1500–1700 | 2,225,730 | 33,370 | 0.0150 | 0.030 | |
| 1700–1900 | 977,391 | 8945 | 0.0092 | −0.374 | |
| 1900–2100 | 121,612 | 73 | 0.0006 | −0.959 | |
| 2100–2300 | 46,744 | 0 | 0.0000 | −1 | |
| >2300 | 11,320 | 0 | 0.0000 | −1 | |
| Profile curvature | −11.54–−1.08 | 197,001 | 1592 | 0.0081 | −0.448 |
| −1.08–−0.43 | 913,652 | 10,276 | 0.0112 | −0.230 | |
| −0.43–0.22 | 1,587,299 | 30,351 | 0.0191 | 0.243 | |
| 0.22–0.95 | 1,085,198 | 13,861 | 0.0128 | −0.124 | |
| 0.95–9.14 | 272,807 | 2951 | 0.0108 | −0.259 | |
| Plan curvature | −5.3–−0.98 | 194,476 | 2913 | 0.0150 | 0.029 |
| −0.98–−0.37 | 896,797 | 15,324 | 0.0171 | 0.151 | |
| −0.37–0.25 | 1,684,370 | 24,543 | 0.0146 | 0.001 | |
| 0.25–0.91 | 1,041,768 | 11,731 | 0.0113 | −0.229 | |
| 0.91–7.68 | 238,546 | 4520 | 0.0189 | 0.236 | |
| Slope aspect | F | 28,771 | 0 | 0.0000 | −1 |
| N | 214,182 | 2853 | 0.0133 | 0.214 | |
| NE | 582,880 | 6117 | 0.0105 | −0.282 | |
| E | 729,709 | 5268 | 0.0072 | −0.508 | |
| SE | 420,997 | 2582 | 0.0061 | −0.582 | |
| S | 387,178 | 8034 | 0.0208 | 0.303 | |
| SW | 467,527 | 6471 | 0.0138 | −0.49 | |
| W | 618,183 | 12,621 | 0.0204 | 0.292 | |
| NW | 455,474 | 9785 | 0.0215 | 0.327 | |
| N | 150,287 | 5301 | 0.0353 | 0.596 | |
| TWI | 2.21–6 | 2,328,468 | 35,112 | 0.0151 | 0.036 |
| 6–10 | 1,451,293 | 21,950 | 0.0151 | 0.039 | |
| 10–14 | 201,447 | 1709 | 0.0085 | −0.420 | |
| 14–18 | 55,808 | 129 | 0.0023 | −0.842 | |
| >18 | 18,942 | 131 | 0.0069 | −0.529 | |
| TPI | −34.64–−7.04 | 324,193 | 4526 | 0.0140 | −0.041 |
| −7.04–−2.2 | 899,770 | 10,850 | 0.0121 | −0.173 | |
| −2.2–1.78 | 1,438,547 | 21,517 | 0.0150 | 0.028 | |
| 1.78–6.34 | 997,182 | 14,002 | 0.0140 | −0.035 | |
| 6.34–37.93 | 396,266 | 8137 | 0.0205 | 0.296 | |
| Distance to roads (m) | 0–100 | 232,634 | 2893 | 0.0124 | −0.147 |
| 100–200 | 207,063 | 10,041 | 0.0485 | 0.710 | |
| 200–300 | 195,015 | 13,289 | 0.0681 | 0.798 | |
| 300–400 | 189,552 | 10,407 | 0.0549 | 0.746 | |
| 400–500 | 179,935 | 5074 | 0.0282 | 0.491 | |
| Distance to rivers (m) | 0–200 | 899,311 | 4349 | 0.0048 | −0.671 |
| 200–400 | 767,341 | 4570 | 0.0060 | −0.594 | |
| 400–600 | 600,724 | 4300 | 0.0072 | −0.512 | |
| 600–800 | 426,497 | 4860 | 0.0114 | −0.219 | |
| 800–1000 | 271,523 | 4276 | 0.0157 | 0.077 | |
| >1000 | 1,078,500 | 36,676 | 0.0340 | 0.581 | |
| NDVI | <0.03 | 6732 | 0 | 0.0000 | −1 |
| 0.03–0.11 | 573,462 | 5068 | 0.0088 | −0.396 | |
| 0.11–0.15 | 2,027,374 | 26,021 | 0.0128 | −0.119 | |
| 0.15–0.19 | 1,180,464 | 23,438 | 0.0199 | 0.271 | |
| 0.19–0.43 | 255,862 | 4506 | 0.0176 | 0.176 | |
| Rainfall (mm/yr) | <450 | 3007 | 0 | 0.0000 | −1 |
| 450–470 | 718,693 | 724 | 0.0010 | −0.932 | |
| 470–490 | 1,544,756 | 8802 | 0.0057 | −0.612 | |
| 490–510 | 1,714,702 | 46,595 | 0.0272 | 0.471 | |
| >510 | 62,471 | 2911 | 0.0466 | 0.698 | |
| Land use | farmland | 1,675,029 | 29,433 | 0.0176 | 0.175 |
| forest | 215,769 | 1698 | 0.0079 | −0.463 | |
| grass | 2,114,613 | 27,901 | 0.0132 | −0.094 | |
| water | 18,869 | 0 | 0.0000 | −1 | |
| residentialareas | 20,311 | 0 | 0.0000 | −1 | |
| Lithology | 1 | 223,561 | 2 | 0.0000 | −0.999 |
| 2 | 3,387,689 | 54,833 | 0.0162 | 0.103 | |
| 3 | 1804 | 10 | 0.0053 | −0.638 | |
| 4 | 1889 | 0 | 0.0000 | −1 | |
| 5 | 70,175 | 1157 | 0.0165 | 0.199 | |
| 6 | 26,678 | 833 | 0.0312 | 0.542 | |
| 7 | 326,333 | 1757 | 0.0054 | −0.633 | |
| 8 | 548 | 440 | 0.8028 | 0.996 | |
| 9 | 81 | 0 | 0.0000 | −1 | |
| SPI | 0–200 | 748,095 | 3344 | 0.0045 | −0.696 |
| 200–400 | 1,239,924 | 25,522 | 0.0206 | 0.297 | |
| 400–600 | 1,151,603 | 17,331 | 0.0150 | 0.034 | |
| 600–800 | 591,663 | 8632 | 0.0146 | 0.003 | |
| >800 | 324,673 | 4202 | 0.0129 | −0.126 | |
| STI | 0–1.89 | 964,332 | 7705 | 0.0080 | −0.833 |
| 1.89–4.12 | 1,275,764 | 20,177 | 0.0158 | 0.088 | |
| 4.12–6.36 | 1,018,068 | 17,450 | 0.0171 | 0.181 | |
| 6.36–9.11 | 597,977 | 11,886 | 0.0199 | 0.374 | |
| 9.11–42.8 | 199,817 | 1813 | 0.0091 | −0.613 |
| NO. | Factor | TOL | VIF |
|---|---|---|---|
| 1 | Slope angle | 0.681 | 1.469 |
| 2 | Elevation | 0.836 | 1.196 |
| 3 | Profile curvature | 0.970 | 1.031 |
| 4 | Plan curvature | 0.981 | 1.020 |
| 5 | Slope aspect | 0.958 | 1.044 |
| 6 | TWI | 0.785 | 1.274 |
| 7 | TPI | 0.944 | 1.060 |
| 8 | Distance to roads | 0.759 | 1.317 |
| 9 | Distance to rivers | 0.680 | 1.470 |
| 10 | NDVI | 0.931 | 1.074 |
| 11 | Rainfall | 0.855 | 1.169 |
| 12 | Landuse | 0.943 | 1.060 |
| 13 | Lithology | 0.799 | 1.251 |
| 15 | STI | 0.586 | 1.705 |
| NO. | Factors | Relevance |
|---|---|---|
| 1 | Rainfall | 0.3534 |
| 2 | Distance to rivers | 0.3287 |
| 3 | Elevation | 0.2899 |
| 4 | Lithology | 0.26 |
| 5 | Slope angle | 0.2347 |
| 6 | SPI | 0.1856 |
| 7 | Slope aspect | 0.112 |
| 8 | Distance to roads | 0.0908 |
| 9 | NDVI | 0.0884 |
| 10 | TPI | 0.0525 |
| 11 | Plan curvature | 0.0483 |
| 12 | STI | 0.0448 |
| 13 | TWI | 0.0435 |
| 14 | Land use | 0.0264 |
| 15 | Profile curvature | 0.0188 |
| Model Type | Levels | Reclassified Value | Area Covered (%) |
|---|---|---|---|
| LR model | Very Low | 0–0.145 | 26.98 |
| Low | 0.145–0.306 | 24.02 | |
| Moderate | 0.306–0.486 | 19.65 | |
| High | 0.486–0.678 | 16.22 | |
| Very High | 0.678–1 | 13.13 | |
| Total | 0–1 | 100 | |
| FT model | Very Low | 0–0.161 | 76.92 |
| Low | 0.161–0.478 | 1.51 | |
| Moderate | 0.478–0.717 | 3.97 | |
| High | 0.717–0.894 | 7.26 | |
| Very High | 0.894–1 | 10.34 | |
| Total | 0–1 | 100 | |
| RSFT model | Very Low | 0–0.147 | 34.72 |
| Low | 0.417–0.311 | 25.42 | |
| Moderate | 0.311–0.512 | 17.67 | |
| High | 0.512–0.734 | 14.22 | |
| Very High | 0.734–0.990 | 7.97 | |
| Total | 0–0.990 | 100 |
| Test Variables | LR | FT | RSFT |
|---|---|---|---|
| ROC Curve Area | 0.811 | 0.776 | 0.844 |
| Standard Error | 0.0116 | 0.0125 | 0.0105 |
| 95% Confidence Interval | 0.789 To 0.832 | 0.752 To 0.797 | 0.823 To 0.863 |
| p Value | <0.0001 | <0.0001 | <0.0001 |
| Test Variables | LR | FT | RSFT |
|---|---|---|---|
| ROC Curve Area | 0.814 | 0.760 | 0.837 |
| Standard Error | 0.0180 | 0.0188 | 0.0163 |
| 95% Confidence Interval | 0.780 To 0.845 | 0.723 To 0.794 | 0.804 To 0.866 |
| p Value | <0.0001 | <0.0001 | <0.0001 |
| Model Type | Susceptibility Levels | Pixels | Pixels (%) | landslides | Landslides (%) | FR | Frequency Ratio Precision |
|---|---|---|---|---|---|---|---|
| LR model | Very low | 1,094,297 | 26.98 | 27 | 2.78 | 0.10 | 0.843 |
| Low | 974,241 | 24.02 | 62 | 6.38 | 0.27 | ||
| Moderate | 796,996 | 19.65 | 128 | 13.17 | 0.67 | ||
| High | 657,876 | 16.22 | 217 | 22.33 | 1.38 | ||
| Very high | 532,142 | 13.12 | 538 | 55.35 | 4.22 | ||
| FT model | Very low | 3,119,843 | 76.92 | 227 | 23.35 | 0.30 | 0.669 |
| Low | 61,245 | 1.51 | 20 | 2.06 | 1.36 | ||
| Moderate | 161,022 | 3.97 | 75 | 7.72 | 1.94 | ||
| High | 294,463 | 7.26 | 198 | 20.37 | 2.81 | ||
| Very high | 419,386 | 10.34 | 452 | 46.50 | 4.50 | ||
| RSFT model | Very low | 1,408,229 | 34.72 | 26 | 2.67 | 0.08 | 0.895 |
| Low | 1,031,025 | 25.42 | 56 | 5.76 | 0.23 | ||
| Moderate | 716,688 | 17.67 | 122 | 12.55 | 0.71 | ||
| High | 576,757 | 14.22 | 220 | 22.63 | 1.59 | ||
| Very high | 323,260 | 7.97 | 548 | 56.38 | 7.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, H.; Su, L.; Chen, W.; Tsangaratos, P.; Ilia, I.; Liu, S.; Cui, S.; Duan, Z. Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China. Remote Sens. 2023, 15, 4952. https://doi.org/10.3390/rs15204952
Shang H, Su L, Chen W, Tsangaratos P, Ilia I, Liu S, Cui S, Duan Z. Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China. Remote Sensing. 2023; 15(20):4952. https://doi.org/10.3390/rs15204952
Chicago/Turabian StyleShang, Hui, Lixiang Su, Wei Chen, Paraskevas Tsangaratos, Ioanna Ilia, Sihang Liu, Shaobo Cui, and Zhao Duan. 2023. "Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China" Remote Sensing 15, no. 20: 4952. https://doi.org/10.3390/rs15204952
APA StyleShang, H., Su, L., Chen, W., Tsangaratos, P., Ilia, I., Liu, S., Cui, S., & Duan, Z. (2023). Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China. Remote Sensing, 15(20), 4952. https://doi.org/10.3390/rs15204952










