Gravity Wave Characterization of Multiple Convections in the Beijing–Tianjin–Hebei Region
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Spectral Analysis Methods
2.3. Methods for Calculating Fluctuation Characteristics
3. Case Analysis
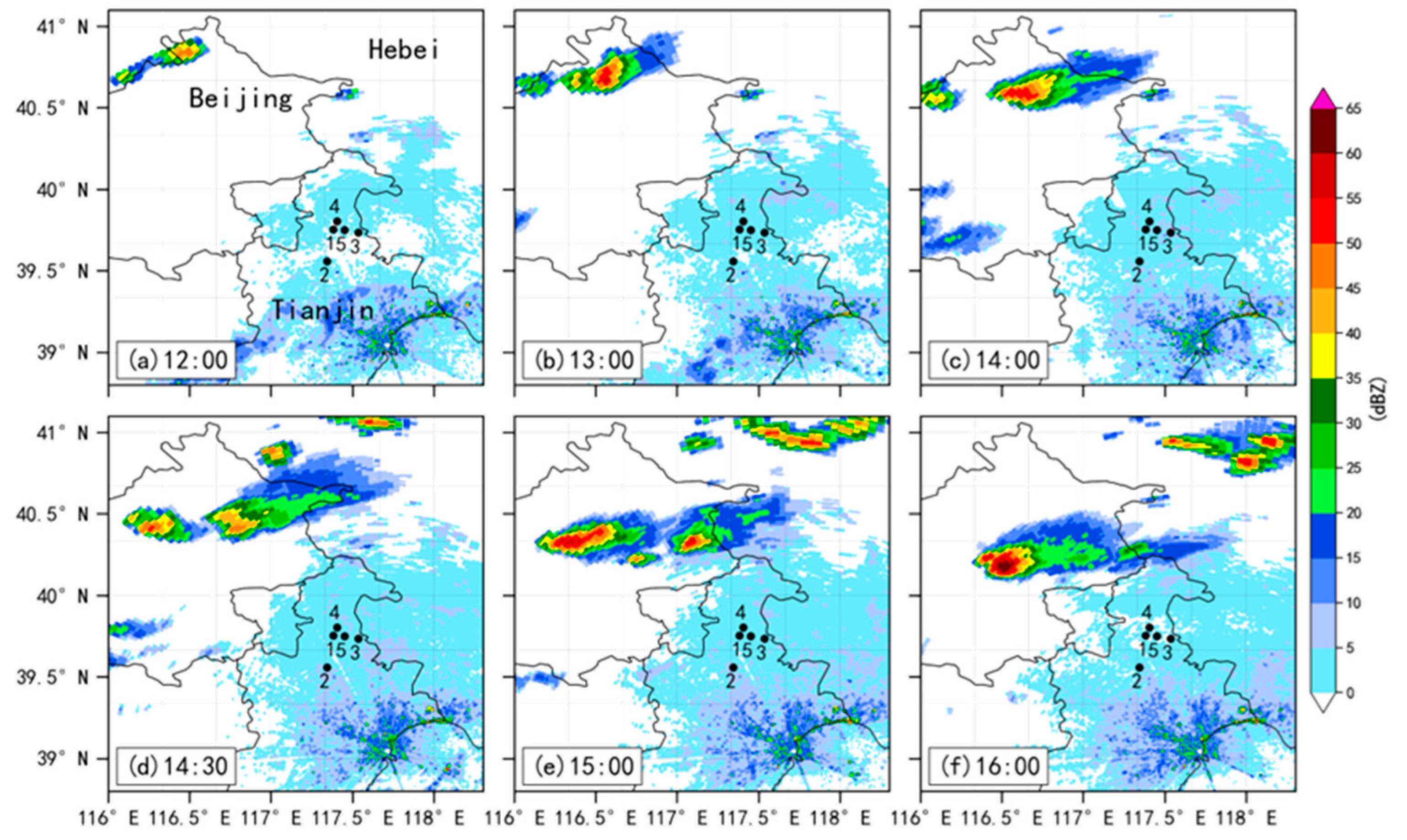
3.1. Convective Process
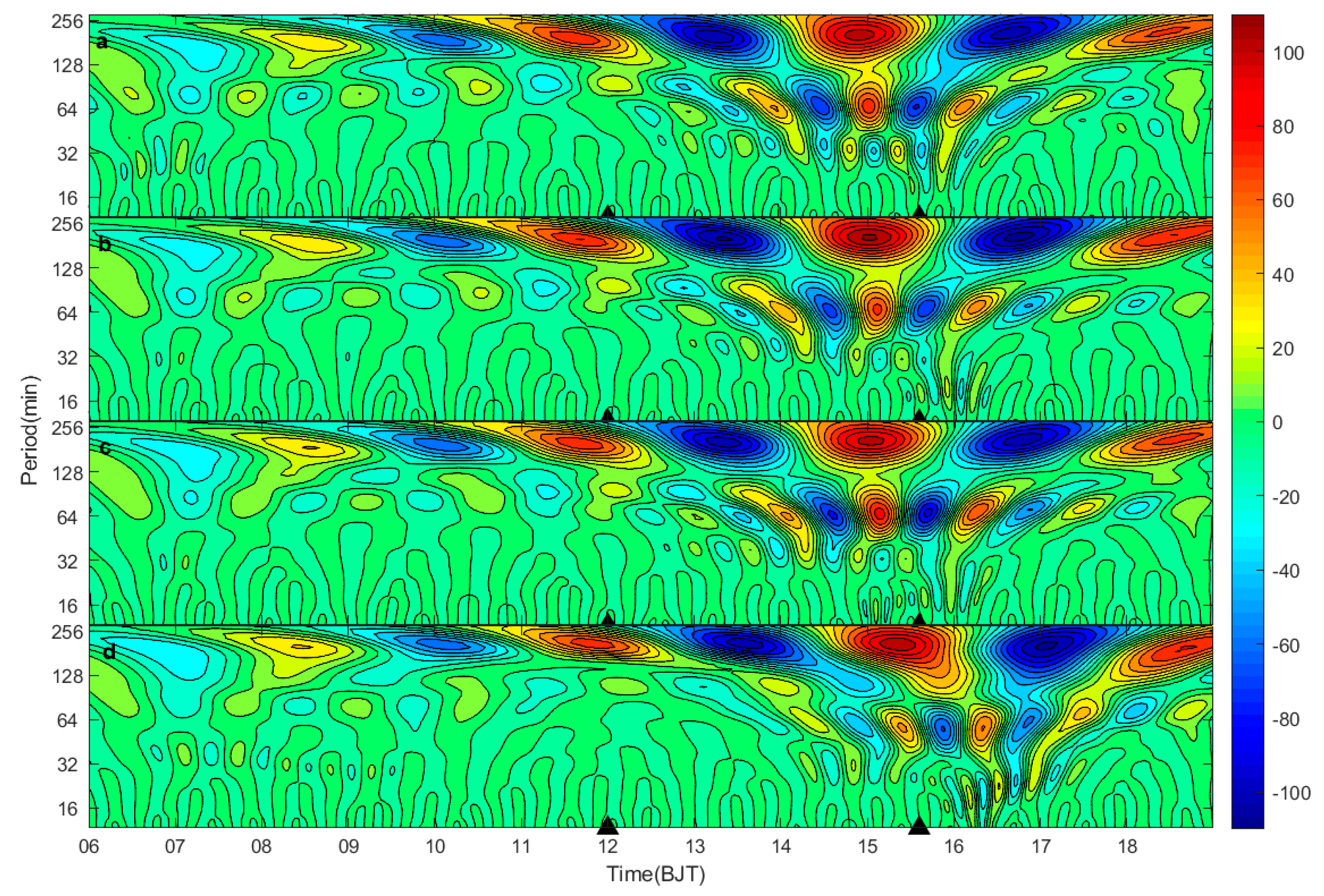
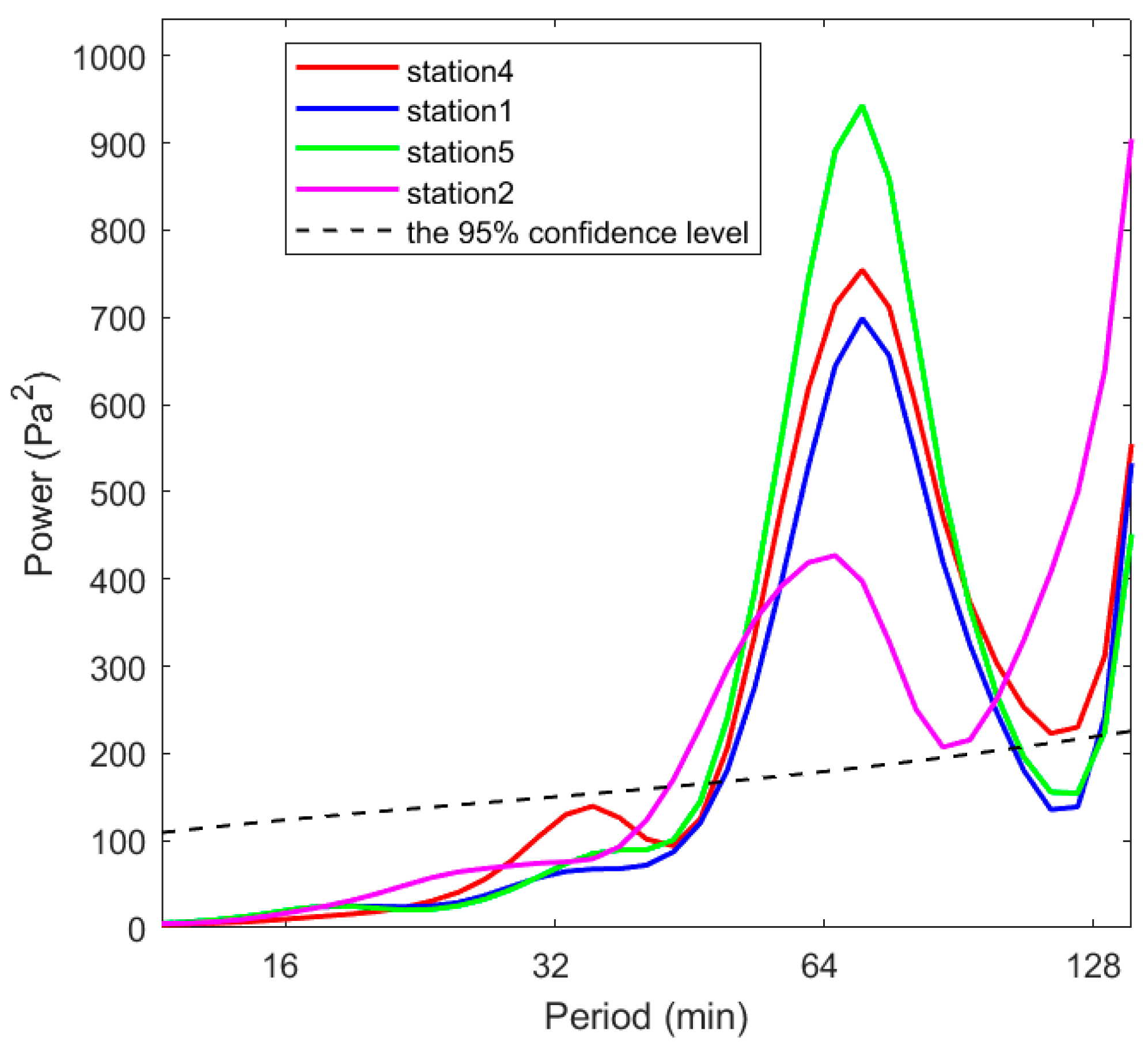
3.2. Gravity Wave Spectral Characteristics
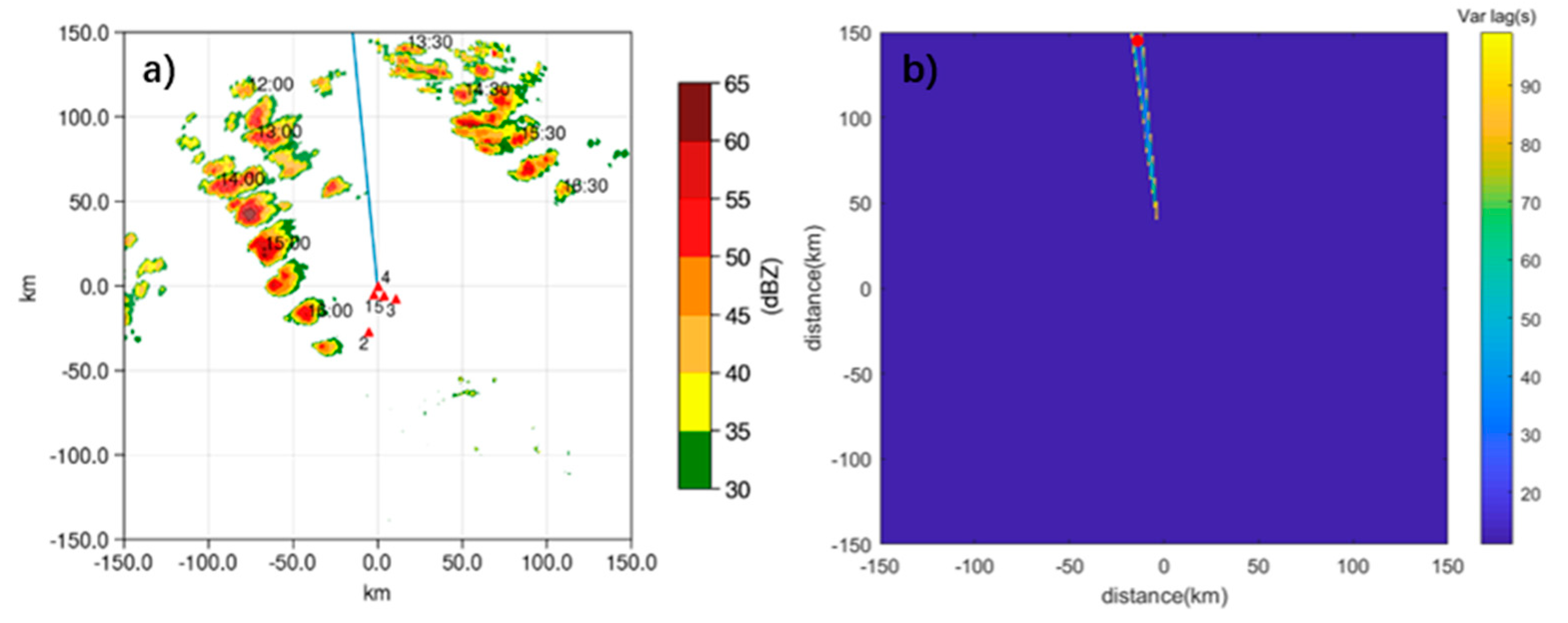
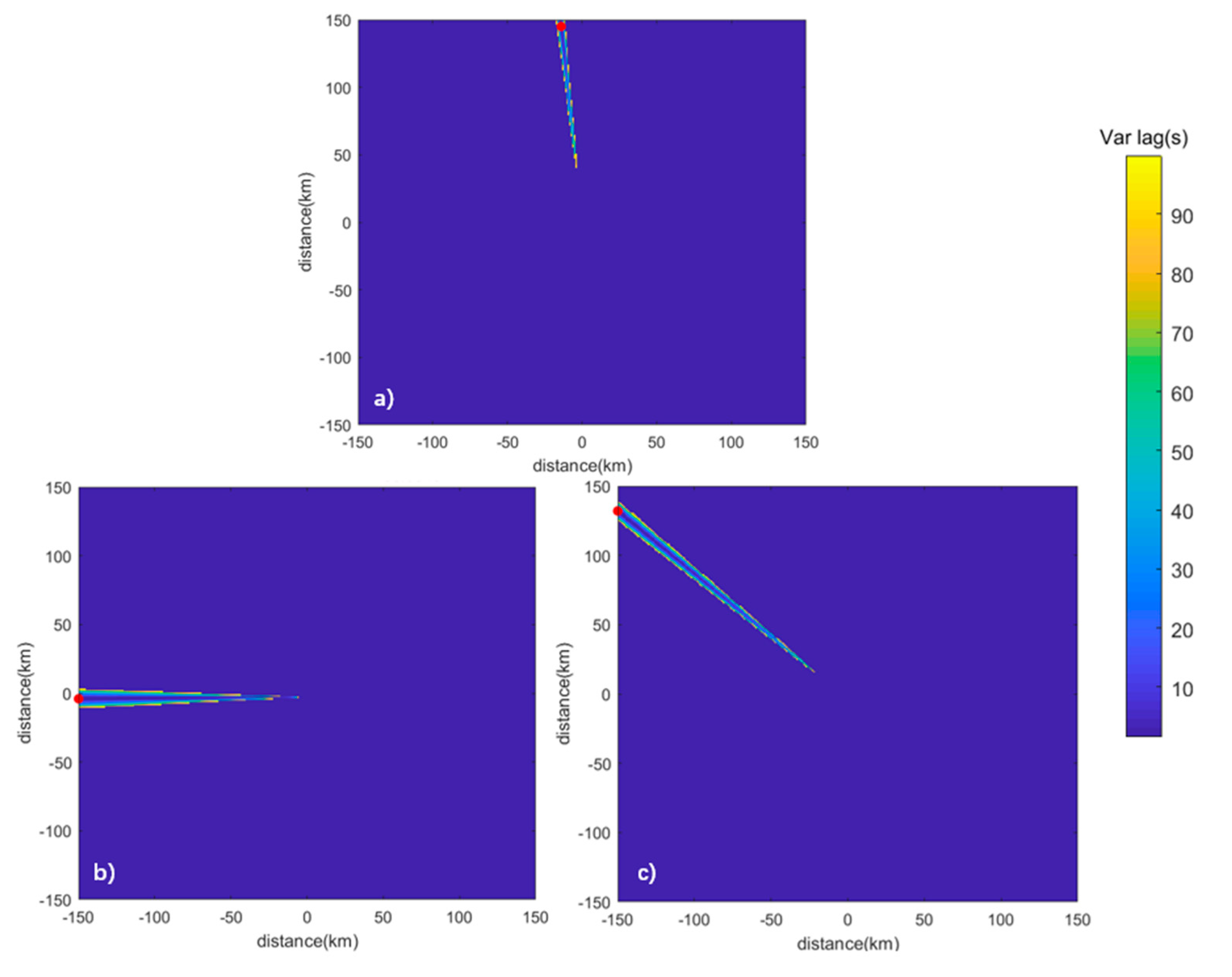
3.3. Characteristics of Gravity Wave Propagation
4. Gravity Wave Characteristics of Multiple Convective Cases
5. Conclusions
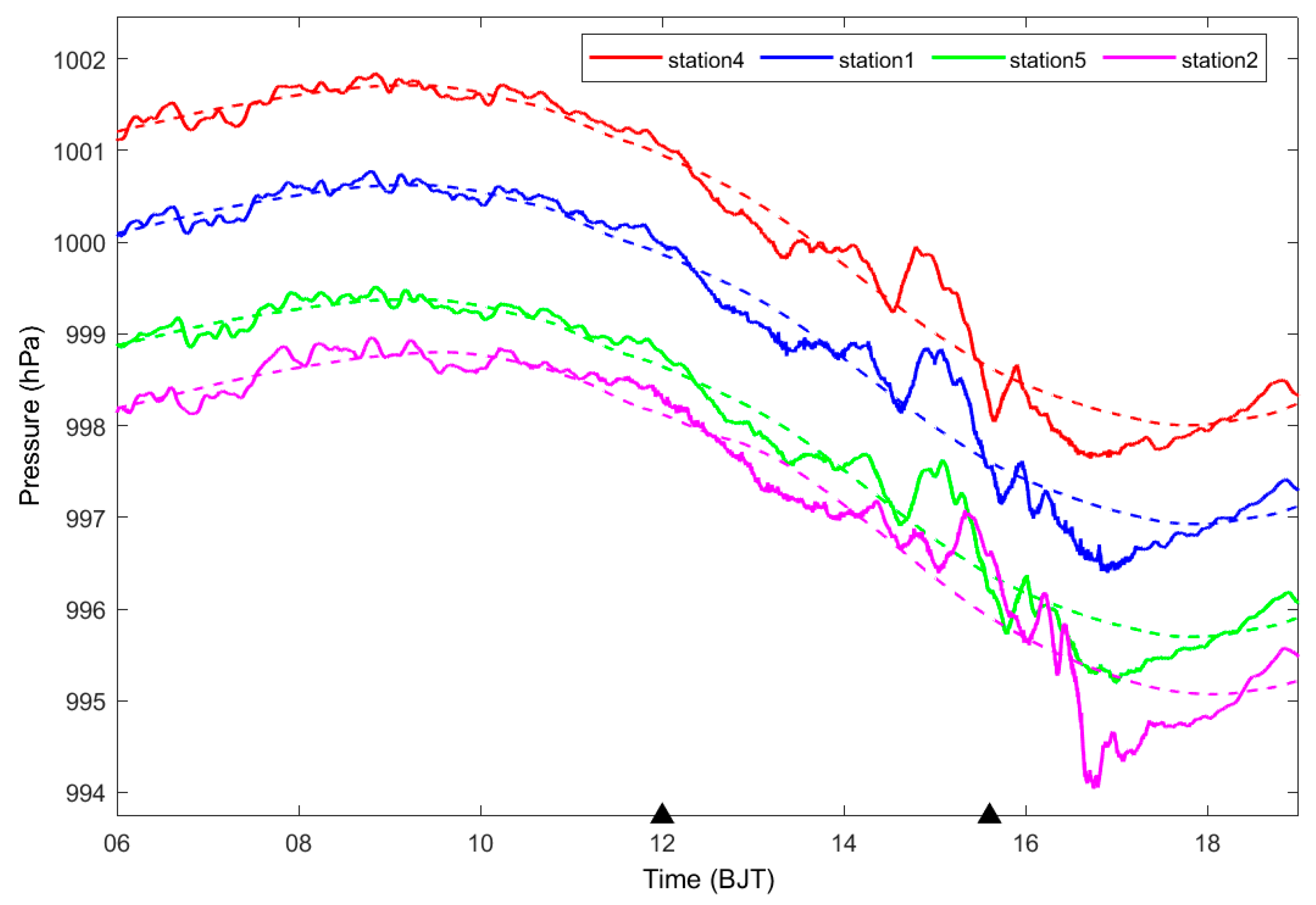
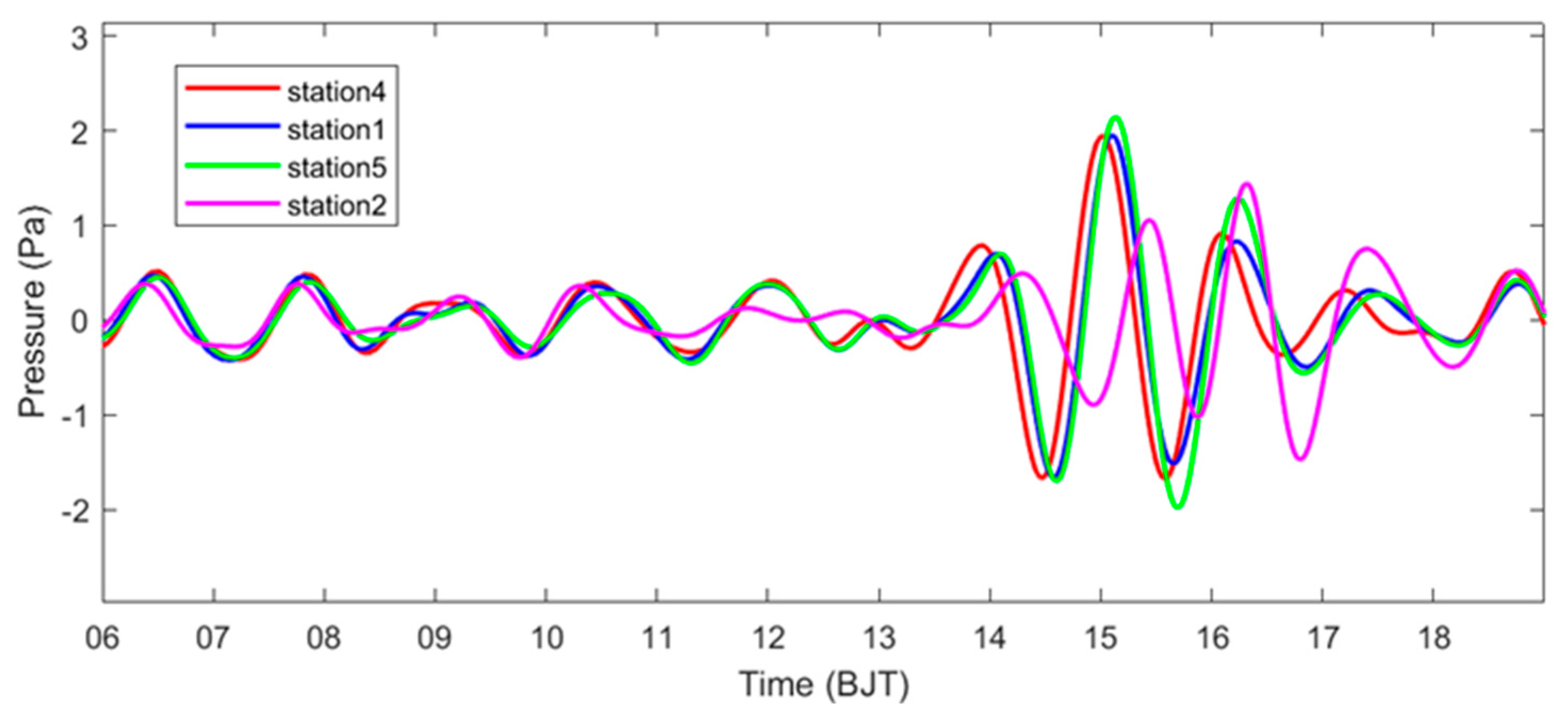
- Multiple micromanometers observe the same convective process, and the accompanying fluctuation signals have a high degree of similarity. The stronger the convection, the larger the amplitude of the barometric pressure observed at the station, and the longer the strong fluctuations appear.
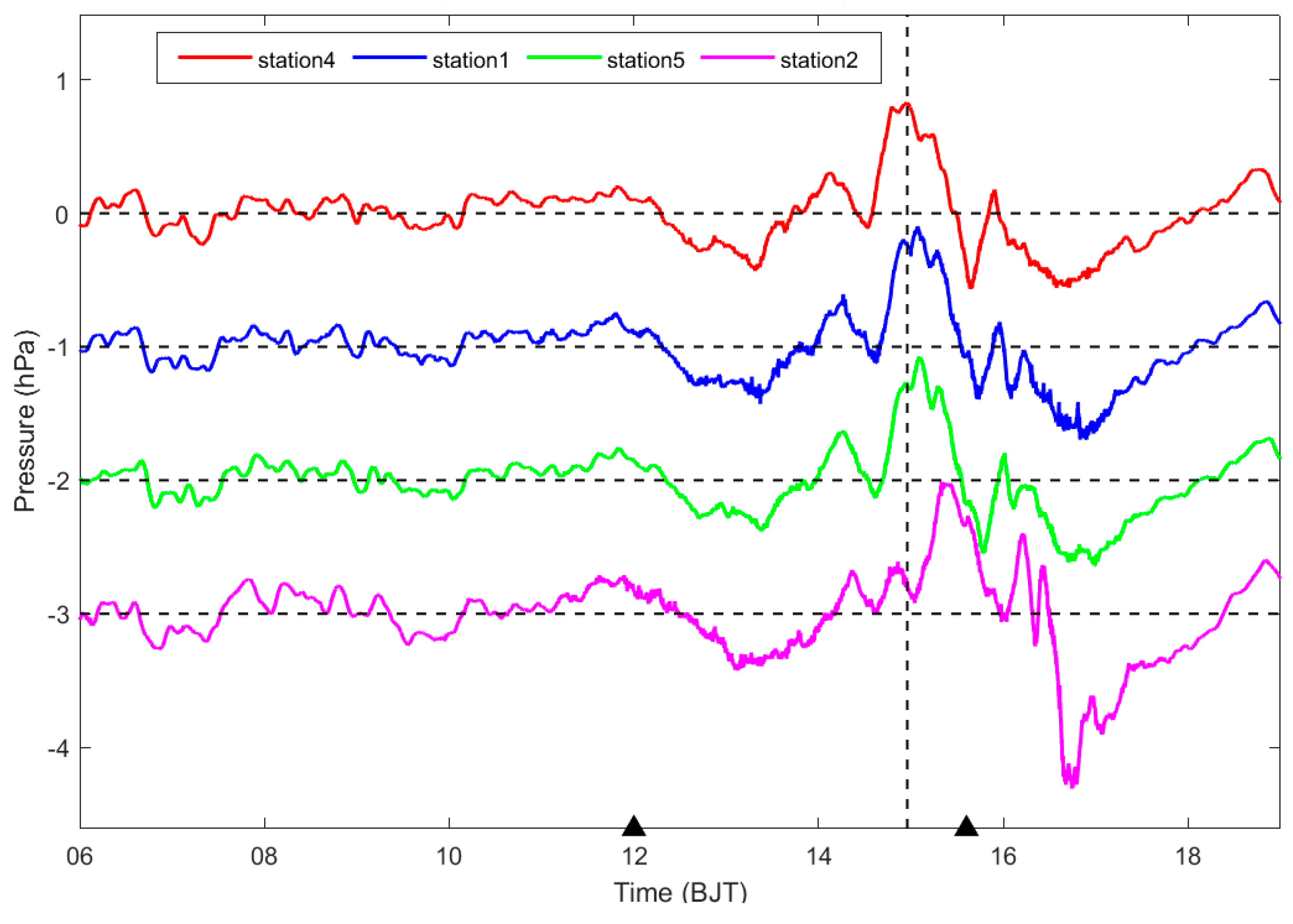
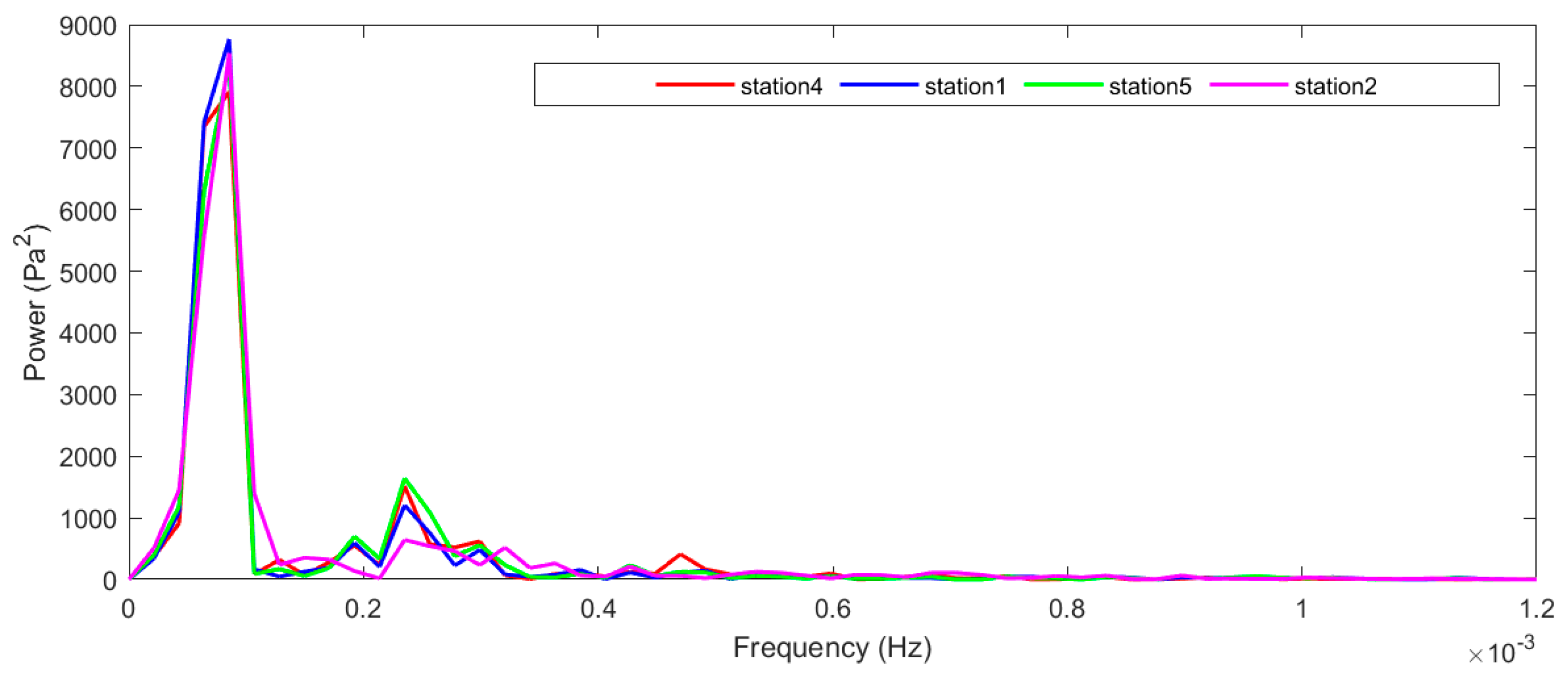
- There are multi-scale spectral characteristics of the fluctuation process. Using Fourier analysis, the fluctuation of the long period was concentrated at 0.903 × 10−4 Hz, and the short period was concentrated at 2.04 × 10−4 Hz; wavelet analysis of the fluctuations found that the strong convection gravity wave period was mainly divided into three bands: 15–40 min, 40–120 min, 120–250 min; the longer period of fluctuations was in advance of the convection, which roughly appeared for 1–4 h, and the time of the short-period fluctuation was more consistent with the convective process. The period of the fluctuation was mostly concentrated at 40–120 min, and the fluctuation frequency broadened when convection was closer to the station. When the convection gradually closed toward the station, the fluctuation frequency broadened, which stimulated a smaller cycle of fluctuations. This conclusion is more consistent with previous studies [58,59,60]. The reconstruction of the 40–120 min period wave shows that the fluctuation characteristics were clearer, and the fluctuation reached its maximum amplitude before the convection was closest to the station and then gradually decreased, which was probably due to the unstable or weakly stable convective environment that can cause the dissipation of the gravity waves in the boundary layer [46].
- The fluctuation propagation characteristics were calculated for the 40–120 min reconstructed signals at stations four, one, and five; the wave speeds during convection were obtained as 14 m/s, 17 m/s, and 37 m/s, respectively, and the azimuthal angles of the wave sources were more consistent with the convective azimuths, but there were still deviations. Generally, the horizontal wave speed of inertial gravity waves ranged from about 10–50 m/s and often occurred in conjunction with convection [48,50,61], with a feedback mechanism between the two. The method of time-delay estimation could roughly estimate the position of the wave source, but the deviation was large, and the localization method still needs to be improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hines, C.O. The upper atmosphere in motion. Q. J. R. Meteorol. Soc. 1963, 89, 1–42. [Google Scholar] [CrossRef]
- James, L. Waves in Fluids. Meas. Sci. Technol. 2002, 13, 1501. [Google Scholar]
- Carmen, J.N. Observations and Measurements of Gravity Waves. In An Introduction to Atmospheric Gravity Waves; Carmen, J.N., Ed.; Academic Press: Cambridge, MA, USA, 2012; Volume 102, pp. 231–278. [Google Scholar]
- Liu, L.; Ran, L.; Gao, S. Analysis of the Characteristics of Inertia-Gravity Waves during an Orographic Precipitation Event. Adv. Atmos. Sci. 2018, 35, 604–620. [Google Scholar] [CrossRef]
- Moffat-Griffin, T. An Introduction to Atmospheric Gravity Wave Science in the Polar Regions and First Results from ANGWIN. J. Geophys. Res. Atmos. 2019, 124, 1198–1199. [Google Scholar] [CrossRef]
- Rees, J.M.; Denholm-Price, J.C.W.; King, J.C.; Anderson, P.S. A Climatological Study of Internal Gravity Waves in the Atmospheric Boundary Layer Overlying the Brunt Ice Shelf, Antarctica. J. Atmos. Sci. 2000, 57, 511–526. [Google Scholar] [CrossRef]
- Jacques, A.A.; Horel, J.D.; Crosman, E.T.; Vernon, F.L. Tracking Mesoscale Pressure Perturbations Using the USArray Transportable Array. Mon. Weather Rev. 2017, 145, 3119–3142. [Google Scholar] [CrossRef]
- Hoffmann, L.; Alexander, M.J. Occurrence frequency of convective gravity waves during the North American thunderstorm season. J. Geophys. Res. Atmos. 2010, 115, D20111. [Google Scholar] [CrossRef]
- de Groot-Hedlin, C.D.; Hedlin, M.A.H.; Hoffmann, L.; Alexander, M.J.; Stephan, C.C. Relationships between Gravity Waves Observed at Earth’s Surface and in the Stratosphere Over the Central and Eastern United States. J. Geophys. Res. Atmos. 2017, 122, 11482–11498. [Google Scholar] [CrossRef]
- Holton, J.R. The Influence of Gravity Wave Breaking on the General Circulation of the Middle Atmosphere. J. Atmos. Sci. 1983, 40, 2497–2507. [Google Scholar] [CrossRef]
- Kim, Y.J.; Eckermann, S.D.; Chun, H.Y. An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models. Atmos. Ocean 2003, 41, 65–98. [Google Scholar]
- Lindzen, R.S. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. Ocean 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Vincent, R.A.; Reid, I.M. HF Doppler Measurements of Mesospheric Gravity Wave Momentum Fluxes. J. Atmos. Sci. 1983, 40, 1321–1333. [Google Scholar] [CrossRef]
- Holton, J.R. The Role of Gravity Wave Induced Drag and Diffusion in the Momentum Budget of the Mesosphere. J. Atmos. Sci. 1982, 39, 791–799. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Lane, T.P.; Zhang, F. Coupling between Gravity Waves and Tropical Convection at Mesoscales. J. Atmos. Sci. 2011, 68, 2582–2598. [Google Scholar] [CrossRef]
- Schmidt, J.M.; Cotton, W.R. Interactions between upper and lower tropospheric gravity waves on squall line structure and maintenance. J. Atmos. Sci. 1990, 47, 1205–1222. [Google Scholar] [CrossRef]
- Pandya, R.E.; Durran, D.R.; Weisman, M.L. The influence of convective thermal forcing on the three-dimensional circulation around squall lines. J. Atmos. Sci. 2000, 57, 29–45. [Google Scholar] [CrossRef]
- Liu, C.; Moncrieff, M.W. Effects of Convectively Generated Gravity Waves and Rotation on the Organization of Convection. J. Atmos. Sci. 2004, 61, 2218–2227. [Google Scholar] [CrossRef]
- Uccelini, L.W. A Case Study of Apparent Gravity Wave Initiation of Severe Convective Storms. Mon. Weather Rev. 1975, 103, 497–513. [Google Scholar] [CrossRef]
- Lindzen, R.S. Wave-CISK in the Tropics. J. Atmos. Sci. 1974, 31, 156–179. [Google Scholar] [CrossRef]
- Raymond, D.J. A Model for Predicting the Movement of Continuously Propagating Convective Storms. J. Atmos. Sci. 1975, 32, 1308–1317. [Google Scholar] [CrossRef]
- Gong, D.; Wu, Z.; Fu, G. Analysis of the Mesoscale Characteristics About a Severe Thunderstorm in North China. Chin. J. Atmos. Sci. 2005, 29, 453–464. [Google Scholar]
- Xie, J.; Li, G. Mechanism Analysis of a Sudden Rainstorm Triggered by the Coupling of Gravity Wave and Convection in Mountainous Area. Chin. J. Atmos. Sci. 2021, 45, 617–632. [Google Scholar]
- Huang, X.; Zhou, Y.; Liu, L. Occurrence and Development of an Extreme Precipitation Event in the Ili Valley, Xinjiang, China and Analysis of Gravity Waves. Atmosphere 2020, 11, 752. [Google Scholar] [CrossRef]
- Su, T.; Zhai, G. The Role of Convectively Generated Gravity Waves on Convective Initiation: A Case Study. Mon. Weather Rev. 2017, 145, 335–359. [Google Scholar] [CrossRef]
- Li, M. Studies on the gravity wave initiation of the excessively heavy rainfall. Chin. J. Atmos. Sci. 1978, 2, 201–209. [Google Scholar]
- Sun, Y.; Li, Z.; Shou, S. A mesoscale analysis of the snowstorm event of 3-5 March 2007 in Liaoning Province. Acta Meteorol. Sin. 2012, 70, 936–948. [Google Scholar]
- Ma, S.; Ran, L.; Cao, J.; Jiao, B.; Zhou, K. Characteristics for the sources and sinks of gravity waves in an orographic heavy snowfall event. Front. Earth Sci. 2023, 17, 604–619. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, J.; Wan, W. Analysis on the Global Morphology of Middle Atmospheric Gravity Waves. Chin. J. Geophys. 2011, 54, 427–435. [Google Scholar] [CrossRef]
- Murphy, D.J.; Alexander, S.P.; Klekociuk, A.R.; Love, P.T.; Vincent, R.A. Radiosonde observations of gravity waves in the lower stratosphere over Davis, Antarctica. J. Geophys. Res. Atmos. 2014, 119, 11,973–11,996. [Google Scholar] [CrossRef]
- Yao, Z.; Hong, J.; Han, Z.; Zhao, Z. Numerical Simulation of Typhoon-generated Gravity Waves Observed by Satellite and its Direct Validationormalsize. Chin. J. Space Sci. 2018, 38, 188–200. [Google Scholar]
- Zhang, N.; Zhao, R.; Sun, D.; Han, Y.; Chen, C. Inertial gravity waves study with Rayleigh Doppler Lidar long-term observation. Infrared Laser Eng. 2020, 49, 20200351. [Google Scholar]
- Yang, C.; Guo, Q.; Cao, X.; Zhang, W. Analysis of gravity wave characteristics in the lower stratosphere based on new round-trip radiosonde. Acta Meteorol. Sin. 2021, 79, 150–167. [Google Scholar]
- Brunk, I.W. The Pressure Pulsation of 11 April 1944. J. Atmos. Sci. 1949, 6, 181–187. [Google Scholar] [CrossRef]
- Bosart, L.F.; Cussen, J.P. Gravity Wave Phenomena Accompanying East Coast Cyclogenesis. Mon. Weather Rev. 1973, 101, 446–454. [Google Scholar] [CrossRef]
- Eom, J.K. Analysis of the Internal Gravity Wave Occurrence of 19 April 1970 in the Midwest. Mon. Weather Rev. 1975, 103, 217–226. [Google Scholar] [CrossRef]
- Donn, W.L.; Rind, D. Natural Infrasound as an Atmospheric Probe. Geophys. J. Int. 1971, 26, 111–133. [Google Scholar] [CrossRef]
- Curry, M.J.; Murty, R.C. Thunderstorm-Generated Gravity Waves. J. Atmos. Sci. 1974, 31, 1402–1408. [Google Scholar] [CrossRef]
- Whitaker, R.W.; Mutschlecner, J.P. A comparison of infrasound signals refracted from stratospheric and thermospheric altitudes. J. Geophys. Res. Atmos. 2008, 113, D08117. [Google Scholar] [CrossRef]
- Jacques, A.A.; Horel, J.D.; Crosman, E.T.; Vernon, F.L. Central and eastern U.S. surface pressure variations derived from the USArray network. Mon. Weather Rev. 2015, 143, 1472–1493. [Google Scholar] [CrossRef]
- Šindelárová, T.; Kozubek, M.; Chum, J.; Potužníková, K. Seasonal and diurnal variability of pressure fluctuation in the infrasound frequency range observed in the Czech microbarograph network. Stud. Geophys. Geod. 2016, 60, 747–762. [Google Scholar] [CrossRef]
- Keliher, T.E. The occurrence of microbarograph-detected gravity waves compared with the existence of dynamically unstable wind shear layers. J. Geophys. Res. 1975, 80, 2967–2976. [Google Scholar] [CrossRef]
- Smart, E.; Flinn, E.A. Fast Frequency-Wavenumber Analysis and Fisher Signal Detection in Real-Time Infrasonic Array Data Processing. Geophys. J. Int. 1971, 26, 279–284. [Google Scholar] [CrossRef]
- Denholm-Price, J.C.W.; Rees, J.M. Detecting Waves Using an Array of Sensors. Mon. Weather Rev. 1999, 127, 57–69. [Google Scholar] [CrossRef]
- Zhang, F.; Davis, C.A.; Kaplan, M.L.; Koch, S.E. Wavelet analysis and the governing dynamics of a large-amplitude mesoscale gravity-wave event along the East Coast of the United States. Q. J. R. Meteorol. Soc. 2001, 127, 2209–2245. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Z.; Lü, D. Spatiotemporal spectrum and momentum flux of the stratospheric gravity waves generated by a typhoon. Sci. China Earth Sci. 2013, 56, 54–62. [Google Scholar] [CrossRef]
- Hauf, T.; Finke, U.; Neisser, J.; Bull, G.; Stangenberg, J.G. A Ground-Based Network for Atmospheric Pressure Fluctuations. J. Atmos. Ocean Technol. 1996, 13, 1001–1023. [Google Scholar] [CrossRef]
- Lu, C.; Koch, S.; Wang, N. Determination of temporal and spatial characteristics of atmospheric gravity waves combining cross-spectral analysis and wavelet transformation. J. Geophys. Res. Atmos. 2005, 110, D01109. [Google Scholar] [CrossRef]
- Li, Q.; Xie, J.; Yang, X. The Dynamic Characteristics of Gravity Waves during Severe Hailstorm Process. Acta Meteorol. Sin. 1993, 51, 361–368. [Google Scholar]
- Wu, L.; Wen, Z.; He, H. Relationship between the Periodic Fluctuations of Pressure and Precipitation during a Rainstorm. Atmos. Ocean Sci. Lett. 2015, 8, 78–81. [Google Scholar]
- Wang, X.; Lei, H.; Jiang, Z.; Zheng, S.; Qi, Y. Frequency Spectrum Dynamic Characteristics of Atmospheric Gravity Waves during Various Types of Thunderstorms in Foshan. Clim. Environ. Res. 2021, 26, 250–262. [Google Scholar]
- Torrence, C.; Webster, P.J. Interdecadal Changes in the ENSO–Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Yang, Q.; Ding, H.; Xia, Y. Source Location of Infrasonic by Tripartite Array Arithmetic. Beijing Gongye Daxue Xuebao/J. Beijing Univ. Technol. 2017, 43, 819–825. [Google Scholar]
- Melissa, J.L.; Martin, J.S. Wavelet analysis of inter-annual variability in the runoff regimes of glacial and nival stream catchments, Bow Lake, Alberta. Hydrol. Process. 2003, 17, 1093–1118. [Google Scholar]
- Koch, S.E.; Siedlarz, L.M. Mesoscale Gravity Waves and Their Environment in the Central United States during STORM-FEST. Mon. Weather Rev. 1999, 127, 2854–2879. [Google Scholar] [CrossRef]
- Wang, X.; Lei, H.; Feng, L.; Zhu, J.; Li, Z.; Jiang, Z. Analysis of the characteristics of gravity waves during a local rainstorm event in Foshan, China. Atmos. Ocean. Sci. Lett. 2020, 13, 163–170. [Google Scholar] [CrossRef]
- Wang, X.; Ran, L.; Qi, Y.; Ma, S.; Mu, X.; Jiang, Z.; Bi, X. Analysis of characteristics of gravity waves of heavy rainfall event based on microbarograph observation. Acta Phys. Sin. 2021, 70, 234702. [Google Scholar] [CrossRef]
- Wang, X.; Ran, L.; Qi, Y.; Jiang, Z.; Yun, T.; Jiao, B. Analysis of Gravity Wave Characteristics during a Hailstone Event in the Cold Vortex of Northeast China. Atmosphere 2023, 14, 412. [Google Scholar] [CrossRef]
- Blanc, E.; Farges, T.; Le Pichon, A.; Heinrich, P. Ten year observations of gravity waves from thunderstorms in western Africa. J. Geophys. Res. Atmos. 2014, 119, 6409–6418. [Google Scholar] [CrossRef]
- Yang, R.; Liu, Y.; Ran, L.; Zhang, Y. Simulation of a torrential rainstorm in Xinjiang and gravity wave analysis. Chin. Phys. B 2018, 27, 059201. [Google Scholar] [CrossRef]

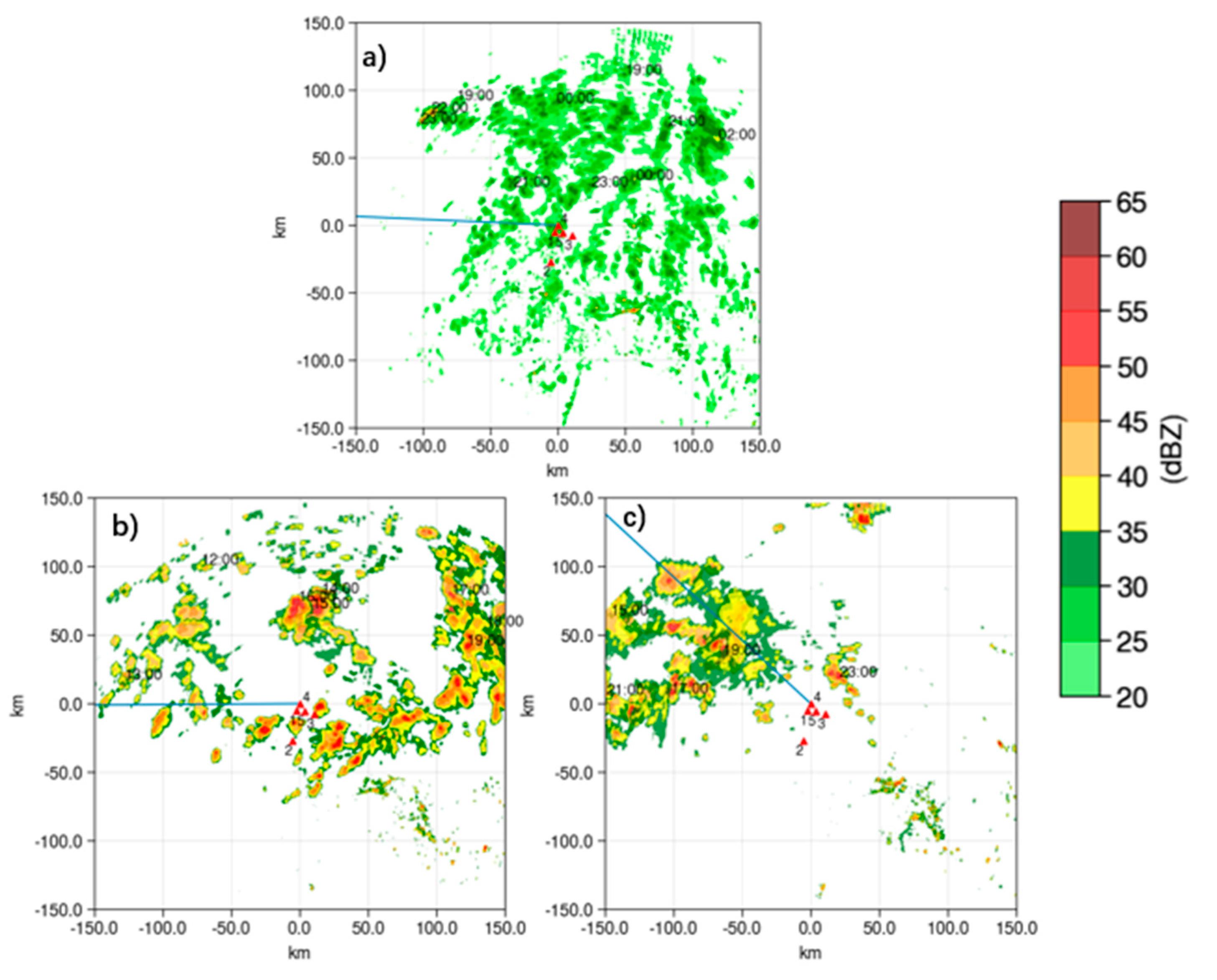
| 22 June 2018 | 26 June 2018 | 29 June 2018 | 30 June 2018 | |
|---|---|---|---|---|
| Time of convection emergence | 18:00 | 12:00 | 12:00 | 15:00 |
| Moment when convection is closest to the stations | 23:00 | 15:36 | 18:00 | 22:00 |
| Maximum combined reflectivity (dBZ) | 40 | 65 | 60 | 60 |
| Maximum amplitude of air pressure (Pa) | 65 | 139.8 | 167.6 | 144 |
| Average frequency (10−4 Hz) | 1.632 | 1.543 | 1.570 | 1.473 |
| Short period range (min) | 46.6–103.5 | 48.3–114.8 | 53.6–110.9 | 46.6–110.9 |
| Wave velocity (m/s) | 14.6 | 14.1 | 36.9 | 17.6 |
| Wave azimuth (°) | 177.5 | 95.6 | 180.4 | 137.3 |
| Wave source location (km) | (−141,4) | (−14,145) | (−150,4) | (−150,132) |
| Estimation error (km) | 110.8 | 69.4, 31.3 | 88 | 67.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Lei, H.; Zhou, K.; Ran, L. Gravity Wave Characterization of Multiple Convections in the Beijing–Tianjin–Hebei Region. Remote Sens. 2023, 15, 5024. https://doi.org/10.3390/rs15205024
Lu Y, Lei H, Zhou K, Ran L. Gravity Wave Characterization of Multiple Convections in the Beijing–Tianjin–Hebei Region. Remote Sensing. 2023; 15(20):5024. https://doi.org/10.3390/rs15205024
Chicago/Turabian StyleLu, Yi, Hengchi Lei, Kuo Zhou, and Lingkun Ran. 2023. "Gravity Wave Characterization of Multiple Convections in the Beijing–Tianjin–Hebei Region" Remote Sensing 15, no. 20: 5024. https://doi.org/10.3390/rs15205024
APA StyleLu, Y., Lei, H., Zhou, K., & Ran, L. (2023). Gravity Wave Characterization of Multiple Convections in the Beijing–Tianjin–Hebei Region. Remote Sensing, 15(20), 5024. https://doi.org/10.3390/rs15205024





