Above Ground Level Estimation of Airborne Synthetic Aperture Radar Altimeter by a Fully Supervised Altimetry Enhancement Network
Abstract
:1. Introduction
- The proposition of a novel label generation algorithm based on a semi-analytical model to implement a fully supervised network for parameter estimation, so that clean and accurate DDMs can be produced by discretizing landforms in the domain of range and Doppler together with empirical scattering theory;
- Accordingly, the estimation is designed by a novel, fully supervised network, which is capable of accessing the AGL parameters for airborne SARAL on complicated landforms;
- The raw data of landscapes are employed in this paper to validate the generalizability and accuracy of the proposed approach.
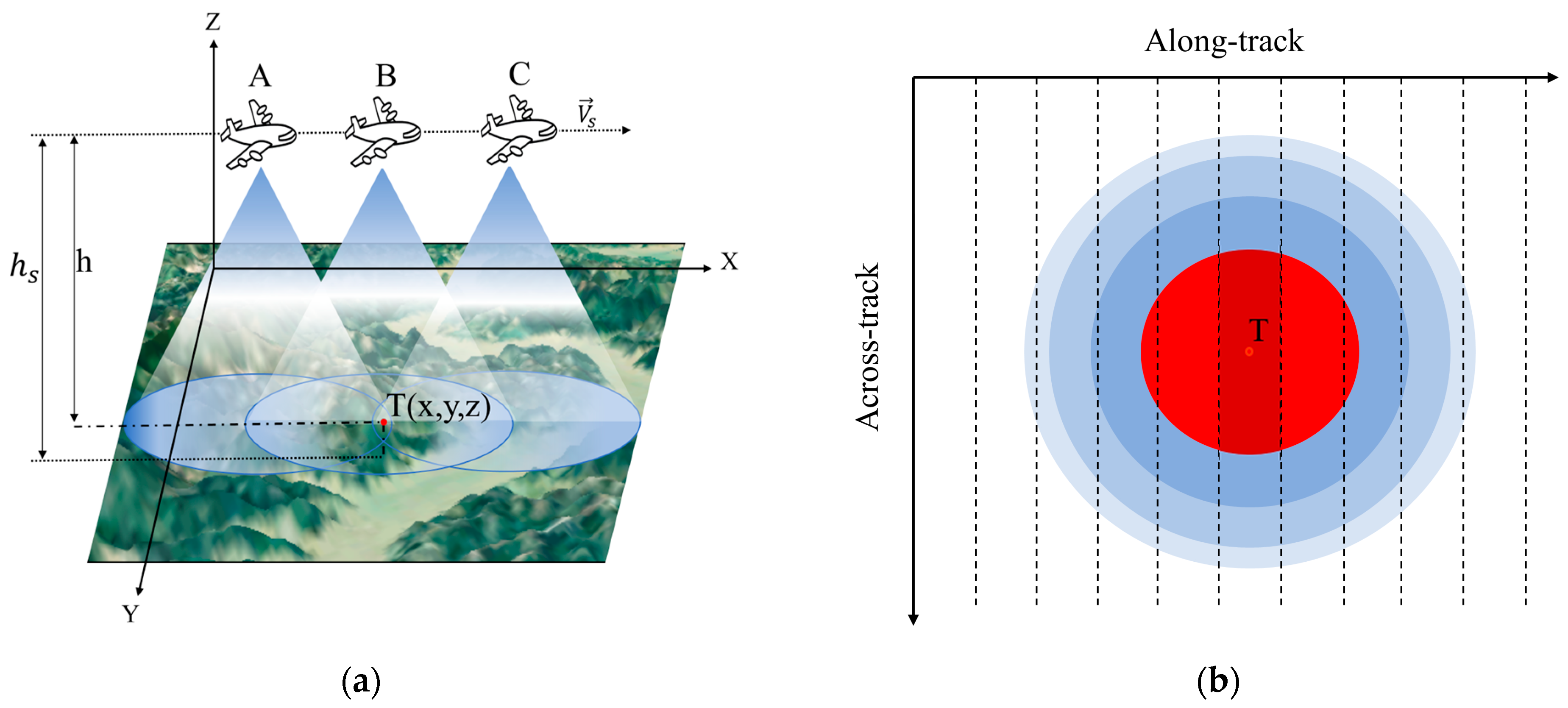
2. Airborne SARAL Geometry and Signal Model
2.1. Airborne SARAL Geometry
2.2. Airborne SARAL Signal Model
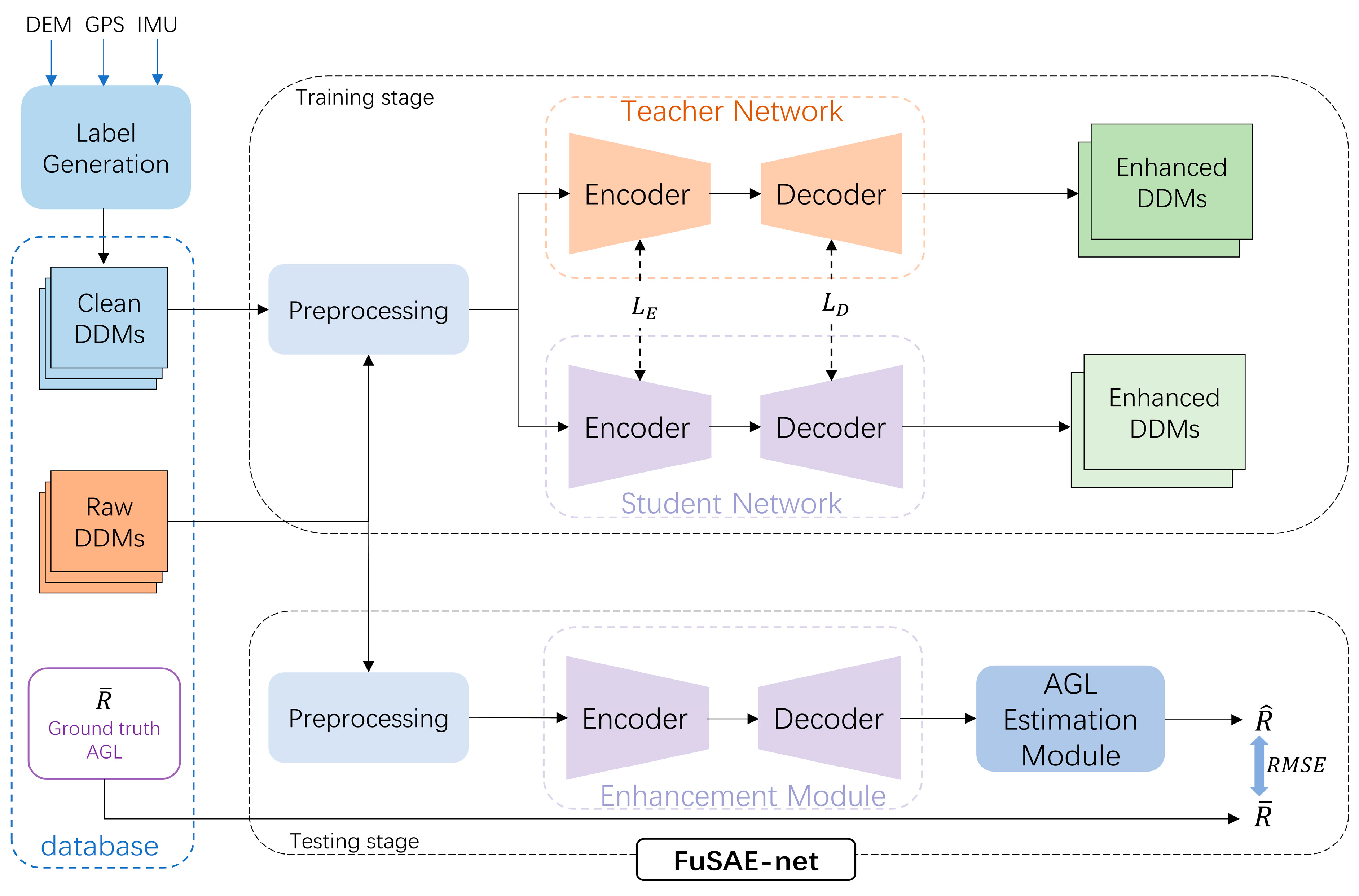
3. Methodology
3.1. Clean Label Generation
| Algorithm 1: Generation process of the clean label. | |
| Input: The coordinates of each scatter: , where is the total set of scatters. Current location and velocity of the platform: and . The wavelength of radar is . The resolution of range gates and Doppler channels as and , respectively. | |
| |
| |
where and depend on the type of land cover medium.
| |
| |
| where and are the index sets with respect to the mth range gate, and nth Doppler channels, correspondingly. | |
| Output: A clean DDM power matrix as , where is the number of pulses and is the number of range gates. | |
3.2. FuSAE-Net
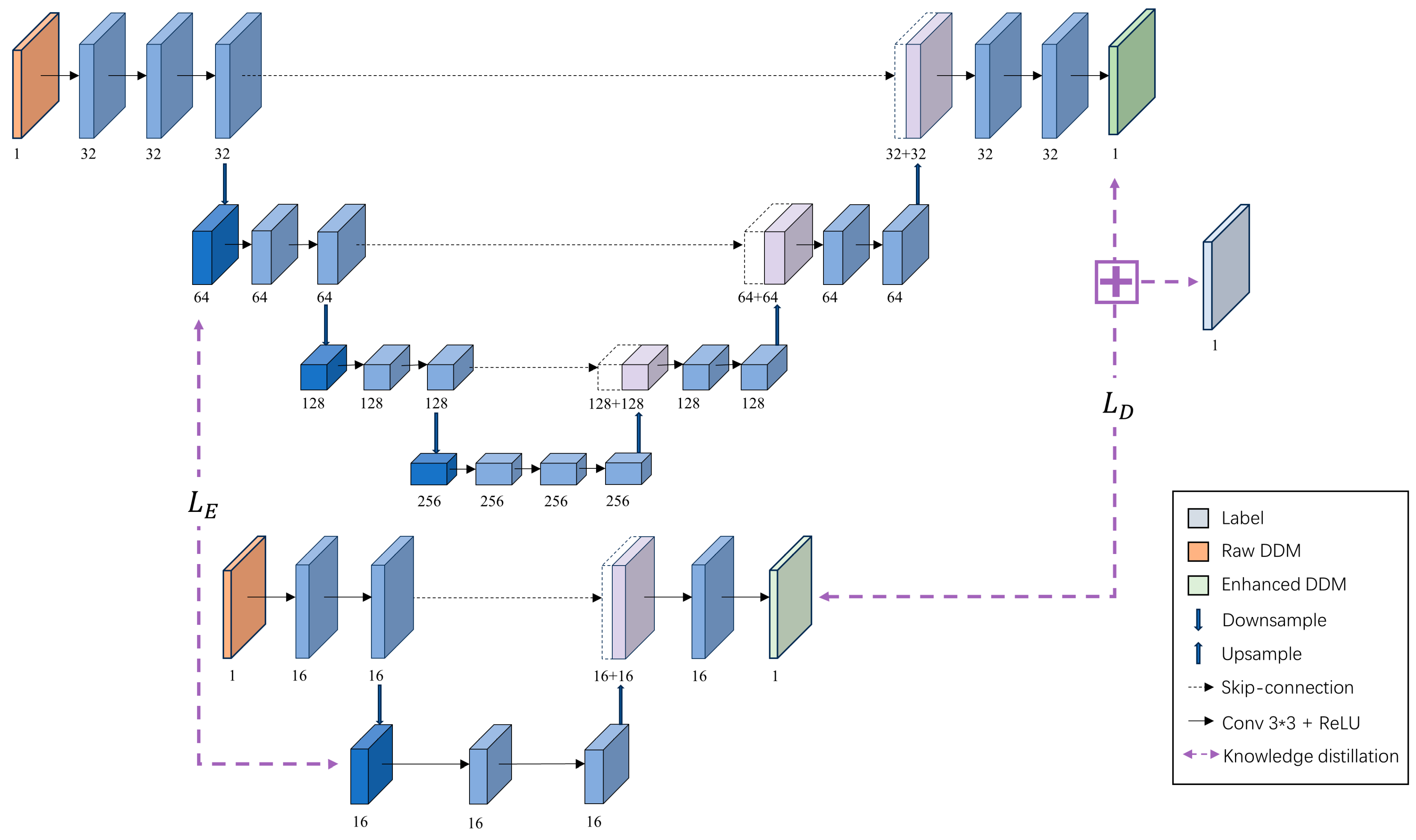
3.2.1. A Lightweight DDM Enhancement Module
- A. Architecture Designation
- B. Training
3.2.2. AGL Estimation Module
4. Experiments
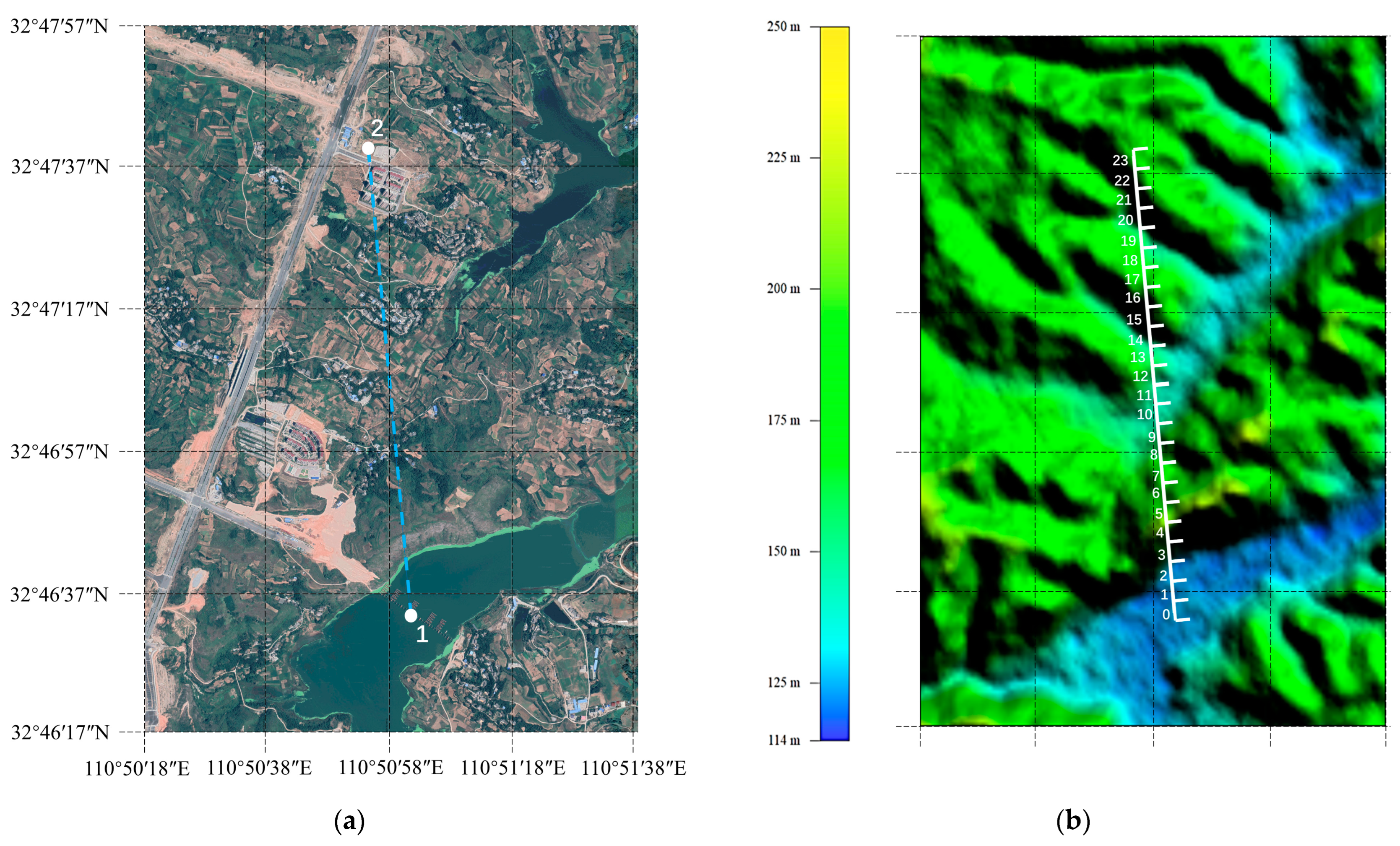
4.1. Data Set Description
4.1.1. Flight Route
4.1.2. Data Collection and Preprocessing
4.2. Evaluation Indicators
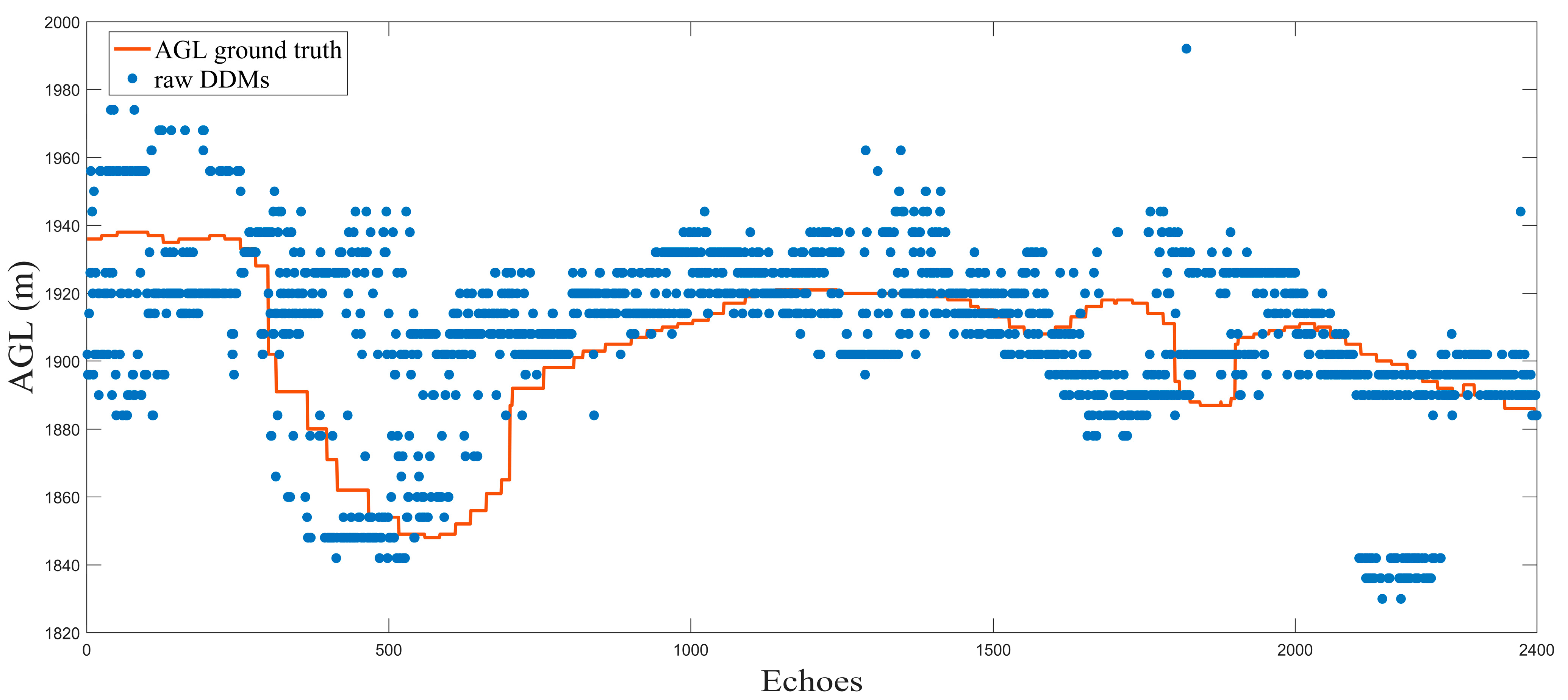
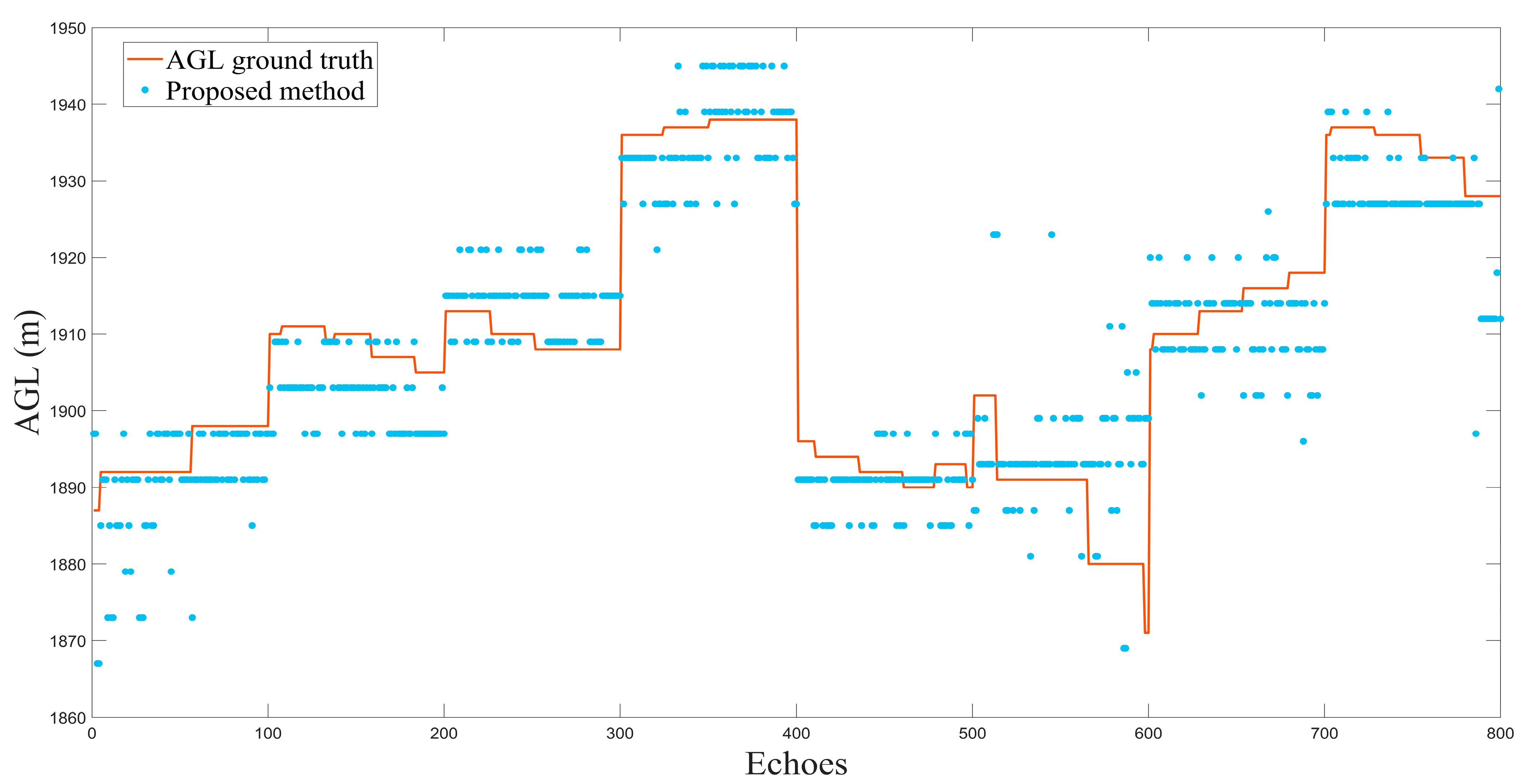
4.3. Performance Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Halimi, A. From conventional to delay/doppler altimetry. Ph.D. dissertation, INP Toulouse, Toulouse, France, 2013. [Google Scholar]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Yang, S.; Zhai, Z.; Xu, K.; Zhisen, W.; Lingwei, S.; Lei, W. The ground process segment of SAR altimeter. Remote Sens. Technol. Appl. 2017, 32, 1083–1092. [Google Scholar]
- Brown, G.S. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Benveniste, J. Coastal SAR and PLRM altimetry in German Bight and West Baltic Sea. Adv. Space Res. 2018, 62, 1371–1404. [Google Scholar] [CrossRef]
- Buchhaupt, C.; Fenoglio-Marc, L.; Dinardo, S.; Scharroo, S.; Becker, M. A fast convolution based waveform model for conventional and unfocused SAR altimetry. Adv. Space Res. 2018, 62, 1445–1463. [Google Scholar] [CrossRef]
- Idris, N.H.; Vignudelli, S.; Deng, X. Assessment of retracked sea levels from Sentinel-3A Synthetic Aperture Radar (SAR) mode altimetry over the marginal seas at Southeast Asia. Int. J. Remote Sens. 2021, 42, 1535–1555. [Google Scholar] [CrossRef]
- Dumont, J.P. Estimation optimale des paramètres altimétriques des signaux radar Poséidon. Ph.D. dissertation, INP Toulouse, Toulouse, France, 1985. [Google Scholar]
- Yang, L.; Zhou, H.; Huang, B.; Liao, X.; Xia, Y. Elevation Estimation for Airborne Synthetic Aperture Radar Altimetry Based on Parameterized Bayesian Learning. J. Electron. Inf. Technol. 2023, 45, 1254–1264. [Google Scholar]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Snoussi, H. Bayesian Estimation of Smooth Altimetric Parameters: Application to Conventional and Delay/Doppler Altimetry. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2207–2219. [Google Scholar] [CrossRef]
- Liao, X.; Zhang, Z.; Jiang, G. Mutant Altimetric Parameter Estimation Using a Gradient-Based Bayesian Method. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhan, Y. Study on the Coastal Echo Processing Method for Satellite Radar Altimeter. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New techniques in satellite altimeter tracking systems. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Zurich, Switzerland, 8–11 September 1986. [Google Scholar]
- Davis, C.H. Growth of the Greenland ice sheet: A performance assessment of altimeter retracking algorithms. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1108–1116. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.; Deng, X.; Hsu, H.Y.; Liu, Y. Coastal gravity anomalies from retracked Geosat/GM altimetry: Improvement, limitation and the role of airborne gravity data. J. Geodesy. 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Lee, H.; Shum, C.K.; Emery, W.; Calmant, S.; Deng, X.; Kuo, C.; Roesler, C.; Yi, Y. Validation of Jason-2 altimeter data by waveform retracking over California coastal ocean. Mar. Geodesy. 2010, 33, 304–316. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H.; Luo, Z.; Shum, C.K.; Tseng, K.-H.; Zhong, B. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms. Remote Sens. 2017, 9, 1077. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Z. Waveform Decontamination for Improving Satellite Radar Altimeter Data Over Nearshore Area: Upgraded Algorithm and Validation. Front. Earth Sci. 2021, 9, 748401. [Google Scholar] [CrossRef]
- Shu, S.; Liu, H.; Beck, R.A.; Frappart, F.; Korhonen, J.; Xu, M.; Yu, B.; Hinkel, K.M.; Huang, Y.; Yu, B. Analysis of Sentinel-3 SAR altimetry waveform retracking algorithms for deriving temporally consistent water levels over ice-covered lakes. Remote Sens. Environ. 2020, 239, 111643. [Google Scholar] [CrossRef]
- Agar, P.; Roohi, S.; Voosoghi, B.; Amini, A.; Poreh, D. Sea Surface Height Estimation from Improved Modified, and Decontaminated Sub-Waveform Retracking Methods over Coastal Areas. Remote Sens. 2023, 15, 804. [Google Scholar] [CrossRef]
- Molini, A.B.; Valsesia, D.; Fracastoro, G.; Magli, E. DeepSUM: Deep Neural Network for Super-Resolution of Unregistered Multitemporal Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3644–3656. [Google Scholar] [CrossRef]
- Xing, D.; Hou, J.; Huang, C.; Zhang, W. Spatiotemporal Reconstruction of MODIS Normalized Difference Snow Index Products Using U-Net with Partial Convolutions. Remote Sens. 2022, 14, 1795. [Google Scholar] [CrossRef]
- Perera, M.V.; Bandara, W.G.C.; Valanarasu, J.M.J.; Patel, V.M. SAR Despeckling Using Overcomplete Convolutional Networks. In Proceedings of the IGARSS 2022 - 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- Wang, P.; Zhang, H.; Patel, V.M. SAR Image Despeckling Using a Convolutional Neural Network. IEEE Signal Process. Lett. 2017, 24, 1763–1767. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Yang, Z.; Ma, X. Learning a Dilated Residual Network for SAR Image Despeckling. Remote Sens. 2018, 10, 196. [Google Scholar] [CrossRef]
- Lattari, F.; Leon, B.G.; Asaro, F.; Rucci, A.; Prati, C.; Matteucci, M. Deep Learning for SAR Image Despeckling. Remote Sens. 2019, 11, 1532. [Google Scholar] [CrossRef]
- Ko, J.; Lee, S. SAR Image Despeckling Using Continuous Attention Module. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3–19. [Google Scholar] [CrossRef]
- Pongrac, B.; Gleich, D. Despeckling of SAR Images Using Residual Twin CNN and Multi-Resolution Attention Mechanism. Remote Sens. 2023, 15, 3698. [Google Scholar] [CrossRef]
- Chierchia, G.; Gheche, M.E.; Scarpa, G.; Verdoliva, L. Multitemporal SAR Image Despeckling Based on Block-Matching and Collaborative Filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5467–5480. [Google Scholar] [CrossRef]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2Noise: Learning Image Restoration without Clean Data. arXiv 2018, arXiv:1803.04189. [Google Scholar]
- Lin, H.; Zhuang, Y.; Huang, Y.; Ding, X. Unpaired Speckle Extraction for SAR Despeckling. IEEE Trans. Geosci. Remote Sens. 2023, 60, 1–14. [Google Scholar] [CrossRef]
- Molini, A.B.; Valsesia, D.; Fracastoro, G.; Magli, E. Speckle2Void: Deep Self-Supervised SAR Despeckling With Blind-Spot Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Laine, S.; Karras, T.; Lehtinen, J.; Aila, T. High-Quality Self-Supervised Deep Image Denoising. arXiv 2019, arXiv:1901.10277. [Google Scholar]
- Tan, S.; Zhang, X.; Wang, H.; Yu, L.; Du, Y.; Yin, J.; Wu, B. A CNN-Based Self-Supervised Synthetic Aperture Radar Image Denoising Approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Moore, R.K.; Williams, C.S. Radar Terrain Return at Near-Vertical Incidence. Proc. IRE 1957, 45, 228–238. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-rayes, M.A. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Landy, J.C.; Tsamados, M.; Scharien, R.K. A Facet-Based Numerical Model for Simulating SAR Altimeter Echoes From Heterogeneous Sea Ice Surfaces. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4164–4180. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, H.; Xu, F. Raw signal simulation of synthetic aperture radar altimeter over complex terrain surfaces. Radio Sci. 2020, 55, 1–17. [Google Scholar] [CrossRef]
- Geng, X.; Wang, L.; Wang, X.; Qin, B.; Liu, T.; Tu, Z. Learning to Refine Source Representations for Neural Machine Translation. arXiv 2018, arXiv:1812.10230. [Google Scholar] [CrossRef]
- Tewari, A.; Zollhoefer, M.; Bernard, F.; Garrido, P.; Kim, H.; Perez, P.; Theobalt, C. High-Fidelity Monocular Face Reconstruction Based on an Unsupervised Model-Based Face Autoencoder. IEEE. Trans. Pattern Anal. Mach. Intell. 2020, 42, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Etten, A.V.; Lindenbaum, D.; Bacastow, T.M. SpaceNet: A remote sensing dataset and challenge series. arXiv 2018, arXiv:1807.01232. [Google Scholar]
- de Rijk, P.; Schneider, L.; Cordts, M.; Gavrila, D.M. Structural Knowledge Distillation for Object Detection. arXiv 2022, arXiv:2211.13133. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]

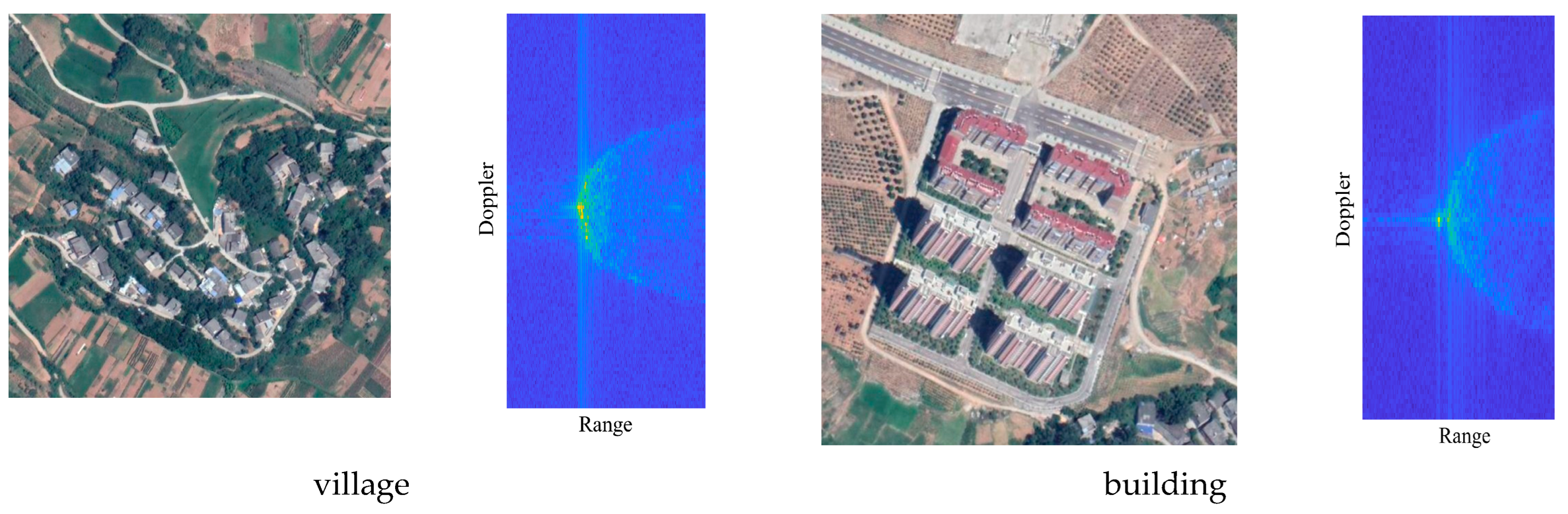


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Altitude | 2.06 km | Bandwidth | 20 MHz |
| Speed | 20 m/s | PRT | 200 μs |
| Band | X | Pulses of each burst | 125 |
| Component | PSNR (dB) | MAE (m) | RMSE (m) | Time (ms) |
|---|---|---|---|---|
| AGL-E-M (Raw data) | 12.7356 | 30.1383 | 25.7765 | 0.4883 |
| Teacher + AGL-E-M | 24.3585 | 6.6338 | 9.2215 | 11.4566 |
| KD + AGL-E-M (Proposed method) | 21.8368 | 6.9163 | 10.3378 | 6.0065 |
| Method | MAE (m) | RMSE (m) | Time (ms) |
|---|---|---|---|
| LS | 23.3591 | 29.3692 | 56,968.2 |
| MAP-smooth | 12.5811 | 23.2932 | 37,782.0 |
| MAP-mutant | 11.0306 | 21.8112 | 36,144.3 |
| Proposed method | 6.9163 | 10.3378 | 6.0065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, M.; Lu, Y.; Wang, Y.; Liu, G.; Tan, L.; Gao, Y.; Li, F.; Jiang, G. Above Ground Level Estimation of Airborne Synthetic Aperture Radar Altimeter by a Fully Supervised Altimetry Enhancement Network. Remote Sens. 2023, 15, 5404. https://doi.org/10.3390/rs15225404
Duan M, Lu Y, Wang Y, Liu G, Tan L, Gao Y, Li F, Jiang G. Above Ground Level Estimation of Airborne Synthetic Aperture Radar Altimeter by a Fully Supervised Altimetry Enhancement Network. Remote Sensing. 2023; 15(22):5404. https://doi.org/10.3390/rs15225404
Chicago/Turabian StyleDuan, Mengmeng, Yanxi Lu, Yao Wang, Gaozheng Liu, Longlong Tan, Yi Gao, Fang Li, and Ge Jiang. 2023. "Above Ground Level Estimation of Airborne Synthetic Aperture Radar Altimeter by a Fully Supervised Altimetry Enhancement Network" Remote Sensing 15, no. 22: 5404. https://doi.org/10.3390/rs15225404
APA StyleDuan, M., Lu, Y., Wang, Y., Liu, G., Tan, L., Gao, Y., Li, F., & Jiang, G. (2023). Above Ground Level Estimation of Airborne Synthetic Aperture Radar Altimeter by a Fully Supervised Altimetry Enhancement Network. Remote Sensing, 15(22), 5404. https://doi.org/10.3390/rs15225404




