Methods to Improve the Accuracy and Robustness of Satellite-Derived Bathymetry through Processing of Optically Deep Waters
Abstract
:1. Introduction
2. Materials and Methods
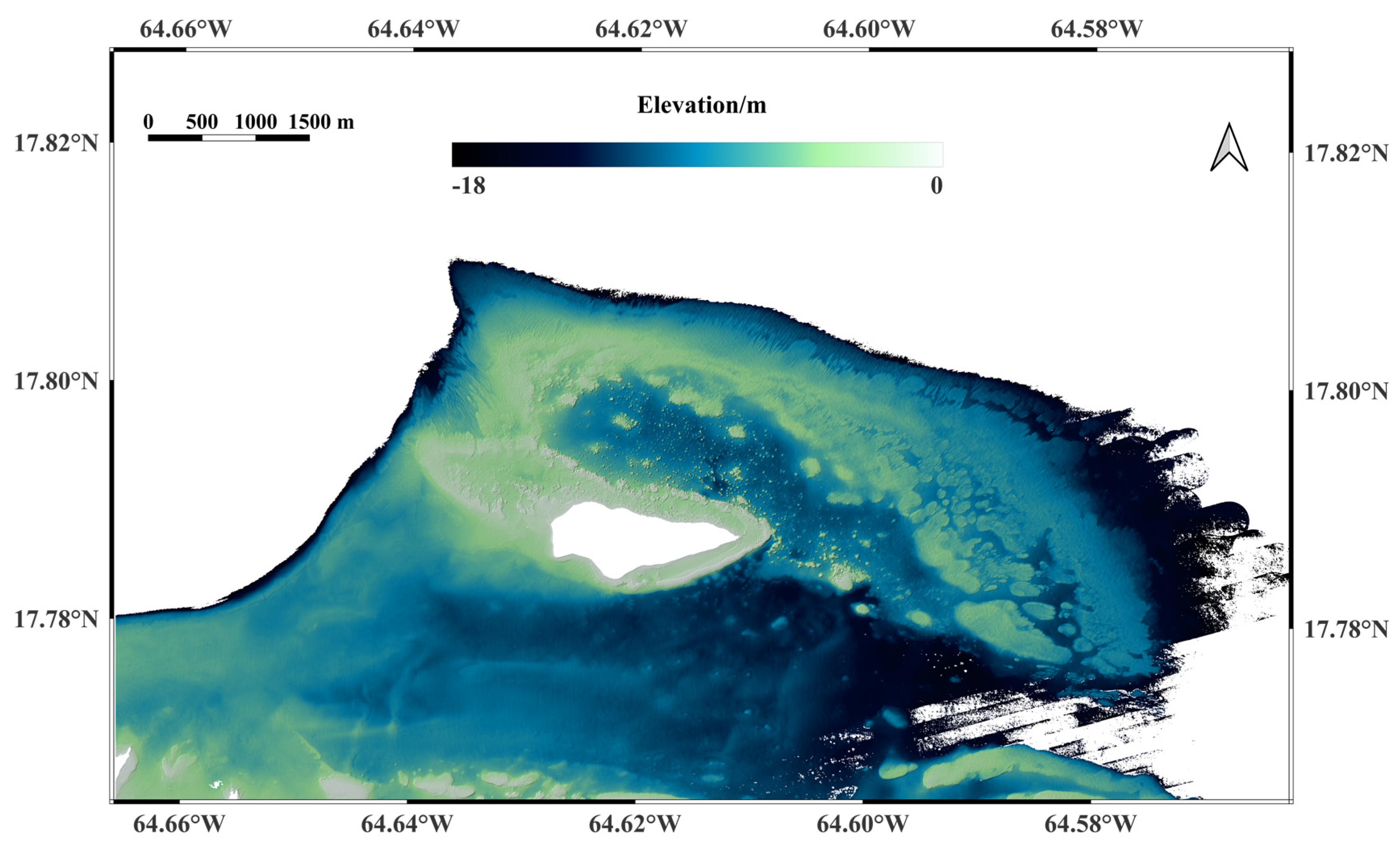
2.1. Study Areas
2.2. Sentinel-2 Imagery
2.3. ICESat-2 Lidar Dataset
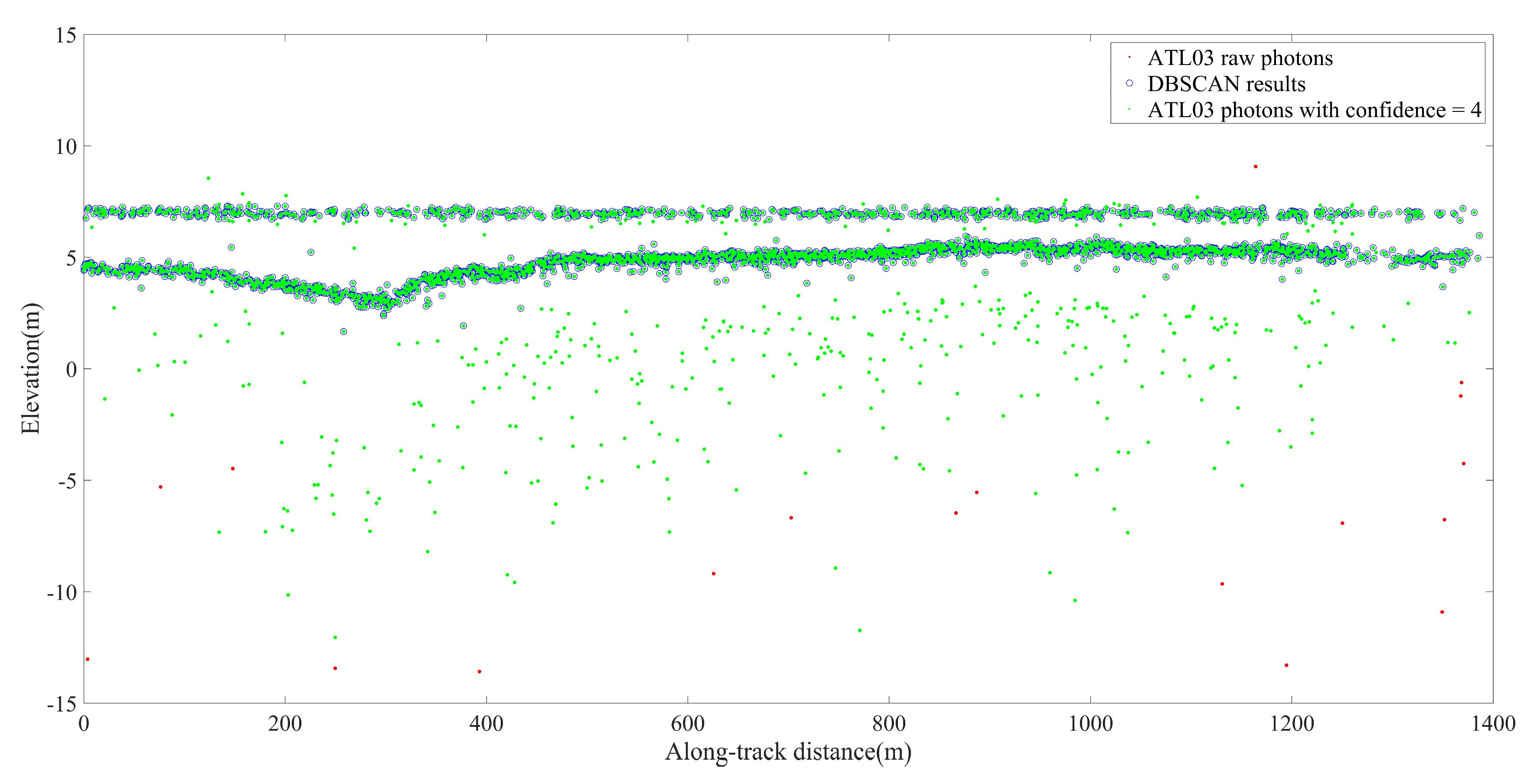
2.4. Detection of Seafloor Topographic Photons in ICESat-2 Data
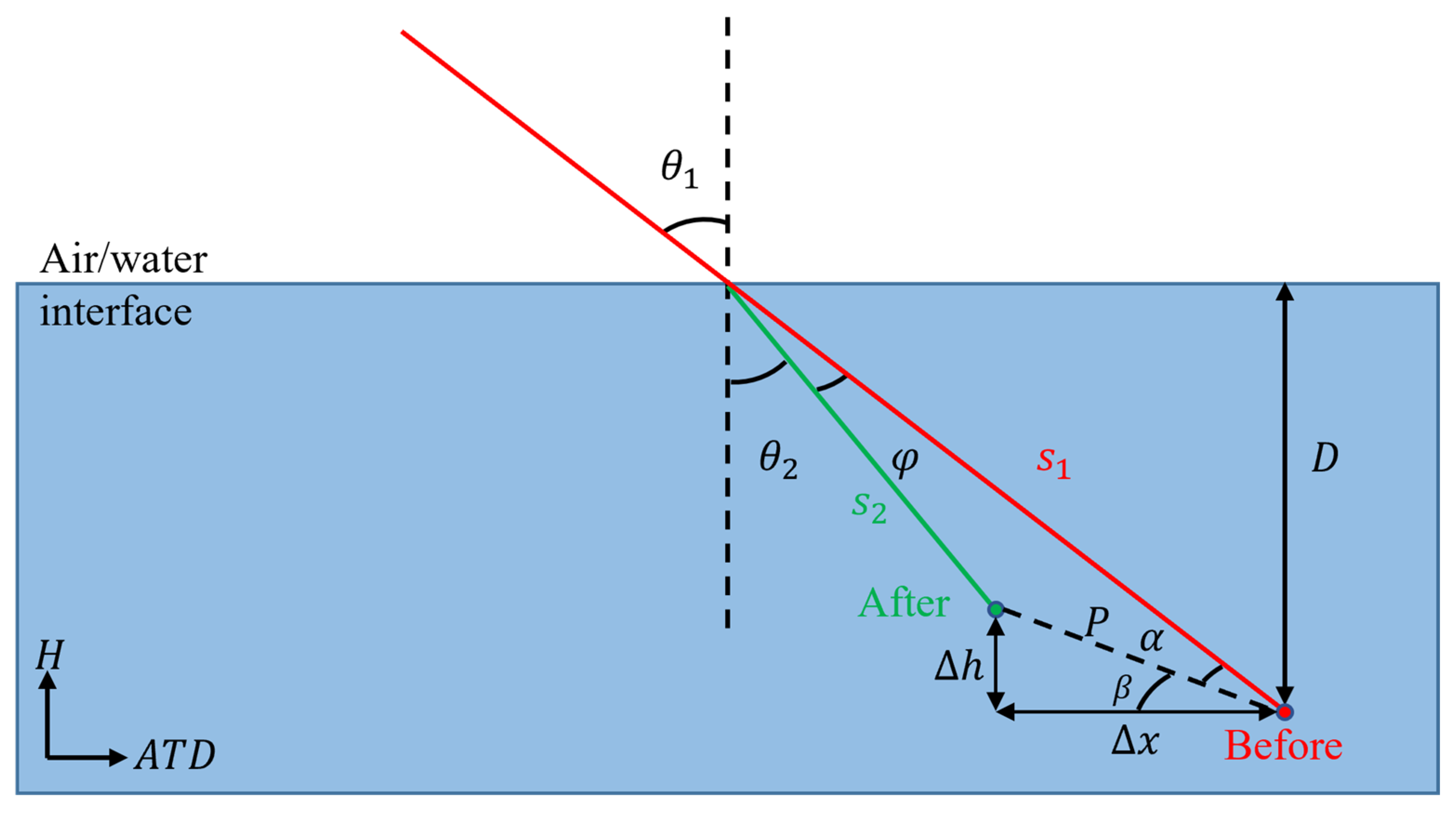
2.5. Bathymetric Correction for Seafloor Photons
2.6. Selection of Optical Deep-Water Areas and Sun Glint Correction
2.7. SDB Method Based on ICESat-2 Water Depth Data
2.8. Evaluation Metrics for SDB Results
3. Results
3.1. ICESat-2 Bathymetric Points
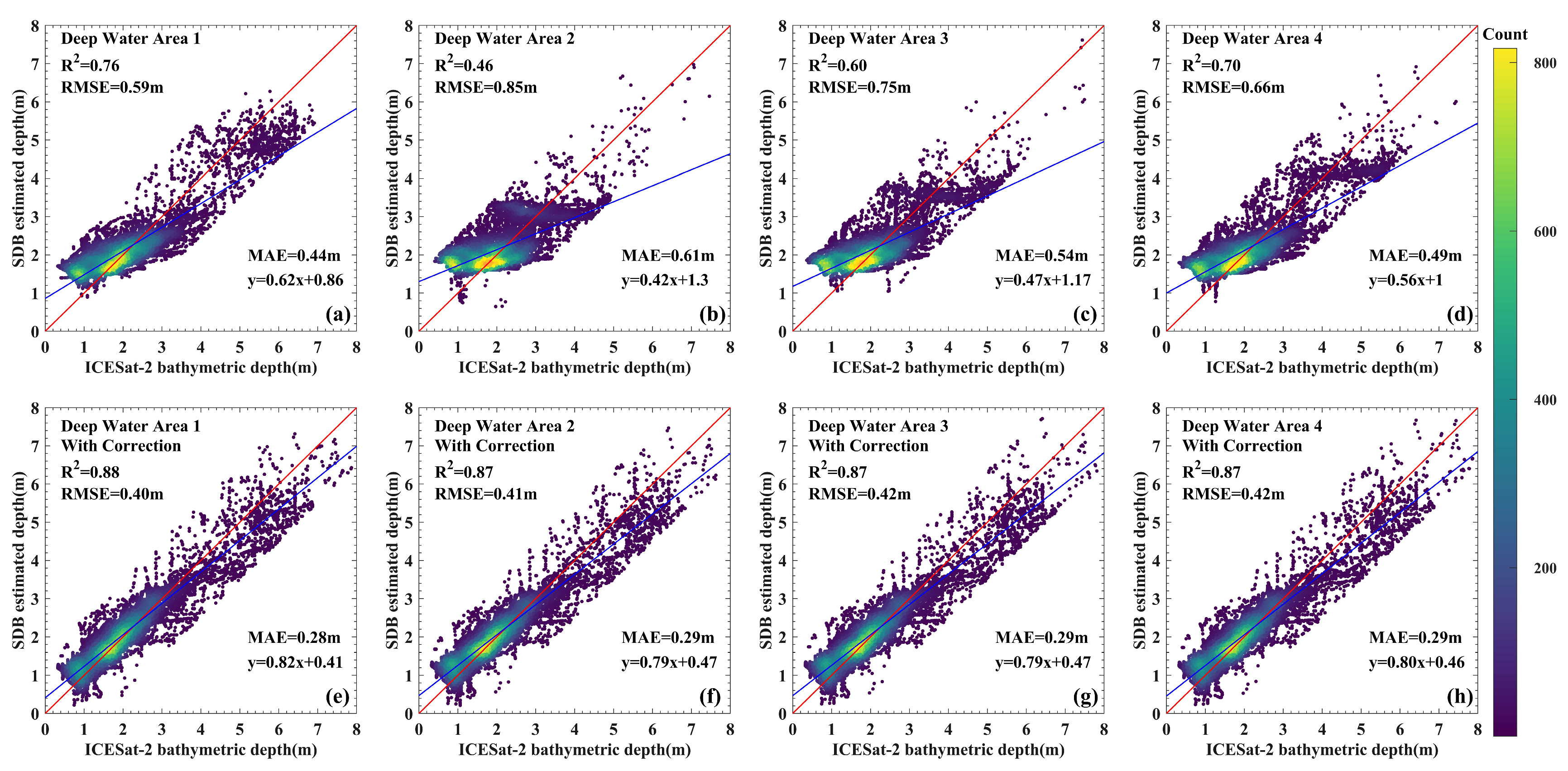
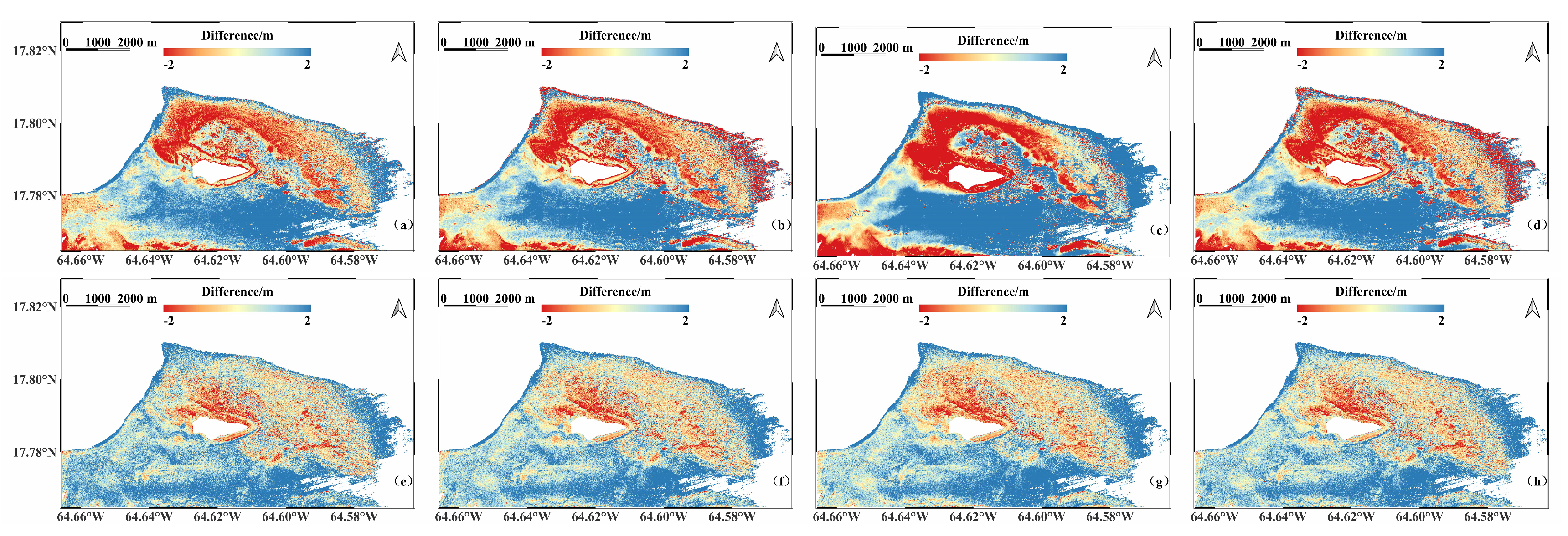
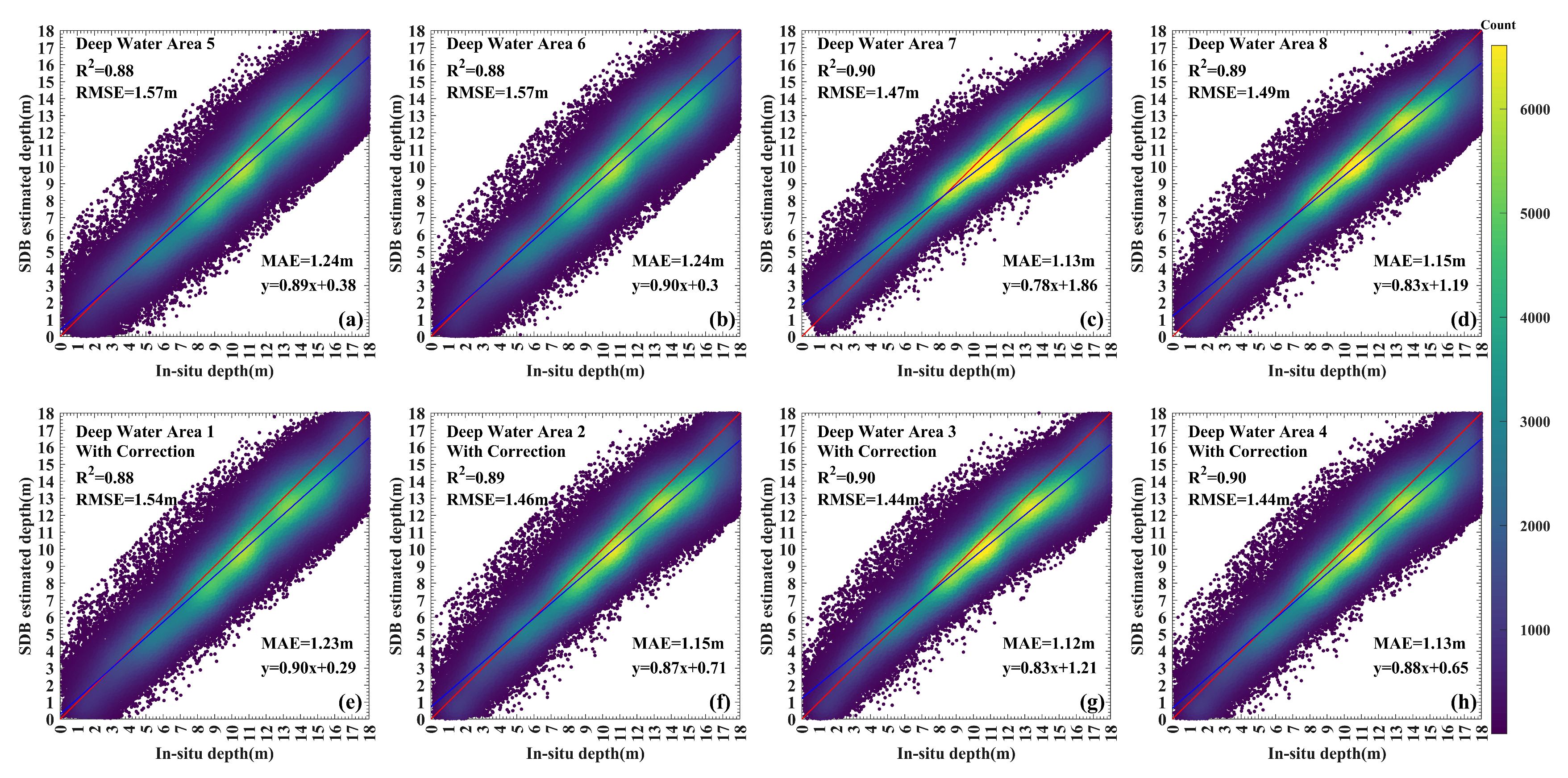
3.2. Bathymetry of Different Optical Deep-Water Areas from the Same Image
3.3. Bathymetry of the Same Optical Deep-Water Areas from Differently Dated Images
4. Discussion
4.1. Availability of High-Confidence Photons in Water for the ATL03 Product
4.2. Equivalent Effect of Sun Glint Correction in Deep-Water Areas and Artificially Identifying Optimal Deep-Water Areas
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kutser, T.; Hedley, J.; Giardino, C.; Roelfsema, C.; Brando, V.E. Remote sensing of shallow waters—A 50 year retrospective and future directions. Remote Sens. Environ. 2020, 240, 111619. [Google Scholar] [CrossRef]
- Lubin, D.; Li, W.; Dustan, P.; Mazel, C.H.; Stamnes, K. Spectral Signatures of Coral Reefs: Features from Space. Remote Sens. Environ. 2001, 75, 127–137. [Google Scholar] [CrossRef]
- McCarthy, M.J.; Otis, D.B.; Hughes, D.; Muller-Karger, F.E. Automated high-resolution satellite-derived coastal bathymetry mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102693. [Google Scholar] [CrossRef]
- Bandini, F.; Kooij, L.; Mortensen, B.K.; Caspersen, M.B.; Thomsen, L.G.; Olesen, D.; Bauer-Gottwein, P. Mapping inland water bathymetry with Ground Penetrating Radar (GPR) on board Unmanned Aerial Systems (UASs). J. Hydrol. 2023, 616, 128789. [Google Scholar] [CrossRef]
- Costa, B.M.; Battista, T.A.; Pittman, S.J. Comparative evaluation of airborne LiDAR and ship-based multibeam SoNAR bathymetry and intensity for mapping coral reef ecosystems. Remote Sens. Environ. 2009, 113, 1082–1100. [Google Scholar] [CrossRef]
- Wang, C.-K.; Philpot, W.D. Using airborne bathymetric lidar to detect bottom type variation in shallow waters. Remote Sens. Environ. 2007, 106, 123–135. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. Measurement of seagrass standing crop using satellite and digital airborne remote sensing. Oceanogr. Lit. Rev. 1998, 45, 1069. [Google Scholar] [CrossRef]
- Kutser, T.; Miller, I.; Jupp, D.L.B. Mapping coral reef benthic substrates using hyperspectral space-borne images and spectral libraries. Estuar. Coast. Shelf Sci. 2006, 70, 449–460. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Kovacs, E.; Roelfsema, C.; Lyons, M.; Zhao, S.; Phinn, S. Seagrass habitat mapping: How do Landsat 8 OLI, Sentinel-2, ZY-3A, and Worldview-3 perform? Remote Sens. Lett. 2018, 9, 686–695. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Acharya, P.K.; Berk, A.; Matthew, M.W.; Gorodetzky, D. Remote bathymetry of the littoral zone from AVIRIS, LASH, and QuickBird imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 337–347. [Google Scholar] [CrossRef]
- Albert, A.; Gege, P. Inversion of irradiance and remote sensing reflectance in shallow water between 400 and 800 nm for calculations of water and bottom properties. Appl. Opt. 2006, 45, 2331–2343. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Chen, R.F.; Peacock, T.G. Properties of the water column and bottom derived from Airborne Visible Infrared Imaging Spectrometer (AVIRIS) data. J. Geophys. Res. Ocean. 2001, 106, 11639–11651. [Google Scholar] [CrossRef]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Benny, A.H.; Dawson, G.J. Satellite Imagery as an Aid to Bathymetric Charting in the Red Sea. Cartogr. J. 2013, 20, 5–16. [Google Scholar] [CrossRef]
- Weidmark, W.C.; Jain, S.C.; Zwick, H.H.; Miller, J.R. Passive bathymetric measurements in the Bruce Peninsula region of Ontario. In Proceeding of the 15th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 11–15 May 1981; pp. 811–822. [Google Scholar]
- Lyzenga, D. Shallow-Water Reflectance Modeling with Applications to Remote Sensing of the Ocean Floor. In Proceeding of the 13th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 23–27 April 1979; Volume 1, pp. 583–602. [Google Scholar]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef]
- Chaoyu, Y.; Dingtian, Y. Improved method to analyze hyperspectral characteristics of coral reefs. Chin. Opt. Lett. 2014, 12, S21001. [Google Scholar] [CrossRef]
- Jay, S.; Guillaume, M. Regularized estimation of bathymetry and water quality using hyperspectral remote sensing. Int. J. Remote Sens. 2016, 37, 263–289. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, L.; He, M.-X. Simulation of shallow water depth data merging for HJ-1A/HSI and EO-1/Hyperion. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2957–2960. [Google Scholar]
- Gülher, E.; Alganci, U. Satellite-Derived Bathymetry Mapping on Horseshoe Island, Antarctic Peninsula, with Open-Source Satellite Images: Evaluation of Atmospheric Correction Methods and Empirical Models. Remote Sens. 2023, 15, 2568. [Google Scholar] [CrossRef]
- Flener, C.; Lotsari, E.; Alho, P.; Käyhkö, J. Comparison of empirical and theoretical remote sensing based bathymetry models in river environments. River Res. Appl. 2012, 28, 118–133. [Google Scholar] [CrossRef]
- Ceyhun, Ö.; Yalçın, A. Remote sensing of water depths in shallow waters via artificial neural networks. Estuar. Coast. Shelf Sci. 2010, 89, 89–96. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef]
- Bué, I.; Catalão, J.; Semedo, Á. Intertidal Bathymetry Extraction with Multispectral Images: A Logistic Regression Approach. Remote Sens. 2020, 12, 1311. [Google Scholar] [CrossRef]
- Prasetya, M.I.; Siregar, V.P.; Agus, S.B. Comparison of Satellite-Derived Bathymetry Algorithm Accuracy Using Sentinel-2 Multispectral Satellite Image. J. Kelaut. Trop. 2023, 26, 113–125. [Google Scholar] [CrossRef]
- Rahman, A. Depth Estimation of Shallow Water Using Multispectral Satellite Imagery Sentinel-2a. J. Segara 2020, 16. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.X.; Su, H.B.; Wang, J. Bathymetry retrieval from optical images with spatially distributed support vector machines. Giscience Remote Sens. 2019, 56, 323–337. [Google Scholar] [CrossRef]
- Misra, A.; Vojinovic, Z.; Ramakrishnan, B.; Luijendijk, A.; Ranasinghe, R. Shallow water bathymetry mapping using Support Vector Machine (SVM) technique and multispectral imagery. Int. J. Remote Sens. 2018, 39, 4431–4450. [Google Scholar] [CrossRef]
- Zhou, W.; Tang, Y.; Jing, W.; Li, Y.; Yang, J.; Deng, Y.; Zhang, Y. A Comparison of Machine Learning and Empirical Approaches for Deriving Bathymetry from Multispectral Imagery. Remote Sens. 2023, 15, 393. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 2010, 2, 71–82. [Google Scholar] [CrossRef]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569–1578. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Yang, H.; Tang, S.; Liu, Y.; Liu, Y. An Appraisal of Atmospheric Correction and Inversion Algorithms for Mapping High-Resolution Bathymetry Over Coral Reef Waters. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4204511. [Google Scholar] [CrossRef]
- Xu, Y.; Cao, B.; Deng, R.; Cao, B.; Liu, H.; Li, J. Bathymetry over broad geographic areas using optical high-spatial-resolution satellite remote sensing without in-situ data. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103308. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote Sens. 2010, 6, 115–125. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Westley, K. Satellite-derived bathymetry for maritime archaeology: Testing its effectiveness at two ancient harbours in the Eastern Mediterranean. J. Archaeol. Sci. Rep. 2021, 38, 103030. [Google Scholar] [CrossRef]
- Harmel, T.; Chami, M.; Tormos, T.; Reynaud, N.; Danis, P.-A. Sunglint correction of the Multi-Spectral Instrument (MSI)-SENTINEL-2 imagery over inland and sea waters from SWIR bands. Remote Sens. Environ. 2018, 204, 308–321. [Google Scholar] [CrossRef]
- Su, H.; Liu, H.; Heyman, W.D. Automated Derivation of Bathymetric Information from Multi-Spectral Satellite Imagery Using a Non-Linear Inversion Model. Mar. Geod. 2008, 31, 281–298. [Google Scholar] [CrossRef]
- Mishra, D.; Narumalani, S.; Rundquist, D.; Lawson, M. Benthic Habitat Mapping in Tropical Marine Environments Using QuickBird Multispectral Data. Photogramm. Eng. Remote Sens. 2006, 72, 1037–1048. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Atmospheric correction for satellite-derived bathymetry in the Caribbean waters: From a single image to multi-temporal approaches using Sentinel-2A/B. Opt. Express 2020, 28, 11742–11766. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Chu, S.; Cheng, L.; Ji, C.; Li, M.; Shen, W. Satellite-derived bathymetry using Landsat-8 and Sentinel-2A images: Assessment of atmospheric correction algorithms and depth derivation models in shallow waters. Opt. Express 2022, 30, 3238–3261. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Xu, N.; Ma, X.; Ma, Y.; Zhao, P.; Yang, J.; Wang, X.H. Deriving Highly Accurate Shallow Water Bathymetry From Sentinel-2 and ICESat-2 Datasets by a Multitemporal Stacking Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6677–6685. [Google Scholar] [CrossRef]
- Chu, S.; Cheng, L.; Ruan, X.; Zhuang, Q.; Zhou, X.; Li, M.; Shi, Y. Technical framework for shallow-water bathymetry with high reliability and no missing data based on time-series sentinel-2 images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8745–8763. [Google Scholar] [CrossRef]
- Abdul Gafoor, F.; Al-Shehhi, M.R.; Cho, C.-S.; Ghedira, H. Gradient Boosting and Linear Regression for Estimating Coastal Bathymetry Based on Sentinel-2 Images. Remote Sens. 2022, 14, 5037. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2007, 27, 3025–3033. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite-2 Mission: A Global Geolocated Photon Product Derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Jasinski, M.F.; Stoll, J.D.; Cook, W.B.; Ondrusek, M.; Stengel, E.; Brunt, K. Inland and Near Shore Water Profiles Derived from the High Altitude Multiple Altimeter Beam Experimental Lidar (MABEL). J. Coast. Res. 2016, 76, 44–55. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Yang, J.; Wang, X.H.; Wang, Y.; Xu, R. Deriving Tidal Flat Topography Using ICESat-2 Laser Altimetry and Sentinel-2 Imagery. Geophys. Res. Lett. 2022, 49, e2021GL096813. [Google Scholar] [CrossRef]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Technical note: Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2007, 26, 2107–2112. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Andrefouet, S.; Tyler, M.R. Sea surface correction of high spatial resolution ikonos images to improve bottom mapping in near-shore environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Thomas, N.; Pertiwi, A.P.; Traganos, D.; Lagomasino, D.; Poursanidis, D.; Moreno, S.; Fatoyinbo, L. Space-Borne Cloud-Native Satellite-Derived Bathymetry (SDB) Models Using ICESat-2 And Sentinel-2. Geophys. Res. Lett. 2021, 48, e2020GL092170. [Google Scholar] [CrossRef]




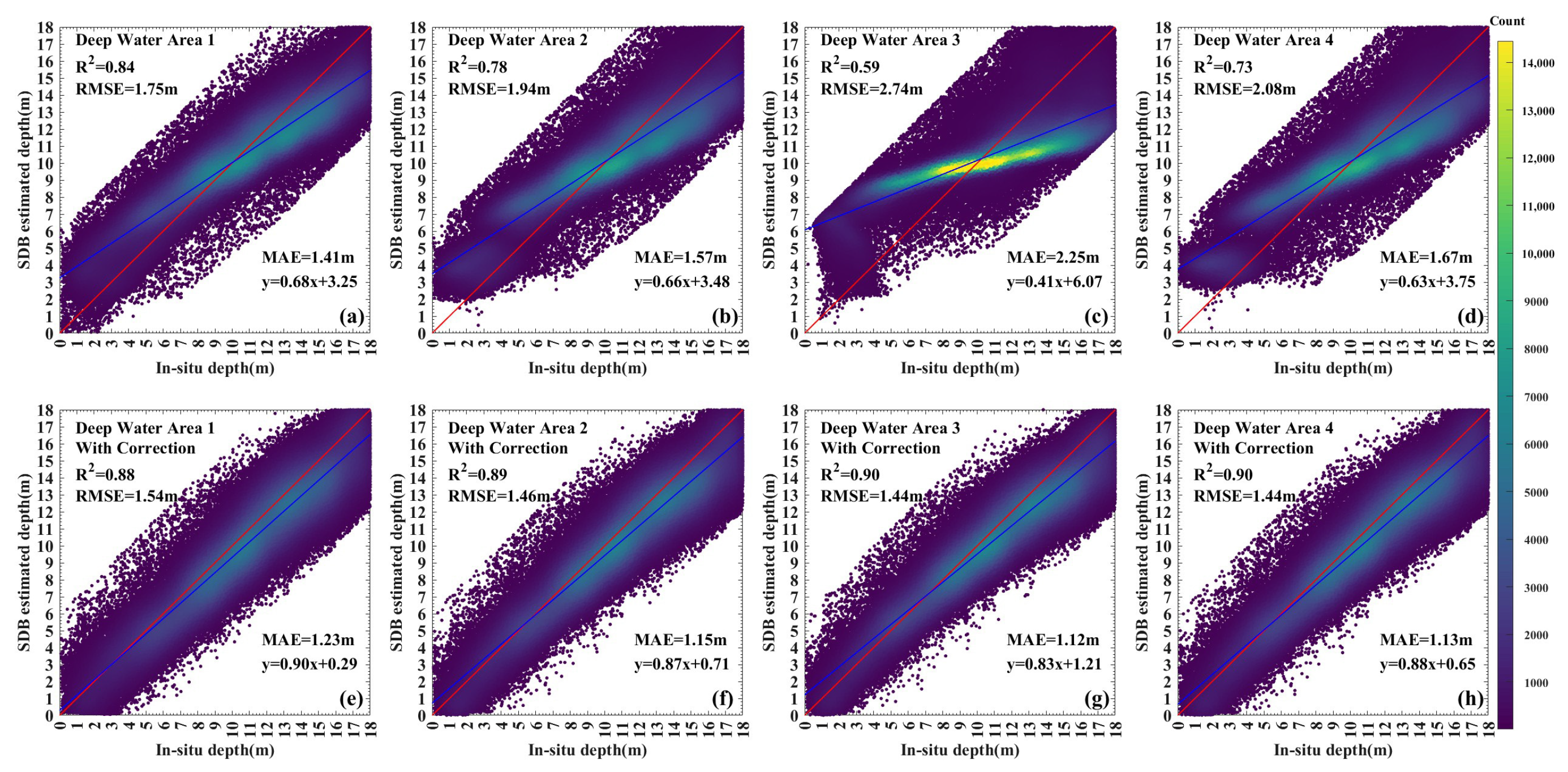
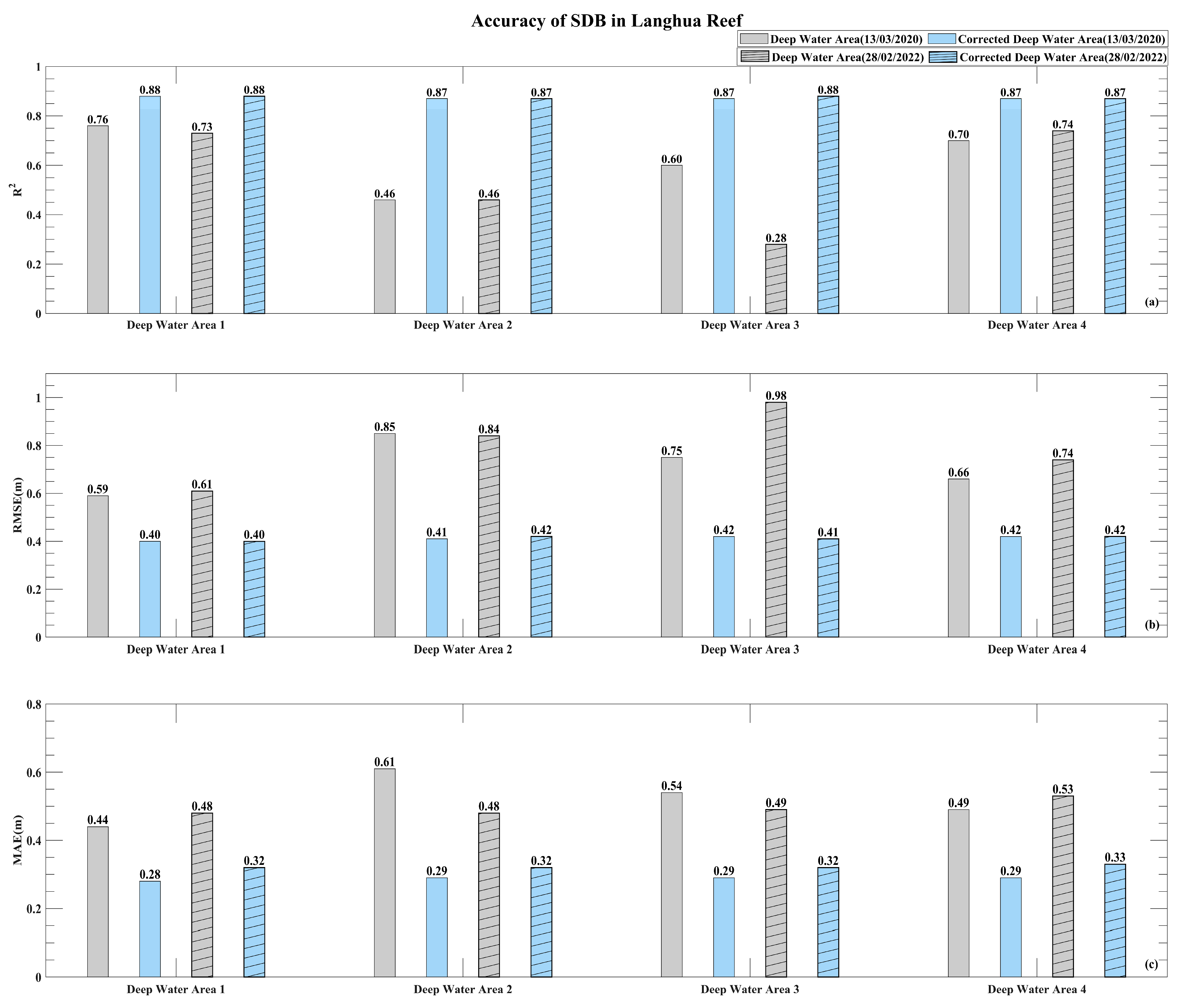
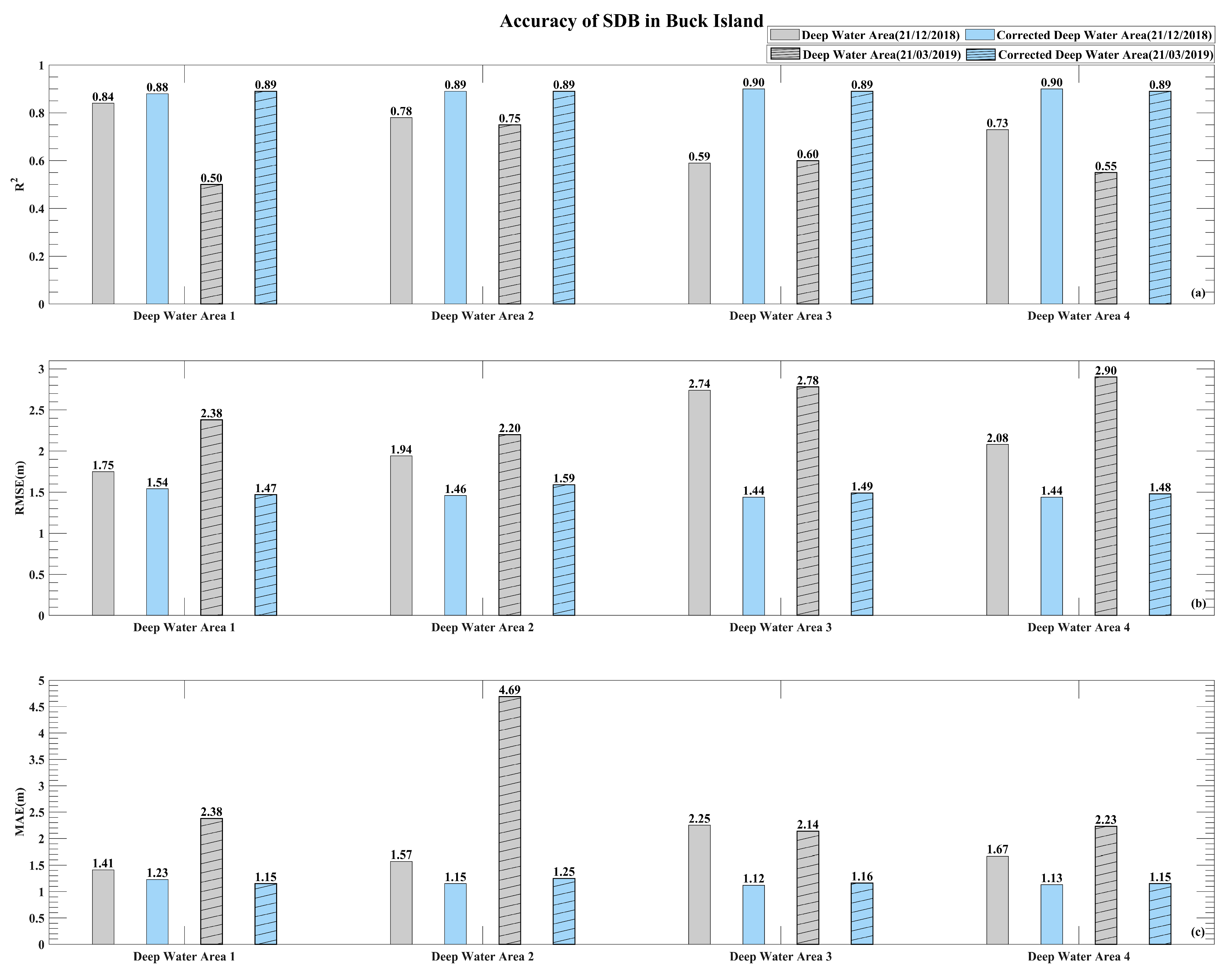

| Study Area | Langhua Jiao | Buck Island |
|---|---|---|
| Location | 16.012–16.087°N | 17.783–17.790°N |
| 112.437–112.079°E | 64.627–64.610°W | |
| Sentinel-2 L2A | 10 March 2020 | 21 December 2018 |
| 28 February 2022 | 21 March 2019 | |
| ICESat-2 ATL03 | 18 October 2018 | 15 October 2019 |
| 15 January 2020 | 14 March 2021 | |
| 12 September 2021 | 12 April 2021 | |
| 12 December 2021 | ||
| In situ data | 30% of ICESat-2 points | NOAA NGS Topo-bathy Lidar DEM |
| Christiansted Harbor Water Level Data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, D.; Li, Y.; He, X.; Yang, Z.; Wu, Y.; Wu, T.; Xu, N. Methods to Improve the Accuracy and Robustness of Satellite-Derived Bathymetry through Processing of Optically Deep Waters. Remote Sens. 2023, 15, 5406. https://doi.org/10.3390/rs15225406
Jia D, Li Y, He X, Yang Z, Wu Y, Wu T, Xu N. Methods to Improve the Accuracy and Robustness of Satellite-Derived Bathymetry through Processing of Optically Deep Waters. Remote Sensing. 2023; 15(22):5406. https://doi.org/10.3390/rs15225406
Chicago/Turabian StyleJia, Dongzhen, Yu Li, Xiufeng He, Zhixiang Yang, Yihao Wu, Taixia Wu, and Nan Xu. 2023. "Methods to Improve the Accuracy and Robustness of Satellite-Derived Bathymetry through Processing of Optically Deep Waters" Remote Sensing 15, no. 22: 5406. https://doi.org/10.3390/rs15225406
APA StyleJia, D., Li, Y., He, X., Yang, Z., Wu, Y., Wu, T., & Xu, N. (2023). Methods to Improve the Accuracy and Robustness of Satellite-Derived Bathymetry through Processing of Optically Deep Waters. Remote Sensing, 15(22), 5406. https://doi.org/10.3390/rs15225406







