High-Accuracy Quasi-Geoid Determination Using Molodensky’s Series Solutions and Integrated Gravity/GNSS/Leveling Data
Abstract
:1. Introduction
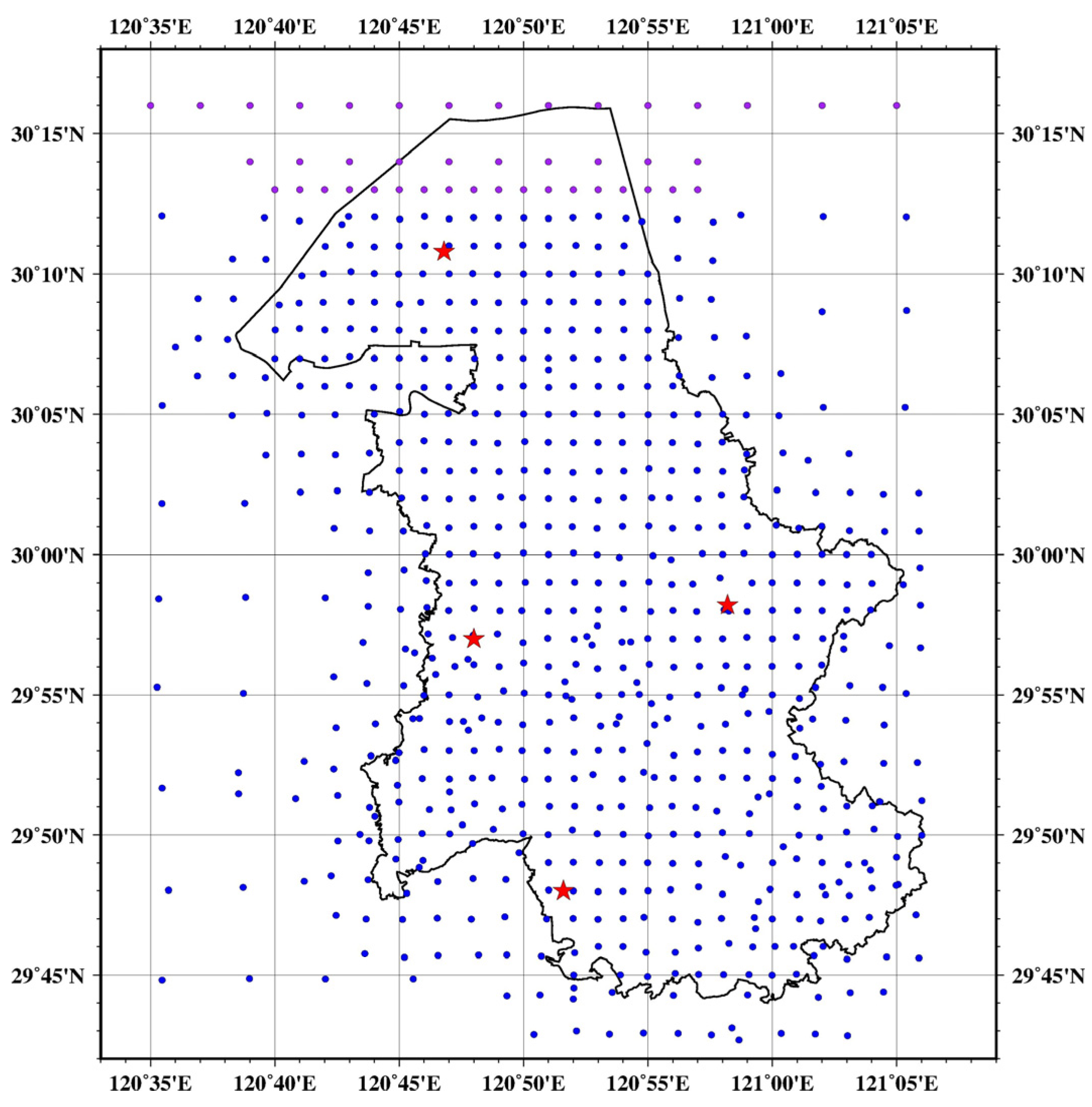
2. Datasets
2.1. Topographic Data
2.2. Ground Gravity Anomaly
2.3. GGM
2.4. GNSS/Leveling Data
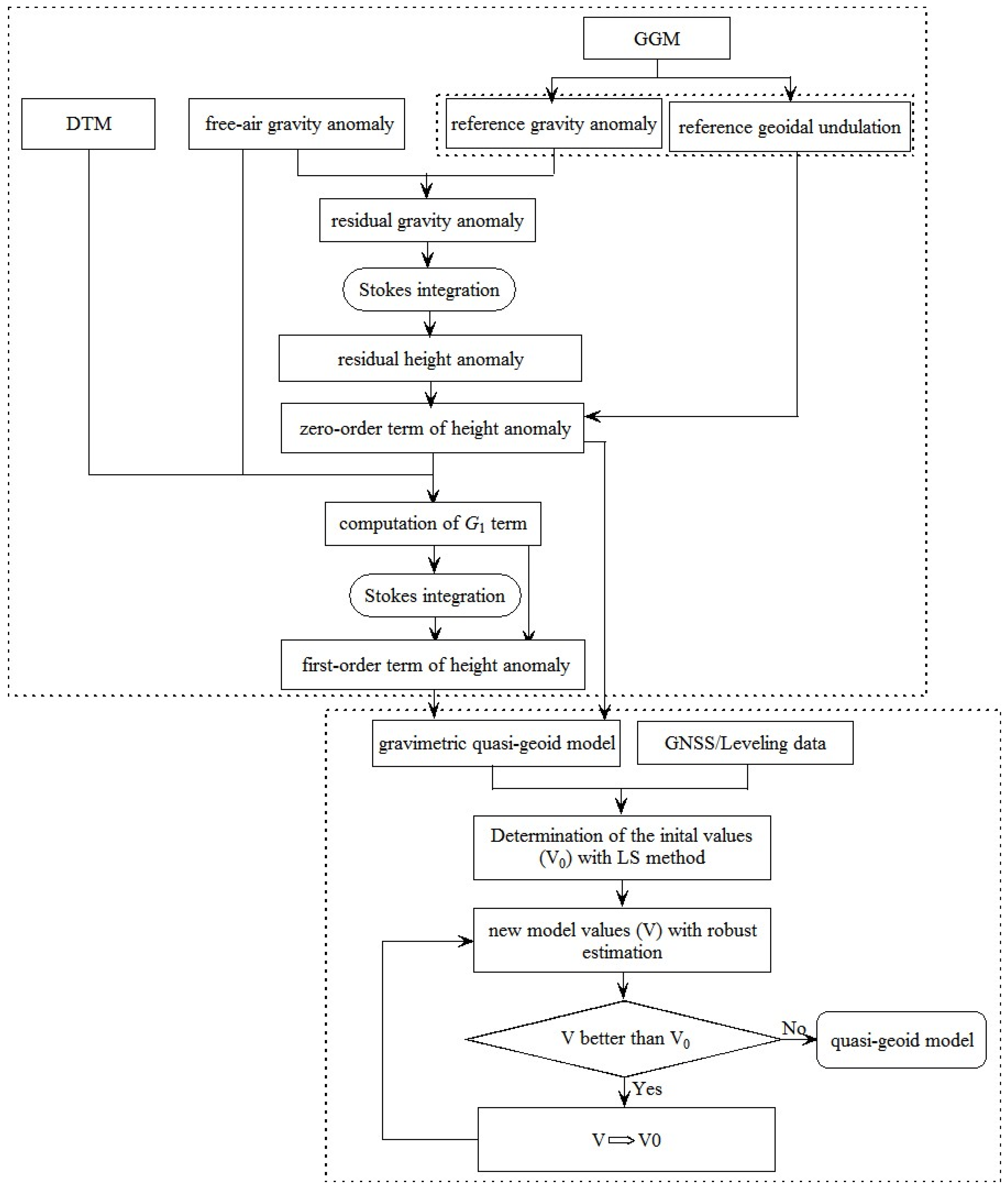
3. Method for Local Quasi-Geoid Determinations
3.1. Linearized Molodensky’s Solution
3.2. Combination of Heights
4. Results and Discussion
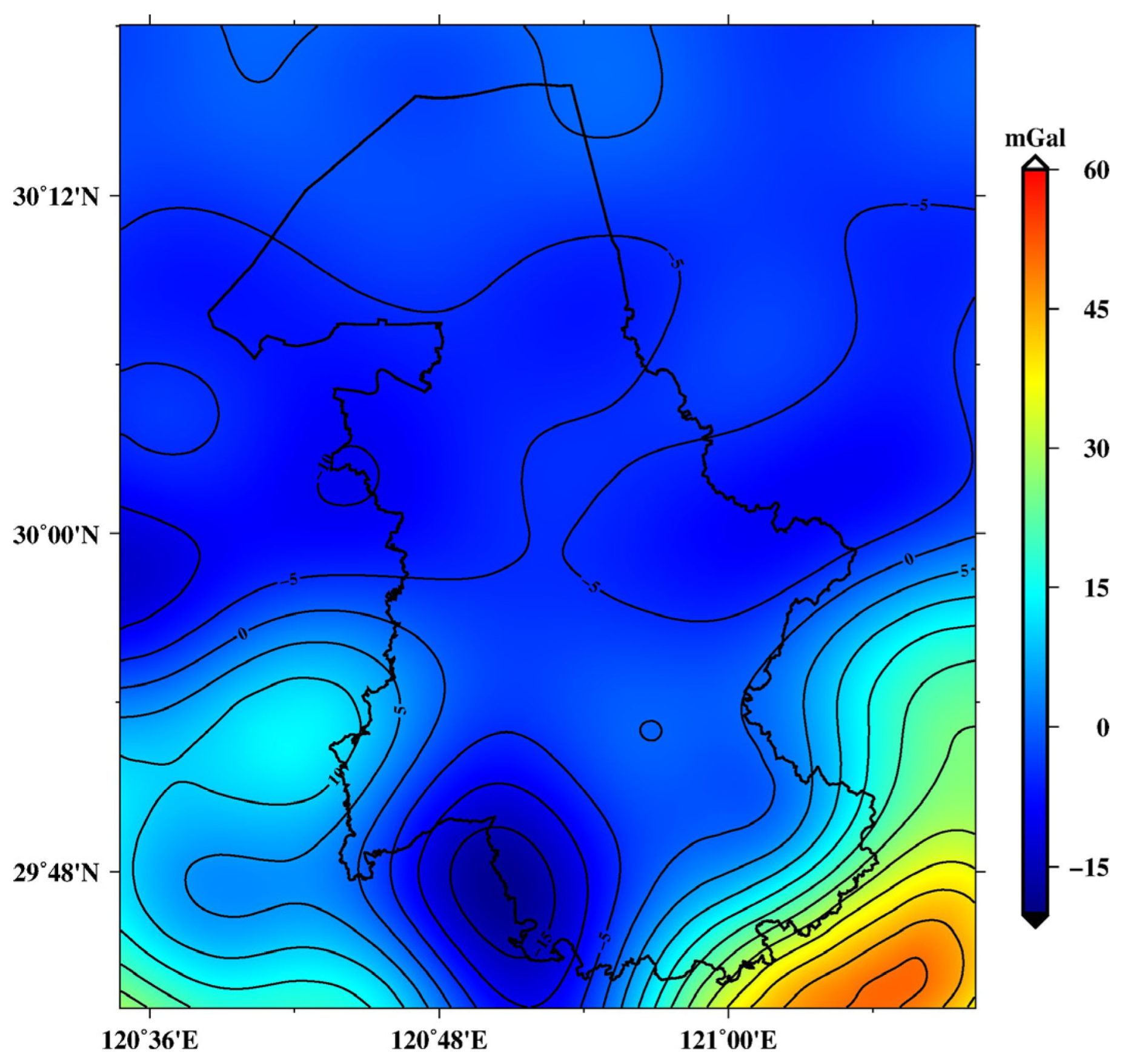
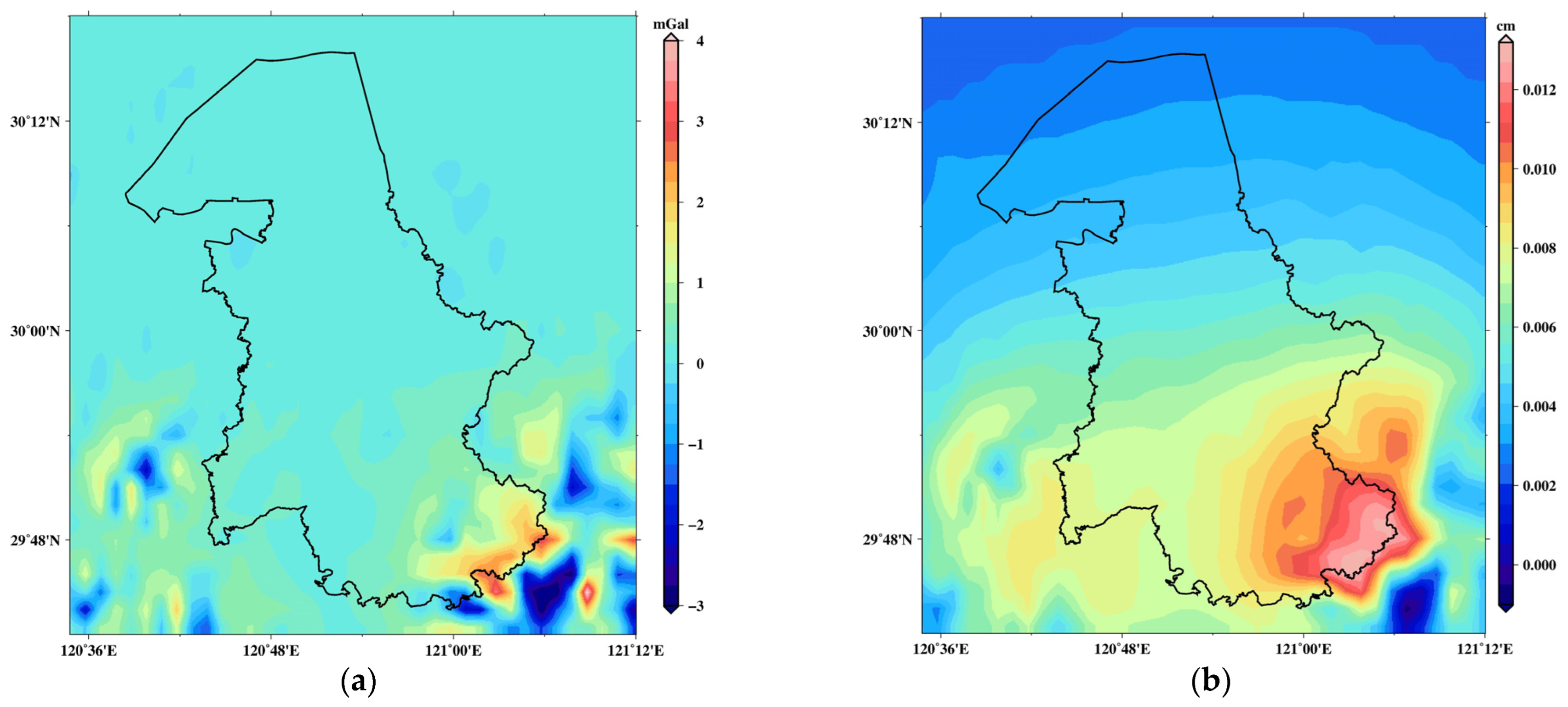
4.1. Computation of Hybrid Quasi-Geoid Model
- Computation of the zero-order term of the height anomaly: The residual height anomaly was computed using Stokes’ theory by taking the difference (residual gravity anomaly) between the free-air and reference gravity anomalies derived from EGM2008. Adding the reference geoidal undulation to the residual height anomaly yielded the zero-order term of the height anomaly, ζ0;
- Computation of the G1 term: Utilizing Equation (13), the G1 term was determined based on the DTM, the gridded free-air anomaly, and the zero-order term of the height anomaly, ζ0;
- Computation of the first-order term of the height anomaly: The effect of the first-order term on height anomaly, denoted as ζ1, was obtained using the spherical Stokes’ integral given by
- 4.
- Computation of the gravimetric quasi-geoid model: The gravimetric quasi-geoid model, denoted as ζgrav is expressed by
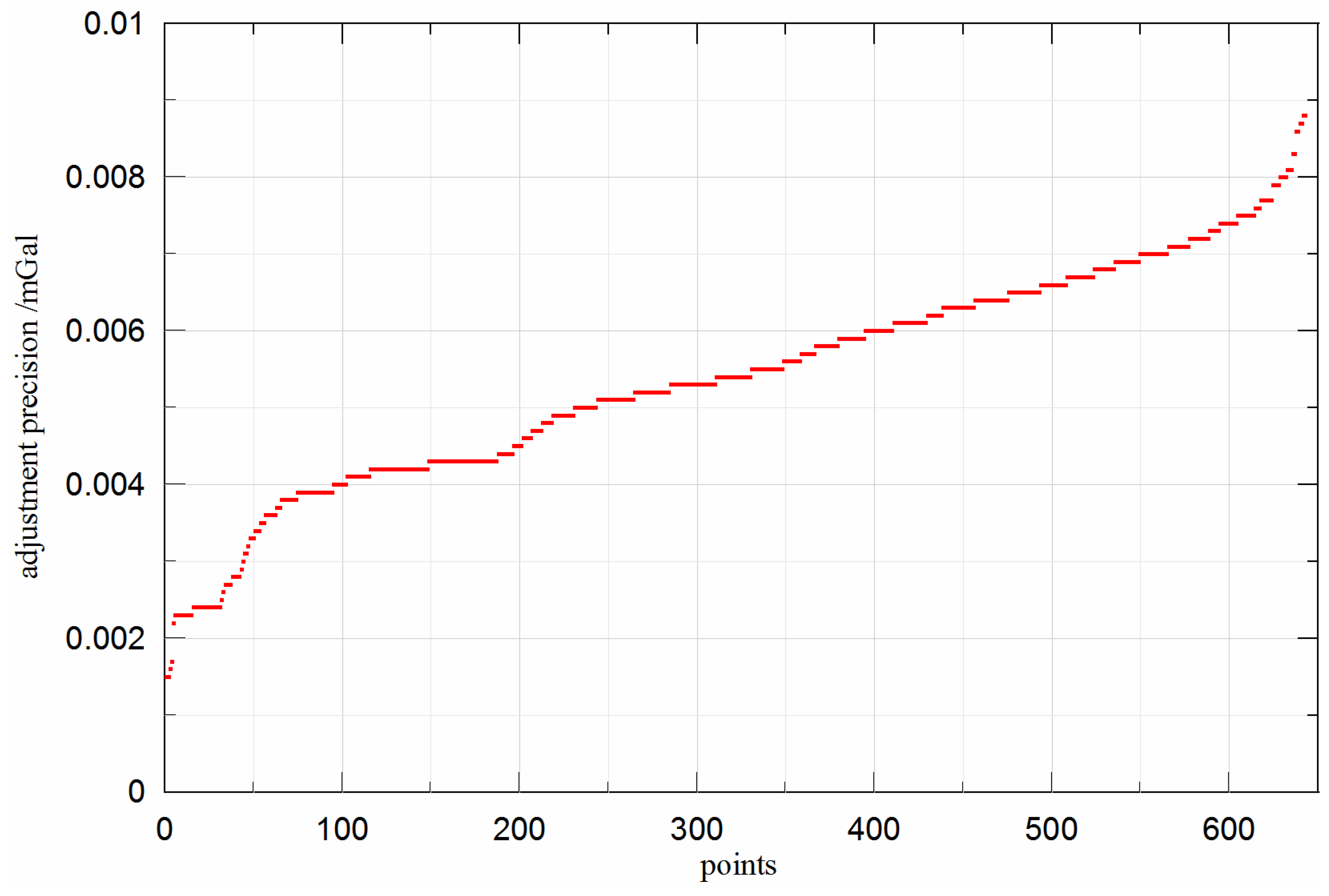
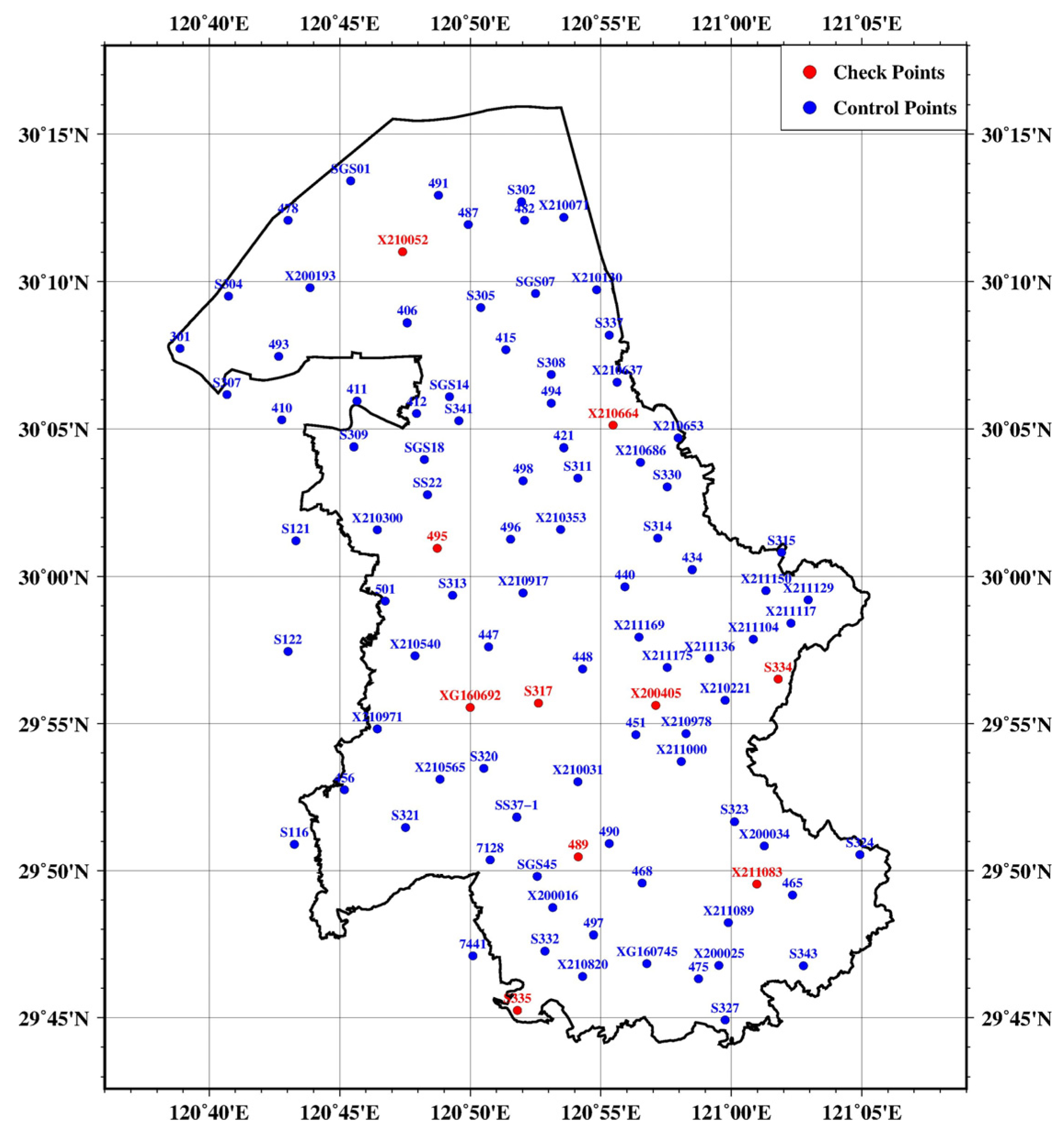
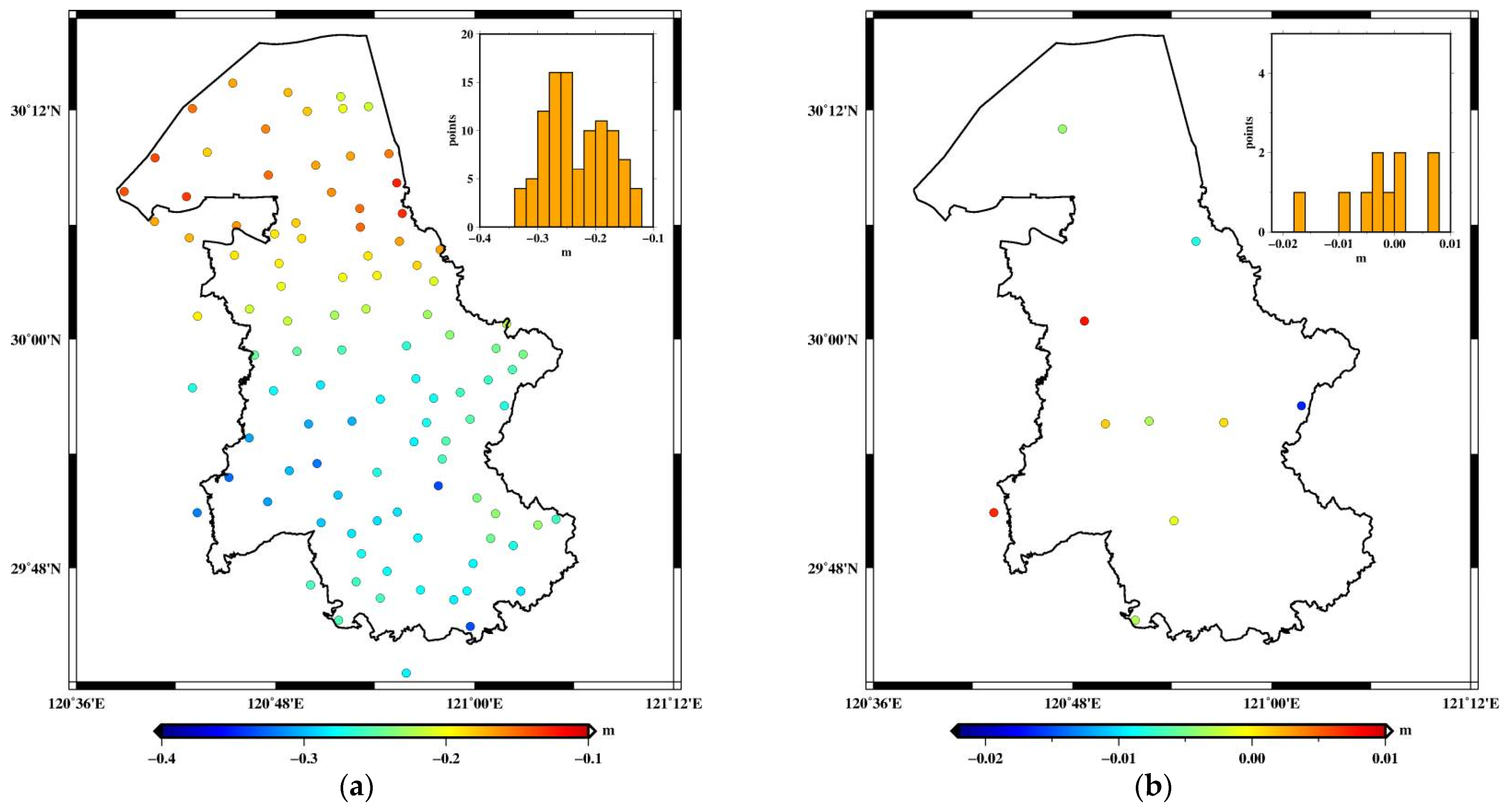
4.2. Accuracy Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brennecke, J.; Groten, E. The deviations of the sea surface from the geoid and their effect on geoid computation. Bull. Geod. 1977, 51, 47–51. [Google Scholar] [CrossRef]
- Sansò, F.; Sideris, M.G. Geoid Determination: Theory and Methods, Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Steinbergerk, B.; Rathnayake, S.; Kendall, E. The Indian Ocean Geoid Low at a plume-slab. Tectonophysics 2021, 817, 229037. [Google Scholar] [CrossRef]
- Falcão, A.P.; Matos, J.; Gonçalves, A.; Casaca, J.; Sousa, J. Preliminary Results of Spatial Modelling of GPS/Levelling Heights: A Local Quasi-Geoid/Geoid for the Lisbon Area. In Gravity, Geoid and Earth Observation; International Association of Geodesy, Symposia; Mertikas, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 135. [Google Scholar]
- Fotopoulos, G. Calibration of geoid error models via a combined adjustment of ellipsoidal, orthometric and gravimetric geoid height data. J. Geod. 2005, 79, 111–123. [Google Scholar] [CrossRef]
- Grigoriadis, V.N.; Vergos, G.S.; Barzaghi, R.; Carrion, D.; Koc, O. Collocation and FFT-based geoid estimation within the Colorado 1 cm geoid experiment. J. Geod. 2021, 95, 52. [Google Scholar] [CrossRef]
- Sansò, F.; Rummel, R. Geodetic Boundary Value Problems in View of the One Centimeter Geoid; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Kotsakis, C.; Tsalis, I. Combination of Geometric and Orthometric Heights in the Presence of Geoid and Quasi-geoid Models. In Gravity, Geoid and Height Systems; International Association of Geodesy, Symposia; Marti, U., Ed.; Springer: Cham, Switzerland, 2014; Volume 141. [Google Scholar]
- Featherstone, W.E.; Olliver, J.G. A method to validate gravimetric-geoid computation software based on Stokes’s integral formula. J. Geod. 1997, 71, 571–576. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Topographic effects by the Stokes-Helmert method of geoid and quasi-geoid determinations. J. Geod. 2000, 74, 255–268. [Google Scholar] [CrossRef]
- Ardestani, V.E.; Martinec, Z. Geoid determination through ellipsoidal Stokes boundary-value problem. Stud. Geophys. Et Geod. 2000, 4, 353–363. [Google Scholar] [CrossRef]
- Molodensky, M.S.; Eremeev, V.F.; Yurkina, M.I. Methods for the Study of the External Gravitational Field and Figure of the Earth; Israeli Program for Scientific Translations: Jerusalem, Israel, 1962. [Google Scholar]
- Brovar, V.V. On the solution of Molodensky’s boundary value problem. Bull. Geod. 1964, 72, 167–173. [Google Scholar] [CrossRef]
- Ardalan, A.A.; Grafarend, E.W.; Ihde, J. Molodensky potential telluroid based on a minimum-distance map. Case study: The quasi-geoid of East Germany in the World Geodetic Datum 2000. J. Geod. 2002, 76, 127–138. [Google Scholar] [CrossRef]
- Kuroishi, Y.; Ando, H.; Fukuda, Y. A new hybrid geoid model for Japan, GSIGE02000. J. Geod. 2002, 76, 428–436. [Google Scholar] [CrossRef]
- Nahavandchi, H.; Soltanpour, A. Improved determination of heights using a conversion surface by combining gravimetric quasi-geoid/geoid and GPS-levelling height differences. Stud. Geophys. Geod. 2006, 50, 165–180. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Vergos, G.S.; Grigoriadis, V.N.; Andritsanos, V.D. Adjustment of Collocated GPS, Geoid and Orthometric Height Observations in Greece. Geoid or Orthometric Height Improvement? In Geodesy for Planet Earth; International Association of Geodesy, Symposia; Kenyon, S., Pacino, M., Marti, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 136. [Google Scholar]
- Hwang, C.; Hsu, H.; Featherstone, W.; Cheng, C.; Yang, M.; Huang, W.; Wang, C.; Huang, J.; Chen, K.; Huang, C.; et al. New gravimetric-only and hybrid geoid models of Taiwan for height modernisation, cross-island datum connection and airborne LiDAR mapping. J. Geod. 2020, 94, 83. [Google Scholar] [CrossRef]
- Yang, Y. Robust estimation of geodetic datum transformation. J. Geod. 1999, 73, 268–274. [Google Scholar] [CrossRef]
- Awange, J.L.; Paláncz, B. Robust Estimation. In Geospatial Algebraic Computations; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Denker, H. Evaluation of SRTM3 and GTOPO30 terrain data in Germany. In International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2005; Volume 129, pp. 218–223. [Google Scholar]
- Amante, C.; Eakins, B.W. ETOPO1, 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS; National Geophysical Data Center, NOAA: Boulder, CO, USA, 2000; Volume 24, p. 19.
- Yang, M.; Hirt, C.; Rexer, M.; Pail, R.; Yamazaki, D. The tree canopy effect in gravity forward modelling. Geophys. J. Int. 2019, 219, 271–289. [Google Scholar] [CrossRef]
- Scherneck, H.G.; Rajner, M.; Engfeldt, A. Superconducting gravimeter and seismometer shedding light on FG5’s offsets, trends and noise: What observations at Onsala Space Observatory can tell us. J. Geod. 2020, 94, 80. [Google Scholar] [CrossRef]
- GB/T 20256-2019; Specifications for the Gravimetry Control. Standards Press of China: Beijing, China, 2019.
- Francis, O. Correction to: Performance assessment of the relative gravimeter Scintrex CG-6. J. Geod. 2022, 96, 2. [Google Scholar] [CrossRef]
- GB/T 17944-2018; Specifications for the Dense Gravity Measurement. Standards Press of China: Beijing, China, 2019.
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Merriam, J.B. Atmospheric pressure and gravity. Geophys. J. Int. 1992, 190, 488–500. [Google Scholar] [CrossRef]
- Spratt, R.S. Modelling the effect of atmospheric pressure variations on gravity. Geophys. J. R. Astron. Soc. 1982, 71, 173–186. [Google Scholar] [CrossRef]
- Wei, S.C.; Xu, J.Q.; Zhou, J.C. Piece-wise linear dynamic adjustment for gravity network. Acta Geod. Cartogr. Sin. 2016, 45, 511–520. [Google Scholar]
- Wijaya, D.D.; Muhammad, N.A.; Prijatna, K.; Sadarviana, V.; Sarsito, D.A.; Pahlevi, A.; Variandy, E.D.; Putra, W. pyGABEUR-ITB: A free software for adjustment of relative gravimeter data. Geomatika 2019, 25, 95–102. [Google Scholar] [CrossRef]
- Hwang, C.; Wang, C.G.; Lee, L.H. Adjustment of relative gravity measurements using weighted and datum-free constraints. Comput. Geosci. 2002, 28, 1005–1015. [Google Scholar] [CrossRef]
- Lagios, E. A Fortran IV program for a least-squares gravity base-station network adjustment. Comput. Geosci. 1983, 10, 263–276. [Google Scholar] [CrossRef]
- Fullea, J.; Fernàndez, M.; Zeyen, H. FA2BOUG-A FORTRAN 90 code to compute Bouguer gravity anomalies from gridded free-air anomalies: Application to the Atlantic-Mediterranean transition zone. Comput. Geosci. 2008, 34, 1665–1681. [Google Scholar] [CrossRef]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly Spaced Data. In Proceedings of the 23rd National Conference ACM, New York, NY, USA, 27–29 August 1968; pp. 517–523. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An earth gravitational model degree 2160: EGM2008. In Proceedings of the 2008 General Assembly of the European Geosciences Union, Vienna, Austria, 13–18 April 2008. [Google Scholar]
- Sánchez, L.; Ågren, J.; Huang, J.; Wang, Y.M.; Forsberg, R. Basic Agreements for the Computation of Station Potential Values as IHRS Coordinates, Geoid Undulations and Height Anomalies within the Colorado 1 cm Geoid Experiment. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems 2018 (GGHS2018), Copenhagen, Denmark, 17–21 September 2018. [Google Scholar]
- Pail, R.; Bruinsma, S.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.-D.; Höck, E.; Reguzzoni, M.; Brockmann, J.M.; Abrikosov, O.; et al. First GOCE gravity field models derived by three different approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
- Vaľko, M.; Mojzeš, M.; Janák, J.; Papčo, J. Comparison of two different solutions to Molodensky’s G1 term. Stud. Geophys. Geod. 2008, 52, 71–86. [Google Scholar] [CrossRef]
- Tiron, M. Some problems regarding the way of solving Molodensky’s integral equation for the earth considered as a plane. Stud. Geophys. Et Geod. 1965, 9, 137–144. [Google Scholar] [CrossRef]
- Moritz, H. Series solutions of Molodensky’s problem. Publ. Deut. Geod. Komm. 1971, A, 70. [Google Scholar] [CrossRef]
- Guo, J.Y. Physical Geodesy. Springer Textbooks in Earth Sciences, Geography and Environment; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Sideris, M.G.; Schwarz, K.P. Solving Molodensky’s series by fast Fourier transform techniques. Bull. Geod. 1986, 60, 51–63. [Google Scholar] [CrossRef]
- Müssle, M.; Heck, B.; Seitz, K.; Grombein, T. On the effect of planar approximation in the Geodetic Boundary Value Problem. Stud. Geophys. Geod. 2014, 58, 536–555. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; Freeman: San Francisco, CA, USA, 1967. [Google Scholar]
- Yu, B.; Guan, Z.; Xu, X.; Yang, L.O. The Application of an Improved Multi-surface Function Based on Earth Gravity Field Model in GPS Leveling Fitting. In Geo-Informatics in Resource Management and Sustainable Ecosystem GRMSE; Communications in Computer and Information, Science; Bian, F., Xie, Y., Cui, X., Zeng, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 399. [Google Scholar]
- Klees, R.; Prutkin, I. The combination of GNSS-levelling data and gravimetric (quasi-) geoid heights in the presence of noise. J. Geod. 2010, 84, 731–749. [Google Scholar] [CrossRef]
- Watson, D.F.; Philip, G.M. A refinement of inverse distance weighted interpolation. Geo-Processing 1985, 2, 315–327. [Google Scholar]
- Kubik, K. An error theory for the Danish method. In Proceedings of the Symp Math Models, Accuracy Aspects and Quality Control, ISPRS Commission III Symposium, Helsinki, Finland, 7–11 June 1982. [Google Scholar]



| Model | Max | Min | Mean | STD |
|---|---|---|---|---|
| GNSS/leveling heights (m) | 11.72 | 9.82 | 10.72 | 0.44 |
| topographic data (m) | 960.38 | −34.81 | 108.80 | 179.74 |
| terrestrial gravity (mGal) | 61.26 | −12.43 | 4.38 | 11.02 |
| reference gravity anomalies (mGal) | 50.97 | −18.51 | 0.99 | 11.93 |
| Model | Max | Min | STD |
|---|---|---|---|
| compared with reference height anomalies | 0.117 | −0.111 | 0.049 |
| compared with gravimetric quasi-geoid | 0.049 | −0.035 | 0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Chen, X.; Xue, Z.; He, H.; Xing, L.; Ma, X.; Niu, X. High-Accuracy Quasi-Geoid Determination Using Molodensky’s Series Solutions and Integrated Gravity/GNSS/Leveling Data. Remote Sens. 2023, 15, 5414. https://doi.org/10.3390/rs15225414
Guo D, Chen X, Xue Z, He H, Xing L, Ma X, Niu X. High-Accuracy Quasi-Geoid Determination Using Molodensky’s Series Solutions and Integrated Gravity/GNSS/Leveling Data. Remote Sensing. 2023; 15(22):5414. https://doi.org/10.3390/rs15225414
Chicago/Turabian StyleGuo, Dongmei, Xiaodong Chen, Zhixin Xue, Huiyou He, Lelin Xing, Xian Ma, and Xiaowei Niu. 2023. "High-Accuracy Quasi-Geoid Determination Using Molodensky’s Series Solutions and Integrated Gravity/GNSS/Leveling Data" Remote Sensing 15, no. 22: 5414. https://doi.org/10.3390/rs15225414
APA StyleGuo, D., Chen, X., Xue, Z., He, H., Xing, L., Ma, X., & Niu, X. (2023). High-Accuracy Quasi-Geoid Determination Using Molodensky’s Series Solutions and Integrated Gravity/GNSS/Leveling Data. Remote Sensing, 15(22), 5414. https://doi.org/10.3390/rs15225414







