MTU2-Net: Extracting Internal Solitary Waves from SAR Images
Abstract
:1. Introduction
2. Methods
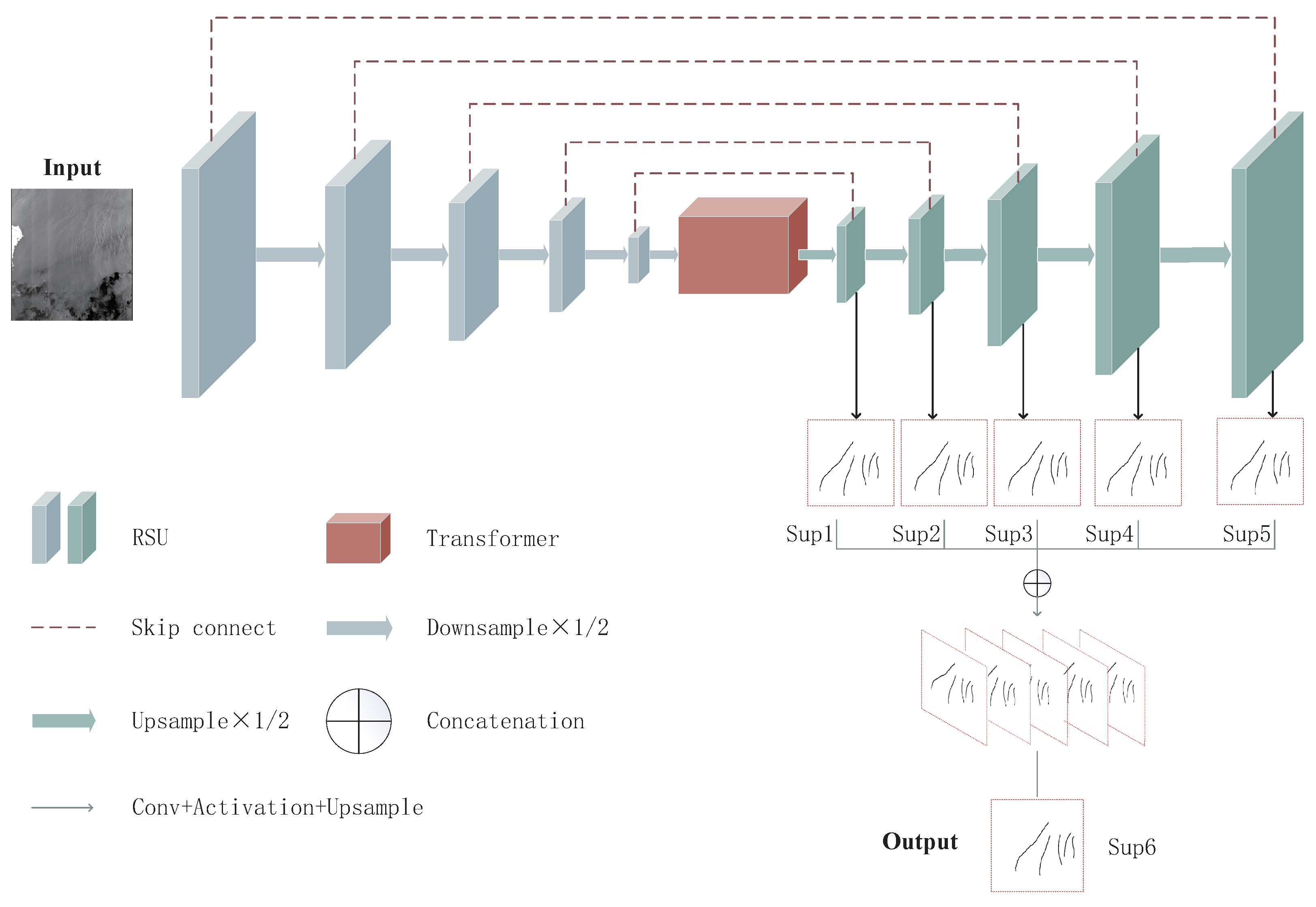
2.1. Network Architecture
- (1)
- Encoder module:
- (2)
- Decoder module:
- (3)
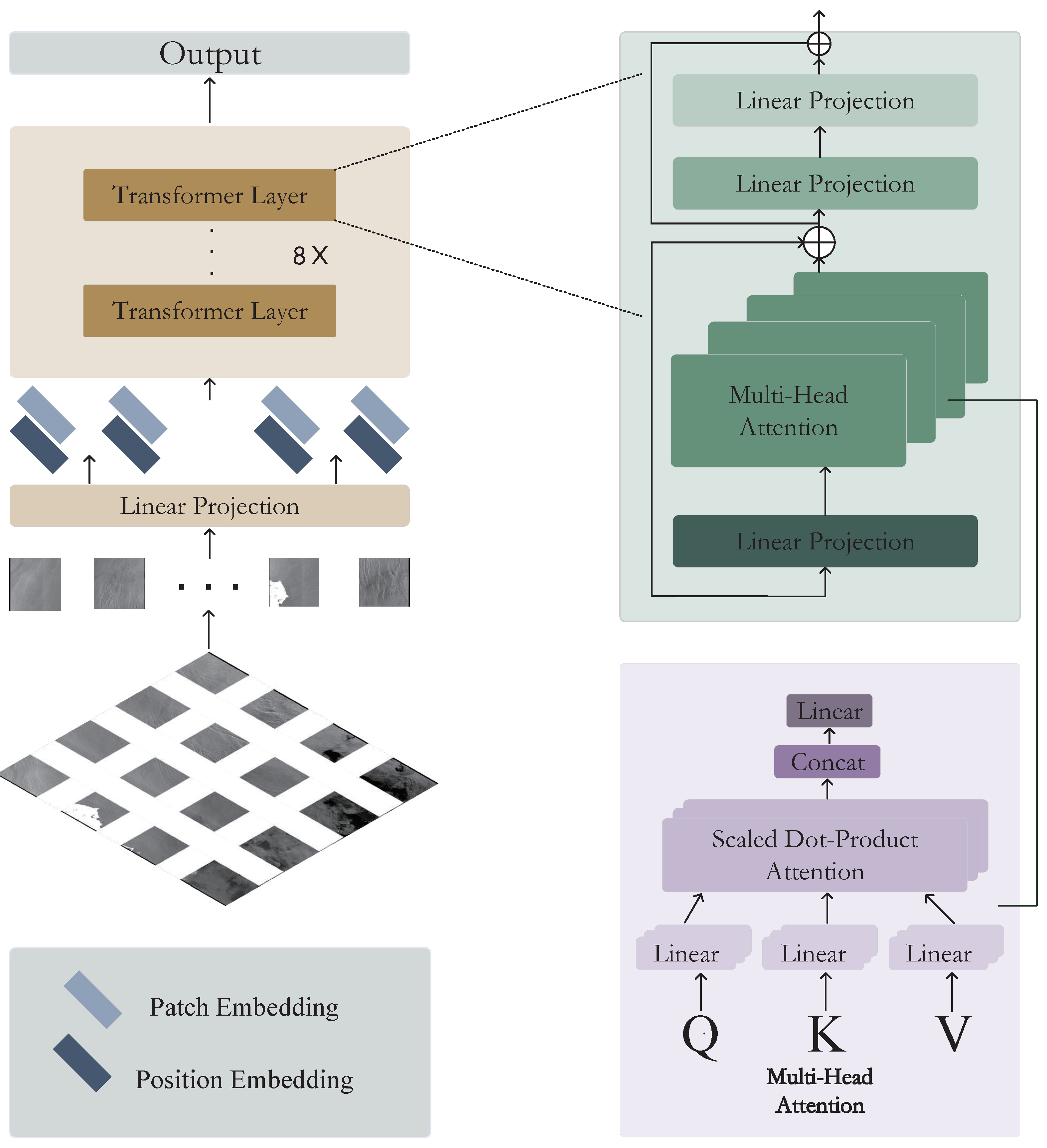
- Transformer module:
- (4)
- Feature Map Fusion module:
2.2. Residual U-Blocks
2.3. Middle-Transformer
2.4. Loss
3. Experimental Section
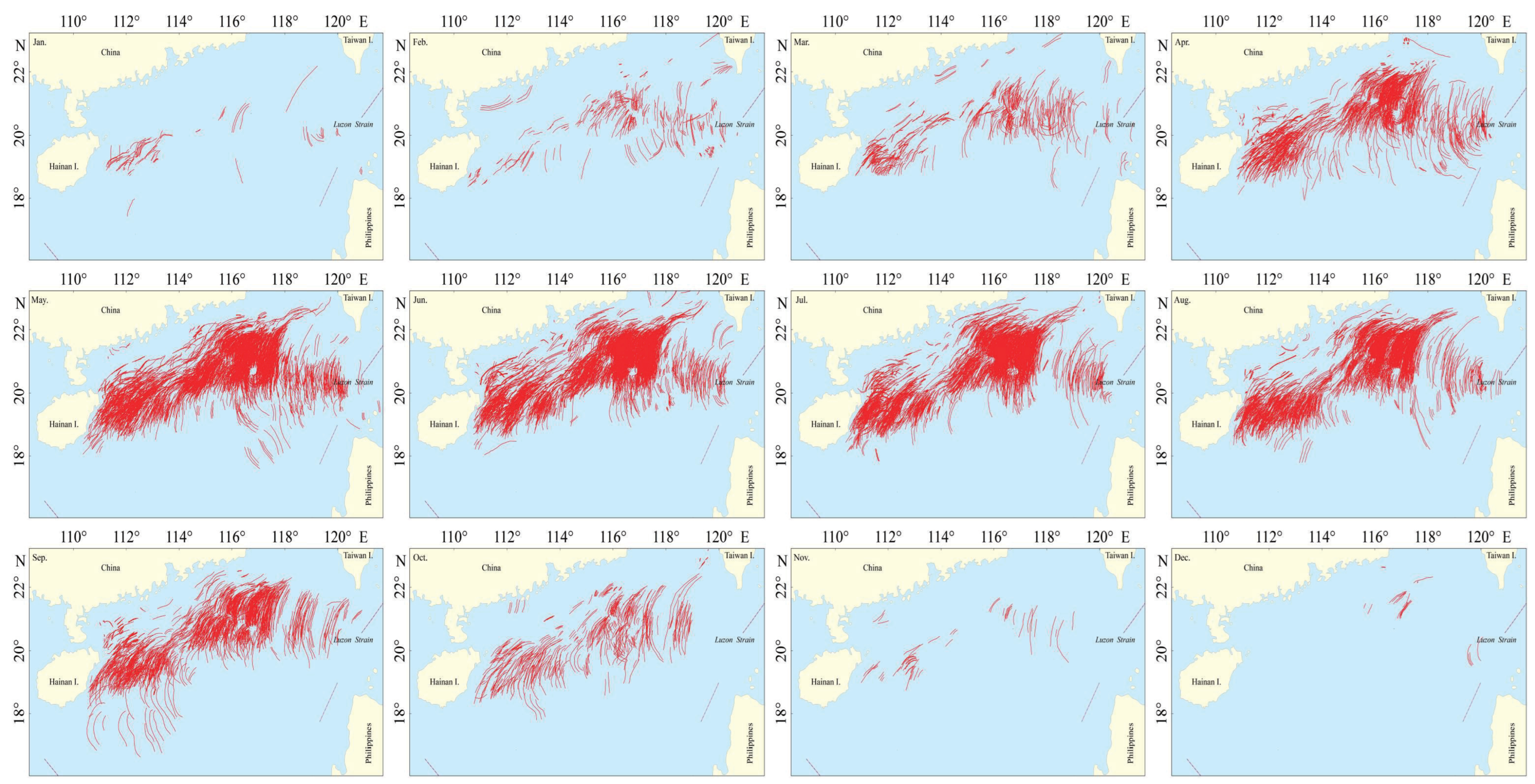
3.1. Data Source
3.2. Dataset
3.3. Experimental Setup
3.4. Evaluation Metrics
4. Experimental Results
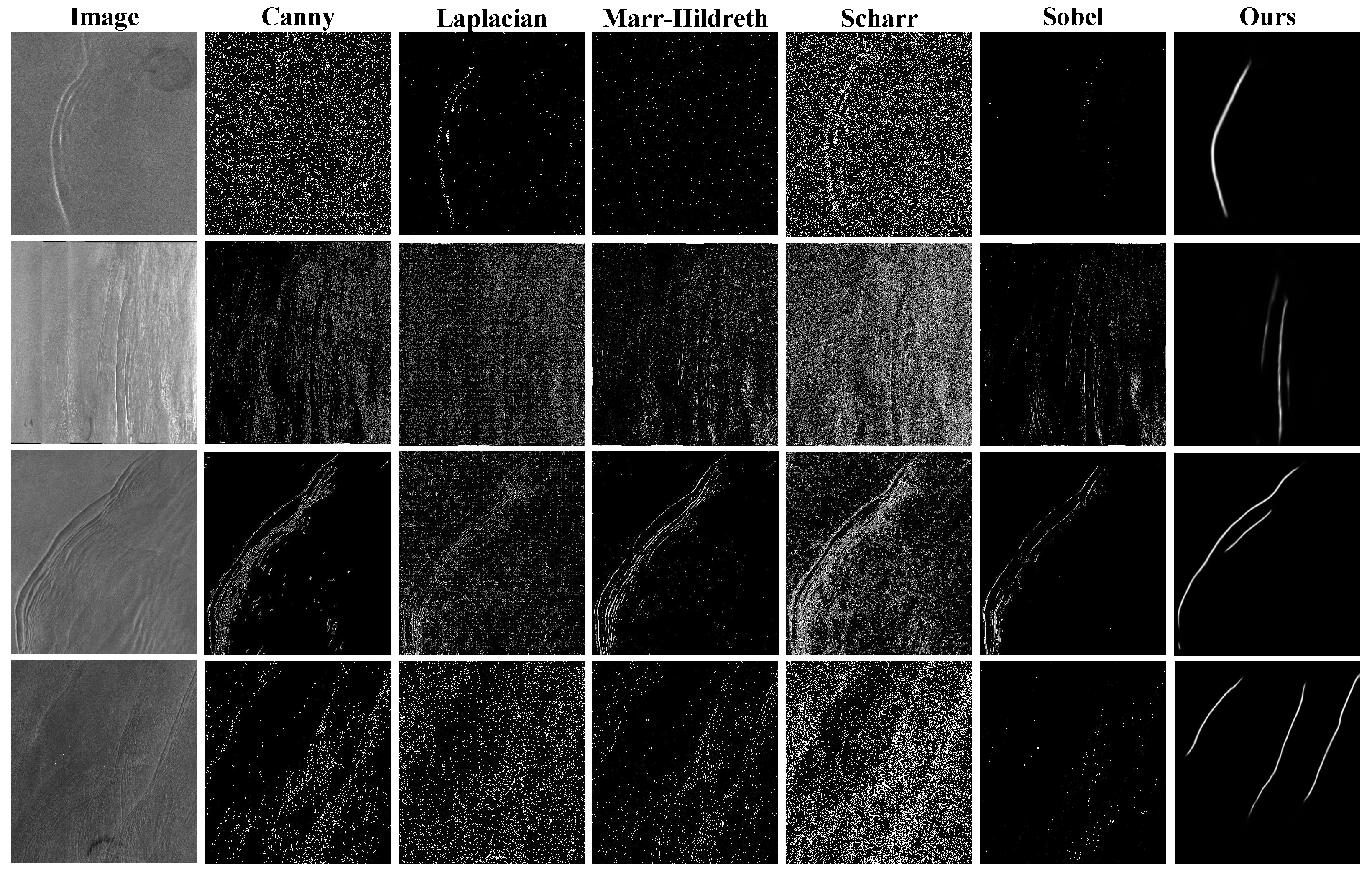
4.1. Comparison with Traditional Methods
4.2. Comparison with Methods of Deep Learning
4.3. Ablation Experiment
4.4. Performance on Another Dataset
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCE | Binary Cross-Entropy |
| ENVISAT ASAR | Environmental Satellite Advanced Synthetic Aperture Radar |
| ISW | Internal Solitary Wave |
| MACC | Mean Accuracy |
| MIoU | Mean Intersection over Union |
| MTU-net | Middle-Transformer U-net |
| RSU | Residual U-block |
| RSU-L | Residual U-block, where L denotes the number of Encoder layers |
| SAR | Synthetic Aperture Radar |
| WSM | Wide Swath Mode |
References
- Reid, E.C.; DeCarlo, T.M.; Cohen, A.L.; Wong, G.T.; Lentz, S.J.; Safaie, A.; Hall, A.; Davis, K.A. Internal waves influence the thermal and nutrient environment on a shallow coral reef. Limnol. Oceanogr. 2019, 64, 1949–1965. [Google Scholar] [CrossRef]
- Fang, X.; Du, T. Fundamentals of Oceanic Internal Waves and Internal Waves in the China Seas; China Ocean University Press: Qingdao, China, 2005; pp. 1–3. [Google Scholar]
- Apel, J.R.; Proni, J.R.; Byrne, H.M.; Sellers, R.L. Near-simultaneous observations of intermittent internal waves on the continental shelf from ship and spacecraft. Geophys. Res. Lett. 1975, 2, 128–131. [Google Scholar] [CrossRef]
- Bao, S.; Meng, J.; Sun, L.; Liu, Y. Detection of ocean internal waves based on Faster R-CNN in SAR images. J. Oceanol. Limnol. 2020, 38, 55–63. [Google Scholar] [CrossRef]
- Zheng, Y.g.; Qi, K.t.; Zhang, H.s. Stripe segmentation of oceanic internal waves in synthetic aperture radar images based on Mask R-CNN. Geocarto Int. 2022, 37, 14480–14494. [Google Scholar] [CrossRef]
- Ma, Y.; Meng, J.; Sun, L.; Ren, P. Oceanic Internal Wave Signature Extraction in the Sulu Sea by a Pixel Attention U-Net: PAU-Net. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3230086. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Jiang, Z.H.; Tay, F.E.; Feng, J.; Yan, S. Tokens-to-token vit: Training vision Transformers from scratch on imagenet. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 558–567. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision Transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF international Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 568–578. [Google Scholar]
- Wu, H.; Xiao, B.; Codella, N.; Liu, M.; Dai, X.; Yuan, L.; Zhang, L. Cvt: Introducing convolutions to vision Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 22–31. [Google Scholar]
- Heo, B.; Yun, S.; Han, D.; Chun, S.; Choe, J.; Oh, S.J. Rethinking spatial dimensions of vision Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 11936–11945. [Google Scholar]
- Chen, Y.; Gu, X.; Liu, Z.; Liang, J. A fast inference vision Transformer for automatic pavement image classification and its visual interpretation method. Remote Sens. 2022, 14, 1877. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Hu, X.; Li, Z.; Li, M. A Novel Lightweight Attention-Discarding Transformer for High Resolution SAR Image Classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4006405. [Google Scholar] [CrossRef]
- Touvron, H.; Cord, M.; Sablayrolles, A.; Synnaeve, G.; Jégou, H. Going deeper with image Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 32–42. [Google Scholar]
- Gong, C.; Wang, D.; Li, M.; Chandra, V.; Liu, Q. Vision Transformers with patch diversification. arXiv 2021, arXiv:2104.12753. [Google Scholar]
- Zhou, D.; Kang, B.; Jin, X.; Yang, L.; Lian, X.; Jiang, Z.; Hou, Q.; Feng, J. Deepvit: Towards deeper vision Transformer. arXiv 2021, arXiv:2103.11886. [Google Scholar]
- Zhou, D.; Shi, Y.; Kang, B.; Yu, W.; Jiang, Z.; Li, Y.; Jin, X.; Hou, Q.; Feng, J. Refiner: Refining Self-Attention for vision Transformers. arXiv 2021, arXiv:2106.03714. [Google Scholar]
- Chu, X.; Tian, Z.; Zhang, B.; Wang, X.; Wei, X.; Xia, H.; Shen, C. Conditional positional encodings for vision Transformers. arXiv 2021, arXiv:2102.10882. [Google Scholar]
- Wu, K.; Peng, H.; Chen, M.; Fu, J.; Chao, H. Rethinking and improving relative position encoding for vision Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10033–10041. [Google Scholar]
- Islam, M.A.; Kowal, M.; Jia, S.; Derpanis, K.G.; Bruce, N.D. Position, padding and predictions: A deeper look at position information in cnns. arXiv 2021, arXiv:2101.12322. [Google Scholar]
- Cordonnier, J.B.; Loukas, A.; Jaggi, M. On the relationship between Self-Attention and convolutional layers. arXiv 2019, arXiv:1911.03584. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical vision Transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Yuan, L.; Hou, Q.; Jiang, Z.; Feng, J.; Yan, S. Volo: Vision outlooker for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 6575–6586. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in Transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Chu, X.; Tian, Z.; Wang, Y.; Zhang, B.; Ren, H.; Wei, X.; Xia, H.; Shen, C. Twins: Revisiting the design of spatial attention in vision Transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 9355–9366. [Google Scholar]
- Dai, Z.; Liu, H.; Le, Q.V.; Tan, M. Coatnet: Marrying convolution and attention for all data sizes. Adv. Neural Inf. Process. Syst. 2021, 34, 3965–3977. [Google Scholar]
- Xiao, T.; Singh, M.; Mintun, E.; Darrell, T.; Dollár, P.; Girshick, R. Early convolutions help Transformers see better. Adv. Neural Inf. Process. Syst. 2021, 34, 30392–30400. [Google Scholar]
- Zhai, X.; Kolesnikov, A.; Houlsby, N.; Beyer, L. Scaling vision Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12104–12113. [Google Scholar]
- Riquelme, C.; Puigcerver, J.; Mustafa, B.; Neumann, M.; Jenatton, R.; Susano Pinto, A.; Keysers, D.; Houlsby, N. Scaling vision with sparse mixture of experts. Adv. Neural Inf. Process. Syst. 2021, 34, 8583–8595. [Google Scholar]
- Chen, M.; Radford, A.; Child, R.; Wu, J.; Jun, H.; Luan, D.; Sutskever, I. Generative pretraining from pixels. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 1691–1703. [Google Scholar]
- Li, Z.; Chen, Z.; Yang, F.; Li, W.; Zhu, Y.; Zhao, C.; Deng, R.; Wu, L.; Zhao, R.; Tang, M.; et al. Mst: Masked self-supervised Transformer for visual representation. Adv. Neural Inf. Process. Syst. 2021, 34, 13165–13176. [Google Scholar]
- Bao, H.; Dong, L.; Piao, S.; Wei, F. Beit: Bert pre-training of image Transformers. arXiv 2021, arXiv:2106.08254. [Google Scholar]
- Chen, X.; Xie, S.; He, K. An empirical study of training self-supervised vision Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9640–9649. [Google Scholar]
- Caron, M.; Touvron, H.; Misra, I.; Jégou, H.; Mairal, J.; Bojanowski, P.; Joulin, A. Emerging properties in self-supervised vision Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9650–9660. [Google Scholar]
- Xie, Z.; Lin, Y.; Yao, Z.; Zhang, Z.; Dai, Q.; Cao, Y.; Hu, H. Self-supervised learning with swin Transformers. arXiv 2021, arXiv:2105.04553. [Google Scholar]
- Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep-learning-based information mining from ocean remote-sensing imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef]
- Wang, S.; Dong, Q.; Duan, L.; Sun, Y.; Jian, M.; Li, J.; Dong, J. A fast internal wave detection method based on PCANet for ocean monitoring. J. Intell. Syst. 2019, 28, 103–113. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, B.; Li, X.; Xu, Q. Automatic extraction of internal wave signature from multiple satellite sensors based on deep convolutional neural networks. In Proceedings of the IGARSS 2020—IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5717–5720. [Google Scholar]
- Zheng, Y.g.; Zhang, H.s.; Qi, K.t.; Ding, L.y. Stripe segmentation of oceanic internal waves in SAR images based on SegNet. Geocarto Int. 2021, 37, 8568–8578. [Google Scholar] [CrossRef]
- Meng, J.; Sun, L.; Zhang, H.; Hu, B.; Hou, F.; Bao, S. Remote sensing survey and research on internal solitary waves in the South China Sea-Western Pacific-East Indian Ocean (SCS-WPAC-EIND). Acta Oceanol. Sin. 2022, 41, 154–170. [Google Scholar] [CrossRef]
- Tao, M.; Xu, C.; Guo, L.; Wang, X.; Xu, Y. An Internal Waves Data Set From Sentinel-1 Synthetic Aperture Radar Imagery and Preliminary Detection. Earth Space Sci. 2022, 9, e2022EA002528. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Hu, Q. Transfuse: Fusing Transformers and cnns for medical image segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part I 24. Springer: Cham, Swizterland, 2021; pp. 14–24. [Google Scholar]
- Dong, B.; Wang, W.; Fan, D.P.; Li, J.; Fu, H.; Shao, L. Polyp-pvt: Polyp segmentation with pyramid vision Transformers. arXiv 2021, arXiv:2108.06932. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: UNet-like pure Transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 205–218. [Google Scholar]
- Qin, X.; Zhang, Z.; Huang, C.; Dehghan, M.; Zaiane, O.R.; Jagersand, M. U2-Net: Going deeper with nested U-structure for salient object detection. Pattern Recognit. 2020, 106, 107404. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Mlsna, P.A.; Rodriguez, J.J. Gradient and Laplacian edge detection. In The Essential Guide to Image Processing; Elsevier: Amsterdam, The Netherlands, 2009; pp. 495–524. [Google Scholar]
- Smith, T., Jr.; Marks, W.; Lange, G.; Sheriff, W., Jr.; Neale, E. Edge detection in images using Marr-Hildreth filtering techniques. J. Neurosci. Methods 1988, 26, 75–81. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, X.; Yang, L.; Liu, H. An improved Sobel edge detection. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 5, pp. 67–71. [Google Scholar]
- Carr, M.; Davies, P.; Hoebers, R. Experiments on the structure and stability of mode-2 internal solitary-like waves propagating on an offset pycnocline. Phys. Fluids 2015, 27, 046602. [Google Scholar] [CrossRef]






| F1-Score | MACC | MIoU | |
|---|---|---|---|
| Swin-UNet | 53.32 | 62.33 | 55.93 |
| Transfuse | 51.64 | 51.91 | 49.15 |
| Polyp-PVT | 55.93 | 58.94 | 53.19 |
| -Net | 52.33 | 61.30 | 52.38 |
| Multi-loss -Net | 53.48 | 62.51 | 53.96 |
| Transformer -Net | 54.39 | 66.23 | 63.83 |
| Ours | 56.03 | 75.20 | 71.57 |
| Different Variants | ||||
|---|---|---|---|---|
| -Net | ✓ | ✓ | ✓ | ✓ |
| Multi-loss | ✓ | ✓ | ||
| Transformer | ✓ | ✓ | ||
| MIoU (%) | 52.38 | 53.96 | 63.83 | 71.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barintag, S.; An, Z.; Jin, Q.; Chen, X.; Gong, M.; Zeng, T. MTU2-Net: Extracting Internal Solitary Waves from SAR Images. Remote Sens. 2023, 15, 5441. https://doi.org/10.3390/rs15235441
Barintag S, An Z, Jin Q, Chen X, Gong M, Zeng T. MTU2-Net: Extracting Internal Solitary Waves from SAR Images. Remote Sensing. 2023; 15(23):5441. https://doi.org/10.3390/rs15235441
Chicago/Turabian StyleBarintag, Saheya, Zhijie An, Qiyu Jin, Xu Chen, Maoguo Gong, and Tieyong Zeng. 2023. "MTU2-Net: Extracting Internal Solitary Waves from SAR Images" Remote Sensing 15, no. 23: 5441. https://doi.org/10.3390/rs15235441
APA StyleBarintag, S., An, Z., Jin, Q., Chen, X., Gong, M., & Zeng, T. (2023). MTU2-Net: Extracting Internal Solitary Waves from SAR Images. Remote Sensing, 15(23), 5441. https://doi.org/10.3390/rs15235441








