Forecasting the Propagation from Meteorological to Hydrological and Agricultural Drought in the Huaihe River Basin with Machine Learning Methods
Abstract
:1. Introduction
2. Study Area and Data
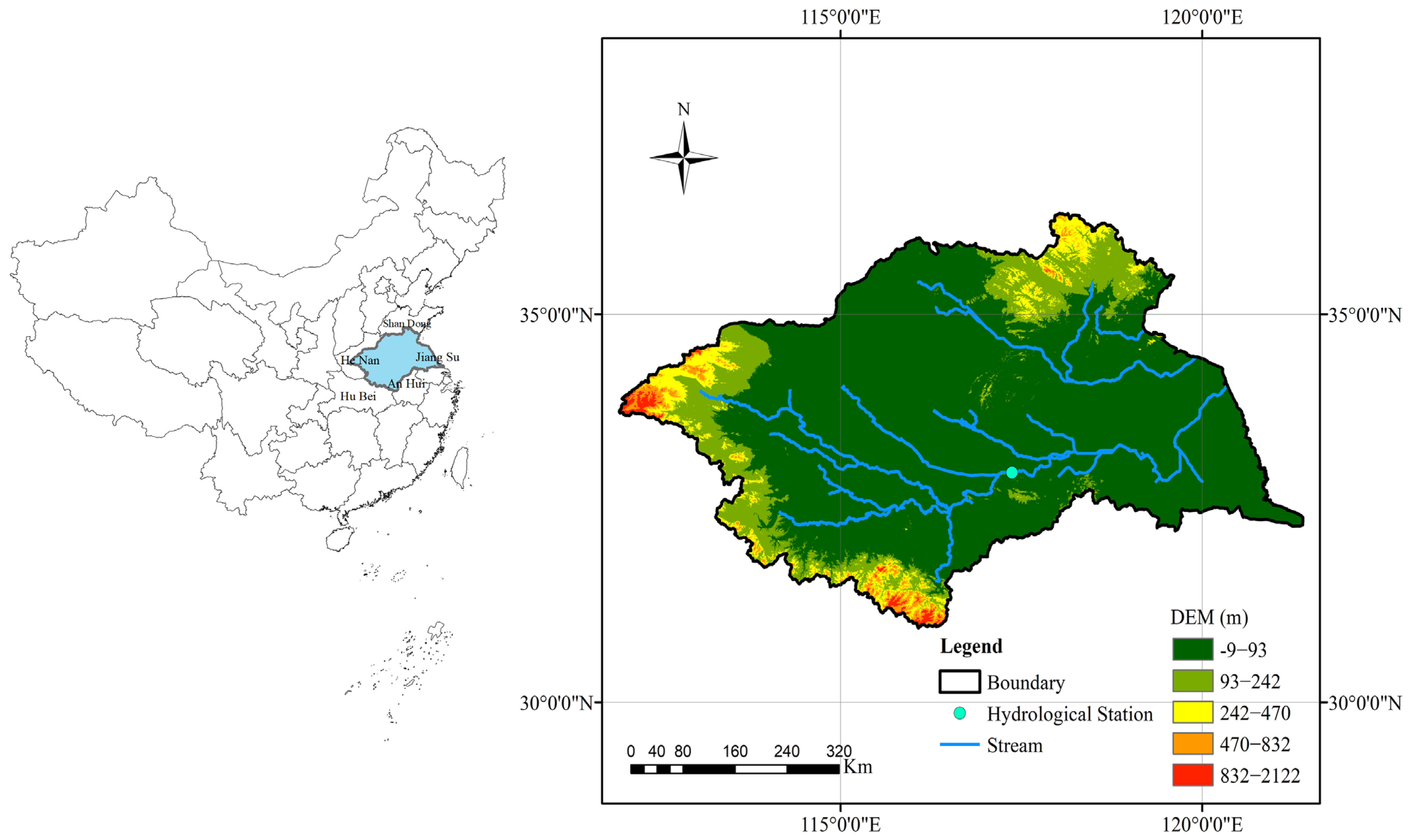
2.1. Study Area
2.2. Data
2.2.1. GPM_3IMERGM
2.2.2. MOD16A2
2.2.3. GLDAS_NOAH025_M 2.1
2.2.4. GRACE/GRACE-FO Mascon
2.2.5. MOD13C2
3. Methods
3.1. Trend Analysis
3.2. Drought Indicators
3.3. Correlation Analysis
3.4. Machine Learning Methods for Drought Forecasting
3.4.1. Long Short-Term Memory Neural Network (LSTM)
3.4.2. Convolutional Neural Network (CNN)
3.4.3. Categorical Boosting (CatBoost)
3.5. Evaluation Criteria
4. Results
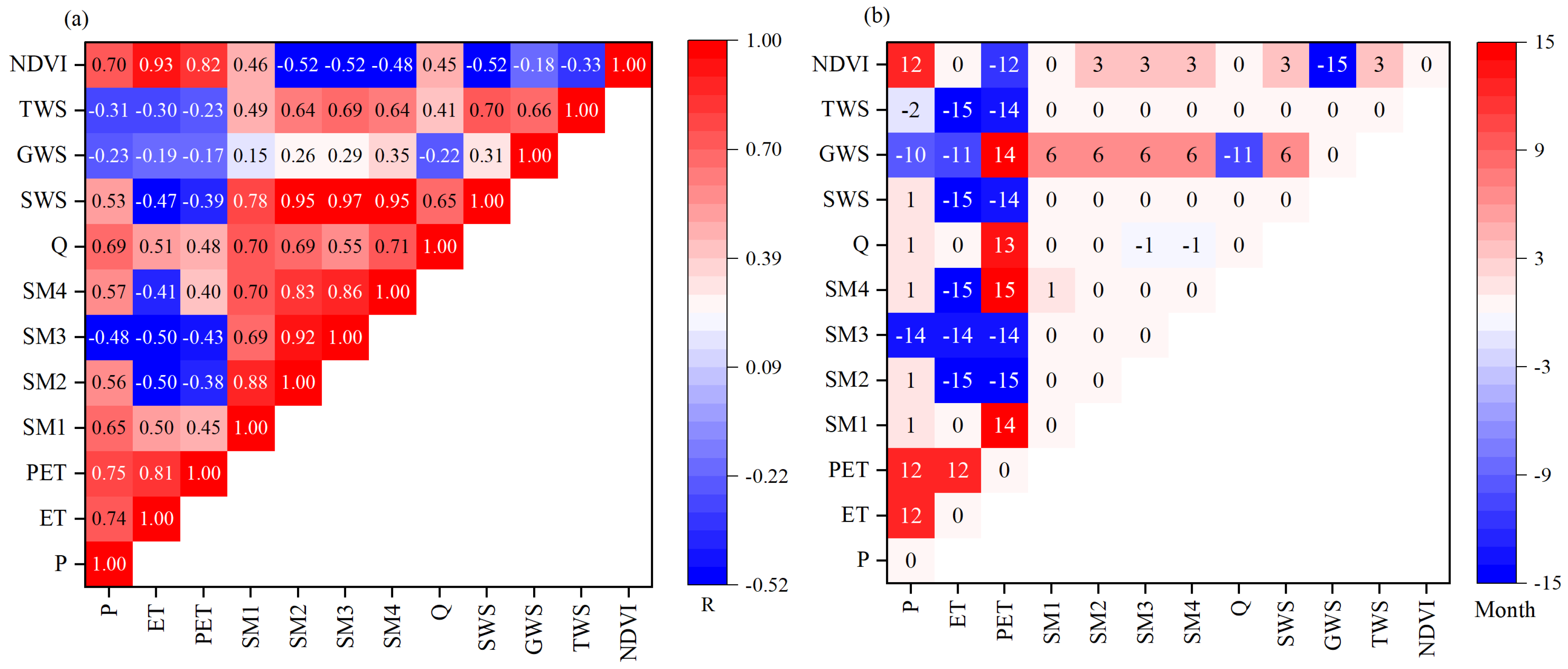
4.1. Trend and Correlation Analysis of Different Variables
4.2. Correlation and Propagation time of Meteorological, Hydrological, and Agricultural Drought
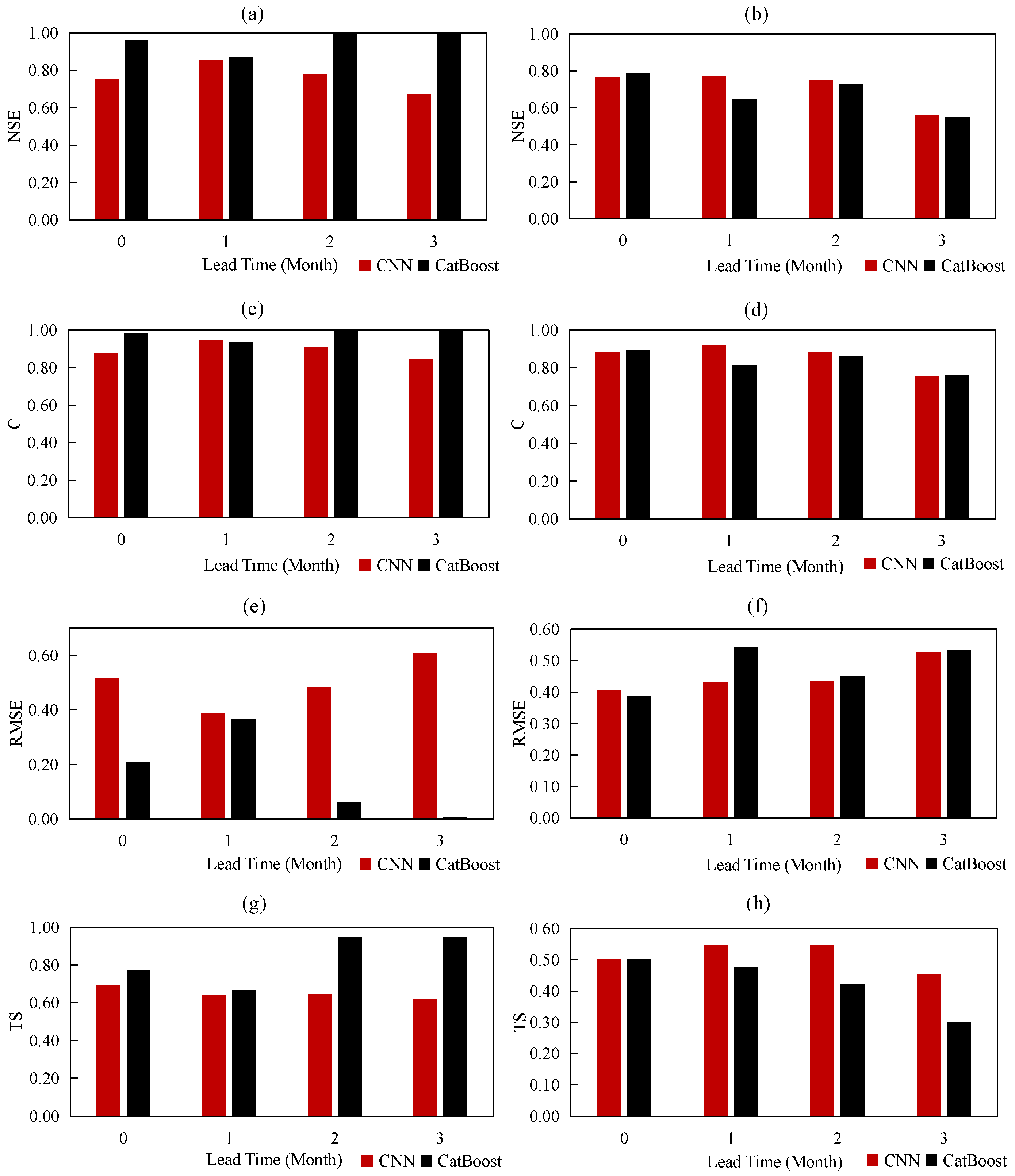
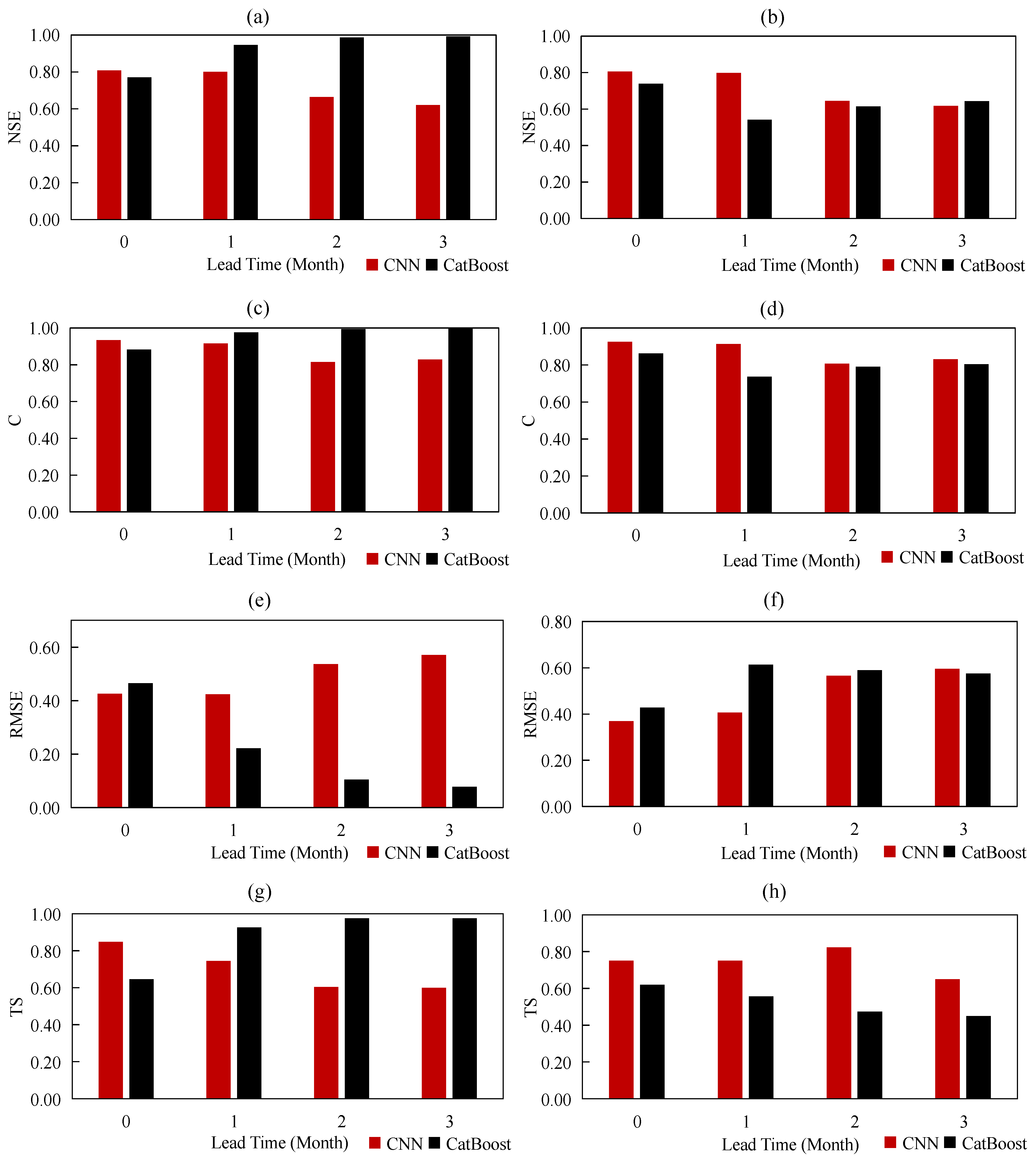
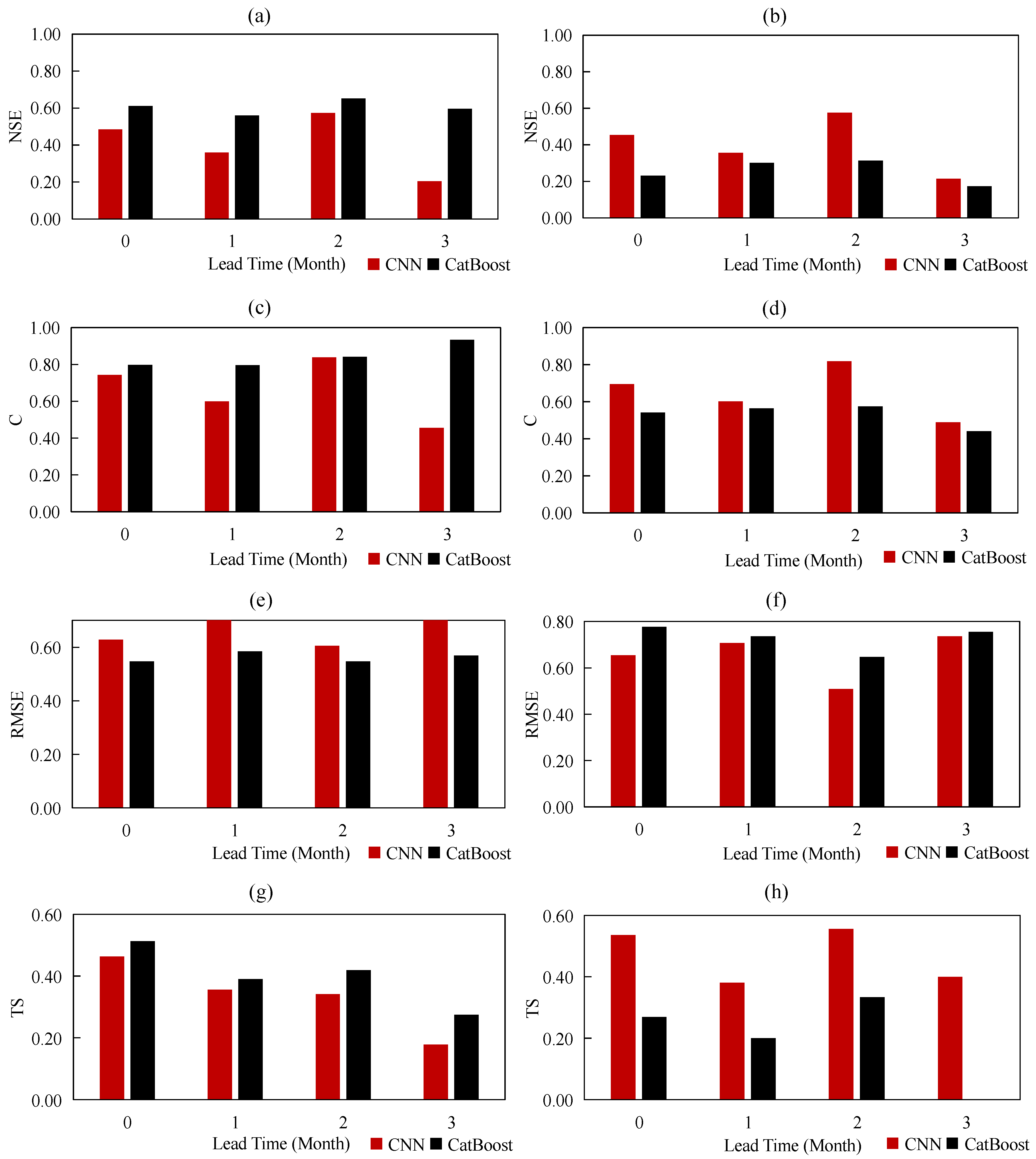
4.3. Performances of Drought Forecasting by LSTM, CNN, and CatBoost
4.4. Performances of Drought Forecasting by CNN and CatBoost with Random Data Splitting for Training and Testing
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jones, R.L.; Guha-Sapir, D.; Ttubeuf, S. Human and economic impacts of natural disasters: Can we trust the global data? Sci. Data 2022, 9, 572. [Google Scholar] [CrossRef] [PubMed]
- Ma, F.; Yuan, X.; Ye, A. Seasonal drought predictability and forecast skill over China. J. Geophys. Res. Atmos. 2015, 120, 8264–8275. [Google Scholar] [CrossRef]
- Escobar, H. Drought triggers alarms in Brazil’s biggest metropolis. Science 2015, 347, 812. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Park, M. Assessment of quantitative standards for mega-drought using data on drought damages. Sustainability 2020, 12, 3598. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- American Meteorological Society (AMS). Statement on meteorological drought. Bull. Am. Meteorol. Soc. 2004, 85, 771–773. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Singh, C.; Jain, G.; Sukhwani, V.; Shaw, R. Losses and damages associated with slow-onset events: Urban drought and water insecurity in Asia. Curr. Opin. Environ. Sustain. 2021, 50, 72–86. [Google Scholar] [CrossRef]
- Crausbay, S.D.; Ramirez, A.R.; Carter, S.L.; Cross, M.S.; Hall, K.R.; Bathke, D.J.; Betancourt, J.L.; Colt, S.; Cravens, A.E.; Dalton, M.S. Defining ecological drought for the twenty-first century. Bull. Amer. Meteor. Soc. 2017, 98, 2543–2550. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Quiring, S.M.; Peña-Gallardo, M.; Yuan, S.; Domínguez-Castro, F. A review of environmental droughts: Increased risk under global warming? Earth-Sci. Rev. 2020, 201, 102953. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. Preprints. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Anaheim, CA, USA, 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Begueria, S.; Lopez-Moreno, J.I. A multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Patel, N.K. Estimating volumetric surface moisture content for cropped soils using a Soil Wetness Index based on surface temperature and NDVI. Agric. For. Meteorol. 2009, 149, 1327–1342. [Google Scholar] [CrossRef]
- Marj, A.F.; Meijerink, A.M. Agricultural drought forecasting using satellite images, climate indices and artificial neural network. Int. J. Remote Sens. 2011, 32, 9707–9719. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Kimball, J.S.; McDowell, N.G.; Running, S.W. A remotely sensed global terrestrial Drought Severity Index. Bull. Am. Meteorol. Soc. 2013, 94, 83–98. [Google Scholar] [CrossRef]
- Zhao, M.; Geruo, A.; Velicogna, I.; Kimball, J.S. A global gridded dataset of GRACE Drought Severity Index for 2002–14: Comparison with PDSI and SPEI and a case study of the Australia millennium drought. J. Hydrometeorol. 2017, 18, 2117–2129. [Google Scholar] [CrossRef]
- Stefanidis, S.; Rossiou, D.; Proutsos, N. Drought Severity and Trends in a Mediterranean Oak Forest. Hydrology 2023, 10, 167. [Google Scholar] [CrossRef]
- Patil, R.; Polisgowdar, B.S.; Rathod, S.; Bandumula, N.; Mustac, I.; Reddy, G.V.S.; Wali, V.; Satishkumar, U.; Rao, S.; Kumar, A. Spatiotemporal characterization of drought magnitude, severity, and return period at various time scales in the Hyderabad Karnataka Region of India. Water 2023, 15, 2483. [Google Scholar] [CrossRef]
- Liu, S.; Chadwick, O.A.; Roberts, D.A.; Still, C.J. Relationships between GPP, satellite measures of greenness and canopy water content with soil moisture in mediterranean-climate grassland and oak savanna. Appl. Environ. Soil Sci. 2011, 2011, 839028. [Google Scholar] [CrossRef]
- Sang, L.; Zhu, G.; Xu, Y.; Sun, Z.; Zhang, Z.; Tong, H. Effects of agricultural large-and medium-sized reservoirs on hydrologic processes in the arid Shiyang River Basin, Northwest China. Water Resour. Res. 2023, 59, e2022WR033519. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Yin, Z.; Liu, M.; Zheng, W. Spatial and wavelet analysis of precipitation and river discharge during operation of the Three Gorges Dam, China. Ecol. Indic. 2023, 154, 110837. [Google Scholar] [CrossRef]
- Li, Y.; Mi, W.; Ji, L.; He, Q.; Yang, P.; Xie, S.; Bi, Y. Urbanization and agriculture intensification jointly enlarge the spatial inequality of river water quality. Sci. Total Environ. 2023, 878, 162559. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Quan, Q.; Yang, S.; Dong, Y. A social-ecological coupling model for evaluating the human-water relationship in basins within the Budyko framework. J. Hydrol. 2023, 619, 129361. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Hao, Z.; Singh, V.P.; Hao, F. Characterization of agricultural drought propagation over China based on bivariate probabilistic quantification. J. Hydrol. 2021, 598, 126194. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, K.; Hu, S.; Liu, J.; Shi, H.; Wei, G.; Chai, H.; Li, J.; Wang, T. Using the global navigation satellite system and precipitation data to establish the propagation characteristics of meteorological and hydrological drought in Yunnan, China. Water Resour. Res. 2023, 59, e2022WR033126. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, F.; Yue, H.; Wang, X.; Fan, Y. Global analysis of the correlation and propagation among meteorological, agricultural, surface water, and groundwater droughts. J. Environ. Manag. 2023, 333, 117460. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.; Tian, L.; Disse, M.; Tuo, Y. A new approach to quantify propagation time from meteorological to hydrological drought. J. Hydrol. 2021, 603, 127056. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, Y.; Liu, S.; Cai, H.; Zhou, Z. A new perspective on drought propagation: Causality. Geophys. Res. Lett. 2022, 49, e2021GL096758. [Google Scholar] [CrossRef]
- Gao, C.; Liu, L.; Zhang, S.L.; Xu, Y.-P.; Wang, X.; Tang, X. Spatiotemporal patterns and propagation mechanism of meteorological droughts over Yangtze River Basin and Pearl River Basin based on complex network theory. Atmos. Res. 2023, 292, 106874. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation thresholds of meteorological drought for triggering hydrological drought at various levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef]
- Yu, M.; Liu, X.; Li, Q. Responses of meteorological drought-hydrological drought propagation to watershed scales in the upper Huaihe River basin, China. Environ. Sci. Pollut. Res. 2020, 27, 17561–17570. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Duan, X.; Guo, Q.; Lu, S.; Hsu, K. The spatiotemporal variations and propagation of droughts in Plateau Mountains of China. Sci. Total Environ. 2022, 805, 150257. [Google Scholar] [CrossRef] [PubMed]
- Gong, R.; Chen, J.; Liang, Z.; Wu, C.; Tian, D.; Wu, J.; Li, S.; Zeng, G. Characterization and propagation from meteorological to groundwater drought in different aquifers with multiple timescales. J. Hydrol. Reg. Stud. 2023, 45, 101317. [Google Scholar] [CrossRef]
- Li, Z.; Huang, S.; Zhou, S.; Leng, G.; Liu, D.; Huang, Q.; Wang, H.; Han, Z.; Liang, H. Clarifying the propagation dynamics from meteorological to hydrological drought induced by climate change and direct human activities. J. Hydrometeorol. 2021, 22, 2359–2378. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Cheng, H.; Wang, H.; Zhu, Y. Propagation from meteorological to hydrological drought and its influencing factors in the Huaihe River Basin. Water 2021, 13, 1985. [Google Scholar] [CrossRef]
- Prodhan, F.A.; Zhang, J.; Hasan, S.S.; Sharma, T.P.T.; Mohana, H.P. A review of machine learning methods for drought hazard monitoring and forecasting: Current research trends, challenges, and future research directions. Environ. Modell. Softw. 2022, 149, 105327. [Google Scholar] [CrossRef]
- Hamitouche, M.; Molina, J. A review of ai methods for the prediction of high-flow extremal hydrology. Water Resour. Manag. 2022, 36, 3859–3876. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Long lead time drought forecasting using lagged climate variables and a stacked long short-term memory model. Sci. Total Environ. 2021, 755, 142638. [Google Scholar] [CrossRef]
- Zhu, S.; Xu, Z.; Luo, X.; Liu, X.; Wang, R.; Zhang, M.; Huo, Z. Internal and external coupling of Gaussian mixture model and deep recurrent network for probabilistic drought forecasting. Int. J. Environ. Sci. Technol. 2021, 18, 1221–1236. [Google Scholar] [CrossRef]
- Adikari, K.E.; Shrestha, S.; Ratnayake, D.T.; Budhathoki, A.; Mohanasundaram, S.; Dailey, M.N. Evaluation of artificial intelligence models for flood and drought forecasting in arid and tropical regions. Environ. Modell. Softw. 2021, 144, 105136. [Google Scholar] [CrossRef]
- Wu, X.; Feng, X.; Wang, Z.; Chen, Y.; Deng, Z. Multi-source precipitation products assessment on drought monitoring across global major river basins. Atmos. Res. 2023, 295, 106982. [Google Scholar] [CrossRef]
- Tian, H.; Huang, N.; Niu, Z.; Qin, Y.; Pei, J.; Wang, J. Mapping winter crops in china with multi-source satellite imagery and phenology-based algorithm. Remote Sens. 2019, 11, 820. [Google Scholar] [CrossRef]
- Mohamed, A.; Faye, C.; Othman, A.; Abdelrady, A. Hydro-Geophysical evaluation of the regional variability of Senegal’s terrestrial water storage using time-variable gravity data. Remote Sens. 2022, 14, 4059. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Zaitchik, B.F.; Reichle, R.H.; Koster, R.D.; van Dam, T.M. Assimilation of GRACE terrestrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe. J. Hydrol. 2012, 446–447, 103–115. [Google Scholar] [CrossRef]
- Lopez, T.; Al Bitar, A.; Biancamaria, S.; Güntner, A.; Jaggi, A. On the use of satellite remote sensing to detect floods and droughts at large scales. Surv. Geophys. 2020, 41, 1461–1487. [Google Scholar] [CrossRef]
- Li, B.L.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; de Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE data assimilation for groundwater and drought monitoring: Advances and challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, W.K. Progress and prospect of GRACE Mascon product and its application. Rev. Geophys. Planet. Phys. 2022, 53, 35–52. (In Chinese) [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Zhong, Y.; Feng, W.; Zhong, M.; Ming, Z. Dataset of Reconstructed Terrestrial Water Storage in China Based on Precipitation (2002–2019); National Tibetan Plateau/Third Pole Environment Data Center: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.; Yong, B.; Hou, A.; Wei, J.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhan, C.; Qiao, Y.; Wang, Y. Monitoring the spatio-temporal changes of terrestrial water storage using GRACE data in the Tarim River basin between 2002 and 2015. Sci. Total Environ. 2017, 595, 218–228. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J.; Liu, X. Drought evaluation using the GRACE terrestrial water storage deficit over the Yangtze River Basin, China. Sci. Total Environ. 2018, 634, 727–738. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Castle, S.L.; Thomas, B.F.; Reager, J.T.; Rodell, M.; Swenson, S.C.; Famiglietti, J.S. Groundwater depletion during drought threatens future water security of the Colorado River Basin. Geophys. Res. Lett. 2014, 41, 5904–5911. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Pei, H.; Shen, Y. Evaluating dynamics of GRACE groundwater and its drought potential in Taihang Mountain Region, China. J. Hydrol. 2022, 612, 128156. [Google Scholar] [CrossRef]
- Didan, K. MOD13C2 MODIS/Terra Vegetation Indices Monthly L3 Global 0.05Deg CMG V006. 2015, Distributed by NASA EOSDIS Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov/products/mod13c2v006/ (accessed on 18 March 2023).
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Blahusiakova, A.; Matouskova, M. Rainfall and runoff regime trends in mountain catchments (Case study area: The upper Hron River basin, Slovakia). J. Hydrol. Hydromech. 2015, 63, 183–192. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H. Long-term trends of annual temperature and precipitation time series in Japan. J. Hydrosci. Hydraul. Eng. 2002, 20, 11–26. [Google Scholar] [CrossRef]
- Das, P.K.; Midya, S.K.; Das, D.K.; Rao, G.S.; Raj, U. Characterizing Indian meteorological moisture anomaly condition using long-term (1901–2013) gridded data: A multivariate moisture anomaly index approach. Int. J. Climatol. 2018, 38, E144–E159. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardized drought index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, J.; Wang, Y.; Zhou, D.; Zhu, Q. Investigation about the correlation and propagation among meteorological, agricultural and groundwater droughts over humid and arid/semi-arid basins in China. J. Hydrol. 2021, 603, 127007. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorín-Molina, C.; Morán-Tejeda, E. Accurate computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Nejadrekabi, M.; Eslamian, S.; Zareian, M.J. Spatial statistics techniques for SPEI and NDVI drought indices: A case study of Khuzestan Province. Int. J. Environ. Sci. Technol. 2022, 19, 6573–6594. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Liu, Y.; Bai, Q.; He, P.; Liang, H.; Shi, W. GRACE-based high-resolution propagation threshold from meteorological to groundwater drought. Agric. For. Meteorol. 2021, 307, 108476. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.; Zhao, T.; Shi, J. Index-based evaluation of vegetation response to meteorological drought in Northern China Normalized Difference Vegetation Index Anomaly (NDVIA). Nat. Hazards 2016, 84, 2179–2193. [Google Scholar] [CrossRef]
- Nygren, M.; Barthel, R.; Allen, D.M.; Giese, M. Exploring groundwater drought responsiveness in lowland post-glacial environments. Hydrogeol. J. 2022, 30, 1937–1961. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Anh, D.T.; Van, S.P.; Dang, T.D.; Hoang, L.P. Downscaling rainfall using deep learning long short-term memory and feedforward neural network. Int. J. Climatol. 2019, 39, 4170–4188. [Google Scholar] [CrossRef]
- Xiang, Z.; Jun, Y.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Hao, R.; Bai, Z. Comparative study for daily streamflow simulation with different machine learning methods. Water 2023, 15, 1179. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Simard, D.; Steinkraus, P.Y.; Platt, J.C. Best practices for convolutional neural networks applied to visual document analysis. In Proceedings of the Seventh International Conference on Document Analysis and Recognition, Edinburgh, UK, 6 August 2003; pp. 958–963. [Google Scholar]
- Taigman, Y.; Yang, M.; Ranzato, M.; Wolf, L. Deepface: Closing the gap to human-level performance in face verification. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1701–1708. [Google Scholar]
- Chen, C.; Hui, Q.; Xie, W.; Wan, S.; Zhou, Y.; Pei, Q. Convolutional Neural Networks for forecasting flood process in Internet-of-Things enabled smart city. Comput. Netw. 2021, 186, 107744. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Guo, Y.; Quan, L.; Song, L.; Liang, H. Construction of rapid early warning and comprehensive analysis models for urban waterlogging based on AutoML and comparison of the other three machine learning algorithms. J. Hydrol. 2022, 605, 127367. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, part 1: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Jollifee, I.T.; Stephenson, D.B. Forecast Verification: A Practitioner’s Guide in Atmospheric Science; John Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- Krause, P.; Boyle, D.P.; Fase, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Mustafa, S.M.T.; Abdollahi, K.; Verbeiren, B.; Huysmans, M. Identification of the influencing factors on groundwater drought and depletion in north-western Bangladesh. Hydrogeol. J. 2017, 25, 1357–1375. [Google Scholar] [CrossRef]
- Forootan, E.; Khaki, M.; Schumacher, M.; Wulfmeyer, V.; Mehrnegar, N.; van Dijk, A.I.J.M.; Brocca, L.; Farzaneh, S.; Akinluyi, F.; Ramillien, G.; et al. Understanding the global hydrological droughts of 2003–2016 and their relationships with teleconnections. Sci. Total Environ. 2019, 650, 2587–2604. [Google Scholar] [CrossRef]
- Yang, L.; Wei, W.; Chen, L.; Jia, F.; Mo, B. Spatial variations of shallow and deep soil moisture in the semi-arid Loess Plateau, China. Hydrol. Earth Syst. Sci. 2012, 16, 3199–3217. [Google Scholar] [CrossRef]
- Xie, X.; He, B.; Guo, L.; Miao, C.; Zhang, Y. Detecting hotspots of interactions between vegetation greenness and terrestrial water storage using satellite observations. Remote Sens. Environ. 2019, 231, 111259. [Google Scholar] [CrossRef]
- Wei, Z.; Wan, X. Spatial and temporal characteristics of NDVI in the Weihe River Basin and its correlation with terrestrial water storage. Remote Sens. 2022, 14, 5532. [Google Scholar] [CrossRef]
- Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Cruz-Nájera, M.A.; Treviño-Berrones, M.G.; Ponce-Flores, M.P.; Terán-Villanueva, J.D.; Castán-Rocha, J.A.; Ibarra-Martínez, S.; Santiago, A.; Laria-Menchaca, J. Short time series forecasting: Recommended methods and techniques. Symmetry 2022, 14, 1231. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, W.; Liu, Y.; Yuan, Y.; Huang, J.; Liu, Y. Identifying spatial extent of meteorological droughts: An examination over a humid region. J. Hydrol. 2020, 591, 125505. [Google Scholar] [CrossRef]
- Dikshit, A.; Dikshit, B.; Huete, A.; Park, H.-J. Spatial based drought assessment: Where are we heading? A review on the current status and future. Sci. Total Environ. 2022, 844, 157239. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Tu, X.; Singh, V.P.; Chen, X.; Lin, K.; Zhou, Z. Drought prediction: Insights from the fusion of LSTM and multi-source factors. Sci. Total Environ. 2023, 902, 166361. [Google Scholar] [CrossRef]
- Bouguerra, H.; Derdous, O.; Tachi, S.E.; Hatzaki, M.; Abida, H. Spatiotemporal investigation of meteorological drought variability over northern Algeria and its relationship with different atmospheric circulation patterns. Theor. Appl. Climatol. 2023. [Google Scholar] [CrossRef]
- Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.V.; Lakshminarayanan, B.; Snoek, J. Can you trust your model’s uncertainty? Evaluating predictive uncertainty under dataset shift. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 14003–14014. [Google Scholar] [CrossRef]
- Kim, T.; Kim, J.; Tae, Y.; Park, C.; Choi, J.-H.; Choo, J. Reversible instance normalization for accurate time-series forecasting against distribution shift. In Proceedings of the ICLR 2022, Virtual Event, 25–29 April 2022. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary Transformers: Exploring the stationarity in time series forecasting. arXiv 2022, arXiv:arXiv:2205.14415. [Google Scholar] [CrossRef]




| Forecasting Variable | Predictors |
|---|---|
| DSI-TWS (t + n) | SPI_12, SEI_12, SPEI_11, SSMI1_11, SSMI2_10, SSMI3_8, SSMI4_10, SSI_10, SNI-12, DSI-TWS (t − 1) |
| DSI-DWS (t + n) | SPI_3, SEI_12, SNI-12, SSMI1_11, SSMI2_11, SSMI3_15, SSMI4_15, SSI_15, DSI-DWS (t − 1) |
| DSI-NDVI (t + n) | SPI_2, SEI_13, SPEI_2, SSMI1_11, SSMI2_9, SSMI3_8, SSMI4_8, SSI_9, DSI-NDVI (t − 1) |
| Model Type | Period | Criteria | T | T + 1 | T + 2 | T + 3 |
|---|---|---|---|---|---|---|
| LSTM | Training (2000–2014) | NSE | 0.56 | 0.50 | 0.42 | 0.43 |
| C | 0.76 | 0.71 | 0.66 | 0.66 | ||
| RMSE | 0.56 | 0.60 | 0.65 | 0.64 | ||
| TS | 0.54 | 0.44 | 0.44 | 0.35 | ||
| Testing (2015–2020) | NSE | 0.52 | 0.40 | 0.33 | 0.30 | |
| C | 0.77 | 0.71 | 0.63 | 0.65 | ||
| RMSE | 0.58 | 0.65 | 0.69 | 0.70 | ||
| TS | 0.39 | 0.51 | 0.45 | 0.42 | ||
| CNN | Training (2000–2014) | NSE | 0.73 | 0.54 | 0.37 | 0.27 |
| C | 0.86 | 0.75 | 0.62 | 0.59 | ||
| RMSE | 0.44 | 0.58 | 0.67 | 0.72 | ||
| TS | 0.54 | 0.43 | 0.33 | 0.46 | ||
| Testing (2015–2020) | NSE | 0.70 | 0.55 | 0.37 | 0.28 | |
| C | 0.87 | 0.75 | 0.69 | 0.54 | ||
| RMSE | 0.46 | 0.57 | 0.67 | 0.71 | ||
| TS | 0.56 | 0.46 | 0.41 | 0.49 | ||
| Catboost | Training (2000–2014) | NSE | 0.95 | 0.99 | 0.98 | 0.92 |
| C | 0.98 | 0.99 | 0.99 | 0.96 | ||
| RMSE | 0.19 | 0.08 | 0.11 | 0.24 | ||
| TS | 0.92 | 0.96 | 0.96 | 0.88 | ||
| Testing (2015–2020) | NSE | −0.13 | −0.33 | −0.56 | −0.66 | |
| C | 0.82 | 0.78 | 0.69 | 0.31 | ||
| RMSE | 0.89 | 0.97 | 1.06 | 1.09 | ||
| TS | 0.39 | 0.39 | 0.18 | 0.09 |
| Model Type | Period | Criteria | T | T + 1 | T + 2 | T + 3 |
|---|---|---|---|---|---|---|
| LSTM | Training (2000–2014) | NSE | 0.57 | 0.54 | 0.51 | 0.24 |
| C | 0.77 | 0.73 | 0.72 | 0.50 | ||
| RMSE | 0.44 | 0.46 | 0.47 | 0.58 | ||
| TS | 0.43 | 0.36 | 0.22 | 0.00 | ||
| Testing (2015–2020) | NSE | 0.38 | 0.31 | 0.24 | 0.25 | |
| C | 0.70 | 0.67 | 0.72 | 0.68 | ||
| RMSE | 0.73 | 0.78 | 0.82 | 0.81 | ||
| TS | 0.52 | 0.54 | 0.35 | 0.58 | ||
| CNN | Training (2000–2014) | NSE | 0.32 | 0.48 | 0.28 | 0.35 |
| C | 0.70 | 0.70 | 0.58 | 0.62 | ||
| RMSE | 0.55 | 0.48 | 0.57 | 0.54 | ||
| TS | 0.52 | 0.18 | 0.27 | 0.25 | ||
| Testing (2015–2020) | NSE | 0.33 | 0.32 | 0.26 | 0.33 | |
| C | 0.59 | 0.68 | 0.65 | 0.70 | ||
| RMSE | 0.76 | 0.77 | 0.81 | 0.77 | ||
| TS | 0.71 | 0.60 | 0.50 | 0.56 |
| Model Type | Period | Criteria | T | T + 1 | T + 2 | T + 3 |
|---|---|---|---|---|---|---|
| LSTM | Training (2000–2014) | NSE | 0.28 | 0.09 | −0.03 | −0.24 |
| C | 0.53 | 0.31 | 0.13 | −0.07 | ||
| RMSE | 0.77 | 0.86 | 0.92 | 0.98 | ||
| TS | 0.37 | 0.20 | 0.18 | 0.07 | ||
| Testing (2015–2020) | NSE | −0.05 | −0.18 | −0.24 | −0.39 | |
| C | 0.15 | 0.20 | −0.17 | 0.06 | ||
| RMSE | 0.74 | 0.78 | 0.79 | 0.84 | ||
| TS | 0.00 | 0.00 | 0.00 | 0.00 | ||
| CNN | Training (2000–2014) | NSE | −0.04 | 0.02 | 0.15 | 0.16 |
| C | 0.23 | 0.30 | 0.40 | 0.41 | ||
| RMSE | 0.92 | 0.89 | 0.83 | 0.81 | ||
| TS | 0.21 | 0.26 | 0.36 | 0.30 | ||
| Testing (2015–2020) | NSE | −0.10 | −0.22 | −0.32 | −0.40 | |
| C | 0.47 | 0.15 | 0.09 | −0.04 | ||
| RMSE | 0.75 | 0.80 | 0.81 | 0.84 | ||
| TS | 0.25 | 0.00 | 0.00 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, R.; Yan, H.; Chiang, Y.-M. Forecasting the Propagation from Meteorological to Hydrological and Agricultural Drought in the Huaihe River Basin with Machine Learning Methods. Remote Sens. 2023, 15, 5524. https://doi.org/10.3390/rs15235524
Hao R, Yan H, Chiang Y-M. Forecasting the Propagation from Meteorological to Hydrological and Agricultural Drought in the Huaihe River Basin with Machine Learning Methods. Remote Sensing. 2023; 15(23):5524. https://doi.org/10.3390/rs15235524
Chicago/Turabian StyleHao, Ruonan, Huaxiang Yan, and Yen-Ming Chiang. 2023. "Forecasting the Propagation from Meteorological to Hydrological and Agricultural Drought in the Huaihe River Basin with Machine Learning Methods" Remote Sensing 15, no. 23: 5524. https://doi.org/10.3390/rs15235524
APA StyleHao, R., Yan, H., & Chiang, Y.-M. (2023). Forecasting the Propagation from Meteorological to Hydrological and Agricultural Drought in the Huaihe River Basin with Machine Learning Methods. Remote Sensing, 15(23), 5524. https://doi.org/10.3390/rs15235524







