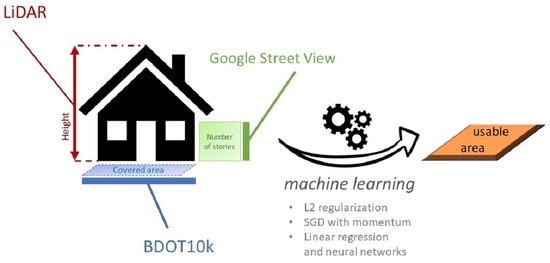
Machine Learning of Usable Area of Gable-Roof Residential Buildings Based on Topographic Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. On Polish Norms for Usable Area Calculation
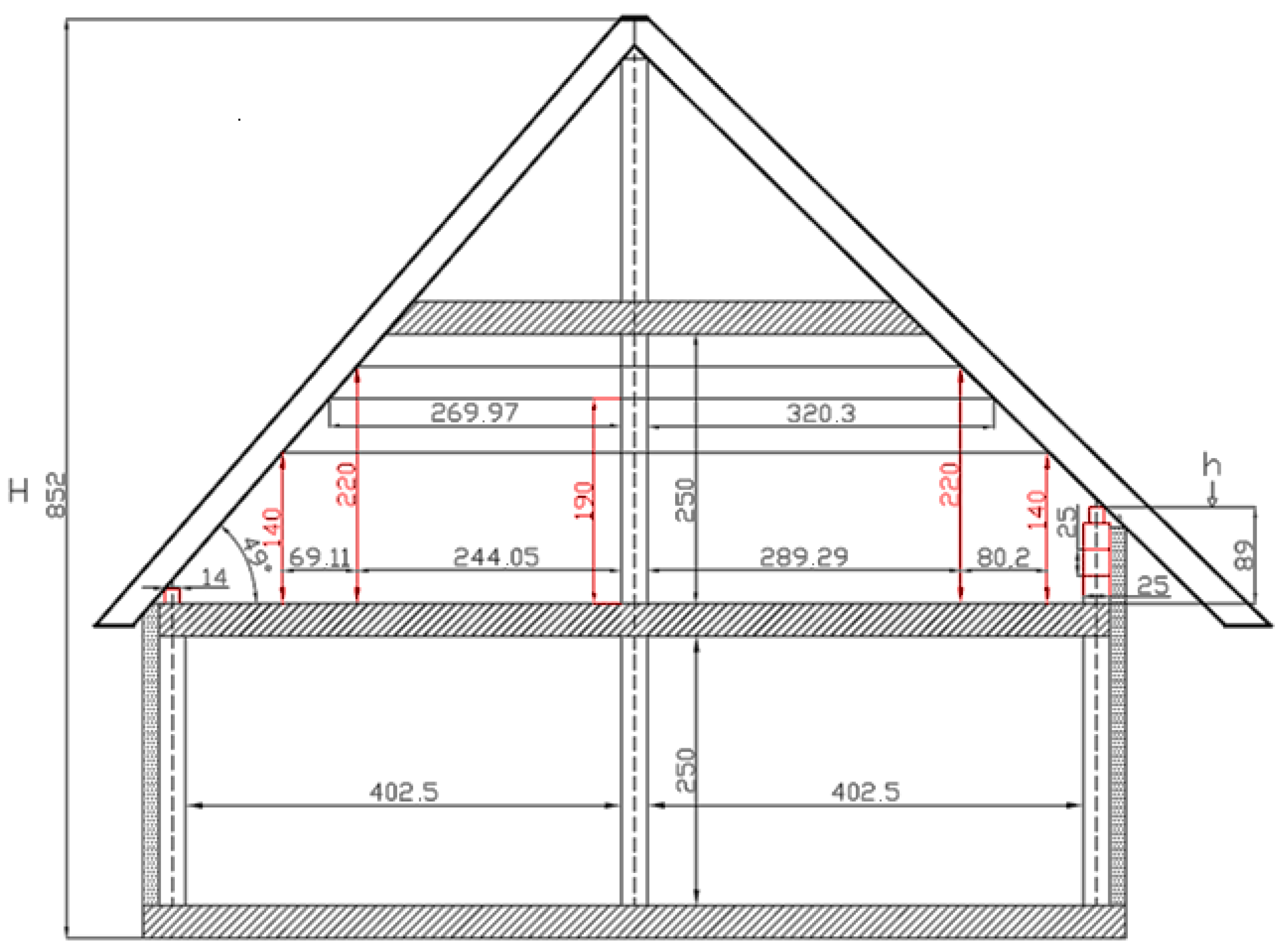
2.2. The Recommended Polish Norm and Gable-Roof Buildings
2.3. Simulation of Knee Wall Height Impact on Usable Area
2.4. Data on Gable-Roof Properties from Architectural Bureaus
2.5. Data on Gable-Roof Residential Buildings in Koszalin from Airborne Laser Scanning
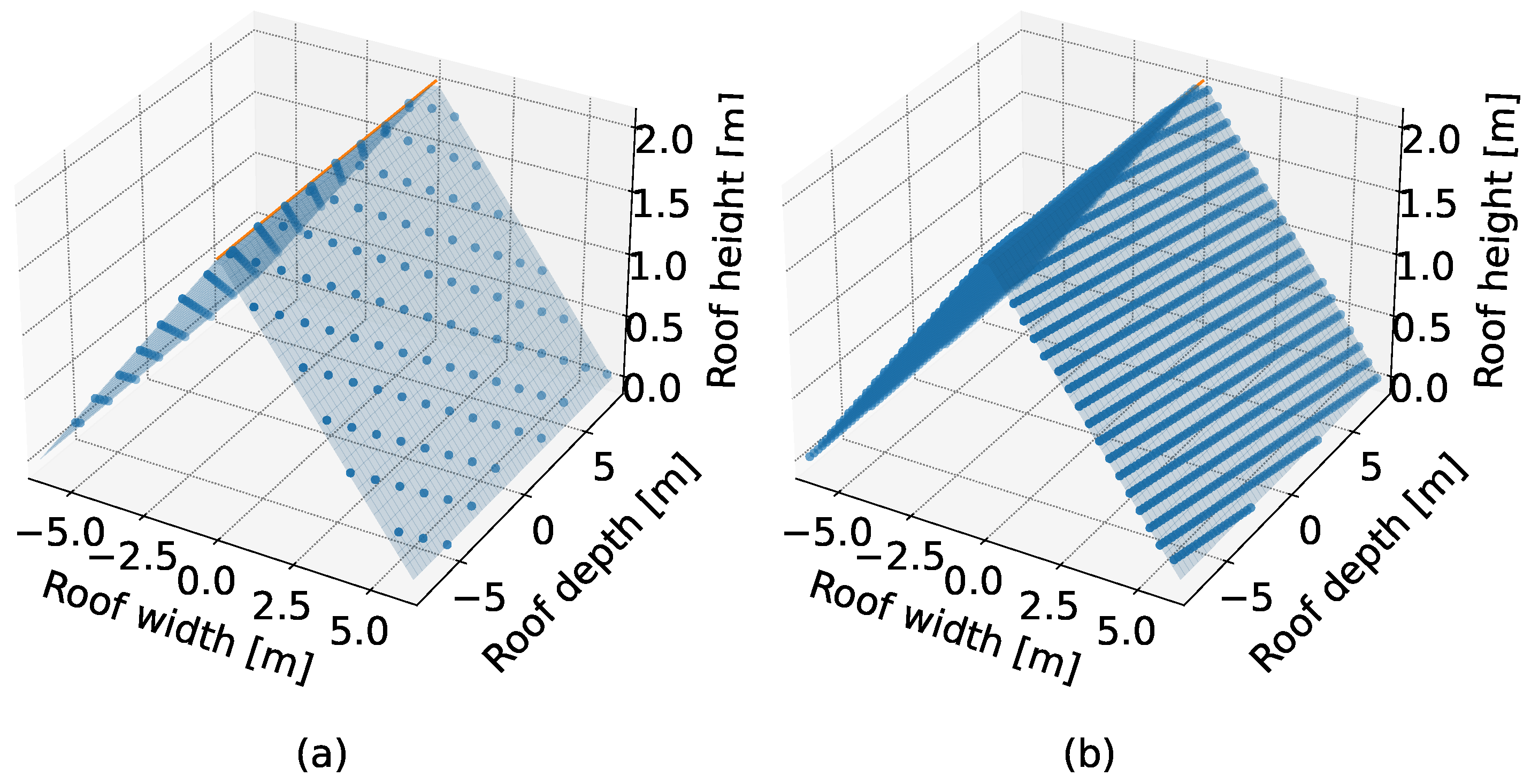
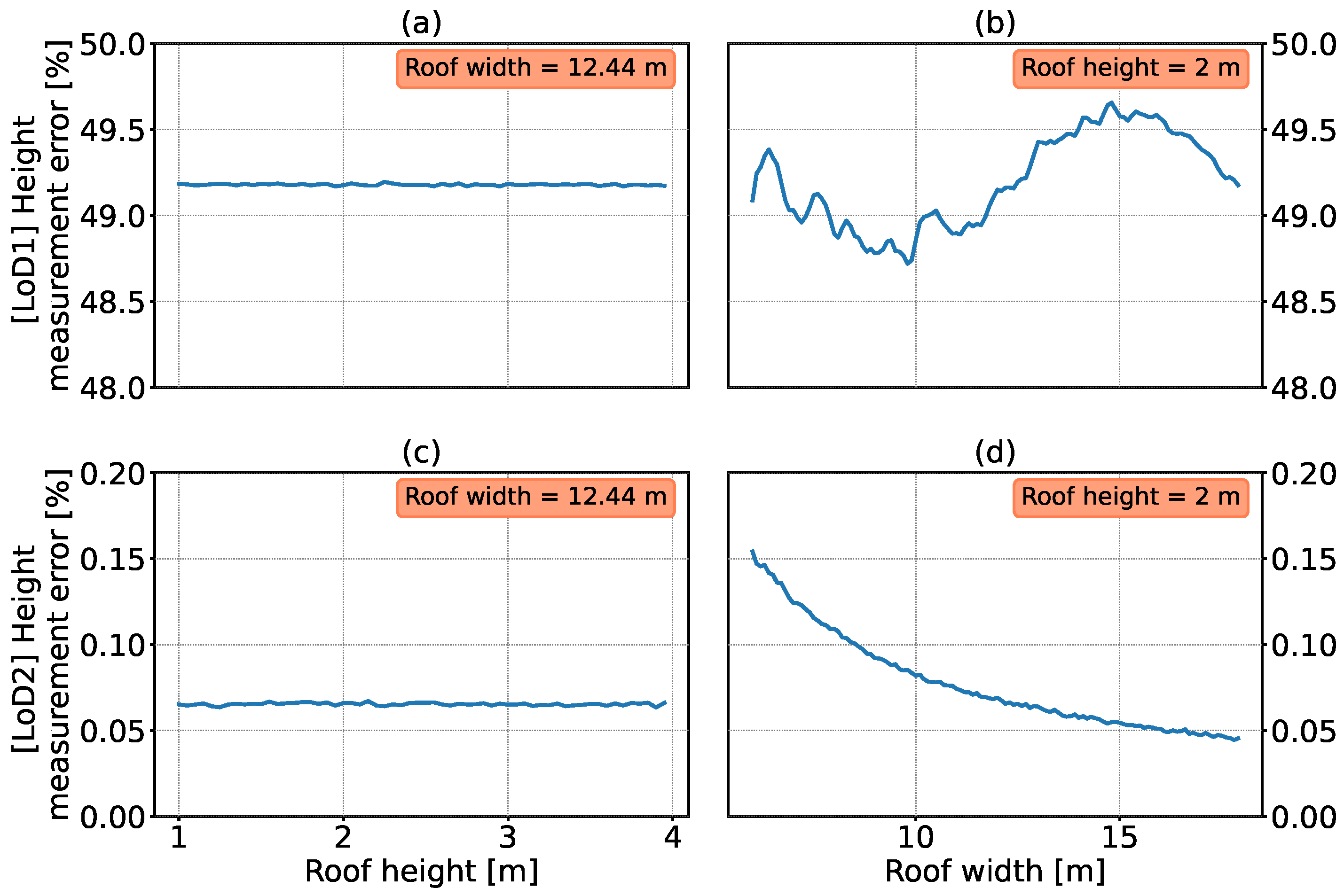
2.6. Monte Carlo Simulation
- We sampled an initial point of the projected measurement grid from the uniform distribution. The point was sampled within a square of dimensions matching the grid’s spacing in the lower left corner of the roof;
- Given this point, we constructed the measurement grid with the spacing representative of LoD1 or LoD2, which covered the whole roof, with 2 m padding on each side of the grid;
- We then measured the height, matching the method to the given LoD:
- For LoD1, the median value among the grid points is was what we modeled as the measured height;
- For LoD2, the maximal value among grid points was what we modeled as the measured height.
- WCSME is the difference between the minimal measured height and the set height;
- MME is the difference between the mean measured height (averaged across Monte Carlo steps for each angle and then averaged over all angles) from the set height.
2.7. Machine Learning Methods
3. Results
3.1. Gable Roofs Impact the Usable Area of the Building
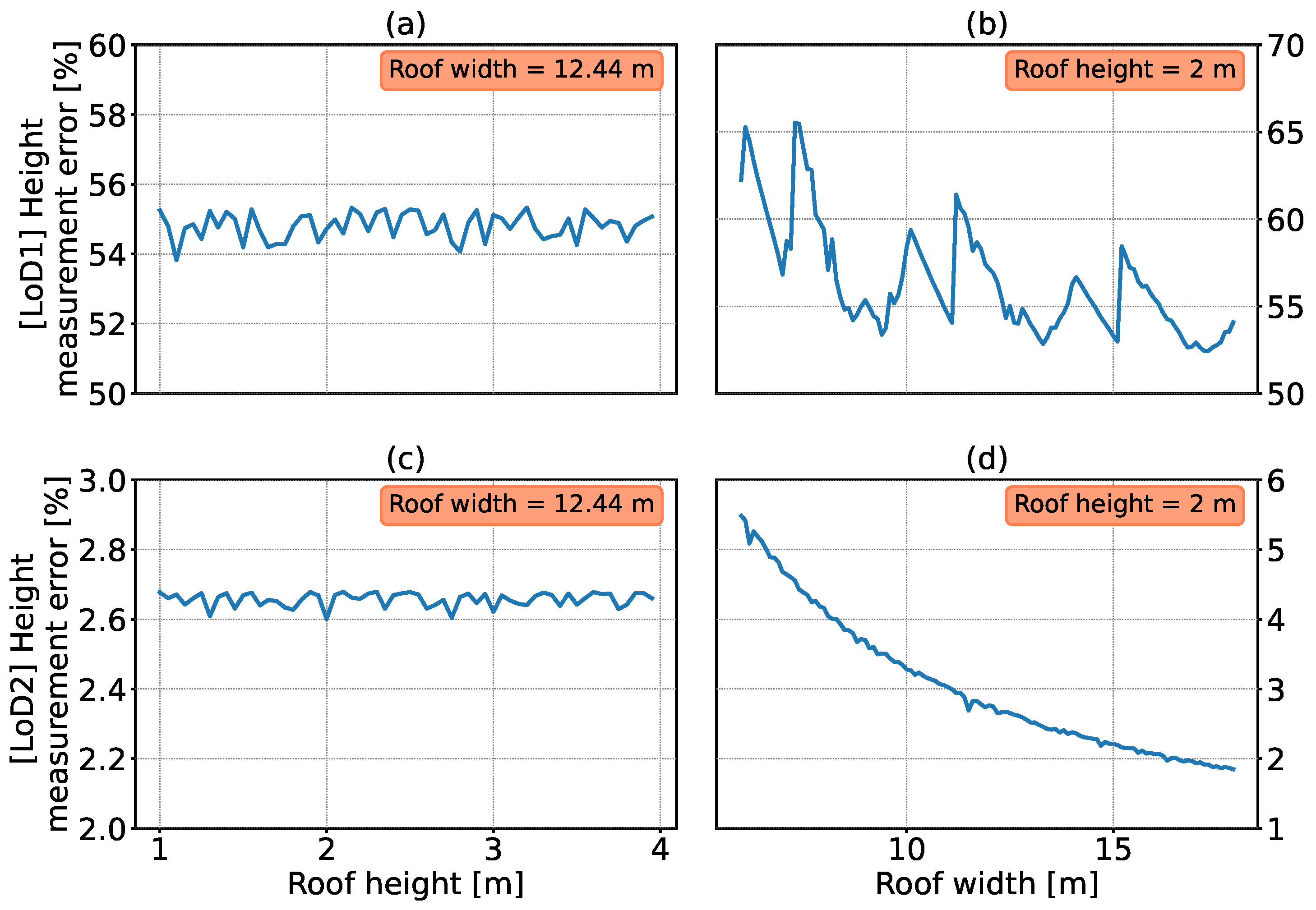
3.2. Errors in the LiDAR-Based Data for Gable-Roof Buildings
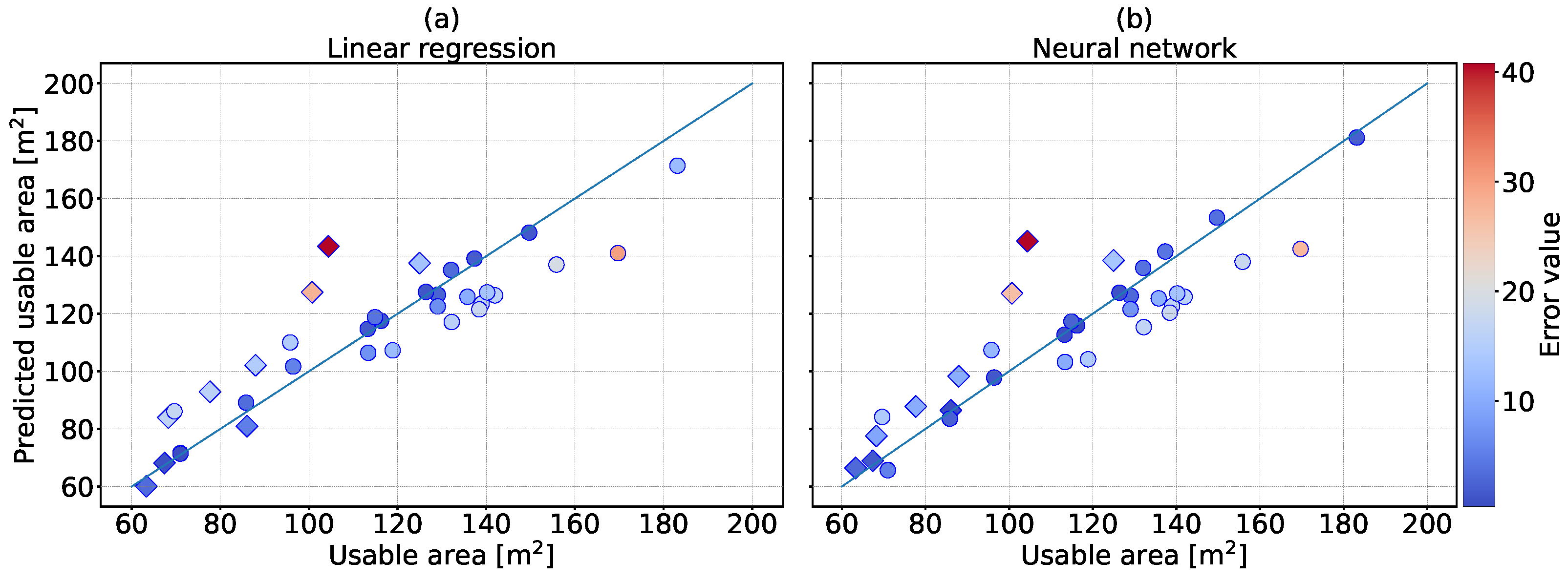
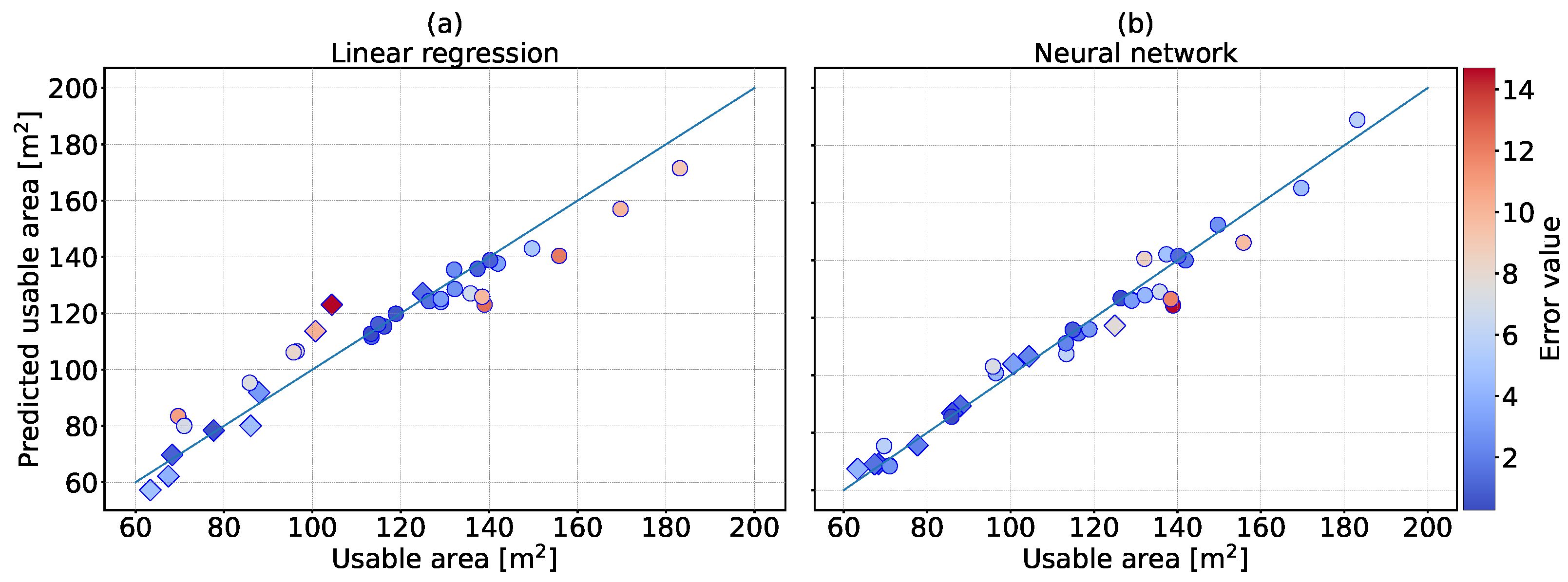
3.3. Machine Learning for Buildings of Architectural Bureaus
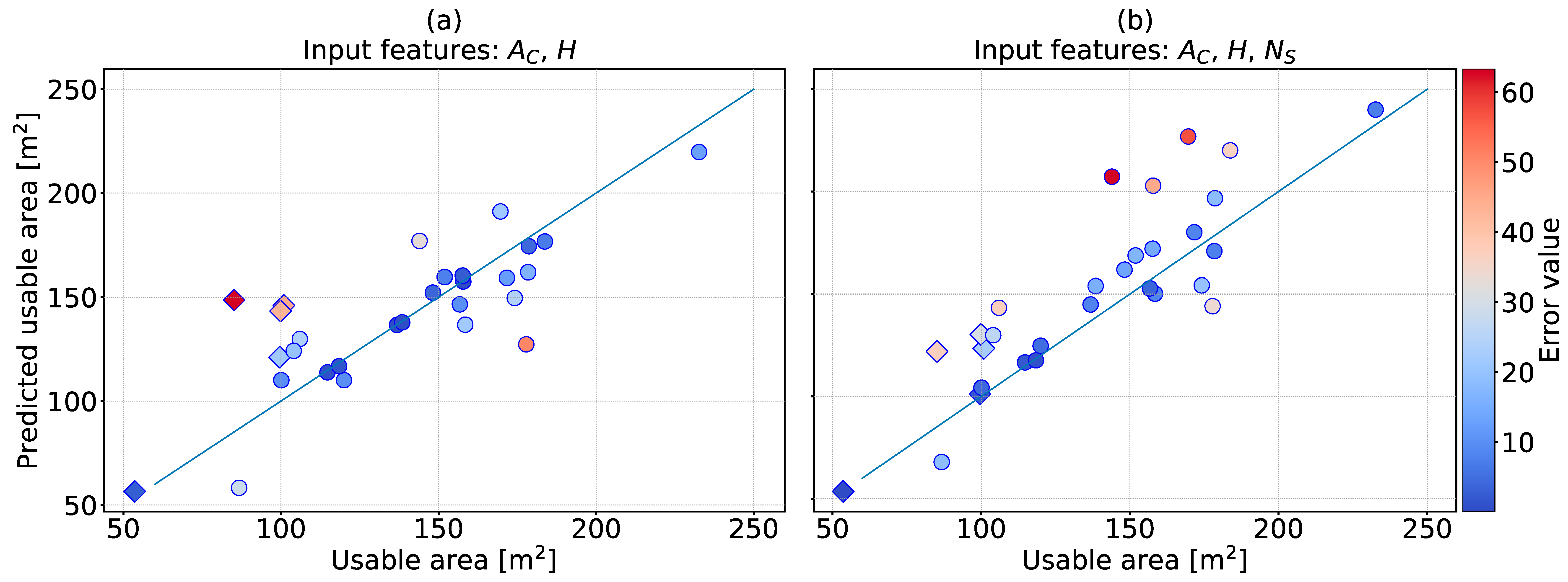
3.4. Machine Learning for Real Buildings in Koszalin
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BDOT10k | Database of Topographic Objects (pol. Baza Danych Obiektów Topologicznych) |
| LiDAR | Light Detection and Ranging |
| LoD | Level of Detail |
| REPR | Real Estate Price Register (pol. Rejestr Cen Nieruchomości) |
| WCSME | Worst-Case Scenario Measurement Error |
| MME | Mean Measurement Error |
| MAE | Mean Absolute Error |
| MedAE | Median Absolute Error |
| MedAPE | Median Absolute Percentage Error |
References
- Czaja, J.; Krysiak, Z.; Nowak, R. Analysis of property valuation methods in comparative approach in the aspect of securing the credit liabilities. Finans. Nieruchom. 2005, 2/2005, 16–28. (In Polish) [Google Scholar]
- Sawiłow, E. Analysis of the real estate valuation methods in comparative approach. Geod. Rev. 2008, 80, 3–7. (In Polish) [Google Scholar]
- Foryś, I.; Kokot, S. Problems with Real Estate Market Analysis. In Microeconomy in Theory and Practice; Scientific Publishing House of the University of Szczecin: Szczecin, Poland, 2001; pp. 175–182. (In Polish) [Google Scholar]
- Applied Econometry with Principles; University of Szczecin: Szczecin, Poland, 2006; pp. 25–31. ISBN 83-913389-7-5. (In Polish)
- Felcenloben, D. Real Estate Cadastre; Gall: Katowice, Poland, 2009; pp. 29–42. (In Polish) [Google Scholar]
- Hycner, R. Basics of the Cadastre; AGH University of Science and Technology Press: Kraków, Poland, 2004; pp. 241–282. (In Polish) [Google Scholar]
- Bennett, R. On the Nature and Utility of Natural Boundaries for Land and Marine Administration. Land Use Policy 2010, 27, 772–779. [Google Scholar]
- Kaufmann, J. Cadastre 2014: A Vision for a Future Cadastral System; International Federation of Surveyors: Copenhagen, Denmark, 1998; pp. 1–38. [Google Scholar]
- Larsson, G. Land Registration and Cadastral Systems; Longman Scientific and Technical: Harlow, UK, 1991; pp. 21–65. [Google Scholar]
- Enemark, S. Building Modern Land Markets in Developed Economies. J. Spat. Sci. 2005, 50, 51–68. [Google Scholar]
- Stoter, J. Towards a 3D Cadastre: Where Do Cadastral Needs and Technical Possibilities Meet? Comput. Environ. Urban Syst. 2003, 27, 395–410. [Google Scholar]
- Kokot, S. Data Quality of Transaction Prices in Real Estate Market. Acta Sci. Adm. Locorum 2015, 14, 43–49. (In Polish) [Google Scholar]
- Dawid, L. Analysis of Completeness of Data from the Price and Value Register on the Example of Kołobrzeg and Koszalin Districts in Years 2010–2017. Stud. Res. FEM SU 2018, 1, 91–102. (In Polish) [Google Scholar]
- Dawid, L. Analysis of Data Completeness in the Register of Real Estate Prices and Values Used for Real Estate Valuation on the Example of Koszalin District in the Years 2010–2016. Folia Econ. Stetin. 2018, 18, 17–26. [Google Scholar]
- Database of Topographic Objects (pol. Baza Danych Obiektów Topologicznych) (BDOT). Available online: https://www.geoportal.gov.pl/dane/baza-danych-obiektow-topograficznych-bdot (accessed on 10 April 2022).
- Wężyk, P. (Ed.) Textbook for Participants of Trainings on Using LiDAR Products; Head Office of Land Surveying and Cartography: Cracow, Poland, 2015. (In Polish)
- Baldominos, A.; Blanco, I.; Moreno, A.J.; Iturrarte, R.; Bernárdez, Ó.; Afonso, C. Identifying Real Estate Opportunities Using Machine Learning. Appl. Sci. 2018, 8, 2321. [Google Scholar] [CrossRef]
- Pinter, G.; Mosavi, A.; Felde, I. Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach. Entropy 2020, 22, 1421. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.; Lee, M.-H.; Hong, S.-Y. A Comparative Study of Machine Learning and Spatial Interpolation Methods for Predicting House Prices. Sustainability 2022, 14, 9056. [Google Scholar] [CrossRef]
- Mora-Garcia, R.-T.; Cespedes-Lopez, M.-F.; Perez-Sanchez, V.R. Housing Price Prediction Using Machine Learning Algorithms in COVID-19 Times. Land 2022, 11, 2100. [Google Scholar] [CrossRef]
- Dawid, L.; Tomza, M.; Dawid, A. Estimation of usable area of flat-roof residential buildings using topographic data with machine learning methods. Remote Sens. 2019, 11, 2382. [Google Scholar] [CrossRef]
- Benduch, P.; Butryn, K. Legal and standard principles of buildings and their parts usable floor area quantity surveying. In Infrastructure and Ecology of Rural Areas; Polish Academy of Sciences: Cracow, Poland, 2018; pp. 225–238. ISSN 1732-5587. (In Polish) [Google Scholar] [CrossRef]
- Benduch, P.; Hanus, P. The Concept of Estimating Usable Floor Area of Buildings Based on Cadastral Data. Rep. Geod. Geoinform. 2018, 105, 29–41. [Google Scholar] [CrossRef] [Green Version]
- Budzyński, T. Calculating the Area of Newly-Built Apartments and Buildings According to Uniform Rules. Geod. R. 2012, 84, 31. (In Polish) [Google Scholar]
- Buśko, M. Analysis of legal regulations upon estimation of usable area of building and residential unit. Geod. R. 2015, 87, 8–12. (In Polish) [Google Scholar]
- Buśko, M. Building contour line in the database of the real estate cadastre in Poland pursuant to applicable laws. Econtechmod Int. Q. J. Econ. Technol. New Technol. Model. Process. 2016, 5, 183–190. [Google Scholar]
- Bydłosz, J.; Cichociński, P.; Piotr, P. Possibilities of the Register of Real Estates Prices and Values Restrictions Overcoming Applying GIS Tools. Stud. Inform. 2010, 31, 229–244. (In Polish) [Google Scholar]
- Ebing, J. Calculating of Area and Cubic Volume of Facilities with Different Intended Use; Verlag Dashofer Sp. z o.o Publishing House: Ljubljana, Slovenia, 2011; ISBN 978-83-7537-108-6. (In Polish) [Google Scholar]
- Polish Committee of Standardization. PN-70/B-02365 Surface Area of Buildings—Classification, Definitions, and Methods of Measurement 1970. Available online: http://rzeczoznawca-zachodniopomorskie.pl/pliki/PN_70_B_02365.pdf (accessed on 22 April 2022). (In Polish).
- Polish Commitee of Standardization. PN-ISO 9836:1997 Performance Standards in Building—Definition and Calculation of Area and Space Indicators 1997. Available online: http://rzeczoznawca-zachodniopomorskie.pl/pliki/PN_ISO_9836_1997.pdf (accessed on 20 April 2022). (In Polish).
- Regulation of the Minister of Transport, Construction and Maritime Economy of April 25, 2012 on Detailed Scope and Form of a Construction Project. Journal of Laws of 2012, Item 462. Available online: http://prawo.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20120000462 (accessed on 20 May 2020). (In Polish)
- Polish Commitee of Standardization. PN-ISO 9836:2015-12 Performance Standards in Building—Definition and Calculation of Area and Space Indicators 2015. Available online: http://sklep.pkn.pl/pn-iso-9836-2015-12p.html (accessed on 25 May 2020). (In Polish).
- Zbroś, D. The Rules for Calculating the Usable Area by Two Current Polish Standards. Saf. Eng. Anthropog. Objects 2016, 3, 19–22. (In Polish) [Google Scholar]
- Project W-0426 for Single-Family Detached House of the Spółdzielczy Ośrodek Budownictwa INWESTPROJEKT Design Bureau, Designed by M.Sc. Eng. Arch. Wojciech Kempiński, issued in 1993 (private archive, accessed on 11 April 2022). 11 April.
- Lipińscy, M.L. Design Office. Houses Projects. Available online: https://lipinscy.pl/ (accessed on 11 April 2022).
- Mendel, B. ARCHON+ Project Office. Available online: https://www.archon.pl/ (accessed on 11 April 2022).
- Head Office of Land Surveying and Cartography. Geoportal of National Spatial Data Infrastructure. Available online: https://www.geoportal.gov.pl/ (accessed on 10 April 2022).
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. Available online: http://qgis.osgeo.org (accessed on 11 April 2022).
- Dawid, L.; Cybiński, K.; Stręk, Ż. GitHub Repository: ML for Usable Area. Available online: https://github.com/kcybinski/ML_for_usable_area_estimation_gable_roofs (accessed on 31 January 2023).
- The Ordinance of the Council of Ministers of September 21, 2004 on Real Estate Valuation and Preparation of Valuation Survey. Journal Laws of 2004, Item 2109. Available online: http://prawo.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20042072109 (accessed on 20 June 2019). (In Polish)
| Feature | Symbol | Values (Design Offices) | Values (Koszalin) |
|---|---|---|---|
| Usable area | 42.47–217.34 m | 53.58–438.90 m | |
| Covered area | 47.18–227.60 m | 66.82–288.39 m | |
| Number of stories | 1–2 | 1–5 | |
| Height | H | 4.54–9.16 m | 6–15.73 m |
| Knee wall’s height | h | 0–2.21 m | no data |
| Usable Area According to the Norm [m] 1 | |||
|---|---|---|---|
| h [cm] | PN 70 | ISO 97 | ISO 2015 |
| 14 | 49.94 | 51.56 | 54.7 |
| 14 + 25 | 53.05 | 56 | 57.9 |
| 14 + 2 × 25 | 56.16 | 59.2 | 61.1 |
| 14 + 3 × 25 | 59.85 | 62.8 | 64.9 |
| 14 + 4 × 25 | 64.03 | 66.8 | 69.2 |
| Metric 1 | Input: , H | Input: , H, | Input: , H, , h | |||
|---|---|---|---|---|---|---|
| LinReg | NN (2-10-1) | LinReg | NN (3-10-1) | LinReg | NN (4-30-1) | |
| [%] | 80 | 81 | 93 | 97 | 95 | 98 |
| MAE [m] | 10.27 | 9.86 | 6.67 | 4.09 | 4.91 | 3.47 |
| MedAE [m] | 9.88 | 9.31 | 5.26 | 2.93 | 3.30 | 3.00 |
| Max error [m] | 39.01 | 40.81 | 18.62 | 14.70 | 17.86 | 11.38 |
| Min error [m] | 0.41 | 0.35 | 0.52 | 0.28 | 0.17 | 0.52 |
| MedAPE [%] | 9 | 9 | 6 | 4 | 5 | 3 |
| Metric 1 | Input: , H | Input: , H, |
|---|---|---|
| [%] | 62 | 56 |
| MAE [m] | 17.29 | 19.40 |
| MedAE [m] | 12.44 | 15.42 |
| Max error [m] | 63.50 | 63.29 |
| Min error [m] | 0.21 | 0.03 |
| MedAPE [%] | 15 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dawid, L.; Cybiński, K.; Stręk, Ż. Machine Learning of Usable Area of Gable-Roof Residential Buildings Based on Topographic Data. Remote Sens. 2023, 15, 863. https://doi.org/10.3390/rs15030863
Dawid L, Cybiński K, Stręk Ż. Machine Learning of Usable Area of Gable-Roof Residential Buildings Based on Topographic Data. Remote Sensing. 2023; 15(3):863. https://doi.org/10.3390/rs15030863
Chicago/Turabian StyleDawid, Leszek, Kacper Cybiński, and Żanna Stręk. 2023. "Machine Learning of Usable Area of Gable-Roof Residential Buildings Based on Topographic Data" Remote Sensing 15, no. 3: 863. https://doi.org/10.3390/rs15030863
APA StyleDawid, L., Cybiński, K., & Stręk, Ż. (2023). Machine Learning of Usable Area of Gable-Roof Residential Buildings Based on Topographic Data. Remote Sensing, 15(3), 863. https://doi.org/10.3390/rs15030863