Early Yield Forecasting of Maize by Combining Remote Sensing Images and Field Data with Logistic Models
Abstract
:1. Introduction
2. Materials and Methodology
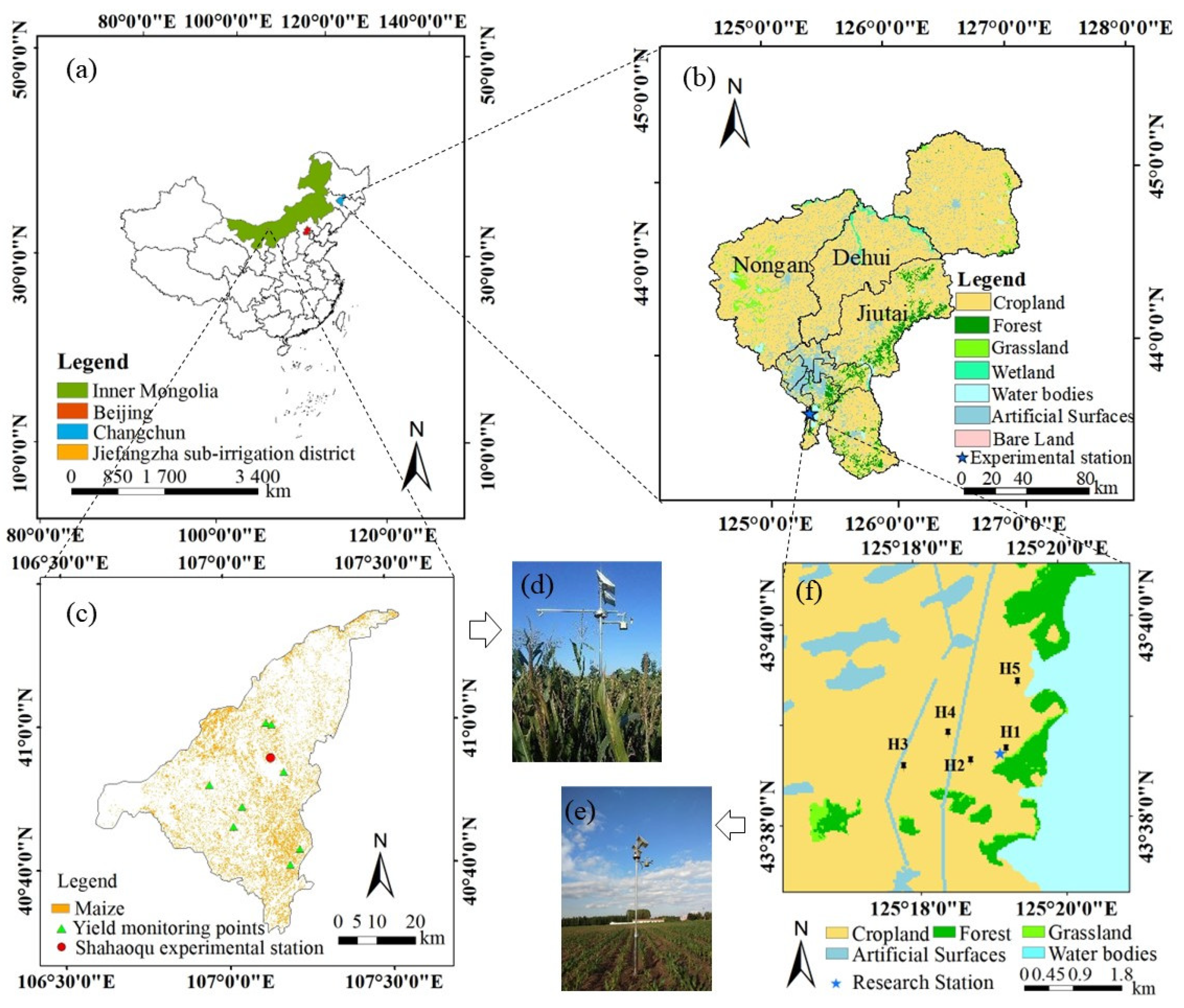
2.1. Study Areas
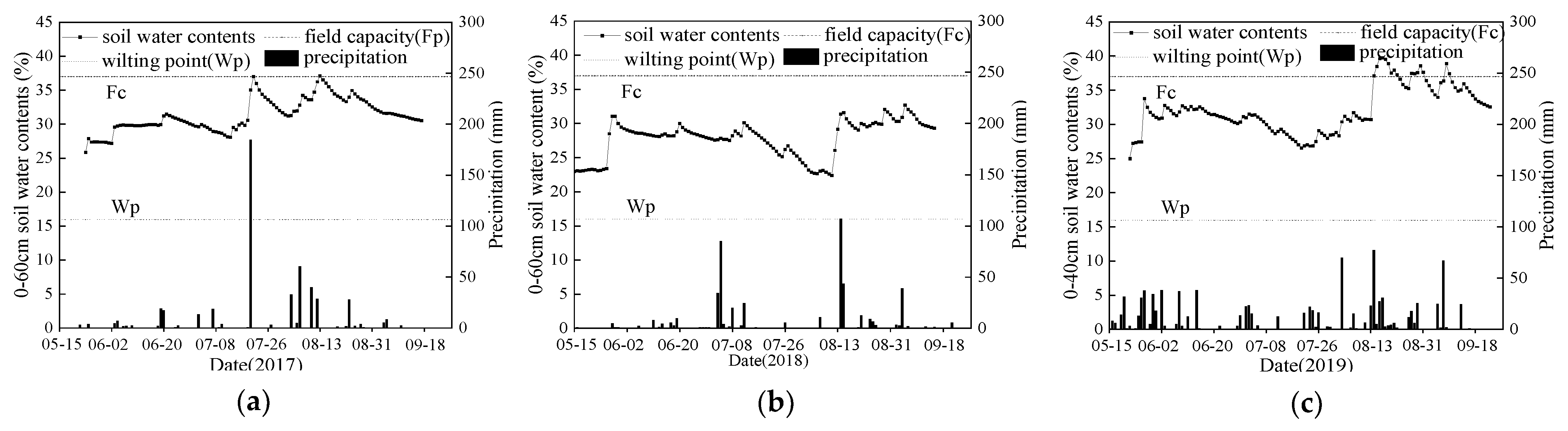
2.2. Field Measurements
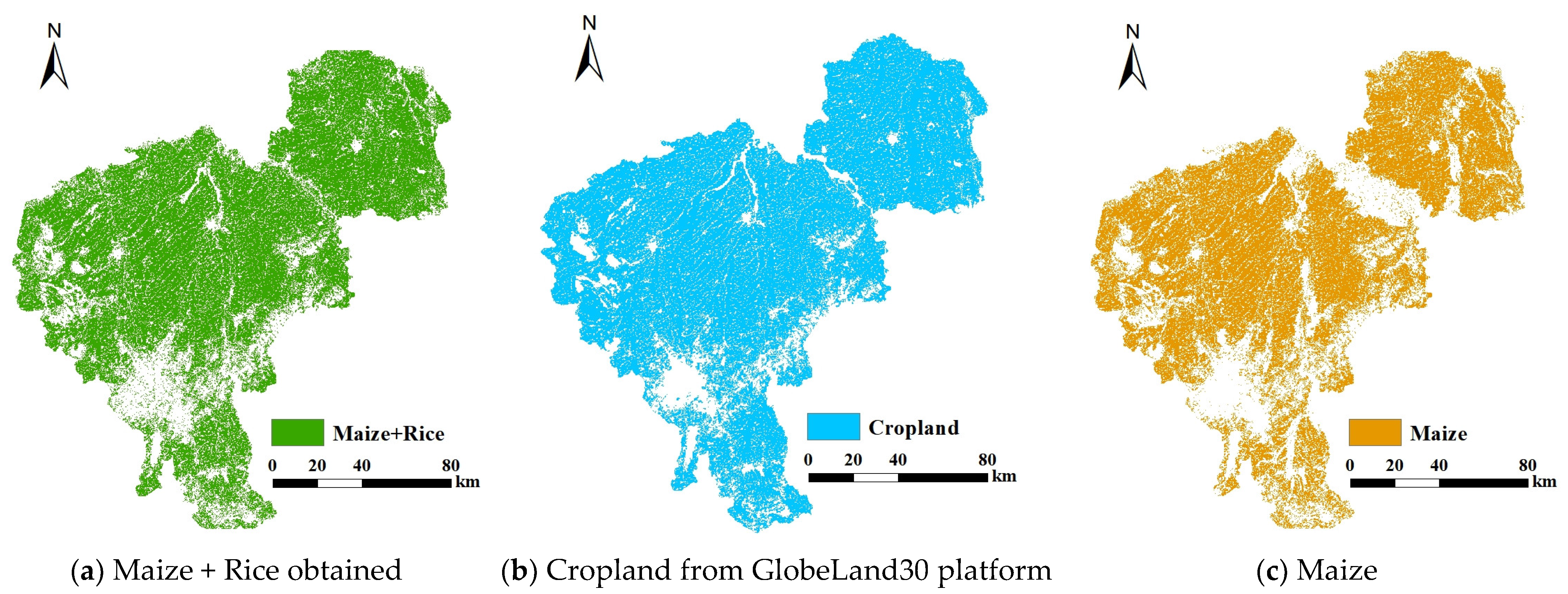
2.3. Remote Sensing Data
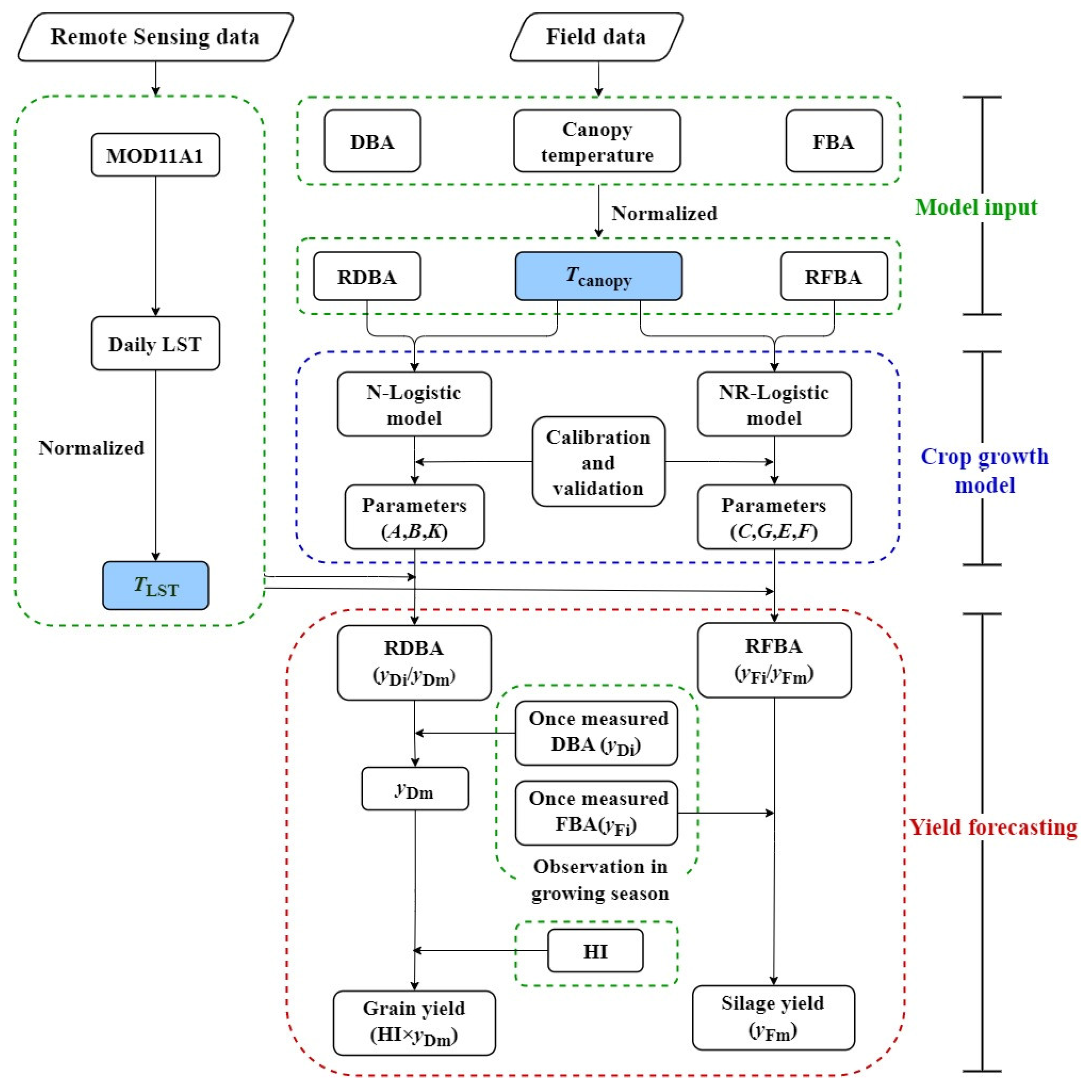
2.4. Logistic Models
2.4.1. Logistic Model
2.4.2. Normalized Logistic Model (N-Logistic Model)
2.4.3. Revised Logistic Model (R-Logistic Model)
2.4.4. Normalized Revised Logistic Model (NR-Logistic Model)
2.5. Yield Forecasting
2.6. Statistical Evaluation
3. Results
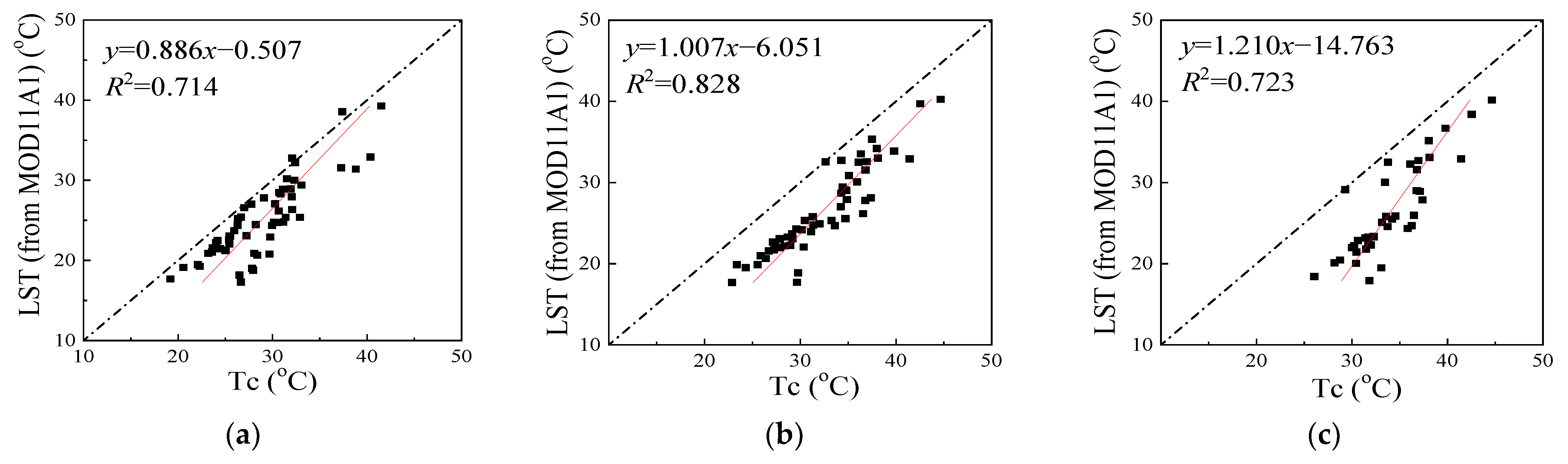
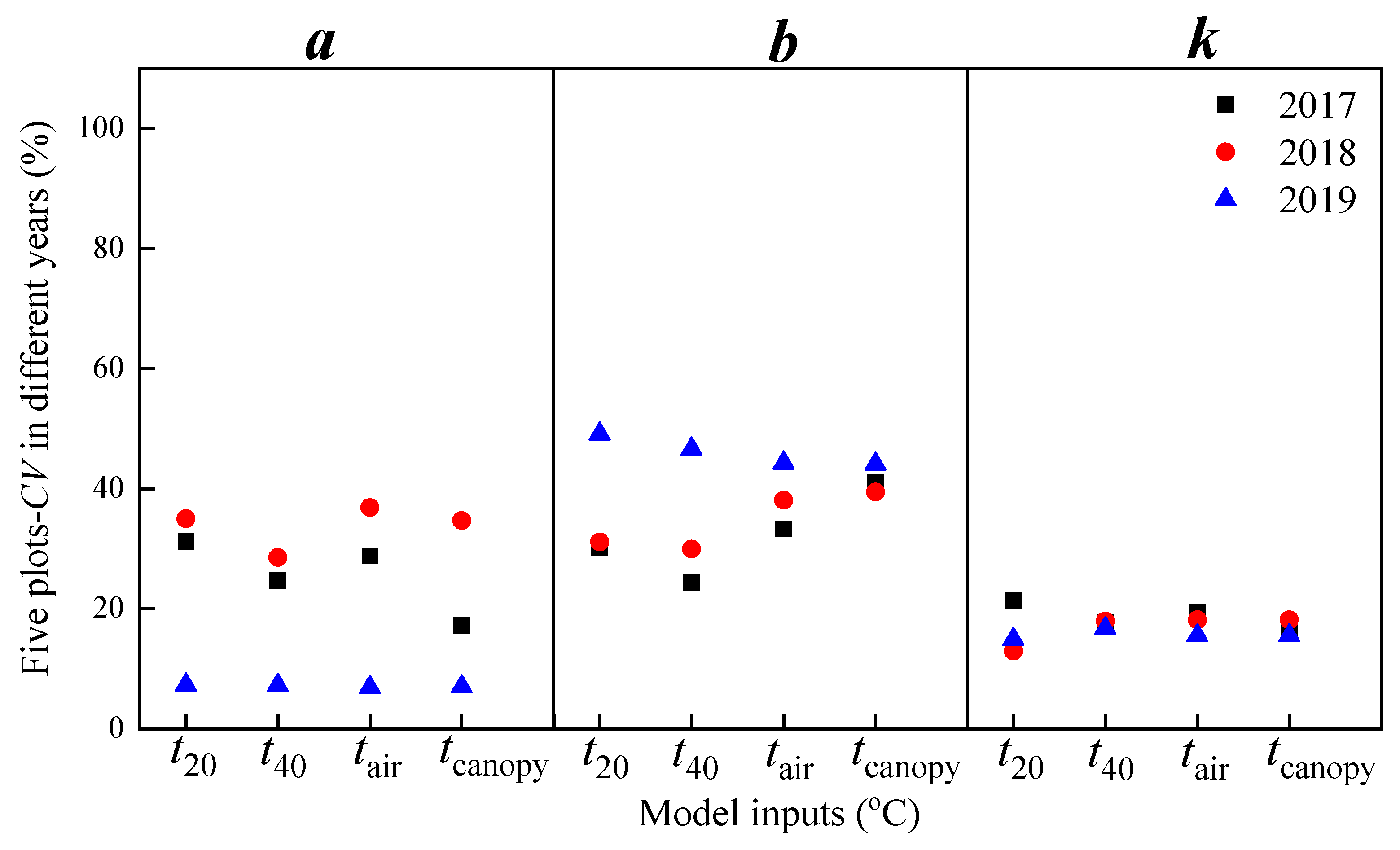
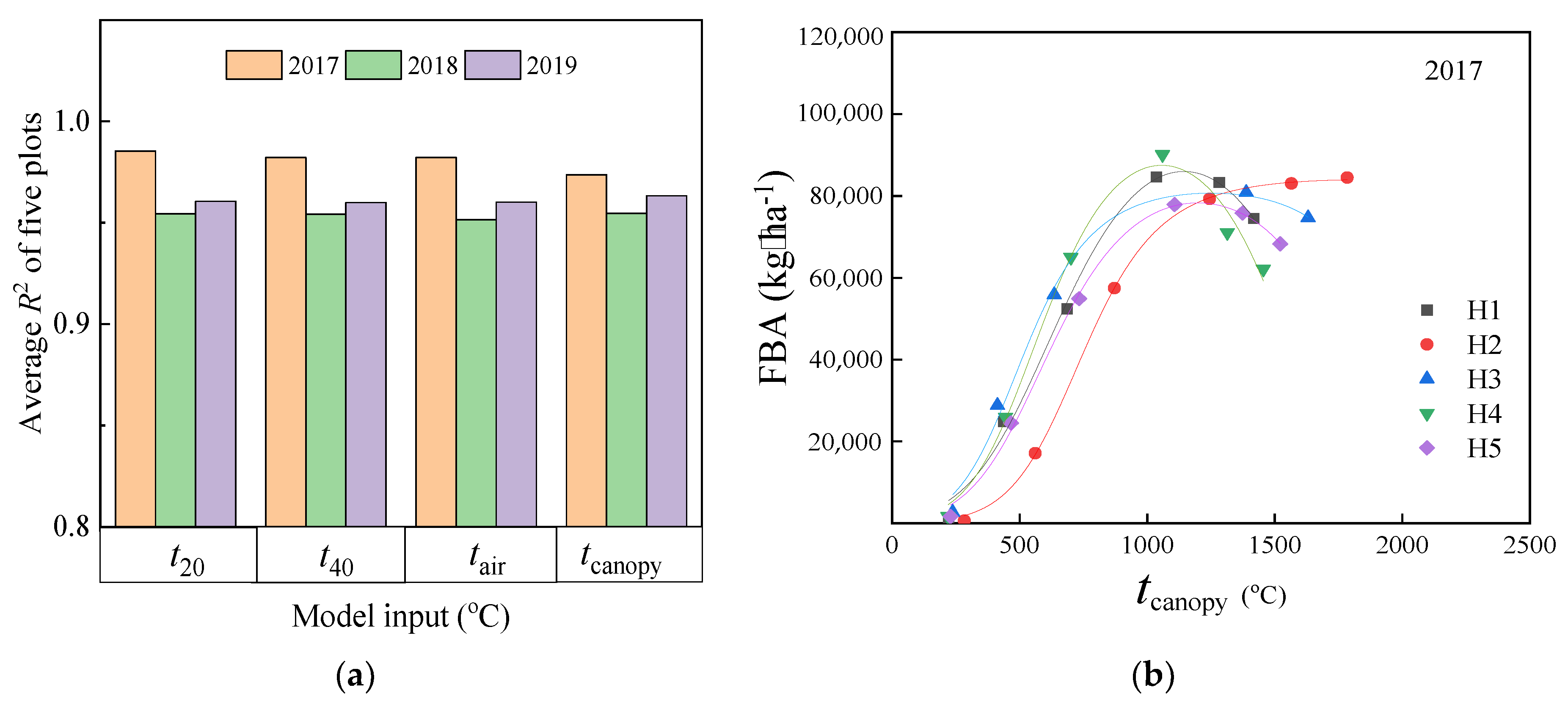
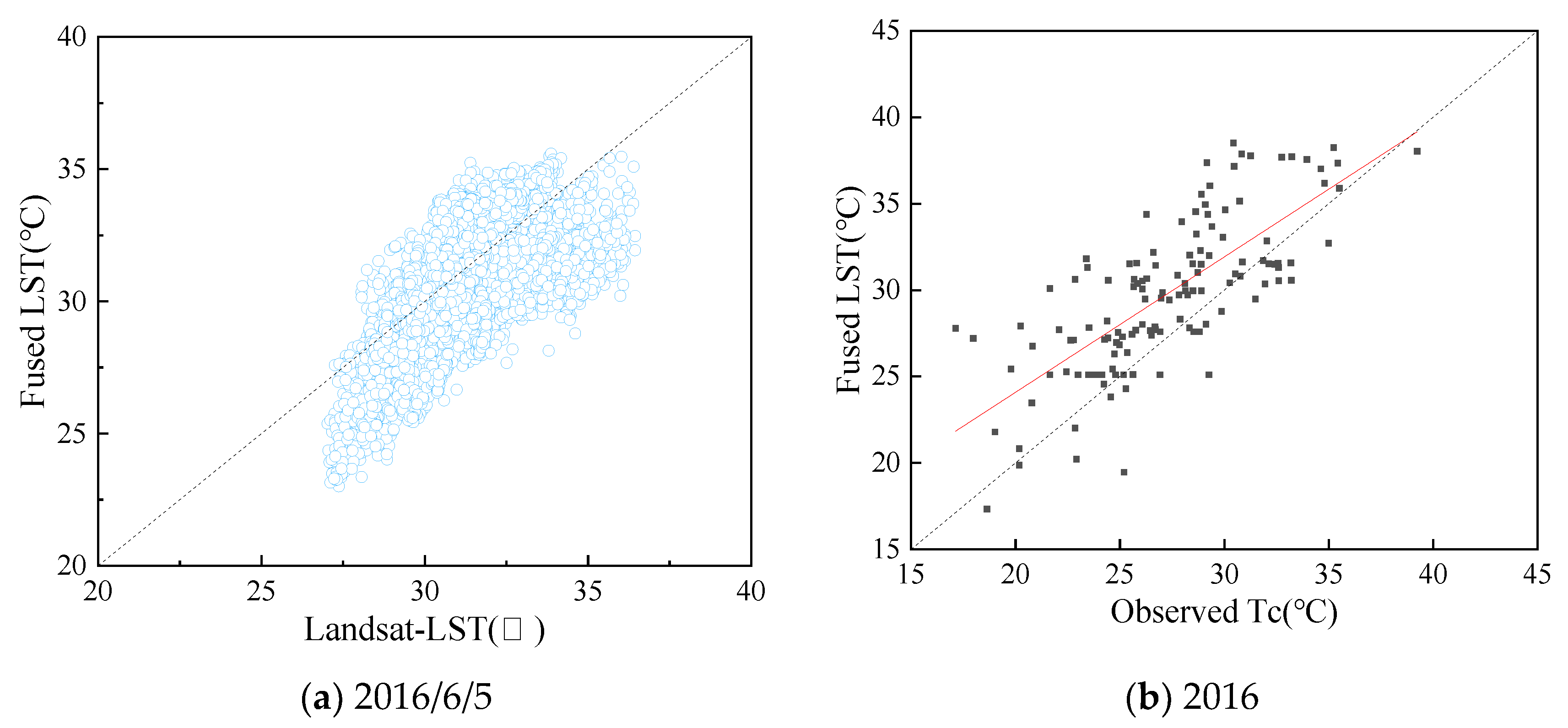
3.1. Evaluating the Values of LST from MOD11A in Changchun
3.2. Grain Yield Forecasting in Changchun
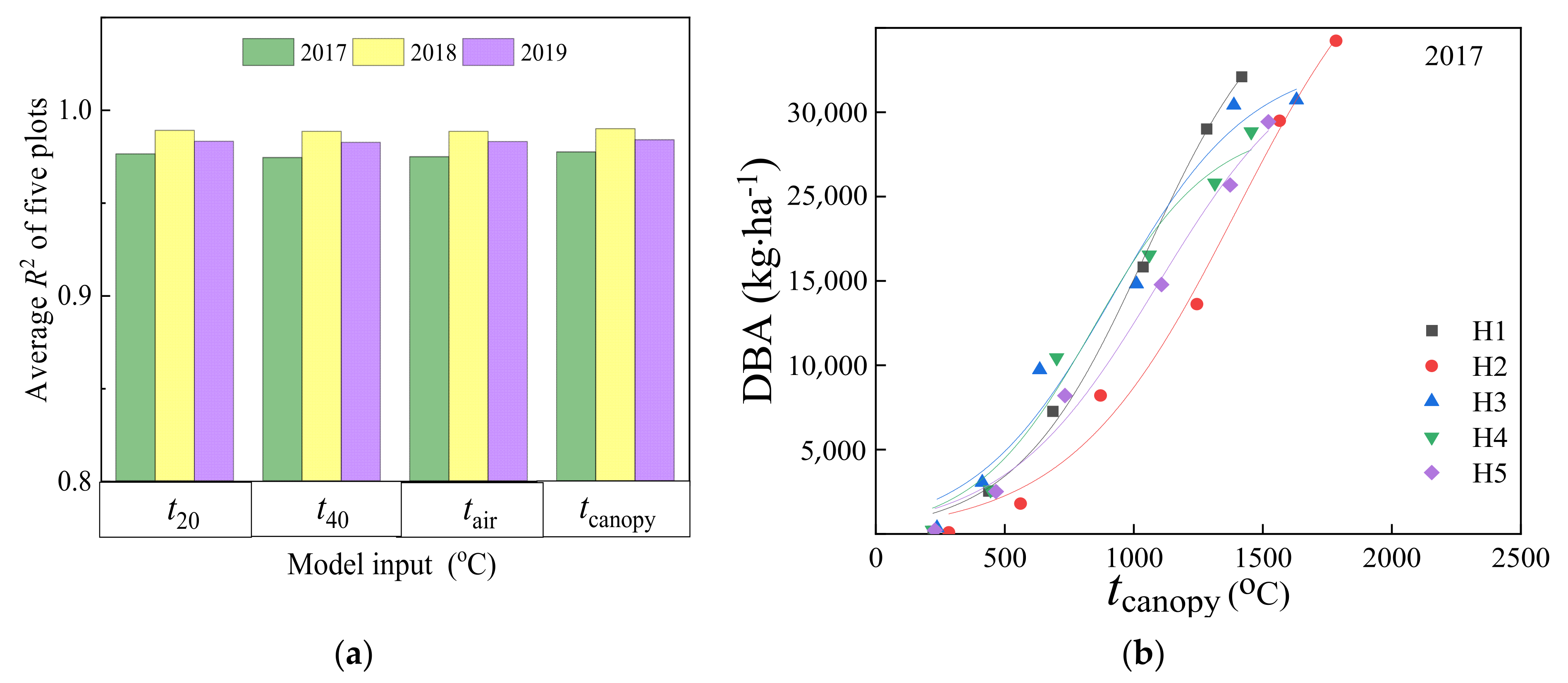
3.2.1. Calibration Results Based on the Logistic Model of DBA
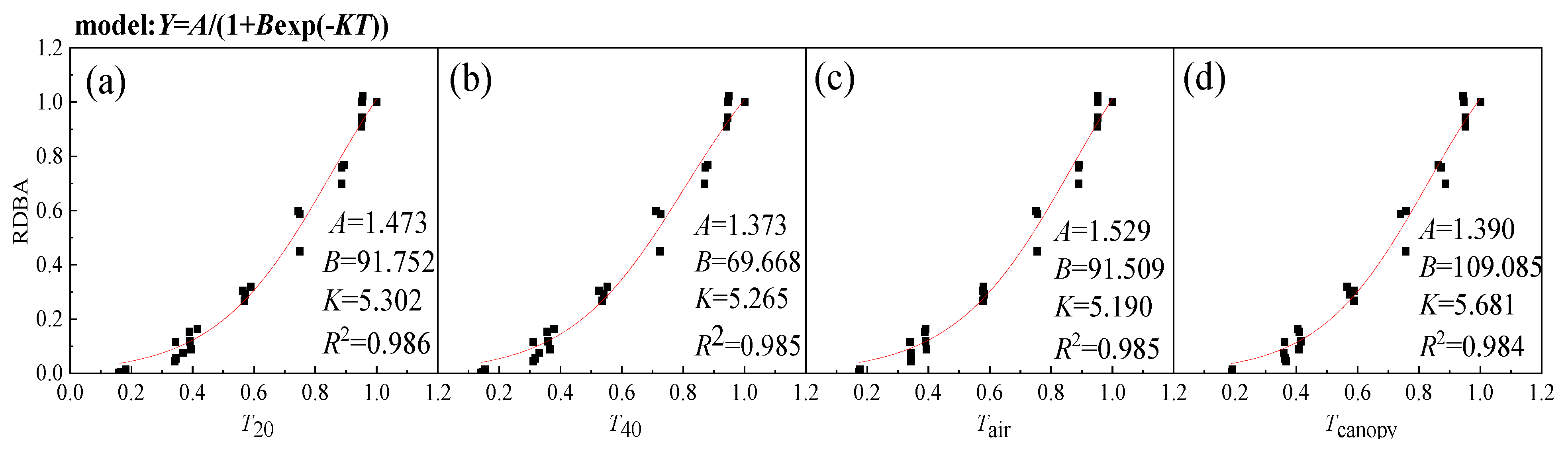
3.2.2. Calibration Results Based on the N-Logistic Model of RDBA
3.2.3. Validation Results Based on the N-Logistic Model of RDBA
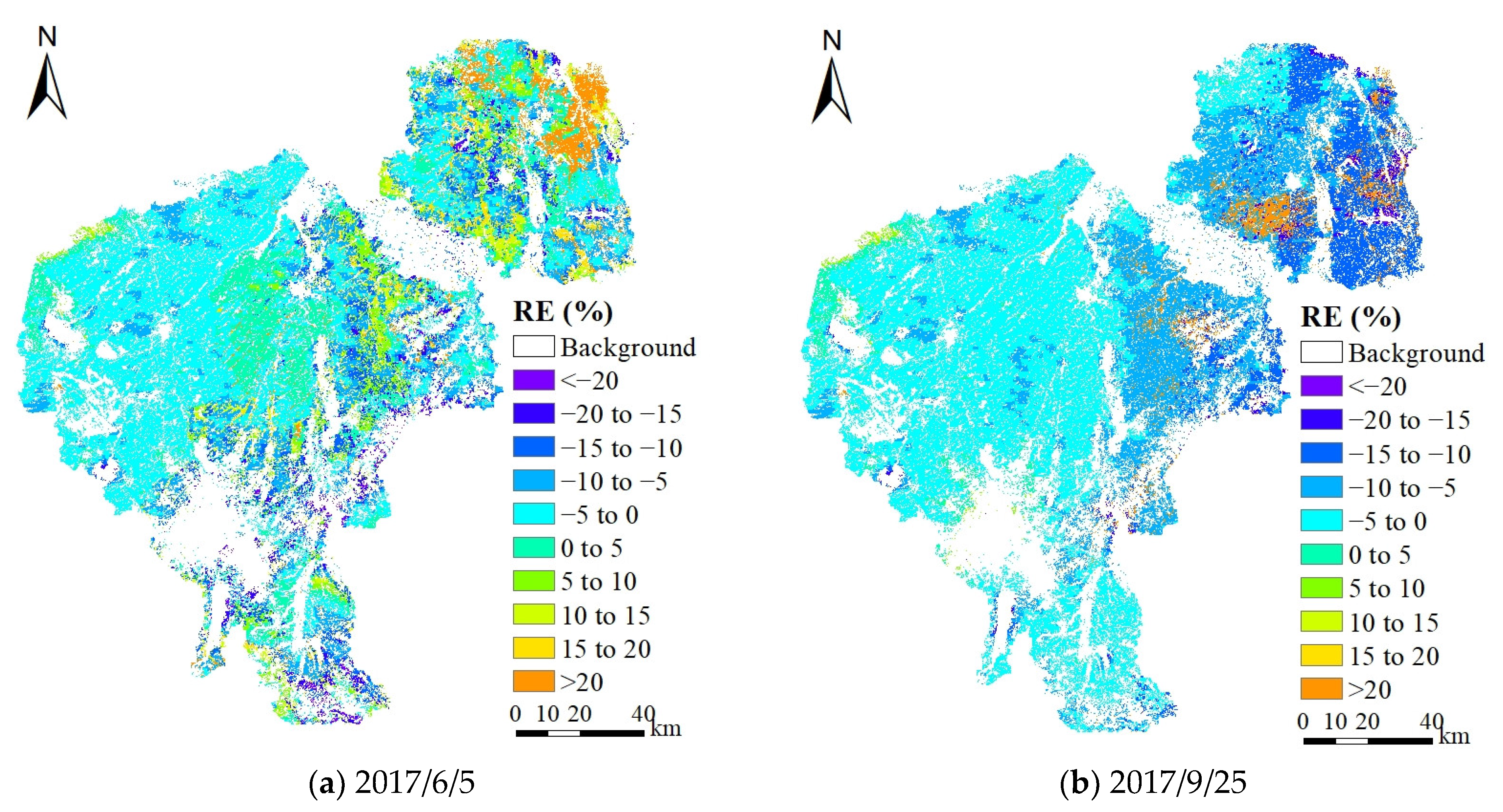
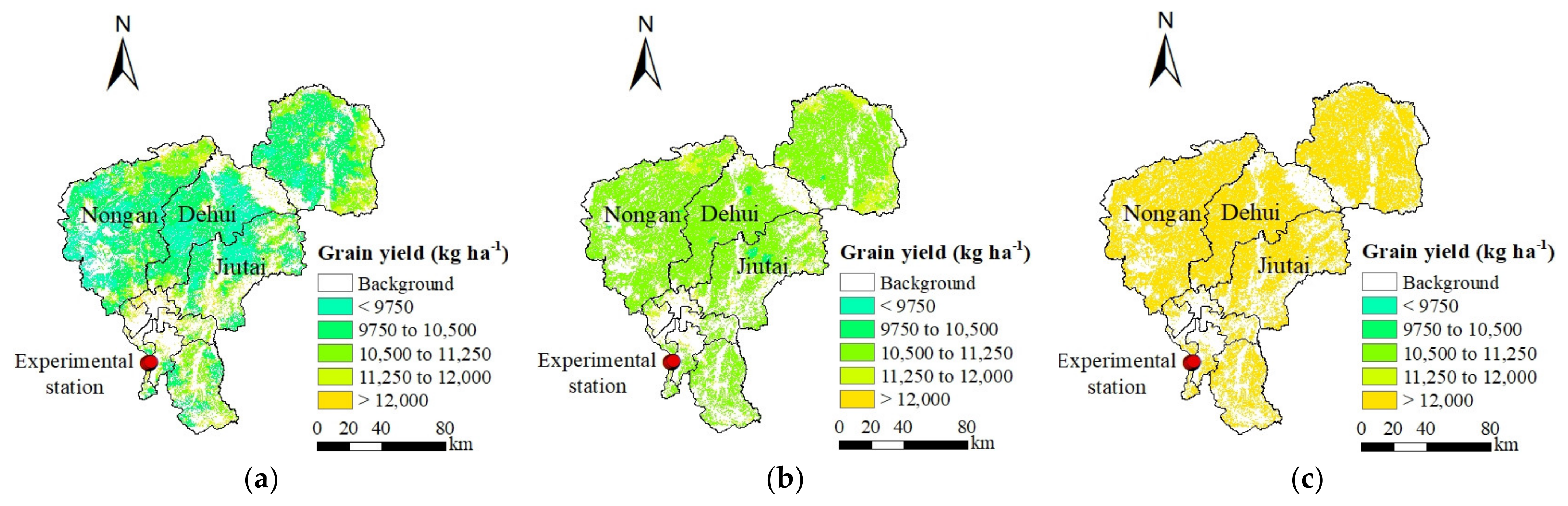
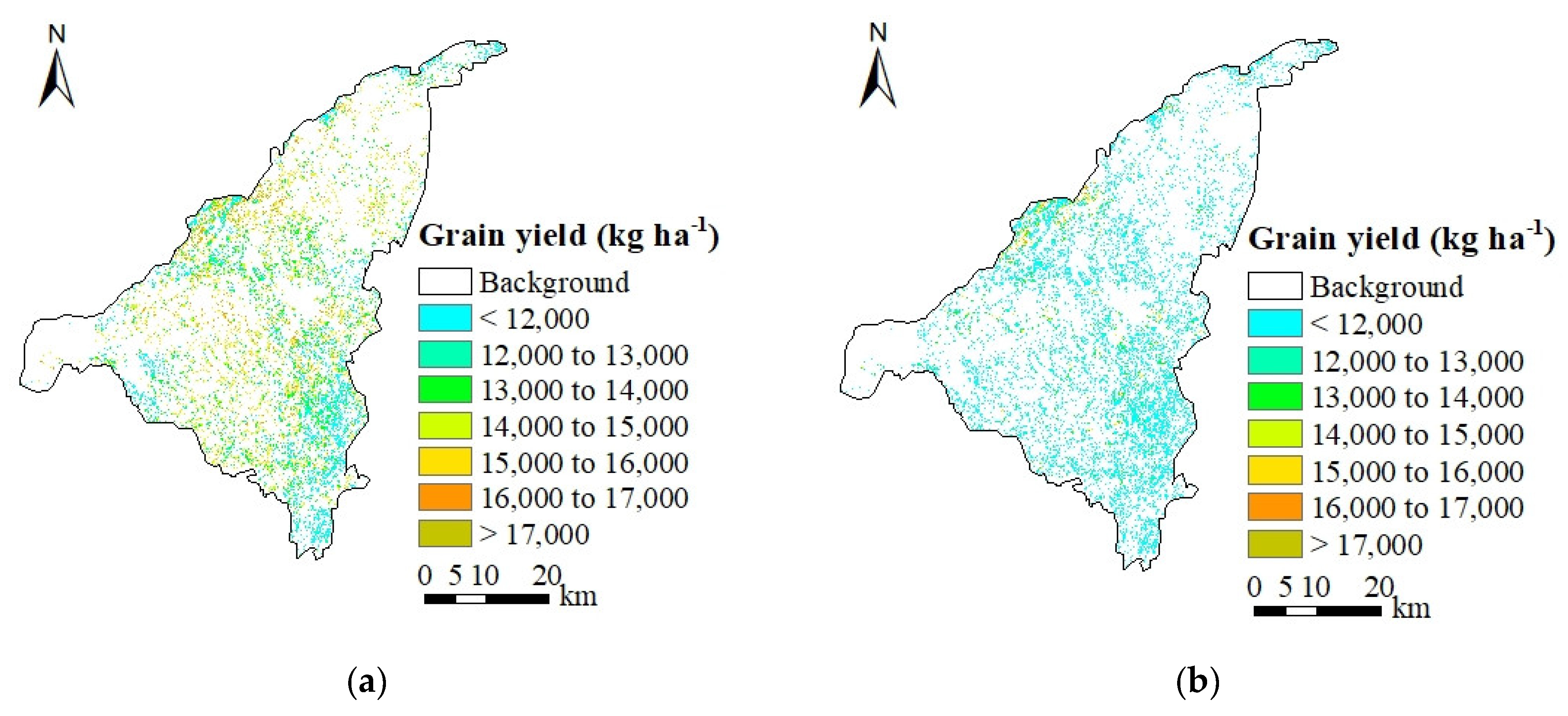
3.2.4. Grain Yield Forecasting in Area by MOD11A1-LST Values
3.3. Silage Yield Forecasting in Changchun
3.3.1. Calibration Results Based on the R-Logistic Model of FBA
3.3.2. Calibration Results Based on the NR-Logistic Model of RFBA
3.3.3. Validation Results Based on the NR-Logistic Model of RFBA
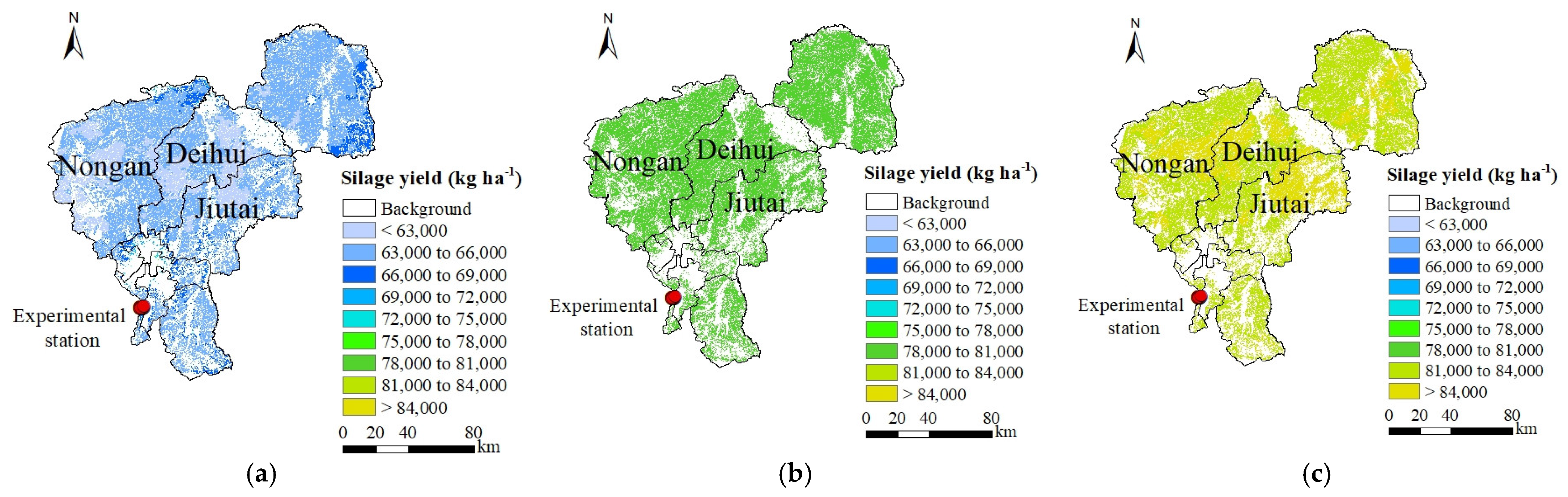
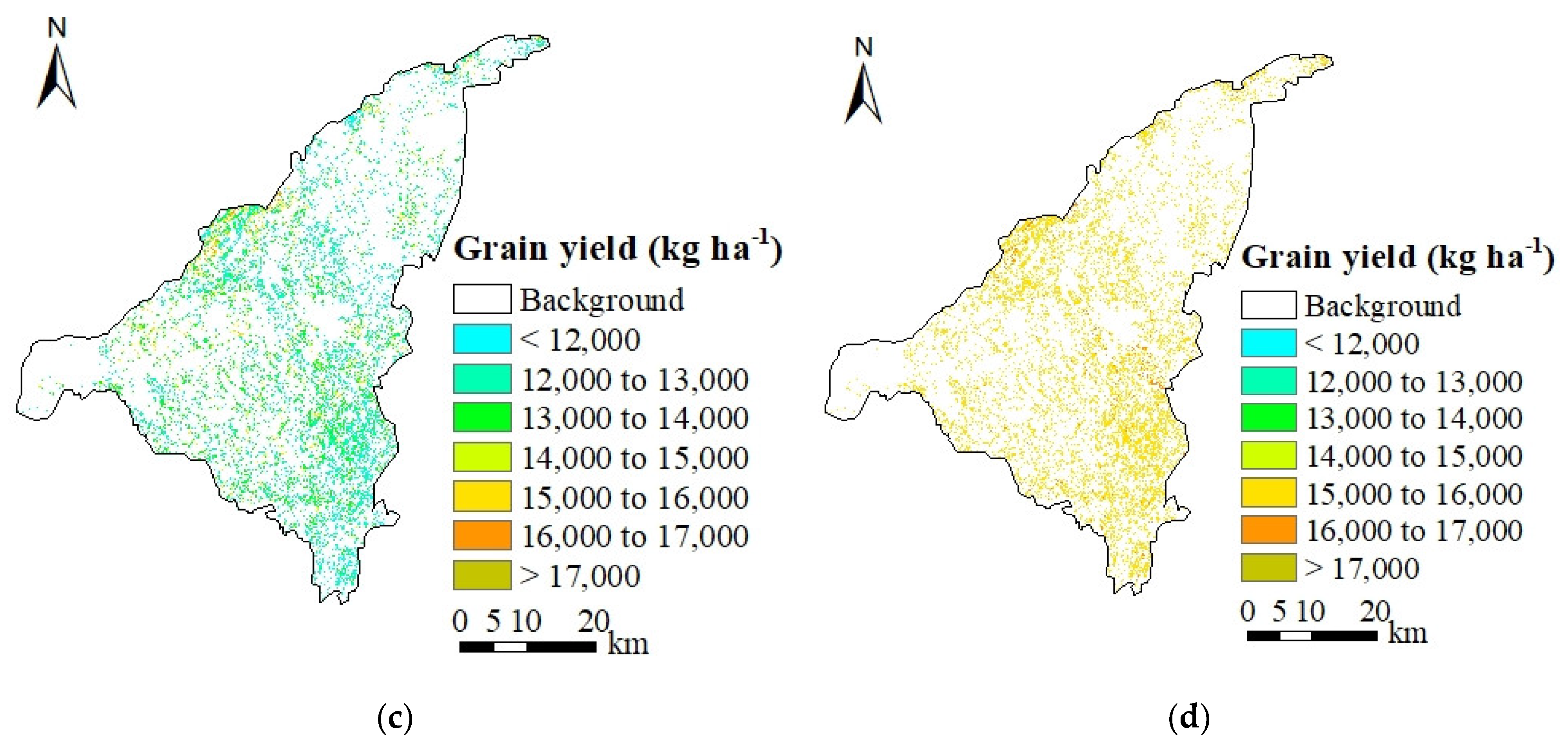
3.3.4. Silage Yield (Maximum FBA) Forecasting in Area by MOD11A1-LST Values
3.4. Verification in Jiefangzha Sub-Irrigation District
4. Discussion
5. Conclusions
- (1)
- The model of 2019 based on Tcanopy performed better result than others. Crop canopy temperature can be used as input parameter in logistic models to simulate DBA and FBA. It is thus a potentially valuable index to facilitate model development in regions.
- (2)
- The normalization method can eliminate the difference in temporal scale between measured daily average values of Tc and instantaneous remote sensing LSTs. Therefore, the normalized LST retrieved from MOD11A1 can be used directly as an independent variable in models to simulate crop biomass for yield forecasting in areas.
- (3)
- The yield forecasting accuracy is reliable in regions with this approach. Satisfactory grain and silage yield forecasting in Changchun were provided by assimilating DBA or FBA measured on 10 August ahead of harvest with RE values of −4.21% and −6.1%, respectively.
- (4)
- The application in the Jiefangzha sub-irrigation district demonstrated that it is possible to apply this approach to predict yield in other regions. These simulation results hold broad potential to provide a real-time reference in maize growing stages for farmers and the grain futures market to make decisions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LST | Land surface temperature, °C |
| Tc | Canopy temperature, °C |
| DBA | Dry biomass accumulation, kg ha−1 |
| FBA | Fresh biomass accumulation, kg ha−1 |
| LAI | Leaf area index |
| RDBA | Relative dry biomass accumulation |
| HI | Harvest index |
| RFBA | Relative fresh biomass accumulation |
| Fc | Field capacity |
| Wp | Wilting point |
| CTMS | Canopy temperature and meteorology monitoring systems |
| NDVI | Normalized difference vegetation index |
| LSWI | Land surface water index |
| ROI | Region of interest |
| Reflectivity of near-infrared band | |
| Reflectivity of red band | |
| Reflectivity of shortwave infrared band | |
| Dependent growth parameter | |
| t | Effective accumulated temperature after emergence, °C |
| Mean daily temperature in the air, canopy, or soil at 20 cm or 40 cm in the root zone, °C | |
| a | The theoretical upper limit of growth of dry biomass accumulation |
| b,k | Parameters of the logistic model |
| tair | Effective accumulative air temperature, °C |
| tcanopy | Effective accumulative canopy temperature, °C |
| t20 | Effective accumulative soil temperature at 20 cm in root zone, °C |
| t40 | Effective accumulative soil temperature at 40 cm in root zone, °C |
| T | Relative effective accumulated temperature |
| YD | Relative dry biomass accumulation |
| Dry biomass accumulation at harvest, kg ha−1 | |
| Effective accumulative temperature at harvest, °C | |
| A | The upper limit of relative dry biomass accumulation |
| B, K | Parameters of the normalized logistic model |
| T20 | Relative effective accumulative soil temperature at 20 cm in root zone |
| T40 | Relative effective accumulative soil temperature at 40 cm in root zone |
| Tcanopy | Relative effective accumulative canopy temperature |
| Tair | Relative effective accumulative air temperature |
| Above-ground fresh biomass accumulation, kg ha−1 | |
| c, g, e, f | Parameters of the revised logistic model |
| Relative fresh biomass accumulation | |
| Maximum relative fresh biomass accumulation | |
| C, G, E, F | Parameters of the normalized revised logistic model |
| Y | Grain yield, kg ha−1 |
| TLST | The relative effective accumulative canopy temperature calculated by the remote sensing instantaneous values of MOD11A1 |
| d | Index of agreement |
| RMSE | Root mean square error |
| RE | Relative error |
| R2 | Coefficient of determination |
| CV | Coefficient of variation |
References
- Chen, Y.; Tao, F.L. Potential of remote sensing data-crop model assimilation and seasonal weather forecasts for early-season crop yield forecasting over a large area. Field Crop. Res. 2022, 276, 108398. [Google Scholar] [CrossRef]
- Ziliani, M.G.; Altaf, M.U.; Aragon, B.; Houborg, R.; Franz, T.E.; Lu, Y.; Sheffield, J.; Hoteit, I.; McCabe, M.F. Early season prediction of within-field crop yield variability by assimilating CubeSat data into a crop model. Agric. For. Meteorol. 2022, 313, 108736. [Google Scholar] [CrossRef]
- Basso, B.; Liu, L. Chapter Four—Seasonal crop yield forecast: Methods, applications, and accuracies. Adv. Agron. 2019, 154, 201–255. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Song, W. Modelling crop yield, water consumption, and water use efficiency for sustainable agroecosystem management. J. Clean. Prod. 2020, 253, 119940. [Google Scholar] [CrossRef]
- Paudel, D.; Boogaard, H.; Wit, A.D.; Janssen, S.; Osinga, S.; Pylianidis, C.; Athanasiadis, I.N. Machine learning for large-scale crop yield forecasting. Agric. Syst. 2021, 187, 103016. [Google Scholar] [CrossRef]
- Hoogenboom, G. Contribution of agrometeorology to the simulation of crop production and its applications. Agric. For. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- Liu, S.; Yang, J.Y.; Drury, C.F.; Liu, H.L.; Reynolds, W.D. Simulating maize (Zea mays L.) growth and yield, soil nitrogen concentration, and soil water content for a long-term cropping experiment in Ontario, Canada. Can. J. Soil Sci. 2014, 94, 435–452. [Google Scholar] [CrossRef]
- Mubeen, M.; Ahmad, A.; Wajid, A.; Khalip, T.; Hammad, H.M.; Sultana, S.R.; Ahmad, S.; Fahad, S.; Nasim, W. Application of CSM-CERES-Maize model in optimizing irrigated conditions. Outlook Agric. 2016, 45, 173–184. [Google Scholar] [CrossRef]
- Wu, W.; Chen, J.L.; Liu, H.B.; Garcia, A.G.; Hoogenboom, G. Parameterizing soil and weather inputs for crop simulation models using the VEMAP database. Agric. Ecosyst. Environ. 2010, 135, 111–118. [Google Scholar] [CrossRef]
- Birch, C.P.D. A new generalized Logistic sigmoid growth equation compared with the Richards growth equation. Ann. Bot. 1999, 83, 713–723. [Google Scholar] [CrossRef] [Green Version]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for ontogenetic growth. Nature 2001, 413, 628–631. [Google Scholar] [CrossRef]
- Bontemps, J.; Duplat, P. A non-asymptotic sigmoid growth curve for top height growth in forest stands. Forestry 2012, 85, 353–368. [Google Scholar] [CrossRef]
- Lewis, J.M.; Lakshmivarahan, S.; Dhall, S. Dynamic Data Assimilation: A Least Squares Approach; Cambridge University Press: Cambridge, UK, 2006; Available online: http://www.gbv.de/dms/goettingen/508439248.pdf (accessed on 16 March 2022).
- Schwalbert, R.A.; Amado, T.J.C.; Nieto, L.; Varela, S.; Corassa, G.M.; Horbe, T.A.N.; Rice, C.W.; Peralta, N.R.; Ciampitti, I.A. Forecasting maize yield at field scale based on high-resolution satellite imagery. Biosyst. Eng. 2018, 171, 179–192. [Google Scholar] [CrossRef]
- Sharifi, A. Yield prediction with machine learning algorithms and satellite images. J. Sci. Food Agric. 2021, 101, 891–896. [Google Scholar] [CrossRef]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Toan, T.L.; Planells, M.; Dejoux, J.-F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Gaso, D.V.; Wit, A.D.; Berger, A.G.; Kooistra, L. Predicting within-field soybean yield variability by coupling Sentinel-2 leaf area index with a crop growth model. Agric. For. Meteorol. 2021, 308–309, 108553. [Google Scholar] [CrossRef]
- Jin, N.; Tao, B.; Ren, W.; He, L.; Zhang, D.Y.; Wang, D.H.; Yu, Q. Assimilating remote sensing data into a crop model improves winter wheat yield estimation based on regional irrigation data. Agric. Water Manag. 2022, 266, 107583. [Google Scholar] [CrossRef]
- Liu, Z.C.; Wang, C.; Bi, R.T.; Zhu, H.F.; He, P.; Jing, Y.D.; Yang, W.D. Winter wheat yield estimation based on assimilated Sentinel-2 images with the CERES-Wheat model. J. Integr. Agric. 2021, 20, 1958–1968. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.X.; Xiao, X.M.; Huang, H.; Bajgain, R.; Wu, X.C.; Gao, X.R.; Wang, J.; Li, X.C.; Wagle, P. Assimilating remote sensing-based VPM GPP into the WOFOST model for improving regional winter wheat yield estimation. Eur. J. Agron. 2022, 139, 126556. [Google Scholar] [CrossRef]
- Junior, I.M.F.; Vianna, M.D.S.; Marin, F.R. Assimilating leaf area index data into a sugarcane process-based crop model for improving yield estimation. Eur. J. Agron. 2022, 136, 126501. [Google Scholar] [CrossRef]
- Klopfenstein, T.J.; Erickson, G.E.; Berger, L.L. Maize is a critically important source of food, feed, energy and forage in the USA. Field Crop. Res. 2013, 153, 5–11. [Google Scholar] [CrossRef]
- Yan, D.C.; Zhu, Y.; Wang, S.H.; Cao, W.X. A quantitative knowledge-based model for designing suitable growth dynamics in rice. Plant Prod. Sci. 2006, 9, 93–105. [Google Scholar] [CrossRef]
- Sheehy, J.E.; Mitchel, P.L.; Allen, L.H.; Ferrer, A.B. Mathematical consequences of using various empirical expressions of crop yield as a function of temperature. Field Crop. Res. 2006, 98, 216–221. [Google Scholar] [CrossRef]
- Singer, J.W.; Meek, D.W.; Sauer, T.J.; Prueger, J.H.; Hatfield, J.L. Variability of light interception and radiation use efficiency in maize and soybean. Field Crop. Res. 2011, 121, 147–152. [Google Scholar] [CrossRef]
- Shi, P.J.; Men, X.Y.; Sandhu, H.S.; Chakraborty, A.; Li, B.L.; Ou-Yang, F.; Sun, Y.C.; Ge, F. The “general” ontogenetic growth model is inapplicable to crop growth. Ecol. Model. 2013, 266, 1–9. [Google Scholar] [CrossRef]
- Bakoglu, A.; Celik, S.; Kokten, K.; Kilic, O. Examination of plant length, dry stem and dry leaf weight of bitter vetch [Vicia ervilia (L) Willd.] with some non-linear growth models. Legume Res. 2016, 39, 533–542. [Google Scholar] [CrossRef]
- Wang, X.L. How to utilize Logistic model in dynamic simulation of crop dry biomass accumulation. Chin. J. Agrometeorol. 1986, 7, 14–19. (In Chinese) [Google Scholar]
- Liu, Y.H.; Su, L.J.; Wang, Q.J.; Zhang, J.H.; Shan, Y.Y.; Deng, M.J. Chapter Six—Comprehensive and quantitative analysis of growth characteristics of winter wheat in China based on growing degree days. Adv. Agron. 2020, 159, 237–273. [Google Scholar] [CrossRef]
- Elings, A. Estimation of leaf area in tropical maize. Agron. J. 2000, 92, 436–444. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, J.D.; Zhang, Y.Q.; Li, J. Simulation of rice biomass accumulation by an extended Logistic model including influence of meteorological factors. Int. J. Biometeorol. 2002, 46, 185–191. [Google Scholar] [CrossRef]
- Sepaskhah, A.R.; Fahandezh-Saadi, S.; Zand-Parsa, S. Logistic model application for prediction of maize yield under water and nitrogen management. Agric. Water Manag. 2011, 99, 51–57. [Google Scholar] [CrossRef]
- Shabani, A.; Sepaskhah, A.R.; Kamgar-Haghighi, A.A. Estimation of yield and dry matter of rapeseed using Logistic model under water, salinity and deficit irrigation. Arch. Agron. Soil Sci. 2014, 60, 951–969. [Google Scholar] [CrossRef]
- Mahbod, M.; Sepaskhah, A.R.; Zand-Parsa, S. Estimation of yield and dry matter of winter wheat using Logistic model under different irrigation water regimes and nitrogen application rates. Arch. Agron. Soil Sci. 2014, 60, 1661–1676. [Google Scholar] [CrossRef]
- Mayer, F.; Gerin, P.A.; Noo, A.; Foucart, G.; Flammang, J.; Lemaigre, S.; Sinnaeve, G.; Dardenne, P.; Delfosse, P. Assessment of factors influencing the biomethane yield of maize silages. Bioresour. Technol. 2014, 153, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Pede, T.; Mountrakis, G.; Shaw, S.B. Improving corn yield prediction across the US Corn Belt by replacing air temperature with daily MODIS land surface temperature. Agric. For. Meteorol. 2019, 276–277, 107615. [Google Scholar] [CrossRef]
- Cai, J.B.; Xu, D.; Si, N.; Wei, Z. Real-time monitoring system of crop canopy temperature and soil moisture for irrigation decision-making. T. Chin. Soc. Agric. Mach. 2015, 46, 133–139, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Qi, L.L. Research on Safety of Water Supply in Chang-Ji Economic Circle. Master’s Thesis, Jilin University, Changchun, China, 2019. (In Chinese with English abstract). [Google Scholar]
- Bai, L.L.; Cai, J.B.; Liu, Y.; Chen, H.; Zhang, B.Z.; Huang, L.X. Responses of field evapotranspiration to the changes of cropping pattern and groundwater depth in large irrigation district of Yellow River basin. Agric. Water Manag. 2017, 188, 1–11. [Google Scholar] [CrossRef]
- Huang, L.X.; Cai, J.B.; Zhang, B.Z.; Chen, H.; Bai, L.L.; Wei, Z.; Peng, Z.G. Estimation of evapotranspiration using the crop canopy temperature at field to regional scales in large irrigation district. Agric. For. Meteorol. 2019, 269–270, 305–322. [Google Scholar] [CrossRef]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of a deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Chandrasekar, K.; Sesha Sai, M.V.R.; Roy, P.S.; Dwevedi, R.S. Land Surface Water Index (LSWI) response to rainfall and NDVI using the MODIS Vegetation Index product. Int. J. Remote Sens. 2010, 31, 3987–4005. [Google Scholar] [CrossRef]
- Zhu, X.L.; Chen, J.; Gao, F.; Chen, X.H.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Wu, R.L.; Ma, C.-X.; Chang, M.; Littell, R.C.; Wu, S.S.; Yin, T.M.; Huang, M.R.; Wang, M.X.; Casella, G. A Logistic mixture model for characterizing genetic determinants causing differentiation in growth trajectories. Genet. Res. 2002, 79, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.F.; Guo, J.P.; Mu, J. Exploring the relationships between climatic variables and climate-induced yield of spring maize in Northeast China. Agric. Ecosyst. Environ. 2015, 207, 79–90. [Google Scholar] [CrossRef]
- Ding, D.Y.; Feng, H.; Zhao, Y.; Hill, R.L.; Yan, H.M.; Chen, H.X.; Hou, H.J.; Chu, X.S.; Liu, J.C.; Wang, N.J.; et al. Effects of continuous plastic mulching on crop growth in a winter wheat-summer maize rotation system on the loess plateau of China. Agric. For. Meteorol. 2019, 271, 385–397. [Google Scholar] [CrossRef]
- Meade, K.A.; Cooper, M.; Beavis, W.D. Modeling biomass accumulation in maize kernels. Field Crop. Res. 2013, 151, 92–100. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.F.; Li, J.S.; Yan, H.J. Effects of mulched drip irrigation on water and heat conditions in field and maize yield in sub-humid region of Northeast China. T. Chin. Soc. Agric. Mach. 2015, 46, 93–104, 135, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- An, Q. Research on Methods of Maize Yield Estimation by Remote Sensing in Changchun Region. Master’s Thesis, Jilin University, Changchun, China, 2018. (In Chinese with English abstract). [Google Scholar]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef] [Green Version]
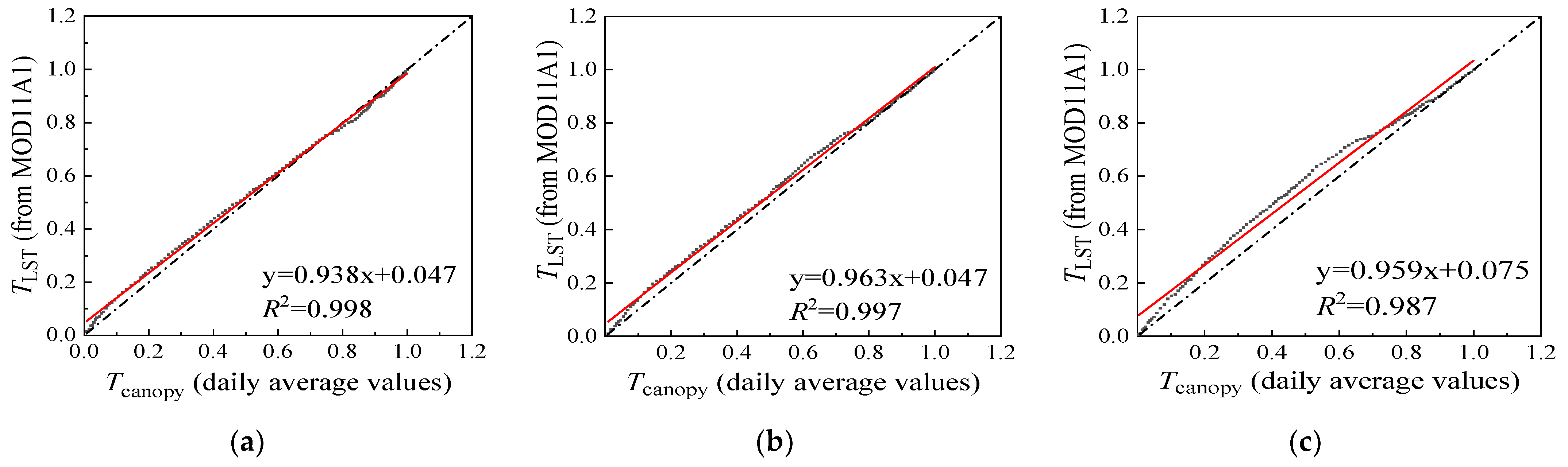

| A | B | K | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | T20 | T40 | Tair | Tcanopy | T20 | T40 | Tair | Tcanopy | T20 | T40 | Tair | Tcanopy |
| 2017 | 1.244 | 1.193 | 1.248 | 1.163 | 33.090 | 27.140 | 31.940 | 41.131 | 4.863 | 4.884 | 4.825 | 5.465 |
| 2018 | 1.473 | 1.373 | 1.529 | 1.390 | 91.752 | 69.668 | 91.509 | 109.085 | 5.302 | 5.265 | 5.190 | 5.681 |
| 2019 | 1.041 | 1.010 | 1.056 | 1.056 | 43.966 | 38.916 | 46.139 | 58.246 | 5.905 | 6.091 | 5.830 | 6.111 |
| CV | 0.173 | 0.152 | 0.186 | 0.142 | 0.555 | 0.485 | 0.550 | 0.509 | 0.098 | 0.114 | 0.096 | 0.057 |
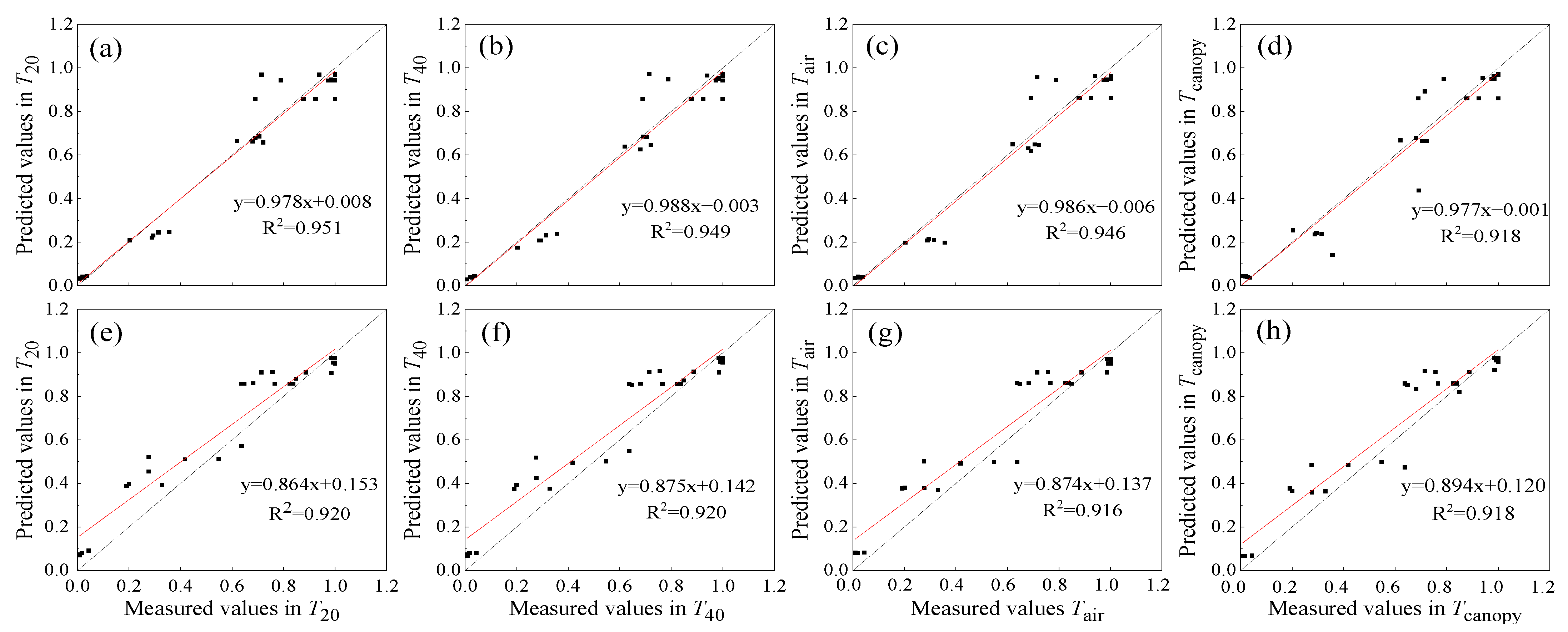
| Calibrated Model | Independent Variable | RMSE | d | R2 | RE (%) | RMSE | d | R2 | RE (%) |
|---|---|---|---|---|---|---|---|---|---|
| In 2017 | Validation by field data of 2018 | Validation by field data of 2019 | |||||||
| T20 | 0.094 | 0.984 | 0.978 | 6.8 | 0.168 | 0.942 | 0.937 | 4.7 | |
| T40 | 0.093 | 0.984 | 0.979 | 6.8 | 0.168 | 0.942 | 0.939 | 5.0 | |
| Tair | 0.098 | 0.982 | 0.976 | 7.3 | 0.170 | 0.941 | 0.946 | 5.7 | |
| Tcanopy | 0.101 | 0.981 | 0.971 | 7.3 | 0.169 | 0.942 | 0.947 | 6.0 | |
| In 2018 | Validation by field data of 2017 | Validation by field data of 2019 | |||||||
| T20 | 0.099 | 0.983 | 0.951 | −5.4 | 0.114 | 0.974 | 0.907 | −3.7 | |
| T40 | 0.098 | 0.983 | 0.952 | −5.3 | 0.111 | 0.974 | 0.909 | −3.4 | |
| Tair | 0.104 | 0.981 | 0.948 | −6.0 | 0.107 | 0.977 | 0.917 | −3.1 | |
| Tcanopy | 0.112 | 0.978 | 0.938 | −6.2 | 0.103 | 0.978 | 0.921 | −2.8 | |
| In 2019 | Validation by field data of 2017 | Validation by field data of 2018 | |||||||
| T20 | 0.068 | 0.991 | 0.969 | −1.3 | 0.096 | 0.994 | 0.963 | 4.8 | |
| T40 | 0.069 | 0.991 | 0.968 | −1.4 | 0.094 | 0.994 | 0.963 | 4.6 | |
| Tair | 0.071 | 0.990 | 0.969 | −2.3 | 0.090 | 0.995 | 0.965 | 4.2 | |
| Tcanopy | 0.079 | 0.988 | 0.963 | −2.8 | 0.085 | 0.996 | 0.968 | 3.7 | |
| Observation Date of Model Simulation Based on | Measured Data in Experimental Station (kg ha−1) 2 | Forecasting Results (kg ha−1) | RE (%) | Measured Data in Three Subareas (kg ha−1) 3 | Forecasting Results (kg ha−1) | RE (%) | |
|---|---|---|---|---|---|---|---|
| Grain yield | 198 (2017/7/16) | 12,442.74 | 10,778.57 | −13.38 | 11,364.30 | 10,126.20 | −10.89 |
| 223 (2017/8/10) | 10,976.90 | −11.78 | 10,885.35 | −4.21 | |||
| 244 (2017/8/31) | 13,501.05 | 8.51 | 13,492.80 | 18.73 |
| Independent Variable | 2017 | 2018 | 2019 | CV | |
|---|---|---|---|---|---|
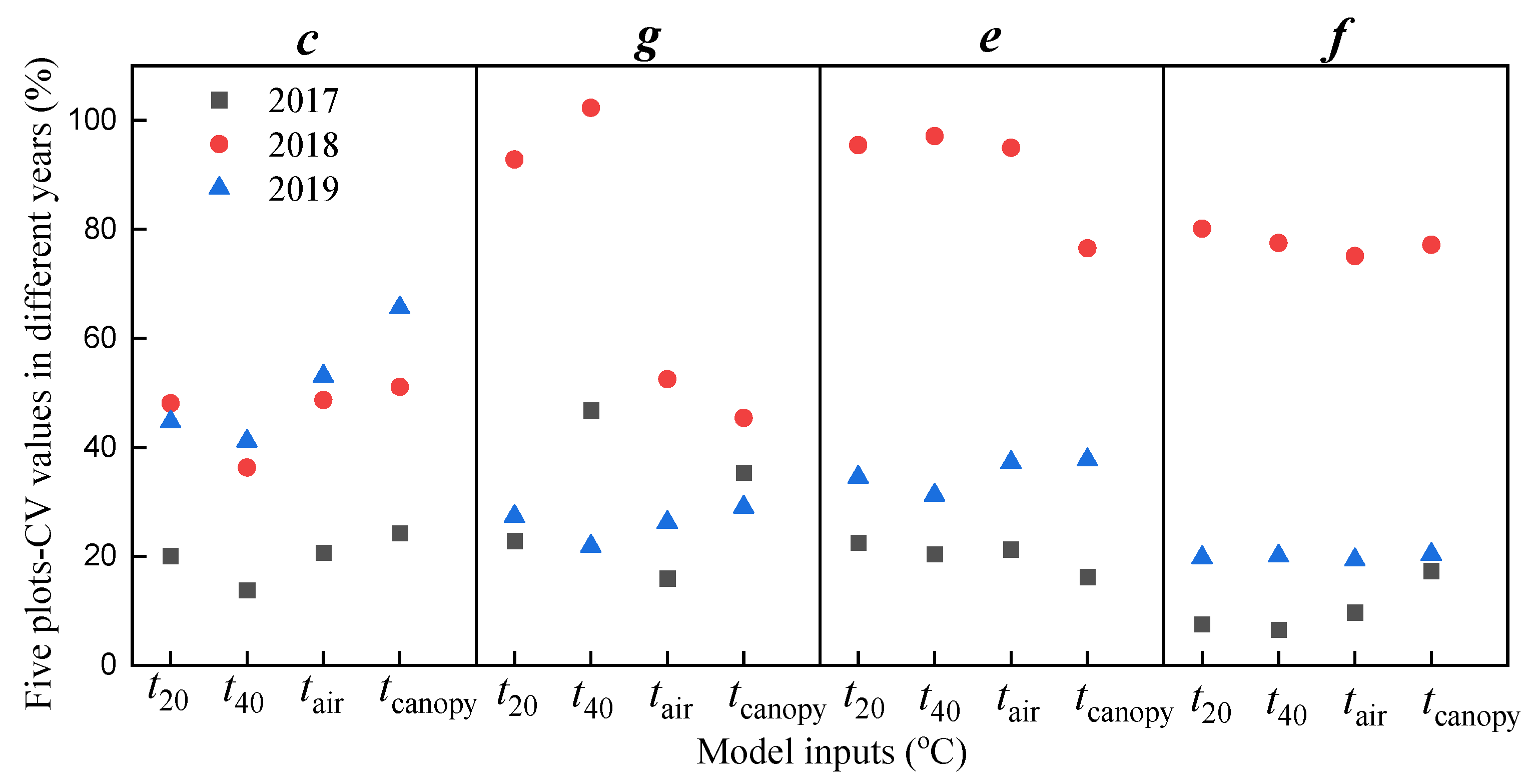
| C | T20 | 1.127 | 2.098 | 1.270 | 0.350 |
| T40 | 1.078 | 1.703 | 1.200 | 0.250 | |
| Tair | 1.122 | 2.086 | 1.276 | 0.346 | |
| Tcanopy | 1.215 | 1.848 | 1.306 | 0.235 | |
| G | T20 | 9.922 | 9.299 | 10.335 | 0.053 |
| T40 | 10.340 | 9.713 | 10.820 | 0.054 | |
| Tair | 9.840 | 8.962 | 10.119 | 0.063 | |
| Tcanopy | 9.864 | 10.375 | 10.845 | 0.047 | |
| E | T20 | −15.934 | −14.554 | −16.214 | −0.057 |
| T40 | −16.233 | −14.855 | −16.653 | −0.059 | |
| Tair | −15.745 | −14.04 | −16.006 | −0.070 | |
| Tcanopy | −15.839 | −16.240 | −17.276 | −0.045 | |
| F | T20 | 4.737 | 5.797 | 5.141 | 0.102 |
| T40 | 4.398 | 5.341 | 4.911 | 0.097 | |
| Tair | 4.614 | 5.603 | 5.152 | 0.097 | |
| Tcanopy | 5.030 | 6.212 | 5.774 | 0.105 |
| Calibrated Model | Independent Variable | RMSE | d | R2 | RE (%) | RMSE | d | R2 | RE (%) |
|---|---|---|---|---|---|---|---|---|---|
| In 2017 | Validation by field data of 2018 | Validation by field data of 2019 | |||||||
| T20 | 0.135 | 0.953 | 0.902 | 13.5 | 0.085 | 0.986 | 0.950 | 3.4 | |
| T40 | 0.139 | 0.950 | 0.899 | 14.0 | 0.088 | 0.985 | 0.951 | 5.3 | |
| Tair | 0.139 | 0.949 | 0.898 | 13.9 | 0.086 | 0.985 | 0.955 | 6.1 | |
| Tcanopy | 0.130 | 0.957 | 0.907 | 12.8 | 0.087 | 0.985 | 0.954 | 5.9 | |
| In 2018 | Validation by field data of 2017 | Validation by field data of 2019 | |||||||
| T20 | 0.121 | 0.972 | 0.916 | −9.9 | 0.111 | 0.976 | 0.936 | −7.8 | |
| T40 | 0.123 | 0.971 | 0.914 | −10.1 | 0.106 | 0.984 | 0.940 | −6.6 | |
| Tair | 0.121 | 0.971 | 0.915 | −9.9 | 0.099 | 0.980 | 0.946 | −5.4 | |
| Tcanopy | 0.120 | 0.972 | 0.915 | −9.6 | 0.096 | 0.987 | 0.947 | −4.5 | |
| In 2019 | Validation by field data of 2017 | Validation by field data of 2018 | |||||||
| T20 | 0.079 | 0.988 | 0.951 | −0.9 | 0.118 | 0.974 | 0.920 | 11.7 | |
| T40 | 0.082 | 0.987 | 0.948 | −1.8 | 0.115 | 0.976 | 0.920 | 11.0 | |
| Tair | 0.084 | 0.986 | 0.946 | −2.4 | 0.114 | 0.976 | 0.916 | 10.1 | |
| Tcanopy | 0.091 | 0.984 | 0.936 | −2.4 | 0.110 | 0.979 | 0.918 | 9.3 | |
| Observation Date of Model Simulation Based on | Measured Data in Experimental Station (kg ha−1) 2 | Forecasting Results (kg ha−1) | RE (%) | |
|---|---|---|---|---|
| Silage yield (maximum FBA) | 198 (2017/7/16) | 84,605.70 | 65,187.70 | −22.95 |
| 223 (2017/8/10) | 79,447.25 | −6.10 | ||
| 244 (2017/8/31) | 83,715.78 | −1.05 |
| Observation Date of Model Simulation Based on | RMSE (kg ha−1) | R2 | RE (%) | d |
|---|---|---|---|---|
| 186 (2016/7/4) | 933 | 0.63 | 3.52 | 0.86 |
| 203 (2016/7/21) | 2334 | 0.77 | −16.14 | 0.56 |
| 217 (2016/8/4) | 1520 | 0.83 | 9.84 | 0.70 |
| 239 (2016/8/26) | 888 | 0.88 | 5.01 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Cai, J.; Zhang, B.; Wei, Z.; Xu, D. Early Yield Forecasting of Maize by Combining Remote Sensing Images and Field Data with Logistic Models. Remote Sens. 2023, 15, 1025. https://doi.org/10.3390/rs15041025
Chang H, Cai J, Zhang B, Wei Z, Xu D. Early Yield Forecasting of Maize by Combining Remote Sensing Images and Field Data with Logistic Models. Remote Sensing. 2023; 15(4):1025. https://doi.org/10.3390/rs15041025
Chicago/Turabian StyleChang, Hongfang, Jiabing Cai, Baozhong Zhang, Zheng Wei, and Di Xu. 2023. "Early Yield Forecasting of Maize by Combining Remote Sensing Images and Field Data with Logistic Models" Remote Sensing 15, no. 4: 1025. https://doi.org/10.3390/rs15041025
APA StyleChang, H., Cai, J., Zhang, B., Wei, Z., & Xu, D. (2023). Early Yield Forecasting of Maize by Combining Remote Sensing Images and Field Data with Logistic Models. Remote Sensing, 15(4), 1025. https://doi.org/10.3390/rs15041025









