Detection of Sargassum from Sentinel Satellite Sensors Using Deep Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Satellite Data
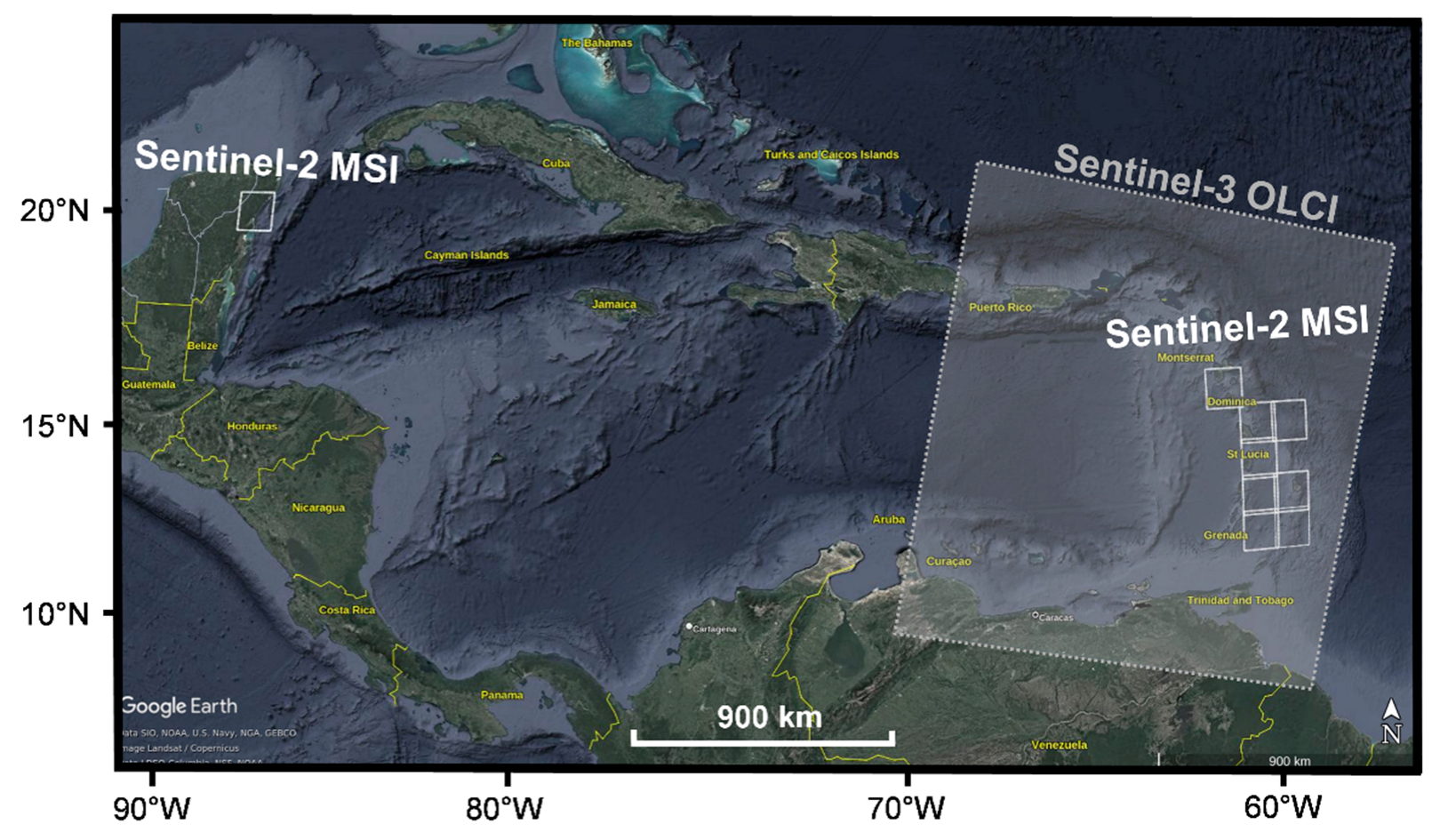
2.2. Study Area and Data Set
2.3. Three Sargassum Detection Methods
2.3.1. Standard Index-Thresholding Method
2.3.2. Convolutional Neural Network (CNN) for Sargassum Retrieval
State of the Art
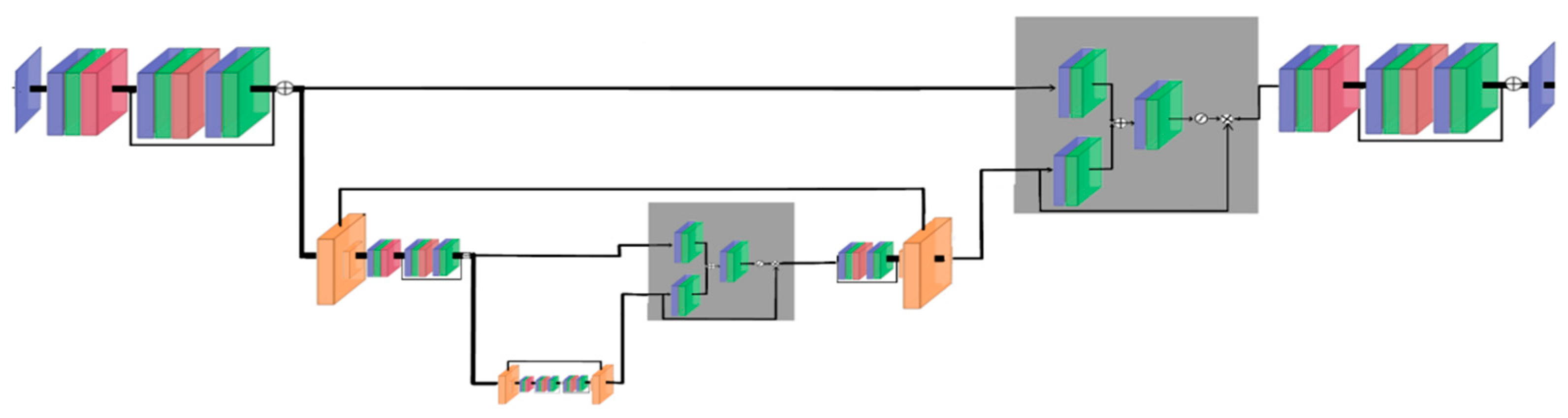
Model Description for MSI and OLCI
Training Process
2.3.3. Visual Analysis to Establish the Ground Truth
2.4. Performance Evaluation
2.4.1. Performance Metrics Using the Ground Truth
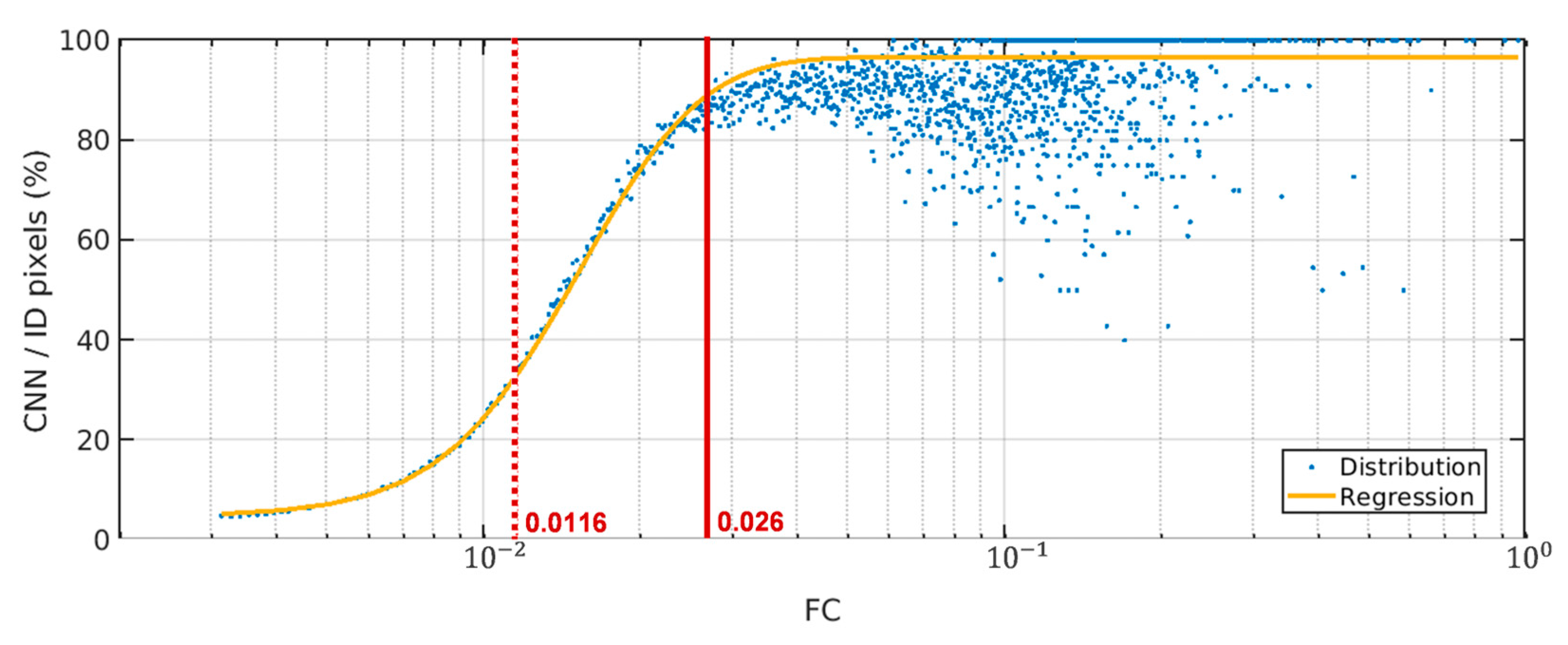
2.4.2. Comparison of CNN and ID Approaches
3. Results
3.1. Model Performances on the Test Dataset
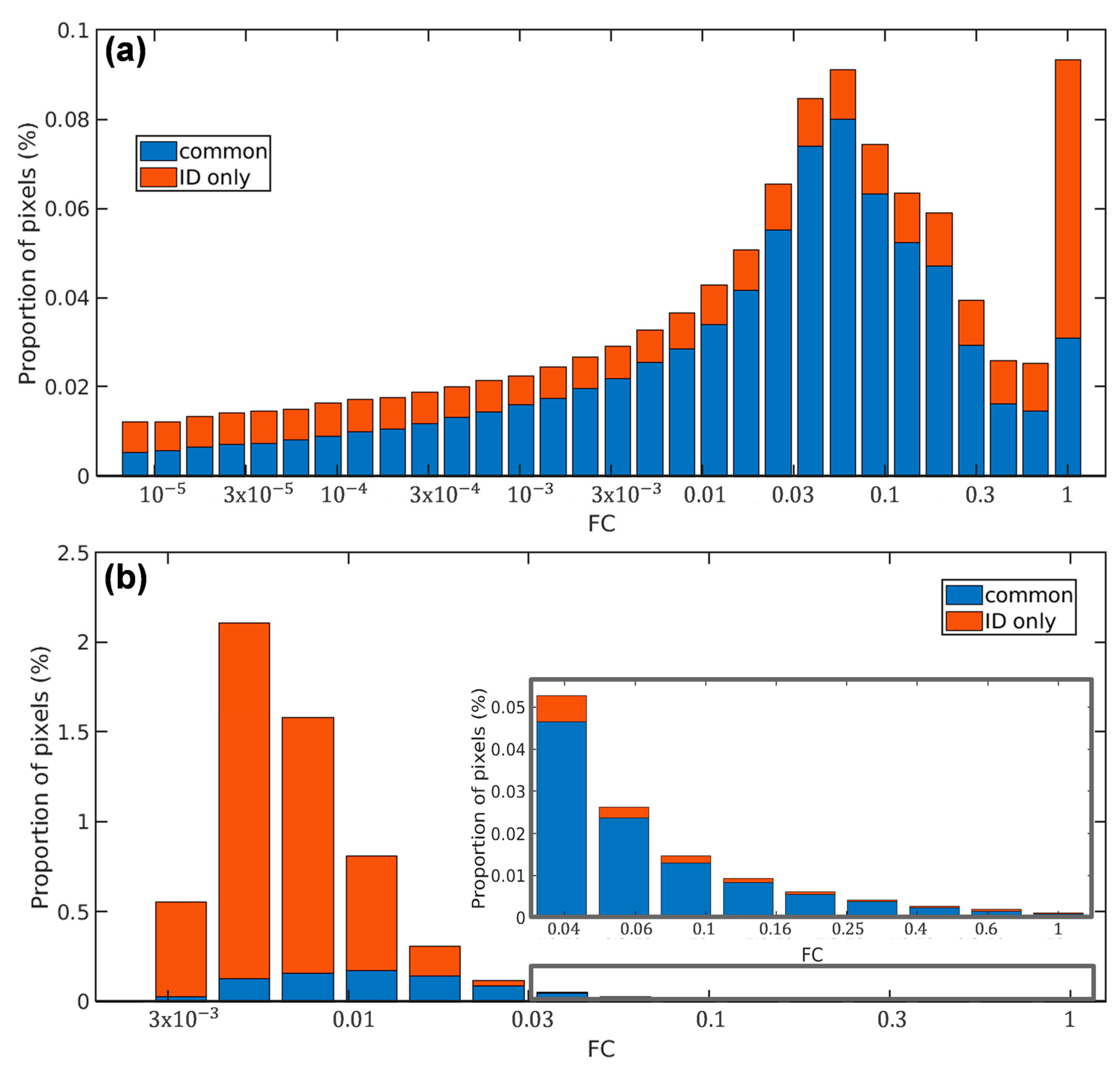
3.2. Comparison with the ID Method
3.3. Comparison with Existing Networks
3.4. Results with the Focus Image Dataset
4. Discussion
4.1. The CNN Reliability on Sargassum Aggregations
4.2. Less False Detections Which Improve Sargassum Coverage Estimation
4.3. Better Estimation of the Aggregation Shape
4.4. Complementarity of MSI and OLCI Images
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.; Hu, C.; Barnes, B.B.; Mitchum, G.; Lapointe, B.; Montoya, J.P. The Great Atlantic Sargassum Belt. Science 2019, 365, 83–87. [Google Scholar] [CrossRef] [PubMed]
- Schell, J.M.; Goodwin, D.S.; Siuda, A.N.S. Recent Sargassum Inundation Events in the Caribbean: Shipboard Observations Reveal Dominance of a Previously Rare Form. Oceanography 2015, 28, 8–11. [Google Scholar] [CrossRef] [Green Version]
- Amaral-Zettler, L.A.; Dragone, N.B.; Schell, J.; Slikas, B.; Murphy, L.G.; Morrall, C.E.; Zettler, E.R. Comparative Mitochondrial and Chloroplast Genomics of a Genetically Distinct Form of Sargassum Contributing to Recent “Golden Tides” in the Western Atlantic. Ecol. Evol. 2017, 7, 516–525. [Google Scholar] [CrossRef] [PubMed]
- Dibner, S.; Martin, L.; Thibaut, T.; Aurelle, D.; Blanfuné, A.; Whittaker, K.; Cooney, L.; Schell, J.M.; Goodwin, D.S.; Siuda, A.N.S. Consistent Genetic Divergence Observed among Pelagic Sargassum Morphotypes in the Western North Atlantic. Mar. Ecol. 2022, 43, e12691. [Google Scholar] [CrossRef]
- Ody, A.; Thibaut, T.; Berline, L.; Changeux, T.; André, J.-M.; Chevalier, C.; Blanfuné, A.; Blanchot, J.; Ruitton, S.; Stiger-Pouvreau, V.; et al. From In Situ to Satellite Observations of Pelagic Sargassum Distribution and Aggregation in the Tropical North Atlantic Ocean. PLoS ONE 2019, 14, e0222584. [Google Scholar] [CrossRef] [Green Version]
- Széchy, M.T.; Baeta-Neves, M.; Guedes, P.; Oliveira, E. Verification of Sargassum Natans (Linnaeus) Gaillon (Heterokontophyta: Phaeophyceae) from the Sargasso Sea off the Coast of Brazil, Western Atlantic Ocean. Check List 2012, 8, 638–641. [Google Scholar] [CrossRef] [Green Version]
- Maréchal, J.-P.; Hellio, C.; Hu, C. A Simple, Fast, and Reliable Method to Predict Sargassum Washing Ashore in the Lesser Antilles. Remote Sens. Appl. Soc. Environ. 2017, 5, 54–63. [Google Scholar] [CrossRef]
- Chávez, V.; Uribe-Martínez, A.; Cuevas, E.; Rodríguez-Martínez, R.E.; van Tussenbroek, B.I.; Francisco, V.; Estévez, M.; Celis, L.B.; Monroy-Velázquez, L.V.; Leal-Bautista, R.; et al. Massive Influx of Pelagic Sargassum Spp. on the Coasts of the Mexican Caribbean 2014–2020: Challenges and Opportunities. Water 2020, 12, 2908. [Google Scholar] [CrossRef]
- Schling, M.; Guerrero Compeán, R.; Pazos, N.; Bailey, A.; Arkema, K.; Ruckelshaus, M. The Economic Impact of Sargassum: Evidence from the Mexican Coast; Inter-American Development Bank: Washington, DC, USA, 2022. [Google Scholar] [CrossRef]
- van Tussenbroek, B.I.; Hernández Arana, H.A.; Rodríguez-Martínez, R.E.; Espinoza-Avalos, J.; Canizales-Flores, H.M.; González-Godoy, C.E.; Barba-Santos, M.G.; Vega-Zepeda, A.; Collado-Vides, L. Severe Impacts of Brown Tides Caused by Sargassum Spp. on near-Shore Caribbean Seagrass Communities. Mar. Pollut. Bull. 2017, 122, 272–281. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, R.E.; Medina-Valmaseda, A.E.; Blanchon, P.; Monroy-Velázquez, L.V.; Almazán-Becerril, A.; Delgado-Pech, B.; Vásquez-Yeomans, L.; Francisco, V.; García-Rivas, M.C. Faunal Mortality Associated with Massive Beaching and Decomposition of Pelagic Sargassum. Mar. Pollut. Bull. 2019, 146, 201–205. [Google Scholar] [CrossRef]
- Maurer, A.S.; Stapleton, S.P.; Layman, C.A.; Burford Reiskind, M.O. The Atlantic Sargassum Invasion Impedes Beach Access for Nesting Sea Turtles. Clim. Chang. Ecol. 2021, 2, 100034. [Google Scholar] [CrossRef]
- Resiere, D.; Mehdaoui, H.; Névière, R.; Mégarbane, B. Sargassum Invasion in the Caribbean: The Role of Medical and Scientific Cooperation. Rev. Panam. Salud Pública 2019, 43, e52. [Google Scholar] [CrossRef] [Green Version]
- Resiere, D.; Mehdaoui, H.; Banydeen, R.; Florentin, J.; Kallel, H.; Nevière, R.; Mégarbane, B. Effets sanitaires de la décomposition des algues sargasses échouées sur les rivages des Antilles françaises. Toxicol. Anal. Clin. 2021, 33, 216–221. [Google Scholar] [CrossRef]
- de Lanlay, D.B.; Monthieux, A.; Banydeen, R.; Jean-Laurent, M.; Resiere, D.; Drame, M.; Neviere, R. Risk of Preeclampsia among Women Living in Coastal Areas Impacted by Sargassum Strandings on the French Caribbean Island of Martinique. Environ. Toxicol. Pharmacol. 2022, 94, 103894. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of Intense Plankton Blooms Using the 709 Nm Band of the MERIS Imaging Spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Hu, C. A Novel Ocean Color Index to Detect Floating Algae in the Global Oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Wang, M.; Hu, C. Mapping and Quantifying Sargassum Distribution and Coverage in the Central West Atlantic Using MODIS Observations. Remote Sens. Environ. 2016, 183, 350–367. [Google Scholar] [CrossRef]
- Gower, J.; Hu, C.; Borstad, G.; King, S. Ocean Color Satellites Show Extensive Lines of Floating Sargassum in the Gulf of Mexico. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3619–3625. [Google Scholar] [CrossRef]
- Gower, J.; King, S. The Distribution of Pelagic Sargassum Observed with OLCI. Int. J. Remote Sens. 2020, 41, 5669–5679. [Google Scholar] [CrossRef]
- Wang, M.; Hu, C. Automatic Extraction of Sargassum Features from Sentinel-2 MSI Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2579–2597. [Google Scholar] [CrossRef]
- Descloitres, J.; Minghelli, A.; Steinmetz, F.; Chevalier, C.; Chami, M.; Berline, L. Revisited Estimation of Moderate Resolution Sargassum Fractional Coverage Using Decametric Satellite Data (S2-MSI). Remote Sens. 2021, 13, 5106. [Google Scholar] [CrossRef]
- Wang, M.; Hu, C. On the Continuity of Quantifying Floating Algae of the Central West Atlantic between MODIS and VIIRS. Int. J. Remote Sens. 2018, 39, 3852–3869. [Google Scholar] [CrossRef]
- Podlejski, W.; Descloitres, J.; Chevalier, C.; Minghelli, A.; Lett, C.; Berline, L. Filtering out False Sargassum Detections Using Context Features. Front. Mar. Sci. 2022, 9, 1–15. [Google Scholar] [CrossRef]
- Chen, C.; Qin, Q.; Zhang, N.; Li, J.; Chen, L.; Wang, J.; Qin, X.; Yang, X. Extraction of Bridges over Water from High-Resolution Optical Remote-Sensing Images Based on Mathematical Morphology. Int. J. Remote Sens. 2014, 35, 3664–3682. [Google Scholar] [CrossRef]
- Kaur, B.; Garg, A. Mathematical Morphological Edge Detection for Remote Sensing Images. In Proceedings of the 2011 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; Volume 5, pp. 324–327. [Google Scholar]
- Siddiqi, M.H.; Ahmad, I.; Sulaiman, S.B. Weed Recognition Based on Erosion and Dilation Segmentation Algorithm. In Proceedings of the 2009 International Conference on Education Technology and Computer, Singapore, 17–20 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 224–228. [Google Scholar] [CrossRef]
- Soille, P.; Pesaresi, M. Advances in Mathematical Morphology Applied to Geoscience and Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2042–2055. [Google Scholar] [CrossRef]
- Cao, H.; Han, L.; Li, L. A Deep Learning Method for Cyanobacterial Harmful Algae Blooms Prediction in Taihu Lake, China. Harmful Algae 2022, 113, 102189. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep-Learning-Based Information Mining from Ocean Remote-Sensing Imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef]
- Ren, Y.; Li, X.; Yang, X.; Xu, H. Development of a Dual-Attention U-Net Model for Sea Ice and Open Water Classification on SAR Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Vasavi, S.; Divya, C.; Sarma, A.S. Detection of Solitary Ocean Internal Waves from SAR Images by Using U-Net and KDV Solver Technique. Glob. Transit. Proc. 2021, 2, 145–151. [Google Scholar] [CrossRef]
- Zheng, G.; Li, X.; Zhang, R.-H.; Liu, B. Purely Satellite Data–Driven Deep Learning Forecast of Complicated Tropical Instability Waves. Sci. Adv. 2020, 6, eaba1482. [Google Scholar] [CrossRef]
- Gao, L.; Li, X.; Kong, F.; Yu, R.; Guo, Y.; Ren, Y. AlgaeNet: A Deep-Learning Framework to Detect Floating Green Algae from Optical and SAR Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2782–2796. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, L.; Li, X. Distribution Characteristics of Green Algae in Yellow Sea Using a Deep Learning Automatic Detection Procedure. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3499–3501. [Google Scholar] [CrossRef]
- Qiu, Z.; Li, Z.; Bilal, M.; Wang, S.; Sun, D.; Chen, Y. Automatic Method to Monitor Floating Macroalgae Blooms Based on Multilayer Perceptron: Case Study of Yellow Sea Using GOCI Images. Opt. Express 2018, 26, 26810–26829. [Google Scholar] [CrossRef] [PubMed]
- Arellano-Verdejo, J.; Lazcano-Hernández, H.E. Collective View: Mapping Sargassum Distribution along Beaches. PeerJ Comput. Sci. 2021, 7, e528. [Google Scholar] [CrossRef] [PubMed]
- Vasquez, J.I.; Uriarte-Arcia, A.V.; Taud, H.; García-Floriano, A.; Ventura-Molina, E. Coastal Sargassum Level Estimation from Smartphone Pictures. Appl. Sci. 2022, 12, 10012. [Google Scholar] [CrossRef]
- Portillo, J.A.L.; Casasola, I.G.; Escalante-Ramírez, B.; Olveres, J.; Arriaga, J.; Appendini, C. Sargassum Detection and Path Estimation Using Neural Networks. In Proceedings of the Optics, Photonics and Digital Technologies for Imaging Applications VII, Strasbourg, France, 6–7 April 2022; SPIE: Strasbourg, France, 2022; Volume 12138, pp. 14–25. [Google Scholar] [CrossRef]
- Cuevas, E.; Uribe-Martínez, A.; Liceaga-Correa, M.d.l.Á. A Satellite Remote-Sensing Multi-Index Approach to Discriminate Pelagic Sargassum in the Waters of the Yucatan Peninsula, Mexico. Int. J. Remote Sens. 2018, 39, 3608–3627. [Google Scholar] [CrossRef]
- Shin, J.; Lee, J.-S.; Jang, L.-H.; Lim, J.; Khim, B.-K.; Jo, Y.-H. Sargassum Detection Using Machine Learning Models: A Case Study with the First 6 Months of GOCI-II Imagery. Remote Sens. 2021, 13, 4844. [Google Scholar] [CrossRef]
- Chen, Y.; Wan, J.; Zhang, J.; Zhao, J.; Ye, F.; Wang, Z.; Liu, S. Automatic Extraction Method of Sargassum Based on Spectral-Texture Features of Remote Sensing Images. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3705–3707. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Colombus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Arellano-Verdejo, J.; Lazcano-Hernandez, H.E.; Cabanillas-Terán, N. ERISNet: Deep Neural Network for Sargassum Detection along the Coastline of the Mexican Caribbean. PeerJ 2019, 7, e6842. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Hu, C. Satellite Remote Sensing of Pelagic Sargassum Macroalgae: The Power of High Resolution and Deep Learning. Remote Sens. Environ. 2021, 264, 112631. [Google Scholar] [CrossRef]
- Gower, J.; Young, E.; King, S. Satellite Images Suggest a New Sargassum Source Region in 2011. Remote Sens. Lett. 2013, 4, 764–773. [Google Scholar] [CrossRef]
- Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 2 December 2022).
- Schamberger, L.; Minghelli, A.; Chami, M.; Steinmetz, F. Improvement of Atmospheric Correction of Satellite Sentinel-3/OLCI Data for Oceanic Waters in Presence of Sargassum. Remote Sens. 2022, 14, 386. [Google Scholar] [CrossRef]
- Rouse, J.W.; Hass, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; E75-10354; NASA/GSFC: Greenbelt, MD, USA, 1974; Type III Final Report. [Google Scholar]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships Between NDVI, Canopy Structure, and Photosynthesis in Three Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the Satellite-Derived NDVI to Assess Ecological Responses to Environmental Change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the Relationship of NDVI with Leaf Area Index in a Deciduous Forest Site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Son, Y.B.; Min, J.-E.; Ryu, J.-H. Detecting Massive Green Algae (Ulva Prolifera) Blooms in the Yellow Sea and East China Sea Using Geostationary Ocean Color Imager (GOCI) Data. Ocean Sci. J. 2012, 47, 359–375. [Google Scholar] [CrossRef]
- Garcia, R.A.; Fearns, P.; Keesing, J.K.; Liu, D. Quantification of Floating Macroalgae Blooms Using the Scaled Algae Index. J. Geophys. Res. Oceans 2013, 118, 26–42. [Google Scholar] [CrossRef] [Green Version]
- Schamberger, L.; Minghelli, A.; Chami, M. Quantification of Underwater Sargassum Aggregations Based on a Semi-Analytical Approach Applied to Sentinel-3/OLCI (Copernicus) Data in the Tropical Atlantic Ocean. Remote Sens. 2022, 14, 5230. [Google Scholar] [CrossRef]
- Yan, K.; Li, J.; Zhao, H.; Wang, C.; Hong, D.; Du, Y.; Mu, Y.; Tian, B.; Xie, Y.; Yin, Z.; et al. Deep Learning-Based Automatic Extraction of Cyanobacterial Blooms from Sentinel-2 MSI Satellite Data. Remote Sens. 2022, 14, 4763. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- PyTorch. Available online: https://www.pytorch.org (accessed on 2 December 2022).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar] [CrossRef]
- Gower, J.; King, S. Satellite Images Show the Movement of Floating Sargassum in the Gulf of Mexico and Atlantic Ocean. Nat. Preced. 2008. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Hardy, R.F.; Hochberg, E.J. Spectral and Spatial Requirements of Remote Measurements of Pelagic Sargassum Macroalgae. Remote Sens. Environ. 2015, 167, 229–246. [Google Scholar] [CrossRef]





| Location | Date | Time (UTC) | Satellite-Sensor | Source |
|---|---|---|---|---|
| Grenadines (Caribbean) | 29 January 2019 | 14:35 | Terra-MODIS | [22] |
| 14:37 | Sentinel-2B-MSI tiles: PQU- PQV-PRU-PRV | [22], us | ||
| 13:38 | Sentinel-3-OLCI | us | ||
| Lesser Antilles | 9 May 2020 | 13:56 | Sentinel-3-OLCI | [52], us |
| 8 July 2017 | 13:55 | Sentinel-3-OLCI | ||
| Martinique | 6 August 2022 | 14:37 | Sentinel-2-MSI tile PRB | us |
| Index | Sensor | (nm) | (nm) | (nm) |
|---|---|---|---|---|
| NDVI | OLCI | 665 | 865 | - |
| MSI | 665 | 833 | - | |
| MCI | OLCI 1 | 681 | 709 | 754 |
| FAI | MODIS 2 | 645 | 859 | 1240 |
| MSI 3 | 655 | 855 | 1609 | |
| AFAI | MODIS 4 | 667 | 748 | 869 |
| MSI 5 | 665 | 740 | 865 |
| ErisNet | UNet | SegNet | Our Proposed Network | ||
|---|---|---|---|---|---|
| MSI | OLCI | ||||
| Layers | 44 | 83 | 91 | 32 | 75 |
| Blocks | 7 | 10 | 10 | 9 | 18 |
| Total Parameters | 455,554 | 13,400,578 | 29,449,350 | 226,762 | 973,145 |
| Sentinel-2/MSI | Sentinel-3/OLCI | |||||
|---|---|---|---|---|---|---|
| Recall | Precision | F1-Score | Recall | Precision | F1-Score | |
| NDVI | 0.835 | 0.085 | 0.154 | 0.910 | 0.105 | 0.188 |
| FAI(MSI)/MCI(OLCI) | 0.587 | 0.120 | 0.200 | 0.619 | 0.167 | 0.320 |
| ErisNet | 0.958 | 0.179 | 0.302 | 0.896 | 0.314 | 0.465 |
| UNet | 0.618 | 0.818 | 0.704 | 0.961 | 0.452 | 0.615 |
| SegNet | 0.599 | 0.840 | 0.699 | 0.931 | 0.493 | 0.645 |
| Our network | 0.819 | 0.942 | 0.876 | 0.735 | 0.785 | 0.760 |
| Satellite-Sensor | Date | Tile | Recall | Precision | F1-Score |
|---|---|---|---|---|---|
| Sentinel-3-OLCI | 29 January 2019 | - | 0.566 | 0.970 | 0.715 |
| 8 July 2017 | - | 0.851 | 0.739 | 0.791 | |
| Sentinel-2B-MSI | 29 January 2019 | PQU | 0.495 | 0.951 | 0.651 |
| PQV | 0.833 | 0.980 | 0.900 | ||
| PRU | 0.786 | 0.999 | 0.880 | ||
| PRV | 0.832 | 0.904 | 0.867 | ||
| 6 August 2022 | PRB | 0.817 | 0.896 | 0.854 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laval, M.; Belmouhcine, A.; Courtrai, L.; Descloitres, J.; Salazar-Garibay, A.; Schamberger, L.; Minghelli, A.; Thibaut, T.; Dorville, R.; Mazoyer, C.; et al. Detection of Sargassum from Sentinel Satellite Sensors Using Deep Learning Approach. Remote Sens. 2023, 15, 1104. https://doi.org/10.3390/rs15041104
Laval M, Belmouhcine A, Courtrai L, Descloitres J, Salazar-Garibay A, Schamberger L, Minghelli A, Thibaut T, Dorville R, Mazoyer C, et al. Detection of Sargassum from Sentinel Satellite Sensors Using Deep Learning Approach. Remote Sensing. 2023; 15(4):1104. https://doi.org/10.3390/rs15041104
Chicago/Turabian StyleLaval, Marine, Abdelbadie Belmouhcine, Luc Courtrai, Jacques Descloitres, Adán Salazar-Garibay, Léa Schamberger, Audrey Minghelli, Thierry Thibaut, René Dorville, Camille Mazoyer, and et al. 2023. "Detection of Sargassum from Sentinel Satellite Sensors Using Deep Learning Approach" Remote Sensing 15, no. 4: 1104. https://doi.org/10.3390/rs15041104
APA StyleLaval, M., Belmouhcine, A., Courtrai, L., Descloitres, J., Salazar-Garibay, A., Schamberger, L., Minghelli, A., Thibaut, T., Dorville, R., Mazoyer, C., Zongo, P., & Chevalier, C. (2023). Detection of Sargassum from Sentinel Satellite Sensors Using Deep Learning Approach. Remote Sensing, 15(4), 1104. https://doi.org/10.3390/rs15041104






