Spatiotemporal Patterns and Regional Differences in Soil Thermal Conductivity on the Qinghai–Tibet Plateau
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.1.1. STC Dataset
2.1.2. Soil Characteristics
2.2. Methodology
2.2.1. Classical Parameterization Schemes
Johansen (1975) Scheme
Côté and Konrad (2005) Scheme
2.2.2. Machine Learning Methods
KNN Method
ELM Method
RF Method
XGBoost Method
2.3. Model Performance Evaluation Parameters
3. Results and Discussion
3.1. Optimal Model for Thermal Conductivity Simulations
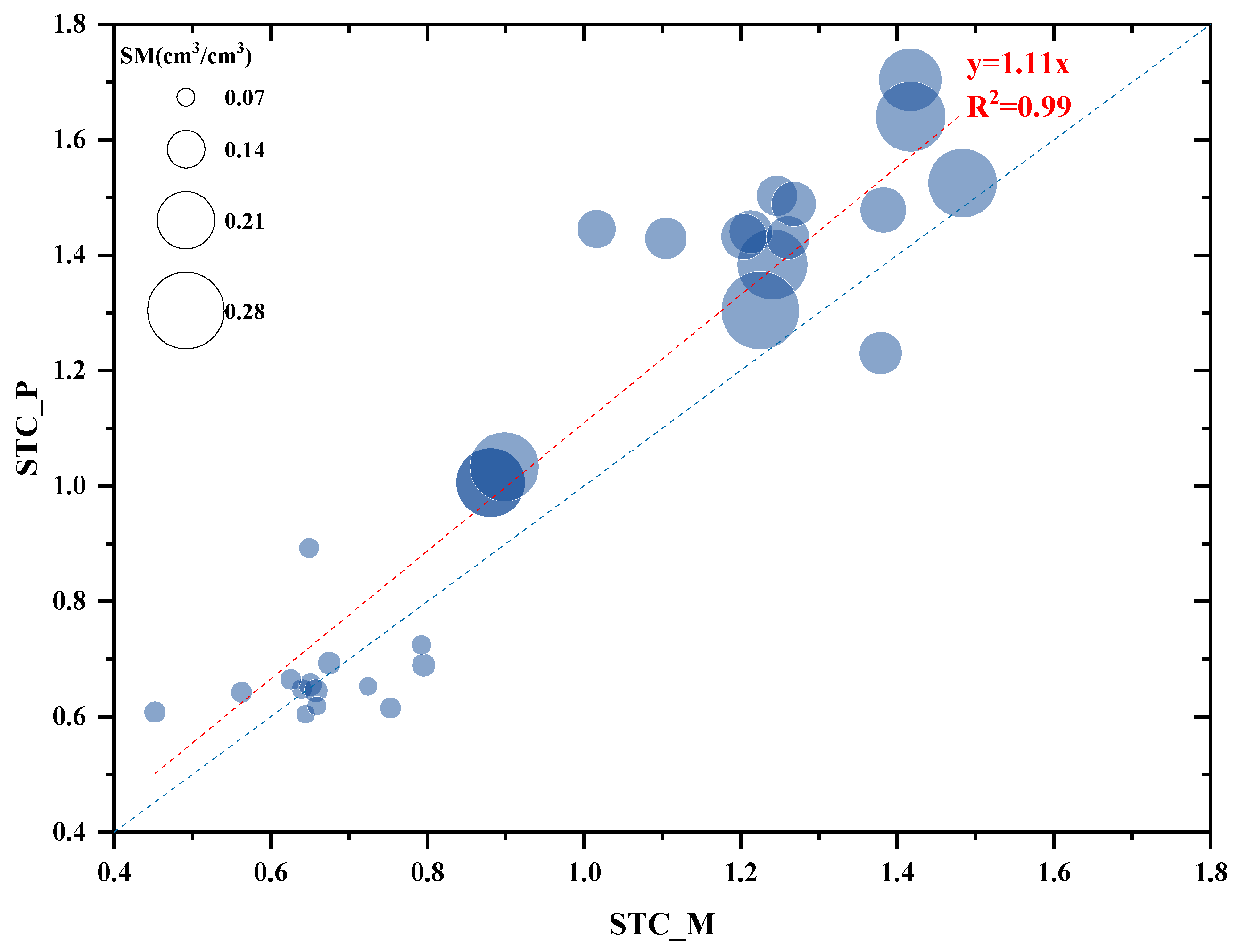
3.2. Verification of Product Reliability
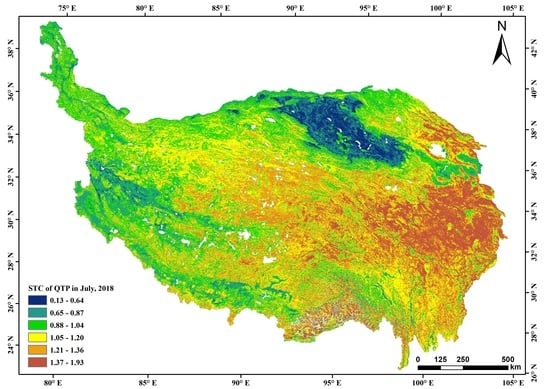
3.3. Spatiotemporal Variation in the Thermal Conductivity by Month
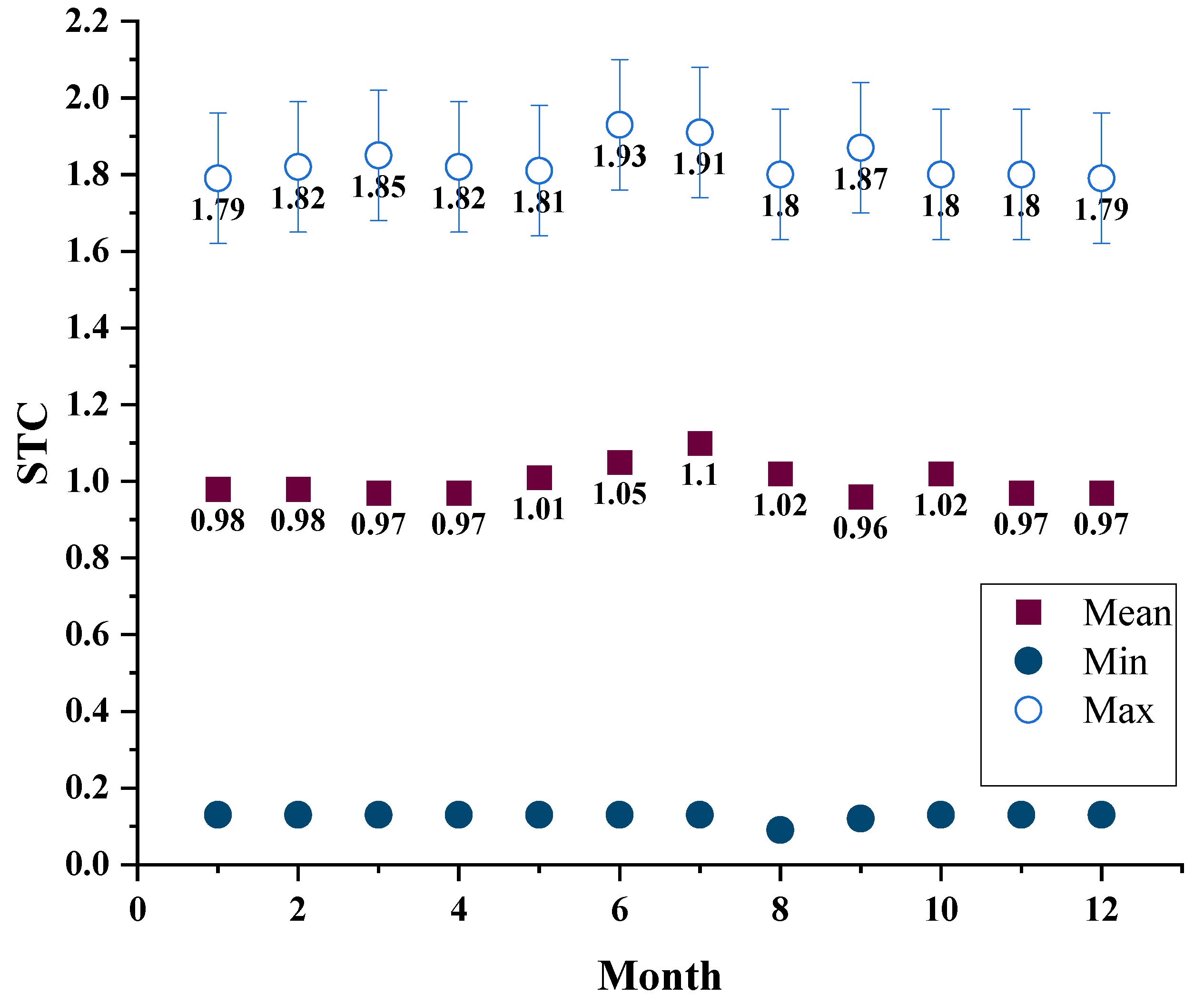
3.3.1. Temporal Variation in the STC
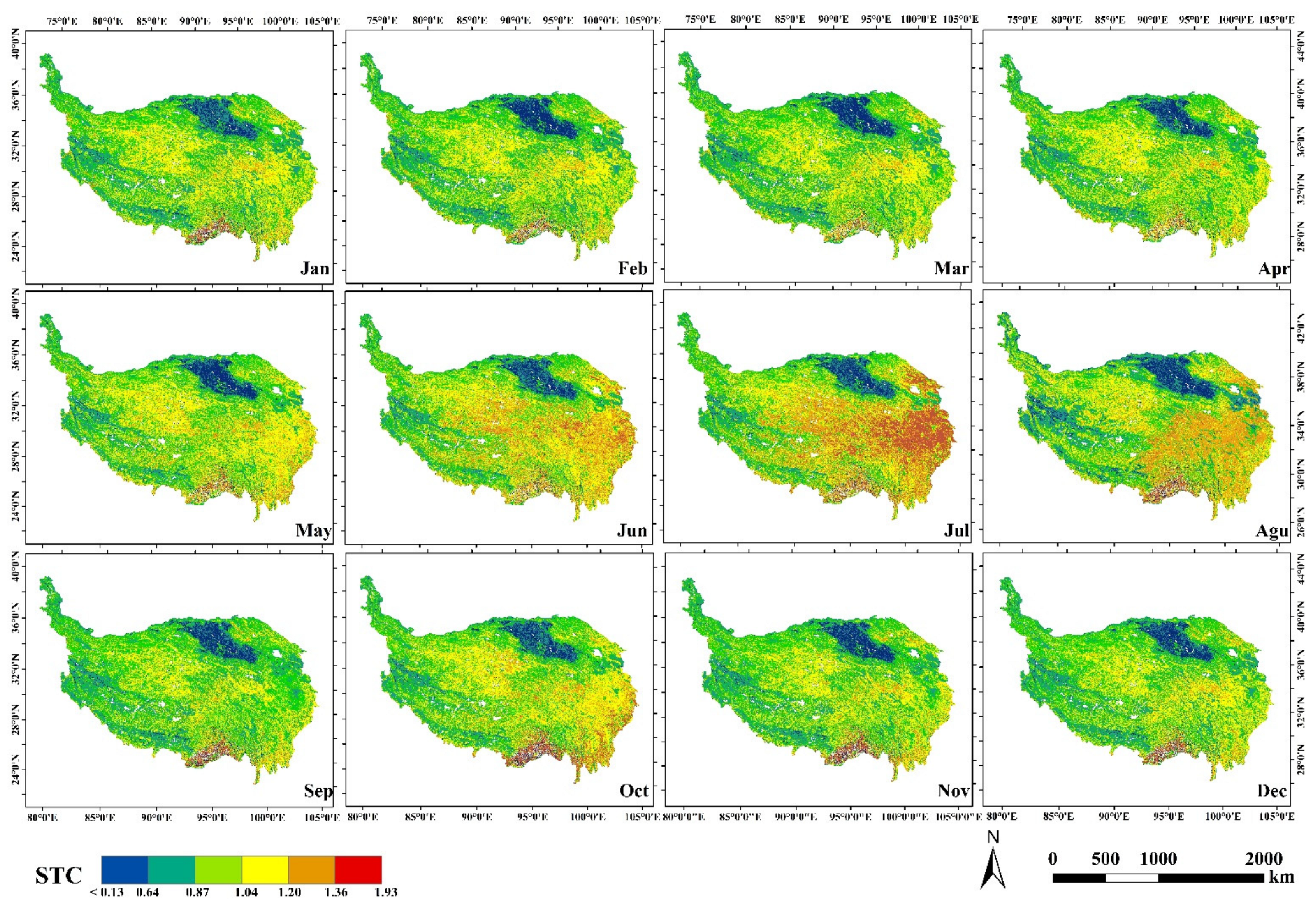
3.3.2. Spatial Variation in the STC in Different Months
3.4. Spatiotemporal Variation in the Thermal Conductivity during the Freezing and Thawing Periods
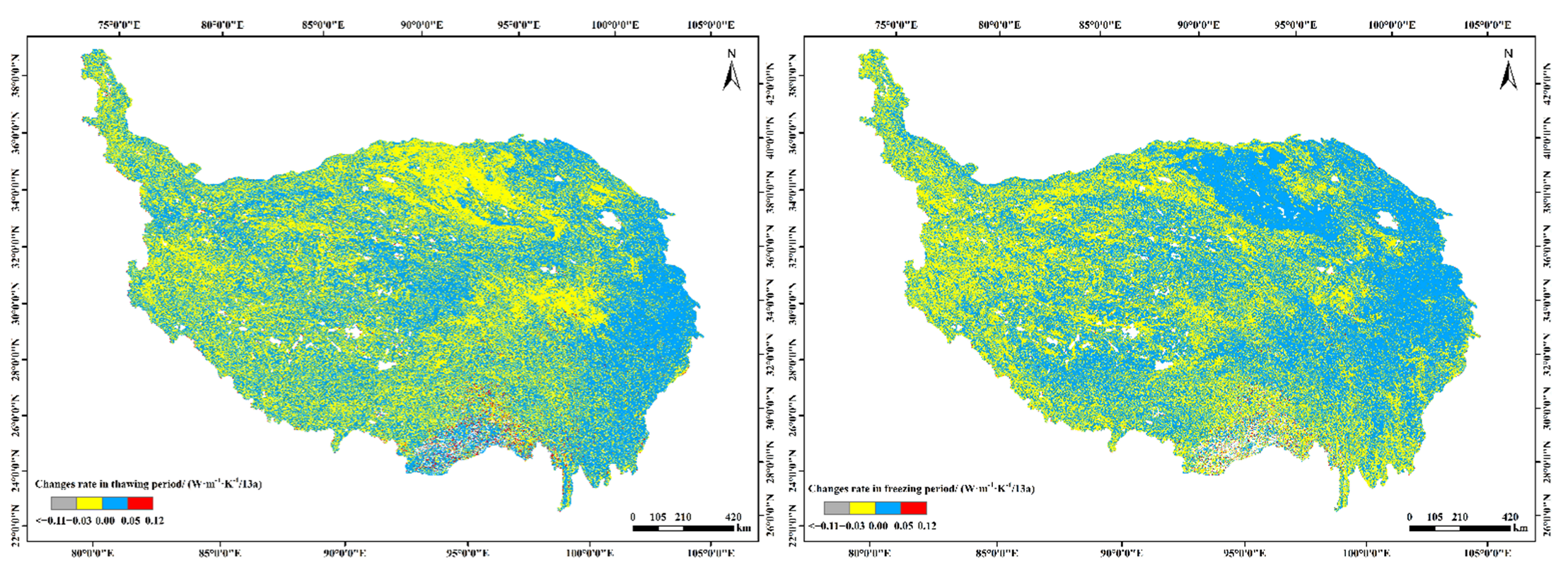
3.5. Interannual Variation in the Thermal Conductivity during the Freezing and Thawing Periods from 2005 to 2018
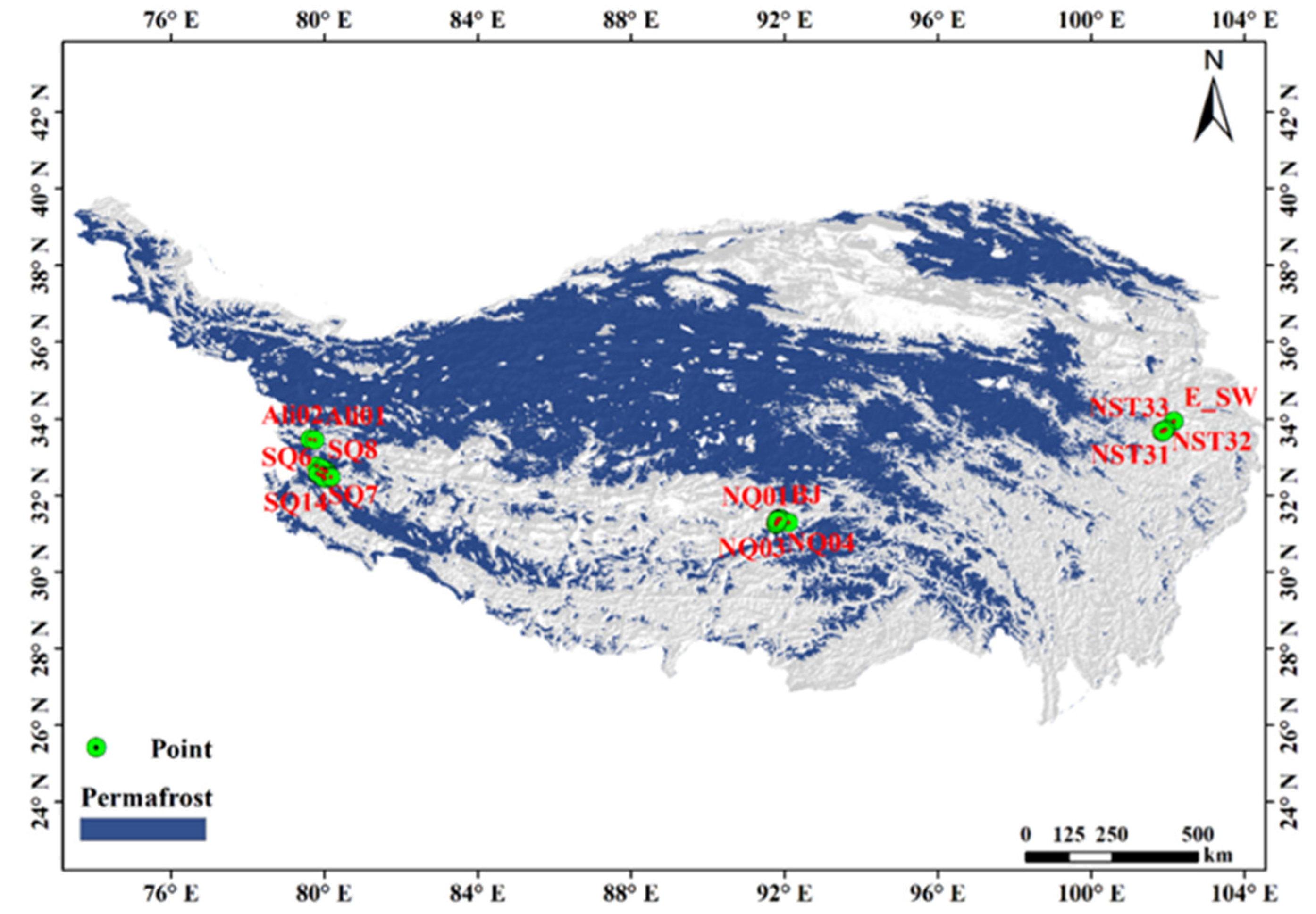
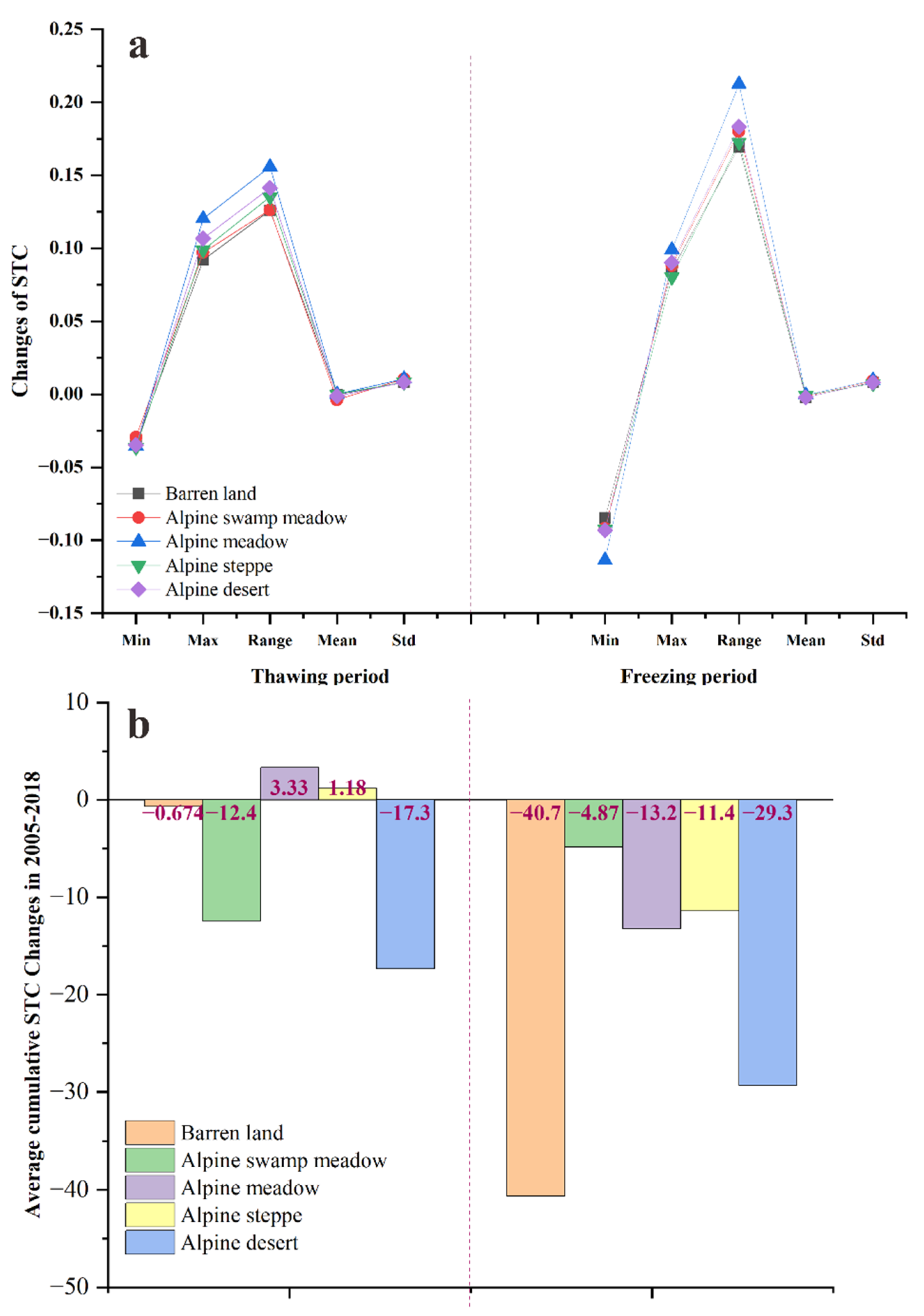
3.6. Distribution and Variation in the Thermal Conductivity of Different Underlying Surfaces in the Permafrost Zone
4. Discussion
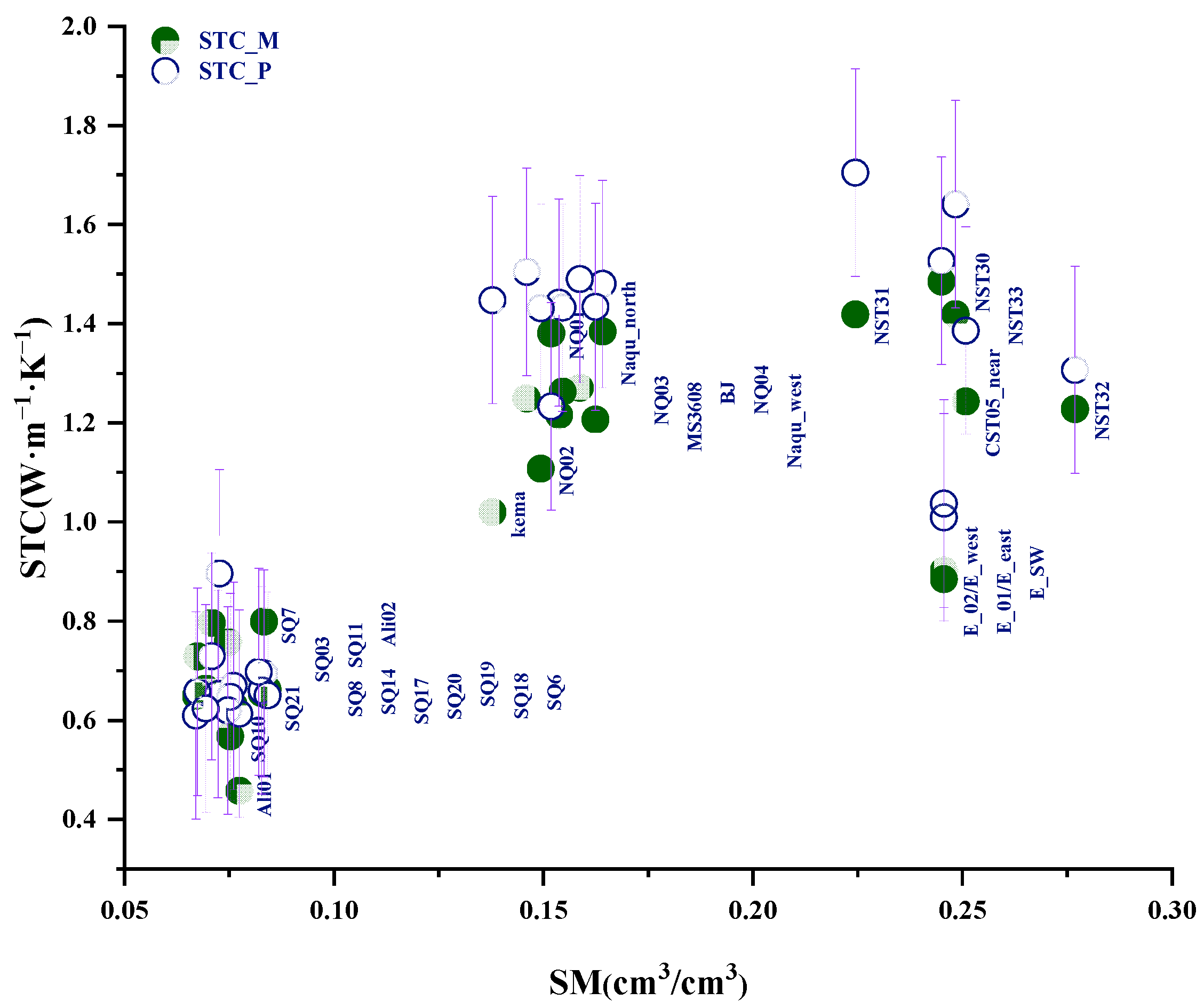
4.1. Soil Moisture Is the Most Important Factor for the Spatial Difference of STC
4.1.1. Precipitation Determines the Monthly Variation of STC
4.1.2. Spatial Differences in Moisture and Heat Determine the Spatial Distribution Pattern of STC during the Thawing and Freezing Periods
4.1.3. Precipitation Causes a Gradual Decrease in the STC Difference between the Thawing and Freezing Periods in the Permafrost Zone
4.2. The Interannual Spatial Distribution Variation of STC from 2005 to 2018 Is Macroscopically Similar and Microscopically Homogeneous
4.3. The Reasons for the Differences in STC Variation Trends in Areas with Special Landforms during the Thawing and Freezing Periods Are Complex
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serikova, S.; Pokrovsky, O.S.; Laudon, H.; Krickov, I.V.; Lim, A.G.; Manasypov, R.M.; Karlsson, J. High Carbon Emissions from Thermokarst Lakes of Western Siberia. Nat. Commun. 2019, 10, 1552. [Google Scholar] [CrossRef] [Green Version]
- Song, C.; Wang, G.; Mao, T.; Dai, J.; Yang, D. Linkage between Permafrost Distribution and River Runoff Changes across the Arctic and the Tibetan Plateau. Sci. China Earth Sci. 2020, 63, 292–302. [Google Scholar] [CrossRef]
- You, Q.; Cai, Z.; Pepin, N.; Chen, D.; Ahrens, B.; Jiang, Z.; Wu, F.; Kang, S.; Zhang, R.; Wu, T. Warming Amplification over the Arctic Pole and Third Pole: Trends, Mechanisms and Consequences. Earth-Sci. Rev. 2021, 217, 103625. [Google Scholar] [CrossRef]
- Pörtner, H.-O.; Roberts, D.C.; Masson-Delmotte, V.; Zhai, P.; Tignor, M.; Poloczanska, E.; Mintenbeck, K.; Nicolai, M.; Okem, A.; Petzold, J. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019; Volume 1. [Google Scholar]
- Bowen, J.C.; Ward, C.P.; Kling, G.W.; Cory, R.M. Arctic Amplification of Global Warming Strengthened by Sunlight Oxidation of Permafrost Carbon to CO2. Geophys. Res. Lett. 2020, 47, e2020GL087085. [Google Scholar] [CrossRef]
- Cheng, G.; Wu, T. Responses of Permafrost to Climate Change and Their Environmental Significance, Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2007, 112, F02S03. [Google Scholar] [CrossRef] [Green Version]
- Miner, K.R.; Turetsky, M.R.; Malina, E.; Bartsch, A.; Tamminen, J.; McGuire, A.D.; Fix, A.; Sweeney, C.; Elder, C.D.; Miller, C.E. Permafrost Carbon Emissions in a Changing Arctic. Nat. Rev. Earth Environ. 2022, 3, 55–67. [Google Scholar] [CrossRef]
- Smith, S.L.; O’Neill, H.B.; Isaksen, K.; Noetzli, J.; Romanovsky, V.E. The Changing Thermal State of Permafrost. Nat. Rev. Earth Environ. 2022, 3, 10–23. [Google Scholar] [CrossRef]
- Hjort, J.; Streletskiy, D.; Doré, G.; Wu, Q.; Bjella, K.; Luoto, M. Impacts of Permafrost Degradation on Infrastructure. Nat. Rev. Earth Environ. 2022, 3, 24–38. [Google Scholar] [CrossRef]
- Ma, J.; Li, R.; Huang, Z.; Wu, T.; Wu, X.; Zhao, L.; Liu, H.; Hu, G.; Xiao, Y.; Du, Y. Evaluation and Spatio-Temporal Analysis of Surface Energy Flux in Permafrost Regions over the Qinghai-Tibet Plateau and Arctic Using CMIP6 Models. Int. J. Digit. Earth 2022, 15, 1948–1966. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Wu, T.; Wang, Q.; Ding, Y.; Yao, J.; Wu, X.; Hu, G.; Xiao, Y.; Du, Y. Soil Thermal Conductivity and Its Influencing Factors at the Tanggula Permafrost Region on the Qinghai–Tibet Plateau. Agric. For. Meteorol. 2019, 264, 235–246. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Slater, A.G. Incorporating Organic Soil into a Global Climate Model. Clim. Dyn. 2008, 30, 145–160. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Leong, W.H. Advanced Geometric Mean Model for Predicting Thermal Conductivity of Unsaturated Soils. Int. J. Thermophys. 2016, 37, 18. [Google Scholar] [CrossRef]
- He, H.; He, D.; Jin, J.; Smits, K.M.; Dyck, M.; Wu, Q.; Si, B.; Lv, J. Room for Improvement: A Review and Evaluation of 24 Soil Thermal Conductivity Parameterization Schemes Commonly Used in Land-Surface, Hydrological, and Soil-Vegetation-Atmosphere Transfer Models. Earth-Sci. Rev. 2020, 211, 103419. [Google Scholar] [CrossRef]
- Comyn-Platt, E.; Hayman, G.; Huntingford, C.; Chadburn, S.E.; Burke, E.J.; Harper, A.B.; Collins, W.J.; Webber, C.P.; Powell, T.; Cox, P.M. Carbon Budgets for 1.5 and 2 C Targets Lowered by Natural Wetland and Permafrost Feedbacks. Nat. Geosci. 2018, 11, 568–573. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Tang, J.; Chen, D.; Wang, S.; Ou, T. Elevation-dependent Warming over the Tibetan Plateau from an Ensemble of CORDEX-EA Regional Climate Simulations. J. Geophys. Res. Atmos. 2021, 126, e2020JD033997. [Google Scholar] [CrossRef]
- Slater, A.G.; Lawrence, D.M. Diagnosing Present and Future Permafrost from Climate Models. J. Clim. 2013, 26, 5608–5623. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Wu, D.; Kong, Y.; Li, R.; Shi, H. Changes of Soil Thermal and Hydraulic Regimes in Northern Hemisphere Permafrost Regions over the 21st Century. Arct. Antarct. Alp. Res. 2017, 49, 305–319. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Yang, K. A New Scheme for Considering Soil Water-heat Transport Coupling Based on Community Land Model: Model Description and Preliminary Validation. J. Adv. Model. Earth Syst. 2018, 10, 927–950. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; Wei, N.; Yuan, H.; Zhang, S.; Shangguan, W.; Liu, S.; Lu, X.; Xin, Y. Evaluation of Soil Thermal Conductivity Schemes for Use in Land Surface Modeling. J. Adv. Model. Earth Syst. 2019, 11, 3454–3473. [Google Scholar] [CrossRef]
- Yang, S.; Li, R.; Wu, T.; Wu, X.; Zhao, L.; Hu, G.; Zhu, X.; Du, Y.; Xiao, Y.; Zhang, Y. Evaluation of Soil Thermal Conductivity Schemes Incorporated into CLM5. 0 in Permafrost Regions on the Tibetan Plateau. Geoderma 2021, 401, 115330. [Google Scholar] [CrossRef]
- Poutou, E.; Krinner, G.; Genthon, C.; de Noblet-Ducoudré, N. Role of Soil Freezing in Future Boreal Climate Change. Clim. Dyn. 2004, 23, 621–639. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Z.; Wei, D. The Sensitivity of Ground Surface Temperature Prediction to Soil Thermal Properties Using the Simple Biosphere Model (SiB2). Adv. Atmos. Sci. 2012, 29, 623–634. [Google Scholar] [CrossRef]
- Su, F.; Duan, X.; Chen, D.; Hao, Z.; Cuo, L. Evaluation of the Global Climate Models in the CMIP5 over the Tibetan Plateau. J. Clim. 2013, 26, 3187–3208. [Google Scholar] [CrossRef] [Green Version]
- Luo, S.; Fang, X.; Lyu, S.; Zhang, Y.; Chen, B. Improving CLM4. 5 Simulations of Land–Atmosphere Exchange during Freeze–Thaw Processes on the Tibetan Plateau. J. Meteorol. Res. 2017, 31, 916–930. [Google Scholar] [CrossRef]
- Zhu, D.; Ciais, P.; Krinner, G.; Maignan, F.; Jornet Puig, A.; Hugelius, G. Controls of Soil Organic Matter on Soil Thermal Dynamics in the Northern High Latitudes. Nat. Commun. 2019, 10, 3172. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Zhao, L.; Dai, Y.; Li, R.; Pang, Q.; Yao, J. Representing Permafrost Properties in CoLM for the Qinghai–Xizang (Tibetan) Plateau. Cold Reg. Sci. Technol. 2013, 87, 68–77. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, L.; Wu, X.; Li, R.; Wu, T.; Xie, C.; Pang, Q.; Xiao, Y.; Li, W.; Qiao, Y. Modeling Permafrost Properties in the Qinghai-Xizang (Tibet) Plateau. Sci. China Earth Sci. 2015, 58, 2309–2326. [Google Scholar] [CrossRef]
- Melton, J.R.; Arora, V.K.; Wisernig-Cojoc, E.; Seiler, C.; Fortier, M.; Chan, E.; Teckentrup, L. CLASSIC v1. 0: The Open-Source Community Successor to the Canadian Land Surface Scheme (CLASS) and the Canadian Terrestrial Ecosystem Model (CTEM)–Part 1: Model Framework and Site-Level Performance. Geosci. Model Dev. 2020, 13, 2825–2850. [Google Scholar] [CrossRef]
- Li, R.; Wu, T.H.; Zhao, L.; Xie, C.; Xiao, Y.; Hu, G.; Du, Y. Investigation on the Soil Thermal Conductivity of Different Land Surface Patterns in the Northern Qinghai-Tibetan Plateau, China. GEO Que. 2015, 548, 1–7. [Google Scholar]
- Zhang, N.; Wang, Z. Review of Soil Thermal Conductivity and Predictive Models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- Malek, K.; Malek, K.; Khanmohammadi, F. Response of Soil Thermal Conductivity to Various Soil Properties. Int. Commun. Heat Mass Transf. 2021, 127, 105516. [Google Scholar] [CrossRef]
- De Vries, D.A. Thermal Properties of Soils. Phys. Plant Environ. 1963, 210–235. [Google Scholar]
- Johansen, O. Thermal Conductivity of Soils. Ph.D. Thesis, Trondheim University, Trondheim, Norway, 1975. [Google Scholar]
- Farouki, O.T. The Thermal Properties of Soils in Cold Regions. Cold Reg. Sci. Technol. 1981, 5, 67–75. [Google Scholar] [CrossRef]
- Côté, J.; Konrad, J.-M. A Generalized Thermal Conductivity Model for Soils and Construction Materials. Can. Geotech. J. 2005, 42, 443–458. [Google Scholar] [CrossRef]
- Lu, S.; Ren, T.; Gong, Y.; Horton, R. An Improved Model for Predicting Soil Thermal Conductivity from Water Content at Room Temperature. Soil Sci. Soc. Am. J. 2007, 71, 8–14. [Google Scholar] [CrossRef]
- He, H.; Zhao, Y.; Dyck, M.F.; Si, B.; Jin, H.; Lv, J.; Wang, J. A Modified Normalized Model for Predicting Effective Soil Thermal Conductivity. Acta Geotech. 2017, 12, 1281–1300. [Google Scholar] [CrossRef]
- He, H.; Flerchinger, G.N.; Kojima, Y.; He, D.; Hardegree, S.P.; Dyck, M.F.; Horton, R.; Wu, Q.; Si, B.; Lv, J. Evaluation of 14 Frozen Soil Thermal Conductivity Models with Observations and SHAW Model Simulations. Geoderma 2021, 403, 115207. [Google Scholar] [CrossRef]
- Du, Y.; Li, R.; Wu, T.; Yang, C.; Zhao, L.; Hu, G.; Xiao, Y.; Yang, S.; Ni, J.; Ma, J. A New Model for Predicting Soil Thermal Conductivity for Dry Soils. Int. J. Therm. Sci. 2022, 176, 107487. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.; Bohn, T.J.; Zhao, L.; Li, J.; Liu, Q.; Zhou, B. Frozen Soil Degradation and Its Effects on Surface Hydrology in the Northern Tibetan Plateau. J. Geophys. Res. Atmos. 2015, 120, 8276–8298. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Wang, P.; Liu, J.; Sparrow, M.; Haginoya, S.; Zhou, X. Variation of Surface Albedo and Soil Thermal Parameters with Soil Moisture Content at a Semi-Desert Site on the Western Tibetan Plateau. Bound.-Layer Meteorol. 2005, 116, 117–129. [Google Scholar] [CrossRef]
- Wang, D.; Wu, T.; Zhao, L.; Mu, C.; Li, R.; Wei, X.; Hu, G.; Zou, D.; Zhu, X.; Chen, J. A 1 Km Resolution Soil Organic Carbon Dataset for Frozen Ground in the Third Pole. Earth Syst. Sci. Data 2021, 13, 3453–3465. [Google Scholar] [CrossRef]
- Cao, X.; Tian, F.; Li, K.; Ni, J.; Yu, X.; Liu, L.; Wang, N. Lake Surface Sediment Pollen Dataset for the Alpine Meadow Vegetation Type from the Eastern Tibetan Plateau and Its Potential in Past Climate Reconstructions. Earth Syst. Sci. Data 2021, 13, 3525–3537. [Google Scholar] [CrossRef]
- Rao, P.; Wang, Y.; Wang, F.; Liu, Y.; Wang, X.; Wang, Z. Daily Soil Moisture Mapping at 1 Km Resolution Based on SMAP Data for Desertification Areas in Northern China. Earth Syst. Sci. Data 2022, 14, 3053–3073. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Hu, Z.; Yu, Z.; Hao, S.; Lei, Z.; Xie, Y. Prediction of Layered Thermal Conductivity Using Artificial Neural Network in Order to Have Better Design of Ground Source Heat Pump System. Energies 2018, 11, 1896. [Google Scholar] [CrossRef] [Green Version]
- Rizvi, Z.H.; Husain, S.M.B.; Haider, H.; Wuttke, F. Effective Thermal Conductivity of Sands Estimated by Group Method of Data Handling (GMDH). Mater. Today Proc. 2020, 26, 2103–2107. [Google Scholar] [CrossRef]
- Rizvi, Z.H.; Zaidi, H.H.; Akhtar, S.J.; Sattari, A.S.; Wuttke, F. Soft and Hard Computation Methods for Estimation of the Effective Thermal Conductivity of Sands. Heat Mass Transf. 2020, 56, 1947–1959. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, C.; Liu, S.; Zhang, N.; Zhang, T. Assessment of Soil Thermal Conduction Using Artificial Neural Network Models. Cold Reg. Sci. Technol. 2020, 169, 102907. [Google Scholar] [CrossRef]
- Wen, H.; Bi, J.; Guo, D. Calculation of the Thermal Conductivities of Fine-textured Soils Based on Multiple Linear Regression and Artificial Neural Networks. Eur. J. Soil Sci. 2020, 71, 568–579. [Google Scholar] [CrossRef]
- Fei, W.; Narsilio, G.A.; Disfani, M.M. Predicting Effective Thermal Conductivity in Sands Using an Artificial Neural Network with Multiscale Microstructural Parameters. Int. J. Heat Mass Transf. 2021, 170, 120997. [Google Scholar] [CrossRef]
- Bayat, H.; Ebrahimzadeh, G.; Mohanty, B.P. Investigating the Capability of Estimating Soil Thermal Conductivity Using Topographical Attributes for the Southern Great Plains, USA. Soil Tillage Res. 2021, 206, 104811. [Google Scholar] [CrossRef]
- Zhang, R.; Xue, X. A New Model for Prediction of Soil Thermal Conductivity. Int. Commun. Heat Mass Transf. 2021, 129, 105661. [Google Scholar] [CrossRef]
- Zhu, C.-Y.; He, Z.-Y.; Du, M.; Gong, L.; Wang, X. Predicting the Effective Thermal Conductivity of Unfrozen Soils with Various Water Contents Based on Artificial Neural Network. Nanotechnology 2021, 33, 065408. [Google Scholar] [CrossRef] [PubMed]
- Orakoglu Firat, M.E.; Atila, O. Investigation of the Thermal Conductivity of Soil Subjected to Freeze–Thaw Cycles Using the Artificial Neural Network Model. J. Therm. Anal. Calorim. 2022, 147, 8077–8093. [Google Scholar] [CrossRef]
- Li, K.-Q.; Kang, Q.; Nie, J.-Y.; Huang, X.-W. Artificial Neural Network for Predicting the Thermal Conductivity of Soils Based on a Systematic Database. Geothermics 2022, 103, 102416. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Tang, W.; Qin, J.; Zhao, L. Parameterizing Soil Organic Carbon’s Impacts on Soil Porosity and Thermal Parameters for Eastern Tibet Grasslands. Sci. China Earth Sci. 2012, 55, 1001–1011. [Google Scholar] [CrossRef]
- Wang, X.; Yang, M.; Pang, G.; Wan, G.; Chen, X. Simulation and Improvement of Land Surface Processes in Nameqie, Central Tibetan Plateau, Using the Community Land Model (CLM3. 5). Environ. Earth Sci. 2015, 73, 7343–7357. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, L.; Wu, X.; Li, R.; Wu, T.; Xie, C.; Pang, Q.; Zou, D. Comparison of the Thermal Conductivity Parameterizations for a Freeze-Thaw Algorithm with a Multi-Layered Soil in Permafrost Regions. Catena 2017, 156, 244–251. [Google Scholar] [CrossRef]
- Chen, S.X. Thermal Conductivity of Sands. Heat Mass Transf. 2008, 44, 1241–1246. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Dane, J.H. Thermal Conductivity of Two Porous Media as a Function of Water Content, Temperature, and Density. Soil Sci. 1986, 142, 187–195. [Google Scholar] [CrossRef]
- Kasubuchi, T.; Momose, T.; Tsuchiya, F.; Tarnawski, V.R. Normalized Thermal Conductivity Model for Three Japanese Soils. Trans. Jpn. Soc. Irrig. Drain. Rural Eng. (Jpn.) 2007, 251, 53–57. [Google Scholar]
- McCombie, M.L.; Tarnawski, V.R.; Bovesecchi, G.; Coppa, P.; Leong, W.H. Thermal Conductivity of Pyroclastic Soil (Pozzolana) from the Environs of Rome. Int. J. Thermophys. 2017, 38, 21. [Google Scholar] [CrossRef]
- McInnes, K.J. Thermal Conductivities of Soils from Dryland Wheat Regions of Eastern Washington. Master’s Thesis, Washington State University, Spokane, DC, USA, 1981. [Google Scholar]
- Tarnawski, V.R.; McCombie, M.L.; Momose, T.; Sakaguchi, I.; Leong, W.H. Thermal Conductivity of Standard Sands. Part III. Full Range of Saturation. Int. J. Thermophys. 2013, 34, 1130–1147. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Momose, T.; McCombie, M.L.; Leong, W.H. Canadian Field Soils III. Thermal-Conductivity Data and Modeling. Int. J. Thermophys. 2015, 36, 119–156. [Google Scholar] [CrossRef]
- Zhao, Y.; Si, B.; Zhang, Z.; Li, M.; He, H.; Hill, R.L. A New Thermal Conductivity Model for Sandy and Peat Soils. Agric. For. Meteorol. 2019, 274, 95–105. [Google Scholar] [CrossRef]
- Barry-Macaulay, D.; Bouazza, A.; Wang, B.; Singh, R.M. Evaluation of Soil Thermal Conductivity Models. Can. Geotech. J. 2015, 52, 1892–1900. [Google Scholar] [CrossRef]
- Gori, F.; Corasaniti, S. New Model to Evaluate the Effective Thermal Conductivity of Three-Phase Soils. Int. Commun. Heat Mass Transf. 2013, 47, 1–6. [Google Scholar] [CrossRef]
- Hiraiwa, Y.; Kasubuchi, T. Temperature Dependence of Thermal Conductivity of Soil over a Wide Range of Temperature (5–75 °C). Eur. J. Soil Sci. 2000, 51, 211–218. [Google Scholar] [CrossRef]
- Kahr, G.; Müller-Vonmoos, M. Wärmeleitfähigkeit von Bentonit MX80 Und von Montigel Nach Der Heizdrahtmethode. Tech. Ber. NTB 82-06, Nagra, Hardstrasse 73, CH-5430 Wettingen, Schweiz. 1982. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/114577 (accessed on 22 November 2022).
- Tang, A.-M.; Cui, Y.-J.; Le, T.-T. A Study on the Thermal Conductivity of Compacted Bentonites. Appl. Clay Sci. 2008, 41, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Yu, W.; Hu, D.; Liu, W. Experimental Study on the Thermal Conductivity of Aeolian Sand from the Tibetan Plateau. Cold Reg. Sci. Technol. 2018, 146, 1–8. [Google Scholar] [CrossRef]
- Nikolaev, I.V.; Leong, W.H.; Rosen, M.A. Experimental Investigation of Soil Thermal Conductivity over a Wide Temperature Range. Int. J. Thermophys. 2013, 34, 1110–1129. [Google Scholar] [CrossRef]
- Singh, D.N.; Devid, K. Generalized Relationships for Estimating Soil Thermal Resistivity. Exp. Therm. Fluid Sci. 2000, 22, 133–143. [Google Scholar] [CrossRef]
- Yamasaki, M.; Kawamura, Y. Thermal Diffusivity and Thermal Conductivity of Mg–Zn–Rare Earth Element Alloys with Long-Period Stacking Ordered Phase. Scr. Mater. 2009, 60, 264–267. [Google Scholar] [CrossRef]
- Zhang, N.; Yu, X.; Pradhan, A.; Puppala, A.J. A New Generalized Soil Thermal Conductivity Model for Sand–Kaolin Clay Mixtures Using Thermo-Time Domain Reflectometry Probe Test. Acta Geotech. 2017, 12, 739–752. [Google Scholar] [CrossRef]
- Mochizuki, H.; Mizoguchi, M.; Miyazaki, T. Effects of NaCl Concentration on the Thermal Conductivity of Sand and Glass Beads with Moisture Contents at Levels below Field Capacity. Soil Sci. Plant Nutr. 2008, 54, 829–838. [Google Scholar] [CrossRef]
- Campbell, G.S.; Jungbauer, J.D., Jr.; Bidlake, W.R.; Hungerford, R.D. Predicting the Effect of Temperature on Soil Thermal Conductivity. Soil Sci. 1994, 158, 307–313. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Tsuchiya, F.; Coppa, P.; Bovesecchi, G. Volcanic Soils: Inverse Modeling of Thermal Conductivity Data. Int. J. Thermophys. 2019, 40, 14. [Google Scholar] [CrossRef]
- Alrtimi, A.; Rouainia, M.; Haigh, S. Thermal Conductivity of a Sandy Soil. Appl. Therm. Eng. 2016, 106, 551–560. [Google Scholar] [CrossRef] [Green Version]
- Tokoro, T.; Ishikawa, T.; Shirai, S.; Nakamura, T. Estimation Methods for Thermal Conductivity of Sandy Soil with Electrical Characteristics. Soils Found. 2016, 56, 927–936. [Google Scholar] [CrossRef]
- Go, G.-H.; Lee, S.-R.; Kim, Y.-S.; Park, H.-K.; Yoon, S. A New Thermal Conductivity Estimation Model for Weathered Granite Soils in Korea. Geomech. Eng 2014, 6, 359–376. [Google Scholar] [CrossRef]
- Bristow, K.L. Measurement of Thermal Properties and Water Content of Unsaturated Sandy Soil Using Dual-Probe Heat-Pulse Probes. Agric. For. Meteorol. 1998, 89, 75–84. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, Y.; Lv, S.; Su, Z. Analysis of Soil Hydraulic and Thermal Properties for Land Surface Modeling over the Tibetan Plateau. Earth Syst. Sci. Data 2018, 10, 1031–1061. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Zhang, W.; Fan, C.; Li, G. Effects of Temperature, Dry Density and Water Content on the Thermal Conductivity of Genhe Silty Clay. Results Phys. 2020, 16, 102830. [Google Scholar] [CrossRef]
- Bachmann, J.; Horton, R.; Van der Ploeg, R.R. Isothermal and Nonisothermal Evaporation from Four Sandy Soils of Different Water Repellency. Soil Sci. Soc. Am. J. 2001, 65, 1599–1607. [Google Scholar] [CrossRef]
- Al-Shammary, A.A.G.; Caballero-Calvo, A.; Jebur, H.A.; Khalbas, M.I.; Fernández-Gálvez, J. A Novel Heat-Pulse Probe for Measuring Soil Thermal Conductivity: Field Test under Different Tillage Practices. Comput. Electron. Agric. 2022, 202, 107414. [Google Scholar] [CrossRef]
- Kersten, M.S. Thermal Properties of Soils; University of Minnesota • Institute of Technology: Minneapolis, MN, USA, 1949. [Google Scholar]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q. A New Map of Permafrost Distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wang, Q.; Zhao, L.; Wu, X.; Yue, G.; Zou, D.; Nan, Z.; Liu, G.; Pang, Q.; Fang, H. Mapping the Vegetation Distribution of the Permafrost Zone on the Qinghai-Tibet Plateau. J. Mt. Sci. 2016, 13, 1035–1046. [Google Scholar] [CrossRef]
- Hu, Z.; Chai, L.; Crow, W.T.; Liu, S.; Zhu, Z.; Zhou, J.; Qu, Y.; Liu, J.; Yang, S.; Lu, Z. Applying a Wavelet Transform Technique to Optimize General Fitting Models for SM Analysis: A Case Study in Downscaling over the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 3063. [Google Scholar] [CrossRef]
- Liu, F.; Wu, H.; Zhao, Y.; Li, D.; Yang, J.-L.; Song, X.; Shi, Z.; Zhu, A.-X.; Zhang, G.-L. Mapping High Resolution National Soil Information Grids of China. Sci. Bull. 2022, 67, 328–340. [Google Scholar] [CrossRef]
- Balland, V.; Arp, P.A. Modeling Soil Thermal Conductivities over a Wide Range of Conditions. J. Environ. Eng. Sci. 2005, 4, 549–558. [Google Scholar] [CrossRef]
- Pan, Y.; Lyu, S.; Li, S.; Gao, Y.; Meng, X.; Ao, Y.; Wang, S. Simulating the Role of Gravel in Freeze–Thaw Process on the Qinghai–Tibet Plateau. Theor. Appl. Climatol. 2017, 127, 1011–1022. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, S.; Xu, J.; He, H.; Wang, D.; Horton, R.; Liu, G. Comparative Analysis of Seven Machine Learning Algorithms and Five Empirical Models to Estimate Soil Thermal Conductivity. Agric. For. Meteorol. 2022, 323, 109080. [Google Scholar] [CrossRef]
- Kang, J.; Yu, Z.; Wu, S.; Zhang, Y.; Gao, P. Feasibility Analysis of Extreme Learning Machine for Predicting Thermal Conductivity of Rocks. Environ. Earth Sci. 2021, 80, 455. [Google Scholar] [CrossRef]
- Kardani, N.; Bardhan, A.; Samui, P.; Nazem, M.; Zhou, A.; Armaghani, D.J. A Novel Technique Based on the Improved Firefly Algorithm Coupled with Extreme Learning Machine (ELM-IFF) for Predicting the Thermal Conductivity of Soil. Eng. Comput. 2022, 38, 3321–3340. [Google Scholar] [CrossRef]
- Kardani, N.; Bardhan, A.; Samui, P.; Nazem, M.; Asteris, P.G.; Zhou, A. Predicting the Thermal Conductivity of Soils Using Integrated Approach of ANN and PSO with Adaptive and Time-Varying Acceleration Coefficients. Int. J. Therm. Sci. 2022, 173, 107427. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land Cover Classification Using Google Earth Engine and Random Forest Classifier—The Role of Image Composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Magidi, J.; Nhamo, L.; Mpandeli, S.; Mabhaudhi, T. Application of the Random Forest Classifier to Map Irrigated Areas Using Google Earth Engine. Remote Sens. 2021, 13, 876. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Dhaliwal, S.S.; Nahid, A.-A.; Abbas, R. Effective Intrusion Detection System Using XGBoost. Information 2018, 9, 149. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance Evaluation of Hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost Models to Predict Blast-Induced Ground Vibration. Eng. Comput. 2022, 38, 4145–4162. [Google Scholar] [CrossRef]
- Jame, Y.-W.; Norum, D.I. Heat and Mass Transfer in a Freezing Unsaturated Porous Medium. Water Resour. Res. 1980, 16, 811–819. [Google Scholar] [CrossRef]
- Tao, Z.X.; Zhang, J.S. The Thermal Conductivity of Thawed and Frozen Soils with High Water (Ice) Content. J. Glaciol. Geocryol. 1983, 5, 75–80. [Google Scholar]
- Li, Y.; Shao, M.A.; Wang, W.Y.; Wang, Q.J.; Zhang, J.F.; Lai, J.B. Influence of Soil Textures on the Thermal Properties. Trans. Chin. Soc. Agric. Eng. 2003, 19, 62–65. [Google Scholar]
- Lin, Z.; Guojie, H.; Defu, Z.; Xiaodong, W.U.; Lu, M.A.; Zhe, S.U.N.; Liming, Y.; Huayun, Z.; Shibo, L.I.U. Permafrost Changes and Its Effects on Hydrological Processes on Qinghai-Tibet Plateau. Bull. Chin. Acad. Sci. 2019, 34, 1233–1246. (In Chinese) [Google Scholar]
- Ma, J.; Li, R.; Liu, H.; Huang, Z.; Wu, T.; Hu, G.; Xiao, Y.; Zhao, L.; Du, Y.; Yang, S. The Surface Energy Budget and Its Impact on the Freeze-Thaw Processes of Active Layer in Permafrost Regions of the Qinghai-Tibetan Plateau. Adv. Atmos. Sci. 2022, 39, 189–200. [Google Scholar] [CrossRef]
- Wang, S.; Li, R.; Wu, T.; Zhao, L.; Wu, X.; Hu, G.; Yao, J.; Ma, J.; Liu, W.; Jiao, Y. Evaluating the Impact of Soil Enthalpy upon the Thawing Process of the Active Layer in Permafrost Regions of the Qinghai–Tibet Plateau Using CLM5. 0. Remote Sens. 2022, 15, 249. [Google Scholar] [CrossRef]
- Gao, H.; Wang, J.; Yang, Y.; Pan, X.; Ding, Y.; Duan, Z. Permafrost Hydrology of the Qinghai-Tibet Plateau: A Review of Processes and Modeling. Front. Earth Sci. 2021, 8, 576838. [Google Scholar] [CrossRef]
- Li, H.; Liu, F.; Zhang, S.; Zhang, C.; Zhang, C.; Ma, W.; Luo, J. Drying–Wetting Changes of Surface Soil Moisture and the Influencing Factors in Permafrost Regions of the Qinghai-Tibet Plateau, China. Remote Sens. 2022, 14, 2915. [Google Scholar] [CrossRef]
- Xu, X.; Wang, J.-C.; Zhang, L.X. Permafrost Physics; Science Press: Beijing, China, 2001; Volume 351. [Google Scholar]
- Zhang, Y.; Ohata, T.; Kadota, T. Land-Surface Hydrological Processes in the Permafrost Region of the Eastern Tibetan Plateau. J. Hydrol. 2003, 283, 41–56. [Google Scholar] [CrossRef]
- Yao, T.; Xue, Y.; Chen, D.; Chen, F.; Thompson, L.; Cui, P.; Koike, T.; Lau, W.K.-M.; Lettenmaier, D.; Mosbrugger, V. Recent Third Pole’s Rapid Warming Accompanies Cryospheric Melt and Water Cycle Intensification and Interactions between Monsoon and Environment: Multidisciplinary Approach with Observations, Modeling, and Analysis. Bull. Am. Meteorol. Soc. 2019, 100, 423–444. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Chen, D.; Piao, S. Reflections and Future Strategies for Third Pole Environment. Nat. Rev. Earth Environ. 2022, 3, 608–610. [Google Scholar] [CrossRef]
- Ma, Y.; Yao, T.; Zhong, L.; Wang, B.; Xu, X.; Hu, Z.; Ma, W.; Sun, F.; Han, C.; Li, M. Comprehensive Study of Energy and Water Exchange over the Tibetan Plateau: A Review and Perspective: From GAME/Tibet and CAMP/Tibet to TORP, TPEORP, and TPEITORP. Earth-Sci. Rev. 2023, 237, 104312. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, X.; Wu, T.; Zhao, L.; Li, R.; Li, W.; Hu, G.; Zou, D.; Ni, J.; Du, Y. Soil Texture and Its Relationship with Environmental Factors on the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 3797. [Google Scholar] [CrossRef]







| Soil Species Quantity | Data Volume | λMean (W m−1 K−1) | Data Sources |
|---|---|---|---|
| 16 | 80 | 1.42 | [60] |
| 1 | 8 | 1.17 | [61] |
| 3 | 25 | 0.87 | [62] |
| 19 | 132 | 0.92 | [37] |
| 2 | 12 | 0.68 | [63] |
| 5 | 76 | 0.57 | [64] |
| 6 | 48 | 1.91 | [65] |
| 40 | 240 | 0.94 | [66] |
| 8 | 48 | 1.29 | [67] |
| 6 | 86 | 0.87 | [68] |
| 32 | 262 | 0.56 | [57] |
| 1 | 6 | 0.89 | [69] |
| 2 | 18 | 0.55 | [70] |
| 7 | 33 | 0.74 | [71,72] |
| 1 | 56 | 1.58 | [73] |
| 2 | 23 | 1.19 | [74] |
| 9 | 131 | 0.59 | [75] |
| 9 | 105 | 0.46 | [76] |
| 6 | 100 | 1.34 | [77] |
| 2 | 21 | 0.71 | [78] |
| 8 | 73 | 0.68 | [79] |
| 1 | 8 | 1.42 | [61] |
| 10 | 10 | 2.12 | [40] |
| 22 | 214 | 0.26 | [80] |
| 1 | 21 | 1.66 | [81] |
| 3 | 30 | 1.02 | [82] |
| 2 | 40 | 0.95 | [49] |
| 12 | 73 | 0.56 | [83] |
| 1 | 27 | 1.99 | [84] |
| 5 | 623 | 0.82 | [85] |
| 1 | 9 | 1.36 | [86] |
| 4 | 72 | 1.57 | [87] |
| 5 | 6 | 0.73 | [88] |
| 18 | 256 | 1.09 | [89] |
| 270 | 2972 | - | [35] |
| Parameter | Mean | Standard Deviation | Min | Max |
|---|---|---|---|---|
| Clay% | 0.122 | 0.202 | 0.000 | 1.000 |
| Silt% | 0.285 | 0.256 | 0.000 | 0.900 |
| Sand% | 0.545 | 0.330 | 0.000 | 1.000 |
| λs | 3.716 | 1.540 | 1.117 | 8.030 |
| Qtz | 0.400 | 0.269 | 0.000 | 1.000 |
| ρs | 2.666 | 0.060 | 2.140 | 2.890 |
| ρb | 1.381 | 0.302 | 0.207 | 2.266 |
| n | 0.483 | 0.115 | 0.151 | 0.923 |
| θw | 0.172 | 0.159 | 0.000 | 0.846 |
| Sr | 0.330 | 0.298 | 0.000 | 1.000 |
| λ | 0.875 | 0.664 | 0.045 | 3.370 |
| Data Type | Product Name | Precision | Years | Sources |
|---|---|---|---|---|
| Soil moisture | Daily 0.01° × 0.01° Land Surface Soil Moisture Dataset of the Qinghai–Tibet Plateau (2005, 2010, 2015, 2017 and 2018) | 0.01° × 0.01° | 2005, 2010, 2015, 2018 | [92] |
| Soil texture | Dataset of digital soil mapping products for the Qinghai–Tibet Plateau (2015–2024) | 250 m 1 km | 2015–2024 | [93] |
| Permafrost extent | A new map of permafrost distribution on the Tibetan Plateau (2017) | 1 km | 2017 | [90] |
| Vegetation map | A new vegetation map for Qinghai–Tibet Plateau by integrated classification from multi-source data products (2020) | 250 m | 2020 | [91] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Li, R.; Wu, T.; Shi, X.; Zhao, L.; Wu, X.; Hu, G.; Yao, J.; Wang, D.; Xiao, Y.; et al. Spatiotemporal Patterns and Regional Differences in Soil Thermal Conductivity on the Qinghai–Tibet Plateau. Remote Sens. 2023, 15, 1168. https://doi.org/10.3390/rs15041168
Liu W, Li R, Wu T, Shi X, Zhao L, Wu X, Hu G, Yao J, Wang D, Xiao Y, et al. Spatiotemporal Patterns and Regional Differences in Soil Thermal Conductivity on the Qinghai–Tibet Plateau. Remote Sensing. 2023; 15(4):1168. https://doi.org/10.3390/rs15041168
Chicago/Turabian StyleLiu, Wenhao, Ren Li, Tonghua Wu, Xiaoqian Shi, Lin Zhao, Xiaodong Wu, Guojie Hu, Jimin Yao, Dong Wang, Yao Xiao, and et al. 2023. "Spatiotemporal Patterns and Regional Differences in Soil Thermal Conductivity on the Qinghai–Tibet Plateau" Remote Sensing 15, no. 4: 1168. https://doi.org/10.3390/rs15041168
APA StyleLiu, W., Li, R., Wu, T., Shi, X., Zhao, L., Wu, X., Hu, G., Yao, J., Wang, D., Xiao, Y., Ma, J., Jiao, Y., Wang, S., Zou, D., Zhu, X., Chen, J., Shi, J., & Qiao, Y. (2023). Spatiotemporal Patterns and Regional Differences in Soil Thermal Conductivity on the Qinghai–Tibet Plateau. Remote Sensing, 15(4), 1168. https://doi.org/10.3390/rs15041168