A Novel Hyperspectral Image Classification Method Using Class-Weighted Domain Adaptation Network

Abstract

With the development of science and technology, hyperspectral image (HSI) classification has been studied in depth by researchers as one of the important means of human cognition in living environments and the exploration of surface information. Nevertheless, the shortage of labeled samples is a major difficulty in HSI classification. To address this issue, we propose a novel HSI classification method called class-weighted domain adaptation network (CWDAN). First, the convolutional domain adaption network (ConDAN) is designed to align the marginal distributions and second-order statistics, respectively, of both domains via multi-kernel maximum mean discrepancy (MK-MMD) and CORAL loss. Then, the class-weighted MMD (CWMMD) is defined to simultaneously consider the conditional distribution discrepancy and changes of class prior distributions, and the CWMMD-based domain adaptation term is incorporated into the classical broad learning system (BLS) to construct the weighted conditional broad network (WCBN). The WCBN is applied to reduce the conditional distribution discrepancy and class weight bias across domains, while performing breadth expansion on domain-invariant features to further enhance representation ability. In comparison with several existing mainstream methods, CWDAN has excellent classification performance on eight real HSI data pairs when only using labeled source domain samples.

1. Introduction

Hyperspectral images (HSIs) can give comprehensive spectral and geographical information, which are commonly employed in astronomy, the military, and agriculture [1,2,3,4,5]. HSI classification is the critical and common technique in these applications. It is designed to use the spectral and spatial information of HSIs to identify surface objects on earth [6,7]. Luo et al. [8] realized the complementation of different features by taking into account the neighborhood, tangential, and statistical distribution of each sample under different features. In addition, an embedded objective function was constructed to effectively complete feature reduction and HSI classification. Classical machine learning [9,10,11] is used for HSI classification. The impressive classification performance of supervised learning methods generally requires the support of abundant labeled samples [12]. However, it is difficult for researchers to obtain accurate HSI labels [13]. Thus, how to accurately classify HSIs using a few labels is a hot topic in remote sensing [14]. Active learning and semi-supervised learning provide a viable solution. Active learning can actively select samples with the largest amount of information from unlabeled samples, and manually label them to increase the amount of training samples [15]. Semi-supervised learning can complete HSI classification with limited labeled samples and a large amount of unlabeled samples [16]. Luo et al. [17] proposed a novel sparse adaptive hypergraph discriminant analysis method, which reveals the structure relationship of HSIs using sparse representation to obtain the discriminative embedded features of HSIs. Zhang et al. [18] proposed a semisupervised classification method based on simple linear iterative cluster segmentation, which effectively explored the spectral features of HSIs and achieved good classification accuracy.

The above techniques can deal with the issue of insufficient training samples due to labeling difficulty to some extent. However, when the distributions of training and testing sample sets are quite different, it is difficult to achieve satisfactory results with the above methods. Domain adaptation (DA) transfers knowledge from a labeled domain (source domain) to a comparable but not identical domain (target domain) by exploring domain-invariant features [19,20]. When the target domain labels are missing or insufficient, DA can exploit similar labeled samples in the source domain to solve the problem of the target domain [21]. According to whether there is a discrepancy between two domains, DA methods can be mainly summarized to fall into two categories: homogeneous and heterogeneous. For the homogeneous DA methods, the feature spaces of both domains are consistent. Kumar et al. [22] developed a theory for gradual domain adaptation and reliably adapted the different distributions between domains with the gradual shift structure. Unlike with homogeneous DA, the main difficulty with heterogeneous DA is that the source and target domain data are located in different feature spaces. To address multi-source heterogeneous unsupervised DA problems, Liu et al. [23] presented a shared-fuzzy-equivalence-relation neural network containing multiple source branches and one target branch.

According to the type of learning model, DA methods can be classified as shallow-learning-based or deep-learning-based. At present, there are a large number of domain adaptation methods based on shallow learning. Since the shallow-learning model cannot fit the data distribution well, it will lead to under-fitting and under-matching problems. The deep neural network has a powerful non-linear representation capability, and thus can extract discriminative and compact features of the input [24,25]. Given the above advantages, DA methods based on deep neural networks have been extensively studied by researchers [26]. Long et al. [27] proposed a deep adaptation network (DAN) to reduce the marginal distribution discrepancy between domains by embedding multiple-kernel maximum mean discrepancy (MK-MMD) into CNNs, which generalized CNNs to the domain adaptation scenario. MMD is one of the most commonly used nonparametric methods to measure the distribution discrepancy across domains. For MMD, kernel selection is very important for ensuring effectiveness. In view of this, Liu et al. [28] proposed a class of non-parametric two-sample tests for learning deep kernels. To detect the discrepancy between natural and adversarial data, Gao et al. [29] further designed a simple and effective semantic-aware MMD based on the two-sample tests. Ganin and Lempitsky [30] applied the adversarial idea to domain adaptation and proposed a domain-adversarial neural network (DANN). Ma et al. [31] proposed a deep domain adaptation network containing three modules: domain alignment module, task allocation module, and domain adaptation module, which successfully achieved the cross-domain classification of HSIs. Wang et al. [32] added a weighted maximum mean-discrepancy-based term and a manifold regularization term into the objective function of the deep neural network, simultaneously achieving domain adaptation. Deng et al. [33] introduced metric learning into a deep embedding network, and achieved same-scene and different-scene HSI classifications.

Recently, the novel broad learning system (BLS) [34] was proposed, which can be viewed as an alternative way of learning in a deep structure. The structure of BLS mainly consists of three parts: the mapped feature (MF) layer for feature mapping of input data, the enhancement node (EN) layer for breadth expansion of the mapping features, and the output layer for solving the weight through ridge regression. Compared with deep learning networks, BLS has the following advantages [35,36]: (1) The structure of the BLS is simple and flexible, and it is easy to integrate with other models; (2) because of EN, BLS is able to achieve feature breadth expansion to enhance the capability of feature representation. Wang et al. [37] fused graph convolution operation and BLS as a unified framework, fully utilizing the flexibility and feature breadth expansion ability of BLS to achieve efficient HSI classification. Guo et al. [38] made full use of the fast training-speed of BLS to pre-train multiple groups of classification models, and then built a dynamic integration structure with multiple classifier groups to determine the class of vehicles. Kong et al. [39] extended the multi-level depth feature using BLS to obtain multi-level features, and introduced block diagonal constraints to enhance the independence between multi-level features. The above model has achieved good results in HSI classification. Feng and Chen [40] achieved good performance in regression and classification tasks by organically combining a Takagi–Sugeno fuzzy system with BLS.

Due to the high label cost of HSIs, HSIs (target domain) are often lacking or even without labels in actual scenes. In order to classify the HSIs of the target domain in this scenario, transfer learning can use the source domain with rich labels to help the target domain complete the classification task. However, due to the differences in equipment, environment and spatial area during the acquisition of different HSIs, there are often large differences in the distribution of the two domains, which causes susceptibility to the phenomenon of difficult knowledge transfer between the two domains. The above problems are difficult to solve with common transfer-learning-based methods because they have the following limitations:

(1)

Common transfer learning methods often only consider aligning the two domain distributions by minimizing the difference between the first or second order statistics of the two domains, with which it is difficult to achieve comprehensive adaptation to the two domain distributions;

(2)

Common transfer learning methods often ignore the difference in conditional distribution between the two domains, which easily leads to confusion of the two domains’ discriminant features, and hinders the improvement of the model’s classification performance;

(3)

Due to the difference between the two HSIs in spatial areas during acquisition, the distribution of their class prior may not be consistent. This phenomenon may lead to insufficient alignment of class distribution. When the two-domain classes are unbalanced, this phenomenon often causes serious performance damage to the model.

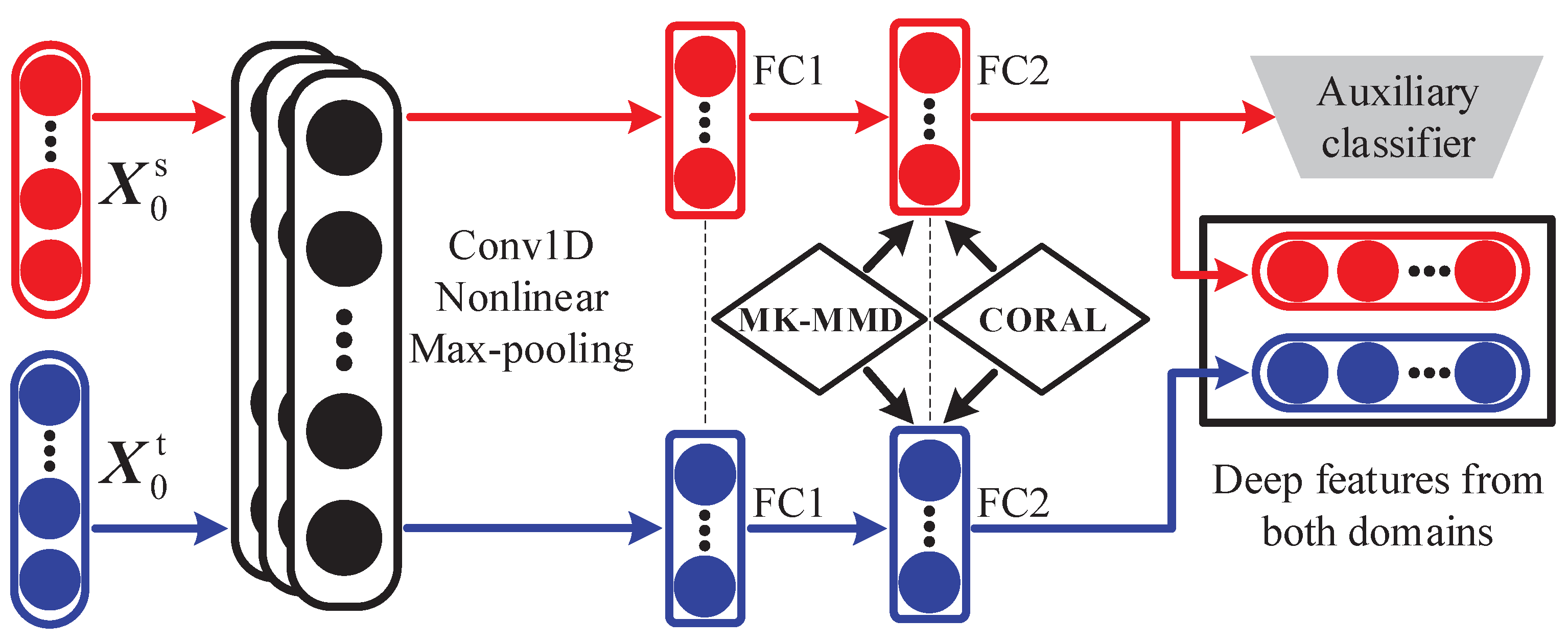
To solve the above problems, we propose CWDAN, which considers the marginal distribution, conditional distribution and class prior distribution of the two domains. Specifically, when aligning the marginal distribution of the two domains, the difference between the first-order statistics and the second-order statistics is minimized through the MMD and CORAL, so as to achieve full alignment of the marginal distribution of the two domains. Then, BLS is used to expand the width of the domain-adaptation features extracted by the ConDAN to further enhance the feature representation ability. In addition, the CWMMD-based domain adaptation term is added to BLS, which reduces the difference between the conditional distributions and class weight bias, so that the model pays more attention to the classes that occupy a higher proportion in the target domain, and thus improves its classification performance in the target domain. The main novel aspects of our work are summarized below:

(1)

We propose a convolutional domain adaptation network (ConDAN); by simultaneously reducing the two-domain difference between the first- and second-order statistics, sufficient and fast marginal distribution alignment was achieved;

(2)

We defined a novel class-weighted maximum mean discrepancy (CWMMD) and further imposed the CWMMD-based domain adaptation term in classical BLS. The weight of each class in the domain adaptation is adjusted based on the class prior distribution, and the training is focused on the important classes in the target domain, which solves the problem of class being unbalanced during conditional distribution alignment;

(3)

Deep learning and broad learning are embedded in a unified framework, and the strong feature extraction ability of deep learning as well as the feature breadth expansion ability of broad learning are fully utilized to achieve the extraction and enhancement of domain-invariant features.

The rest of this paper is organized as follows. The flowchart of CWDAN for HSI classification is presented in Section 2. The experimental results on eight real HSI data pairs are presented and analyzed, followed by a conclusion in Section 4.

2. Classification of HSIs Based on CWDAN

2.1. Network Overview

ConDAN consists of a band selection module, a feature extractor and an auxiliary classifier. The band selection module reduces the two-domain dimensions by selecting spectral bands to reduce the redundancy. The feature extractor is composed of a conv1d, nonlinear layer, and a pooling layer, which is used to extract features from two domains. The auxiliary classifier consists of FCs and Softmax layers, which can obtain the target domain pseudo labels.

WCBN consists of an MF layer, an EN layer and a classifier. The MF layer based on CWMMD can simultaneously reduce the conditional distribution discrepancy and class weight bias. The EN layer is used for feature breadth expansion. The classifier can obtain predicted results.

2.2. Flowchart of CWDAN for HSI Classification

The structure diagram of the proposed CWDAN consisting of five stages is shown in Figure 1.

(1)

Use band selection to reduce the dimensions and eliminate redundant features of the original HSIs and unify the HSIs of two domains into the same dimension;

(2)

Input the preprocessed HSIs of the source and target domains into ConDAN for model training, and extract the deep features of HSIs with the trained ConDAN, which servers as the auxiliary classifier by minimizing the difference between the first- and second-order statistics of the two domains through marginal and covariance adaptation terms;

(3)

First, exploit the auxiliary classifier trained on the source domain to obtain the target domain pseudo labels, and based on that, calculate the class importance parameter. Then, input the deep features extracted by ConDAN to WCBN, and weighted-align the conditional distributions between two domains based on CWMMD. Thus, the domain-invariant features of the source and target HSIs, i.e., source MFs and target MFs, can be extracted;

(4)

Map source and target MFs to ENs with randomly generated weights for feature breadth expansion, which is helpful for further enhancing the representation ability of the features;

(5)

Calculate the output layer weights with ridge region theory, and then calculate the class probability vector of the input samples and obtain the predicted results.

2.3. Band-Selection-Based HSI Dimensionality Reduction

HSIs contains a great deal of bands and there is usually a high correlation between bands, which may result in the problem known as the curse of dimensionality [41]. Therefore, it is necessary to investigate effective dimensionality reduction (DR) methods before HSI classification. The commonly used DR methods include band selection and band extraction, and the former directly selects some bands from the original band space based on certain searching strategies. Motivated by [42], a simple band selection method is implemented to reduce the dimension of HSIs. Denoting the number of bands in original HSIs, $N_{\mathrm{b}}$, d is the dimension after band selection. $⌊N_{\mathrm{b}}/\phantom{N_{\mathrm{b}}d}d⌋$ and $⌊N_{\mathrm{b}}/\phantom{N_{\mathrm{b}}d}d⌋+1$ as intervals are exploited to select bands, where $⌊.⌋$ represents the floor operation. Then we have:

$$\left\{\begin{array}{c}c+b=d\hfill \\ ⌊N_{\mathrm{b}}/d⌋\ast c+\left(⌊N_{\mathrm{b}}/d⌋+1\right)\ast b=N_{\mathrm{b}}\hfill \end{array}\right.$$

(1)

where c and b are the numbers of the selected bands. ${\mathit{X}}_0\in {\mathbb{R}}^{n\times d}$ denotes the samples after dimension reduction, ${\mathit{X}}_0^{\mathrm{s}}$ = $\left\{{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_{n_{\mathrm{s}}}\right\}\in {\mathbb{R}}^{n_{\mathrm{s}}\times d}$ and ${\mathit{X}}_0^{\mathrm{t}}=\left\{{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_{n_{\mathrm{t}}}\right\}\in {\mathbb{R}}^{n_{\mathrm{t}}\times d}$ represent samples from the source and target domains, respectively, and ${\mathit{Y}}_{\mathrm{s}}$ represents the sample labels of the source domain.

2.4. Deep Feature Extracting Based on ConDAN

Although deep neural networks are more powerful for extracting deep and discriminative features of original HSIs, the higher task-specific layers of CNNs can barely learn the transferable knowledge if the distribution of training data and testing data are different [27]. Dataset shift has functioned as a bottleneck for the transferability of deep neural networks, resulting in statistically unbounded risk for the target task [43,44]. In view of this, we propose the ConDAN by adding a domain adaptation layer in the CNN.

The ConDAN is composed of a convolution layer, nonlinear layer, pooling layer, fully connected layer, domain adaptation layer and Softmax layer, as shown in Figure 2.

The domain adaptation layer is added to reduce the distribution discrepancy between two domains, and the output of the domain adaptation layer is connected to the Softmax layer. The loss function of ConDAN can be expressed as:

$$\begin{array}{cc}\hfill L\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}},{\mathit{Y}}_{\mathrm{s}};\mathsf{\theta }\right)=& {\alpha }_1{L}_{\mathrm{MMD}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}};\mathsf{\theta }\right)\hfill \\ & +{\alpha }_2{L}_{\mathrm{CORAL}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}};\mathsf{\theta }\right)\hfill \\ & +L_{\mathrm{src}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{Y}}_{\mathrm{s}};\mathsf{\theta }\right)\hfill \end{array}$$

(2)

where $L_{\mathrm{MMD}}({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}};\mathsf{\theta })$ and $L_{\mathrm{CORAL}}({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}};\mathsf{\theta })$ are the marginal and covariance adaptation terms, which are used to align the marginal distribution of the two domains. ${\alpha }_1$ and ${\alpha }_2$ are the marginal and covariance adaptation parameters, which are used to adjust the importance of first-order statistic difference and second- order statistic difference, respectively. $L_{\mathrm{src}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{Y}}_{\mathrm{s}};\mathsf{\theta }\right)$ is the classification loss on the labeled source domain.

The marginal adaptation term is:

$$\begin{array}{c}\hfill L_{\mathrm{MMD}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}};\mathsf{\theta }\right)={∥\frac{{\sum }_{i=1}^{n_{\mathrm{s}}}\vartheta \left({\mathit{X}}_i^{\mathrm{s}}\right)}{n_{\mathrm{s}}}-\frac{{\sum }_{j=1}^{n_{\mathrm{t}}}\vartheta \left({\mathit{X}}_j^{\mathrm{t}}\right)}{n_{\mathrm{t}}}∥}_{\mathcal{H}}^2\end{array}$$

(3)

The covariance adaptation term is defined as:

$$L_{\mathrm{CORAL}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{X}}_0^{\mathrm{t}};\mathsf{\theta }\right)=\frac{1}{4d_1}∥{\mathit{C}}_{\mathrm{s}}-{\mathit{C}}_{\mathrm{t}}∥$$

(4)

where $d_1$ is the input dimension of the domain adaptation layer, ${\mathit{C}}_{\mathrm{s}}$ and ${\mathit{C}}_{\mathrm{t}}$ are the covariance matrices of the source and target domains.

The classification loss on the labeled source data can be expressed as:

$$L_{\mathrm{src}}\left({\mathit{X}}_0^{\mathrm{s}},{\mathit{Y}}_{\mathrm{s}};\mathsf{\theta }\right)=-\sum _{k\in {\mathit{Y}}_{\mathrm{s}}}\sum _{c=1}^C{\mathit{Y}}_{kc}^{\mathrm{s}}ln{\mathit{S}}_{kc}^{\mathrm{s}}$$

(5)

where C is the number of classes, $\mathit{Y}$ is the class matrix, and $\mathit{S}$ is the prediction result of ConDAN.

2.5. Class-Weighted Domain Adaptation and Breadth Expansion Based on WCBN

ConDAN only adapts the marginal distributions of both domains, but ignores the difference of conditional distribution between the two domains, which will lead to confusion of the discriminative features. However, most of the existing methods for aligning the conditional distribution do not take into account the changes of class prior distributions, i.e., class weight bias across domains. The above problem easily leads to confusion of the two-domain discriminative features, and hinders the improvement of the model’s classification performance.

To address this concern, the CWMMD is proposed, and the domain adaptation term based on CWMMD is added to the MF during feature mapping, and then the WCBN is obtained. On the one hand, WCBN helps the model to achieve more fine-grained domain-invariant feature extraction by aligning the conditional distribution of the two domains. On the other hand, the changes of class prior distributions are considered. CWMMD is used to weight-adapt the conditional distribution according to the class importance of the target domain, so that the model pays more attention to the class with a high proportion of the target domain, so as to obtain the domain-invariant features more applicable to the target domain.

The workflow of WCBN can be described as follows: Map the deep features $\mathit{X}=\left[{\mathit{X}}_{\mathrm{s}};{\mathit{X}}_{\mathrm{t}}\right]\in {\mathbb{R}}^{n\times d_2}$ extracted by ConDAN with $\mathit{A}$ to MF, and the i-th group MF is:

$${\mathit{Z}}_i=\mathit{X}\mathit{A}+{\beta }_{ei},i=1,\dots ,d^{\mathrm{M}}$$

(6)

where ${\mathit{Z}}_i\in {\mathbb{R}}^{\left(n_{\mathrm{s}}+n_{\mathrm{t}}\right)\times G^{\mathrm{M}}}$, $\mathit{A}$ and ${\beta }_{ei}$ are the connecting weight and bias from $\mathit{X}$ to MF, $d^{\mathrm{M}}$ is the number of nodes in MF, $G^{\mathrm{M}}$ is the feature dimension of each group. Similar to SAE, the optimization equation is:

$$\underset{{\mathit{A}}_i}{argmin}{∥\mathit{X}{\mathit{A}}_i-{\mathit{Z}}_i∥}_2^2+\lambda {∥{\mathit{A}}_i∥}_1$$

(7)

where $\lambda$ denotes the regularization parameter. To simultaneously consider the conditional distribution divergences and the changes of class prior distributions, the domain adaptation term $D_{cf}\left(P_{\mathrm{s}},P_{\mathrm{t}}\right)$ based on CWMMD is used to constrain the stacked autoencoder (SAE) which is exploited to fine-tune the weights mapped from input data to MF in the original BLS, obtaining the weighted conditional distribution SAE (WCDSAE):

$$\underset{{\mathit{A}}_i}{argmin}{∥\mathit{X}{\mathit{A}}_i-{\mathit{Z}}_i∥}_2^2+\lambda {∥{\mathit{A}}_i∥}_1+\gamma D_{cf}\left(P_{\mathrm{s}},P_{\mathrm{t}}\right)$$

(8)

where $\gamma$ is the domain adaptation parameter, $c\in \left\{1,2,\dots ,C\right\}$ is the class index, and $D_{cf}\left(P_{\mathrm{s}},P_{\mathrm{t}}\right)$ can be expressed as:

$$\begin{array}{cc}\hfill D_{cf}\left(P_{\mathrm{s}},P_{\mathrm{t}}\right)& =\sum _{c=1}^C{\omega }_c{∥\mathrm{E}\left[f\left({\mathit{z}}_{\mathrm{s}}^{\left(c\right)}\right)\right]-\mathrm{E}\left[f\left({\mathit{z}}_{\mathrm{t}}^{\left(c\right)}\right)\right]∥}_{\mathrm{H}}^2\hfill \\ & =tr\left({\mathit{A}}^{\mathrm{T}}{\mathit{X}}^{\mathrm{T}}\mathit{M}\mathit{X}\mathit{A}\right)\hfill \end{array}$$

(9)

where ${\omega }_{\mathit{c}}=\sqrt{\frac{n_c^{\mathrm{t}}/\phantom{{n^{\mathrm{t}}}_c{n}_{\mathrm{t}}}{n}_{\mathrm{t}}}{n_c^{\mathrm{s}}/\phantom{{n^{\mathrm{s}}}_c{n}_{\mathrm{s}}}{n}_{\mathrm{s}}}}$ is the class importance weight. When c has a high proportion in the target domain and a low proportion in the source domain, the class will get a larger ${\omega }_c$. In this way, the model will pay more attention to the classes that occupy a high proportion in the target domain, and thus improves its classification performance in the target domain, $\mathit{M}={\displaystyle \sum _{c=1}^C}{\omega }_{\mathit{c}}{\mathit{M}}_c$, ${\mathit{M}}_c$ can be written as:

$${\left({\mathit{M}}_c\right)}_{ij}=\left\{\begin{array}{cc}\frac{1}{{\left(n_c^{\mathrm{s}}\right)}^2},\hfill & {\mathit{x}}_i,{\mathit{x}}_j\in D_{\mathrm{s}}^{\left(c\right)}\\ \frac{1}{{\left(n_c^{\mathrm{t}}\right)}^2},\hfill & {\mathit{x}}_i,{\mathit{x}}_j\in D_{\mathrm{t}}^{\left(c\right)}\\ -\frac{1}{\left(n_c^{\mathrm{s}}\right)\left(n_c^{\mathrm{t}}\right)},\hfill & \left\{\begin{array}{c}{\mathit{x}}_i\in D_{\mathrm{s}}^{\left(c\right)},{\mathit{x}}_j\in D_{\mathrm{t}}^{\left(c\right)}\hfill \\ {\mathit{x}}_i\in D_{\mathrm{t}}^{\left(c\right)},{\mathit{x}}_j\in D_{\mathrm{s}}^{\left(c\right)}\hfill \end{array}\right.\\ 0,\hfill & \mathrm{otherwise}\end{array}\right.$$

(10)

Thus, Equation (7) can be expressed as:

$$\underset{{\mathit{A}}_i}{argmin}{∥\mathit{X}{\mathit{A}}_i-{\mathit{Z}}_i∥}_2^2+\lambda {∥{\mathit{A}}_i∥}_1+\gamma tr\left({\mathit{A}}_i^{\mathrm{T}}{\mathit{X}}^{\mathrm{T}}\mathit{M}\mathit{X}{\mathit{A}}_i\right)$$

(11)

According to the alternating direction method of multipliers, Equation (11) can be solved to get ${\mathit{A}}_i$. ${\mathit{Z}}_i$ can be calculated by:

$${\mathit{Z}}_i=\mathit{X}{\mathit{A}}_i$$

(12)

For clarity, we denote the mapped features from the source and target domains as ${\mathit{Z}}_i^{\mathrm{s}}={\mathit{X}}_{\mathrm{s}}{\mathit{A}}_i$ and ${\mathit{Z}}_i^{\mathrm{t}}={\mathit{X}}_{\mathrm{t}}{\mathit{A}}_i$, respectively. Afterwards, we use randomly generated weight ${\mathit{W}}^{\mathrm{E}}$ to map $\mathit{Z}$ to EN for breadth expansion:

$$\mathit{H}=\sigma \left(\mathit{Z}{\mathit{W}}^{\mathrm{E}}\right)$$

(13)

where $\mathit{Z}=\left[{\mathit{Z}}_1,{\mathit{Z}}_2,\dots ,{\mathit{Z}}_{d^{\mathrm{M}}}\right]$, $\sigma \left(·\right)$ is the TanSig function here, $\mathit{H}\in {\mathbb{R}}^{\left(n_{\mathrm{s}}+n_{\mathrm{t}}\right)\times d^{\mathrm{E}}}$ are features of EN, and $d^{\mathrm{E}}$ is the number of nodes in EN. Both MF and EN are connected to the output layer, and the objective function of WCBN can be expressed as:

$$\underset{\mathit{W}}{argmin}{∥{\mathit{Q}}_{\mathrm{s}}\mathit{W}-{\mathit{Y}}_{\mathrm{s}}∥}_2^2+\delta {\parallel \mathit{W}\parallel }_2^2$$

(14)

where ${\mathit{Q}}_{\mathrm{s}}=\left[{\mathit{Z}}_{\mathrm{s}}|{\mathit{H}}_{\mathrm{s}}\right]$, $\delta$ is the regularization parameter. Calculate Equation (14) with ridge regression theory to get:

$$\mathit{W}=\frac{{\mathit{Q}}_{\mathrm{s}}^{\mathrm{T}}{\mathit{Y}}_{\mathrm{s}}}{\delta \mathit{I}+{\mathit{Q}}_{\mathrm{s}}^{\mathrm{T}}{\mathit{Q}}_{\mathrm{s}}}$$

(15)

The predicted result can be calculated as:

$${\mathit{Y}}_{\mathrm{t}}={\mathit{Q}}_{\mathrm{t}}\mathit{W}$$

(16)

where ${\mathit{Q}}_{\mathrm{t}}=\left[{\mathit{Z}}_{\mathrm{t}}|{\mathit{H}}_{\mathrm{t}}\right]$.

3. Experiments and Analysis

3.1. HSI Datasets

Two real HSI datasets including BOT and KSC were used for experiments. The sample size of per-class surface object is described in

Table 1. Class names and number of samples of BOT and KSC data.

BOT					KSC
Class	Surface Object	BOT5	BOT6	BOT7	Class	Surface Object	KSC1	KSC3
1	Exposed soils	215	229	615	1	Water	927	1392
2	Firescar	354	335	433	2	Scrub	761	422
3	Island interior	337	370	664	3	Slash pine	161	166
4	Riparian	448	303	438	4	Harwood swamp	105	248
5	Savanna	330	342	710	5	Willow swamp	243	180
6	Short mopane	239	299	330	6	Graminoid marsh	432	453
7	Primary floodplain	437	308	584	7	Salt marsh	419	156
8	Woodlands	357	324	633	8	Oak/broadleaf hammock	229	274
9	Water	297	361	590	9	CP/oak hammock	252	132
					10	CP hammock	256	431
	Total	3014	2871	4997		Total	3784	3854

. There are three groups of hyperspectral data (BOT5, BOT6, and BOT7) in the BOT dataset in total, which were collected in May, June, and July, respectively over the Okavango Delta, Botswana. Any two of the three BOT data groups can be selected as the source and target domains, and thus six data pairs can be used for experiments. We selected two groups of hyperspectral data (KSC1 and KSC3) from the KSC dataset for experiment; each dataset is treated as the source domain and target domain, respectively, for the experiment.

3.2. Experimental Setting

The following methods are used for comparison, including non-transfer learning methods, shallow-learning-based DA methods and deep-learning-based DA methods:

(1)

Non-transfer learning method: BLS [34];

(2)

Shallow-learning-based DA methods: TCA [21], JDA [45], and DABL [46];

(3)

Deep-learning-based DA methods: DANN [30], DAN [27], DCORAL [47], CDAN [48], DDA-Net [31], DDME [32], and SG-CNN [42].

The experimental settings are as follows: the configuration of ConDAN is shown in

Table 2. Configuration of ConDAN.

BOT		KSC
C1	Covn1D: size = 5 × 64	C1	Covn1D: size = 5 × 64
P1	Pooling: size = 2	P1	Pooling: size = 2
N1	Tanh	N1	Tanh
C2	Conv1D: size = 5 × 64	C2	Covn1D: size = 5 × 64
N2	Tanh	N2	Tanh
C3	Covn1D: size = 3 × 64	C3	Covn1D: size = 3 × 64
P2	Pooling: size = 2	N3	Tanh
FC1	size = 64	C4	Covn1D: size = 3 × 64
FC2	size = 9	N4	Tanh
		FC1	size = 32
		FC2	size = 10

. In CWDAN, ${\alpha }_1$ = 1, ${\alpha }_2$ = 0.6, $\gamma$ = 0.5, $\lambda$ = 0.01, $G^{\mathrm{M}}$ = 25, $d^{\mathrm{M}}$ = 55, and $d^{\mathrm{E}}$ = 700; a total of 8 data pairs were used for experiments: BOT5–6, BOT6–5, BOT5–7, BOT7–5, BOT6–7, BOT7–6, KSC1–3, and KSC3–1. The former in each set of data pairs represent the source domain, and the latter represent the target domain.

3.3. Comparative Experiments

OA is the abbreviation for overall accuracy. The overall classification accuracy is obtained by dividing the number of correctly classified samples by the total number of samples. The comparison of OA achieved by different classification methods on eight data pairs is reported in

Table 3. Comparison of classification performance (OA, %).

Data Pairs		BLS [34]	TCA [21]	JDA [45]	DANN [30]	DAN [27]	DCORAL [47]	CDAN [48]
BOT	5–6	73.18	80.29	82.51	87.81	88.37	88.33	90.18
	6–5	62.74	67.85	67.88	85.47	85.77	87.13	89.12
	5–7	57.89	61.98	66.16	75.35	75.97	75.17	76.19
	7–5	64.70	66.09	66.17	76.68	76.61	79.06	80.57
	6–7	67.30	70.68	71.00	79.19	80.37	80.53	82.45
	7–6	74.57	75.62	78.06	86.45	85.89	87.84	89.31
KSC	1–3	63.08	64.58	65.75	72.21	71.20	71.67	73.72
	3–1	59.21	67.12	68.18	69.48	69.05	71.06	71.54
Data Pairs		DDA-Net [31]	DDME [32]	DABL [46]	SG-CNN [42]	ConDAN	CWDAN
BOT	5–6	90.84	89.10	86.66	90.67	90.80	92.09
	6–5	88.96	87.92	85.17	88.65	88.89	90.34
	5–7	76.41	75.47	70.28	76.36	77.93	78.62
	7–5	82.16	77.25	79.13	81.57	81.98	83.30
	6–7	82.89	80.81	81.25	82.09	83.09	83.85
	7–6	89.79	86.45	88.16	88.37	88.38	90.90
KSC	1–3	73.79	71.41	72.01	72.74	72.78	75.16
	3–1	72.16	70.65	70.51	72.17	72.49	73.86

.

Table 4. Comparison of classification performance (BOT5-6).

Surface Object	BLS [34]	TCA [21]	JDA [45]	DANN [30]	DAN [27]	DCORAL [47]	CDAN [48]
Exposed soils	12.22	83.41	79.48	79.48	85.59	82.10	82.97
Firescar	99.10	99.40	99.70	99.70	99.70	99.70	99.40
Island interior	88.11	74.05	83.24	92.43	91.89	94.32	96.49
Riparian	65.02	61.72	63.37	78.22	83.50	80.20	75.25
Savanna	78.07	86.26	89.18	91.52	83.33	91.81	95.03
Short mopane	55.18	93.65	96.99	96.32	98.33	94.65	99.00
Primary floodplain	86.36	88.31	87.99	93.83	98.38	99.35	98.38
Woodlands	50.93	34.57	38.89	54.01	52.78	49.07	60.49
Water	98.34	100	100	100	100	100	100
Surface Object	DDA-Net [31]	DDME [32]	DABL [46]	SG-CNN [42]	ConDAN	CWDAN
Exposed soils	93.89	81.22	66.38	99.13	97.82	97.38
Firescar	100	99.70	100	98.81	98.81	100
Island interior	97.84	95.68	95.68	93.51	98.11	99.46
Riparian	82.51	69.31	66.67	72.61	84.49	87.46
Savanna	94.74	94.74	94.15	89.77	94.44	97.66
Short mopane	97.66	99.33	95.65	94.98	96.32	99.67
Primary floodplain	98.05	97.73	92.21	99.68	99.03	99.03
Woodlands	50.62	58.95	59.26	67.91	48.15	47.84
Water	100	100	100	100	99.72	100

lists the classification accuracy of each surface object in the BOT5–6 and BOT7–6 data pairs respectively. The following observations can be made:

(1)

Since BOT5–7, BOT7–5, KSC1–3, and KSC3–1 have big spectral drift, OA achieved by all evaluation methods on these data pairs is low;

(2)

Because BLS belongs to the non-transferable method, it achieves the lowest OA on all BOT and KSC data pairs;

(3)

Among three shallow-learning-based DA methods, DABL achieves the highest OA while TCA has the lowest. The main reasons for the above experimental results can be summarized as: JDA additionally adapts the conditional distribution compared to TCA, and DABL performs the breadth expansion of features compared to JDA;

(4)

Compared with DAN and DCORAL, our ConDAN achieves higher OA because it comprehensively takes full advantage of DAN and DCORAL, i.e., it simultaneously aligns the marginal distributions and covariance matrices of the source and target domains;

(5)

Both DANN and CDAN are adversarial adaptation methods. The DANN only pays attention to aligning the feature distributions across domains, while CDAN tries to capture the cross-covariance between features and classifier predictions. Therefore, CDAN achieves higher OAs than DANN.

We used the BOT5–6, BOT6–5, and BOT7–6 data pairs for visualization illustration. The original features and the features extracted by CWDAN were visualized to obtain Figure 3. For example, the red hollow circle and red solid square denote the sample points of Class 1 in the source and target domains, respectively. From Figure 3a–c, it is easily observed that not only do some original features have large within-class variance, but also that different classes may have considerable overlapping features, which is not conducive to HSI classification. Compared with original HSI features, the features extracted by CWDAN have smaller within-class variance and larger inter-class variance, which makes it easy to distinguish different classes of surface objects.

To further verify the effect of CWDAN, Figure 4 visibly shows the alignment results of Classes 2–4, i.e., Firescar, Island interior, and Riparian in the BOT5–6 data pair, where the data from different domains are displayed in circles with different colors, and the bigger orange and green rhombi represent the means of classes from the source and target domains respectively. It can be observed from Figure 4a–c that the distribution discrepancy between domains is large, since BLS does not apply the domain adaptation strategy. As shown in Figure 4d–f, with the help of CWDAN, the features of all three classes are better aligned and the centroids of the same class from different domains become closer.

3.4. Ablation for Band Selection

To determine the number of selected bands, we conducted experiments on eight HSI data pairs, CWDAN-32 (d = 32), CWDAN (d = 64), CWDAN-128 (d = 128) and CWDAN-O (CWDAN without band selection), as shown in

Table 5. Classification performance (OA, %) with different numbers of bands.

Data Pair	BOT5–6	BOT6–5	BOT6–7	BOT7–6	BOT5–7	BOT7–5	KSC1–3	KSC3–1
CWDAN-32	90.03	87.26	76.12	81.26	80.34	88.36	73.27	70.72
CWDAN	92.09	90.34	78.62	83.30	83.85	90.90	75.16	73.86
CWDAN-128	91.15	89.14	77.35	82.27	81.87	89.36	74.02	71.05
CWDAN-O	90.85	88.83	76.93	81.86	81.35	88.91	73.65	70.81

.

It can be seen from Table 5 that:

(1)

CWDAN-32 has the lowest classification accuracy, because the number of bands selected is small at this time, which will lead to an excessive interval of band selection, causing serious loss of spectral information;

(2)

Compared with CWDAN-O, the classification accuracy of CWDAN-128 is improved, but optimal classification accuracy is not achieved. This is because higher band selection will result in excessively small intervals of band selection, which can only alleviate the phenomenon of information redundancy between bands to a certain extent, and can hinder the improvement of model classification accuracy;

(3)

The classification accuracy of CWDAN is the highest because at this time, the spectral information loss is small, and the spectral bands have low redundancy, so that the model can achieve effective feature extraction and complete the HSI classification task more accurately.

3.5. Ablation Study

To verify the impact of BS (band selection), MMD, CORAL, CDA (conditional distribution adaptation) and CWMMD on the CWDAN classification performance, we added ablation experiments, as shown in

Table 6. Ablation experiments.

Technique	CWDAN-A	CWDAN-B	CWDAN-C	CWDAN-D	CWDAN-E	CWDAN
BS		√	√	√	√	√
MMD			√	√	√	√
CORAL				√	√	√
CDA					√	√
CWMMD						√

and

Table 7. Impact of different techniques on OA (%).

Data Pairs		CWDAN-A	CWDAN-B	CWDAN-C	CWDAN-D	CWDAN-E	CWDAN
BOT	5–6	86.89	88.12	90.31	90.84	91.64	92.09
	6–5	85.71	87.26	88.84	89.25	89.52	90.34
	5–7	73.68	75.12	77.35	77.97	78.10	78.62
	7–5	77.85	79.35	81.68	82.23	82.88	83.30
	6–7	79.36	80.27	82.67	83.16	83.57	83.85
	7–6	83.28	85.34	88.73	89.52	90.16	90.90
KSC	1–3	69.12	70.61	72.86	73.34	74.10	75.16
	3–1	68.87	70.28	72.03	72.68	72.87	73.86

.

It can be observed from Table 6 and Table 7 that:

(1)

Compared with CWDAN-A, CWDAN-B shows higher classification accuracy, which is because band selection can effectively alleviate the problem of HSI band information redundancy and help the model achieve more identifiable feature extraction;

(2)

Compared with CWDAN-B, CWDAN-C achieved better classification performance. This is because reducing the difference between the first-order statistics of the two domains can effectively align the distribution, helping to achieve knowledge transfer between the two domains;

(3)

Compared with CWDAN-C, CWDAN-D has better classification performance, which indicates that reducing the difference between the first- and second-order statistics simultaneously can effectively align the marginal distribution of the two domains;

(4)

Compared with CWDAN-D, CWDAN-E has higher classification accuracy, which additionally adapts the conditional distribution, and helps the model extract more fine-grained domain-invariant features;

(5)

Compared with CWDAN-E, CWDAN achieved better classification performance. This is because CWMMD can alleviate the effect of class weight bias based on the changes of class prior distributions.

3.6. The Impact of Noise on CWDAN

Finally, we analyze the impact of noisy source domain labels on the OA of CWDAN. We took BOT5–6 as an example and randomly assigned 10%, 20%, 30%, 40%, and 50% labels of training samples as the wrong ones.

Table 8. Comparison of decline rate of OA (%) on BOT5–6.

Method	0% Noisy	10% Noisy		20% Noisy		30% Noisy		40% Noisy		50% Noisy
	OA	OA	Rate	OA	Rate	OA	Rate	OA	Rate	OA	Rate
CWDAN	92.09	91.92	0.18	91.26	0.90	89.79	2.50	88.02	4.42	82.24	10.70
CDAN [48]	90.18	88.47	1.90	86.73	3.83	85.34	5.37	84.01	6.84	78.65	12.79
DAN [27]	88.37	85.34	3.43	83.07	6.00	79.97	9.51	76.45	13.49	75.51	14.55

shows the comparison of the decline rate of OA (%) achieved by CWDAN, CDAN, and DAN, where “0%” noisy means that all labels of training samples are correct, i.e., clean labels. It can be observed that: (1) OA generally decreases as the number of noisy labels increases; (2) compared with CDAN and DAN, the decline rates of OA of CWDAN under different amounts of noisy labels are relatively small, indicating the robustness of CWDAN against noisy labels.

3.7. Computational Cost

In this section, we show the running time and number of network parameters for different methods in

Table 9. Running time and number of parameters for all the networks.

Dataset	Index	BLS	TCA	JDA	DANN	DAN	DCORAL
BOT	Time (s)	8.65	4.21	81.32	2327.21	3187.26	2213.83
	Parameters (M)	~	~	~	42.31	42.19	38.02
KSC	Time (s)	10.32	5.16	124.26	2216.34	3314.62	2361.32
	Parameters (M)	~	~	~	48.14	48.07	47.02
Dataset	Index	CDAN	DDA-Net	DDME	DAB	SG-CNN	CWDAN
BOT	Time (s)	2532.14	2678.35	2563.45	18.92	3215.25	2109.36
	Parameters (M)	46.48	93.30	38.02	~	74.75	39.40
KSC	Time (s)	2645.25	2958.21	2236.47	19.67	3421.83	2197.28
	Parameters (M)	46.75	52.13	47.02	~	71.39	48.39

.

It can be seen from Table 9 that:

(1)

Compared with shallow learning methods, such as BLS, TCA, DABL, and JDA, CWDAN has longer running time. This is because when aligning the marginal distribution, CWDAN needs to optimize the model parameters through back-propagation, which increases the running time;

(2)

CWDAN takes less time than deep-learning-based DA methods such as DANN, CDAN, DDA-Net, and SG-CNN. This is because CWDAN consists of ConDAN and WCBN, where ConDAN quickly aligns the marginal distribution from the first and second order statistics at the same time, while WCBN aligns the two-domain conditional distribution without updating the network parameters through back-propagation.

4. Discussion

The HSI dimension reduction method usually consists of two categories: feature-learning-based and band-selection-based. The feature-learning-based method maps the original data to a low-dimensional subspace for dimension reduction. Common techniques include maximum noise fraction [49] and principal component analysis [50]. The band-selection-based method selects bands with large amounts of information according to a certain standard. Common techniques include equal interval band selection [42] and progressive band selection [51]. However, the operation of image transformation with the feature-learning-based method makes the transformed data no longer have the original physical attributes, which is not conducive to understanding the original data. Compared with the above method, the advantages of band selection include [52,53]: (1) the selected band not only contains useful detailed data information, but also maintains the integrity of its physical attributes; (2) the operation of band selection is relatively simple.

The common methods for alleviating the class distribution misalignment caused by class unbalance are divided into two categories: data-resampling-based [54,55] and sample-reweighting-based [56,57]. The first method alleviates the class distribution misalignment by oversampling the minority classes or undersampling the majority classes. However, the oversampling of minority classes may easily lead to over-fitting, while the undersampling of majority classes may lead to information loss. The other method alleviates the class distribution misalignment by assigning the corresponding weight to each class in the process of domain adaptation. However, most of the sample reweighting-based methods tend to pay the same attention to each class when designing the weight factor, without considering the relationship between the weight factor and the class prior distribution in the target domain. Considering that the classification task is targeted at the target domain, the proposed method designs the weight factor based on the prior distribution of the target class, and focuses the training of the model on the important classes of the target domain during domain adaptation, which improves the accuracy of the model in the task of cross-domain HSI classification.

The OA of CWDAN in all data pairs is the highest, with a little sacrifice in terms of running time and number of parameters, which is due to the advantages of the proposed method. The advantages of CWDAN are summarized as follows: (1) By simultaneously reducing the two-domain difference between the first and second order statistics, sufficient and fast marginal distribution alignment is achieved; (2) the weight of each class in the domain adaptation is adjusted based on the class prior distribution of the two domains, and the training is focused on the important classes in the target domain, which solves the problem of class unbalanced during the conditional distribution alignment; (3) deep learning and broad learning are embedded in a unified framework, and the strong feature extraction ability of deep learning and the feature breadth expansion ability of broad learning are fully utilized to achieve the extraction and enhancement of domain-invariant features.

The disadvantages of CWDAN are summarized as follows: the model cannot adaptively adjust ${\alpha }_1$ and ${\alpha }_2$, which makes it difficult to adapt to the marginal distribution differences according to importance, thus hindering the further improvement of domain adaptation performance.

5. Conclusions

As remote sensing technology advances, more and more hyperspectral images can be collected and analyzed. The classification of hyperspectral images is a basic foundation for its further application in land resource evaluation and analysis. One of the most challenging problems faced by HSI classification is the scarcity of sample labels. To address this concern, we have investigated the effectiveness of CWDAN for HSI classification. The proposed CWDAN can achieve satisfactory classification performance, since it aligns the deep-feature marginal distributions, second-order statistics, and conditional distributions between two domains, and reduces the class weight bias via CWMMD. Extensive experiments conducted with eight real HSI data pairs demonstrate that our proposed CWDAN is superior to several advanced domain adaptation methods.