Matchup Strategies for Satellite Sea Surface Salinity Validation
Abstract
:1. Introduction
2. Data and Methods
2.1. The Global Model
2.2. Simulated SSS Data
2.2.1. Simulated Satellite Data
2.2.2. Simulated Argo Float Data
2.3. Matchup Criteria
2.3.1. Single Salinity Difference Closest in Time Method (SSDT)
2.3.2. Single Salinity Difference Closest in Space Method (SSDS)
2.3.3. All Salinity Difference Method (ASD)
2.3.4. N-Closest Optimized Averaging Method (NCLO)
3. Results
3.1. Optimization of NCLO Parameters
3.2. Relative Effectiveness of Each Matchup Strategy
3.3. Impact of Simulated Instrumental Errors
3.4. The Effect of Matchup Method on the Spatial and Temporal Distance of the Satellite Observations Picked for Comparison
4. Discussion
4.1. The Effect of Region and Satellite Track on Ideal Matchup Strategy
4.2. Feasibility of Each Method
4.3. The Effect of Averaging on Instrumental Noise
4.4. Success of ASD, SSDS, SSDT and Recommendations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loew, A.; Bell, W.; Brocca, L.; Bulgin, C.E.; Burdanowitz, J.; Calbet, X.; Donner, R.V.; Ghent, D.; Gruber, A.; Kaminski, T.; et al. Validation practices for satellite-based Earth observation data across communities. Rev. Geophys. 2017, 55, 779–817. [Google Scholar] [CrossRef] [Green Version]
- Dinnat, E.P.; Le Vine, D.M.; Boutin, J.; Meissner, T.; Lagerloef, G. Remote Sensing of Sea Surface Salinity: Comparison of Satellite and In Situ Observations and Impact of Retrieval Parameters. Remote Sens. 2019, 11, 750. [Google Scholar] [CrossRef] [Green Version]
- Kao, H.-Y.; Lagerloef, G.S.E.; Lee, T.; Melnichenko, O.; Meissner, T.; Hacker, P. Aquarius Salinity Validation Analysis, Data Version 5.0; Aquarius/SAC-D: Seattle, WA, USA, 2018; Volume 45. [Google Scholar] [CrossRef] [Green Version]
- Abe, H.; Ebuchi, N. Evaluation of sea surface salinity observed by Aquarius. J. Geophys. Res. Oceans 2014, 119, 8109–8121. [Google Scholar] [CrossRef]
- Tang, W.; Yueh, S.H.; Fore, A.G.; Hayashi, A. Validation of Aquarius sea surface salinity with in situ measurements from Argo floats and moored bouys. J. Geophys. Res. Oceans 2014, 119, 6171–6189. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.; Le Vine, D.M. The salinity retrieval algorithms for the NASA Aquarius version 5 and SMAP version 3 releases. Remote Sens. 2018, 10, 1121. [Google Scholar] [CrossRef] [Green Version]
- Dinnat, E.P.; Boutin, J.; Yin, X.; Le Vine, D.M. Inter-comparison of SMOS and aquarius Sea Surface Salinity: Effects of the dielectric constant and vicarious calibration. In Proceedings of the 2014 13th IEEE Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad), Pasadena, CA, USA, 24–27 March 2014. [Google Scholar] [CrossRef] [Green Version]
- Hernandez, O.; Boutin, J.; Kolodziejczyk, N.; Reverdin, G.; Martin, N.; Gaillard, F.; Reul, N.; Vergely, J.L. SMOS salinity in the subtropical North Atlantic salinity maximum: 1. Comparison with Aquarius and in situ salinity. J. Geophys. Res. Oceans 2014, 119, 8878–8896. [Google Scholar] [CrossRef] [Green Version]
- Bao, S.; Wang, H.; Zhang, R.; Yan, H.; Chen, J. Comparison of Satellite-Derived Sea Surface Salinity Products from SMOS, Aquarius, and SMAP. J. Geophys. Res. Oceans 2019, 124, 1932–1944. [Google Scholar] [CrossRef]
- Qin, S.; Wang, H.; Zhu, J.; Wan, L.; Zhang, Y.; Wang, H. Validation and correction of sea surface salinity retrieval from SMAP. Acta Oceanol. Sin. 2020, 39, 148–158. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Olmedo, E.; Gabarró, C.; González-Gambau, V.; Martínez, J.; Turiel, A.; Ballabrera, P.J.; Portabella, M.; Fournier, S.; Lee, T. Seven Years of SMOS Sea Surface Salinity at High Latitudes: Variability in Arctic and Sub-Arctic Regions. Remote Sens. 2018, 10, 1772. [Google Scholar] [CrossRef] [Green Version]
- Olmedo, E.; Taupier-Letage, I.; Turiel, A.; Alvera-Azcárate, A. Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea Through Multi-Variate and Multi-Fractal Analysis. Remote Sens. 2018, 10, 485. [Google Scholar] [CrossRef] [Green Version]
- Olmedo, E.; González-Haro, C.; Hoareau, N.; Umbert, M.; González-Gambau, V.; Martínez, J.; Gabarró, C.; Turiel, A. Nine years of SMOS sea surface salinity global maps at the Barcelona Expert Center. Earth Syst. Sci. Data 2021, 13, 857–888. [Google Scholar] [CrossRef]
- Tang, W.; Fore, A.; Yueh, S.; Lee, T.; Hayashi, A.; Sanchez-Franks, A.; Martinez, J.; King, B.; Baranowski, D. Validating SMAP SSS with in situ measurements. Remote Sens. Environ. 2017, 200, 326–340. [Google Scholar] [CrossRef] [Green Version]
- Fournier, S.; Lee, T.; Tang, W.; Steele, M.; Olmedo, E. Evaluation and Intercomparison of SMOS, Aquarius, and SMAP Sea Surface Salinity Products in the Arctic Ocean. Remote Sens. 2019, 11, 3043. [Google Scholar] [CrossRef] [Green Version]
- Vazquez-Cuervo, J.; Fournier, S.; Dzwonkowski, B.; Reager, J. Intercomparison of In-Situ and Remote Sensing Salinity Products in the Gulf of Mexico, a River-Influenced System. Remote Sens. 2018, 10, 1590. [Google Scholar] [CrossRef] [Green Version]
- Vazquez-Cuervo, J.; Gomez-Valdes, J.; Bouali, M.; Miranda, L.E.; Van der Stocken, T.; Tang, W.; Gentemann, C. Using Saildrones to Validate Satellite-Derived Sea Surface Salinity and Sea Surface Temperature along the California/Baja Coast. Remote Sens. 2019, 11, 1964. [Google Scholar] [CrossRef] [Green Version]
- Vazquez-Cuervo, J.; Gomez-Valdes, J.; Bouali, M. Comparison of Satellite-Derived Sea Surface Salinity Gradients Using the Saildrone California/Baja and North Atlantic Gulf Stream Deployments. Remote Sens. 2020, 12, 1839. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; Gentemann, C.; Tang, W.; Carroll, D.; Zhang, H.; Menemenlis, D.; Gomez-Valdes, J.; Bouali, M.; Steele, M. Using Saildrones to Validate Arctic Sea-Surface Salinity from the SMAP Satellite and from Ocean Models. Remote Sens. 2021, 13, 831. [Google Scholar] [CrossRef]
- Hall, K.; Daley, A.; Whitehall, S.; Sandiford, S.; Gentemann, C.L. Validating Salinity from SMAP and HYCOM Data with Saildrone Data during EUREC A-OA/ATOMIC. Remote Sens. 2022, 14, 3375. [Google Scholar] [CrossRef]
- Schanze, J.J.; Le Vine, D.M.; Dinnat, E.P.; Kao, H.-Y. Comparing Satellite Salinity Retrievals with In Situ Measurements: A Recommendation for Aquarius and SMAP (Version 1); Earth & Space Research: Seattle, WA, USA, 2020; Volume 20. [Google Scholar] [CrossRef]
- Bingham, F.M.; Fournier, S.; Brodnitz, S.; Ulfsax, K.; Zhang, H. Matchup Characteristics of Sea Surface Salinity Using a High-Resolution Ocean Model. Remote Sens. 2021, 13, 2995. [Google Scholar] [CrossRef]
- Bingham, F.M.; Brodnitz, S.; Fournier, S.; Ulfsax, K.; Hayashi, A.; Zhang, H. Sea Surface Salinity Sub Footprint Variability from a Global High Resolution Model. Remote Sens. 2021, 13, 4410. [Google Scholar] [CrossRef]
- Su, Z.; Wang, J.; Klein, P.; Thompson, A.F.; Menemenlis, D. Ocean submesoscales as a key component of the global heat budget. Nat. Commun. 2018, 9, 775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Menemenlis, D. Pre-SWOT Ocean Simulation LLC4320 Version 1 User Guide; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2021. [Google Scholar]
- Rocha, C.B.; Gille, S.T.; Chereskin, T.K.; Menemenlis, D. Seasonality of submesoscale dynamics in the Kuroshio Extension. Geophys. Res. Lett. 2016, 43, 11304–11311. [Google Scholar] [CrossRef]
- Drucker, R.; Riser, S. Validation of Aquarius Sea Surface Salinity with Argo: Analysis of Error Due to Depth of Measurement and Vertical Salinity Stratification. J. Geophys. Res. Oceans 2014, 119, 4626–4637. [Google Scholar] [CrossRef]
- Akhil, V.P.; Vialard, J.; Lengaigne, M.; Keerthi, M.G.; Boutin, J.; Vergely, J.L.; Papa, F. Bay of Bengal Sea surface salinity variability using a decade of improved SMOS re-processing. Remote Sens. Environ. 2020, 248, 11196. [Google Scholar] [CrossRef]
- Clayson, C.A.; Edson, J.B.; Paget, A.; Graham, R.; Greenwood, B. Effects of rainfall on the atmosphere and the ocean during SPURS-2. Oceanography 2019, 32, 86–97. [Google Scholar] [CrossRef] [Green Version]












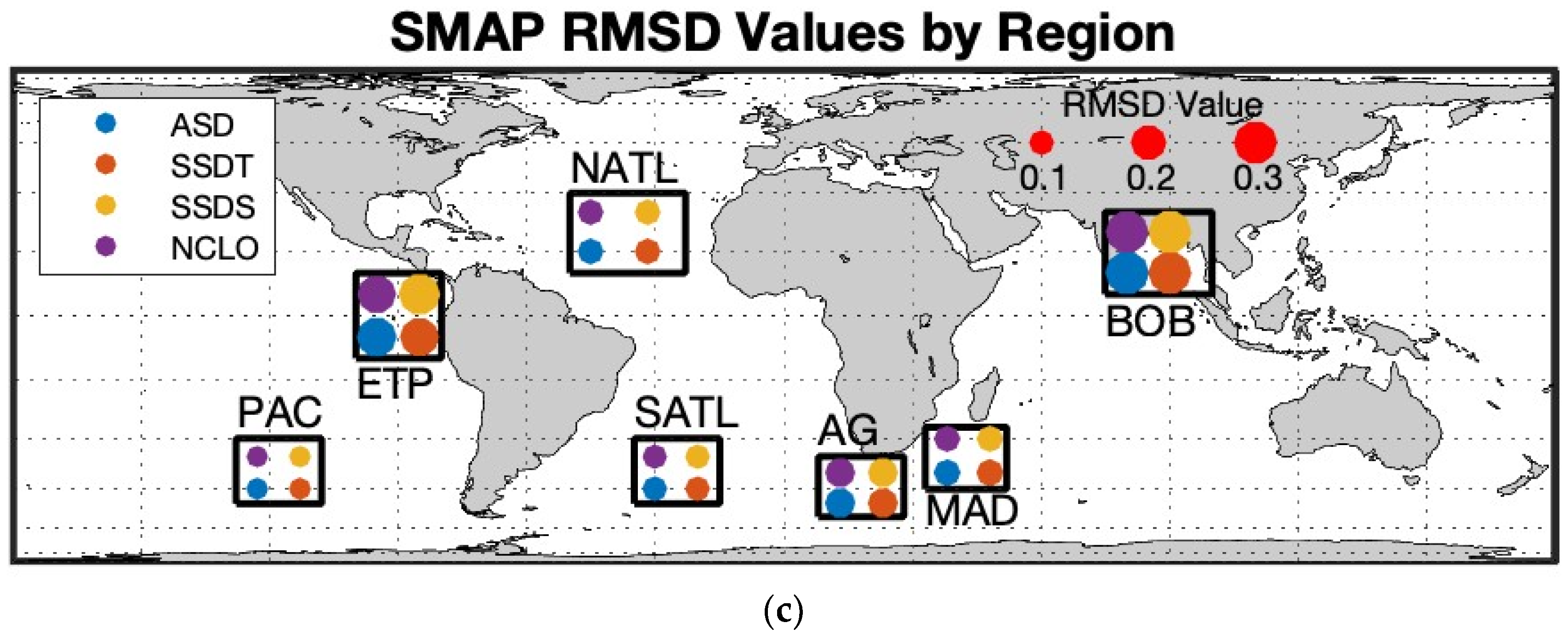

| Region Name | Region Latitudes | Region Longitudes |
|---|---|---|
| Pacific (PAC) | 30°S–50°S | 128°W–108°W |
| South Atlantic (SATL) | 30°S–50°S | 15°W–35°W |
| Agulhas (AG) | 35°S–55°S | 8°E–28°E |
| North Atlantic (NATL) | 10°N–30°N | 23°W–50°W |
| MAD (Madagascar) | 45°S–27°S | 33°E–52°E |
| Bay of Bengal (BOB) | 5°N–25°N | 75°E–100°E |
| Eastern Tropical Pacific (ETP) | 10°S–10°N | 100°W–80°W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Westbrook, E.E.; Bingham, F.M.; Fournier, S.; Hayashi, A. Matchup Strategies for Satellite Sea Surface Salinity Validation. Remote Sens. 2023, 15, 1242. https://doi.org/10.3390/rs15051242
Westbrook EE, Bingham FM, Fournier S, Hayashi A. Matchup Strategies for Satellite Sea Surface Salinity Validation. Remote Sensing. 2023; 15(5):1242. https://doi.org/10.3390/rs15051242
Chicago/Turabian StyleWestbrook, Elizabeth E., Frederick M. Bingham, Severine Fournier, and Akiko Hayashi. 2023. "Matchup Strategies for Satellite Sea Surface Salinity Validation" Remote Sensing 15, no. 5: 1242. https://doi.org/10.3390/rs15051242
APA StyleWestbrook, E. E., Bingham, F. M., Fournier, S., & Hayashi, A. (2023). Matchup Strategies for Satellite Sea Surface Salinity Validation. Remote Sensing, 15(5), 1242. https://doi.org/10.3390/rs15051242






