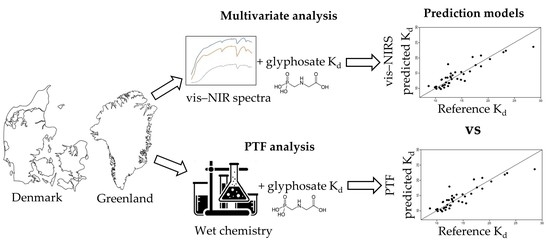
Visible Near-Infrared Spectroscopy and Pedotransfer Function Well Predict Soil Sorption Coefficient of Glyphosate
Abstract
1. Introduction
2. Materials and Methods
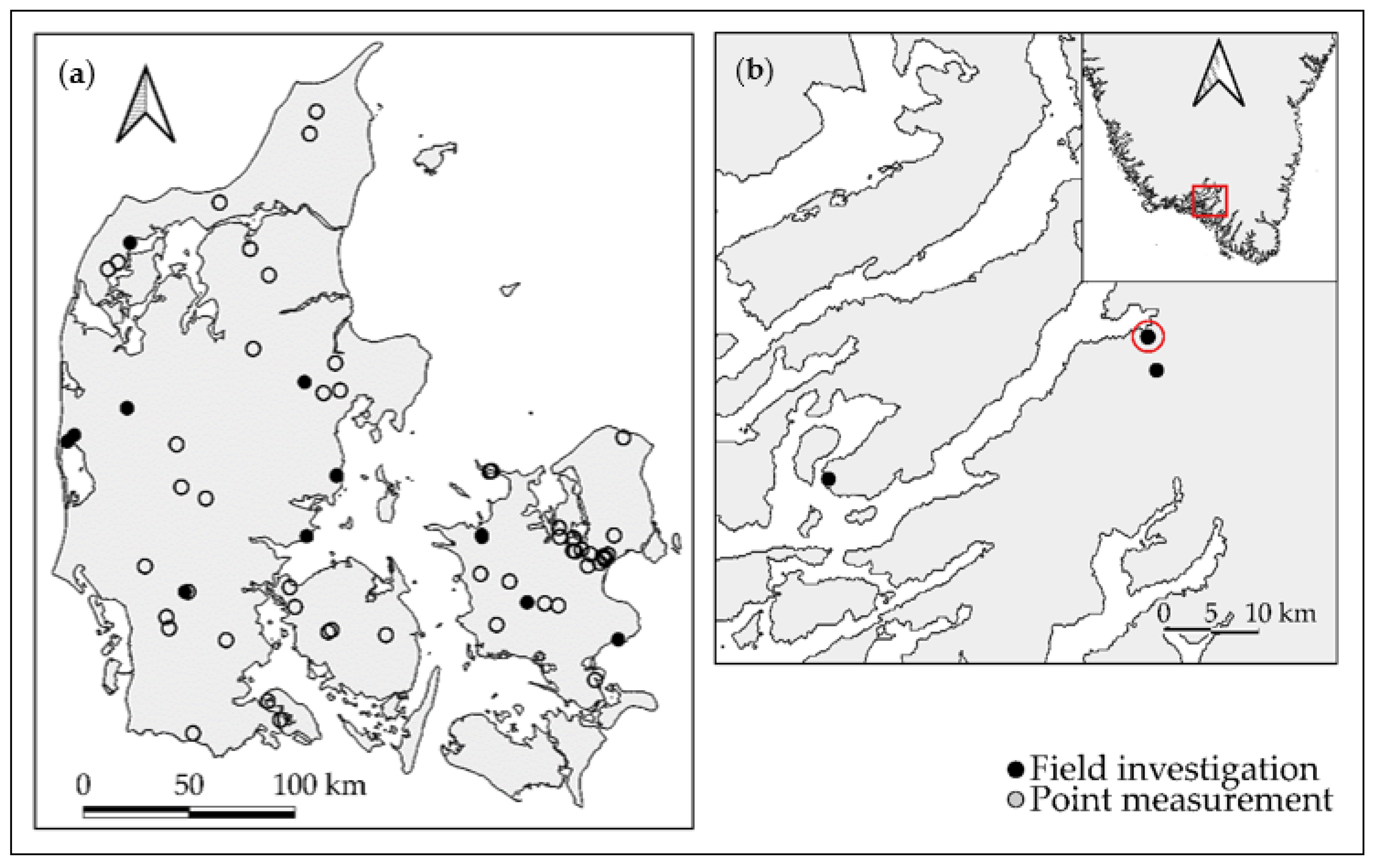
2.1. Soil Samples
2.2. Laboratory Analysis
2.3. Visible Near-Infrared Measurements and Analysis
2.4. Data Subdivision and Exploratory Analysis
2.5. Pedotransfer Function (PTF)
2.6. Spectral Modeling
2.7. Models’ Validation
3. Results
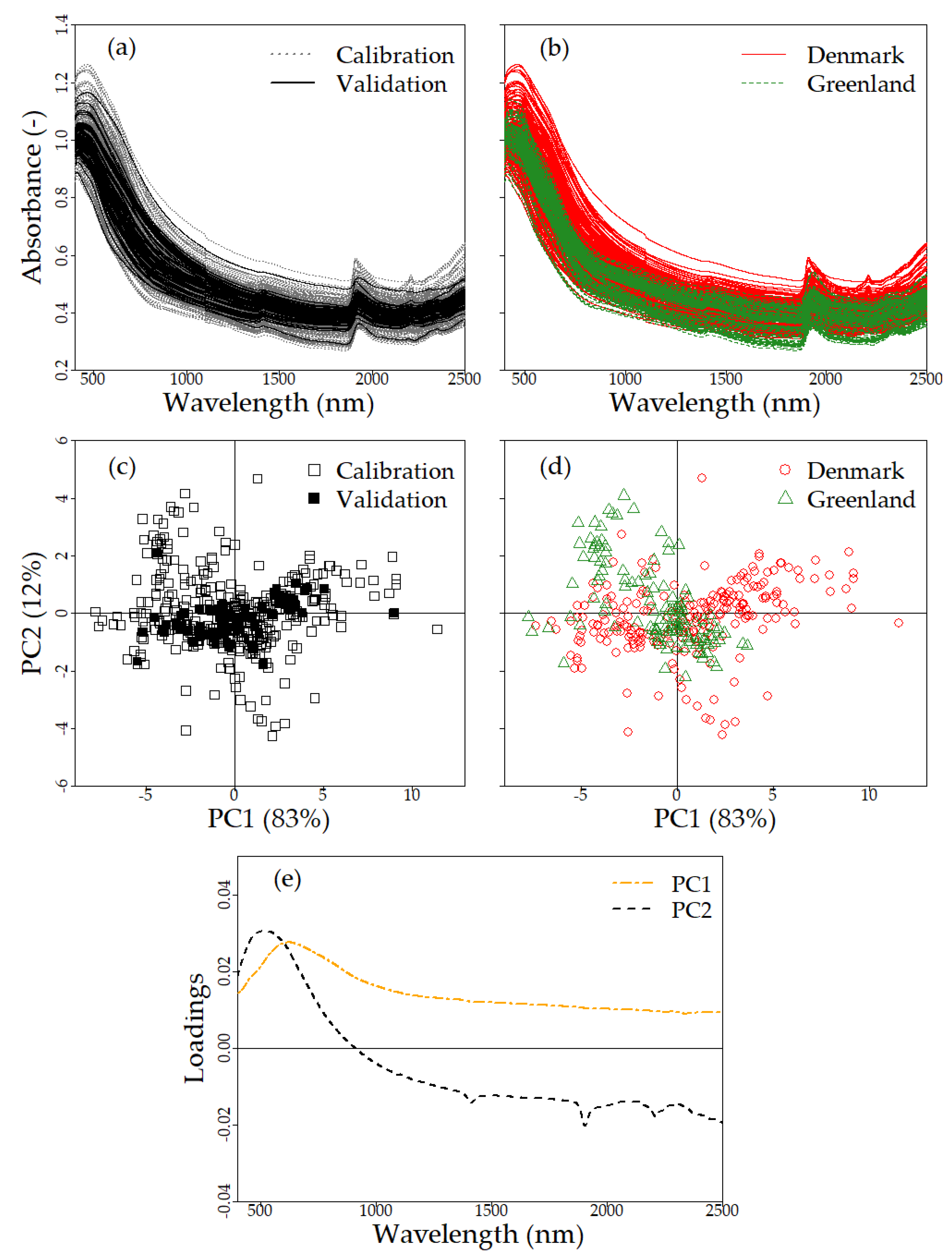
3.1. Exploratory Analysis
3.1.1. Soil Properties
3.1.2. Soil Spectra
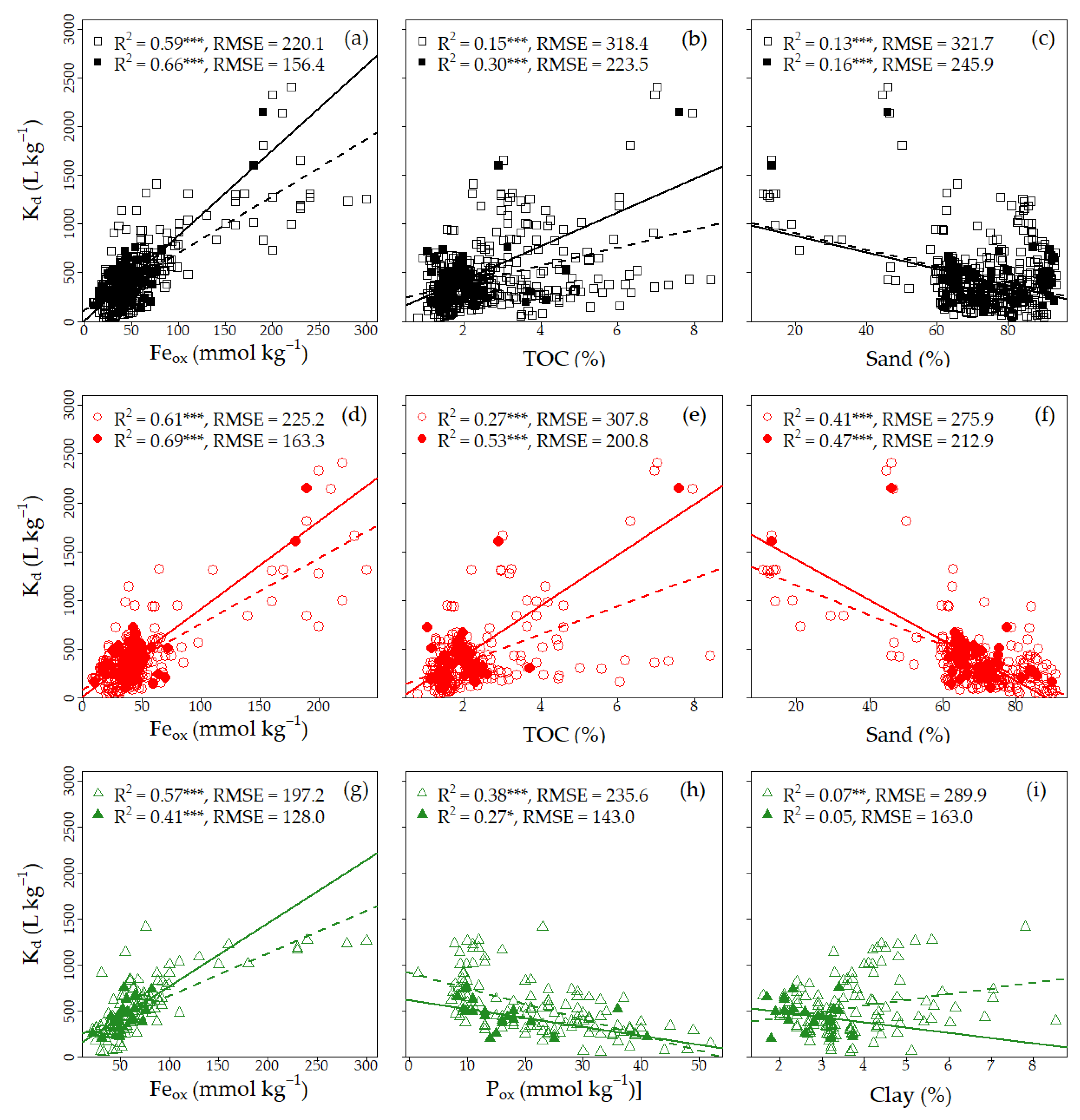
3.1.3. Single Linear Regression (SLR) Analysis
3.2. Prediction of the Kd of Glyphosate
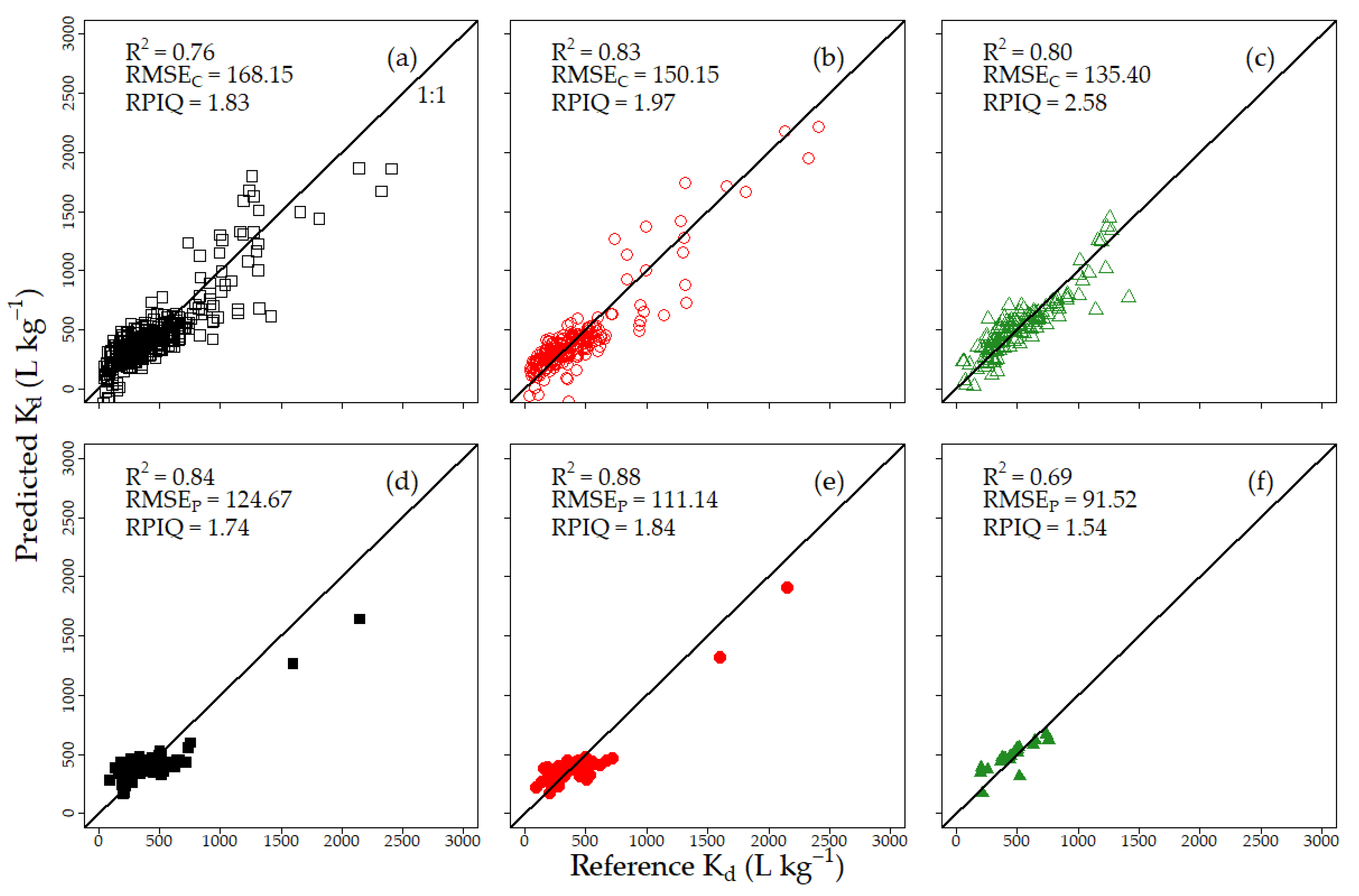
3.2.1. Pedotransfer Functions
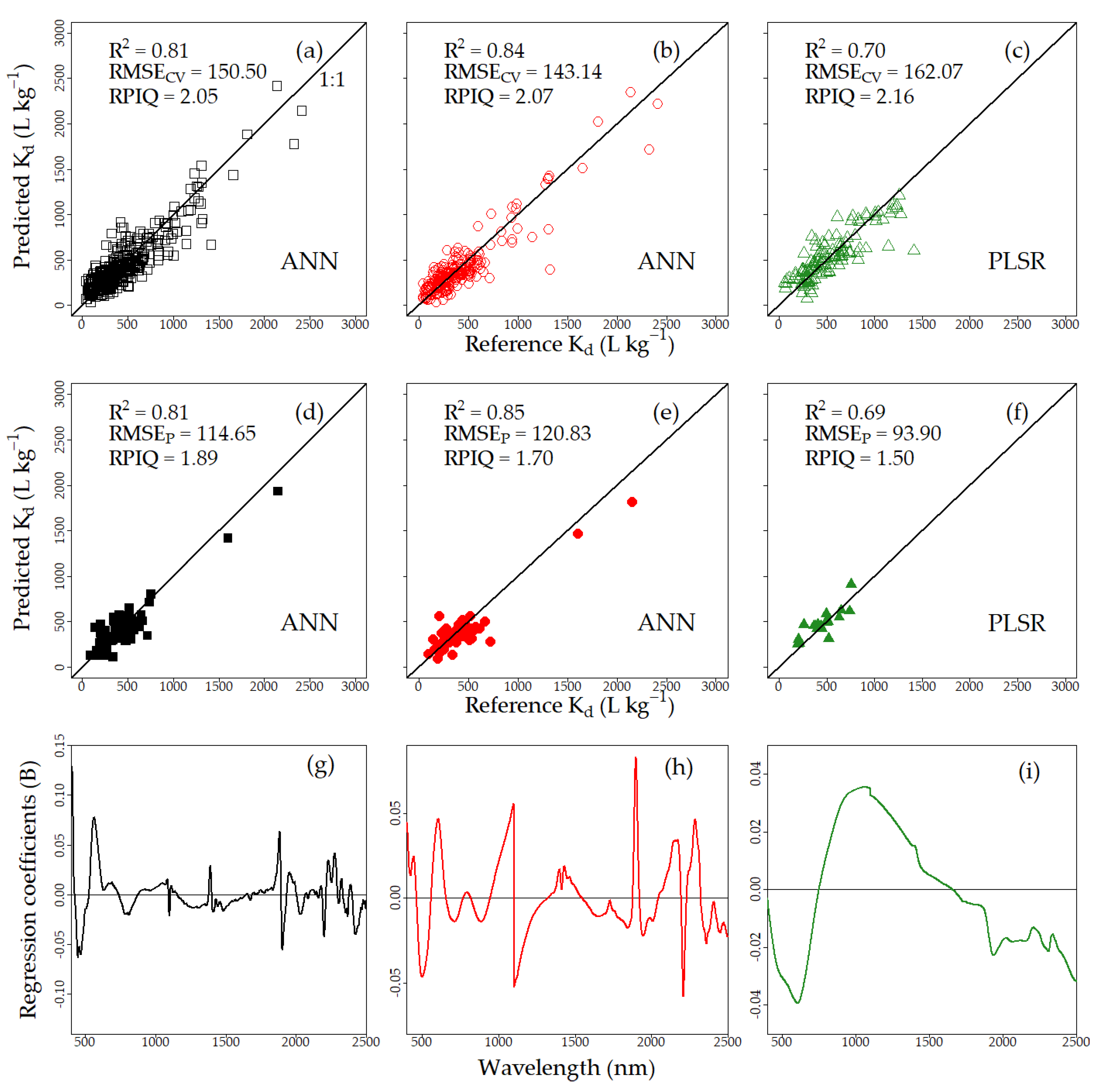
3.2.2. Spectral Model
3.2.3. Assessing the Advantages of Developing Individual Models
4. Discussion
4.1. Evaluation of Exploratory Analysis Results
4.2. Evaluation of Kd Predictions by PTF and Vis–NIRS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Clay | Silt | Sand | TOC a | pH | EC b | Feox c | Alox c | Pox c | Kd d | |
|---|---|---|---|---|---|---|---|---|---|---|
| Combined dataset, n = 439 (Calibration, n = 351) (Validation, n = 88) | ||||||||||
| Clay | 1 | 0.66 ***,e,f (0.62 ***,g) (0.95 ***,h) | −0.92 *** (−0.92 ***) (−0.98 ***) | −0.08 (−0.10) (0.12) | 0.58 *** (0.55 ***) (0.76 ***) | 0.37 *** (0.36 ***) (0.52 ***) | 0.33 *** (0.34 ***) (0.30 **) | −0.29 *** (−0.27 ***) (−0.45 ***) | −0.19 *** (−0.17 **) (−0.34 **) | 0.32 *** (0.31 **) (0.37 **) |
| Silt | 1 | −0.87 *** (−0.85 ***) (−0.98 ***) | −0.06 (−0.06) (0.10) | 0.49 *** (0.45 ***) (0.73 ***) | 0.35 *** (0.35 ***) (0.51 ***) | 0.16 *** (0.17 **) (0.23 *) | −0.31 *** (−0.28 ***) (−0.43 ***) | −0.17 *** (−0.14 *) (−0.34 **) | 0.21 *** (0.20 **) (0.30 **) | |
| Sand | 1 | −0.09 (−0.08) (−0.23 *) | −0.55 *** (−0.51 ***) (−0.73 ***) | −0.43 *** (−0.42 ***) (−0.55 ***) | −0.34 *** (−0.35 ***) (−0.32 **) | 0.24 *** (0.21 ***) (0.43 ***) | 0.13 *** (0.10) (0.30 **) | −0.36 ** (−0.36 **) (−0.40 **) | ||
| TOC | 1 | −0.29 *** (−0.31 ***) (−0.13) | 0.21 *** (0.17 **) (0.31 **) | 0.32 *** (0.30 ***) (0.47 ***) | 0.49 *** (0.52 ***) (0.02) | 0.41 *** (0.40 ***) (0.30 **) | 0.40 *** (0.38 ***) (0.55 ***) | |||
| pH | 1 | 0.37 *** (0.38 ***) (0.37 ***) | −0.13 ** (−0.13 *) (−0.05) | −0.43 *** (−0.42 ***) (−0.51 ***) | −0.26 *** (−0.25 ***) (−0.36 ***) | −0.21 *** (−0.23 ***) (−0.06) | ||||
| EC | 1 | 0.18 *** (0.15 **) (0.36 ***) | −0.06 (−0.07) (−0.24 *) | 0.13 ** (0.12 *) (−0.01) | 0.02 (0.00) (0.20) | |||||
| Feox | 1 | 0.18 *** (0.18 ***) (0.09) | 0.10 * (0.08) (0.18) | 0.77 *** (0.77 ***) (0.81 ***) | ||||||
| Alox | 1 | 0.54 *** (0.51 ***) (0.63 ***) | 0.10 * (0.12 *) (−0.03) | |||||||
| Pox | 1 | −0.15 ** (−0.16 **) (−0.15) | ||||||||
| Kd | 1 | |||||||||
| Denmark, n = 296 (Calibration, n = 228) (Validation, n = 68) | ||||||||||
| Clay | 1 | 0.58 *** (0.56 ***) (0.90 ***) | −0.93 *** (−0.93 ***) (−0.97 ***) | 0.15 ** (0.14 *) (0.33 **) | 0.40 *** (0.40 ***) (0.48 ***) | 0.32 *** (0.32 ***) (0.33 **) | 0.74 *** (0.75 ***) (0.67 ***) | −0.07 (−0.05) (−0.33 **) | 0.13 * (0.18 **) (−0.33 **) | 0.57 *** (0.57 ***) (0.67 ***) |
| Silt | 1 | −0.82 *** (−0.81 ***) (−0.96 ***) | 0.01 (0.01) (0.16) | 0.35 *** (0.33 ***) (0.48 ***) | 0.23 *** (0.24 ***) (0.31 **) | 0.52 *** (0.53 ***) (0.51 ***) | −0.32 *** (−0.32 ***) (−0.30 *) | −0.28 *** (−0.25 ***) (−0.41 ***) | 0.45 *** (0.43 ***) (0.52 ***) | |
| Sand | 1 | −0.25 *** (−0.24 ***) (−0 37 **) | −0.39 *** (−0.38 ***) (−0.48 ***) | −0.33 *** (−0.34 ***) (−0.37 **) | −0.76 *** (−0.77 ***) (−0.67 ***) | 0.13 * (0.10) (0.31 *) | 0.03 (−0.02) (0.34 **) | −0.64 *** (−0.64 ***) (−0.69 ***) | ||
| TOC | 1 | −0.15 ** (−0.16 *) (−0.09) | 0.14 * (0.11) (0.27 *) | 0.34 *** (0.30 ***) (0.61 ***) | 0.42 *** (0.49 ***) (−0.11) | 0.07 (0.07) (−0.02) | 0.54 *** (0.52 ***) (0.73 ***) | |||
| pH | 1 | 0.27 *** (0.29 ***) (0.14) | 0.10 (0.10) (0.09) | −0.25 *** (−0.22 ***) (−0.41 ***) | −0.01 (0.03) (−0.22) | −0.13 * (−0.15 *) (−0.05) | ||||
| EC | 1 | 0.36 *** (0.34 ***) (0.52 ***) | −0.02 (−0.02) (−0.15) | 0.10 (0.10) (−0.04) | 0.12 * (0.10) (0.30 *) | |||||
| Feox | 1 | −0.04 (−0.05) (0.02) | 0.31 *** (0.32 ***) (0.22) | 0.78 *** (0.78 ***) (0.83 ***) | ||||||
| Alox | 1 | 0.45 *** (0.41 ***) (0.65 ***) | −0.03 (−0.03) (−0.06) | |||||||
| Pox | 1 | −0.05 (−0.04) (−0.11) | ||||||||
| Kd | 1 | |||||||||
| Greenland, n = 143 (Calibration, n = 123) (Validation, n = 20) | ||||||||||
| Clay | 1 | 0.79 *** (0.78 ***) (0.59 **) | −0.85 *** (−0.83 ***) (−0.74 ***) | 0.41 *** (0.34 ***) (0.69 ***) | 0.11 (0.12) (−0.43) | 0.47 *** (0.40 ***) (0.76 ***) | 0.28 *** (0.26 **) (0.04) | 0.62 *** (0.59 ***) (0.42) | 0.31 *** (0.25 **) (0.67 **) | 0.26 ** (0.26 **) (−0.21) |
| Silt | 1 | −0.93 *** (−0.93 ***) (−0.96 ***) | 0.36 *** (0.29 **) (0.88 ***) | 0.13 (0.13) (0.03) | 0.53 *** (0.48 ***) (0.87 ***) | −0.12 (−0.17) (−0.01) | 0.50 *** (0.45 ***) (0.67 **) | 0.50 *** (0.46 ***) (0.84 ***) | −0.06 (−0.08) (−0.20) | |
| Sand | 1 | −0.66 *** (−0.60 ***) (−0.97 ***) | −0.11 (−0.11) (0.14) | −0.68 *** (−0.64 ***) (−0.96 ***) | −0.02 (0.02) (0.07) | −0.57 *** (−0.53 ***) (−0.59 **) | −0.57 *** (−0.53 ***) (−0.86 ***) | −0.01 (0.01) (0.24) | ||
| TOC | 1 | −0.02 (−0.03) (−0.20) | 0.70 *** (0.65 ***) (0.96 ***) | 0.16 (0.14) (−0.17) | 0.38 *** (0.32 ***) (0.47 *) | 0.52 *** (0.47 ***) (0.80 ***) | 0.03 (0.01) (−0.24) | |||
| pH | 1 | 0.43 *** (0.46 ***) (−0.11) | −0.09 (−0.10) (−0.05) | −0.04 (−0.05) (−0.03) | 0.11 (0.12) (−0.20) | −0.17 * (−0.19 *) (0.06) | ||||
| EC | 1 | 0.00 (−0.04) (−0.18) | 0.26 ** (0.19 *) (0.50 *) | 0.57 *** (0.54 ***) (0.82 ***) | −0.13 (−0.16) (−0.31) | |||||
| Feox | 1 | 0.30 *** (0.28 **) (0.27) | −0.29 *** (−0.33 ***) (−0.06) | 0.75 *** (0.75 ***) (0.64 **) | ||||||
| Alox | 1 | 0.42 *** (0.38 ***) (0.67 **) | 0.18 ** (0.17) (0.04) | |||||||
| Pox | 1 | −0.58 *** (−0.62 ***) (−0.52 *) | ||||||||
| Kd | 1 | |||||||||
| All Samples of the Combined Dataset | All Samples of the Danish Dataset | All Samples of the Greenlandic Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| Variables | R2 a | RMSE b | Variables | R2 a | RMSE b | Variables | R2 a | RMSE b |
| Constant | 329.73 | Constant | 343.52 | Constant | 284.81 | |||
| Feox | 0.59 | 211.29 | Feox | 0.61 | 214.36 | Feox | 0.56 | 188.76 |
| Pox | 0.64 | 197.25 | Pox | 0.71 | 186.94 | Pox | 0.71 | 154.84 |
| TOC | 0.72 | 176.07 | TOC | 0.78 | 161.01 | Sand | 0.79 | 132.69 |
| pH | 0.73 | 170.73 | EC | 0.82 | 148.45 | Alox | 0.80 | 129.77 |
| Sand | 0.77 | 160.02 | pH | 0.83 | 141.70 | pH | 0.81 | 128.07 |
| EC | 0.78 | 156.56 | Clay | 0.84 | 139.71 | |||
| Dataset | PTFs |
|---|---|
| Combined calibration subset | Kd a = 1524.34 − (5.87 × sand) + (55.62 × TOC b) − (131.54 × pH) + (4.56 × Feox c) − (13.39 × Pox c) |
| Danish calibration subset | Kd = 761.25 + (76.46 × TOC) − (78.32 × pH) − (129.20 × EC d) + (7.46 × Feox) − (20.70 × Pox) |
| Greenlandic calibration subset | Kd = 1521.14 − (11.53 × sand) + (3.12 × Feox) + (2.82 × Alox c) − (17.52 × Pox) |
| Dataset | No of LVs a | R2 b | RMSEP c in L kg−1 | RPIQ d |
|---|---|---|---|---|
| Combined | 13 e (14 f) | 0.69 (0.81) | 162.01 (114.65) | 1.34 (1.89) |
| Denmark | 15 (15) | 0.82 (0.85) | 130.12 (120.83) | 1.58 (1.70) |
| Greenland | 03 (04) | 0.69 (0.62) | 93.90 (97.98) | 1.50 (1.44) |
References
- De Gerónimo, E.; Aparicio, V.C.; Costa, J.L. Glyphosate sorption to soils of Argentina. Estimation of affinity coefficient by pedotransfer function. Geoderma 2018, 322, 140–148. [Google Scholar] [CrossRef]
- Duke, S.O. The history and current status of glyphosate. Pest Manag. Sci. 2018, 74, 1027–1034. [Google Scholar] [CrossRef] [PubMed]
- Duke, S.O.; Powles, S.B. Glyphosate: A once-in-a-century herbicide. Pest Manag. Sci. 2008, 64, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Mensink, H.; Janseen, P. (Eds.) Environmental Health Criteria. In Glyphosate; World Health Organization: Geneva, Switzerland, 1994; ISBN 978-92-4-157159-3. [Google Scholar]
- Szekacs, A.; Darvas, B. Forty Years with Glyphosate. In Herbicides—Properties, Synthesis and Control of Weeds; Hasaneen, M.N., Ed.; InTech: London, UK, 2012; ISBN 978-953-307-803-8. [Google Scholar]
- Cheah, U.B.; Kirkwood, R.C.; Lum, K.Y. Adsorption, desorption and mobility of four commonly used pesticides in Malaysian agricultural soils. Pestic. Sci. 1997, 50, 53–63. [Google Scholar] [CrossRef]
- de Jonge, L.W.; Kjaergaard, C.; Moldrup, P. Colloids and colloid-facilitated transport of contaminants in soils: An introduction. Vadose Zone J. 2004, 3, 321–325. [Google Scholar] [CrossRef]
- Norgaard, T.; Moldrup, P.; Ferré, T.P.A.; Olsen, P.; Rosenbom, A.E.; de Jonge, L.W. Leaching of glyphosate and aminomethylphosphonic acid from an agricultural field over a twelve-year period. Vadose Zone J. 2014, 13, vzj2014.05.0054. [Google Scholar] [CrossRef]
- Vereecken, H. Mobility and leaching of glyphosate: A review. Pest Manag. Sci. 2005, 61, 1139–1151. [Google Scholar] [CrossRef]
- Borggaard, O.K.; Gimsing, A.L. Fate of glyphosate in soil and the possibility of leaching to ground and surface waters: A review. Pest Manag. Sci. 2008, 64, 441–456. [Google Scholar] [CrossRef]
- Farenhorst, A.; Papiernik, S.K.; Saiyed, I.; Messing, P.; Stephens, K.D.; Schumacher, J.A.; Lobb, D.A.; Li, S.; Lindstrom, M.J.; Schumacher, T.E. Herbicide sorption coefficients in relation to soil properties and terrain attributes on a cultivated prairie. J. Environ. Qual. 2008, 37, 1201–1208. [Google Scholar] [CrossRef]
- Farenhorst, A.; McQueen, D.A.R.; Saiyed, I.; Hilderbrand, C.; Li, S.; Lobb, D.A.; Messing, P.; Schumacher, T.E.; Papiernik, S.K.; Lindstrom, M.J. Variations in soil properties and herbicide sorption coefficients with depth in relation to PRZM (pesticide root zone model) calculations. Geoderma 2009, 150, 267–277. [Google Scholar] [CrossRef]
- Gevao, B.; Semple, K.T.; Jones, K.C. Bound pesticide residues in soils: A review. Environ. Pollut. 2000, 108, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Wauchope, R.D.; Yeh, S.; Linders, J.B.H.J.; Kloskowski, R.; Tanaka, K.; Rubin, B.; Katayama, A.; Kördel, W.; Gerstl, Z.; Lane, M.; et al. Pesticide soil sorption parameters: Theory, measurement, uses, limitations and reliability. Pest Manag. Sci. 2002, 58, 419–445. [Google Scholar] [CrossRef] [PubMed]
- Ololade, I.A.; Oladoja, N.A.; Oloye, F.F.; Alomaja, F.; Akerele, D.D.; Iwaye, J.; Aikpokpodion, P. Sorption of glyphosate on soil components: The roles of metal oxides and organic materials. Soil Sediment Contam. Int. J. 2014, 23, 571–585. [Google Scholar] [CrossRef]
- Dollinger, J.; Dagès, C.; Voltz, M. Glyphosate sorption to soils and sediments predicted by pedotransfer functions. Environ. Chem. Lett. 2015, 13, 293–307. [Google Scholar] [CrossRef]
- Morillo, E.; Undabeytia, T.; Maqueda, C.; Ramos, A. Glyphosate adsorption on soils of different characteristics. Influence of copper addition. Chemosphere 2000, 40, 103–107. [Google Scholar] [CrossRef]
- Piccolo, A.; Celano, G.; Conte, P. Adsorption of glyphosate by humic substances. J. Agric. Food Chem. 1996, 44, 2442–2446. [Google Scholar] [CrossRef]
- Arroyave, J.M.; Waiman, C.C.; Zanini, G.P.; Avena, M.J. Effect of humic acid on the adsorption/desorption behavior of glyphosate on goethite. Isotherms and kinetics. Chemosphere 2016, 145, 34–41. [Google Scholar] [CrossRef]
- Day, G.M.; Hart, B.T.; McKelvie, I.D.; Beckett, R. Influence of natural organic matter on the sorption of biocides onto goethite, II. Glyphosate. Environ. Technol. 1997, 18, 781–794. [Google Scholar] [CrossRef]
- de Jonge, H.; de Jonge, L.W.; Jacobsen, O.H.; Yamaguchi, T.; Moldrup, P. Glyphosate sorption in soils of different pH and phosphorus content. Soil Sci. 2001, 166, 230–238. [Google Scholar] [CrossRef]
- de Jonge, H.; de Jonge, L.W. Influence of pH and solution composition on the sorption of glyphosate and prochloraz to a sandy loam soil. Chemosphere 1999, 39, 753–763. [Google Scholar] [CrossRef]
- Gimsing, A.L.; Borggaard, O.K.; Bang, M. Influence of soil composition on adsorption of glyphosate and phosphate by contrasting Danish surface soils. Eur. J. Soil Sci. 2004, 55, 183–191. [Google Scholar] [CrossRef]
- Paradelo, M.; Norgaard, T.; Moldrup, P.; Ferré, T.P.A.; Kumari, K.G.I.D.; Arthur, E.; de Jonge, L.W. Prediction of the glyphosate sorption coefficient across two loamy agricultural fields. Geoderma 2015, 259–260, 224–232. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; McBratney, A. Near-infrared (NIR) and mid-infrared (MIR) spectroscopic techniques for assessing the amount of carbon stock in soils—Critical review and research perspectives. Soil Biol. Biochem. 2011, 43, 1398–1410. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; Macdonald, L.M.; McLaughlin, M.J. The performance of visible, near-, and mid-infrared reflectance spectroscopy for prediction of soil physical, chemical, and biological properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2010; Volume 107, pp. 163–215. ISBN 978-0-12-381033-5. [Google Scholar]
- Ben-Dor, E. Quantitative remote sensing of soil properties. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2002; Volume 75, pp. 173–243. ISBN 978-0-12-000793-6. [Google Scholar]
- Paradelo, M.; Hermansen, C.; Knadel, M.; Moldrup, P.; Greve, M.H.; de Jonge, L.W. Field-scale predictions of soil contaminant sorption using visible–near infrared spectroscopy. J. Infrared Spectrosc. 2016, 24, 281–291. [Google Scholar] [CrossRef]
- Horta, A.; Malone, B.; Stockmann, U.; Minasny, B.; Bishop, T.F.A.; McBratney, A.B.; Pallasser, R.; Pozza, L. Potential of integrated field spectroscopy and spatial analysis for enhanced assessment of soil contamination: A prospective review. Geoderma 2015, 241–242, 180–209. [Google Scholar] [CrossRef]
- Goldshleger, N.; Chudnovsky, A.; Ben-Dor, E. Using reflectance spectroscopy and artificial neural network to assess water infiltration rate into the soil profile. Appl. Environ. Soil Sci. 2012, 2012, 439567. [Google Scholar] [CrossRef]
- Janik, L.J.; Forrester, S.T.; Rawson, A. The prediction of soil chemical and physical properties from mid-infrared spectroscopy and combined partial least-squares regression and neural networks (PLS-NN) analysis. Chemom. Intell. Lab. Syst. 2009, 97, 179–188. [Google Scholar] [CrossRef]
- Hermansen, C.; Norgaard, T.; Wollesen de Jonge, L.; Moldrup, P.; Müller, K.; Knadel, M. Predicting glyphosate sorption across New Zealand pastoral soils using basic soil properties or vis–NIR spectroscopy. Geoderma 2020, 360, 114009. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Fouad, Y.; Lagacherie, P. Sentinel-2 Image Capacities to Predict Common Topsoil Properties of Temperate and Mediterranean Agroecosystems. Remote Sens. Environ. 2019, 223, 21–33. [Google Scholar] [CrossRef]
- Ge, Y.; Thomasson, J.A.; Sui, R. Remote Sensing of Soil Properties in Precision Agriculture: A Review. Front. Earth Sci. 2011, 5, 229–238. [Google Scholar] [CrossRef]
- Yu, H.; Kong, B.; Wang, Q.; Liu, X.; Liu, X. Hyperspectral Remote Sensing Applications in Soil: A Review. In Hyperspectral Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2020; pp. 269–291. ISBN 978-0-08-102894-0. [Google Scholar]
- Ben-Dor, E.; Chabrillat, S.; Demattê, J.A.M.; Taylor, G.R.; Hill, J.; Whiting, M.L.; Sommer, S. Using Imaging Spectroscopy to Study Soil Properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, Y.; Wang, H.; Li, F.; Jin, H. Heterogeneous Knowledge Distillation for Simultaneous Infrared-Visible Image Fusion and Super-Resolution. IEEE Trans. Instrum. Meas. 2022, 71, 5004015. [Google Scholar] [CrossRef]
- Wang, P.; Wang, L.; Leung, H.; Zhang, G. Super-Resolution Mapping Based on Spatial–Spectral Correlation for Spectral Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2256–2268. [Google Scholar] [CrossRef]
- Breuning-Madsen, H.; Jensen, N.H. Soil map of Denmark according to the revised FAO legend 1990. Geogr. Tidsskr.-Dan. J. Geogr. 1996, 96, 51–59. [Google Scholar] [CrossRef]
- Moberg, J.P. Composition and development of the clay fraction in Danish soils. An overview/Composition et évolution de la fraction argileuse des sols danois. Un Aperçu. Sci. Géologiques Bull. Mémoires 1990, 43, 193–202. [Google Scholar] [CrossRef]
- Garde, A.A.; Hamilton, M.A.; Chadwick, B.; Grocott, J.; McCaffrey, K.J. The Ketilidian orogen of South Greenland: Geochronology, tectonics, magmatism, and fore-arc accretion during Palaeoproterozoic oblique convergence. Can. J. Earth Sci. 2002, 39, 765–793. [Google Scholar] [CrossRef]
- Ogrič, M.; Knadel, M.; Kristiansen, S.M.; Peng, Y.; De Jonge, L.W.; Adhikari, K.; Greve, M.H. Soil organic carbon predictions in subarctic Greenland by visible–near infrared spectroscopy. Arct. Antarct. Alp. Res. 2019, 51, 490–505. [Google Scholar] [CrossRef]
- Gee, G.W.; Or, D. Partcle-Size Analysis. In Methods of Soil Analysis; SSSA: Madison, WI, USA, 2002; pp. 255–293. [Google Scholar]
- Thomas, G.W. Soil pH and Soil Acidity. In Methods of Soil Analysis; Sparks, D.L., Page, A.L., Helmke, P.A., Loeppert, R.H., Soltanpour, P.N., Tabatabai, M.A., Johnston, C.T., Sumner, M.E., Eds.; SSSA Book Series; Soil Science Society of America, American Society of Agronomy: Madison, WI, USA, 1996; pp. 475–490. ISBN 978-0-89118-866-7. [Google Scholar]
- Schoumans, O.F.; Breeuwsma, A.; Vries, W.D. Use of soil survey information for assessing the phosphate sorption capacity of heavily manured soils. In Proceedings of the International Conference on Vulnerability of Soil and Groundwater to Pollutants, Amsterdam, The Netherlands, 26–29 October 1987; pp. 1079–1088. [Google Scholar]
- Soares, A.A.; Moldrup, P.; Minh, L.N.; Vendelboe, A.L.; Schjonning, P.; de Jonge, L.W. Sorption of phenanthrene on agricultural soils. Water Air Soil Pollut. 2013, 224, 1519. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Martens, H.; Naes, T. Multivariate Calibration; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Gowen, A.A.; Downey, G.; Esquerre, C.; O’Donnell, C.P. Preventing Over-Fitting in PLS Calibration Models of near-Infrared (NIR) Spectroscopy Data Using Regression Coefficients. J. Chemom. 2011, 25, 375–381. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Neurocomputing; Addison-Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Galvao, L.S.; Vitorello, I. Role of organic matter in obliterating the effects of iron on spectral reflectance and colour of Brazilian tropical soils. Int. J. Remote Sens. 1998, 19, 1969–1979. [Google Scholar] [CrossRef]
- Post, J.L.; Nobel, P.N. The near-infrared combination band frequencies of dioctahedral smectites, micas, and illites. Clays Clay Miner. 1993, 41, 639–644. [Google Scholar] [CrossRef]
- Sherman, D.M.; Waite, T.D. Electronic spectra of Fe3+ oxides and oxide hydroxides in the near IR to near UV. Am. Mineral. 1985, 70, 1262–1269. [Google Scholar]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses. 2. Application to simulated and glass spectral data. Anal. Chem. 1988, 60, 1202–1208. [Google Scholar] [CrossRef]
- Piccolo, A.; Celano, G.; Arienzo, M.; Mirabella, A. Adsorption and desorption of glyphosate in some European soils. J. Environ. Sci. Health Part B 1994, 29, 1105–1115. [Google Scholar] [CrossRef]
- Rampazzo, N.; Todorovic, G.R.; Mentler, A.; Blum, W.E.H. Adsorption of glyphosate and aminomethylphosphonic acid in soils. Int. Agrophys. 2013, 27, 203–209. [Google Scholar] [CrossRef]
- Sprankle, P.; Meggitt, W.F.; Penner, D. Adsorption, mobility, and microbial degradation of glyphosate in the soil. Weed Sci. 1975, 23, 229–234. [Google Scholar] [CrossRef]
- Freese, D.; Van Der Zee, S.E.A.T.M.; Van Riemsdijk, W.H. Comparison of different models for phosphate sorption as a function of the iron and aluminium oxides of soils. Eur. J. Soil Sci. 1992, 43, 729–738. [Google Scholar] [CrossRef]
- Ige, D.V.; Akinremi, O.O.; Flaten, D.N. Direct and indirect effects of soil properties on phosphorus retention capacity. Soil Sci. Soc. Am. J. 2007, 71, 95–100. [Google Scholar] [CrossRef]
- Scheinost, A.C.; Chavernas, A.; Barrón, V.; Torrent, J. Use and limitations of second-derivative diffuse reflectance spectroscopy in the visible to near-infrared range to identify and quantify Fe oxide minerals in soils. Clays Clay Miner. 1998, 46, 528–536. [Google Scholar] [CrossRef]
- Clark, R.N. Spectroscopy of rocks and minerals, and principles of spectroscopy. In Manual of Remote Sensing, Remote Sensing for the Earth Sciences; Rencz, A.N., Ed.; John Wiley & Sons: New York, NY, USA, 1999; pp. 3–58. [Google Scholar]
- Clark, R.N.; King, T.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. Solid Earth 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- Hunt, G.R. Spectral signatures of particulate minerals in the visible and near infrared. Geophysics 1977, 42, 501–513. [Google Scholar] [CrossRef]

| Statistical Parameters | Clay | Silt | Sand | TOC a | Kd b | pH | EC c | Feox d | Alox d | Pox d |
|---|---|---|---|---|---|---|---|---|---|---|
| % | L kg−1 | (-) | mS cm−1 | mmol kg−1 | ||||||
| Combined dataset, n = 439 (Calibration, n = 351) (Validation, n = 88) | ||||||||||
| Mean | 11 e (11 f) (11 g) | 11 (11) (12) | 73 (74) (73) | 2.6 (2.7) (2.0) | 448 (452) (431) | 6.3 (6.3) (6.4) | 0.6 (0.7) (0.5) | 54.4 (56.2) (47.2) | 37.0 (38.5) (31.1) | 15.9 (16.6) (13.1) |
| Max | 69 (69) (40) | 43 (43) (42) | 94 (94) (93) | 8.4 (8.4) (7.6) | 2409 (2409) (2149) | 8.3 (8.3) (7.7) | 3.9 (3.9) (2.1) | 300.0 (300.0) (190.0) | 130.0 (130.0) (110.0) | 52.0 (52.0) (41.0) |
| Min | 2 (2) (2) | 2 (2) (2) | 11 (11) (13) | 0.8 (0.8) (1.1) | 37 (37) (93) | 4.4 (4.4) (4.8) | 0.1 (0.1) (0.2) | 8.3 (8.3) (9.9) | 11.0 (11.0) (16.0) | 1.5 (1.5) (7.1) |
| Median | 10 (9) (13) | 11 (11) (14) | 74 (75) (70) | 2.1 (2.2) (1.9) | 378 (369) (423) | 6.4 (6.3) (6.6) | 0.5 (0.6) (0.5) | 44.0 (45.0) (44.0) | 33.0 (35.0) (29.0) | 12.0 (13.0) (11.0) |
| CV h | 0.8 (0.9) (0.5) | 0.6 (0.6) (0.5) | 0.2 (0.2) (0.2) | 0.5 (0.5) (0.4) | 0.7 (0.8) (0.6) | 0.1 (0.1) (0.1) | 0.6 (0.6) (0.5) | 0.8 (0.8) (0.5) | 0.4 (0.4) (0.4) | 0.5 (0.5) (0.5) |
| Q1 i | 4 (4) (6) | 6 (6) (5) | 66 (66) (65) | 1.6 (1.7) (1.6) | 242 (238) (277) | 5.7 (5.7) (5.9) | 0.4 (0.4) (0.4) | 33.0 (32.0) (36.0) | 26.0 (26.0) (25.0) | 9.9 (10.0) (9.5) |
| Q3 j | 15 (15) (15) | 16 (15) (16) | 84 (84) (83) | 3.0 (3.3) (2.1) | 519 (546) (494) | 6.8 (6.8) (6.8) | 0.8 (0.8) (0.6) | 60.0 (62.2) (50.0) | 46.0 (48.0) (36.0) | 20.0 (21.0) (13.0) |
| Denmark, n = 296 (Calibration, n = 228) (Validation, n = 68) | ||||||||||
| Mean | 14 e (15 f) (14 g) | 13 (13) (15) | 68 (69) (68) | 2.2 (2.3) (2.0) | 410 (406) (424) | 6.6 (6.6) (6.6) | 0.7 (0.7) (0.6) | 47.4 (48.0) (45.3) | 31.7 (32.5) (28.7) | 13.1 (13.5) (12.0) |
| Max | 69 (69) (40) | 43 (43) (42) | 91 (91) (90) | 8.4 (8.4) (7.6) | 2409 (2409) (2149) | 8.3 (8.3) (7.7) | 3.9 (3.9) (2.1) | 240.0 (240.0) (190.0) | 130.0 (130.0) (110.0) | 32.0 (32.0) (28.0) |
| Min | 3 (3) (3) | 3 (3) (3) | 11 (11) (13) | 0.8 (0.8) (1.1) | 37 (37) (93) | 4.9 (4.9) (5.5) | 0.2 (0.2) (0.3) | 8.3 (8.3) (9.9) | 11.0 (11.0) (16.0) | 3.9 (3.9) (7.1) |
| Median | 13 (13) (14) | 14 (13) (16) | 69 (70) (66) | 1.9 (1.9) (0.2) | 345 (310) (408) | 6.7 (6.6) (6.7) | 0.5 (0.6) (0.5) | 40.0 (39.0) (43.0) | 28.0 (28.0) (28.0) | 11.0 (11.0) (11.0) |
| CV h | 0.6 (0.7) (0.3) | 0.5 (0.5) (0.3) | 0.2 (0.2) (0.1) | 0.5 (0.5) (0.4) | 0.8 (0.9) (0.7) | 0.1 (0.1) (0.1) | 0.6 (0.6) (0.5) | 0.8 (0.9) (0.6) | 0.5 (0.5) (0.4) | 0.4 (0.4) (0.4) |
| Q1 i | 10 (9) (12) | 10 (9) (13) | 64 (64) (65) | 1.6 (1.6) (1.6) | 208 (197) (272) | 6.3 (6.2) (6.4) | 0.4 (0.5) (0.4) | 29.0 (28.0) (34.8) | 23.1 (23.7) (22.8) | 9.6 (9.8) (9.4) |
| Q3 j | 16 (17) (15) | 16 (16) (17) | 76 (77) (72) | 2.3 (2.4) (2.1) | 485 (493) (477) | 6.9 (7.0) (6.8) | 0.8 (0.9) (0.6) | 48.0 (49.0) (47.3) | 35.3 (37.3) (30.0) | 15.0 (16.0) (13.0) |
| Greenland, n = 143 (Calibration, n = 123) (Validation, n = 20) | ||||||||||
| Mean | 4 e (4 f) (3 g) | 7 (8) (4) | 84 (83) (90) | 3.2 (3.4) (2.1) | 526 (537) (455) | 5.6 (5.6) (5.5) | 0.5 (0.5) (0.3) | 68.9 (71.4) (53.9) | 48.1 (49.5) (39.4) | 21.5 (22.3) (16.6) |
| Max | 9 (9) (4) | 30 (30) (9) | 94 (94) (93) | 7.8 (7.8) (4.7) | 1414 (1414) (757) | 7.4 (7.4) (6.0) | 1.4 (1.4) (0.7) | 300.0 (300.0) (82.0) | 97.0 (97.0) (53.0) | 52.0 (52.0) (41.0) |
| Min | 2 (2) (2) | 2 (2) (2) | 58 (58) (80) | 0.9 (0.9) (1.2) | 57 (57) (197) | 4.4 (4.4) (4.8) | 0.1 (0.1) (0.2) | 22.0 (22.0) (22.0) | 18.0 (18.0) (30.0) | 1.5 (1.5) (8.2) |
| Median | 3 (4) (3) | 6 (7) (3) | 84 (83) (91) | 3.0 (3.1) (1.8) | 472 (472) (469) | 5.5 (5.5) (5.4) | 0.4 (0.5) (0.2) | 57.0 (60) (55.0) | 46.0 (46.0) (38.0) | 21.0 (22.0) (14.5) |
| CV h | 0.3 (0.3) (0.2) | 0.7 (0.6) (0.5) | 0.1 (0.1) (0.0) | 0.4 (0.4) (0.5) | 0.5 (0.6) (0.4) | 0.1 (0.1) (0.1) | 0.6 (0.6) (0.5) | 0.7 (0.7) (0.3) | 0.3 (0.3) (0.2) | 0.5 (0.5) (0.5) |
| Q1 i | 3 (3) (2) | 4 (4) (3) | 79 (78) (89) | 2.1 (2.4) (1.5) | 321 (319) (376) | 5.2 (5.2) (5.3) | 0.3 (0.3) (0.2) | 46.5 (46.5) (46.5) | 38.0 (39.0) (35.3) | 11.0 (12.0) (10.7) |
| Q3 j | 4 (4) (3) | 9 (9) (4) | 90 (89) (92) | 4.1 (4.3) (2.2) | 656 (669) (517) | 5.9 (5.9) (5.8) | 0.7 (0.7) (0.3) | 74.0 (77.0) (63.3) | 54.0 (57.5) (42.0) | 29.0 (30.0) (18.0) |
| Combined | Denmark | Greenland | ||||||
|---|---|---|---|---|---|---|---|---|
| Variables | R2 a | RMSEC b | Variables | R2 a | RMSEC b | Variables | R2 a | RMSEC b |
| Constant | 344.00 | Constant | 358.29 | Constant | 298.92 | |||
| Feox | 0.59 | 220.15 | Feox | 0.61 | 225.18 | Feox | 0.57 | 197.24 |
| Pox | 0.64 | 206.68 | Pox | 0.70 | 197.36 | Pox | 0.72 | 159.21 |
| TOC | 0.71 | 185.21 | TOC | 0.78 | 169.07 | Sand | 0.79 | 138.13 |
| pH | 0.73 | 179.16 | EC | 0.81 | 156.71 | Alox | 0.80 | 135.40 |
| Sand | 0.76 | 168.15 | pH | 0.83 | 150.15 | pH | 0.81 | 133.56 |
| EC | 0.77 | 164.92 | Clay | 0.84 | 147.63 | |||
| Pre-Processing Technique | No of LVs a | R2 b | RMSECV cin L kg−1 | RPIQ d |
|---|---|---|---|---|
| Combined dataset (n = 351) | ||||
| No pre-processing | 14 | 0.66 e (0.81 f) | 199.52 (150.50) | 1.54 (2.05) |
| SNV g | 13 | 0.57 (0.70) | 234.29 (189.83) | 1.31 (1.62) |
| MSC h | 11 | 0.57 (0.68) | 226.18 (198.45) | 1.36 (1.55) |
| SG 1st derivative i | 11 | 0.69 (0.79) | 193.09 (158.30) | 1.60 (1.95) |
| SG 2nd derivative i | 11 | 0.62 (0.76) | 211.80 (166.83) | 1.45 (1.85) |
| SG 1st derivative + MSC | 11 | 0.64 (0.74) | 206.82 (176.67) | 1.49 (1.74) |
| SG 1st derivative + SNV | 13 | 0.73 (0.77) | 182.44 (164.52) | 1.69 (1.87) |
| Danish dataset (n = 228) | ||||
| No pre-processing | 15 | 0.80 (0.84) | 162.44 (143.14) | 1.82 (2.07) |
| SNV | 14 | 0.70 (0.80) | 201.36 (163.55) | 1.47 (1.81) |
| MSC | 15 | 0.78 (0.80) | 168.68 (157.71) | 1.75 (1.88) |
| SG 1st derivative | 10 | 0.77 (0.82) | 172.19 (151.87) | 1.72 (1.95) |
| SG 2nd derivative | 11 | 0.77 (0.83) | 173.63 (145.63) | 1.70 (2.05) |
| SG 1st derivative + MSC | 12 | 0.74 (0.82) | 182.39 (151.72) | 1.62 (1.95) |
| SG 1st derivative + SNV | 09 | 0.64 (0.77) | 221.55 (173.55) | 1.34 (1.71) |
| Greenlandic dataset (n = 123) | ||||
| No pre-processing | 03 | 0.70 (0.68) | 162.07 (168.14) | 2.16 (2.08) |
| SNV | 07 | 0.66 (0.63) | 183.60 (183.23) | 1.91 (1.91) |
| MSC | 03 | 0.48 (0.46) | 215.18 (218.69) | 1.63 (1.60) |
| SG 1st derivative | 03 | 0.66 (0.66) | 173.78 (173.84) | 2.01 (2.01) |
| SG 2nd derivative | 04 | 0.70 (0.69) | 162.99 (166.52) | 2.15 (2.10) |
| SG 1st derivative + MSC | 04 | 0.59 (0.59) | 191.90 (190.71) | 1.82 (1.84) |
| SG 1st derivative + SNV | 03 | 0.67 (0.68) | 172.63 (171.70) | 2.03 (2.04) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akter, S.; de Jonge, L.W.; Møldrup, P.; Greve, M.H.; Nørgaard, T.; Weber, P.L.; Hermansen, C.; Mouazen, A.M.; Knadel, M. Visible Near-Infrared Spectroscopy and Pedotransfer Function Well Predict Soil Sorption Coefficient of Glyphosate. Remote Sens. 2023, 15, 1712. https://doi.org/10.3390/rs15061712
Akter S, de Jonge LW, Møldrup P, Greve MH, Nørgaard T, Weber PL, Hermansen C, Mouazen AM, Knadel M. Visible Near-Infrared Spectroscopy and Pedotransfer Function Well Predict Soil Sorption Coefficient of Glyphosate. Remote Sensing. 2023; 15(6):1712. https://doi.org/10.3390/rs15061712
Chicago/Turabian StyleAkter, Sonia, Lis Wollesen de Jonge, Per Møldrup, Mogens Humlekrog Greve, Trine Nørgaard, Peter Lystbæk Weber, Cecilie Hermansen, Abdul Mounem Mouazen, and Maria Knadel. 2023. "Visible Near-Infrared Spectroscopy and Pedotransfer Function Well Predict Soil Sorption Coefficient of Glyphosate" Remote Sensing 15, no. 6: 1712. https://doi.org/10.3390/rs15061712
APA StyleAkter, S., de Jonge, L. W., Møldrup, P., Greve, M. H., Nørgaard, T., Weber, P. L., Hermansen, C., Mouazen, A. M., & Knadel, M. (2023). Visible Near-Infrared Spectroscopy and Pedotransfer Function Well Predict Soil Sorption Coefficient of Glyphosate. Remote Sensing, 15(6), 1712. https://doi.org/10.3390/rs15061712