Breach Progression Observation in Rockfill Dam Models Using Photogrammetry
Abstract
:1. Introduction
2. Methods and Materials
2.1. Physical Model Description
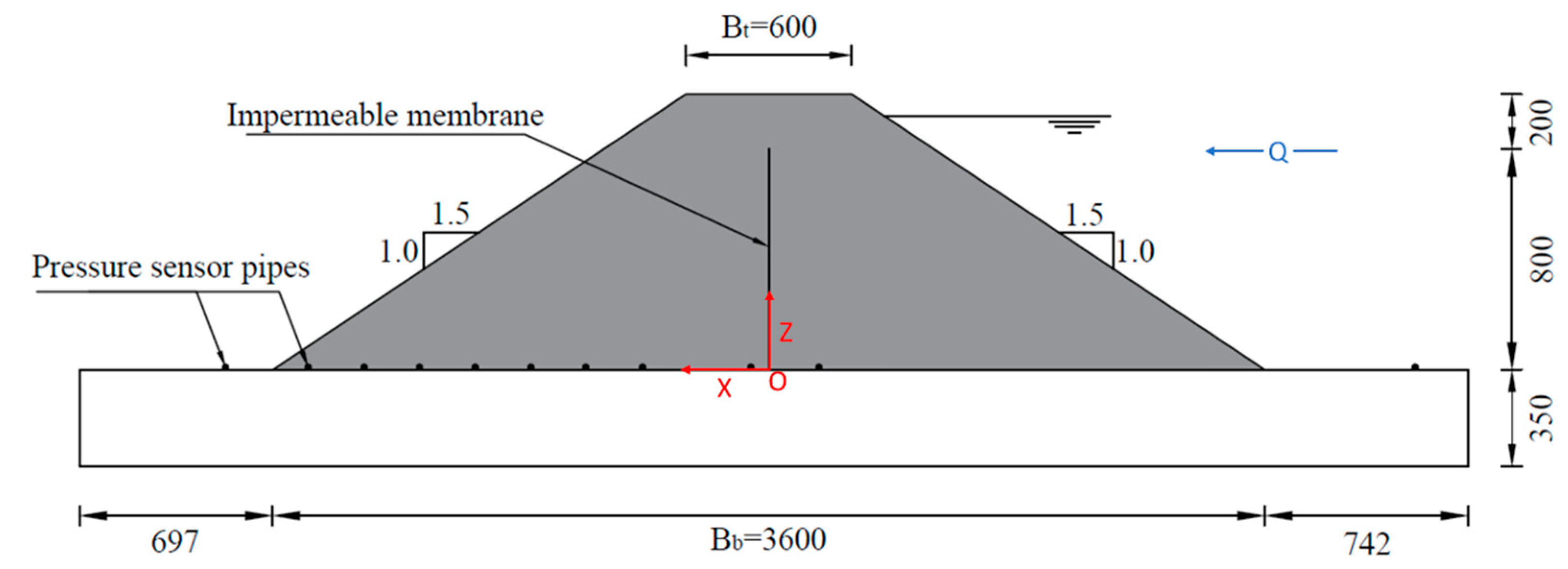
2.1.1. The Dam Model
2.1.2. Sensor Data Collection
2.1.3. Video Cameras Setup and Type
2.2. Materials
2.2.1. Core Material
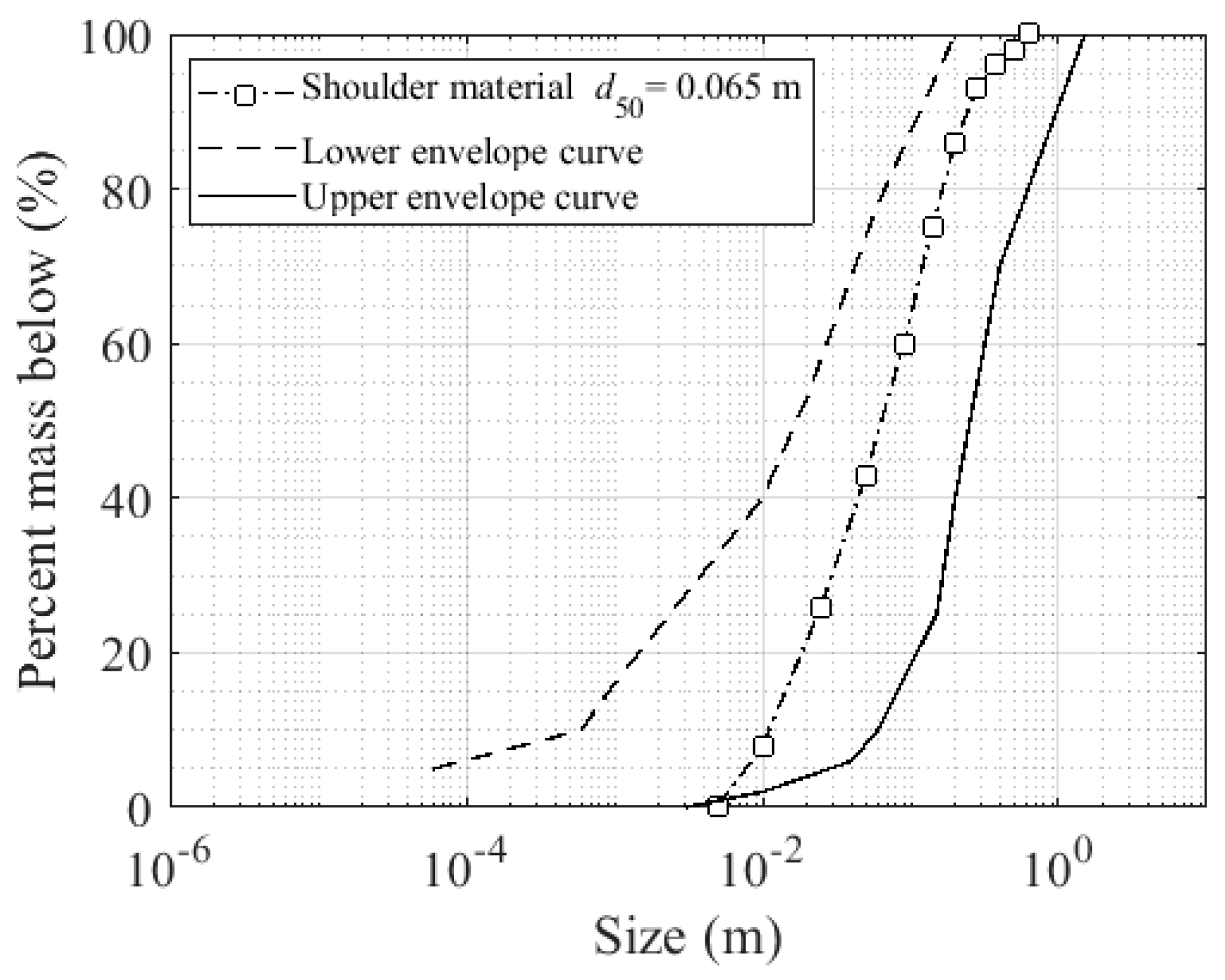
2.2.2. Rockfill
2.3. Testing Procedure
2.4. Sensor Data Analysis
2.5. Image Analysis and Photogrammetry
3. Results
3.1. Visual Observation
3.1.1. Dam Model with a Central Core
3.1.2. Dam Model without a Core
3.2. Side-View Video Analysis
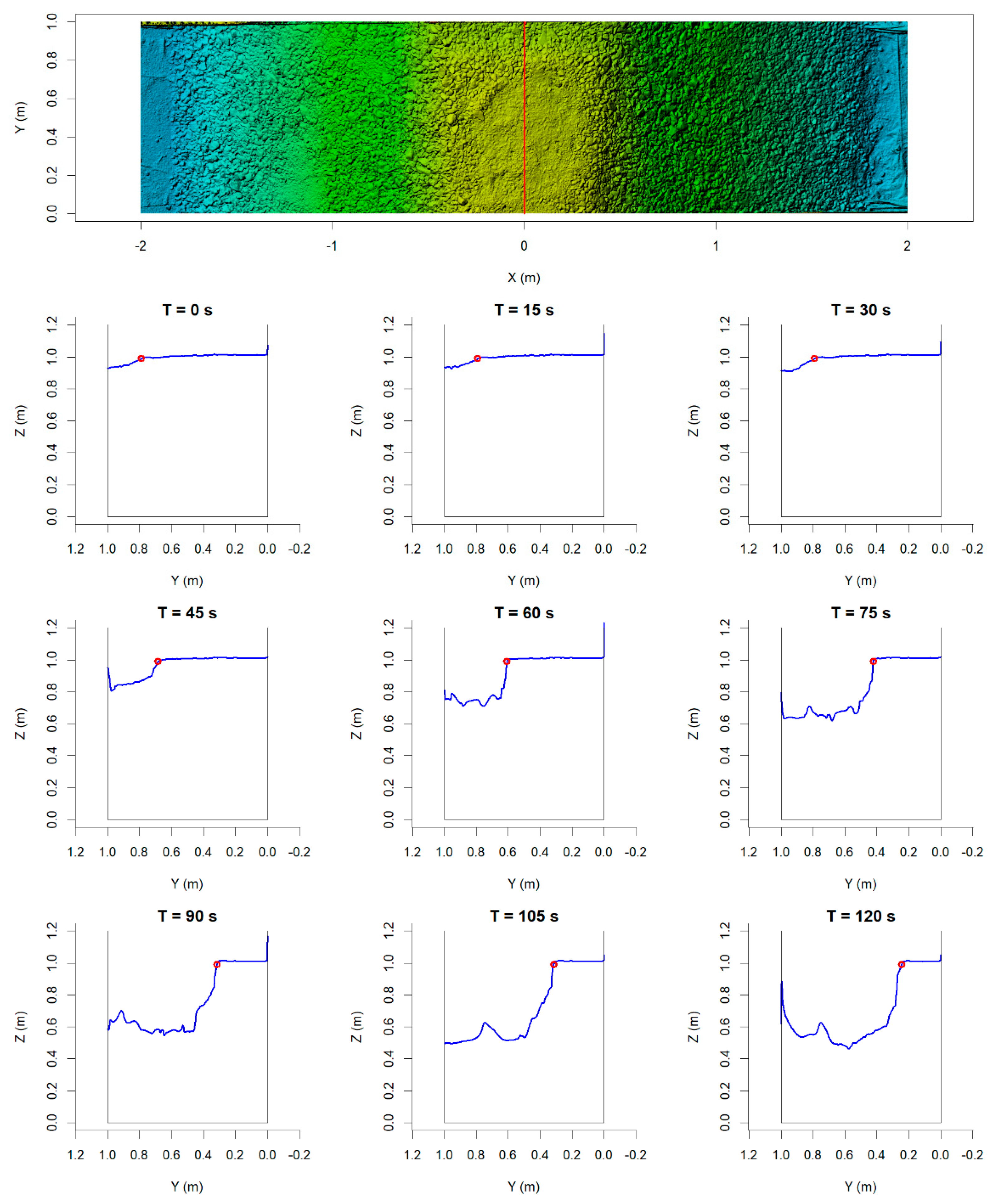
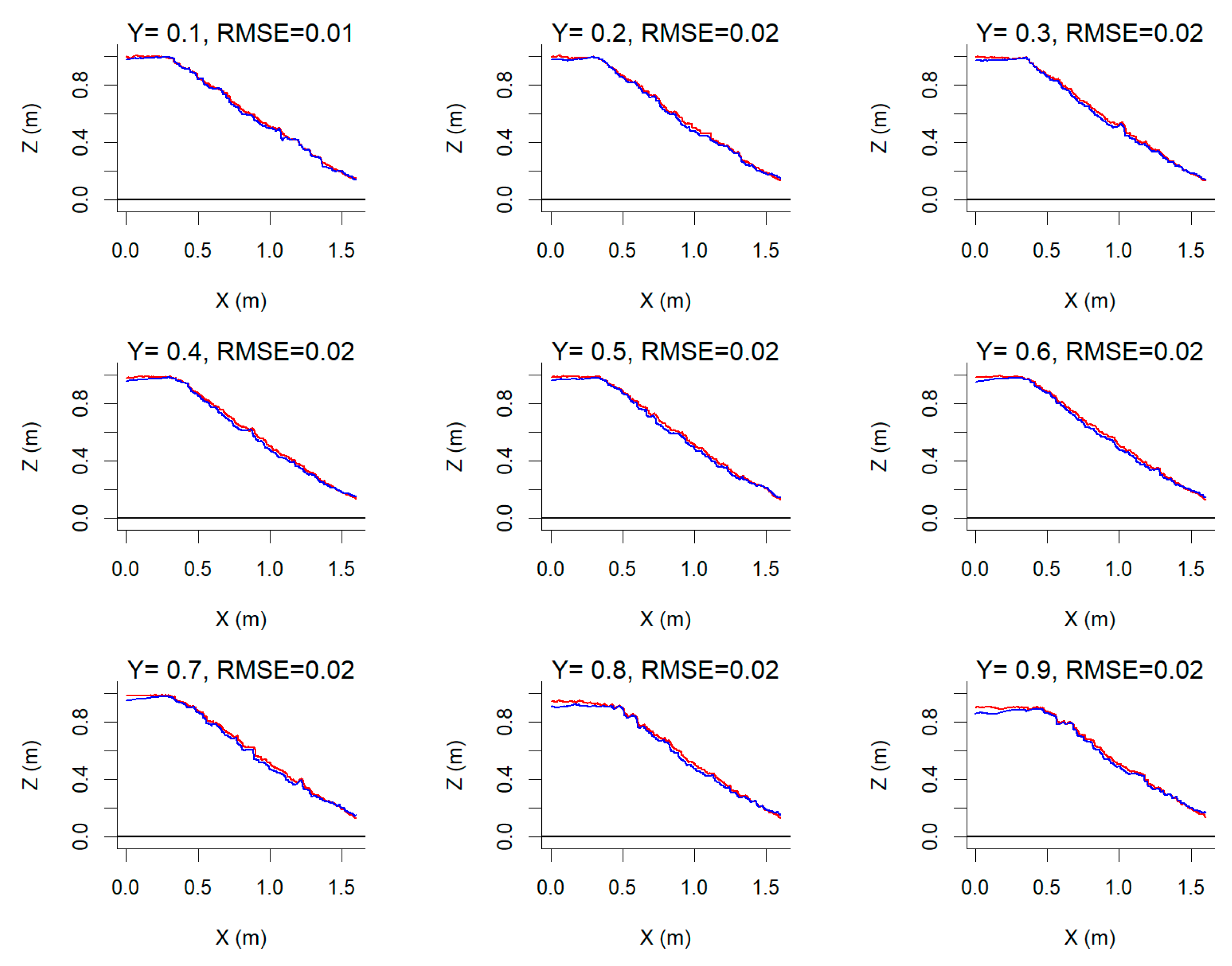
3.3. Analysis of 3D Models
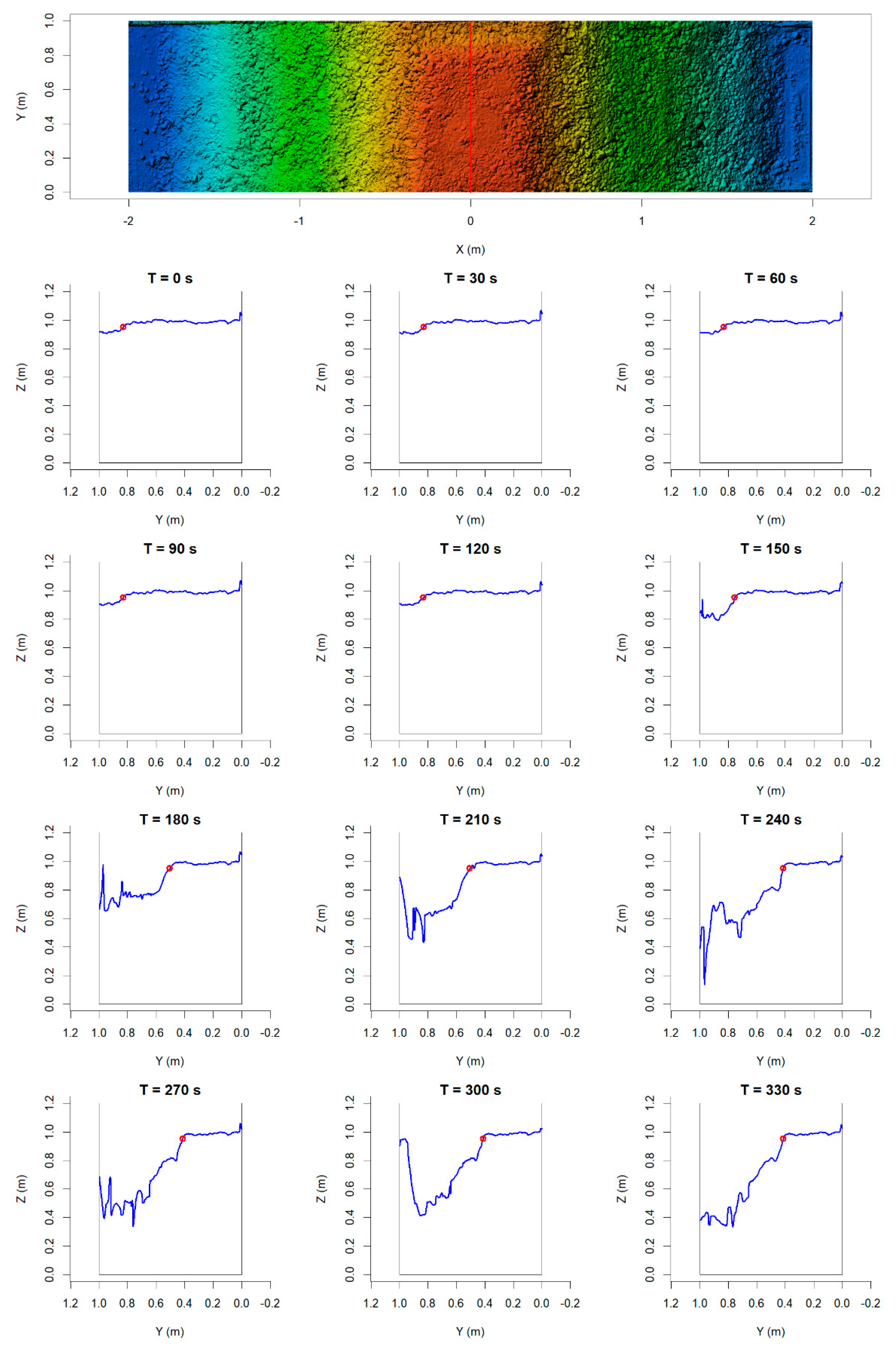
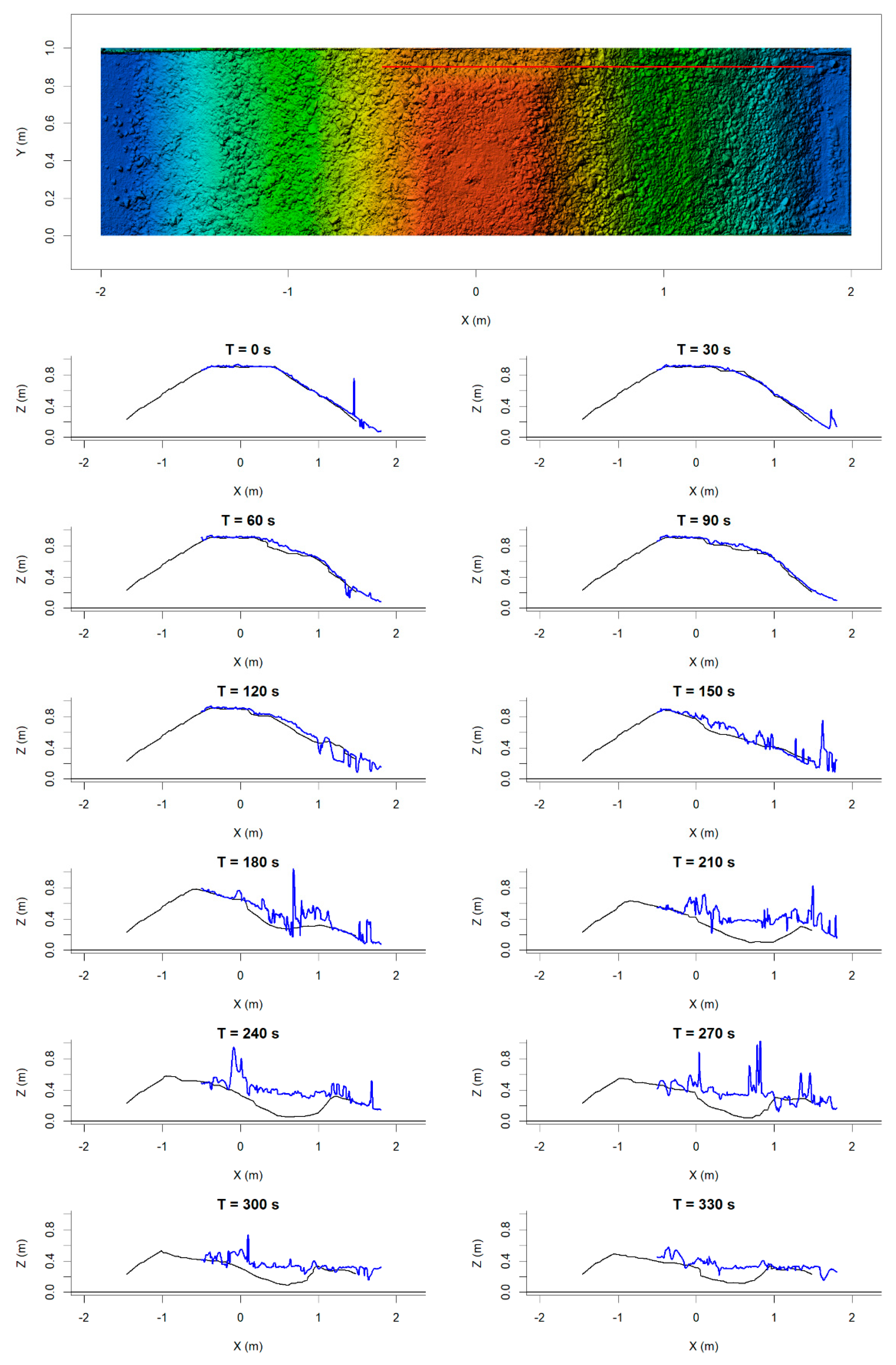
3.3.1. Profiles from DEM Models
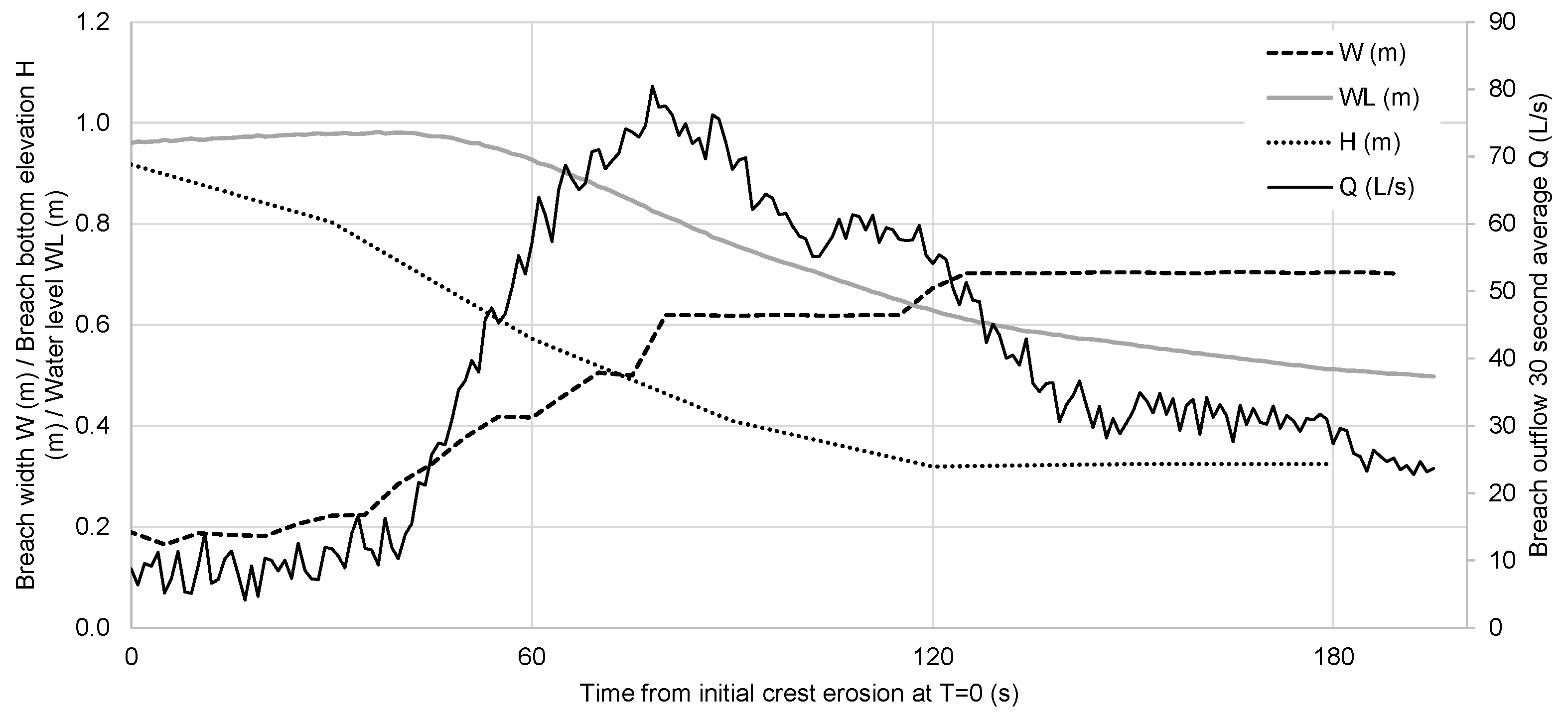
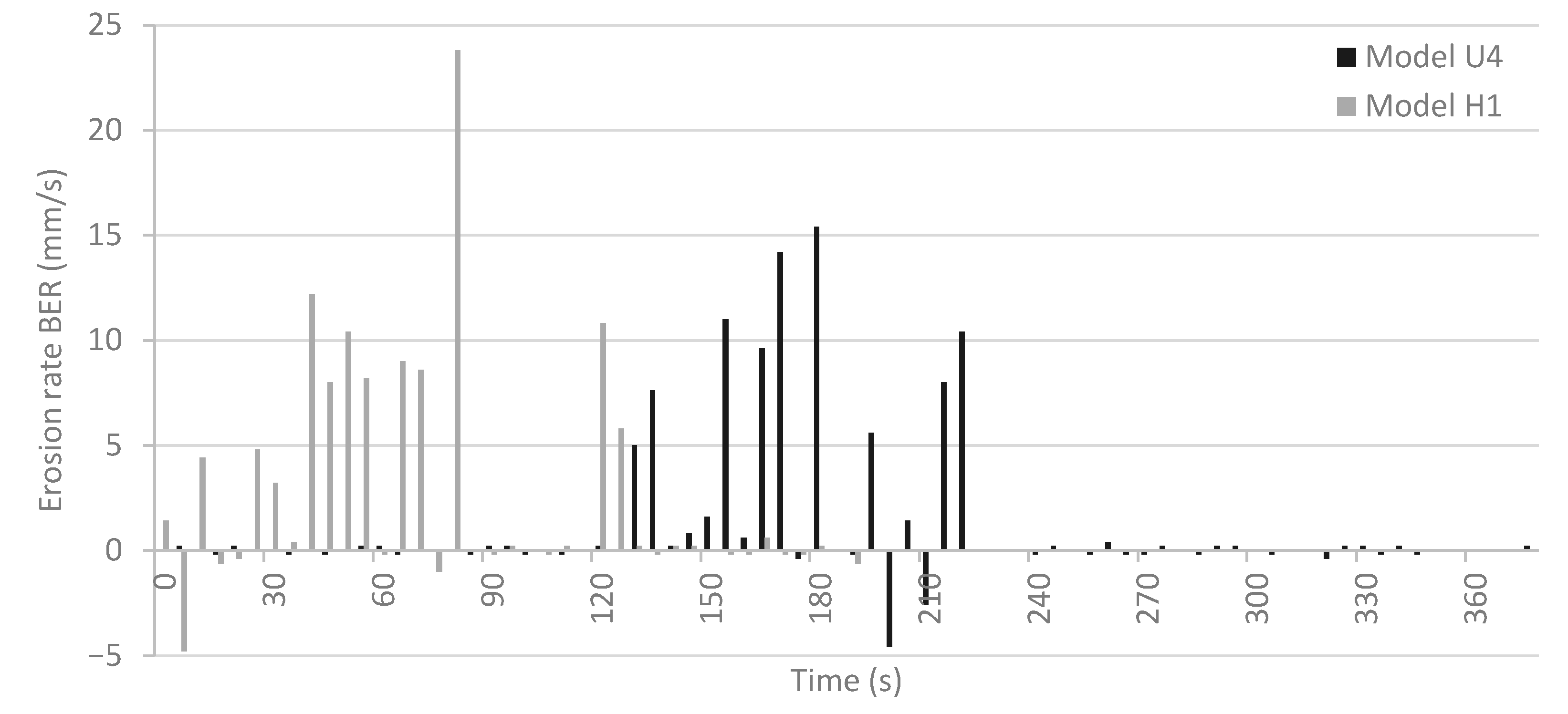
3.3.2. Breach Edge Tracking
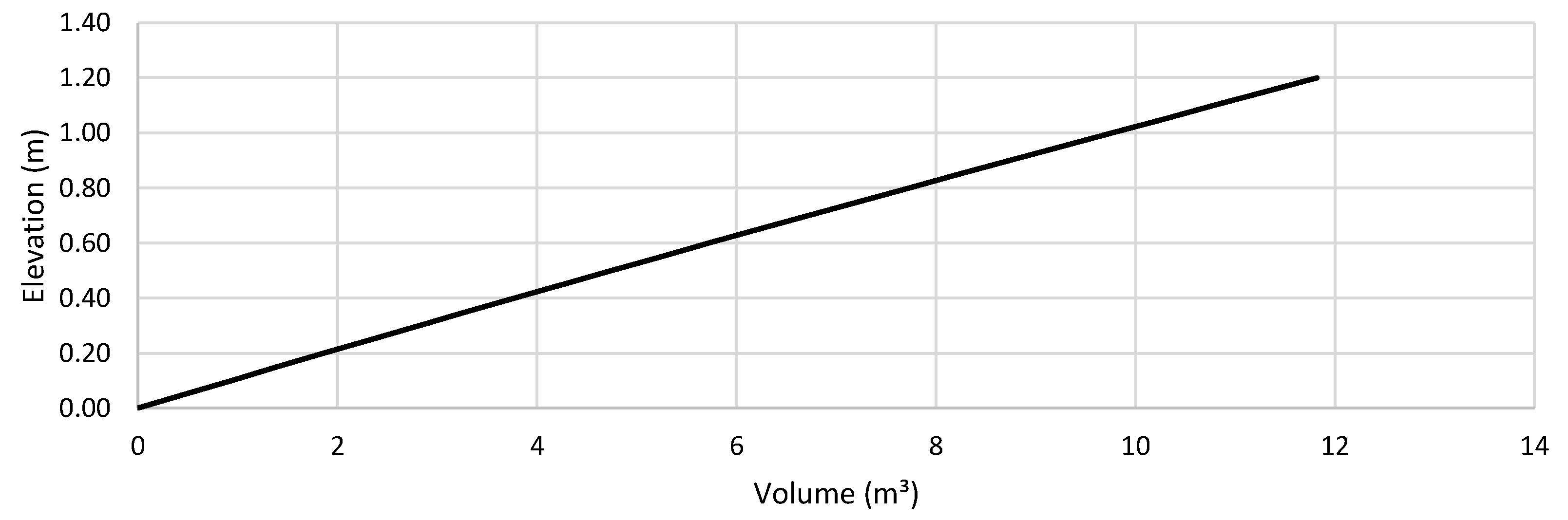
3.3.3. Volume Change
3.4. Dynamic DEM Validation
4. Discussion
4.1. Advantages and Limitations of Photogrammetric Methods
4.2. Breaching Process Compared to the Literature
4.3. Comparison between Models of the Present Study
4.4. Limitation of the Breaching Results
4.5. Further Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Bb | Bottom width of dam (fundamental units L) |
| Bt | Top width of dam (fundamental units L) |
| BER | Breach expansion rate (fundamental units L·T−1) |
| Cu | Coefficient of uniformity, the ratio D60/D10 where D60 and D10 are the sieve sizes through which 60% and 10% of the material passes (dimensionless) |
| CV | Coefficient of variation |
| D50 | Sieve size passing 50% of the particles (fundamental units L) |
| DEM | Digital Elevation Model |
| DSM | Digital Surface Model |
| g | Acceleration of gravity (fundamental units L·T−2) |
| Hd | Height of the dam (fundamental units L) |
| L | Length, fundamental dimension |
| Ld | Transverse length of the embankment (fundamental units L) |
| M | Mass, fundamental dimension |
| MVS | Multi View Stereo (photogrammetric method) |
| n | Porosity (dimensionless) |
| Q | Discharge (fundamental units L3·T−1) |
| R | Correlation coefficient |
| RMSE | Root mean square error |
| ρ | Density (fundamental units M·L−3) |
| SFM | Structure from Motion (photogrammetric method) |
| SPH | Smoothed Particle Hydrodynamics (numerical simulation technique) |
| T | Time, fundamental dimension |
| V | Volume (fundamental units L3) |
| Vdiff | Volume difference (fundamental units L3) |
| W | Breach top width (fundamental units L) |
| WL | Water level (fundamental units L) |
| X | Coordinate system axis (fundamental units L) |
| Y | Coordinate system axis (fundamental units L) |
| Z | Coordinate system axis (fundamental units L) |
| Zdss | Slope of the downstream rockfill shoulder (dimensionless) |
| Zuss | Slope of the upstream rockfill shoulder (dimensionless) |
Appendix A
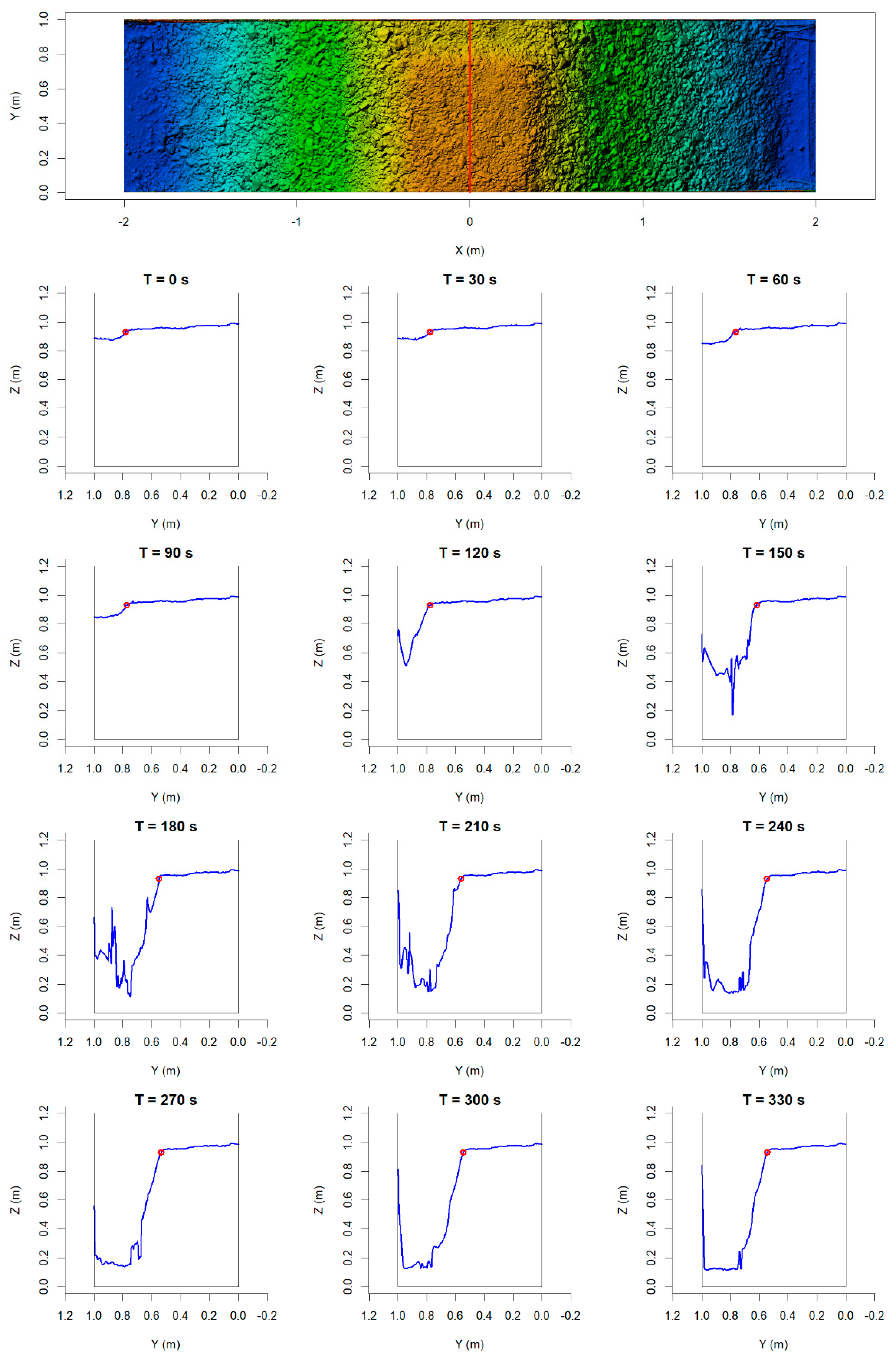
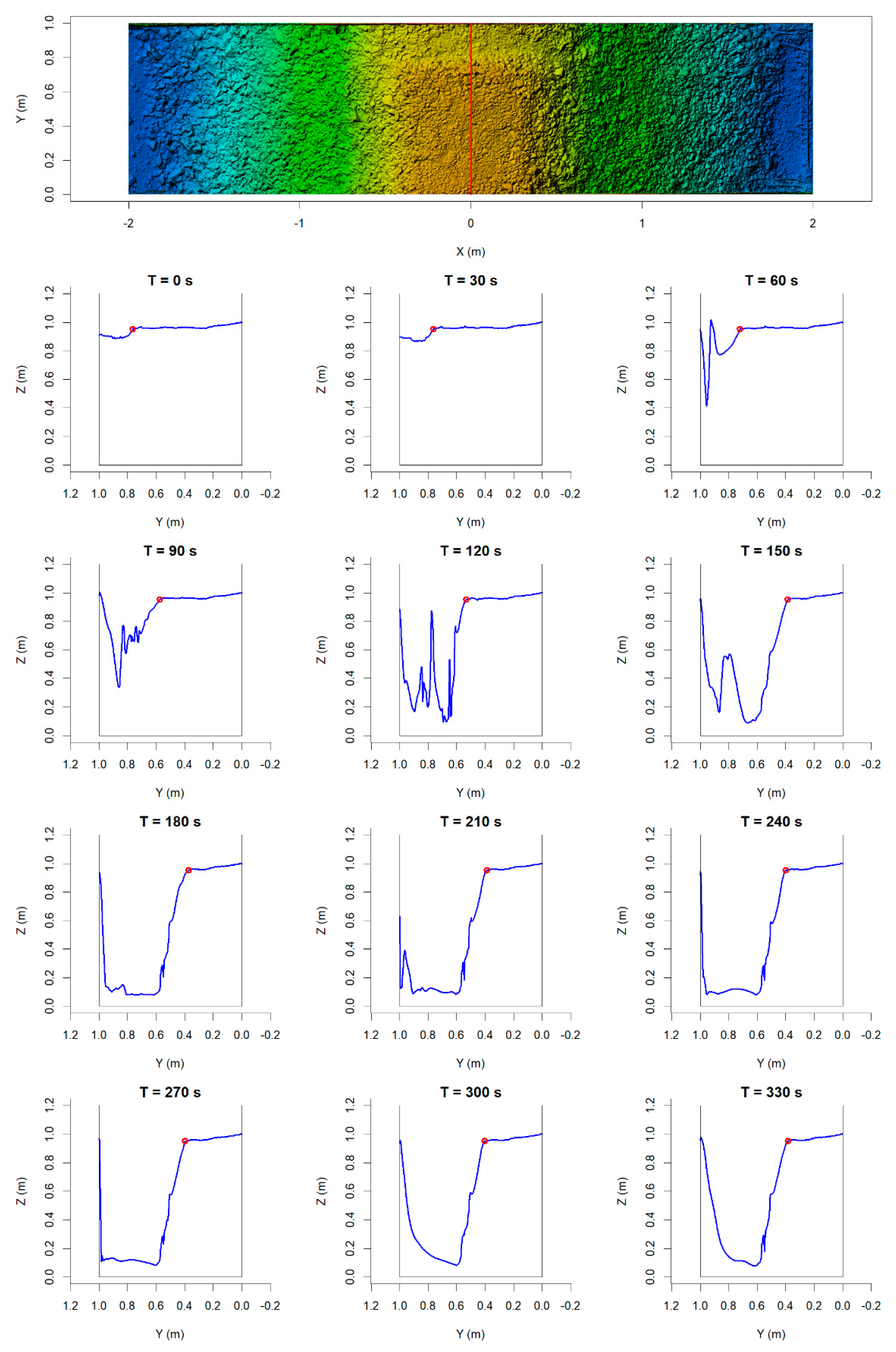


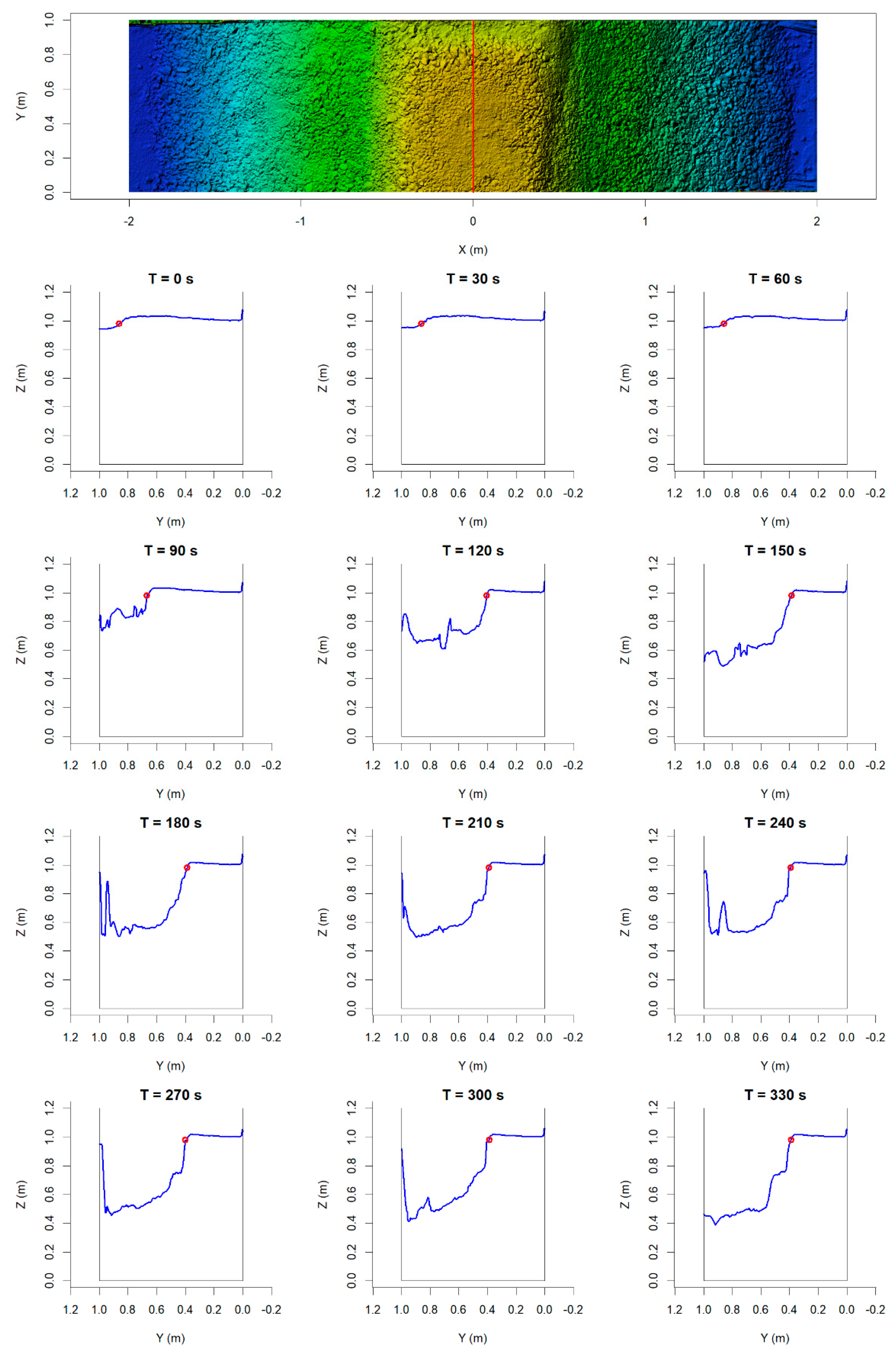
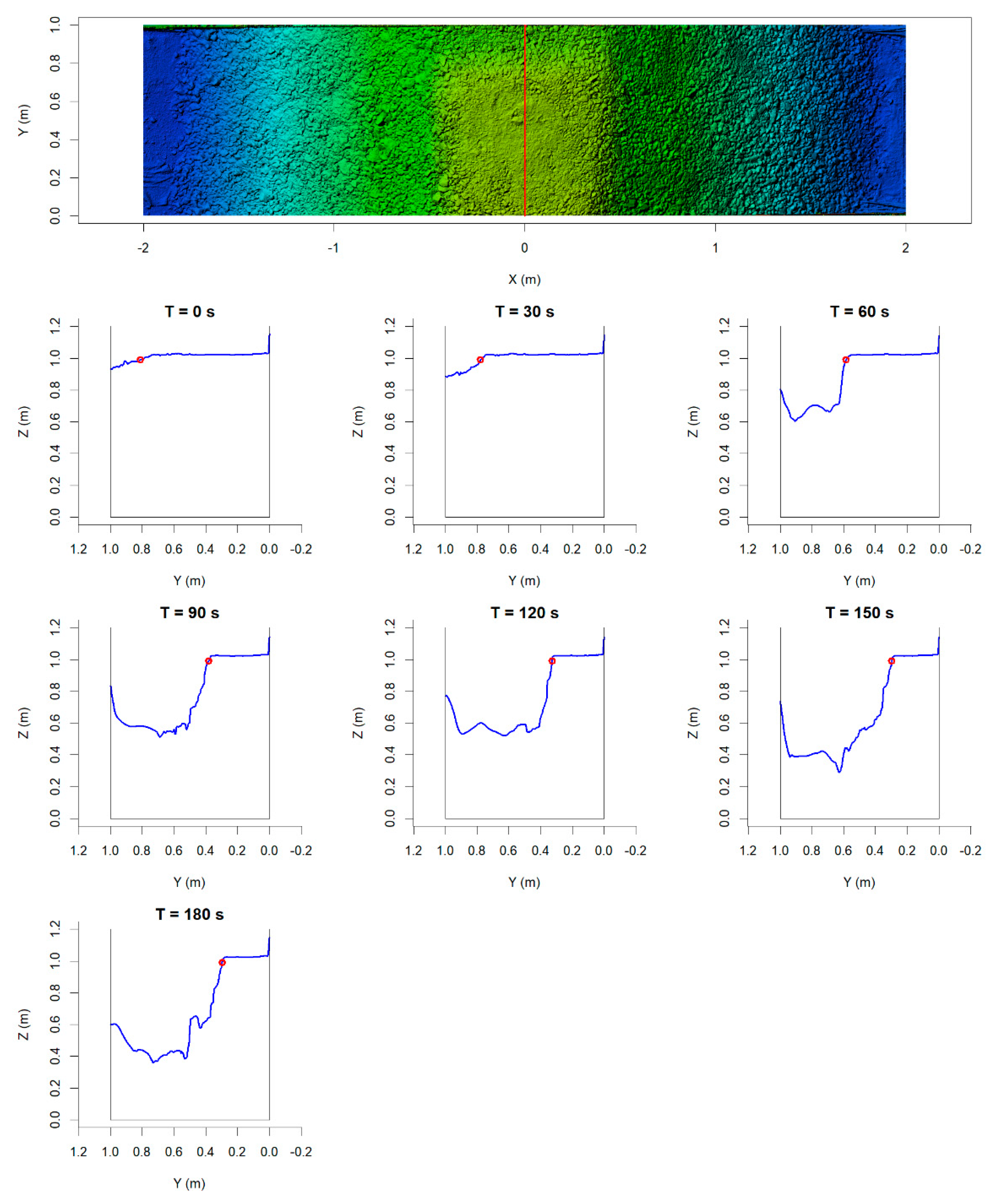

References
- ICOLD. ICOLD Incident Database Bulletin 99 Update Statistical Analysis of Dam Failures; ICOLD: Paris, France, 2019. [Google Scholar]
- Sigurjonsson, S.; Sigtryggsdottir, F.G.; Kiplesund, G.H. Pertinence of parametric based breach models for rockfill dams. In Proceedings of the 20th International Conference on Soil Mechanics and Geotechnical Engineering, Sydney, Australia, 1–5 May 2022; Australian Geomechanics Society: Sydney, Australia; SIMSG; ISSMGE: London, UK, 2022; pp. 2753–2758. [Google Scholar]
- West, M.; Morris, M.; Hassan, M. A Guide to Breach Prediction; HR Wallingford: Oxford, UK, 2018. [Google Scholar]
- ICOLD World Register of Dams-General Synthesis. Available online: https://www.icold-cigb.org/GB/world_register/general_synthesis.asp (accessed on 26 September 2022).
- Pörtner, H.; Roberts, D.; Tignor, M.; Poloczanska, E.; Mintenbeck, K.; Alegría, A.; Craig, M.; Langsdorf, S.; Löschke, S.; Möller, V.; et al. Climate Change 2022: Impacts, Adaptation and Vulnerability Working Group II Contribution to the IPCC Sixth Assessment Report; IPCC: Geneva, Switzerland, 2022; ISBN 9781009325844. [Google Scholar]
- Monteiro-Alves, R.; Toledo, M.Á.; Moran, R.; Balairón, L. Failure of the Downstream Shoulder of Rockfill Dams Due to Overtopping or Throughflow. Water 2022, 14, 1624. [Google Scholar] [CrossRef]
- Larese, A.; Rossi, R.; Oñate, E.; Toledo, M.Á.; Morán, R.; Campos, H. Numerical and Experimental Study of Overtopping and Failure of Rockfill Dams. Int. J. Geomech. 2015, 15, 04014060. [Google Scholar] [CrossRef]
- Chinnarasri, C.; Jirakitlerd, S.; Wongwises, S. Embankment dam breach and its outflow characteristics. Civ. Eng. Environ. Syst. 2004, 21, 247–264. [Google Scholar] [CrossRef]
- Asghari Tabrizi, A.; Elalfy, E.; Elkholy, M.; Chaudhry, M.H.; Imran, J. Effects of compaction on embankment breach due to overtopping. J. Hydraul. Res. 2017, 55, 236–247. [Google Scholar] [CrossRef]
- Wahl, T.L. Erosion Testing of Zoned Rockfill Embankments; United States Bureau of Reclamation: Washington, DC, USA, 2019.
- Morris, M.W.; Hassan, M.A.A.M.; Vaskinn, K.A. Breach formation: Field test and laboratory experiments. J. Hydraul. Res. 2007, 45, 9–17. [Google Scholar] [CrossRef]
- Cao, Z.; Yue, Z.; Pender, G. Landslide dam failure and flood hydraulics. Part I: Experimental investigation. Nat. Hazards 2011, 59, 1003–1019. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, Y.; Wu, L.; Lei, Y. Experimental investigation of failure modes and breaching characteristics of natural dams. Geomat. Nat. Hazards Risk 2018, 9, 33–48. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, G.; Peng, M.; Zhang, Q.; Zhou, Y.; Zhou, M. Experimental Investigation on the Breaching Process of Landslide Dams with Differing Materials under Different Inflow Conditions. Materials 2022, 15, 2029. [Google Scholar] [CrossRef]
- Awal, R.; Nakagawa, H.; Fujita, M.; Kawaike, K.; Baba, Y.; Zhang, H. Experimental Study on Glacial Lake Outburst Floods Due to Waves Overtopping and Erosion of Moraine Dam. Annu. Disas. Prev. Res. Inst. Kyoto Univ. 2010, 53, 583–594. [Google Scholar]
- Vaskinn, K.A.; Løvoll, A.; Höeg, K.; Morris, M.; Hanson, G.J.; Hassan, M.A. Physical modeling of breach formation: Large scale field tests. Proc. Dam Saf. 2004, 1–16. [Google Scholar]
- Amaral, S.; Viseu, T.; Ferreira, R. Experimental methods for local-scale characterization of hydro-morphodynamic dam breach processes. Breach detection, 3D reconstruction, flow kinematics and spatial surface velocimetry. Flow Meas. Instrum. 2019, 70, 101658. [Google Scholar] [CrossRef]
- James, M.R.; Chandler, J.H.; Eltner, A.; Fraser, C.; Miller, P.E.; Mills, J.P.; Noble, T.; Robson, S.; Lane, S.N. Guidelines on the use of structure-from-motion photogrammetry in geomorphic research. Earth Surf. Process. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Abellan, A.; Schindewolf, M. Time lapse structure-from-motion photogrammetry for continuous geomorphic monitoring. Earth Surf. Process. Landf. 2017, 42, 2240–2253. [Google Scholar] [CrossRef]
- Cucchiaro, S.; Maset, E.; Fusiello, A.; Cazorzi, F. 4D-SFM photogrammetry for monitoring sediment dynamics in a debris-flow catchment: Software testing and results comparison. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; International Society for Photogrammetry and Remote Sensing, Istanbul, Turkey, 18–21 March 2018; Volume 42, pp. 281–288. [Google Scholar]
- Pacheco-Ruiz, R.; Adams, J.; Pedrotti, F. 4D modelling of low visibility Underwater Archaeological excavations using multi-source photogrammetry in the Bulgarian Black Sea. J. Archaeol. Sci. 2018, 100, 120–129. [Google Scholar] [CrossRef] [Green Version]
- Dezert, T.; Kiplesund, G.H.; Sigtryggsdóttir, F.G. Riprap Protection Exposed to Overtopping Phenomena: A Review of Laboratory Experimental Models. Water 2022, 14, 2722. [Google Scholar] [CrossRef]
- Hiller, P.H.; Aberle, J.; Lia, L. Displacements as failure origin of placed riprap on steep slopes. J. Hydraul. Res. 2018, 56, 141–155. [Google Scholar] [CrossRef] [Green Version]
- Kiplesund, G.H.; Sigtryggsdóttir, F.G. Laboratory Investigations into Stability and Breaching of Rockfill Dams Using Dynamic Structure from Motion. In Proceedings of the 39th IAHR World Congress, Granada, Spain, 19–24 June 2022; IAHR: Granada, Spain, 2022; pp. 5079–5088. [Google Scholar]
- Hyllestad, E.; Andersen, R.; Østvold, H.M.; Rystad, V. Veileder for Fyllingsdammer; NVE: Oslo, Norway, 2012. [Google Scholar]
- Kiplesund, G.H.; Ravindra, G.H.R.; Rokstad, M.M.; Sigtryggsdóttir, F.G. Effects of toe configuration on throughflow properties of rockfill dams. J. Appl. Water Eng. Res. 2021, 9, 277–292. [Google Scholar] [CrossRef]
- ICOLD. Geomembrane Sealing Systems for Dams—Design Principles and Review of Experience Bulletin 135; International Commission on Large Dams: Paris, France, 2010. [Google Scholar]
- Demirdogen, S.; Gunaratne, M. Stability analysis of embankment dams with defective internal geomembrane liners. Int. J. Geotech. Eng. 2022, 16, 1165–1175. [Google Scholar] [CrossRef]
- Wang, W.; Höeg, K. Simplified material model for analysis of asphalt core in embankment dams. Constr. Build. Mater. 2016, 124, 199–207. [Google Scholar] [CrossRef]
- Høeg, K. Asphaltic Concrete Cores for Embankment Dams; Norwegian Geotechnical Institute: Oslo, Norway, 1993; ISBN 82-546-0163-1. [Google Scholar]
- NTNU. Course Compendium for VM6001-Dam Safety; Department of Civil and Environmental Engineering, NTNU: Singapore, 2020. [Google Scholar]
- USDA. Natural Resources Conservation Service Gradation Design of Sand and Gravel Filters. In National Engineering Handbook Part 633; USDA: Washington, DC, USA, 2017. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 20 September 2022).
- FFmpeg Developers FFmpeg. Available online: https://ffmpeg.org/ (accessed on 16 September 2022).
- Agisoft LLC. Agisoft Metashape User Manual Professional Edition, Version 2.0.; Agisoft LLC: St. Petersburg, Russia, 2022; p. 160. [Google Scholar]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef] [Green Version]
- Hendrickx, H.; Vivero, S.; De Cock, L.; De Wit, B.; De Maeyer, P.; Lambiel, C.; Delaloye, R.; Nyssen, J.; Frankl, A. The reproducibility of SfM algorithms to produce detailed Digital Surface Models: The example of PhotoScan applied to a high-alpine rock glacier. Remote Sens. Lett. 2018, 10, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Pock, T.; Zebedin, L.; Bischof, H. TGV-Fusion. In Rainbow of Computer Science. Lecture Notes in Computer Science; Calude, C.S., Rozenberg, G., Salomaa, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6570, pp. 245–258. ISBN 9783642193903. [Google Scholar]
- Poliarnyi, N.; Agisoft, L. Out-of-Core Surface Reconstruction via Global T GV Minimization. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 5641–5650. [Google Scholar]
- Kingsland, K. Comparative analysis of digital photogrammetry software for cultural heritage. Digit. Appl. Archaeol. Cult. Herit. 2020, 18, e00157. [Google Scholar] [CrossRef]
- Kloc, B.; Mazur, A.; Szumiło, M. Comparison of Free and Commercial Software in the Processing of Data Obtained from Non-Metric Cameras. J. Ecol. Eng. 2021, 22, 213–225. [Google Scholar] [CrossRef]
- QGIS Development Team QGIS Software. Available online: https://www.qgis.org/ (accessed on 20 September 2022).
- Pugh, C.A. Report No. REC-ERC-85-7, “Hydraulic Model Studies of Fuse Plug Embankments”; USBR: Denver, CO, USA, 1985.
- Franca, M.J.; Almeida, A.B. Experimental Tests on Rockfill Dam Breaching Process. In Proceedings of the IAHR-International Symposium on Hydraulic and Hydrological Aspects of Reliability and Safety Assessment of Hydraulic Structures, St. Petersburg, Russia, 29 May–2 June 2002. [Google Scholar]









| Model | Date | Core Material | Leakage Flow (L/s) | Inflow (L/s) | No. of Cameras Total/SFM | Ground Control Points | No. of Dynamic Frames | No. of Start Images | No. of End Images |
|---|---|---|---|---|---|---|---|---|---|
| U1 | 2020-10-01 | Rubber | 1 | 5.1 | 6/3 | 8 | 120 | 38 | 52 |
| U2 | 2020-10-10 | Rubber | 0.7 | 5.1 | 6/3 | 8 | 168 | 34 | 54 |
| U3 | 2021-01-05 | Rubber | 0.7 | 10.3 | 6/3 | 8 | 120 | 39 | 48 |
| U4 | 2021-08-10 | Rubber | 0.2 | 5.0 | 6/5 | 7 | 132 | 34 | 88 |
| U5 | 2022-01-14 | Rubber | 0.3 | 15.2 | 9/7 | 7 | 108 | 48 | 67 |
| H1 | 2022-02-03 | None | NA | 15.0 | 9/7 | 6 | 60 | 62 | 92 |
| H2 | 2022-02-10 | None | NA | 20.5 | 9/7 | 6 | 36 | 49 | 90 |
| H3 | 2022-02-23 | None | NA | 15 * | 9/7 | 6 | 48 | 64 | 103 |
| Test | Test Inflow (L/s) | Vdiff (m³) | Breach Time (s) |
|---|---|---|---|
| U1 | 5.1 | 0.45 | 170 |
| U2 | 5.1 | 0.47 | 145 |
| U3 | 10.3 | 0.59 | 85 |
| U4 | 5 | 0.49 | 220 |
| U5 | 15.2 | 0.64 | 120 |
| Coefficient of correlation (R) | 0.97 | −0.66 | |
| H1 | 15 | 0.69 | 125 |
| H2 | 20.5 | 0.75 | 120 |
| H3 | 15 | 0.70 | 175 |
| Coefficient of correlation (R) | 0.99 | −0.57 | |
| Model U1 | Model U2 | Model U3 | Model U4 | Model U5 | Model H1 | Model H2 | Model H3 | |
|---|---|---|---|---|---|---|---|---|
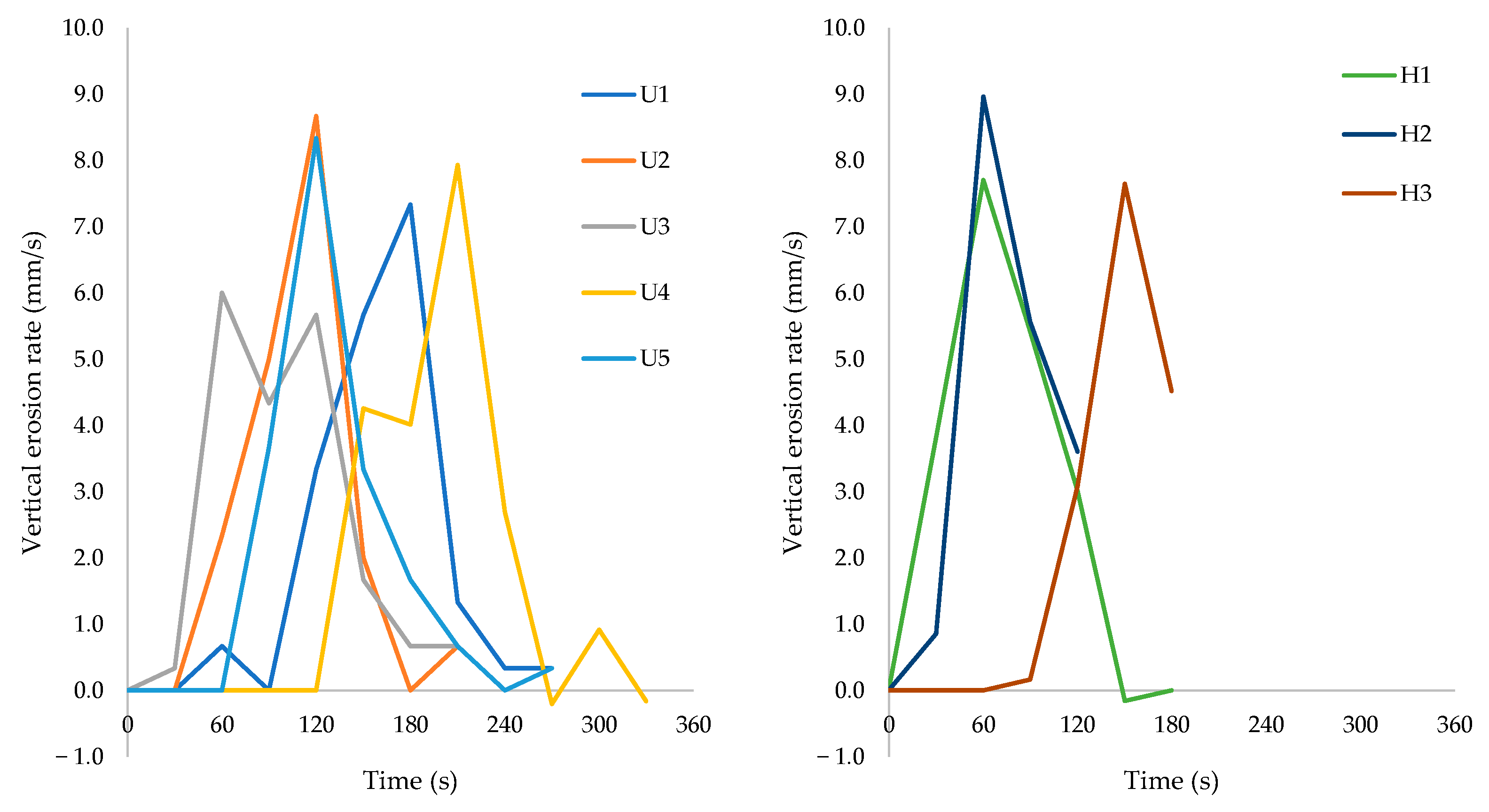
| Max 30 s vertical erosion rate (mm/s) | 7.3 | 8.7 | 6.0 | 7.9 | 8.3 | 7.3 | 6.0 | 6.3 |
| Average vertical erosion rate (mm/s) | 4.4 | 4.5 | 4.4 | 4.7 | 4.3 | 6.2 | 5.1 | 4.3 |
| Max 30 s lateral erosion rate (mm/s) | 7.6 | 5.2 | 13.0 | 8.8 | 8.7 | 7.3 | 11.3 | 9.7 |
| Average lateral erosion rate (mm/s) | 4.4 | 4.2 | 11.4 | 4.7 | 7.1 | 6.2 | 6.2 | 7.2 |
| Average inflow (L/s) | 5.1 | 5.1 | 10.3 | 5.0 | 15.2 | 15.0 | 20.5 | Ca 15 |
| Max 30 s outflow (L/s) | 55.8 | 56.5 | 56.0 | 60.9 | 73.9 | 80.4 | 81.3 | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiplesund, G.H.; Sigtryggsdottir, F.G.; Lia, L. Breach Progression Observation in Rockfill Dam Models Using Photogrammetry. Remote Sens. 2023, 15, 1715. https://doi.org/10.3390/rs15061715
Kiplesund GH, Sigtryggsdottir FG, Lia L. Breach Progression Observation in Rockfill Dam Models Using Photogrammetry. Remote Sensing. 2023; 15(6):1715. https://doi.org/10.3390/rs15061715
Chicago/Turabian StyleKiplesund, Geir Helge, Fjola Gudrun Sigtryggsdottir, and Leif Lia. 2023. "Breach Progression Observation in Rockfill Dam Models Using Photogrammetry" Remote Sensing 15, no. 6: 1715. https://doi.org/10.3390/rs15061715
APA StyleKiplesund, G. H., Sigtryggsdottir, F. G., & Lia, L. (2023). Breach Progression Observation in Rockfill Dam Models Using Photogrammetry. Remote Sensing, 15(6), 1715. https://doi.org/10.3390/rs15061715






