Yield Adjustment Using GPR-Derived Spatial Covariance Structure in Cassava Field: A Preliminary Investigation
Abstract
:1. Introduction
- (a)
- Plan and execute an experimental design based on a multi-antenna GPR array;
- (b)
- Evaluate the ability of GPR to account for spatial variation at the field scale;
- (c)
- Evaluate the improvement in yield estimation after adjustment for GPR-derived spatial variation.
2. Materials and Methods
2.1. Ground-Penetrating Radar (GPR)
2.2. Field Trial
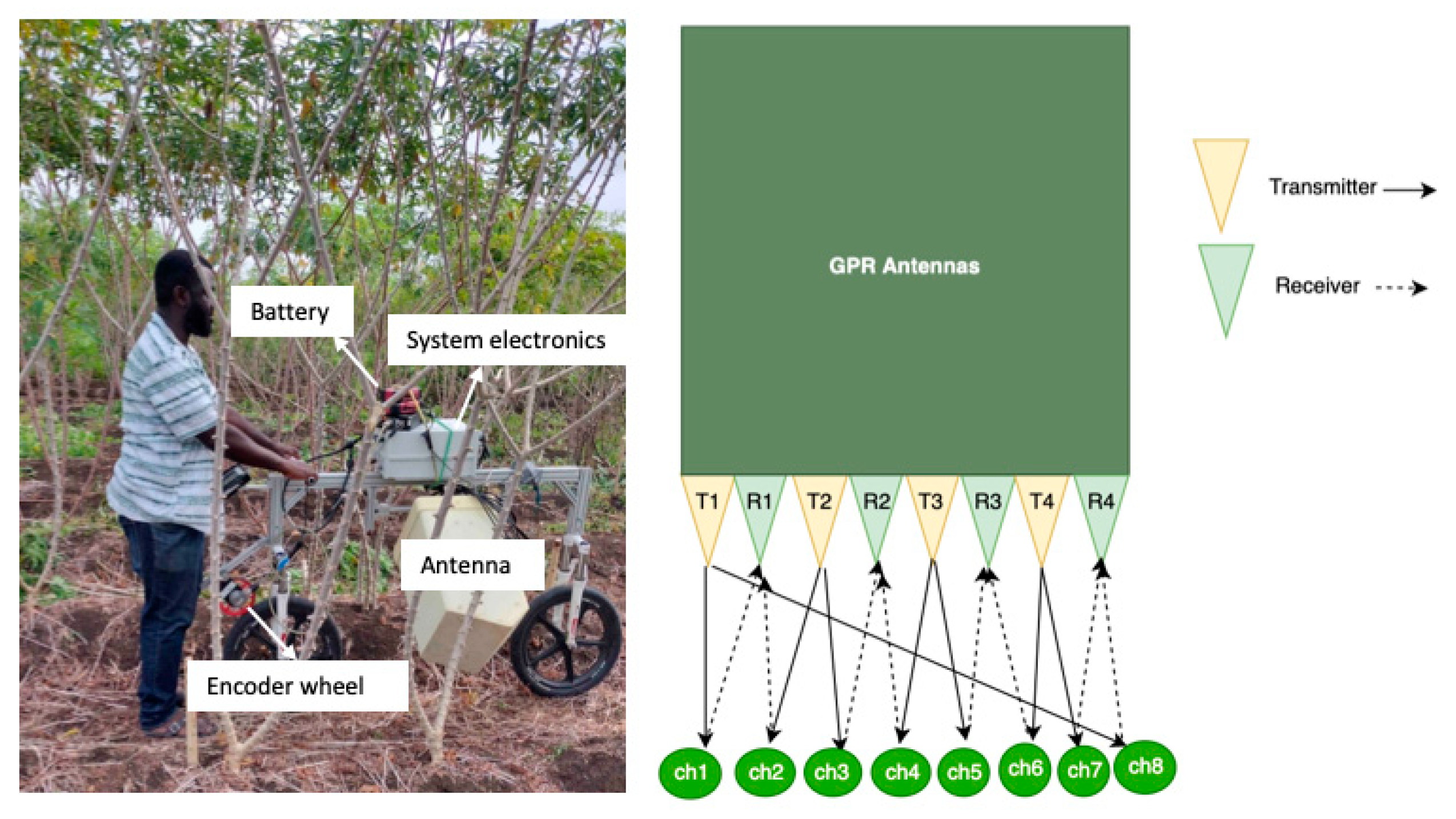
2.3. Radar Acquisition Device
2.4. Sampling Strategy and Fresnel Zone Footprint
2.5. Test for Spatial Dependency
2.5.1. Spatial Neighborhood Matrices
2.5.2. Global Moran’s I Statistic
2.6. Spatial Process Model
2.7. Spatial Model for Yield Adjustment
2.8. Spatial Krigging
3. Results
3.1. Spatial Distribution of VOA and FYLD
3.2. Spatial Model Comparison
3.3. Adjusting Estimation of Fyld Using VOA-Defined Covariance Structure
3.4. Prediction in Untested Locations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hardie, M. Review of novel and emerging proximal soil moisture sensors for use in agriculture. Sensors 2020, 20, 6934. [Google Scholar] [CrossRef]
- Abbas, F.; Afzaal, H.; Farooque, A.A.; Tang, S. Crop yield prediction through proximal sensing and machine learning algorithms. Agronomy 2020, 10, 1046. [Google Scholar] [CrossRef]
- Tonukari, N.J. Cassava and the future of starch. Electron. J. Biotechnol. 2004, 7, 12–15. [Google Scholar] [CrossRef]
- Chiona, M.; Ntawuruhunga, P.; Mukuka, I.; Chalwe, A.; Phiri, N.; Chikoti, P.; Simwambana, M. Growing Cassava: Training Manual for Extension & Farmers in Zambia; International Institute of Tropical Agriculture (IITA): Lusaka, Zambia, 2016; pp. 1–77. [Google Scholar]
- Teeken, B.; Olaosebikan, O.; Haleegoah, J.; Oladejo, E.; Madu, T.; Bello, A.; Parkes, E.; Egesi, C.; Kulakow, P.; Kirscht, H.; et al. Cassava Trait Preferences of Men and Women Farmers in Nigeria: Implications for Breeding. Econ. Bot. 2018, 72, 263–277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agbona, A.; Teare, B.; Ruiz-Guzman, H.; Dobreva, I.D.; Everett, M.E.; Adams, T.; Montesinos-Lopez, O.A.; Kulakow, P.A.; Hays, D.B. Prediction of root biomass in cassava based on ground penetrating radar phenomics. Remote Sens. 2021, 13, 4908. [Google Scholar] [CrossRef]
- Delgado, A.; Hays, D.B.; Bruton, R.K.; Ceballos, H.; Novo, A.; Boi, E.; Selvaraj, M.G. Ground penetrating radar: A case study for estimating root bulking rate in cassava (Manihot esculenta Crantz). Plant Methods 2017, 13, 65. [Google Scholar] [CrossRef] [Green Version]
- Elias, A.A.; Rabbi, I.; Kulakow, P.; Jannink, J.L. Improving genomic prediction in cassava field experiments using spatial analysis. G3 Genes Genomes Genet. 2018, 8, 53–62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Papadakis, J. Méthode statistique pour des expériences sur champ. Bull. Inst. Amél. Plantes Salonique 1937, 30, 23. [Google Scholar]
- Lill, W.J.; Gleeson, A.C.; Cullis, B.R. Relative accuracy of a neighbour method for field trials. J. Agric. Sci. 1988, 111, 339–346. [Google Scholar] [CrossRef] [Green Version]
- Cullis, B.R.; Gleeson, A.C. Spatial Analysis of Field Experiments—An Extension to Two Dimensions. Biometrics 1991, 47, 1449–1460. [Google Scholar] [CrossRef]
- Gilmour, A.R.; Cullis, B.R.; Verbyla, A.P. Accounting for Natural and Extraneous Variation in the Analysis of Field Experiments. J. Agric. Biol. Environ. Stat. 1997, 2, 269–293. [Google Scholar] [CrossRef] [Green Version]
- Radočaj, D.; Jug, I.; Vukadinović, V.; Jurišić, M.; Gašparović, M. The effect of soil sampling density and spatial autocorrelation on interpolation accuracy of chemical soil properties in arable cropland. Agronomy 2021, 11, 2430. [Google Scholar] [CrossRef]
- Canal Filho, R.; Molin, J.P. Spatial distribution as a key factor for evaluation of soil attributes prediction at field level using online near-infrared spectroscopy. Front. Soil Sci. 2022, 2, 984963. [Google Scholar] [CrossRef]
- Shit, P.K.; Bhunia, G.S.; Maiti, R. Spatial analysis of soil properties using GIS based geostatistics models. Model. Earth Syst. Environ. 2016, 2, 107. [Google Scholar] [CrossRef] [Green Version]
- Kiani, M.; Hernandez-ramirez, G.; Quideau, S.A.M. Spatial variation of soil quality indicators as a function of land use and topography. Can. J. Soil Sci. 2020, 100, 463–478. [Google Scholar] [CrossRef]
- Negassa, W.; Baum, C.; Schlichting, A.; Müller, J.; Leinweber, P. Small-scale spatial variability of soil chemical and biochemical properties in a rewetted degraded Peatland. Front. Environ. Sci. 2019, 7, 116. [Google Scholar] [CrossRef] [Green Version]
- Corwin, D.L.; Lesch, S.M. Characterizing soil spatial variability with apparent soil electrical conductivity: I. Survey protocols. Comput. Electron. Agric. 2005, 46, 103–133. [Google Scholar] [CrossRef]
- Li, S.L.; Liang, W.L. Spatial-temporal soil water dynamics beneath a tree monitored by tensiometer-time domain reflectometry probes. Water 2019, 11, 1662. [Google Scholar] [CrossRef] [Green Version]
- Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Mapping spatial variation in surface soil water content: Comparison of ground-penetrating radar and time domain reflectometry. J. Hydrol. 2002, 269, 194–207. [Google Scholar] [CrossRef]
- Weihermüller, L.; Huisman, J.A.; Lambot, S.; Herbst, M.; Vereecken, H. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques. J. Hydrol. 2007, 340, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Campos, J.R.d.R.; Vidal-Torrado, P.; Modolo, A.J. Use of Ground Penetrating Radar to study spatial variability and soil stratigraphy. Eng. Agric. 2019, 39, 358–364. [Google Scholar] [CrossRef]
- Wollschläger, U.; Gerhards, H.; Yu, Q.; Roth, K. Multi-channel ground-penetrating radar to explore spatial variations in thaw depth and moisture content in the active layer of a permafrost site. Cryosphere 2010, 4, 269–283. [Google Scholar] [CrossRef] [Green Version]
- Redman, D.; Galagedara, L.; Parkin, G. Measuring Soil Water Content with the Ground Penetrating Radar Surface Reflectivity Method: Effects of Spatial Variability. In 2003 ASAE Annual Meeting; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2013; p. 0300. [Google Scholar] [CrossRef]
- De Benedetto, D.; Barca, E.; Castellini, M.; Popolizio, S.; Lacolla, G.; Stellacci, A.M. Prediction of Soil Organic Carbon at Field Scale by Regression Kriging and Multivariate Adaptive Regression Splines Using Geophysical Covariates. Land 2022, 11, 381. [Google Scholar] [CrossRef]
- Fedorova, L.L.; Sokolov, K.O.; Savvin, D.V.; Kulyandin, G.A. Analysis of Variance Amplitudes of Signals for Detecting Structural Permafrost Heterogeneities by Ground Penetrating Radar. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 301–304. [Google Scholar]
- Solla, M.; Lagüela, S.; Riveiro, B.; Lorenzo, H. Non-destructive testing for the analysis of moisture in the masonry arch bridge of Lubians (Spain). Struct. Control Health Monit. 2013, 20, 1366–1376. [Google Scholar] [CrossRef]
- Rasol, M.A.; Pérez-Gracia, V.; Fernandes, F.M.; Pais, J.C.; Santos-Assunçao, S.; Santos, C.; Sossa, V. GPR laboratory tests and numerical models to characterize cracks in cement concrete specimens, exemplifying damage in rigid pavement. Meas. J. Int. Meas. Confed. 2020, 158, 107662. [Google Scholar] [CrossRef]
- Annan, A.P. GPR—History, Trends, and Future Developments. Subsurf. Sens. Technol. Appl. 2002, 3, 253–270. [Google Scholar] [CrossRef]
- Turpin, N.; Stapleton, L.; Perret, E.; Van Der Heide, C.M.; Garrod, G.; Brouwer, F.; Voltr, V.; Cairol, D. Assessment of multifunctionality and jointness of production. In Environmental and Agricultural Modelling: Integrated Approaches for Policy Impact Assessment; Springer: Dordrecht, Netherlands, 2010; pp. 11–35. ISBN 9789048136186. [Google Scholar]
- Zhu, S.; Huang, C.; Su, Y.; Sato, M. 3D Ground Penetrating Radar to Detect Tree Roots and Estimate Root Biomass in the Field. Remote Sens. 2014, 6, 5754–5773. [Google Scholar] [CrossRef] [Green Version]
- Dobreva, I.D.; Ruiz-Guzman, H.A.; Barrios-Perez, I.; Adams, T.; Teare, B.L.; Payton, P.; Everett, M.E.; Burow, M.D.; Hays, D.B. Thresholding Analysis and Feature Extraction from 3D Ground Penetrating Radar Data for Noninvasive Assessment of Peanut Yield. Remote Sens. 2021, 13, 1896. [Google Scholar] [CrossRef]
- Butnor, J.R.; Doolittle, J.A.; Kress, L.; Cohen, S.; Johnsen, K.H. Use of ground-penetrating radar to study tree roots in the southeastern United States. Tree Physiol. 2001, 21, 1269–1278. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Dong, X.; Xue, Q.; Leskovar, D.I.; Jifon, J.; Butnor, J.R.; Marek, T. Ground penetrating radar (GPR) detects fine roots of agricultural crops in the field. Plant Soil 2018, 423, 517–531. [Google Scholar] [CrossRef]
- Jol, H.M. Ground Penetrating Radar Theory and Applications, 1st ed.; Elsevier: Oxford, UK, 2009; ISBN 9780080951843. [Google Scholar]
- Everett, M.E. Near-Surface Applied Geophysics; Cambridge University Press: New York, NY, USA, 2013; ISBN 978-1-107-01877-8. [Google Scholar]
- Kim, K.; Scott, W.R. Design of a resistively loaded vee dipole for ultrawide-band ground-penetrating radar applications. IEEE Trans. Antennas Propag. 2005, 53, 2525–2532. [Google Scholar]
- Nuzzo, L.; Alli, G.; Guidi, R.; Cortesi, N.; Sarri, A.; Manacorda, G.; Ingegneria, I.D.S.; Sistemi, D. A new densely-sampled Ground Penetrating Radar array for landmine detection. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 969–974. [Google Scholar]
- Cropphenomics. Crop Phenomics LLC, College Station, TX, USA. Available online: https://cropphenomics.com (accessed on 18 January 2023).
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Tsai, P.J.; Lin, M.L.; Chu, C.M.; Perng, C.H. Spatial autocorrelation analysis of health care hotspots in Taiwan in 2006. BMC Public Health 2009, 9, 464. [Google Scholar] [CrossRef] [Green Version]
- Bivand, R.S.; Wong, D.W.S. Comparing implementations of global and local indicators of spatial association. Test 2018, 27, 716–748. [Google Scholar] [CrossRef]
- Paula, M. Geospatial Health Data: Modelling and Visualization with R-INLA and Shiny. Available online: https://www.paulamoraga.com/book-geospatial/sec-arealdatatheory.html (accessed on 10 January 2023).
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer Nature: Berlin, Germany, 2022; ISBN 9783030890094. [Google Scholar]
- Pinheiro, J.; Bates, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. Available online: https://cran.r-project.org/package=nlme (accessed on 10 December 2022).
- Rodriguez, L.S.; Munoz, F. breedR: Statistical Methods for Forest Genetic Resources Analysts. In IUFRO Genomics and Forest Tree Genetics; Hindustan Aeronautics Limited: Arcachon, France, 2016. [Google Scholar]
- Simpson, T.W. Comparison of Response Surface and Kriging Models in the Multidisciplinary Design of an Aerospike Nozzle; NASA ICASE Rep.; NASA: Washington, DC, USA, 1998.
- Finley, A.O.; Banerjee, S.; Carlin, B.P. spBayes: An R Package for Univariate and Multivariate Hierarchical Point-referenced Spatial Models. J. Stat. Softw. 2007, 19, 1–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Sugiura, N. Further Analysis of the Data by Anaike’s Information Criterion and the Finite Corrections. Commun. Stat. Theory Methods 1978, 7, 13–26. [Google Scholar] [CrossRef]
- Shekhar, S.; Xiong, H. Encyclopedia of GIS. Available online: https://books.google.com/books?id=6q2lOfLnwkAC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false (accessed on 13 February 2023).
- Metzner, R.; van Dusschoten, D.; Bühler, J.; Schurr, U.; Jahnke, S. Belowground plant development measured with magnetic resonance imaging (MRI): Exploiting the potential for non-invasive trait quantification using sugar beet as a proxy. Front. Plant Sci. 2014, 5, 469. [Google Scholar] [CrossRef] [Green Version]
- Agbona, A.; Peteti, P.; Teeken, B.; Olaosebikan, O.; Bello, A.; Parkes, E.; Rabbi, I.; Mueller, L.; Egesi, C.; Kulakow, P. Data Management in Multi-disciplinary African RTB Crop Breeding Programs. In Towards Responsible Plant Data Linkage: Data Challenges for Agricultural Research and Development; Williamson, H.F., Leonelli, S., Eds.; Springer: Cham, Switzerland, 2022; p. 19. ISBN 978-3-031-13275-9. [Google Scholar]










| Field Measurement Input Parameter | Value | |
|---|---|---|
| 1 | Frequency range (est.) | 1.3–2.3 GHz |
| 2 | Central frequency | 1.8 GHz |
| 3 | Effective depth penetration | ~0.8 m |
| 4 | Spatial resolution | 0.01 m |
| 5 | Number of samples | 512 |
| 6 | Temporal resolution | 18 ns |
| 7 | Antenna spacing | 0.04 m |
| Neighborhood Parameter | Value |
|---|---|
| Number of regions | 380 |
| Number of non-zero links | 1822 |
| Percentage of non-zero weights | 1.26 |
| Average number of links | 4.80 |
| SAR | CAR | IID | |
|---|---|---|---|
| Intercept | 17.47 | 17.43 | 17.37 |
| rho | 0.27 | 0.48 | N/A |
| Sigma2 | 0.01 | 0.01 | 0.07 |
| Log likelihood | 313.97 | 313.79 | 317.98 |
| AICC | −619.71 | −619.34 | −627.73 |
| Model | avgBLUE | AICC | avgSE | Majority Voting (MV) | |
|---|---|---|---|---|---|
| GPR-VOA | 27.09 | −17,911.01 | 9.57 | 88.33 | |
| AR1 AR1 | 22.23 | −932.48 | 10.15 | 10.56 | |
| GPR-VOA | 27.09 | −17,911.01 | 9.57 | 100 | |
| IID | 21.81 | −378.99 | 17.37 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agbona, A.; Montesinos-Lopez, O.A.; Everett, M.E.; Ruiz-Guzman, H.; Hays, D.B. Yield Adjustment Using GPR-Derived Spatial Covariance Structure in Cassava Field: A Preliminary Investigation. Remote Sens. 2023, 15, 1771. https://doi.org/10.3390/rs15071771
Agbona A, Montesinos-Lopez OA, Everett ME, Ruiz-Guzman H, Hays DB. Yield Adjustment Using GPR-Derived Spatial Covariance Structure in Cassava Field: A Preliminary Investigation. Remote Sensing. 2023; 15(7):1771. https://doi.org/10.3390/rs15071771
Chicago/Turabian StyleAgbona, Afolabi, Osval A. Montesinos-Lopez, Mark E. Everett, Henry Ruiz-Guzman, and Dirk B. Hays. 2023. "Yield Adjustment Using GPR-Derived Spatial Covariance Structure in Cassava Field: A Preliminary Investigation" Remote Sensing 15, no. 7: 1771. https://doi.org/10.3390/rs15071771
APA StyleAgbona, A., Montesinos-Lopez, O. A., Everett, M. E., Ruiz-Guzman, H., & Hays, D. B. (2023). Yield Adjustment Using GPR-Derived Spatial Covariance Structure in Cassava Field: A Preliminary Investigation. Remote Sensing, 15(7), 1771. https://doi.org/10.3390/rs15071771






