Spatio-Temporal Changes of Mangrove-Covered Tidal Flats over 35 Years Using Satellite Remote Sensing Imageries: A Case Study of Beibu Gulf, China
Abstract
1. Introduction
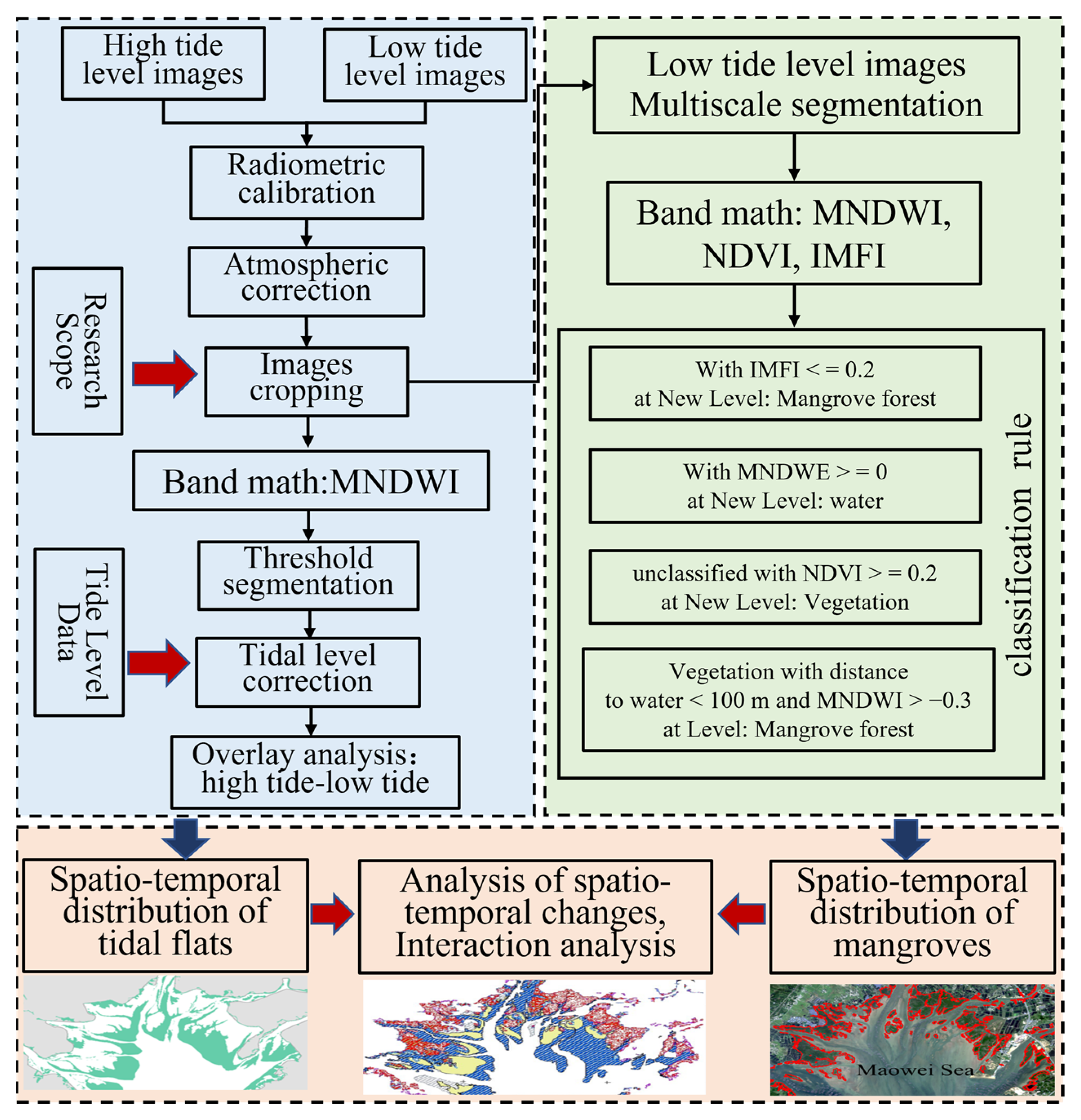
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition and Pre-Processing
2.3. Extraction of Tidal Flats
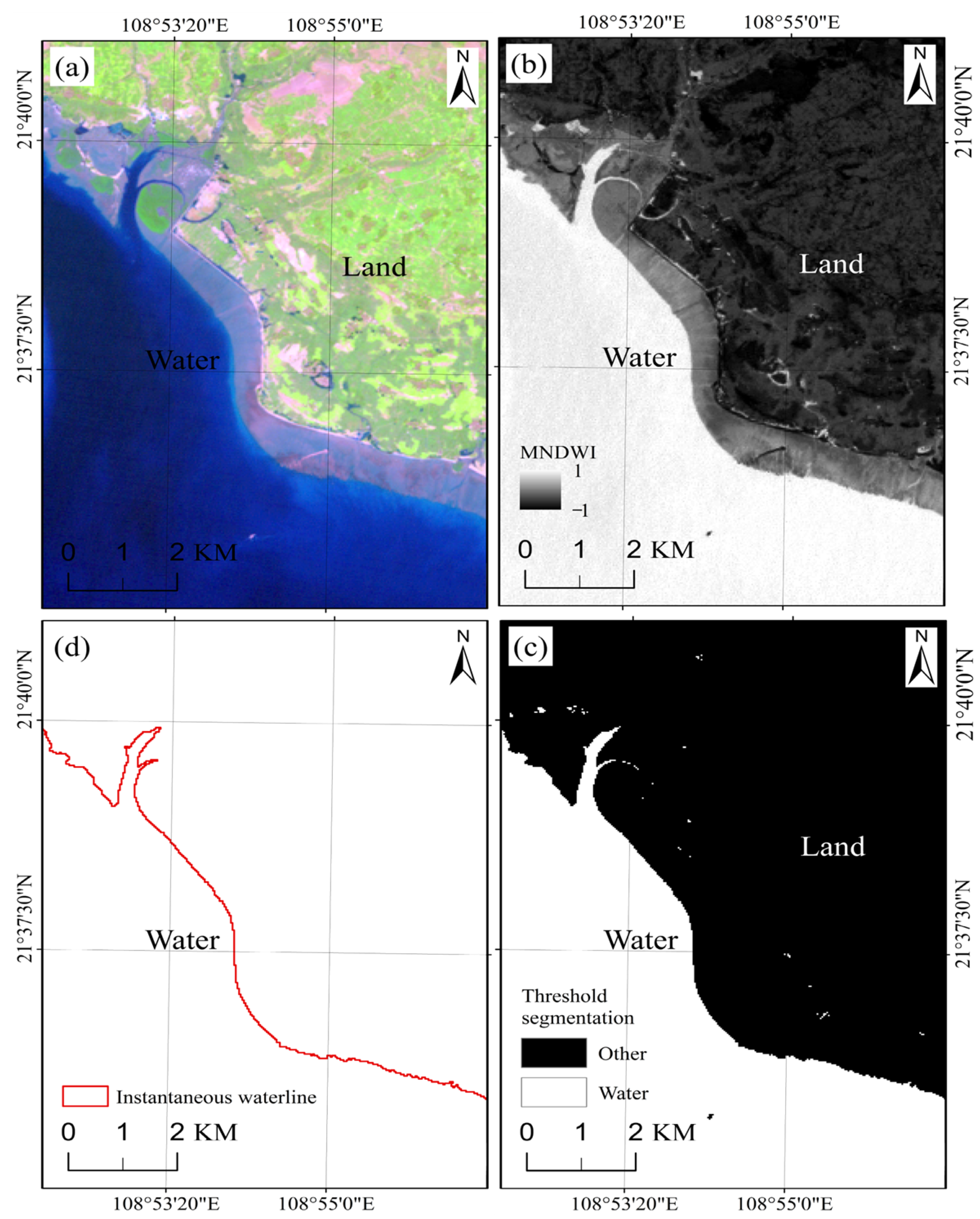
2.3.1. Instantaneous Water-Edge Line Extraction
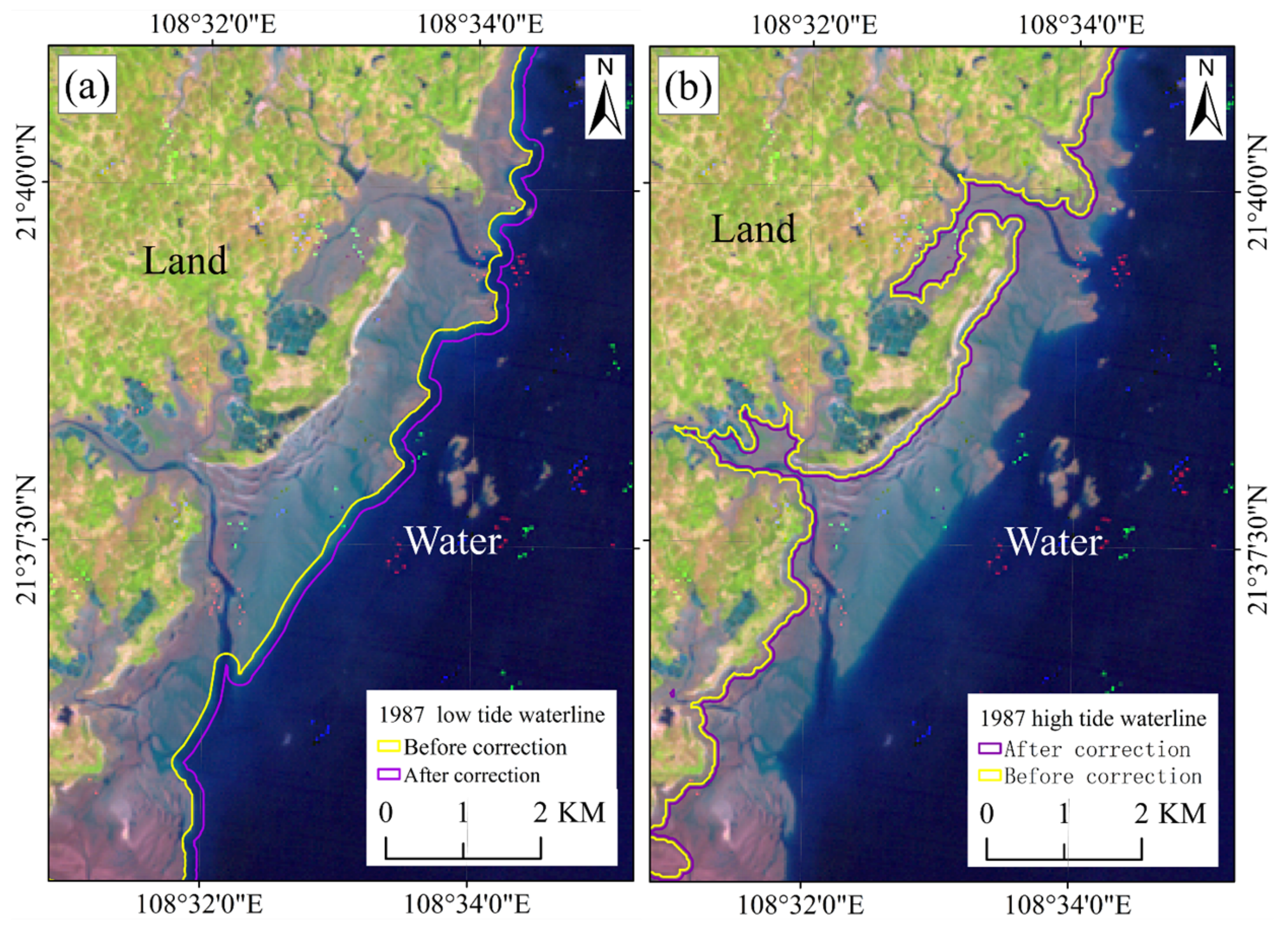
2.3.2. Tidal-Level Correction
2.3.3. Spatial Distribution of Mangroves in Tidal Flats
3. Results and Discussion
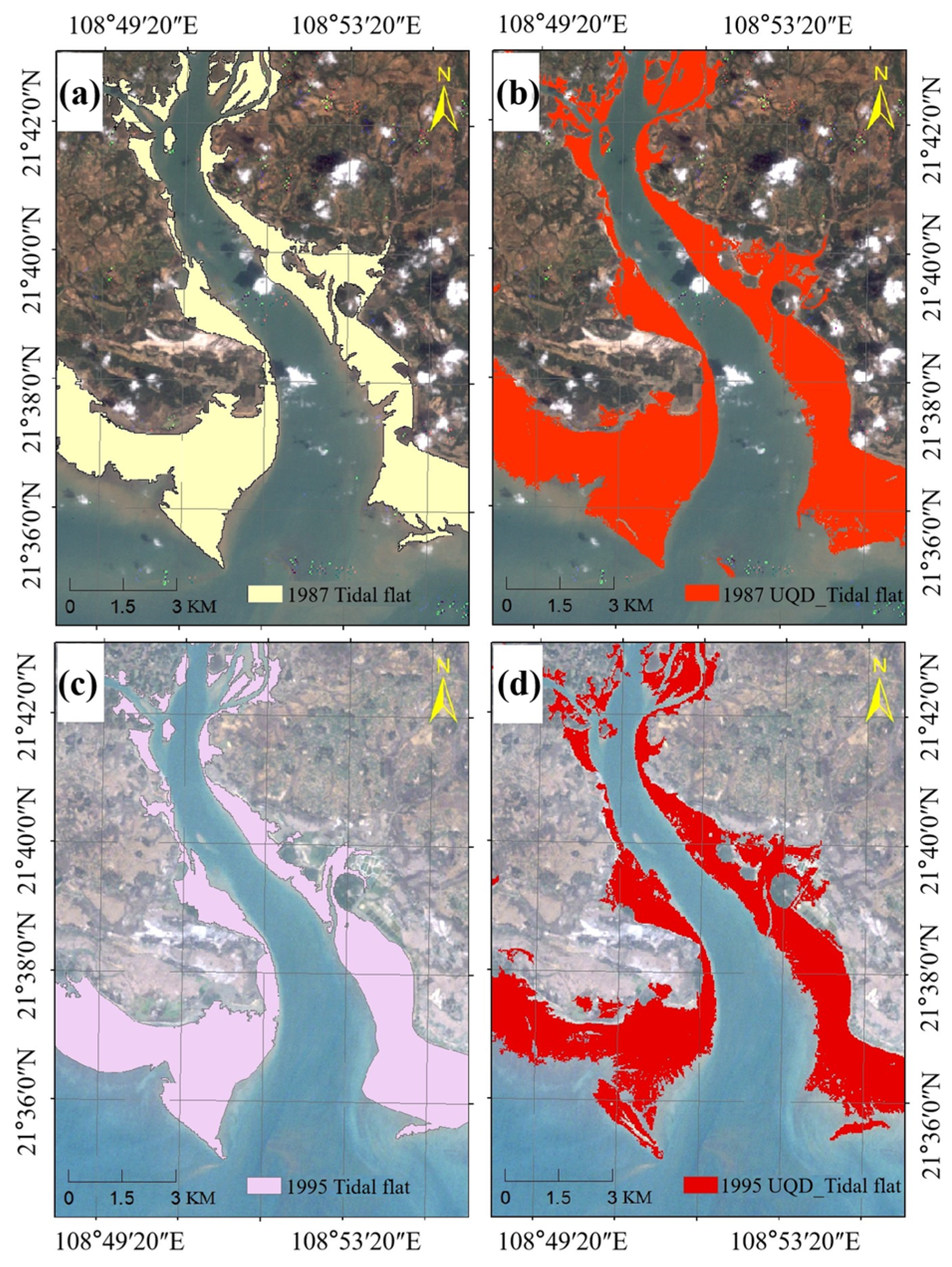
3.1. Reliability Analysis of Tidal Flat Extraction Results
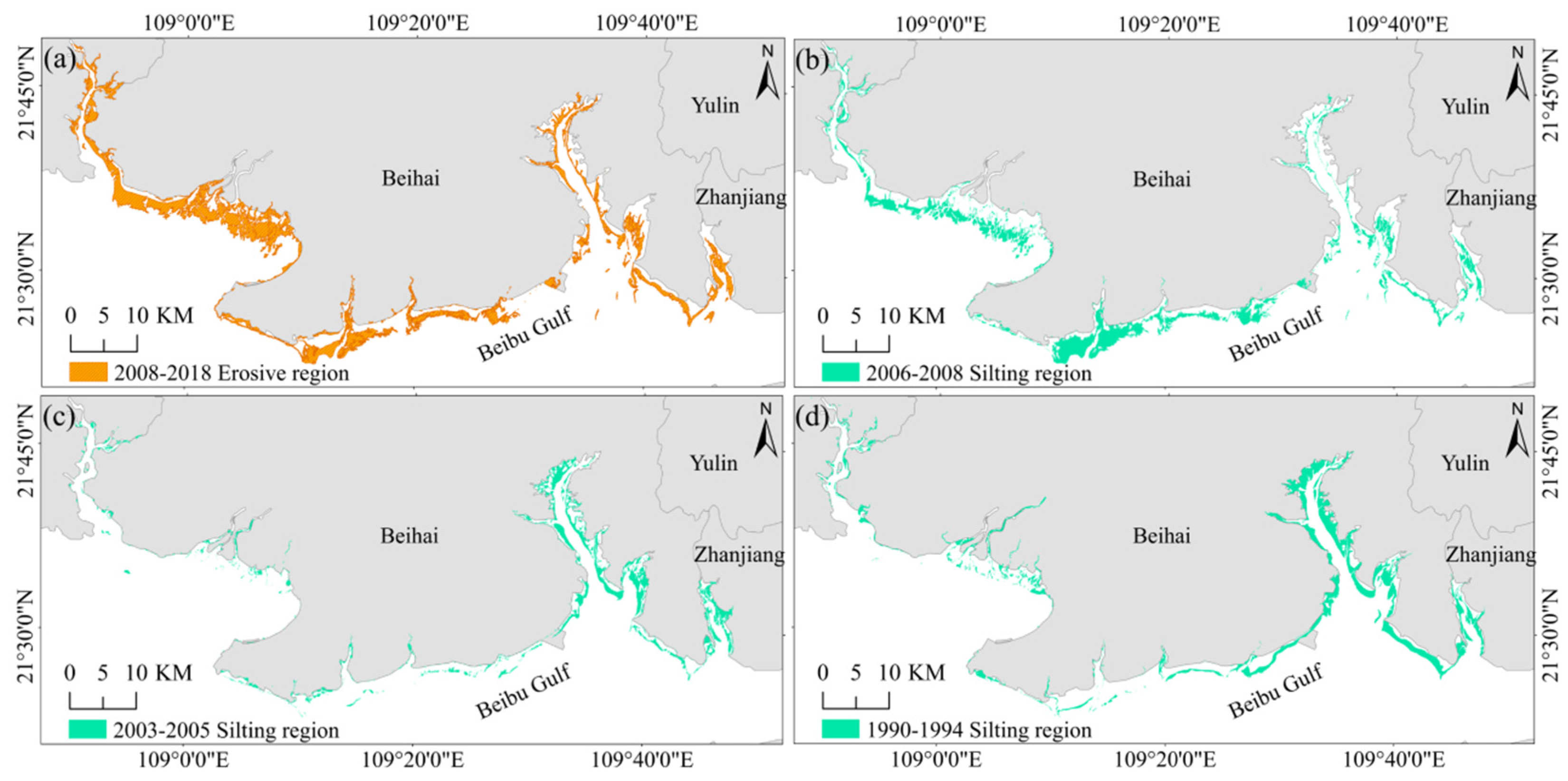
3.2. Spatio-Temporal Variation of Tidal Flats in Beibu Gulf
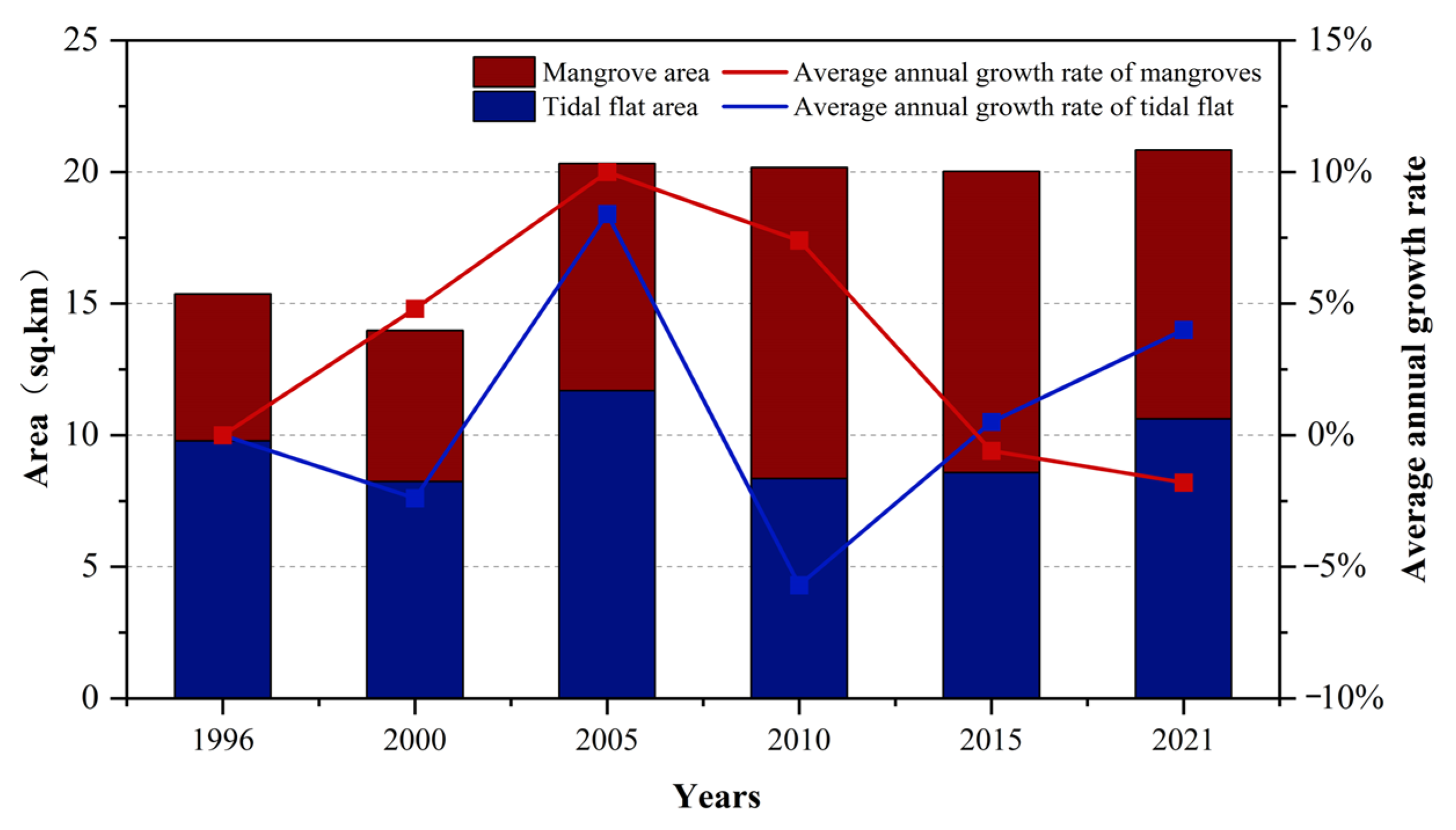
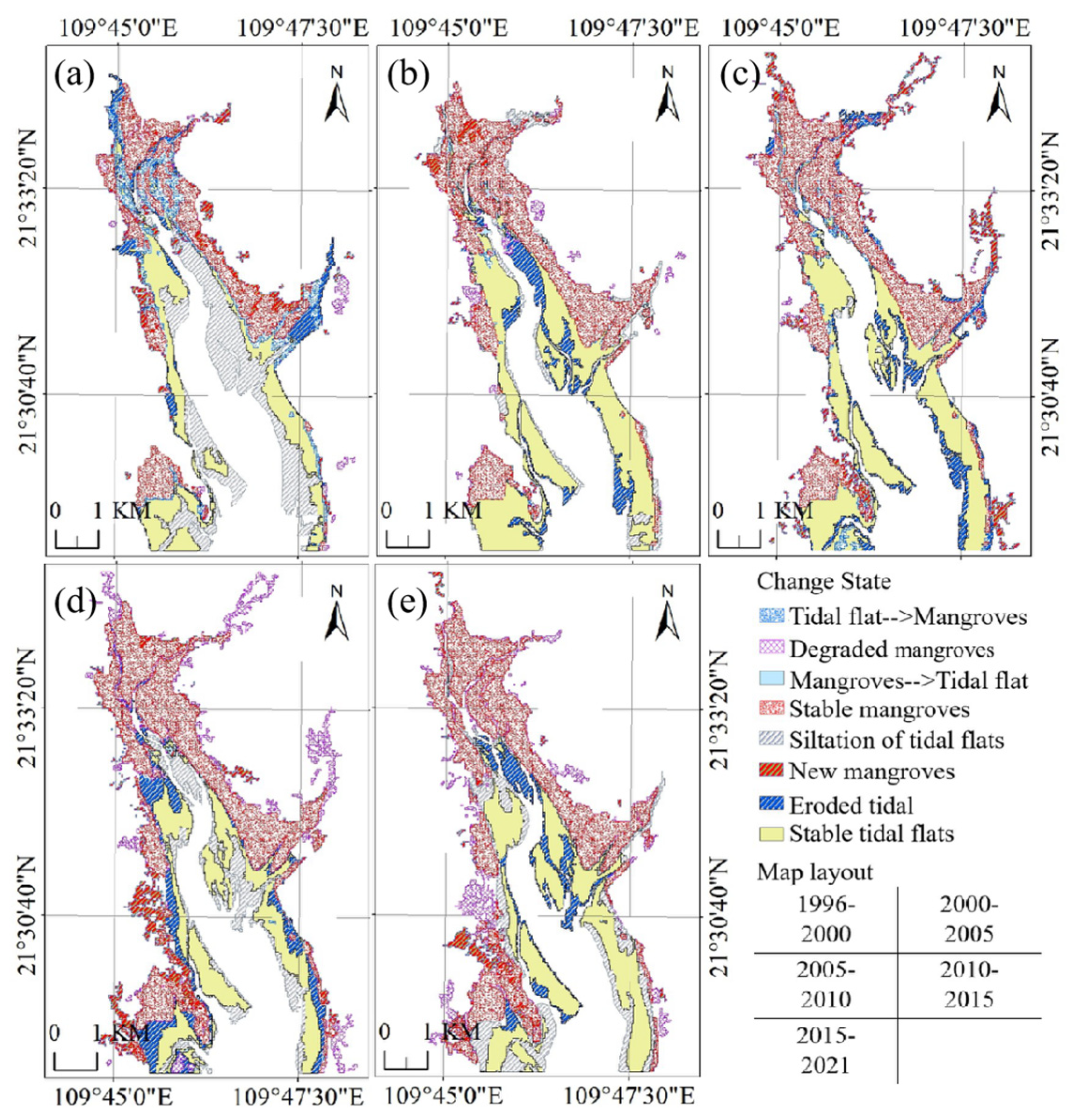
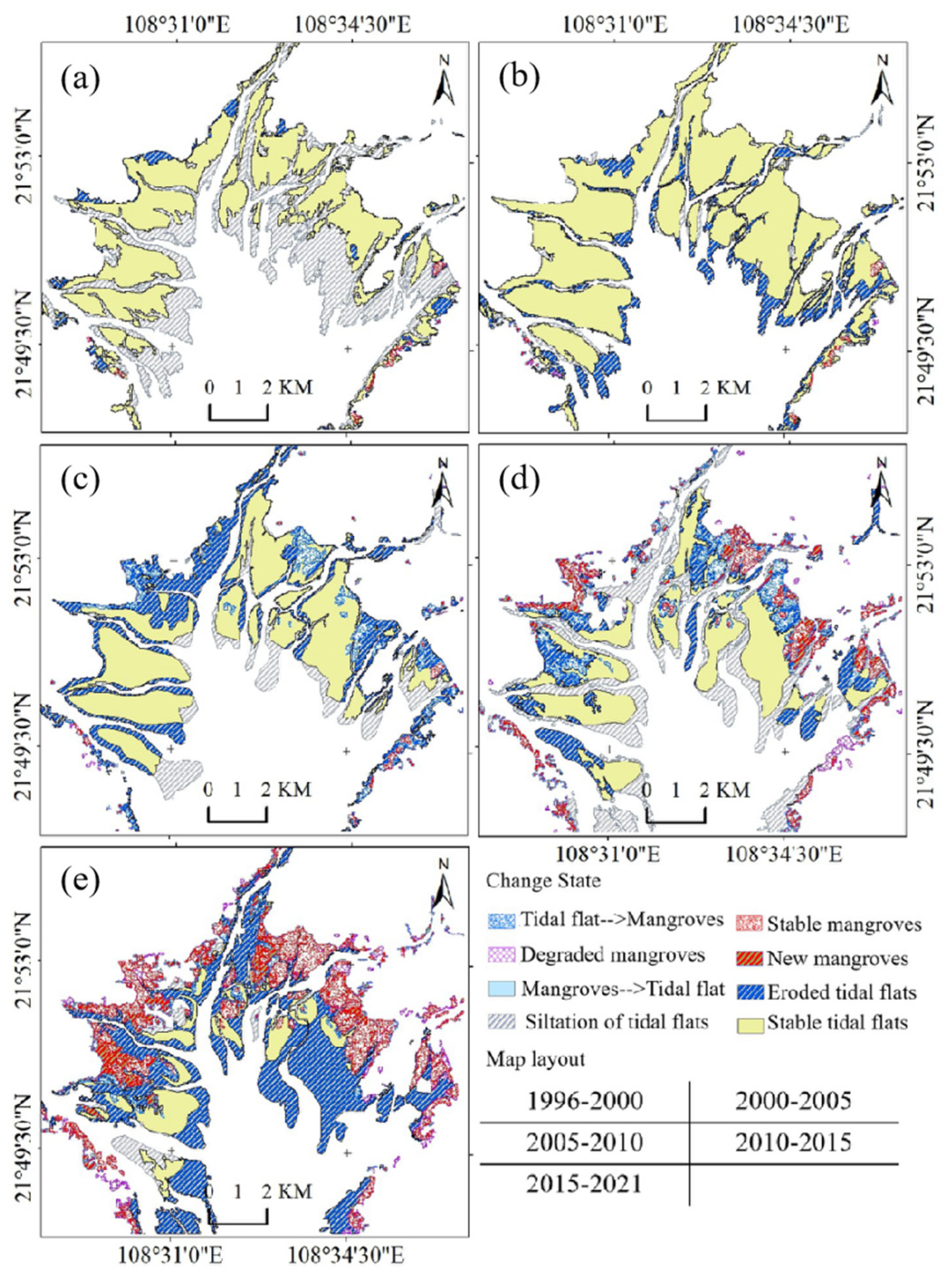
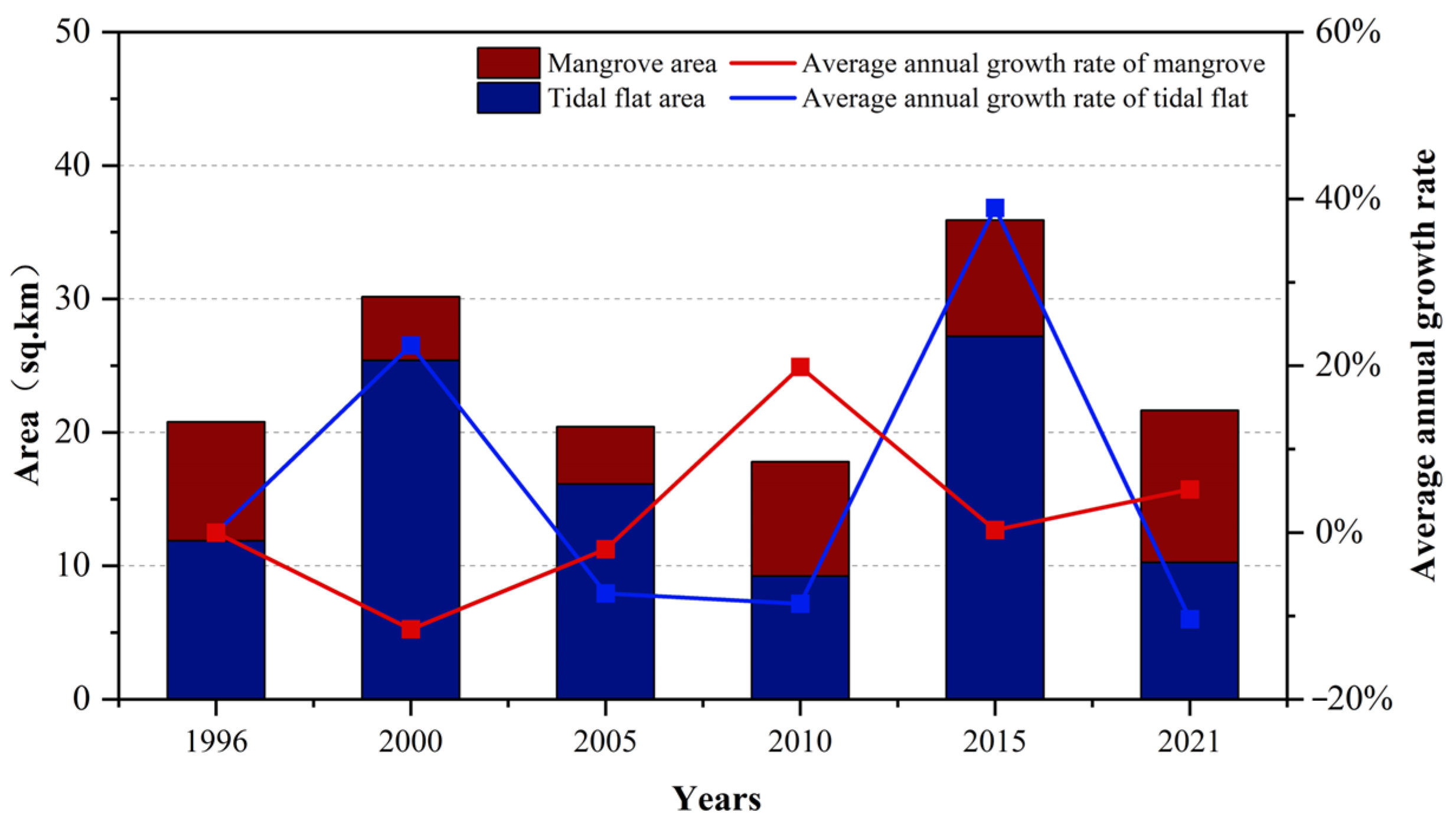
3.3. Analysis of Spatio-Temporal Changes in Tidal Flats as Influenced by Temporal Changes in Mangrove Forests
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Xiao, X.; Zou, Z.; Hou, L.; Qin, Y.; Dong, J.; Doughty, R.; Chen, B.; Zhang, X.; Chen, Y.; et al. Mapping coastal wetlands of China using time series Landsat images in 2018 and Google Earth Engine. ISPRS-J. Photogramm. Remote Sens. 2020, 163, 312–326. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xiao, X.; Zou, Z.; Chen, B.; Ma, J.; Dong, J.; Doughty, R.; Zhong, Q.; Qin, Y.; Dai, S.; et al. Tracking annual changes of coastal tidal flats in China during 1986–2016 through analyses of Landsat images with Google Earth Engine. Remote Sens. Environ. 2020, 238, 110987. [Google Scholar] [CrossRef] [PubMed]
- Yuan, R.; Zhang, H.; Qiu, C.; Wang, Y.; Guo, X.; Wang, Y.; Chen, S. Mapping Morphodynamic Variabilities of a Meso-Tidal Flat in Shanghai Based on Satellite-Derived Data. Remote Sens. 2022, 14, 4123. [Google Scholar] [CrossRef]
- Chang, M.; Li, P.; Li, Z.; Wang, H. Mapping Tidal Flats of the Bohai and Yellow Seas Using Time Series Sentinel-2 Images and Google Earth Engine. Remote Sens. 2022, 14, 1789. [Google Scholar] [CrossRef]
- Ghosh, S.; Mishra, D.; Gitelson, A. Long-term monitoring of biophysical characteristics of tidal wetlands in the northern Gulf of Mexico-A methodological approach using MODIS. Remote Sens. Environ. 2016, 173, 39–58. [Google Scholar] [CrossRef]
- Murray, N.; Phinn, S.; DeWitt, M.; Ferrari, R.; Johnston, R.; Lyons, M.; Clinton, N.; Thau, D.; Richard, A. The global distribution and trajectory of tidal flats. Nature 2019, 565, 222–225. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Mao, D.; Ren, C.; Wang, C.; Wang, Y. Rapid, robust, and automated mapping of tidal flats in China using time series Sentinel-2 images and Google Earth Engine. Remote Sens. Environ. 2021, 255, 112285. [Google Scholar] [CrossRef]
- Ren, C.; Wang, Z.; Zhang, Y.; Zhang, B.; Chen, L.; Xi, Y.; Xiao, X.; Doughty, R.; Liu, M.; Jia, M.; et al. Rapid expansion of coastal aquaculture ponds in China from Landsat observations during 1984–2016. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101902. [Google Scholar] [CrossRef]
- Mao, D.; Wang, Z.; Wu, J.; Wu, B.; Zeng, Y.; Song, K.; Yi, K.; Luo, L. China’s wetlands loss to urban expansion. Land Degrad. 2018, 29, 2644–2657. [Google Scholar] [CrossRef]
- Zhou, G.; Huang, J.; Yue, T.; Luo, Q.; Zhang, G. Temporal-spatial distribution of wave energy: A case study of Beibu Gulf, China. Renew. Energy 2015, 74, 344–356. [Google Scholar] [CrossRef]
- Xu, N.; Gong, P. Significant coastline changes in China during 1991–2015 tracked by Landsat data. Sci. Bull. 2018, 63, 883–886. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Zhou, Y.; Li, R.; Li, X. Mapping changes in coastlines and tidal flats in developing islands using the full time series of Landsat images. Remote Sens. Environ. 2020, 239, 111665. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, M. Three-dimensional (3D) GIS-based topographically morphological analysis and dynamical visualization of Assateague Island National Seashore. J. Coast. Res. 2009, 25, 435–447. [Google Scholar] [CrossRef]
- Zhou, G.; Li, C.; Zhang, D.; Liu, D.; Zhou, X.; Zhan, J. Overview of Underwater Transmission Characteristics of Oceanic LiDAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8144–8159. [Google Scholar] [CrossRef]
- Zhou, G. Urban High-Resolution Remote Sensing: Algorithms and Modelling, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021; pp. 3–15. [Google Scholar]
- Zhou, G.; Zhou, X. Seamless Fusion of LiDAR and Aerial Imagery for Building Extraction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7393–7407. [Google Scholar] [CrossRef]
- Murray, N.; Clemens, R.; Phinn, S.; Possingham, H.; Fuller, R. Tracking the rapid loss of tidal wetlands in the Yellow Sea. Front. Ecol. Environ. 2014, 12, 267–272. [Google Scholar] [CrossRef]
- Murray, N.; Phinn, S.; Clemens, R.; Roelfsema, C.; Fuller, R. Continental Scale Mapping of Tidal Flats across East Asia Using the Landsat Archive. Remote Sens. 2012, 4, 3417–3426. [Google Scholar] [CrossRef]
- Li, T.; Wang, J.; Wu, F.; Zhao, Z.; Zhang, W. Construction of tidal flat DEM based on multi-algorithm waterline extraction. Remote Sens. Nat. Resour. 2021, 33, 38–44. [Google Scholar] [CrossRef]
- Han, Q.; Niu, Z. Remote-sensing monitoring and analysis of China intertidal zone changes based on tidal correction. Chin. Sci. Bull. 2019, 64, 456–473. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Q.; Xu, J. Coastline Extraction Using Support Vector Machine from Remote Sensing Image. J. Multimedia 2013, 8, 175–182. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, X.; Liu, Z.; Gao, W.; Hu, Z.; Wu, G. Mapping Tidal Flats with Landsat 8 Images and Google Earth Engine: A Case Study of the China’s Eastern Coastal Zone circa 2015. Remote Sens. 2019, 11, 924. [Google Scholar] [CrossRef]
- Wang, X. Remote sensing monitoring of the Caofeidian tidal zone evolution. Mar. Sci. Bull. 2014, 33, 559–565. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Aedla, R.; Dwarakish, G.; Venkat, R. Automatic Shoreline Detection and Change Detection Analysis of Netravati-GurpurRivermouth Using Histogram Equalization and Adaptive Thresholding Techniques. Aquat. Procedia 2015, 4, 563–570. [Google Scholar] [CrossRef]
- Fu, B.; Xie, S.; He, H.; Zuo, P.; Sun, J.; Liu, L.; Huang, L.; Fan, D.; Gao, E. Synergy of multi-temporal polarimetric SAR and optical image satellite for mapping of marsh vegetation using object-based random forest algorithm. Ecol. Indic. 2021, 131, 108173. [Google Scholar] [CrossRef]
- Campbell, A.; Wang, Y.; Christiano, M.; Stevens, S. Salt marsh monitoring in Jamaica Bay, New York from 2003 to 2013: A decade of change from restoration to hurricane sandy. Remote Sens. 2017, 9, 131. [Google Scholar] [CrossRef]
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Fu, B.; He, X.; Yao, H.; Liang, Y.; Deng, T.; He, H.; Fan, D.; Lan, G.; He, W. Comparison of RFE-DL and stacking ensemble learning algorithms for classifying mangrove species on UAV multispectral images. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102890. [Google Scholar] [CrossRef]
- Li, Y.; Fu, B.; Sun, X.; Fan, D.; Wang, Y.; He, H.; Gao, E.; He, W.; Yao, Y. Comparison of Different Transfer Learning Methods for Classification of Mangrove Communities Using MCCUNet and UAV Multispectral Images. Remote Sens. 2022, 14, 5533. [Google Scholar] [CrossRef]
- Zhang, R.; Jia, M.; Wang, Z.; Zhou, Y.; Wen, X.; Tan, Y.; Cheng, L. A Comparison of Gaofen-2 and Sentinel-2 Imagery for Mapping Mangrove Forests Using Object-Oriented Analysis and Random Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4185–4193. [Google Scholar] [CrossRef]
- Lee, S.; Ryu, J. High-Accuracy Tidal Flat Digital Elevation Model Construction Using TanDEM-X Science Phase Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2713–2724. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, G.; Zhang, W.; Luo, S. Study on Local to Global Radiometric Balance for Remotely Sensed Imagery. Remote Sens. 2021, 13, 2068. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Huang, R.; Pan, H.; Xu, M. Recent Evolution of Coastal Tidal Flats and the Impacts of Intensified Human Activities in the Modern Radial Sand Ridges, East China. Int. J. Environ. Res. Public Health 2020, 17, 3191. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, G.; Su, S.; Cao, Q.; Tian, Z. The Development of A Rigorous Model for Bathymetric Mapping from Multispectral Satellite-Images. Remote Sens. 2022, 14, 2495. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Ning, J.; Yu, X.; Zhang, Y. An Improved Method for Mapping Tidal Flats Based on Remote Sensing Waterlines: A Case Study in the Bohai Rim, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5123–5129. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, R.; Huang, S. Generalized Buffering Algorithm. IEEE Access 2021, 9, 27140–27157. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, M.; Allen, T. Assateague Island National Seashore Coastline Monitoring via LIDAR Series Datasets. In Proceedings of the International Colloquium Series on Land Use/Cover Change Science and Applications—Studying Land Use Effects in Coastal Zones with Remote Sensing and GIS, Istanbul, Turkey, 13–16 August 2003. [Google Scholar]
- Campbell, A.; Wang, Y. Examining the Influence of Tidal Stage on Salt Marsh Mapping Using High-Spatial-Resolution Satellite Remote Sensing and Topobathymetric LiDAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5169–5176. [Google Scholar] [CrossRef]
- Choi, C.; Kim, D. Optimum Baseline of a Single-Pass In-SAR System to Generate the Best DEM in Tidal Flats. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 919–929. [Google Scholar] [CrossRef]
- Xia, Q.; He, T.-T.; Qin, C.-Z.; Xing, X.-M.; Xiao, W. An Improved Submerged Mangrove Recognition Index-Based Method for Mapping Mangrove Forests by Removing the Disturbance of Tidal Dynamics and S. alterniflora. Remote Sens. 2022, 14, 3112. [Google Scholar] [CrossRef]
- Peng, W.; Wang, Q.; Cao, Y.; Xing, X.; Hu, W. Evaluation of Tidal Effect in Long-Strip DInSAR Measurements Based on GPS Network and Tidal Models. Remote Sens. 2022, 14, 2954. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Yang, B.; Zhuang, Z.; Shang, K. Coastline extraction using remote sensing based on coastal type and tidal correction. Remote Sens. Nat. Resour. 2013, 25, 91–97. [Google Scholar] [CrossRef]
- Wang, J.; Niu, Z. Remote-sensing analysis of Yancheng intertidal zones based on tidal correction. Acta Oceanol Sin. 2017, 39, 149–160. [Google Scholar] [CrossRef]
- Guan, M.; Li, Q.; Zhu, J.; Wang, C.; Zhou, L.; Huang, C.; Ding, K. A method of establishing an instantaneous water level model for tide correction. Ocean Eng. 2019, 171, 324–331. [Google Scholar] [CrossRef]
- Wicaksono, A.; Wicaksono, P.; Khakhim, N.; Farda, N.; Marfai, M. Tidal Correction Effects Analysis on Shoreline Mapping in Jepara Regency. J. Appl. Geospat. Inf. 2018, 2, 145–151. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, T.; Liu, M.; Jia, M.; Lin, H.; Chu, L.; Devlin, A.T. Potential of Combining Optical and Dual Polarimetric SAR Data for Improving Mangrove Species Discrimination Using Rotation Forest. Remote Sens. 2018, 10, 467. [Google Scholar] [CrossRef]
- Lee, K.; Shih, S.; Huang, Z. Mangrove colonization on tidal flats causes straightened tidal channels and consequent changes in the hydrodynamic gradient and siltation potential. J Environ. Manag. 2022, 314, 115058. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Xiao, X.; Li, X.; Pan, L.; Doughty, R.; Ma, J.; Dong, J.; Qin, Y.; Zhao, B.; Wu, Z.; et al. A mangrove forest map of China in 2015: Analysis of time series Landsat 7/8 and Sentinel-1A imagery in Google Earth Engine cloud computing platform. ISPRS-J. Photogramm. Remote Sens. 2017, 131, 104–120. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Zhang, Y.; Ren, C.; Song, K. Landsat-Based Estimation of Mangrove Forest Loss and Restoration in Guangxi Province, China, Influenced by Human and Natural Factors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 311–323. [Google Scholar] [CrossRef]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-Based Mangrove Species Classification Using Unmanned Aerial Vehicle Hyperspectral Images and Digital Surface Models. Remote Sens. 2018, 10, 89. [Google Scholar] [CrossRef]
- He, Z.; Shi, Q.; Liu, K.; Cao, J.; Zhan, W.; Cao, B. Object-Oriented Mangrove Species Classification Using Hyperspectral Data and 3-D Siamese Residual Network. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2150–2154. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Li, L.; Song, K.; Ren, C.; Liu, B.; Mao, D. Mapping China’s mangroves based on an object-oriented classification of Landsat imagery. Wetlands 2014, 34, 277–283. [Google Scholar] [CrossRef]
- Zhao, D.; Xiao, M.; Huang, C.; Liang, Y.; Yang, Z. Land Use Scenario Simulation and Ecosystem Service Management for Different Regional Development Models of the Beibu Gulf Area, China. Remote Sens. 2021, 13, 3161. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.; Shi, H.; Lv, X. Spatio-temporal changes and driving forces of reclamation based on remote sensing: A case study of the Guangxi Beibu Gulf. Front. Mar. Sci. 2023, 10, 1112487. [Google Scholar] [CrossRef]
- Song, S.; Wu, Z.; Wang, Y.; Cao, Z.; He, Z.; Su, Y. Mapping the rapid decline of the intertidal wetlands of China over the past half century based on remote sensing. Front. Earch Sci. 2020, 8, 36. [Google Scholar] [CrossRef]












| Sensors | Resolution (m) | Year of Acquisition | Source of Images | Number |
|---|---|---|---|---|
| Landsat 5-TM | 30 | 1987–1999 | GSCloud | 76 |
| 2002–2005 | ||||
| 2008–2009 | ||||
| 2011 | ||||
| Landsat 7-ETM | 30 | 2000–2001 | USGS | 24 |
| 2006–2007 | ||||
| 2010–2012 | ||||
| Landsat 8-OLI | 30 | 2013–2021 | USGS | 36 |
| Landsat 9-OLI2 | 30 | 2021 | USGS | 4 |
| Sentinel-2 | 10 | 2018–2020 | ESA | 8 |
| Visual Interpretation | Classification Result | Mapping Accuracy | ||
|---|---|---|---|---|
| Tidal Flats | Others | Total | ||
| Tidal flats | 1024 | 169 | 1193 | 85.8% |
| Others | 174 | 4286 | 4460 | 96.1% |
| Total | 1198 | 4455 | 5653 | |
| User accuracy | 85.5% | 96.2% | ||
| Overall accuracy | 93.9% | Kappa | 0.82 | |
| Year | Overall Accuracy | Kappa | Year | Overall Accuracy | Kappa | Year | Overall Accuracy | Kappa |
|---|---|---|---|---|---|---|---|---|
| 1987 | 93.7% | 0.83 | 1999 | 95.3% | 0.88 | 2011 | 95.7% | 0.89 |
| 1988 | 90.4% | 0.76 | 2000 | 95.2% | 0.88 | 2012 | 92.5% | 0.82 |
| 1989 | 91.5% | 0.79 | 2001 | 95.2% | 0.85 | 2013 | 94.4% | 0.80 |
| 1990 | 96.0% | 0.83 | 2002 | 94.2% | 0.83 | 2014 | 93.1% | 0.79 |
| 1991 | 93.4% | 0.78 | 2003 | 95.6% | 0.81 | 2015 | 95.9% | 0.87 |
| 1992 | 93.6% | 0.77 | 2004 | 94.4% | 0.81 | 2016 | 93.4% | 0.82 |
| 1993 | 96.3% | 0.82 | 2005 | 94.5% | 0.81 | 2017 | 95.4% | 0.89 |
| 1994 | 94.9% | 0.81 | 2006 | 94.4% | 0.84 | 2018 | 93.3% | 0.81 |
| 1995 | 92.3% | 0.83 | 2007 | 95.2% | 0.86 | 2019 | 93.3% | 0.78 |
| 1996 | 92.4% | 0.80 | 2008 | 92.8% | 0.83 | 2020 | 93.4% | 0.87 |
| 1997 | 91.1% | 0.75 | 2009 | 94.6% | 0.82 | 2021 | 91.8% | 0.80 |
| 1998 | 96.6% | 0.90 | 2010 | 96.8% | 0.90 |
| Time | Mangrove Area of Shankou Area | Mangrove Area of Maowei Sea | Mangrove Area of Pearl Bay |
|---|---|---|---|
| 1996 | 4.6 | 0.4 | 8.9 |
| 2000 | 5.8 | 0.5 | 4.8 |
| 2005 | 8.6 | 0.5 | 4.3 |
| 2010 | 11.8 | 4.2 | 8.3 |
| 2015 | 11.4 | 13.3 | 8.7 |
| 2021 | 10.2 | 18.5 | 11.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, E.; Zhou, G. Spatio-Temporal Changes of Mangrove-Covered Tidal Flats over 35 Years Using Satellite Remote Sensing Imageries: A Case Study of Beibu Gulf, China. Remote Sens. 2023, 15, 1928. https://doi.org/10.3390/rs15071928
Gao E, Zhou G. Spatio-Temporal Changes of Mangrove-Covered Tidal Flats over 35 Years Using Satellite Remote Sensing Imageries: A Case Study of Beibu Gulf, China. Remote Sensing. 2023; 15(7):1928. https://doi.org/10.3390/rs15071928
Chicago/Turabian StyleGao, Ertao, and Guoqing Zhou. 2023. "Spatio-Temporal Changes of Mangrove-Covered Tidal Flats over 35 Years Using Satellite Remote Sensing Imageries: A Case Study of Beibu Gulf, China" Remote Sensing 15, no. 7: 1928. https://doi.org/10.3390/rs15071928
APA StyleGao, E., & Zhou, G. (2023). Spatio-Temporal Changes of Mangrove-Covered Tidal Flats over 35 Years Using Satellite Remote Sensing Imageries: A Case Study of Beibu Gulf, China. Remote Sensing, 15(7), 1928. https://doi.org/10.3390/rs15071928







