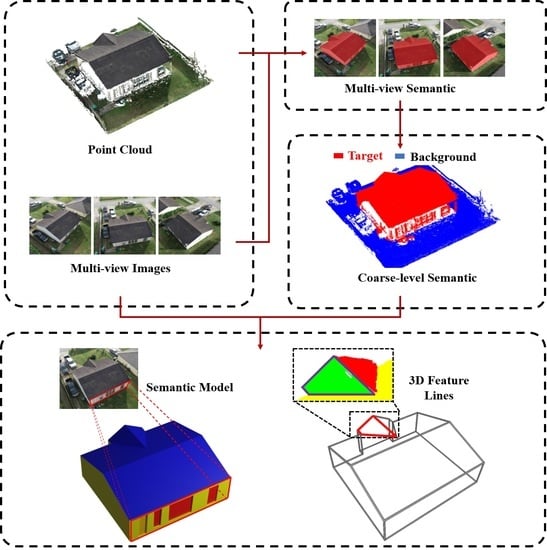
1. Introduction
Accurate 3D understanding and presentation technology of complex urban scenes play an important role in addressing issues of unmanned localization, unmanned aerial vehicle (UAV) autonomous navigation, and urban scene planning. Among them, the 3D semantic modeling of buildings is particularly necessary for 3D scene perception because the architectures occupy a large proportion of urban scenes. However, existing mainstream 3D semantic modeling methods, such as PointNet by Qi et al. [
1] and PointNet++ by Qi et al. [
2], rely heavily on a large amount of semantic labeled training data, which are severely lacking in urban 3D point cloud scenes. In addition, the lack of fine-grained semantic information of buildings cannot meet the requirements of high-precision scene localization and perception (the robots need to be parked accurately in front of a specific unit door of a building). Furthermore, the number of point clouds in a real urban scene is generally beyond the million level. Even if accurate semantic information can be extracted, the vast amount of discrete point cloud data need to occupy large storage resources, which are not suitable for low-power embedded robot devices. Therefore, further lightweight processing of point cloud data is necessary. Existing lightweight modeling techniques, such as Poisson reconstruction Kazhdan and Hoppe [
3] and VSA Cohen-Steiner et al. [
4], utilize 3D point clouds to produce a lightweight mesh of the scene. However, building edges directly extracted from discrete point clouds are serrated and not smooth enough. Additionally, given that these methods construct a unified mesh of the whole scene, each building target in the mesh is connected and indistinguishable, thereby interrupting the generation of fine-grained semantics for the target building. None of them can directly generate lightweight models with semantic information and smooth building edges. In summary, the existing methods cannot achieve high-precision building lightweight modeling with fine-grained semantic information. Hence, they are still far from being used in practical applications.
Focusing on the above issues, this paper proposes a fine-grained segmentation-based lightweight semantic modeling framework. Combining the semantic information of multi-view images with the geometric structure of the 3D point cloud, a complex urban scene is first segmented coarse-grained to extract each building point cloud in the scene. Second, constrained by 3D feature lines, a vectorized 3D model that contains building element details is generated by using the multi-view fine-grained segmentation-based lightweight modeling method. In practical applications, our lightweight fine-grained semantic model cannot only significantly reduce the storage load but also improve the understanding of semantic details of 3D architecture. The main contributions can be summarized as follows:
Joint 2D–3D Semi-supervised Semantic Object Segmentation: The existing dataset that can be applied to the semantic segmentation of large-scale complex urban scenes is extremely limited, thus seriously affecting the generalization ability and segmentation accuracy of networks. Moreover, urban scene data sets are accompanied by a large number of manual semantic annotations, and constructing new data sets is also highly labor intensive. To solve the aforementioned issues, we propose a semi-supervised 2D-3D joint semantic segmentation method that learns robust 3D scene semantic representations without requiring semantic labeling of the point cloud. Our method enforces multi-view consistency and geometric co-planarity constraints, ensuring that pixels obtained by projecting the same 3D point or belonging to the same plane onto multiple views have the same semantics. Using only a limited amount of image semantic labeling, our semi-supervised method effectively trains a robust semantic segmentation model. Our approach effectively addresses the problem of limited labeled data and outperforms complex 3D or KNN convolutions, as it relies on more efficient 2D convolutions.
Plane Constrained Multi-view Accurate 3D Feature Lines Extraction and Optimization: For vectorization modeling, a highly accurate plane fitting of the building point cloud should be constrained by an accurate geometric boundary. However, 3D point cloud data are discrete and sparse, and are not smooth enough to extract the boundary directly. In addition, boundaries extracted from 2D images are smooth but discontinuous due to occlusions and shadows. To solve the above problems, we project the multi-view edge information to the 3D reference plane to generate continuous and smooth 3D feature lines of the building based on the edge detection of multi-view images and point cloud reference plane parameters. Among them, the introduction of multi-view image consistency not only ensures the smooth edge but also solves the boundary discontinuity caused by occlusion. Finally, point clouds are replaced with vector planes generated by the shortest loop algorithm, which achieves a highly accurate 3D vector modeling of building targets in complex scenes.
Lightweight Semantic Modeling Framework in Fine-grained Elements Segmentation Level: The existing semantic modeling approach for the urban scene is a global meshing of the overall scene, where each element (e.g., buildings, road, trees, etc.) mesh is interconnected and indistinguishable. However, this kind of modeling cannot process and analyze individual objects separately, thereby significantly limiting the flexibility of semantic modeling. The worst factor is that more complex geometric representations and a large number of planes and points are required, which will waste more storage resources and are not suitable for practical applications. To solve the above problems, we propose a novel semantic modeling framework for buildings. Neglecting the fact that we use the plain modeling method, the accurate building models are generated provided with the aforementioned precise point cloud segments and 3D feature lines.In the building modeling stage, multi-view images and 3D point cloud clustering information are referenced to extract each building and vectorized individually. This not only guarantees the accuracy of the 3D geometric structure of the building but also reduces modeling complexity. Finally, a feature line that constraints fine-grained element segmentation method is proposed to obtain detailed semantics of building elements (doors and windows) and integrated with the lightweight model to achieve a highly accurate 3D vectorization modeling of individual buildings with fine-grained semantic information.
2. Related Work
We explore generate accurate point cloud segmentation and detect precise 3D feature lines to aid semantic and lightweight architecture modeling. Given the emphasis on building modeling and semantic segmentation, we view the related works on two main aspects: lightweight modeling and semantic segmentation of buildings.
2.1. Vectorized Modeling
Building modeling is a popular research topic because of its various applications and development of point cloud generation techniques.
Several early works concentrate on robust and accurate modeling. Kazhdan and Hoppe [
3] proposed a faster and higher-quality surface reconstruction method by extending the Poisson surface reconstruction algorithm. Driven by geometric error, Cohen-Steiner et al. [
4] and Garland and Heckbert [
5] tended to simplify surface mesh to reduce model complexity. However, relying on accurate surface meshes, these methods are sensitive to outliers.
Considering that building models are composed of fixed geometric primitives, several works use bounding boxes to represent building models under the Manhattan World assumption. Li et al. [
6] fitted buildings with bounding boxes and formulated building modeling as a linear integer programming problem. Nan et al. [
7] adopted a similar strategy and solved the building modeling problem in a way that minimized energy.
Viewing the building modeling reconstruction as a labeling problem, Li et al. [
8] selected a subset of candidate boxes in Markov random field formulation, which could be easily solved by the graph-cut algorithm. Although most buildings can be reconstructed by the above-mentioned bounding box-based methods, modeling for buildings with complex architecture remains a challenge.
To solve this problem, few works emphasized the modeling of complex building roofs. Zhou and Neumann [
9], under the hypothesis of vertical walls, extended classic dual contour into a 2.5D method to recover buildings with a complex roof structure. By solving an energy minimization problem of 2.5D roof section arrangement, Lafarge and Mallet [
10] modeled complex roof and vertical walls with a hybrid representation that is combined with mesh patches and regular geometric primitives. Nevertheless, under the vertical wall assumption, building facade details, which are important in building modeling, are neglected.
PolyFit [
11], which was developed by Nan and Wonka [
11], proposed a method for modeling random building surfaces that were composed of planes. In PolyFit, taking organized point clouds as input, the building surface is composed of faces that are selected from a large set of face candidates by solving an energy minimization problem using binary linear programming. In spite of its robustness on most building models, the time cost of binary linear programming is unacceptable for buildings with a large number of faces.
2.2. Semantic Segmentation
Semantic segmentation has been a popular topic in computer vision, robotics, and remote sensing for decades and plays a vital role in building reconstruction. Segmentation on point clouds is a common method to reconstruct buildings with semantic information, and most algorithms can be categorized into supervised and unsupervised formula.
2.2.1. Unsupervised Point Cloud Semantic Segmentation
Region growing [
12] was first proposed to segment 2D images and is widely used in point cloud segmentation today. It grows regions from seed points and determines whether near points belong or not to the region according to the criteria that combine features between two points to measure distances among points. Gorte [
13] applied the region-growing algorithm to clustering LiDAR generating building point clouds into planar facets. Vo et al. [
14] proposed a building point cloud segmentation algorithm, which first applied a region-growing step and then refined cluster in a coarse to fine manner, based on voxelized point clouds.
Random sample consensus (RANSAC) by Fischler and Bolles [
15] is a popular modeling fitting method. Considering that buildings are made up of parameterized 3D geometric primitives, RANSAC-based algorithms are suitable for segment building point clouds. In application, RANSAC-based algorithms are widely used to detect planar building faces. Efficient RANSAC developed by Schnabel et al. [
16] aims to detect basic geometric primitives from unorganized point clouds and show fine robustness in the presence of many outliers and a high degree of noise. Adam et al. [
17] took point clouds produced by overlapped images as inputs and leveraged RANSAC on 3D geometry and 2D segmentation to achieve more accurate results.
Even for unsupervised segmentation algorithms, determining the semantic label of point clouds directly is difficult, and it can be applied in the preprocessing step in building semantic segmentation and modeling.
2.2.2. Supervised Point Cloud Segmentation
Compared with unsupervised point cloud segmentation algorithm that focuses on cluster points with co-geometric primitives, supervised segmentation methods aim to classify point clouds into different semantic labels.
Traditional machine learning has been commonly used in point cloud semantic segmentation. Wang et al. [
18] and Lodha et al. [
19] applied Adaboost classifier to segment point clouds. Chehata et al. [
20] used random forest algorithm to classify urban LiDAR point clouds. These classifiers depend on hand-crafted features and neglect contextual information, which is useful for classification. Additionally, these methods take point clouds whose ground is in parallel with the x–y plane as inputs. This approach is unusual for multi-view generating point clouds. In contrast to the above classifiers, conditional random field (CRF) can capture more specific relations of object classes and model contextual information. Niemeyer et al. [
21] adopted CRF classifier in complex urban LiDAR point clouds. To speed up the problem solving of CRF, Lim and Suter [
22] over-segmented and classified point clouds into supervoxels. Restricted by domain-specific parameters of CRF, these methods show fine robustness in LiDAR point clouds, yet failed to hold generalization on multi-view generated point clouds.
With the increasing popularity of deep learning techniques, a growing number of works have been leveraging deep learning models on the point cloud segmentation task. PointNet, which was proposed by Qi et al. [
1], incorporated non-local information into point cloud segmentation by maxpooling operation on point feature vectors. Based on PointNet, Qi et al. [
2] used hierarchical network to capture more local features and proposed PointNet++. To recover the topological connection between points, DGCNN, which was developed by Wang et al. [
23], leveraged EdgeConv for point cloud segmentation. Our closest related work is Genova et al. [
24], who generated sparse 3D point cloud semantic labels by combining image semantic labeling with pose information, and densified scene semantics further using 3D convolutions. However, this approach still requires a significant amount of labeled image data to obtain a robust semantic segmentation model, and its multi-stage segmentation method poses deployment challenges in practical applications. Deep-learning-based methods are enjoying increasing popularity on point cloud segmentation. However, limited by the need for massive training data, applying deep learning techniques in building point cloud segmentation is difficult.
3. Methodology
3.1. Overview
We propose a unified framework for producing accurate segmentation results and extracting precise 3D feature lines for building models from complex urban scenes. Notably, the input data, including 2D multi-view images and 3D dense point cloud, are multi-source and heterogeneous, and the output is a lightweight building model with fine-grained semantic annotations. To address the challenges of extracting object-level segmentation results from noisy and cluttered point clouds, we propose a novel joint 2D-3D semi-supervised object segmentation algorithm. Our approach leverages the complementary strengths of multi-view images and 3D point clouds by combining photometric consistency with geometric consistency. However, the point cloud is memory costly. To generate lightweight 3D building models, we generate a lightweight contour for each building facet based on the 3D plane constrained multi-view accurate feature line extraction and optimization algorithm. Finally, to enrich the fine-grained semantic information of the acquired lightweight model, we designed a lightweight semantic modeling framework to produce lightweight models with fine-grained and lightweight semantic annotations. The detailed pipeline of our framework is shown in
Figure 1.
3.2. Joint 2D-3D Semi-Supervised Semantic Object Segmentation
Previous works mainly focus on segment point clouds by supervised learning methods, which require a large amount of labeled training data [
18,
19,
20,
21,
22,
25,
26]. However, constructing a training dataset for urban scene semantic segmentation is labor intensive for the complexity and discreteness of urban scene point clouds. When confronted with dense and complex urban point cloud semantic segmentation tasks, no methods are deemed effective yet.
A joint 2D-3D semi-supervised semantic object segmentation method for dense point clouds is designed to overcome the aforementioned issues. To extract target building pixels from multi-view images, we utilize the HRNet [
27] as our backbone for object segmentation. Additionally, we employ the unsupervised clustering algorithm proposed in [
28] to perform coplanar clustering of point clouds. This approach enables us to obtain coplanar image pixels through multiview projection of coplanar point clouds. These pixels are then bounded by semantic consistency during the training process. To ensure multi-view photometric consistency, we enforce the constraint that the projections of the same point cloud on different images belong to the same semantic class. By combining the constraints of multi-view segmentation information and point cloud clustering information, we effectively reduce the errors that may arise from discrete point clouds. This approach improves the accuracy and quality of the segmentation results and enables us to obtain more reliable and robust segmentation output for various downstream applications. Notably, 2D multi-view segmentation only needs to provide a handful of labeled 2D images as the training set, which reduces the dependence on semantic annotation of the point cloud greatly. Meanwhile, it can provide photometric consistency to reduce the occlusion problem. Then, co-planar geometric consistency from point cloud clustering can also guarantee the details of the accuracy of the dense point cloud segmentation, which does not need any supervised information.
Notably, we propose a semi-supervised high-accuracy architecture modeling framework. To achieve more accurate building modeling, segmentation and meshing modules in our framework, not limited by methods in this work, are upgradeable and alternative.
3.2.1. Multi-View Image Segmentaion
A lack of training data remains one of the main challenges of existing segmentation methods. Most open-source segmentation datasets are captured in front views. However, the input images in our tasks are mostly bird-eye views, which cannot directly utilize the existing data set for training. To overcome this problem, we use some manually annotated images from Dataset I to train an HRNet [
27] from scratch. We annotated collected images with two categories, namely,
building, and
background clutter. Given an image as input, our network outputs a probability
for every pixel
image
i, where
. Thus, our loss function can be defined as follows:
y is the ground truth label represented by a vector of 0 or 1.
3.2.2. Photo-Metric Semantic Constraint
By providing image location and point visibility information, we can easily incorporate photometric consistency and semantic constraints from multi-view images into the training framework. This intuitive approach enhances the accuracy and reliability of the segmentation results and allows for more effective training of the algorithm. With known image intrinsic matrix
, rotation matrix
and translation vector
, projection matrix is defined as
,
denotes the image from image sets
, 2D images pixel
location
on image
according to
as:
where
is the location of
.
and
are the homogeneous coordinates. Visibility is denote as an image set
for each 3D point
. The photometric loss is computed as:
3.2.3. Co-Planar Geometric Constraint
The simplest way to decide the final classification for point clouds is by fetching the label with max probability for point . Nevertheless, these methods neglect the facts that multi-view image segmentation results are inevitably noisy. As such, the training framework can be further improved combined with 3D geometric consistency constraints. Building on the assumption that co-planar points belong to the same object, we introduce a novel loss function that is based on self-supervised signals. Our proposed loss function enhances the performance of the algorithm by enforcing the constraint that co-planar points are assigned to the same semantic class.
Clustering point clouds with similar geometric features is an unsupervised segmentation problem that has been heavily researched for decades. Commonly used algorithms for segmentation point clouds include region-growing-based [
12] and RANSAC-based [
15] approaches. These methods are efficient for detecting clusters with similar features. However, these algorithms are designed to neglect hypothesized outliers, and the segmentation completeness is not ensured. Our inputs are noisy multi-view generated point clouds, and segmentation completeness is critical to this task. For consideration, we adopt a newly proposed method called pairwise-linkage by Lu et al. [
28], which can detect co-planar segmentation and guarantee the segmentation completeness.
We used the pairwise-linkage algorithm to segment point clouds into different co-planar clusters. For each cluster
and projected image
i, we compute geometric loss as follows:
Thus, our final training loss is a linear combination of the above three losses, expressed as follows:
In this way, the background and noise point clouds can be removed in the later facet plane fitting and facet contour generating steps. In addition, after removing the background point clouds, the connection among different target buildings is eliminated, which is more beneficial to model and generate fine-grained semantics for target building independently.
3.3. Plane Constrained Multi-View Accurate 3D Feature Line Extraction and Optimization
After determining the architecture point clouds, our target in this step is to generate lightweight architecture polygon contour to replace the original point cloud architecture facet. In this way, we can avoid the use of memory costly point cloud on lower energy cost applications. Several early works focus on lightweight modeling based on point clouds. Cohen-Steiner et al. [
4] and Kazhdan and Hoppe [
3] attempted to detect building edges from 3D point clouds. However, for the discrete and noise of point clouds, the obtained building edges are generally jagged and non-smooth. The building edges extracted from the images are smooth but discontinuous and hence cannot compose valid 3D building edges. In summary, generating accurate and smooth edges and being robust to noisy point clouds are the main challenges on the architecture modeling of urban dense point cloud scenes.
To relieve the aforementioned issues, we proposed a 3D plane constrained multiview accurate feature line extraction and optimization algorithm. In our methods, architecture facet contour is constrained and generated from 3D feature lines. First, leveraging multi-view image information to extract edges can avoid the generation of architecture facet contour from point clouds, which eliminates the noise of major edges. Second, multi-view images have more 3D edge details than point clouds, which can considerably boost robustness and precision on architecture modeling.
3.3.1. Ground Calibration
In the urban scene segmentation stage, point clouds are classified into coplanar clusters and labeled with different classes. Before extracting architecture facets, the world coordinates of point clouds must be calibrated to satisfy the Manhattan-world assumption. We take point clouds belonging to
ground and use RANSAC [
15] to estimate the normal of ground point clouds. Given the estimated ground normal vector
and center point
, we generate two vectors, namely,
,
and
are pair-wise orthogonal. The rotation matrix
and translation vector
is defined as:
By applying rotation and translation, point clouds are calibrated to the Manhattan-world coordinate.
3.3.2. Inner 3D Feature Line Generation
The parameterization of roof facets is implemented using RANSAC [
15]. We define inner 3D feature edges as the intersection line segments of parameterized architecture facets. To determine the intersection line segments of facets, hypothesis intersection lines are computed on the basis of parametrized facets. After obtaining a hypothesis line, we select two sets of intersection facet points, which are under the distance threshold
t to the intersection line. A line segment can be acquired by reprojecting one set of points to an intersection line and fetching endpoints. Intersection line segments are obtained by computing the common interval of two line segments. Considering that most facets have common intersection points, we refine the endpoint intersection segments to the common intersection point.
3.3.3. Multi-View 2D Feature Line Detection
In this stage, our main goal is to extract edge line segments of facets on 2D images. We apply LSD Von Gioi et al. [
29] to detect candidate 2D feature lines. For each facet, two steps must be followed to obtain the final facet contour, view selection, and multi-view segment fusion.
View Selection: For each architecture facet, a subset of visible images
is selected according to the visibility file. With known visibility image set
for each point
, we define visibility set
for each facet
as:
Multi-view 2D Feature Line Fusion: We use LSD to extract a large amount of candidate line segments from
. Aiming to transfer 2D line segments to 3D facet plane, end points of the line segments extracted from image
are projected to 3D roof facet using projection Matrix
and parametrized facet plane equation
as:
where
is the endpoint of the line segment, and
is the 3D coordinate location of projected
. Through this projection method, the 2D line segments from different images are gathered to the target facet 3D plane.
3D Feature Line Filtering: However, most of these line segments are not valid contour of the target facet, and the filtering process is essential to reduce the solving time of contour arrangement optimization. In common sense, edge line segments are always close to point clouds, and the point cloud densities between two sides of the line segment have a huge difference. Based on the two aforementioned assumptions, we design a robust and simple strategy to filter out invalid line segments. Facet point clouds are projected to the facet plane. Given a line segment with length
L, we construct a bounding box parallel to the line segment and centered on the middle point of the line segment with an aspect ratio of
. All points located in the bounding box are counted and divided into the negative side
and positive side
. Line segments with
and
are retained. The intuitive explanation is shown in
Figure 2.
3D Feature Line Merging: Although the majority of invalid 3D feature lines are filtered out, a large number of candidate edge line segments of target facet is conserved yet. To further speed up the 2D contour arrangement optimization problem, merging is vital to duplicate line segments. When determining whether line segments are duplicated, parallel and proximity are our main considerations. Given two line segments
,
with middle points
,
, and direction vector
and
, parallel is defined as:
The defined
and
are parameterized by
and
. Proximity can be defined as:
With the definition of parallel and proximity, we cluster all the duplicated segments. We determine the direction and middle point of the new line segment merged from segment clusters as the average direction and middle point of original segment clusters. Moreover, the endpoints of the new segment are the max interval of endpoints of original segment clusters. With the average operation, the noise is eliminated, and boundary precision is improved.
3.3.4. Geometric-Based Contour Optimization
In this step, our main goal is to construct a complete facet polygon contour from inner intersection line segments and outer candidate edge line segments for each facet. We emphasize the generation of low complexity polygons and fitted the shape to the real roof facet. Viewing the contour arrangement problem as the shortest circle path problem of directed graph which is natural to roof contour, we developed an efficient algorithm to solve it.
We define the Graph as .
Node definition: Given the inner and edge line segments, we define their intersection points as node .
Edge definition: After generating nodes, we define the directed edge
between two nodes located on the same line segment
in the same direction. To determine the edge direction, we extract the rough 2D contour of target facet using the alpha-shape algorithm implemented by CGAL [
30]. Then, a simplified contour
based on the extracted contour is computed by Douglas-Peucker algorithm. For each edge in
, we select a direction to guarantee that only one circular path exist. The direction of the line segment
in
is consistent with the direction of the edge
in
with maximum matching score. The matching score between edge
and
is defined as:
where
and
are the normal vectors of
and
, respectively. Moreover,
and
are the middle points of
and
, respectively. See
Figure 3 for a straight-forward explanation.
Edge weight definition: Edge weight definition is auxiliary for guiding the algorithm to solve the correct contour shape of the roof facet. Edges with accurate contour, compact, and edge preserving have two main features. For compactness, we designed a factor to measure the compactness reduction for adding the edge
to the contour,
where
s the length of edge
. Edge
located on line le is defined. For edge preserving, line segments with more confidence semantic boundary will be detected in more images. We calculate
as the edge-preserving factor. Because line
is merged from a number line segments
,
is the number of set
. The final edge weight for edge
is defined as:
Contour Rearrangement: We view the contour arrangement as the shortest circular path algorithm. The algorithm to solve this problem is described as Algorithm 1.
With the building facet contour composed of 3D feature lines, the smoothness and lightweight of the building edge are guaranteed, thereby avoiding the use of dense point clouds or complex mesh to represent the building model. Further, lightweight models are the fundamental of lightweight fine-grained semantic representation of buildings. In practice, lightweight models can reduce computation and storage consumption of applications significantly and is beneficial to energy conservation.
| Algorithm 1 Shortest Circular Path Algorithm |
Input: Graph , Adjacent Table
Output: Shortest Circular Path
Initialization: Set for each i, j, for each i, dist[i][j] is the shortest distance from node i to node j.
Step 1. Use Floyd-Warshall Algorithm to compute dist[i][j].
Step 2. , ,
for in E do:
i, j, w = start node of , end node of , weight of e.
if w + dist[j][i] then:
= w + dist[j][i]
Step 3.
while do:
for g, w in do:
if dist[g][v] + w = dist[u][v] then:
= + g
break;
= + v
Return |
3.4. Light Weight Semantic Modeling Framework in Fine–Grained Element Segmentation Level
Currently, many applications not only require accurate 3D building model parameters but also fine-grained building semantic information. However, to be utilized by lower-cost devices, a lightweight representation of semantic information is necessary. Therefore, our main goal is to generate lightweight fine-grained semantics of the target building. To enrich the semantic information of building models, we proposed a lightweight semantic modeling framework with fine-grained element segmentation.
The majority of recent works [
3,
4,
11] on modeling building mainly produce a unified mesh of the whole scene where each target building is inseparable. Recently proposed methods [
31,
32,
33] for segmentation of building facades show excellent results. However, the outputs of these works are pixel-wise, which is not compact enough for vectorized model representation. To eliminate these disadvantages, we train a DeepLabv3 [
34] network to output pixel-wise labeled results and adopt Algorithm 1 to achieve the polygonal segmentation. Finally, we combine the polygonal segmentation with the obtained lightweight model to generate lightweight semantic models.
3.4.1. Candidate View Selection
A candidate image must be selected for each architecture facet to detect fine-grained semantic instances. To extract complete fine-grained semantics, we attempt to select the image that contains the majority of points of the target architecture facet. The candidate view image
for facet
is defined as follows.
3.4.2. Fine-Grained Semantic Instance Detection
We first detect fine-grained semantic instance
on candidate view
using a trained neural network.
is defined as the 2D semantic pixel belonging to
, the 3D back projection location
to facet
of
can be computed as follows.
is the 2D location of pixel
.
After obtaining the fine-grained semantic 3D point cloud
, we use the method in
Section 3.3.3 to collect the 3D feature lines and apply algorithm in
Section 3.3.4 to generate light weight polygonal fine-grained semantic representation.
3.4.3. Framework Designation
The designed framework can solve the fine-grained semantic modeling problem for urban scenes. The concise data stream and independent modules of our framework bring fine extensibility and utility. For utility, our framework can take reconstruction results of most multi-view stereo algorithms as input data. For extensibility, our current fine-grained semantic elements can extend to more classes, such as stairs and balconies, by replacing the fine-grained segmentation network. Based on our framework, developing more semantic modeling applications, such as indoor semantic modeling or urban street semantic modeling, is possible.
Through the above steps, the semantic and 3D structure of the produced model is lightweight, thereby extending the application range and enabling the lower-cost devices to process fine-grained building semantics effectively.
4. Results
We have applied our methods on several datasets of real-world buildings and conducted qualitative and quantitative measurements of the proposed method. It should be noted that we use the vanilla modeling approach to show the superior benefits of point cloud segmentation and 3D feature line detection for architecture modeling. Evaluation Dataset I is a collection of multi-view images captured from an unmanned aerial vehicle (UAV). The point clouds are generated using COLMAP [
35,
36,
37]. The dataset [
38] used is an open dataset for fine-grained building facade image segmentation. The point clouds inputted to our methods are noisy with incomplete building facades and uneven densities. Results show that our method is robust to complex building structures and meanwhile with fine-grained semantic information. We evaluate our methods around our three tasks, namely, object-level point cloud semantic segmentation, elements level vectorized semantic segmentation and vectorized building modeling.
4.1. Point Cloud Segmentation
In these experiments, we test point cloud semantic segmentation performance in different models. We compare our results with the SOTA method, PointNet [
1], PointNet++ [
2], and RandLA-Net [
39] on our test data. The test scenes are selected from Dataset I with an average of million points. We selected 9 scenes from Dataset I, and 6 of them were selected as the training data of PointNet [
1], PointNet++ [
2], RandLA-Net [
39], Point Transformer [
40] and PointNeXt [
41], and three of them were selected as the test data. For our methods that take multi-view images as input data, we manually annotated 40 images to train HRNet [
42] to produce segmentation results on 2D images.
Table 1 shows the accuracy and IoU of our multi-view fusion model, PointNet, PointNet++, RandLA-Net, Point Transformer and PointNeXt. We achieve the best performance and dense semantic segmentation results (
Figure 4).
As shown in
Figure 5, the top left and bottom left of the figure is the collected multi-view images and generated dense scene point clouds, and the bottom right of the figure is the semantic segmentation result of the scene point clouds where redpoint clouds denote building, and blue point clouds denote background. Finally, the top right of the figure corresponds to the produced fine-grained semantic included vectorized building models after extracting the building point clouds from the scene point clouds.
4.1.1. Fine-Grained Semantic Segmentation
We mainly focus on generating precise and lightweight fine-grained semantic contour from pixel-wise segmentation results, combined with the lightweight architecture model.
In this experiment, we set DeepLabv3+ [
34] as our base model and train it on Dataset from the 3D Semantic Segmentation and Procedural Modelling Challenge [
38] to detect pixel-wise segmentation results on 2D images.
In
Table 2, we train our models using the training set labeling information of dataset [
38], including windows and doors. The results in the table correspond to the performance of our model on the test set of the dataset. We show that we can generate more accurate contour and improve the segmentation accuracy based on rough pixel-wise segmentation results with the geometric-based contour optimization algorithm. As shown in
Figure 6, through our fine-grained segmentation-based lightweight semantic modeling framework, the architecture model can be enhanced with richer and more lightweight fine-grained semantic annotation.
Figure 7 shows that the fine-grained semantic contour generated by our optimization is more lightweight and compact than the neural network segmentation result.
Figure 7 shows that our boundary optimization algorithm can extract accurate and compact semantic contour from raw pixel-wise segmentation results. After applying our optimization algorithm, the semantic segmentation can be represented by a polygon which is more lightweight than pixel-wise information. Simultaneously, the edge of the optimized segmentation is smoother and more similar to the true semantic annotation.
4.1.2. Vectorized Modeling
In this section, our main goal is to evaluate the generated model in terms of accuracy and lightweight. We selected Dataset I as the test data. In our model generation experiments, weight parameters and are set to 1.0 and 1.0, thresholds t and are set to 0.001 and 200 for both datasets, respectively. We conduct our experiment in terms of quality and quantity. For quantity evaluation, we select six scenes from dataset I and compute the errors and facet numbers of the model among different methods.
Table 3 shows that our results, which are combined with few lightweight facets, are more compact than models generated from PolyFit [
11], VSA [
4], and QEM [
5]. Two main metrics are
, the distance from the origin point cloud to the building mesh, and
, the facet number of the building mesh. Generally, smaller
represent higher modeling precision. As an indicator of lightweight,
should be smaller under the constraint of accurate modeling (smaller
). Considering the complex structure and limited precision of the point cloud, the
should be less than 0.1, and
should range from 50 to 200. Furthermore, our algorithm is robust to simple and complex roof structures. Nevertheless the raw point clouds with sparse and incomplete walls can still acquire good vectorized models using our algorithm.
In
Figure 5, we show the modeling results applied on Dataset I, large downtown area. Compared with the original point clouds, the models produced by our method are more lightweight, and each facet of the buildings can be described by a polygon. Besides, the edge of the generated model is smooth, and no intersection exists between different buildings. We also extend our experiment to Dataset [
38].
Figure 8 shows the model reconstruction results on Dataset [
38] with vectorized semantic segmentation. Compared with the original mesh, our reconstruction result is preferable with lightweight architecture facades.
5. Discussion
Regarding the segmentation results, we observed that PointNet [
1] and PointNet++ [
2] performed poorly in semantic segmentation experiments of building point clouds. The networks failed to obtain effective semantic information of the buildings, possibly due to heavy downsampling during the segmentation process (
Figure 4). However, our approach, which combines multi-view information and 2D convolutional neural networks, outperformed PointNeXt [
41] and RandLANet [
39] in the segmentation of building geometric corners, producing more precise and sharper segmentation results (
Figure 4, highlighted in orange).
PointFormer showed clear segmentation results of building corners. However, this was based on a global attention mechanism that required
computational complexity and consumed large amounts of memory. In contrast, our approach achieved good segmentation results even in cases of severe point cloud loss. For example, in
Figure 4 highlighted in green, most of the building points were not reconstructed, and only a corner of the building was visible. However, our approach accurately segmented these points into buildings, showing its robustness to loss and occlusion. This robustness could be attributed to the complementary nature of the missing parts in multi-view images.
Regarding the lightweight modeling results (
Table 3), our approach outperformed other methods in terms of modeling accuracy. The high accuracy was due to the extraction of multi-view 3D feature lines, which avoided direct surface fitting on the point cloud, leading to better results than methods based on pure point clouds. In terms of modeling lightweightness, our approach was comparable to the PolyFit [
11] method, while the VSA [
4] and QEM [
5] methods did not consider prior knowledge about building modeling, such as the fact that buildings are typically composed of geometric planes. Our approach effectively utilized this prior knowledge, strengthening the 3D plane constraint during building face generation, resulting in more lightweight models.
Concerning the smoothness of the models, our approach and PolyFit [
11] outperformed the other methods. However, it is important to note that PolyFit [
11] generated building models that did not match real building shapes. This was due to the optimization problem of constructing a watertight geometry, which requires complete point clouds without significant occlusion or loss; otherwise, the optimization problem becomes ill-conditioned. However, buildings reconstructed using multi-view geometry collection methods are usually incomplete and occluded, making our approach more suitable for lightweight modeling.
6. Conclusions
In this paper, a novel lightweight semantic modeling framework is designed to achieve a highly accurate 3D vectored modeling of buildings with fine-grained semantic information. A joint 2D-3D semi-supervised semantic object segmentation framework is proposed to improve the semantic accuracy and richness of buildings through 2D segmentation and unsupervised clustering. Meanwhile, semi-supervised building semantic segmentation can also reduce the labeling work of training data without affecting the quality of segmentation significantly. Subsequently, a 3D plane-constrained multi-view accurate feature line extraction and optimization method is proposed to achieve continuous, multi-view, consistent, and smooth 3D lines of the buildings. The introduction of multi-view image consistency not only solves the boundary discontinuity caused by occlusion but also improves the accuracy of single building surface vector modeling. Finally, a lightweight semantic modeling framework with fine-grained element segmentation is designed carefully. Each building in complex urban scenes will be extracted accurately and finely vectorized independently, thereby not only improving the details of the 3D geometric structure of the building but also solving the issue of buildings in urban scene mesh models that cannot be processed and analyzed separately. A feature line that constraints fine-grained element segmentation is also introduced into the modeling framework to achieve a highly accurate 3D vectorization modeling of individual buildings with fine-grained semantic information (doors and windows). Of course, our framework has shortcomings.
In the current reconstruction process, we only make use of segmentation and 3D feature lines by using a plain approach to generate 3D building mesh. By extending our framework to a more complex and well-designed modeling method, we may attain better meshing results. Another interesting problem is that the piece-wise planar roof structure assumption becomes overly restrictive when dealing with atypical architectures. Moreover, the point clouds used in this work, mostly generated by multi-view reconstruction, have some missing parts, which will slightly affect the meshing process. Furthermore, the 3D feature line detection also requires high-accuracy camera poses from multi-view reconstruction. In future work, we would like to enhance our method to incorporate more types of geometric primitives, such as cylinders and spheres, to describe more complex and diverse building vector models. We also expect to extend our framework to more fine-grained semantic elements, such as exterior building decorations, geometric structural details of doors, windows, balconies and others, and apply our method to more practical applications, such as animation, movie making, and autonomous driving.
Author Contributions
Conceptualization, S.X. and J.S.; methodology, S.X.; software, J.S.; validation, J.Z., W.M. and X.Z.; formal analysis, S.X.; investigation, S.X. and J.Z.; resources, X.Z. and W.M.; data curation, J.S.; writing—original draft preparation, S.X.; writing—review and editing, S.X. and J.Z.; visualization, J.S.; supervision, X.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Nos. U21A20515, 61972459, 61971418, U2003109, 62171321, 62071157 and 62162044) and in part by the Open Research Fund of Key Laboratory of Space Utilization, Chinese Academy of Sciences (No. LSU-KFJJ-2021-05), and this work was supported by the Open Projects Program of National Laboratory of Pattern Recognition.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the fact that the data collected for this study are intended for commercial use and are therefore considered proprietary information.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. (ToG) 2013, 32, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Steiner, D.; Alliez, P.; Desbrun, M. Variational shape approximation. In ACM SIGGRAPH 2004 Papers; ACM Press: New York, NY, USA, 2004; pp. 905–914. [Google Scholar]
- Garland, M.; Heckbert, P.S. Surface simplification using quadric error metrics. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 3–8 August 1997; ACM Press: New York, NY, USA, 1997; pp. 209–216. [Google Scholar]
- Li, M.; Nan, L.; Liu, S. Fitting boxes to Manhattan scenes using linear integer programming. Int. J. Digit. Earth 2016, 9, 806–817. [Google Scholar] [CrossRef] [Green Version]
- Nan, L.; Jiang, C.; Ghanem, B.; Wonka, P. Template assembly for detailed urban reconstruction. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2015; Volume 34, pp. 217–228. [Google Scholar]
- Li, M.; Wonka, P.; Nan, L. Manhattan-world urban reconstruction from point clouds. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin, Germany, 2016; pp. 54–69. [Google Scholar]
- Zhou, Q.Y.; Neumann, U. 2.5 d dual contouring: A robust approach to creating building models from aerial lidar point clouds. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–10 September 2010; Springer: Berlin, Germany, 2010; pp. 115–128. [Google Scholar]
- Lafarge, F.; Mallet, C. Creating large-scale city models from 3D-point clouds: A robust approach with hybrid representation. Int. J. Comput. Vis. 2012, 99, 69–85. [Google Scholar] [CrossRef] [Green Version]
- Nan, L.; Wonka, P. Polyfit: Polygonal surface reconstruction from point clouds. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2353–2361. [Google Scholar]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 641–647. [Google Scholar] [CrossRef] [Green Version]
- Gorte, B. Segmentation of TIN-structured surface models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 465–469. [Google Scholar]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2007; Volume 26, pp. 214–226. [Google Scholar]
- Adam, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. H-RANSAC: A hybrid point cloud segmentation combining 2D and 3D data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2018, 4, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, L.; Fang, T.; Mathiopoulos, P.T.; Tong, X.; Qu, H.; Xiao, Z.; Li, F.; Chen, D. A multiscale and hierarchical feature extraction method for terrestrial laser scanning point cloud classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2409–2425. [Google Scholar] [CrossRef]
- Lodha, S.K.; Fitzpatrick, D.M.; Helmbold, D.P. Aerial lidar data classification using adaboost. In Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling (3DIM 2007), Montreal, QC, Canada, 21–23 August 2007; IEEE: New York, NY, USA, 2007; pp. 435–442. [Google Scholar]
- Chehata, N.; Guo, L.; Mallet, C. Airborne lidar feature selection for urban classification using random forests. In Proceedings of the Laserscanning, Paris, France, 1–2 September 2009. [Google Scholar]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Conditional random fields for lidar point cloud classification in complex urban areas. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2012, 1, 263–268. [Google Scholar] [CrossRef] [Green Version]
- Lim, E.H.; Suter, D. 3D terrestrial LIDAR classifications with super-voxels and multi-scale Conditional Random Fields. Comput.-Aided Des. 2009, 41, 701–710. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. (ToG) 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Genova, K.; Yin, X.; Kundu, A.; Pantofaru, C.; Cole, F.; Sud, A.; Brewington, B.; Shucker, B.; Funkhouser, T. Learning 3D semantic segmentation with only 2D image supervision. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; IEEE: New York, NY, USA, 2021; pp. 361–372. [Google Scholar]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Vosselman, G.; Coenen, M.; Rottensteiner, F. Contextual segment-based classification of airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 354–371. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Lu, X.; Yao, J.; Tu, J.; Li, K.; Li, L.; Liu, Y. Pairwise Linkage for Point Cloud Segmentation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3. [Google Scholar]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 722–732. [Google Scholar] [CrossRef]
- Fabri, A.; Pion, S. CGAL: The computational geometry algorithms library. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 538–539. [Google Scholar]
- Liu, H.; Zhang, J.; Zhu, J.; Hoi, S.C. Deepfacade: A Deep Learning Approach to Facade Parsing; IJCAI: San Francisco, CA, USA, 2017. [Google Scholar]
- Mathias, M.; Martinović, A.; Van Gool, L. ATLAS: A three-layered approach to facade parsing. Int. J. Comput. Vis. 2016, 118, 22–48. [Google Scholar] [CrossRef] [Green Version]
- Schmitz, M.; Mayer, H. A convolutional network for semantic facade segmentation and interpretation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 709. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Schönberger, J.L.; Price, T.; Sattler, T.; Frahm, J.M.; Pollefeys, M. A Vote-and-Verify Strategy for Fast Spatial Verification in Image Retrieval. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 20–24 November 2016. [Google Scholar]
- Riemenschneider, H.; Bódis-Szomorú, A.; Weissenberg, J.; Van Gool, L. Learning where to classify in multi-view semantic segmentation. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 516–532. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Online, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.A.A.K.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. arXiv 2022, arXiv:2206.04670. [Google Scholar]
- Sun, K.; Zhao, Y.; Jiang, B.; Cheng, T.; Xiao, B.; Liu, D.; Mu, Y.; Wang, X.; Liu, W.; Wang, J. High-resolution representations for labeling pixels and regions. arXiv 2019, arXiv:1904.04514. [Google Scholar]
- Yi, H.; Wei, Z.; Ding, M.; Zhang, R.; Chen, Y.; Wang, G.; Tai, Y.W. Pyramid multi-view stereo net with self-adaptive view aggregation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin, Germany, 2020; pp. 766–782. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).