Author Contributions
Conceptualization, J.W., J.X. and Q.C.; methodology, J.W., J.X. and Q.C.; software, J.W.; validation, Z.L. and W.Y.; formal analysis, H.X.; investigation, Q.X.; resources, Q.C.; data curation, Z.L.; writing—original draft preparation, J.W. and Q.C.; writing—review and editing, J.X. and M.N.; visualization, H.X.; supervision, Q.X. and M.N.; project administration, W.Y.; funding acquisition, J.X. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Workflow of the conventional AE unmixing network.
Figure 1.
Workflow of the conventional AE unmixing network.
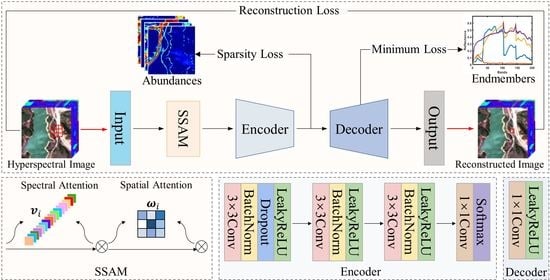
Figure 2.
Network architecture of the proposed SSANet.
Figure 2.
Network architecture of the proposed SSANet.
Figure 3.
Detailed workflow of the SEAM.
Figure 3.
Detailed workflow of the SEAM.
Figure 4.
Detailed workflow of the SAAM.
Figure 4.
Detailed workflow of the SAAM.
Figure 5.
Geometric interpretation of minimum volume regularization. Each vertex of the simplex is considered as an endmember, and the initial endmembers are oriented toward the centroid of the simplex determined by the real endmembers.
Figure 5.
Geometric interpretation of minimum volume regularization. Each vertex of the simplex is considered as an endmember, and the initial endmembers are oriented toward the centroid of the simplex determined by the real endmembers.
Figure 6.
RGB images of the synthetic and real HSIs adopted in the experiments. (a) Synthetic data. (b) Samson. (c) Jasper Ridge. (d) Houston. (e) Urban.
Figure 6.
RGB images of the synthetic and real HSIs adopted in the experiments. (a) Synthetic data. (b) Samson. (c) Jasper Ridge. (d) Houston. (e) Urban.
Figure 7.
Convergence curves during 50 epochs.
Figure 7.
Convergence curves during 50 epochs.
Figure 8.
Experimental results of SSANet with various noise values (20, 30, and 40 dB) for the synthetic dataset. (a) Mean RMSE. (b) Mean SAD.
Figure 8.
Experimental results of SSANet with various noise values (20, 30, and 40 dB) for the synthetic dataset. (a) Mean RMSE. (b) Mean SAD.
Figure 9.
Visualization results of the abundances of the synthetic data (SNR 40 dB). (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) Ground truth (GT).
Figure 9.
Visualization results of the abundances of the synthetic data (SNR 40 dB). (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) Ground truth (GT).
Figure 10.
Visualization results of the endmembers of the synthetic data (SNR 40 dB). (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 10.
Visualization results of the endmembers of the synthetic data (SNR 40 dB). (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 11.
Visualization results of the abundances of Samson data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 11.
Visualization results of the abundances of Samson data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 12.
Visualization results of the endmembers of Samson data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) MTAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 12.
Visualization results of the endmembers of Samson data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) MTAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 13.
Visualization results of the abundances of Jasper Ridge data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 13.
Visualization results of the abundances of Jasper Ridge data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 14.
Visualization results of the endmembers of Jasper Ridge data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 14.
Visualization results of the endmembers of Jasper Ridge data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 15.
Visualization results of the abundances of Houston data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 15.
Visualization results of the abundances of Houston data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 16.
Visualization results of the endmembers of Houston data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 16.
Visualization results of the endmembers of Houston data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 17.
Visualization results of the abundances of Urban data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 17.
Visualization results of the abundances of Urban data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet. (i) GT.
Figure 18.
Visualization results of the endmembers of Urban data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Figure 18.
Visualization results of the endmembers of Urban data. (a) VCA-FCLS. (b) SGCNMF. (c) DAEU. (d) MTAEU. (e) CNNAEU. (f) CyCU-Net. (g) MiSiCNet. (h) SSANet.
Table 1.
Hyperparameter settings for the proposed SSANet.
Table 1.
Hyperparameter settings for the proposed SSANet.
| Parameter | | | Epoch | Batch Size | Encoder Learning Rate | Decoder Learning Rate |
|---|
| Synthetic data | 1 × 10−2 | 1 × 10−2 | 50 | 32 | 1 × 10−5 | 1 × 10−5 |
| Samson | 5 × 10−2 | 0.5 | 50 | 128 | 1 × 10−3 | 1 × 10−3 |
| Jasper Ridge | 5 × 10−2 | 0.5 | 50 | 128 | 1 × 10−3 | 1 × 10−3 |
| Houston | 5 × 10−2 | 0.5 | 50 | 256 | 1 × 10−4 | 1 × 10−5 |
| Urban | 5 × 10−2 | 0.5 | 50 | 64 | 1 × 10−3 | 1 × 10−3 |
Table 2.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Samson data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 2.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Samson data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| RMSE | Soil | 26.50 | 17.86 | 11.02 | 13.36 | 19.9 | 18.27 | 18.18 | 4.06 |
| Tree | 25.11 | 24.49 | 9.89 | 9.49 | 25.01 | 19.19 | 17.91 | 3.41 |
| Water | 42.35 | 35.77 | 10.71 | 7.08 | 27.91 | 15.78 | 31.31 | 1.90 |
| Mean RMSE | 31.32 | 26.04 | 10.54 | 9.98 | 24.27 | 17.75 | 22.47 | 3.12 |
Table 3.
SAD (×100) and mean SAD (×100) of endmembers acquired by various unmixing approaches on Samson data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 3.
SAD (×100) and mean SAD (×100) of endmembers acquired by various unmixing approaches on Samson data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| SAD | Soil | 2.36 | 0.98 | 1.53 | 3.20 | 6.13 | 1.06 | 1.03 | 0.92 |
| Tree | 4.33 | 4.60 | 4.52 | 6.21 | 4.01 | 2.50 | 3.54 | 3.55 |
| Water | 15.04 | 22.97 | 3.39 | 4.98 | 16.09 | 5.37 | 40.08 | 2.96 |
| Mean SAD | 7.24 | 9.51 | 3.15 | 4.80 | 8.74 | 2.97 | 14.88 | 2.48 |
Table 4.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Jasper Ridge data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 4.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Jasper Ridge data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| RMSE | Road | 14.48 | 11.99 | 19.03 | 20.83 | 44.82 | 11.75 | 24.94 | 5.11 |
| Soil | 12.69 | 14.82 | 15.90 | 26.99 | 37.48 | 14.09 | 22.13 | 6.18 |
| Tree | 15.63 | 15.80 | 16.32 | 21.75 | 23.64 | 9.66 | 9.60 | 5.27 |
| Water | 18.73 | 26.27 | 8.05 | 5.19 | 30.65 | 10.04 | 11.42 | 2.25 |
| Mean RMSE | 15.39 | 17.22 | 14.95 | 18.69 | 34.15 | 11.38 | 17.02 | 4.70 |
Table 5.
SAD (×100) and mean SAD (×100) of endmembers acquired by various unmixing approaches on Jasper Ridge data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 5.
SAD (×100) and mean SAD (×100) of endmembers acquired by various unmixing approaches on Jasper Ridge data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| SAD | Road | 9.01 | 14.39 | 29.57 | 11.64 | 15.07 | 3.85 | 32.97 | 2.10 |
| Soil | 22.34 | 22.45 | 6.03 | 15.80 | 9.52 | 3.70 | 6.63 | 7.52 |
| Tree | 14.81 | 20.76 | 3.20 | 4.61 | 9.17 | 3.23 | 4.32 | 6.56 |
| Water | 54.59 | 27.79 | 3.40 | 7.06 | 3.51 | 15.40 | 29.04 | 4.06 |
| Mean SAD | 25.19 | 21.35 | 10.55 | 9.78 | 9.32 | 6.44 | 18.24 | 5.06 |
Table 6.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Houston data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 6.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Houston data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| RMSE | Running Track | 7.74 | 9.47 | 15.19 | 21.45 | 14.33 | 40.12 | 10.36 | 5.96 |
| Grass Healthy | 12.66 | 7.02 | 15.52 | 6.84 | 16.23 | 13.18 | 5.99 | 9.24 |
| Parking Lot1 | 24.76 | 23.86 | 30.66 | 22.05 | 43.68 | 25.07 | 14.21 | 12.49 |
| Parking Lot2 | 25.68 | 25.60 | 15.81 | 22.04 | 43.46 | 47.64 | 16.77 | 14.62 |
| Mean RMSE | 17.71 | 16.49 | 19.29 | 18.09 | 29.42 | 31.50 | 11.83 | 10.58 |
Table 7.
SAD (×100) and mean SAD (×100) of endmembers acquired by various unmixing approaches on Houston data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 7.
SAD (×100) and mean SAD (×100) of endmembers acquired by various unmixing approaches on Houston data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| SAD | Running Track | 16.34 | 36.79 | 20.56 | 23.39 | 42.56 | 33.73 | 7.24 | 15.23 |
| Grass Healthy | 11.85 | 12.54 | 7.00 | 4.19 | 0.97 | 7.30 | 9.05 | 8.48 |
| Parking Lot1 | 2.59 | 4.06 | 2.73 | 4.17 | 7.46 | 2.55 | 1.10 | 3.00 |
| Parking Lot2 | 26.64 | 12.49 | 5.90 | 6.82 | 3.14 | 10.50 | 19.40 | 9.39 |
| Mean SAD | 14.35 | 16.47 | 9.05 | 9.64 | 13.53 | 13.52 | 9.20 | 9.02 |
Table 8.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Urban data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 8.
RMSE (×100) and mean RMSE (×100) of abundances acquired by various unmixing approaches on Urban data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| RMSE | Asphalt | 27.54 | 39.26 | 16.59 | 15.35 | 23.56 | 33.41 | 37.70 | 13.73 |
| Grass | 40.10 | 33.83 | 15.21 | 15.06 | 29.81 | 44.90 | 31.64 | 13.51 |
| Tree | 45.85 | 25.48 | 11.19 | 9.39 | 20.08 | 39.59 | 24.53 | 7.58 |
| Roof | 17.08 | 18.93 | 8.68 | 8.55 | 13.70 | 15.15 | 15.64 | 8.23 |
| Mean RMSE | 32.64 | 29.37 | 12.92 | 12.09 | 21.79 | 33.27 | 27.38 | 10.76 |
Table 9.
SAD (×100) and mean SAD (×100) of endmembers acquired by different unmixing approaches on Urban data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
Table 9.
SAD (×100) and mean SAD (×100) of endmembers acquired by different unmixing approaches on Urban data. Annotation: bold red text indicates the best results and bold blue text indicates the suboptimal results.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| SAD | Asphalt | 20.95 | 102.34 | 11.48 | 8.13 | 6.02 | 20.66 | 76.25 | 7.51 |
| Grass | 26.03 | 44.42 | 6.85 | 5.06 | 10.05 | 34.99 | 39.12 | 3.69 |
| Tree | 34.59 | 9.28 | 3.39 | 6.95 | 13.99 | 20.88 | 9.88 | 3.80 |
| Roof | 82.28 | 16.45 | 30.91 | 14.83 | 6.29 | 9.86 | 4.52 | 26.31 |
| Mean SAD | 40.96 | 43.12 | 13.16 | 8.74 | 9.09 | 21.60 | 32.45 | 10.33 |
Table 10.
Mean RMSE (×100) and mean SAD (×100) results of ablation experiments with various losses. Annotation: bold black text indicates the best results.
Table 10.
Mean RMSE (×100) and mean SAD (×100) results of ablation experiments with various losses. Annotation: bold black text indicates the best results.
| | | | | |
|---|
| Mean RMSE | 14.53 | 6.27 | 9.54 | 4.70 |
| Mean SAD | 23.58 | 6.75 | 14.96 | 5.06 |
Table 11.
Mean RMSE (×100) and mean SAD (×100) results of ablation experiments with various network modules. Annotation: bold black text indicates the best results.
Table 11.
Mean RMSE (×100) and mean SAD (×100) results of ablation experiments with various network modules. Annotation: bold black text indicates the best results.
| | None | SEAM | SAAM | SEAM + SAAM |
|---|
| Mean RMSE | 6.87 | 6.48 | 5.46 | 4.70 |
| Mean SAD | 5.91 | 5.37 | 5.24 | 5.06 |
Table 12.
Consumption time (in seconds) for all the unmixing approaches.
Table 12.
Consumption time (in seconds) for all the unmixing approaches.
| Methods | VCA-FCLS | SGCNMF | DAEU | MTAEU | CNNAEU | CyCU-Net | MiSiCNet | SSANet |
|---|
| Time(s) | 1.75 | 26.82 | 15.35 | 23.26 | 1152.97 | 23.74 | 92.39 | 71.53 |