Comparative Study on Remote Sensing Methods for Forest Height Mapping in Complex Mountainous Environments
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area Overview
2.2. Data
2.2.1. ICESat-2/ATL03 Data
2.2.2. Sentinel-2 Data
2.2.3. Other Auxiliary Data
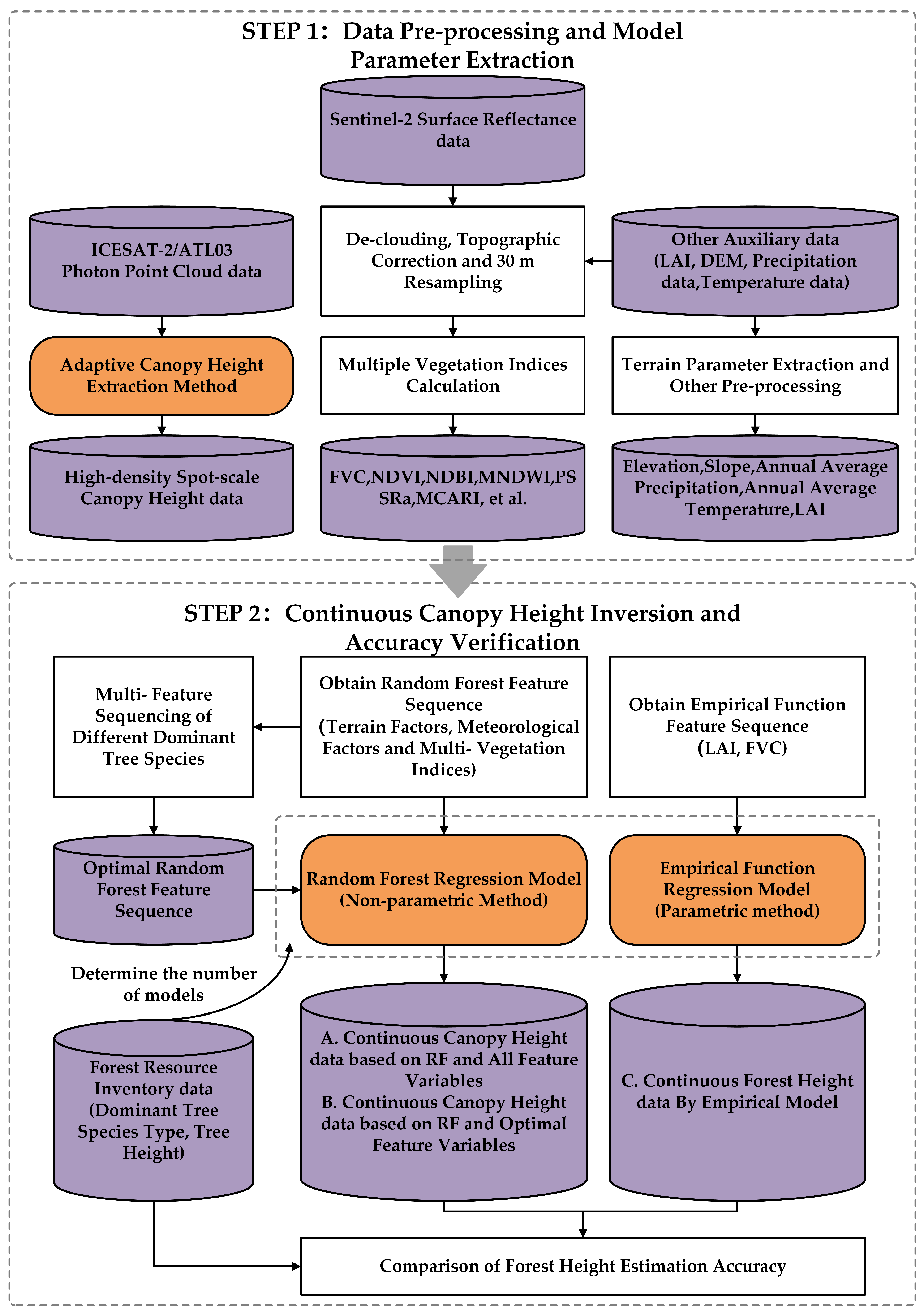
3. Research Methods
3.1. Forest Canopy Height Extraction Algorithm of ICESat-2/ATL03
3.2. Forest Canopy Height Inversion Model Based on the Empirical Function Regression
3.3. Forest Canopy Height Inversion Model Based on the Random Forest Regression
3.3.1. Random Forest Model Construction
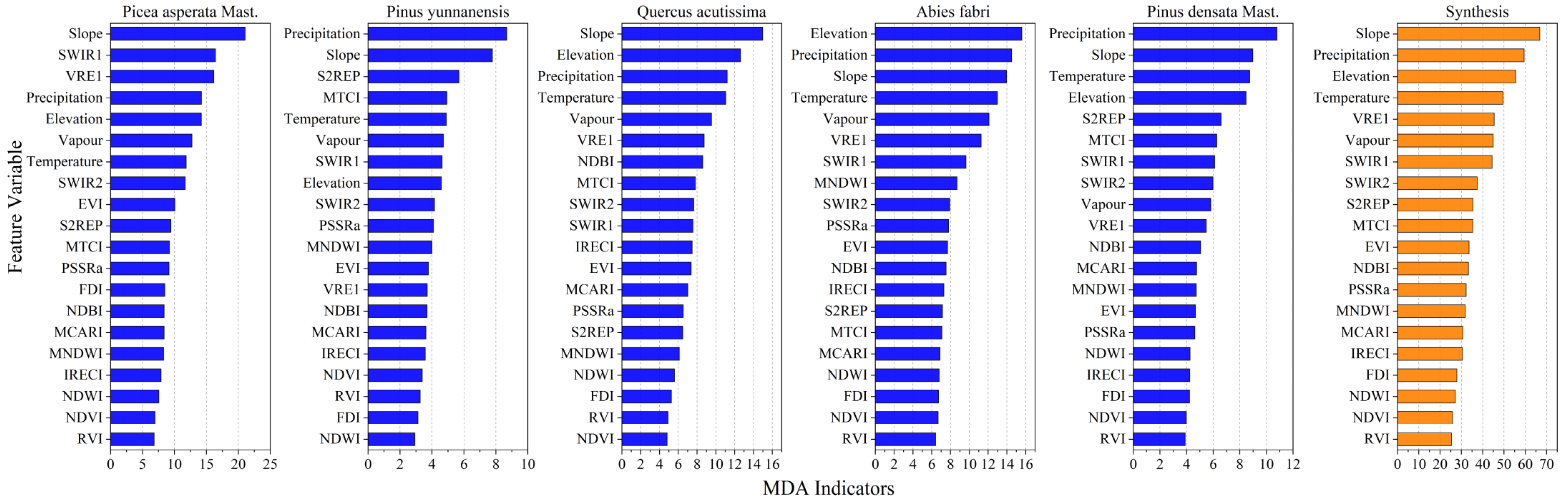
3.3.2. Selection and Ranking of Feature Variables
| Feature Name | The Description of the Feature Variable | Reference |
|---|---|---|
| Slope | Topographic slope estimated based on elevation data. | - |
| Precipitation | Annual average precipitation data for the Shangri-La region. | - |
| Elevation | Shangri-la 30 m elevation data extracted by ASTER GDEM product mask. | - |
| Temperature | Annual average temperature data for the Shangri-La region. | - |
| Vapour | B9(Water Vapour) | - |
| SWIR1 | B11(ShortWave InfraRed1) | - |
| VRE1 | B5(Vegetation Red Edge1) | - |
| SWIR2 | B12(ShortWave InfraRed2) | - |
| MTCI | VRE2-B6(Vegetation Red Edge2)/VRE1-B5(Vegetation Red Edge1)/R-B4(Red) | Dash et al. [44] |
| S2REP | R-B4(Red)/VRE3-B7(Vegetation Red Edge3)/VRE1-B5(Vegetation Red Edge1)/VRE2-B6(Vegetation Red Edge2) | Guyot et al. [45] |
| EVI | NIR-B8(Near InfraRed)/R-B4(Red) | Liu et al. [46] |
| NDBI | SWIR1-B11(ShortWave InfraRed1)/NIR-B8(Near InfraRed) | Zha et al. [47] |
| PSSRa | VRE3-B7(Vegetation Red Edge3)/R-B4(Red) | Blackburn [48] |
| MNDWI | G-B3(Green)/SWIR1-B11(ShortWave InfraRed1) | Xu [49] |
| MCARI | VRE1-B5(Vegetation Red Edge1)/R-B4(Red)/G-B3(Green) | Daughtry et al. [50] |
| IRECI | VRE1-B5(Vegetation Red Edge1)/VRE2-B6(Vegetation Red Edge2)/VRE3-B7(Vegetation Red Edge3)/R-B4(Red) | Clevers et al. [51] |
| FDI | NIR-B8(Near InfraRed)/G-B3(Green)/R-B4(Red) | Bunting et al. [52] |
| NDWI | G-B3(Green)/NIR-B8(Near InfraRed) | McFeeters [53] |
| NDVI | NIR-B8(Near InfraRed)/R-B4(Red) | Rouse et al. [54] |
| RVI | NIR-B8(Near InfraRed)/R-B4(Red) | Major et al. [55] |
4. Results and Analysis
4.1. Inversion Results of the Forest Canopy Height Based on the Empirical Function Regression
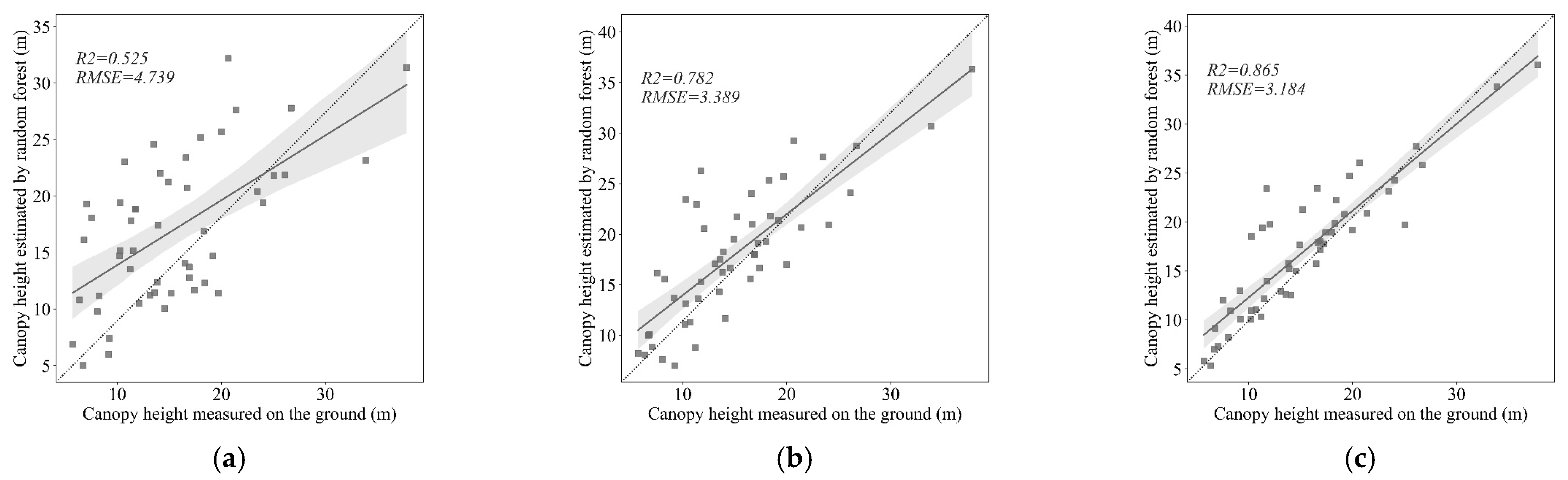
4.2. Inversion Results of the Forest Canopy Height Based on the Random Forest Regression
5. Conclusions
- The empirical function model cited in this paper has poor applicability under different terrain conditions, especially in complex terrain conditions where the fitting effect is relatively poor. In addition, during the fitting process of the empirical function model for each dominant tree species, the fitting effect is poor in Quercus acutissima and Pinus yunnanensis. At the meantime, because the ecological range of Quercus acutissima and Pinus yunnanensis in Shangri-La is wide, and the habitat limitation is small, it can be judged that their forest types are mostly mixed forests, which is similar to the results in previous research [16].
- It was found that the topographic and meteorological factors played a dominant role in canopy height inversion in evaluating the importance of explanatory variables in the random forest regression model.
- There are usually two problems when using random forest regression for canopy height inversion: the explanatory variables calculated from optical images can be subject to saturation, and there may be errors between the predicted results and the canopy height samples estimated by ICESat-2, especially in Quercus acutissima and Pinus yunnanensis. Furthermore, there may be an accumulation of errors in the random forest regression by applying multiple feature variables.
- Combining empirical function regression and random forest regression models, the highest precision canopy height data in Shangri-La can be obtained in the random forest regression model with the optimal feature variables, with an R2 of 0.865 and an RMSE of only 3.184 m. In addition, the poor inversion effect of the parametric model is primarily due to the lack of consideration of topographical and meteorological factors, which is unsuitable for canopy height inversion under complex terrain conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, T.; Wang, C.; Li, G.; Luo, S.; Xi, X.; Gao, S.; Zeng, H. Forest Canopy Height Mapping over China Using GLAS and MODIS Data. Sci. China Earth Sci. 2015, 58, 96–105. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Q. Impacts of the Carbon Emission Trading System on China’s Carbon Emission Peak: A New Data-Driven Approach. Nat. Hazards 2021, 107, 2487–2515. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Luo, T.; Gao, J. The Effect of Emission Trading Policy on Carbon Emission Reduction: Evidence from an Integrated Study of Pilot Regions in China. J. Clean. Prod. 2020, 265, 121843. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping Forest Canopy Height Globally with Spaceborne Lidar. J. Geophys. Res. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Balzter, H.; Rowland, C.; Saich, P. Forest Canopy Height and Carbon Estimation at Monks Wood National Nature Reserve, UK, Using Dual-Wavelength SAR Interferometry. Remote Sens. Environ. 2007, 108, 224–239. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth Obs. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Pierce, A.D.; Farris, C.A.; Taylor, A.H. Use of Random Forests for Modeling and Mapping Forest Canopy Fuels for Fire Behavior Analysis in Lassen Volcanic National Park, California, USA. For. Ecol. Manag. 2012, 279, 77–89. [Google Scholar] [CrossRef]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and Validating Leaf Area Index (LAI) at Multiple Spatial Scales through Lidar Remote Sensing: A Case Study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Gupta, R.; Sharma, L.K. Mixed Tropical Forests Canopy Height Mapping from Spaceborne LiDAR GEDI and Multisensor Imagery Using Machine Learning Models. Remote Sens. Appl. Soc. Environ. 2022, 27, 100817. [Google Scholar] [CrossRef]
- Sothe, C.; Gonsamo, A.; Lourenço, R.B.; Kurz, W.A.; Snider, J. Spatially Continuous Mapping of Forest Canopy Height in Canada by Combining GEDI and ICESat-2 with PALSAR and Sentinel. Remote Sens. 2022, 14, 5158. [Google Scholar] [CrossRef]
- Selkowitz, D.J.; Green, G.; Peterson, B.; Wylie, B. A Multi-Sensor Lidar, Multi-Spectral and Multi-Angular Approach for Mapping Canopy Height in Boreal Forest Regions. Remote Sens. Environ. 2012, 121, 458–471. [Google Scholar] [CrossRef]
- Yue, C.Y.; Zheng, Y.C.; Xing, Y.Q.; Pang, Y.; Li, S.M.; Cai, L.T.; He, H.Y. Technical and application development study of space-borne LiDAR in forestry remote sensing. Infrared Laser Eng. 2020, 49, 20200235. [Google Scholar]
- Liao, K.T. Estimation of Forest Aboveground Biomass in Jiangxi Province Using GLAS and Landsat Data. Master’s Thesis, Jiangxi Normal University, Nanchang, China, 2015. [Google Scholar]
- Zhang, R.H. Model on Remote Sensing and the Basic Experiments; Sciences Press: Beijing, China, 1996; pp. 20–60. [Google Scholar]
- Ghosh, S.M.; Behera, M.D.; Paramanik, S. Canopy Height Estimation Using Sentinel Series Images through Machine Learning Models in a Mangrove Forest. Remote Sens. 2020, 12, 1519. [Google Scholar] [CrossRef]
- Dong, L.X.; Li, G.C.; Tang, S.H. Inversion of forest canopy height in south of China by integrating GLAS and MERSI: The case of Jiangxi province in China. J. Remote Sens. 2011, 15, 1301–1314. [Google Scholar]
- Ni, X.; Zhou, Y.; Cao, C.; Wang, X.; Shi, Y.; Park, T.; Choi, S.; Myneni, R.B. Mapping Forest Canopy Height over Continental China Using Multi-Source Remote Sensing Data. Remote Sens. 2015, 7, 8436–8452. [Google Scholar] [CrossRef]
- Ni, X.; Park, T.; Choi, S.; Shi, Y.; Cao, C.; Wang, X.; Lefsky, M.A.; Simard, M.; Myneni, R.B. Allometric Scaling and Resource Limitations Model of Tree Heights: Part 3. Model Optimization and Testing over Continental China. Remote Sens. 2014, 6, 3533–3553. [Google Scholar] [CrossRef]
- Zhu, X.X. Based on ICESat-2 and GEDI Data, Research on Forest Height Retrieval with 30 m Resolution in China. Ph.D. Thesis, The Institute of Remote Sensing and Digital Earth (RADI), Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Luo, S.; Wang, C.; Xi, X.; Nie, S.; Fan, X.; Chen, H.; Ma, D.; Liu, J.; Zou, J.; Lin, Y.; et al. Estimating Forest Aboveground Biomass Using Small-Footprint Full-Waveform Airborne LiDAR Data. Int. J. Appl. Earth Obs. 2019, 83, 101922. [Google Scholar] [CrossRef]
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global Canopy Height Regression and Uncertainty Estimation from GEDI LIDAR Waveforms with Deep Ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Alcarde Alvares, C.; Stape, J.L.; Bailly, J.S.; Scolforo, H.F.; Cegatta, I.R.; Zribi, M.; Le Maire, G. Terrain Slope Effect on Forest Height and Wood Volume Estimation from GEDI Data. Remote Sens. 2021, 13, 2136. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance Evaluation of GEDI and ICESat-2 Laser Altimeter Data for Terrain and Canopy Height Retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Tian, X.; Shan, J. Comprehensive Evaluation of the ICESat-2 ATL08 Terrain Product. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8195–8209. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the Agreement of ICESat-2 Terrain and Canopy Height with Airborne Lidar over US Ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Huang, X.; Cheng, F.; Wang, J.; Duan, P.; Wang, J. Forest Canopy Height Extraction Method Based on ICESat-2/ATLAS Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5700814. [Google Scholar] [CrossRef]
- Wang, J.L.; Cheng, F.; Wang, C.; Chen, L.J.; Wang, X.H. Primary Discussion on the Potential of Forest Volume Estimating Using ICESat/GLAS Data in Complex Terrain Area—A Case Study of Shangri-la Yunnan Province. Remote Sens. Technol. Appl. 2012, 27, 45–50. [Google Scholar]
- Zhu, X.X.; Wang, C.; Xi, X.H.; Nie, S.; Yang, X.B.; Li, D. Research progress of ICESat-2/ATLAS data processing and appli-cations. Infrared Laser Eng. 2020, 47, 76–85. [Google Scholar]
- Khalsa, S.J.S.; Borsa, A.; Nandigam, V.; Phan, M.; Lin, K.; Crosby, C.; Fricker, H.; Baru, C.; Lopez, L. OpenAltimetry-Rapid Analysis and Visualization of Spaceborne Altimeter Data. Earth Sci. Inform. 2022, 15, 1471–1480. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A Modified Sun-Canopy-Sensor Topographic Correction in Forested Terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Fang, P.F.; Wang, L.G.; Xu, W.H.; Ou, G.L.; Dai, Q.L.; Li, R.N. Decision Fusion Classification of Forest Dominant Tree Species in Shangri-La Area of Yunnan Province. Remote Sens. Technol. Appl. 2022, 37, 638–650. [Google Scholar]
- Ma, R.B.; Cheng, F.; Yi, B.J.; Fu, L.; Jiang, L.F. Analysis of vertical differentiation of land use in Shangri-La. J. Yunnan Norm. Univ. Nat. Sci. 2011, 31, 70–75. [Google Scholar]
- Yu, Y.; Wang, J.; Liu, G.; Cheng, F. Forest Leaf Area Index Inversion Based on Landsat OLI Data in the Shangri-La City. J. Indian Soc. Remote Sens. 2019, 47, 967–976. [Google Scholar] [CrossRef]
- Li, M.M. The Method of Vegetation Fraction Estimation by Remote Sensing. Master’s Thesis, The Institute of Remote Sensing and Digital Earth (RADI), Chinese Academy of Sciences, Beijing, China, 2003. [Google Scholar]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The Interpretation of Spectral Vegetation Indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Wang, H.; Seaborn, T.; Wang, Z.; Caudill, C.C.; Link, T.E. Modeling Tree Canopy Height Using Machine Learning over Mixed Vegetation Landscapes. Int. J. Appl. Earth Obs. 2021, 101, 102353. [Google Scholar] [CrossRef]
- Torres de Almeida, C.; Gerente, J.; Rodrigo dos Prazeres Campos, J.; Caruso Gomes Junior, F.; Providelo, L.A.; Marchiori, G.; Chen, X. Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning. Remote Sens. 2022, 14, 4112. [Google Scholar] [CrossRef]
- Deng, Y.; Pan, J.; Wang, J.; Liu, Q.; Zhang, J. Mapping of Forest Biomass in Shangri-La City Based on LiDAR Technology and Other Remote Sensing Data. Remote Sens. 2022, 14, 5816. [Google Scholar] [CrossRef]
- Nandy, S.; Srinet, R.; Padalia, H. Mapping Forest Height and Aboveground Biomass by Integrating ICESat-2, Sentinel-1 and Sentinel-2 Data Using Random Forest Algorithm in Northwest Himalayan Foothills of India. Geophys. Res. Lett. 2021, 48, e2021GL093799. [Google Scholar] [CrossRef]
- Moudrý, V.; Gdulová, K.; Gábor, L.; Šárovcová, E.; Barták, V.; Leroy, F.; Špatenková, O.; Rocchini, D.; Prošek, J. Effects of Environmental Conditions on ICESat-2 Terrain and Canopy Heights Retrievals in Central European Mountains. Remote Sens. Environ. 2022, 279, 113112. [Google Scholar] [CrossRef]
- Jindal, R.; Leekha, M.; Manuja, M.; Goswami, M. What Makes a Better Companion? Towards Social & Engaging Peer Learning. In Proceedings of the 24th European Conference on Artificial Intelligence (ECAI), Santiago de Compostela, Spain, 29 August–8 September 2020; pp. 482–489. [Google Scholar]
- Hur, J.-H.; Ihm, S.-Y.; Park, Y.-H. A Variable Impacts Measurement in Random Forest for Mobile Cloud Computing. Wirel. Commun. Mob. Comput. 2017, 2017, e6817627. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. Evaluation of the MERIS Terrestrial Chlorophyll Index (MTCI). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F. Utilisation de la haute resolution spectrale pour suivre l’etat des couverts vegetaux. In Proceedings of the Spectral Signatures of Objects in Remote Sensing, Aussois, France, 18–22 January 1988; p. 279. [Google Scholar]
- Liu, H.Q.; Huete, A. A Feedback Based Modification of the NDVI to Minimize Canopy Background and Atmospheric Noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey Iii, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; De Jong, S.; Epema, G.F.; Addink, E.; Van, F.; Meer, D.; Bakker, W.; Skidmore, A. MERIS and the Red-Edge Index. In Proceedings of the Second EARSeL Workshop on Imaging Spectroscopy, Enschede, The Netherlands, 11–13 July 2000. [Google Scholar]
- Bunting, P.; Lucas, R. The Delineation of Tree Crowns in Australian Mixed Species Forests Using Hyperspectral Compact Airborne Spectrographic Imager (CASI) Data. Remote Sens. Environ. 2006, 101, 230–248. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Major, D.J.; Baret, F.E.D.E.; Guyot, G. A ratio vegetation index adjusted for soil brightness. Int. J. Remote Sens. 1990, 11, 727–740. [Google Scholar] [CrossRef]
- Joy, S.M.; Reich, R.M.; Reynolds, R.T. A Non-Parametric, Supervised Classification of Vegetation Types on the Kaibab National Forest Using Decision Trees. Int. J. Remote Sens. 2003, 24, 1835–1852. [Google Scholar] [CrossRef]
- Chirici, G.; McRoberts, R.E.; Fattorini, L.; Mura, M.; Marchetti, M. Comparing Echo-Based and Canopy Height Model-Based Metrics for Enhancing Estimation of Forest Aboveground Biomass in a Model-Assisted Framework. Remote Sens. Environ. 2016, 174, 1–9. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural Network Guided Interpolation for Mapping Canopy Height of China’s Forests by Integrating GEDI and ICESat-2 Data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]

| Number | ICESat-2/ATL03 Info Date/RGT Number/Cycle Number/Segment Number | Strong Tracks |
|---|---|---|
| NW-SE_01 | 20181217/1216/01/02 | gt1r/gt2r/gt3r |
| SW-NE_01 | 20190130/0507/02/06 | gt1l/gt2l/gt3l |
| NW-SE_02 | 20181016/0271/01/02 | gt1r/gt2r/gt3r |
| SW-NE_02 | 20181129/0949/01/06 | gt1r/gt2r/gt3r |
| NW-SE_03 | 20190213/0713/02/02 | gt1l/gt2l/gt3l |
| SW-NE_03 | 20181228/0004/02/06 | gt1l/gt2l/gt3l |
| Dominant Tree Species | Number of Training and Testing Samples | Model Information | R2 | Regression t-Test (p-Value) | ||
|---|---|---|---|---|---|---|
| Equation | α | β | ||||
| Abies fabri | 200 | −21.16577 | −0.38467 | 0.616 | 5.337 × 10−9 | |
| Pinus densata Mast. | 200 | −36.42064 | −0.57092 | 0.665 | 3.764 × 10−9 | |
| Quercus acutissima | 200 | −18.11949 | −0.27552 | 0.545 | 1.471 × 10−6 | |
| Pinus yunnanensis | 200 | −10.17889 | −0.32941 | 0.526 | 1.401 × 10−9 | |
| Picea asperata Mast. | 200 | −19.65823 | −0.51156 | 0.623 | 3.396 × 10−6 | |
| Dominant Tree Species | Feature Selection for Random Forest Regression Models | RMSE (m) | R2 |
|---|---|---|---|
| Picea asperata Mast. | Slope/SWIR1/VRE1/Precipitation/Elevation/Vapour(S2 B9)/Temperature | 4.086 | 0.736 |
| Slope/Precipitation/Elevation/Temperature/Vapour(S2 B9) | 3.994 | 0.756 | |
| All feature vectors | 4.254 | 0.712 | |
| Pinus densata Mast. | Precipitation/Slope/Temperature/Elevation/S2REP/MTCI/SWIR1/SWIR2/Vapour(S2 B9) | 3.774 | 0.725 |
| Slope/Precipitation/Elevation/Temperature/Vapour(S2 B9)/SWIR1 | 3.210 | 0.762 | |
| All feature vectors | 3.893 | 0.712 | |
| Abies fabri | Elevation/Precipitation/Slope/Temperature/Vapour(S2 B9)/VRE1/SWIR1/MNDWI/SWIR2 | 3.796 | 0.760 |
| Slope/Precipitation/Elevation/Temperature/Vapour(S2 B9)/SWIR1/VRE1/SWIR2/MTCI | 3.820 | 0.757 | |
| All feature vectors | 4.739 | 0.748 | |
| Pinus yunnanensis | Precipitation/Slope/S2REP/MTCI/Temperature/Vapour(S2 B9)/SWIR1/Elevation/SWIR2/PSSRa/MNDWI | 3.997 | 0.681 |
| Slope/Precipitation/Elevation/Temperature/Vapour(S2 B9)/SWIR1 | 3.868 | 0.704 | |
| All feature vectors | 4.084 | 0.668 | |
| Quercus acutissima | Slope/Elevation/Precipitation/Temperature/Vapour(S2 B9) | 5.103 | 0.720 |
| Slope/Precipitation/Elevation/Temperature/Vapour(S2 B9) | 5.108 | 0.713 | |
| All feature vectors | 5.365 | 0.677 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Cheng, F.; Wang, J.; Yi, B.; Bao, Y. Comparative Study on Remote Sensing Methods for Forest Height Mapping in Complex Mountainous Environments. Remote Sens. 2023, 15, 2275. https://doi.org/10.3390/rs15092275
Huang X, Cheng F, Wang J, Yi B, Bao Y. Comparative Study on Remote Sensing Methods for Forest Height Mapping in Complex Mountainous Environments. Remote Sensing. 2023; 15(9):2275. https://doi.org/10.3390/rs15092275
Chicago/Turabian StyleHuang, Xiang, Feng Cheng, Jinliang Wang, Bangjin Yi, and Yinli Bao. 2023. "Comparative Study on Remote Sensing Methods for Forest Height Mapping in Complex Mountainous Environments" Remote Sensing 15, no. 9: 2275. https://doi.org/10.3390/rs15092275
APA StyleHuang, X., Cheng, F., Wang, J., Yi, B., & Bao, Y. (2023). Comparative Study on Remote Sensing Methods for Forest Height Mapping in Complex Mountainous Environments. Remote Sensing, 15(9), 2275. https://doi.org/10.3390/rs15092275








