A Cost-Effective GNSS Solution for Continuous Monitoring of Landslides
Abstract
1. Introduction
1.1. Dual-Frequency Low-Cost GNSS Receivers
1.2. Objective and Study Organization
2. Material and Methods
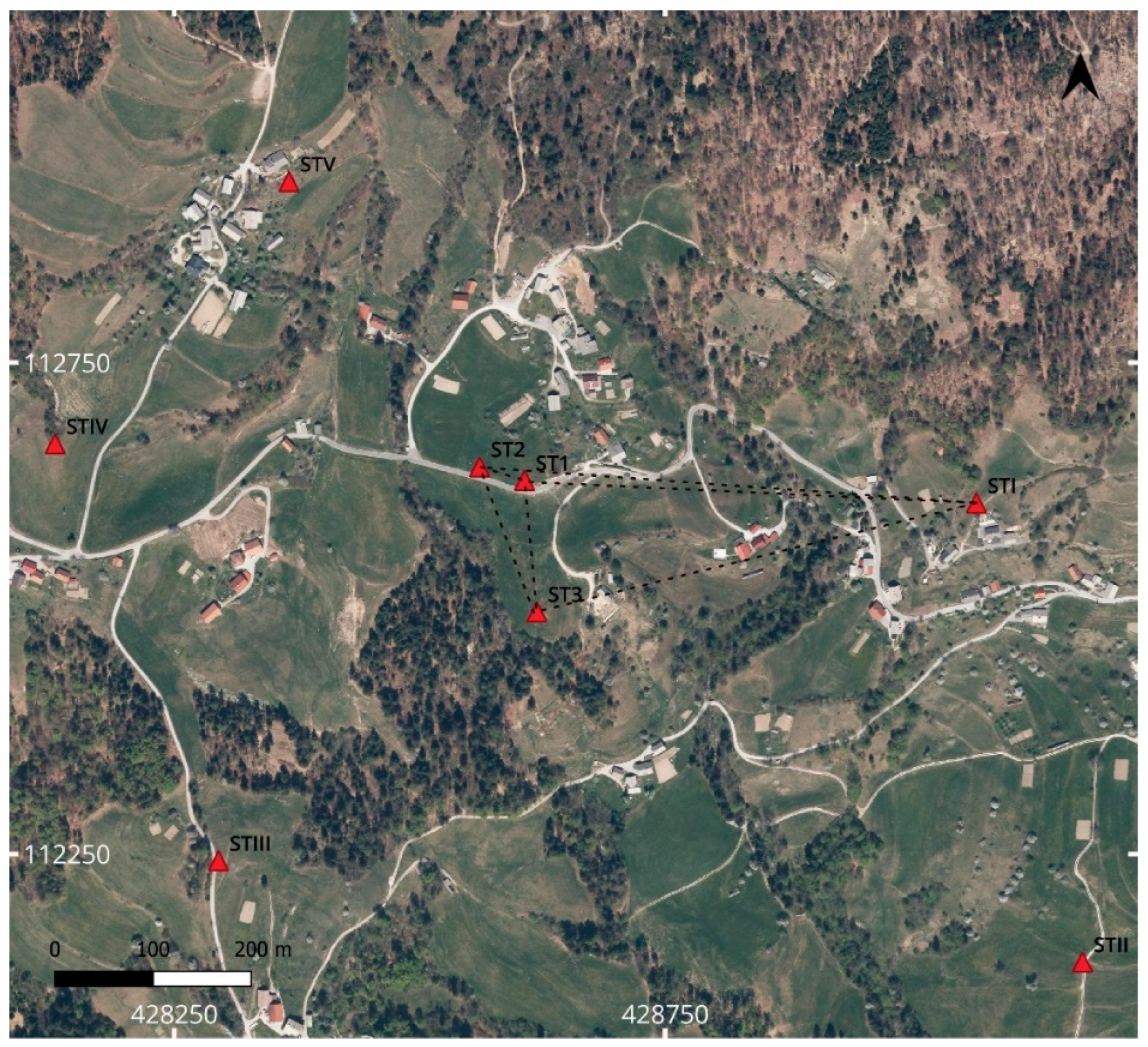
2.1. Laze Landslide
2.2. Geodetic Network
2.3. GNSS Equipment
2.4. Data Processing
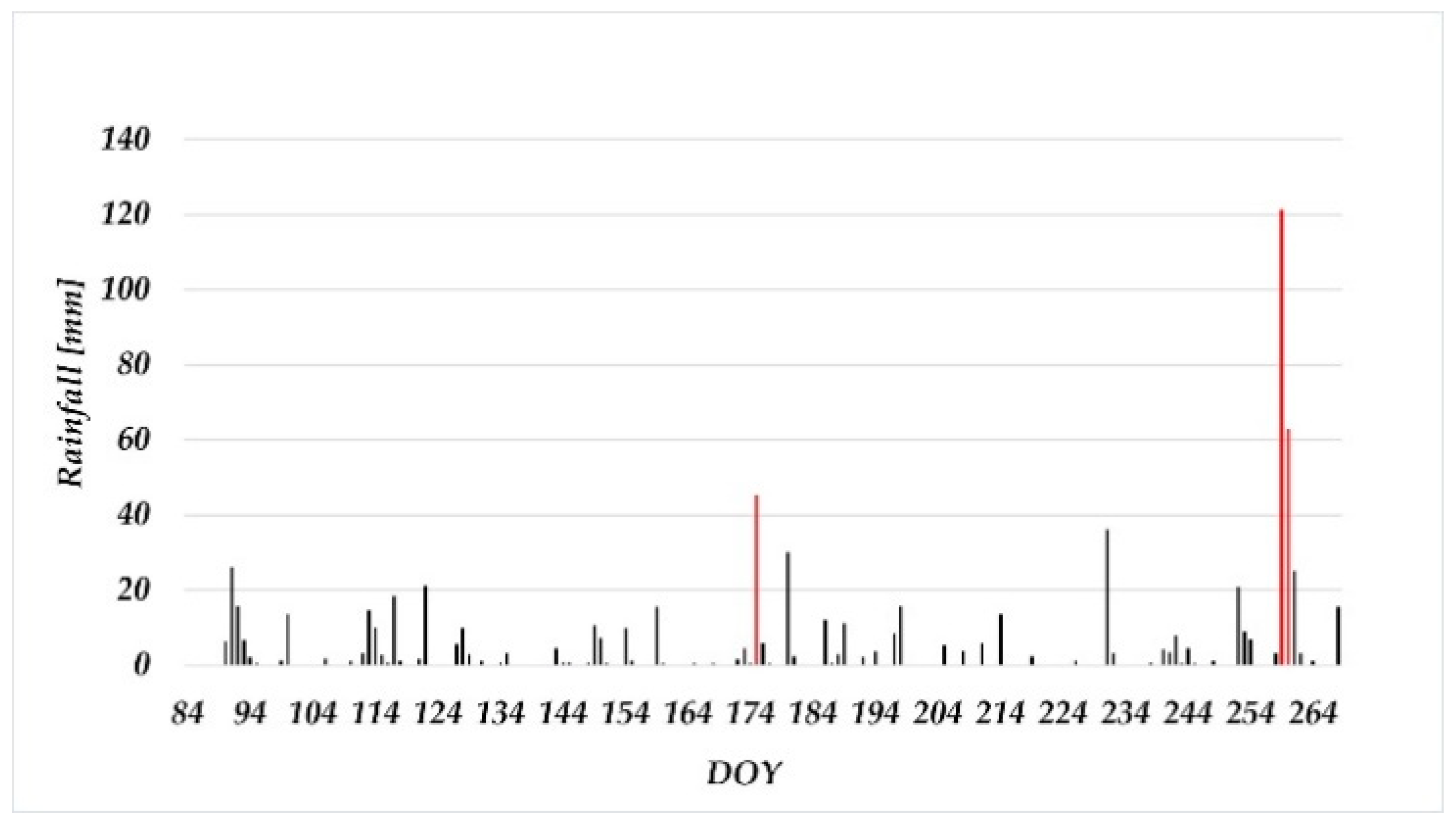
2.5. Rainfall Data
2.6. RTK Displacement Detection
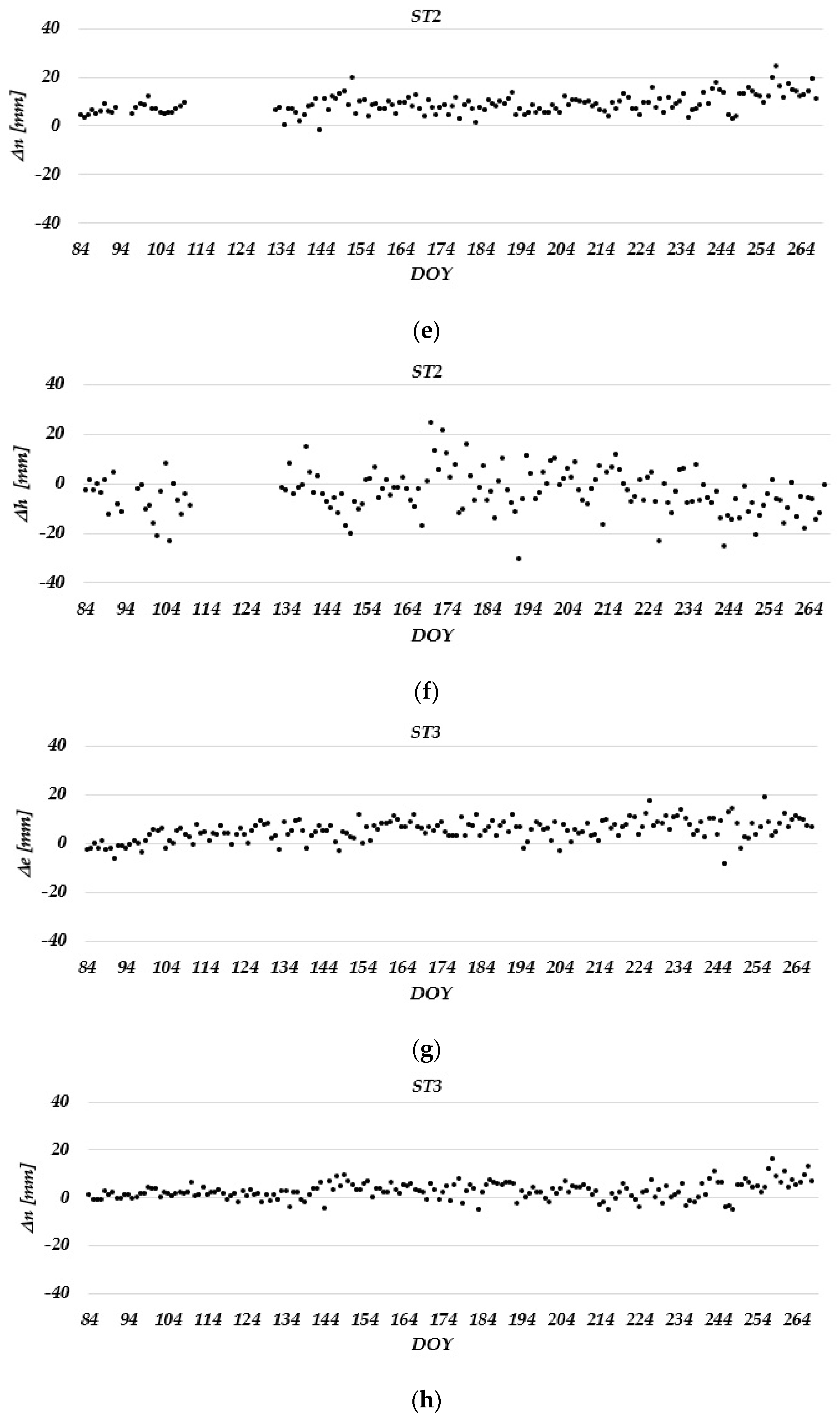
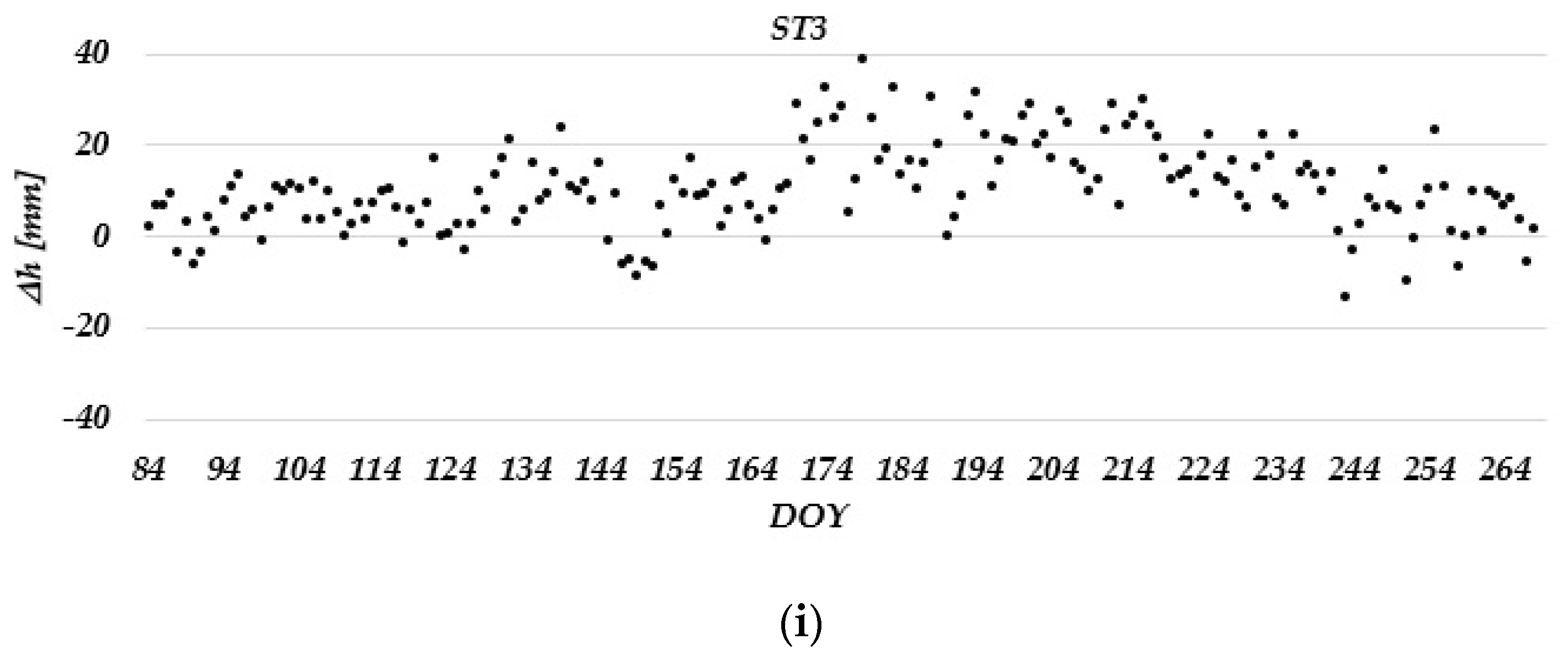
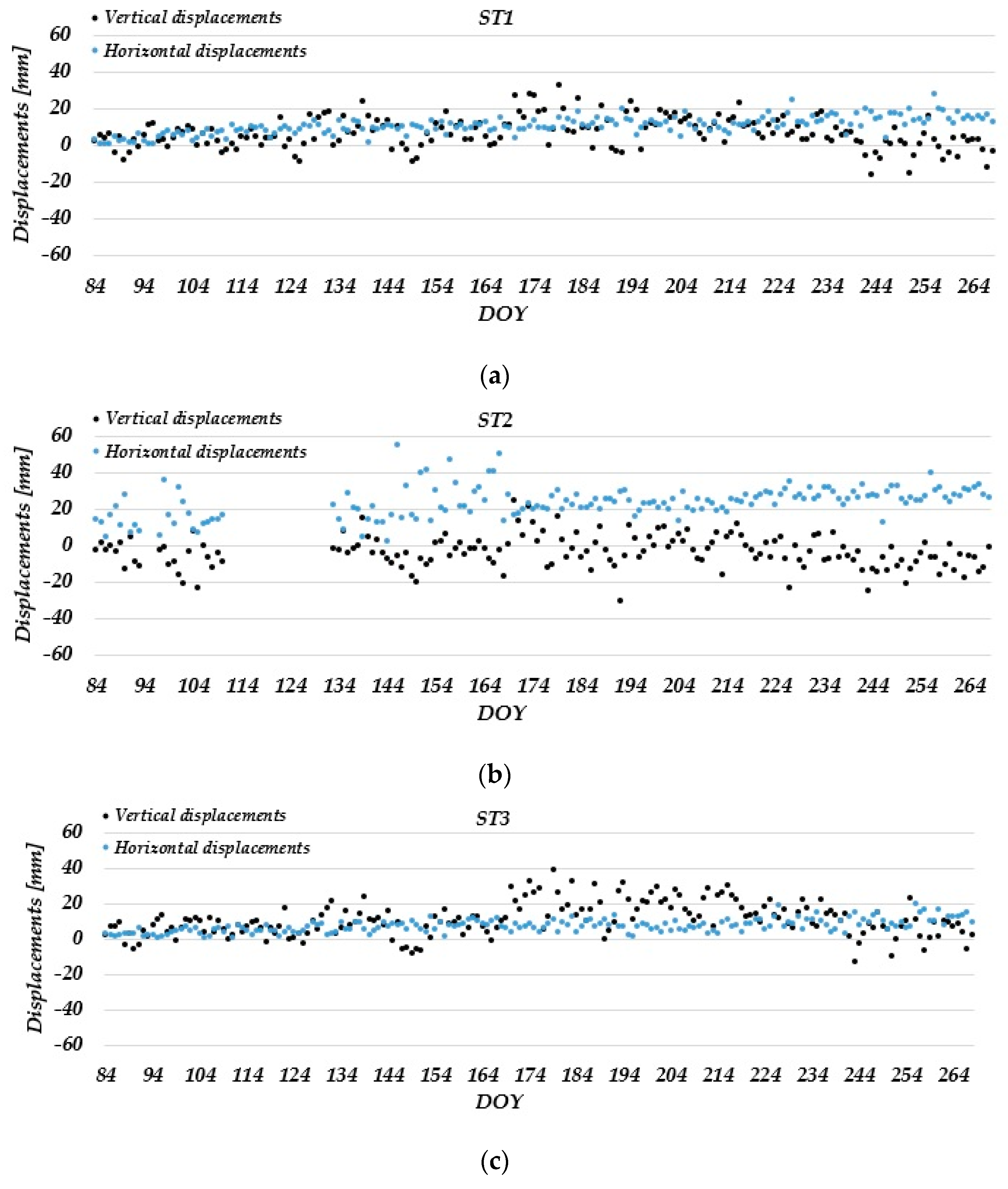
3. Results and Discussion
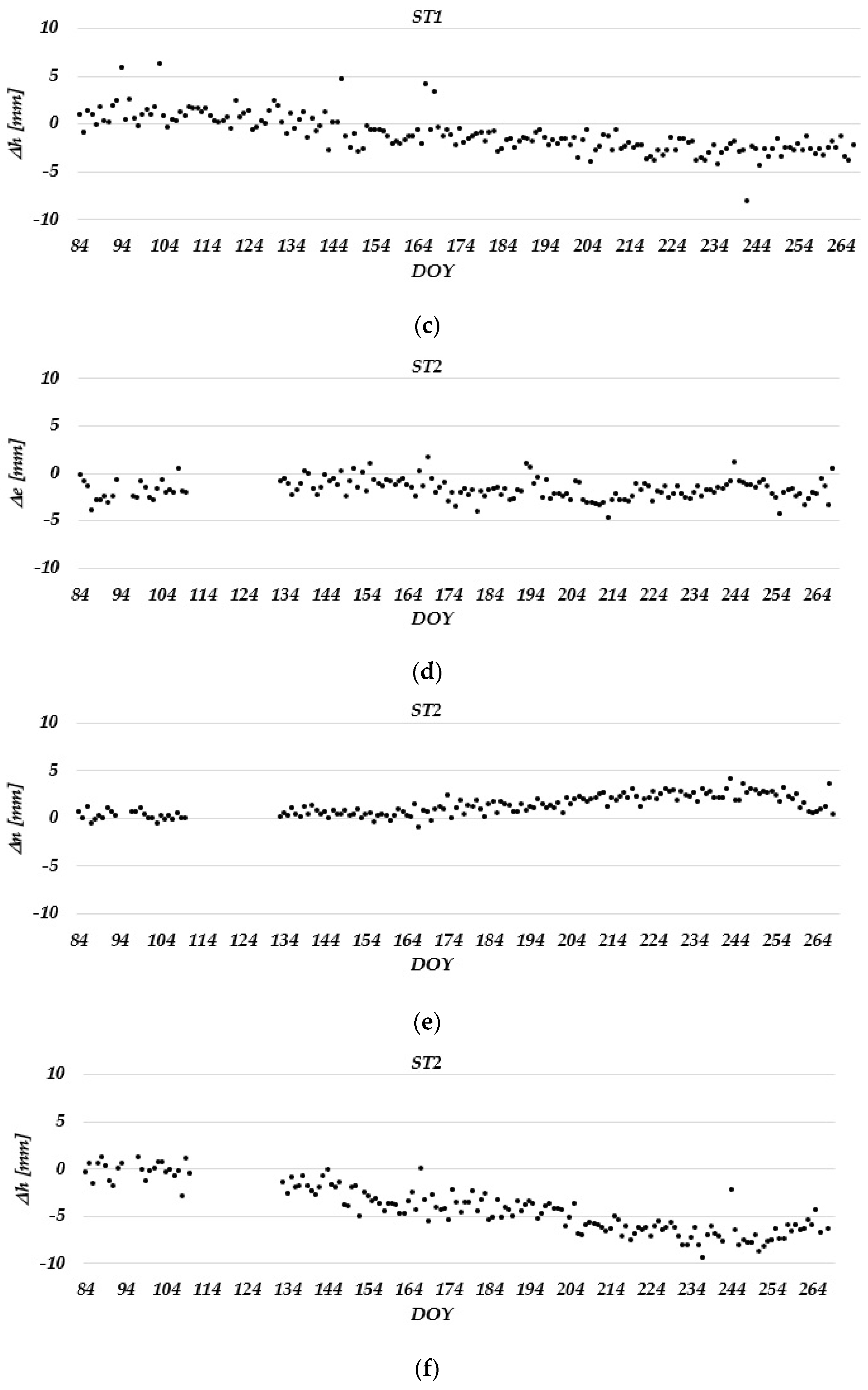
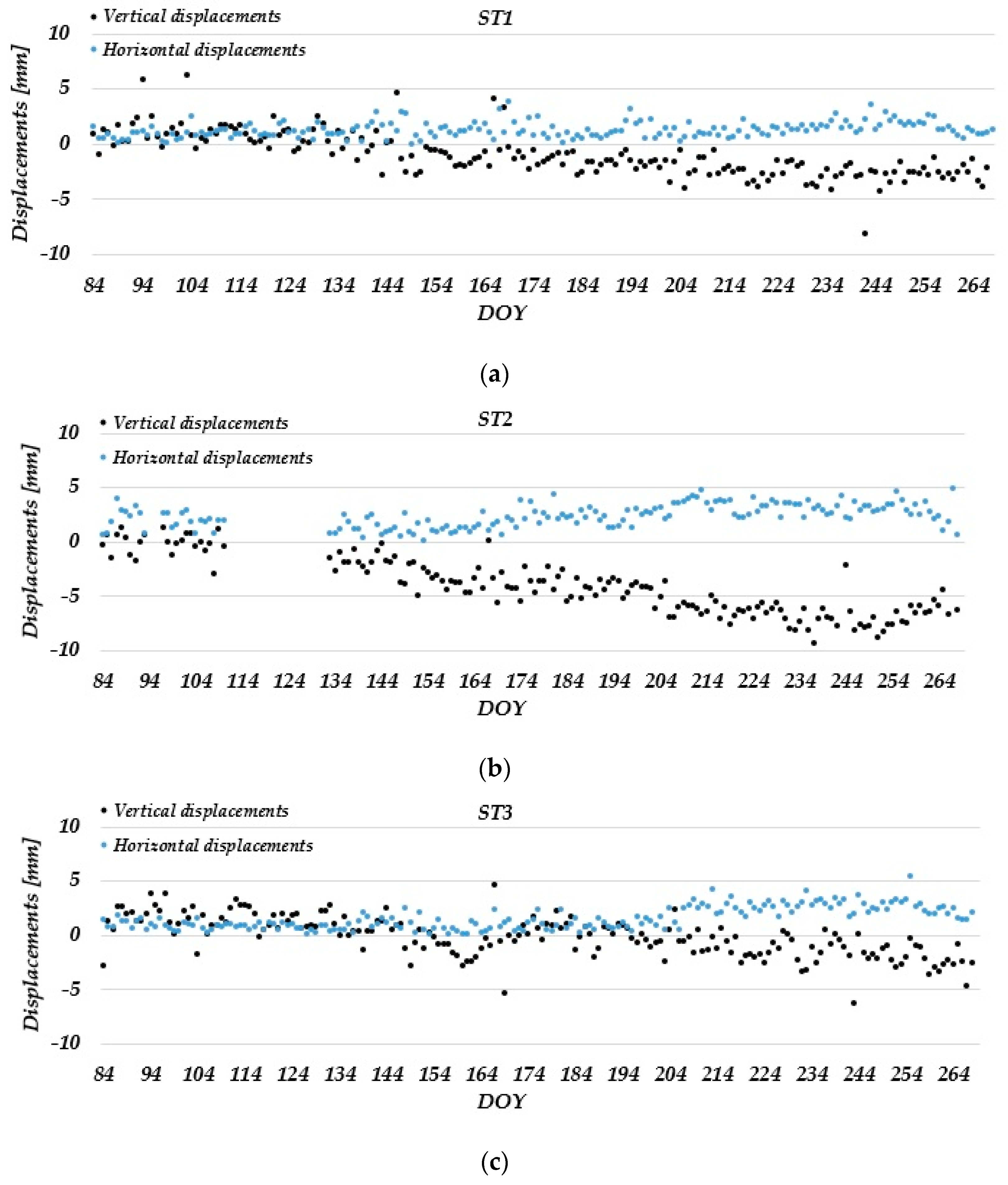
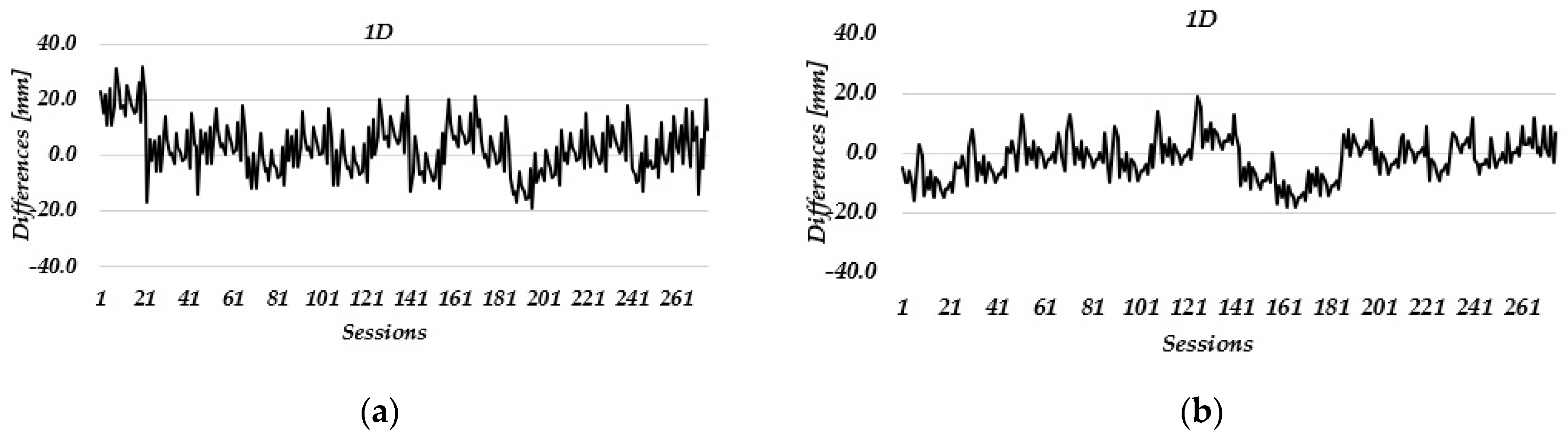
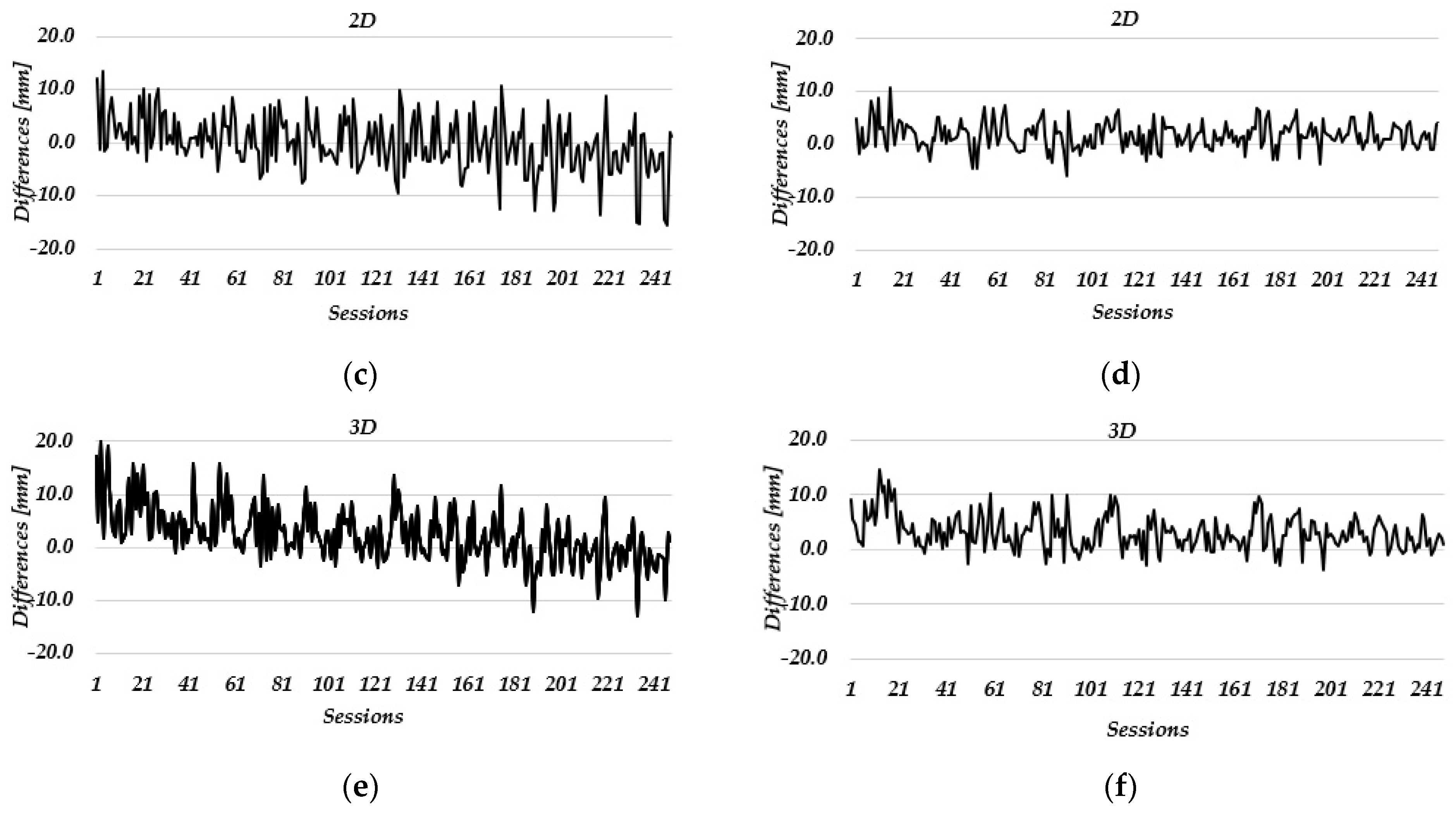
3.1. Static Relative Method
3.2. PPP Method
3.3. Rainfall
3.4. RTK Displacement Detection
4. Conclusions
- Low-cost GNSS receivers are suitable for setting up a low-cost GNSS monitoring system with high positioning accuracy and provide near-real-time continuous monitoring of landslides or other buildings while meeting the accuracy requirements.
- Low-cost GNSS instruments are several times cheaper than are geodetic instruments; therefore, a denser monitoring network can be established, providing more information on landslide dynamics.
- The positioning quality of low-cost GNSS instruments over short baselines is comparable to high-end GNSS receivers and comes with decreased costs. Coordinate differences obtained in the static relative positioning mode between low-cost and high-end geodetic GNSS receivers are within the accuracy range of GNSS technology.
- The estimated daily coordinate differences in the static relative positioning mode in the Laze landslide did not show displacements of the measuring stations in the horizontal direction. In the vertical direction, the determined ellipsoid heights decreased over time, which could be seen more clearly in one monitoring station (ST 2). These changes were not detected in PPP due to the lower accuracy of the method itself. However, low-cost GNSS receivers can be used to achieve positioning solutions with a quality that meets landslide monitoring requirements.
- The extreme rainfall in mid-September did not trigger movements in the Laze landslide, as the coordinate differences variations obtained with LGMS were in the same range as previously observed for both horizontal and vertical components.
- Low-cost GNSS instruments are more sensitive and of lower quality compared to geodetic GNSS ones. This could lead to difficulties in data collection and consequently in the functioning of the GNSS monitoring system itself. Therefore, more reliable, rigorous, and longer tests must be conducted to evaluate their performance.
- Low-cost GNSS receivers have integrated RTK engines. The experimental test showed that these sensors can detect 20 mm spatial displacements and therefore may be suitable for developing real-time GNSS monitoring systems.
- Low-cost GNSS technology could be the solution to the increased monitoring needs caused by extreme weather events, reducing costs and thus enabling surface movements monitoring of more natural hazards in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, R.; Shi, H.; He, X.; Li, Z.; Jia, D.; Yang, Z. Deformation Monitoring of Reservoir Dams Using GNSS: An Application to South-to-North Water Diversion Project, China. IEEE Access 2019, 7, 54981–54992. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Gu, M. Experimental Assessment of High-Rate GPS Receivers for Deformation Monitoring of Bridge. Measurement 2013, 46, 420–432. [Google Scholar] [CrossRef]
- Kaloop, M.; Elbeltagi, E.; Hu, J.; Elrefai, A. Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review. ISPRS Int. J. Geo-Inf. 2017, 6, 382. [Google Scholar] [CrossRef]
- Im, S.B.; Hurlebaus, S.; Kang, Y.J. Summary Review of GPS Technology for Structural Health Monitoring. J. Struct. Eng. 2013, 139, 1653–1664. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Ambrožič, T.; Turk, G.; Sterle, O. Testing Multi-Frequency Low-Cost GNSS Receivers for Geodetic Monitoring Purposes. Sensors 2020, 20, 4375. [Google Scholar] [CrossRef]
- Lin, C.; Wu, G.; Feng, X.; Li, D.; Yu, Z.; Wang, X.; Gao, Y.; Guo, J.; Wen, X.; Jian, W. Application of Multi-System Combination Precise Point Positioning in Landslide Monitoring. Appl. Sci. 2021, 11, 8378. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Ambrožič, T.; Sterle, O. Performance Evaluation of Low-Cost Multi-Frequency GNSS Receivers and Antennas for Displacement Detection. Appl. Sci. 2021, 11, 6666. [Google Scholar] [CrossRef]
- Ardusimple Survey Calibrated. Available online: https://www.ardusimple.com/product/calibrated-survey-gnss-multiband-antenna-ip67/ (accessed on 3 January 2023).
- Ardusimple SimpleRTK2B. Available online: https://www.ardusimple.com/simplertk2b-receivers/ (accessed on 2 January 2023).
- Samboko, H.T.; Schurer, S.; Savenije, H.H.G.; Makurira, H.; Banda, K.; Winsemius, H. Evaluating Low-Cost Topographic Surveys for Computations of Conveyance. Geosci. Instrum. Method. Data Syst. 2022, 11, 1–23. [Google Scholar] [CrossRef]
- Lăpădat, A.M.; Tiberius, C.C.J.M.; Teunissen, P.J.G. Experimental Evaluation of Smartphone Accelerometer and Low-Cost Dual Frequency GNSS Sensors for Deformation Monitoring. Sensors 2021, 21, 7946. [Google Scholar] [CrossRef]
- Romero-Andrade, R.; Trejo-Soto, M.E.; Vázquez-Ontiveros, J.R.; Hernández-Andrade, D.; Cabanillas-Zavala, J.L. Sampling Rate Impact on Precise Point Positioning with a Low-Cost GNSS Receiver. Appl. Sci. 2021, 11, 7669. [Google Scholar] [CrossRef]
- Stępniak, K.; Paziewski, J. On the Quality of Tropospheric Estimates from Low-Cost GNSS Receiver Data Processing. Measurement 2022, 198, 111350. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Cho, W.; Hayashi, K. Performance Evaluation of a Typical Low-Cost Multi-Frequency Multi-GNSS Device for Positioning and Navigation in Agriculture—Part 1: Static Testing. Smart Agric. Technol. 2021, 1, 100004. [Google Scholar] [CrossRef]
- Broekman, A.; Gräbe, P.J. A Low-Cost, Mobile Real-Time Kinematic Geolocation Service for Engineering and Research Applications. HardwareX 2021, 10, e00203. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Sterle, O. Testing the Performance of Multi-Frequency Low-Cost GNSS Receivers and Antennas. Sensors 2021, 21, 2029. [Google Scholar] [CrossRef] [PubMed]
- Janos, D.; Kuras, P. Evaluation of Low-Cost GNSS Receiver under Demanding Conditions in RTK Network Mode. Sensors 2021, 21, 5552. [Google Scholar] [CrossRef] [PubMed]
- Wielgocka, N.; Hadas, T.; Kaczmarek, A.; Marut, G. Feasibility of Using Low-Cost Dual-Frequency GNSS Receivers for Land Surveying. Sensors 2021, 21, 1956. [Google Scholar] [CrossRef]
- Romero-Andrade, R.; Trejo-Soto, M.E.; Vega-Ayala, A.; Hernández-Andrade, D.; Vázquez-Ontiveros, J.R.; Sharma, G. Positioning Evaluation of Single and Dual-Frequency Low-Cost GNSS Receivers Signals Using PPP and Static Relative Methods in Urban Areas. Appl. Sci. 2021, 11, 10642. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Sterle, O.; Pavlovčič-Prešeren, P. Low-Cost Dual-Frequency GNSS Receivers and Antennas for Surveying in Urban Areas. Sensors 2023, 23, 2861. [Google Scholar] [CrossRef]
- Krietemeyer, A.; van der Marel, H.; van de Giesen, N.; ten Veldhuis, M.-C. High Quality Zenith Tropospheric Delay Estimation Using a Low-Cost Dual-Frequency Receiver and Relative Antenna Calibration. Remote Sens. 2020, 12, 1393. [Google Scholar] [CrossRef]
- Krietemeyer, A.; van der Marel, H.; van de Giesen, N.; ten Veldhuis, M.-C. A Field Calibration Solution to Achieve High-Grade-Level Performance for Low-Cost Dual-Frequency GNSS Receiver and Antennas. Sensors 2022, 22, 2267. [Google Scholar] [CrossRef]
- Šegina, E.; Peternel, T.; Urbančič, T.; Realini, E.; Zupan, M.; Jež, J.; Caldera, S.; Gatti, A.; Tagliaferro, G.; Consoli, A.; et al. Monitoring Surface Displacement of a Deep-Seated Landslide by a Low-Cost and near Real-Time GNSS System. Remote Sens. 2020, 12, 3375. [Google Scholar] [CrossRef]
- Notti, D.; Cina, A.; Manzino, A.; Colombo, A.; Bendea, I.H.; Mollo, P.; Giordan, D. Low-Cost GNSS Solution for Continuous Monitoring of Slope Instabilities Applied to Madonna Del Sasso Sanctuary (NW Italy). Sensors 2020, 20, 289. [Google Scholar] [CrossRef] [PubMed]
- Manzini, N.; Orcesi, A.; Thom, C.; Brossault, M.-A.; Botton, S.; Ortiz, M.; Dumoulin, J. Performance Analysis of Low-Cost GNSS Stations for Structural Health Monitoring of Civil Engineering Structures. Struct. Infrastruct. Eng. 2020, 18, 595–611. [Google Scholar] [CrossRef]
- Xue, C.; Psimoulis, P.A.; Meng, X. Feasibility Analysis of the Performance of Low-Cost GNSS Receivers in Monitoring Dynamic Motion. Measurement 2022, 202, 111819. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y.; Xiang, Z.; Zhang, S.; Li, X.; Wang, X.; Ma, X.; Hu, C.; Pan, J.; Zhou, Y.; et al. A Novel Low-Cost GNSS Solution for the Real-Time Deformation Monitoring of Cable Saddle Pushing: A Case Study of Guojiatuo Suspension Bridge. Remote Sens. 2022, 14, 5174. [Google Scholar] [CrossRef]
- Barzaghi, R.; Reguzzoni, M.; De Gaetani, C.I.; Caldera, S.; Rossi, L. CULTURAL HERITAGE MONITORING BY LOW-COST GNSS RECEIVERS: A FEASIBILITY STUDY FOR SAN GAUDENZIO’S CUPOLA, NOVARA. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W11, 209–216. [Google Scholar] [CrossRef]
- Poluzzi, L.; Tavasci, L.; Corsini, F.; Barbarella, M.; Gandolfi, S. Low-Cost GNSS Sensors for Monitoring Applications. Appl. Geomat. 2020, 12, 35–44. [Google Scholar] [CrossRef]
- Tunini, L.; Zuliani, D.; Magrin, A. Applicability of Cost-Effective GNSS Sensors for Crustal Deformation Studies. Sensors 2022, 22, 350. [Google Scholar] [CrossRef]
- Günter, J.; Heunecke, O.; Pink, S.; Schuhbäck, S. Developments towards a Low-Cost GNSS Based Sensor Network for the Monitoring of Landslides. In Proceedings of the 13th FIG International Symposium on Deformation Measurements and Analysis, Lisbon, Portugal, 12 May 2008. [Google Scholar]
- Glabsch, J.; Heunecke, O.; Schuhbäck, S. Monitoring the Hornbergl Landslide Using a Recently Developed Low Cost GNSS Sensor Network. J. Appl. Geod. 2009, 3, 179–192. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GPS/GNSS and Radar Interferometric Data for a 3D Surface Displacement Monitoring of Landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Carlà, T.; Tofani, V.; Lombardi, L.; Raspini, F.; Bianchini, S.; Bertolo, D.; Thuegaz, P.; Casagli, N. Combination of GNSS, Satellite InSAR, and GBInSAR Remote Sensing Monitoring to Improve the Understanding of a Large Landslide in High Alpine Environment. Geomorphology 2019, 335, 62–75. [Google Scholar] [CrossRef]
- Cina, A.; Piras, M. Performance of Low-Cost GNSS Receiver for Landslides Monitoring: Test and Results. Geomat. Nat. Hazards Risk 2015, 6, 497–514. [Google Scholar] [CrossRef]
- Hohensinn, R.; Stauffer, R.; Glaner, M.F.; Herrera Pinzón, I.D.; Vuadens, E.; Rossi, Y.; Clinton, J.; Rothacher, M. Low-Cost GNSS and Real-Time PPP: Assessing the Precision of the u-Blox ZED-F9P for Kinematic Monitoring Applications. Remote Sens. 2022, 14, 5100. [Google Scholar] [CrossRef]
- ARSO Leskovica Rain Station. Available online: https://meteo.arso.gov.si/met/sl/app/webmet/#webmet==8Sdwx2bhR2cv0WZ0V2bvEGcw9ydlJWblR3LwVnaz9SYtVmYh9iclFGbt9SaulGdugXbsx3cs9mdl5WahxXYyNGapZXZ8tHZv1WYp5mOnMHbvZXZulWYnwCchJXYtVGdlJnOn0UQQdSf (accessed on 7 November 2022).
- Lazar, A.; Beguš, T.; Vulić, M. Integration of Measurement Techniques in Monitoring of the Laze Landslide in Slovenia. AGS 2020, 17, 33–45. [Google Scholar] [CrossRef]
- Everett, T. RTKLIB Demo5_b33b. Available online: https://rtkexplorer.com/downloads/rtklib-code/ (accessed on 3 January 2022).
- IGS (Institution for a Global Society). IGS Products. Available online: https://cddis.nasa.gov/archive/gnss/products/ (accessed on 2 January 2023).
- Koch, K.-R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer: Berlin/Heidelberg, Germany, 1999; ISBN 978-3-642-08461-4. [Google Scholar]
- Kuang, S. Geodetic Network Analysis and Optimal Design: Concepts and Applications; Ann Arbor Press: Chelsea, MI, USA, 1996; ISBN 978-1-57504-044-8. [Google Scholar]
- Caspary, W.F. Concepts of Network and Deformation Analysis; Monograph, 2nd. corrected impression ed.; Rüeger, J.M., Ed.; School of Surveying, University of New South Wales: Kensington, Australia, 1988; ISBN 978-0-85839-044-7. [Google Scholar]
- Savšek, S. An Alternative Approach to Testing Displacements in a Geodetic Network. Geod. Vestn. 2017, 61, 387–411. [Google Scholar] [CrossRef]








| Characteristics | |
|---|---|
| GNSS board | SimpleRTK2B |
| GNSS antenna | Survey Calibrated GNSS antenna |
| Constellations and frequencies | GPS (L1C/A, L2C), GLONASS (L1OF, L2OF), Galileo (E1-b/C, E5b), BeiDou (B1l, B2l), QZSS (L1C/A, L2C) |
| Observations | Code, Carrier phase, Doppler frequency, SNR |
| Channels | 184 |
| Antenna calibration | Yes (NGS) |
| Configuration | U-center |
| Data storage | 32GB |
| Basic system price | 500 EUR |
| Operating temperature | −40 to +85 °C |
| Interfaces | Micro USB, UART |
| Raw messages | UBX |
| Positioning accuracy | Hz, Hv < 1 cm, 1 km baseline, RTKLIB postprocessing |
| Power consumption | 150 mA@5 V |
| Antenna IP rating | IP67 |
| Solar panel | 25 W |
| Lithium battery | 30 Ah, 12 V |
| Parameters | RTKLIB |
|---|---|
| Filter type | Combined |
| Elevation mask | 10° |
| Iono correction | Broadcast |
| Troposphere correction | Sastamoinen |
| Satellite ephemeris/clock | Broadcast |
| Ambiguity | Continuous |
| Satellites | GPS, GLO, Galileo |
| Antenna | AS-ANT2BCAL |
| Station | ∆e | ∆n | ∆h | ∆2D | ∆3D |
|---|---|---|---|---|---|
| Station 1 | −2.7 mm | 3.7 mm | 0.2 mm | 4.6 mm | 4.6 mm |
| Station 2 | −2.3 mm | 6.0 mm | 0.1 mm | 6.3 mm | 6.3 mm |
| Station 3 | −4.8 mm | 4.9 mm | −0.8 mm | 6.9 mm | 6.9 mm |
| Station | GSR1-FGG1 | VRS-FGG1 |
|---|---|---|
| Not detected | 95% | 94% |
| Detected | 5% | 6% |
| Displacements | GSR1-FGG1 | VRS-FGG1 |
|---|---|---|
| 5 mm | 7% | 0% |
| 10 mm | 28% | 30% |
| 15 mm | 79% | 81% |
| 20 mm | 94% | 100% |
| 25 mm | 100% | 100% |
| Displacements | GSR1-FGG1 | VRS-FGG1 |
|---|---|---|
| 5 mm | 9% | 2% |
| 10 mm | 25% | 15% |
| 15 mm | 56% | 75% |
| 20 mm | 97% | 100% |
| 25 mm | 100% | 100% |
| Antenna | GSR1-FGG1 | VRS-FGG1 | ||||
|---|---|---|---|---|---|---|
| Dimension | 1D | 2D | 3D | 1D | 2D | 3D |
| MAE (mm) | 7.7 | 4.0 | 4.3 | 5.8 | 2.4 | 3.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamza, V.; Stopar, B.; Sterle, O.; Pavlovčič-Prešeren, P. A Cost-Effective GNSS Solution for Continuous Monitoring of Landslides. Remote Sens. 2023, 15, 2287. https://doi.org/10.3390/rs15092287
Hamza V, Stopar B, Sterle O, Pavlovčič-Prešeren P. A Cost-Effective GNSS Solution for Continuous Monitoring of Landslides. Remote Sensing. 2023; 15(9):2287. https://doi.org/10.3390/rs15092287
Chicago/Turabian StyleHamza, Veton, Bojan Stopar, Oskar Sterle, and Polona Pavlovčič-Prešeren. 2023. "A Cost-Effective GNSS Solution for Continuous Monitoring of Landslides" Remote Sensing 15, no. 9: 2287. https://doi.org/10.3390/rs15092287
APA StyleHamza, V., Stopar, B., Sterle, O., & Pavlovčič-Prešeren, P. (2023). A Cost-Effective GNSS Solution for Continuous Monitoring of Landslides. Remote Sensing, 15(9), 2287. https://doi.org/10.3390/rs15092287







