First Open-Coast HF Radar Observations of a 2-Phase Volcanic Tsunami, Tonga 2022
Abstract
:1. Introduction
2. Materials and Methods
2.1. Tsunami Generation Mechanisms
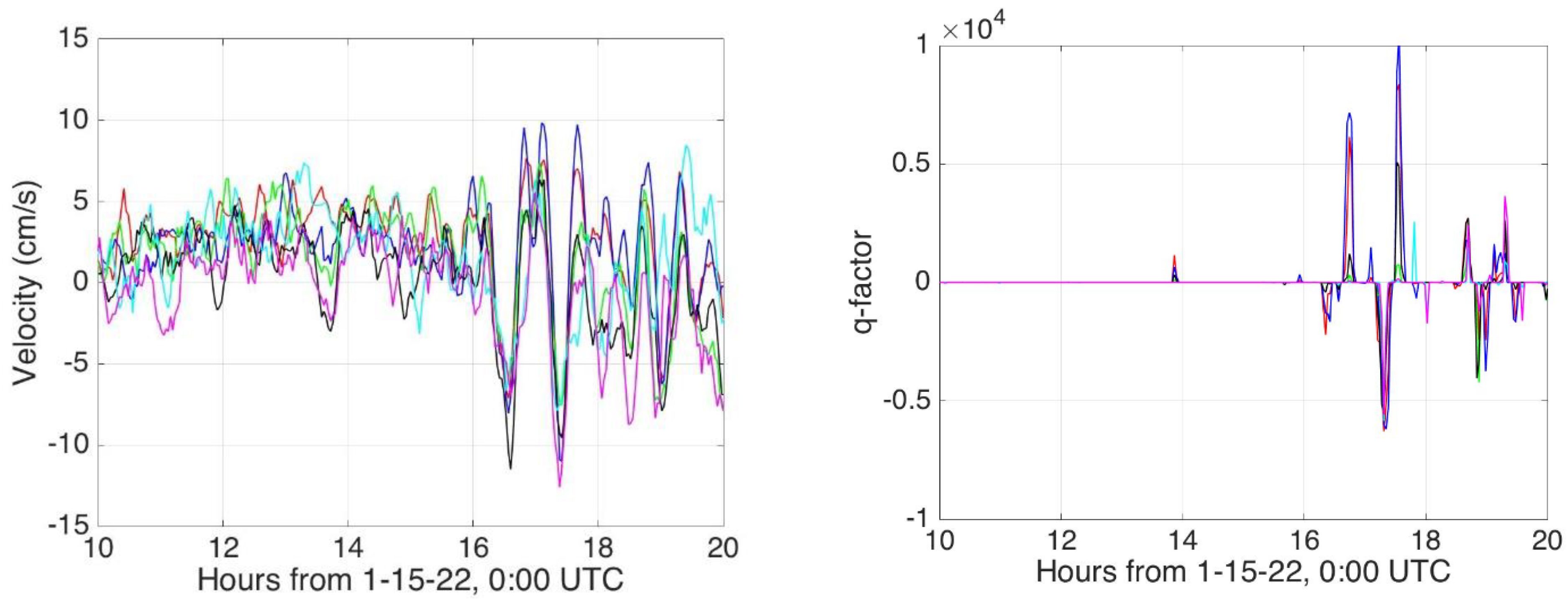
2.2. Radar Tsunami Detection
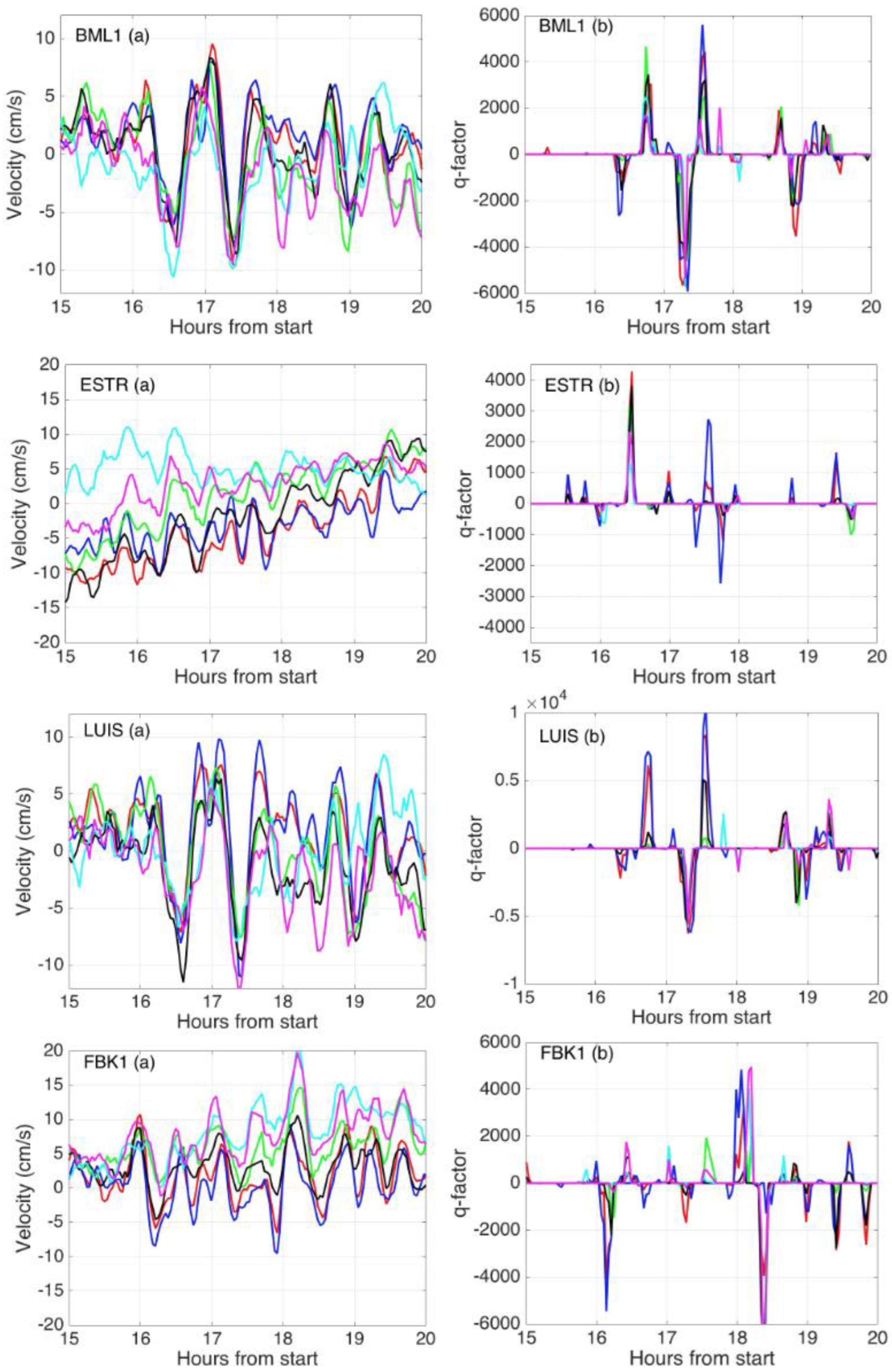
- Within each band, if the velocity increment over two consecutive time intervals (typically 2 min each) has increased/decreased by an amount greater than a preset level, the q-factor for that band is incremented/decremented.
- If the maximum/minimum velocities for neighboring bands coincide within a preset value for consecutive time intervals, the q-factor level is further increased/decreased for those bands.
- Finally, if the velocity has increased/decreased over two consecutive time intervals for three adjacent area bands, the q-factor level is further incremented/decremented for those bands.
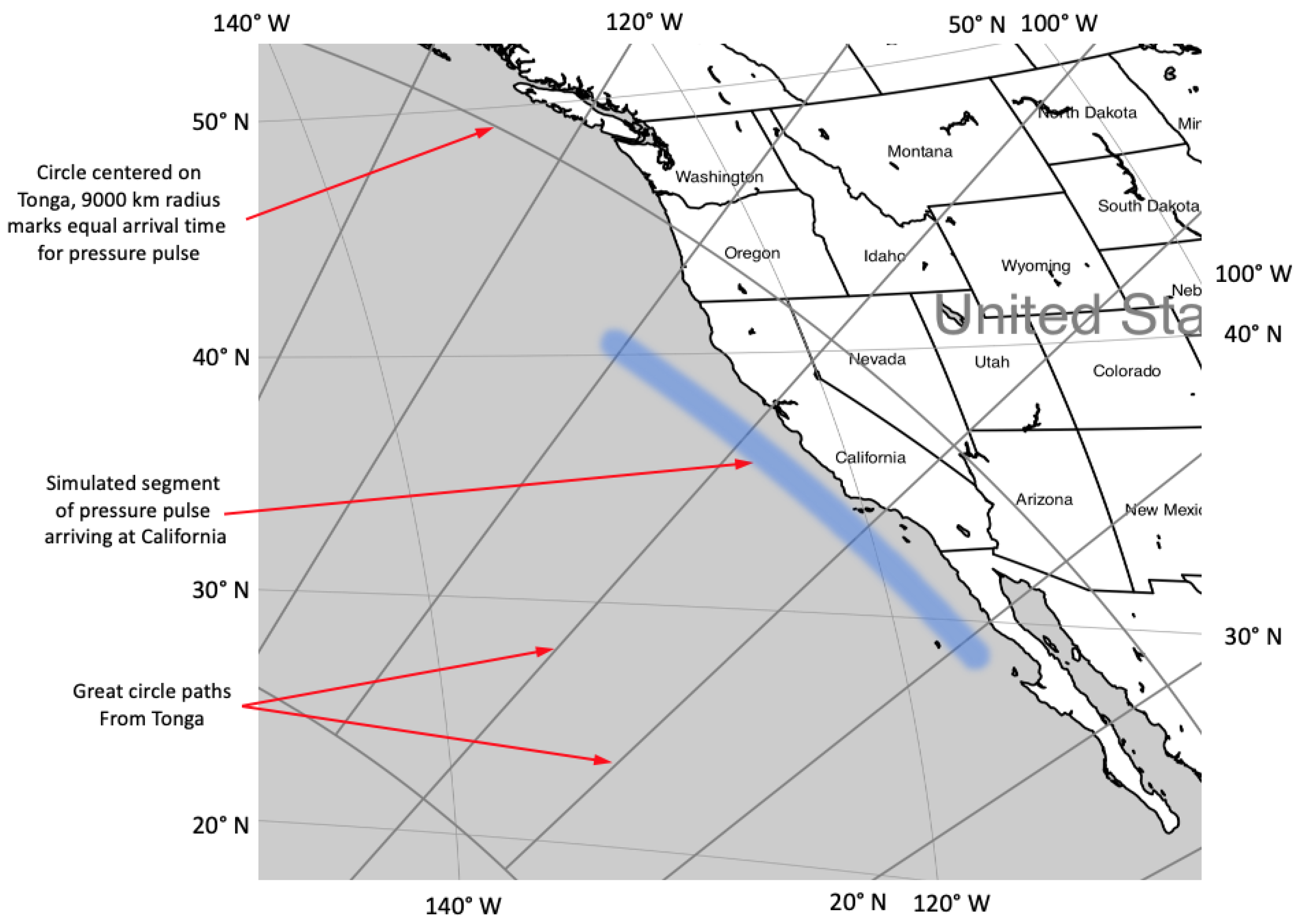
2.3. Radar Site Locations and Offshore Water Depths
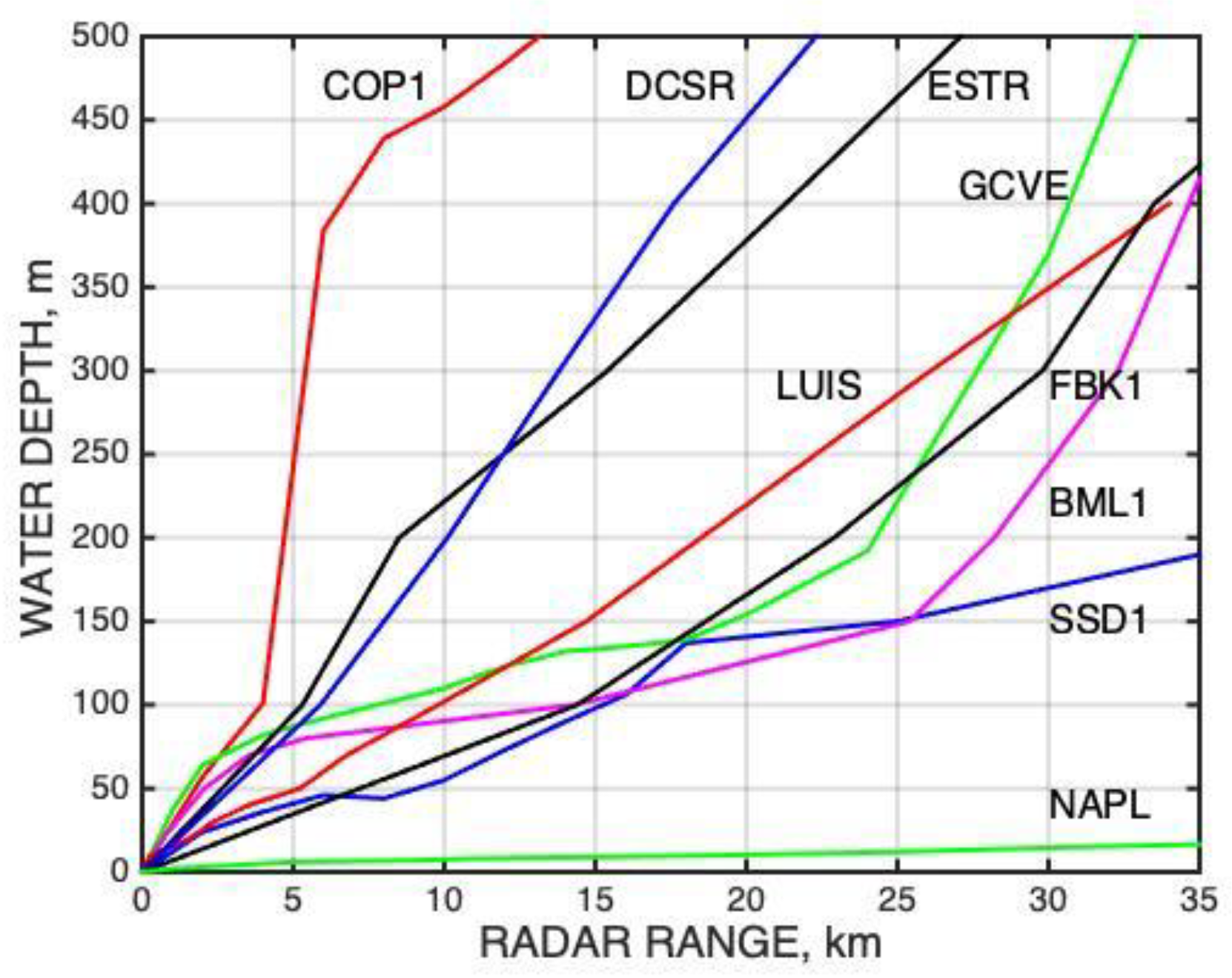
2.4. The Effect of Water Depth on Tsunami Parameters
3. Results
3.1. Radar Tsunami Detection on the U.S. West Coast and Florida: Band Velocities and q-Factors
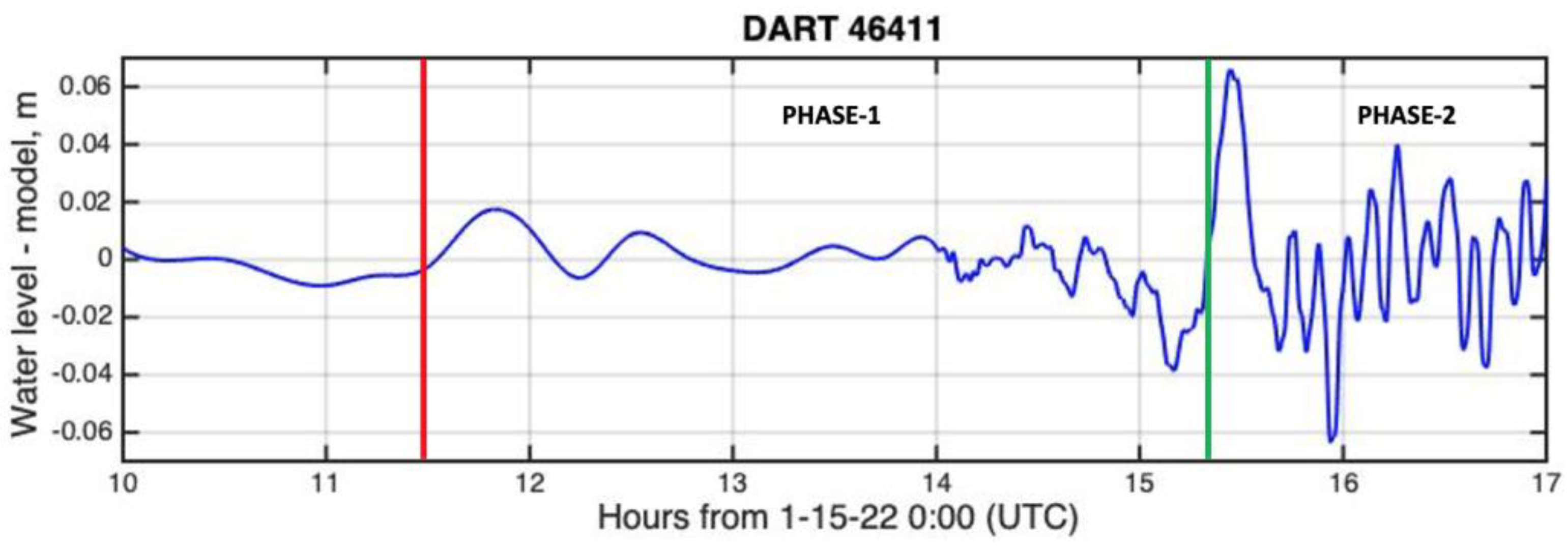
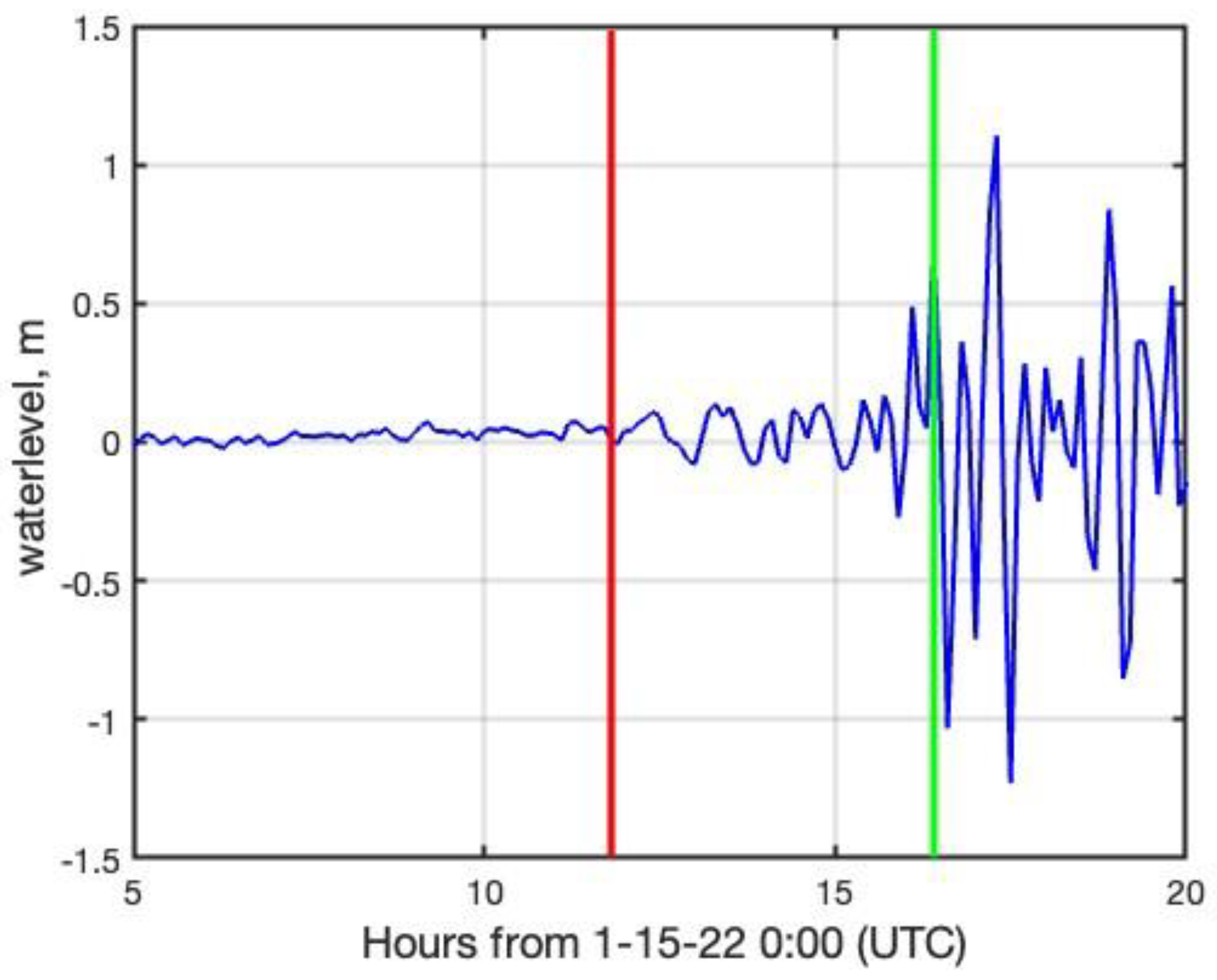
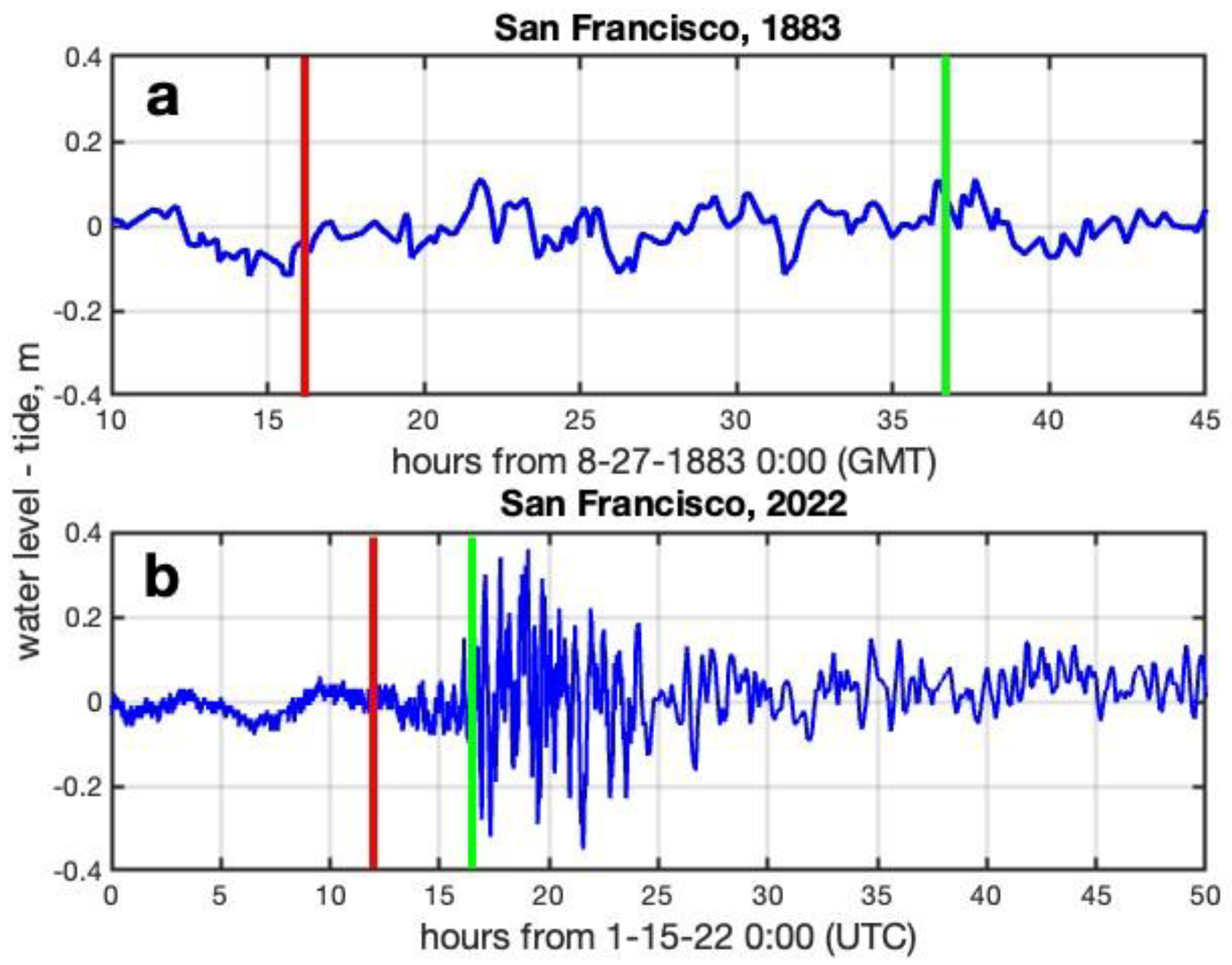
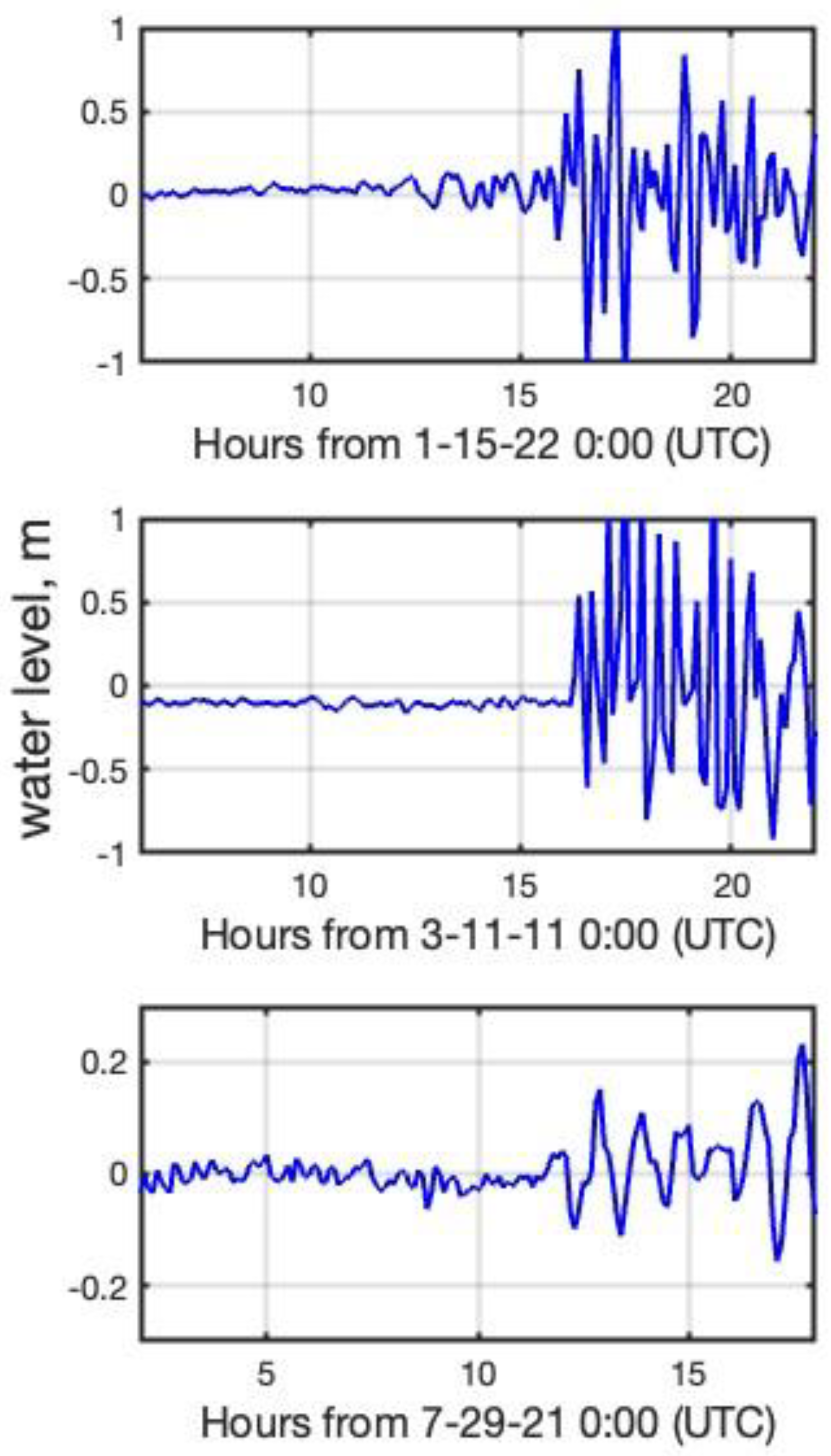
3.2. Tide Gauge Water Levels
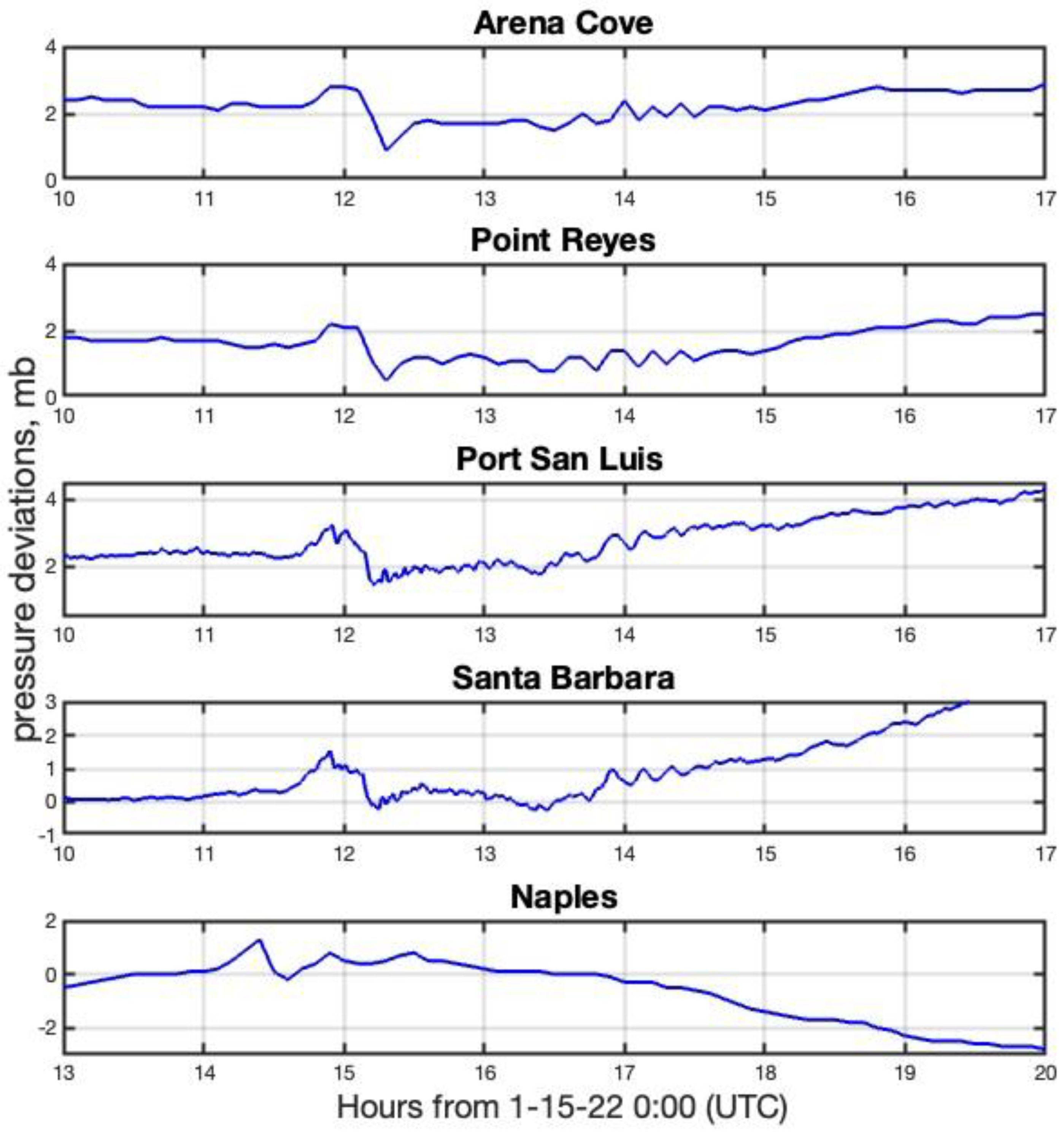
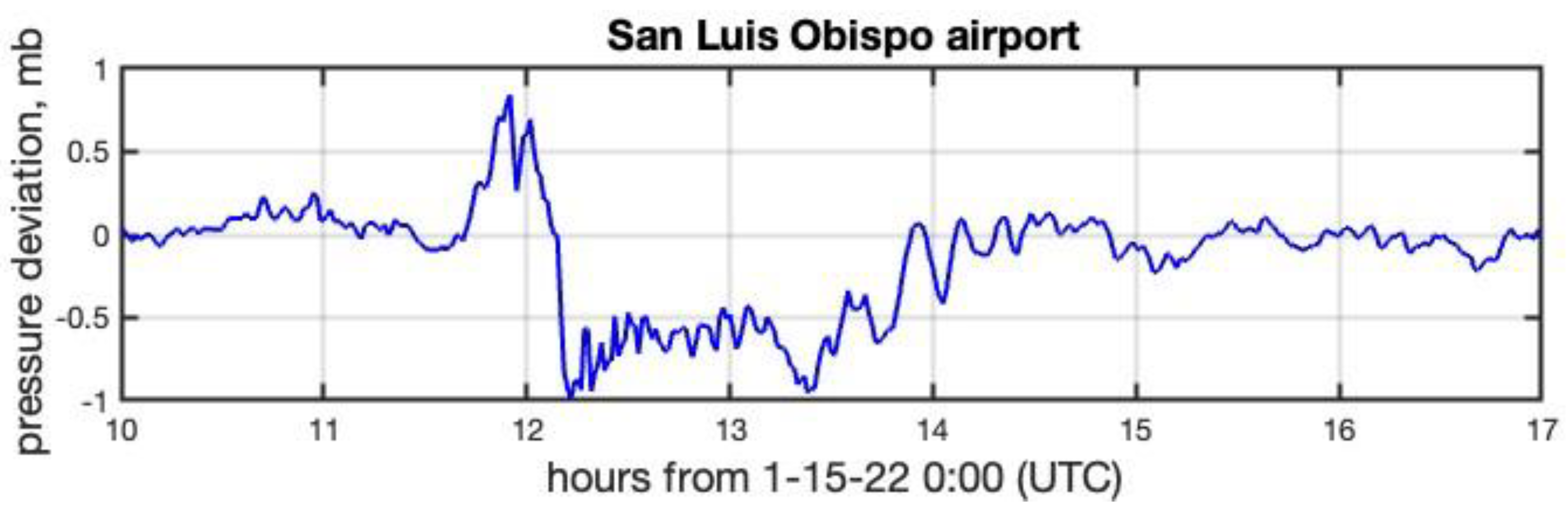
3.3. Barometric Pressure Observations
3.4. Tsunami Arrival Times
3.5. Tsunami Wave Height
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
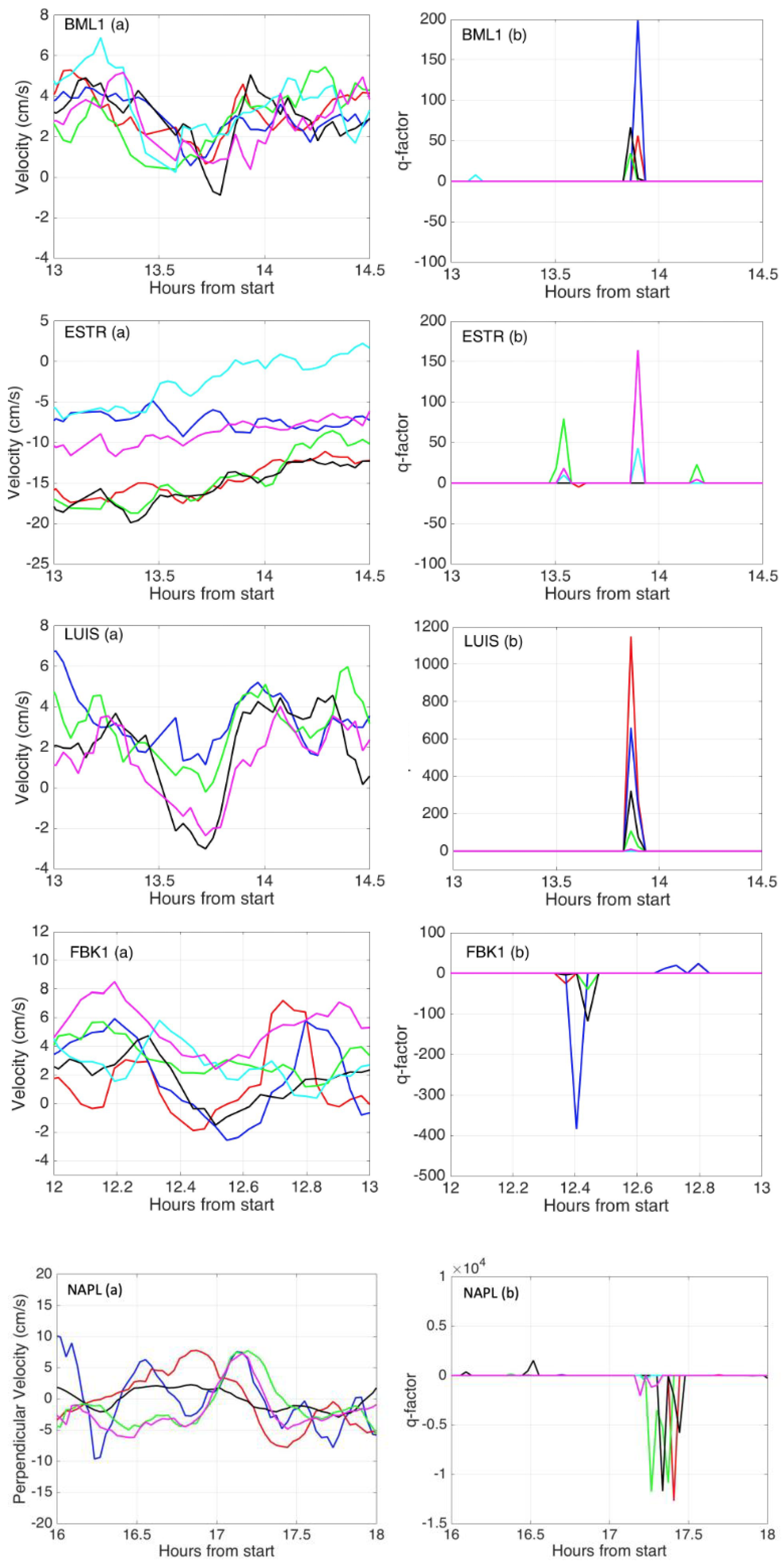
Appendix B
References
- Rabinovich, A.B. Twenty-Seven Years of Progress in the Science of Meteorological Tsunamis Following the 1992 Daytona Beach Event. Pure Appl. Geophys. 2020, 177, 1193–1230. [Google Scholar] [CrossRef]
- Rabinovich, A.B. Seiches and harbor oscillations. In Handbook of Coastal and Ocean Engineering; Kim, Y.C., Ed.; World Scientific Publ.: Singapore, 2009; Chapter 9; pp. 193–236. [Google Scholar]
- Han, P.; Yu, X. An unconventional tsunami: 2022 Tonga event. Phys. Fluids 2022, 34, 116607. [Google Scholar] [CrossRef]
- Wang, Y.; Imai, K.; Mulia, I.E.; Ariyoshi, K.; Takahashi, N.; Sasaki, K.; Kaneko, H.; Abe, H.; Sato, Y. Data Assimilation Using High-Frequency Radar for Tsunami Early Warning: A Case Study of the 2022 Tonga Volcanic Tsunami. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025153. [Google Scholar] [CrossRef]
- Wright, C.J.; Hindley, N.P.; Alexander, M.J.; Barlow, M.; Hoffmann, L.; Mitchell, C.N.; Prata, F.; Bouillon, M.; Carstens, J.; Clerbaux, C.; et al. Surface-to-space atmospheric waves from Hunga Tonga-Hunga Ha’apai eruption. Nature 2022, 609, 741–746. [Google Scholar] [CrossRef] [PubMed]
- Gusman, A.R.; Roger, J. Hunga Tonga-Hunga Ha’apai Volcano-Induced Sea Level Oscillations and Tsunami Simulations. GNS Science Webpage. 2022. Available online: https://www.gns.cri.nz/Home/Our-Science/Natural-Hazards-and-Risks/Tsunami/2022-Hunga-Tonga-Tsunami (accessed on 3 August 2022).
- Hunga Tonga Hunga-Ha’apai Volcano-Generated Tsunami, 15 January 2022 UTC. Main Event Page. Available online: https://nctr.pmel.noaa.gov/tonga20220115/ (accessed on 3 August 2022).
- Carvajal, M.; Sepúlveda, I.; Gubler, A.; Garreaud, R. Worldwide Signature of the 2022 Tonga Volcanic Tsunami. Geophys. Res. Lett. 2022, 49, e2022GL098153. [Google Scholar] [CrossRef]
- Harrison, G. Pressure anomalies from the January 2022 Hunga Tonga-Hunga Ha’apai eruption. Weather 2022, 77, 87–90. [Google Scholar] [CrossRef]
- Matoza, R.S.; Fee, D.; Assink, J.D.; Iezzi, A.M.; Green, D.N.; Kim, K.; Toney, L.; Lecocq, T.; Krishnamoorthy, S.; Lalande, J.M.; et al. Atmospheric waves and global seismo-acoustic observations of the January 2022 Hunga eruption, Tonga. Science 2022, 277, 6601. [Google Scholar] [CrossRef]
- Omira, R.; Ramalho, R.S.; Kim, J.; González, P.J.; Kadri, U.; Miranda, J.M.; Carrilho, F.; Baptista, M.A. Global Tonga tsunami explained by a fast-moving atmospheric source. Nature 2022, 609, 734–740. [Google Scholar] [CrossRef]
- Prata, F.; AIRES Pty Ltd. Available online: https://zenodo.org/record/6575810#.YuMEg_HMKZ0https:%2F%2Fzenodo.org%2Frecord%2F6575810%2Ffiles%2Famerican_samoa.png%3Fdownload=1 (accessed on 10 November 2022).
- Iowa State University, Environmental Mesonet. Available online: https://mesonet.agron.iastate.edu/request/asos/1min.phtml#://doi.org/10.1186/s40562-022-00232-z (accessed on 10 November 2022).
- Ewings, M.; Press, F. Tide Gauge Disturbances from the Great Eruption of KRAKATOA; Tech. Report on Seismology No. 27; Columbia University: New York, NY, USA, 1953. [Google Scholar]
- Lowe, D.J.; De Lange, W.P. Volcano-meteorological tsunamis, the c. AD 200 Taupo eruption (New Zealand) and the possibility of a global tsunami. Holocene 2000, 10, 401–407. [Google Scholar] [CrossRef]
- Terry, J.; Goff, J.; Winspear, N.; Bongolan, V.; Fisher, S. Tonga volcanic eruption and tsunami, January 2022: Globally the most significant opportunity to observe an explosive and tsunamigenic submarine eruption since AD 1883 Krakatau. Geosci. Lett. 2022, 9, 24. [Google Scholar] [CrossRef]
- DART® (Deep-Ocean Assessment and Reporting of Tsunamis). Available online: https://nctr.pmel.noaa.gov/Dart/ (accessed on 20 September 2022).
- Harkrider, D.; Press, F. The Krakatoa air-sea waves: An example of pulse propagation in coupled systems. Geophys. J. R. Astron. Soc. 1967, 13, 149–158. [Google Scholar] [CrossRef]
- Lynett, P.; McCann, M.; Zhou, Z.; Renteria, W.; Borrero, J.; Greer, D.; Cinar, G.E. Diverse tsunamigenesis triggered by the Hunga Tonga-Hunga Ha’apai eruption. Nature 2022, 609, 728. [Google Scholar] [CrossRef] [PubMed]
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 MHz. Nature 1955, 75, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.B. First-order theory and analysis of MF/HF/VHF scatter from the Sea. IEEE Trans. Antenna Propag. 1972, AP-20, 2–10. [Google Scholar] [CrossRef]
- Lipa, B.; Nyden, B.; Ullman, B.D.; Terrill, E. SeaSonde Radial Velocities: Derivation and Internal Consistency. IEEE J. Ocean. Eng. 2006, 31, 850–861. [Google Scholar] [CrossRef]
- Lipa, B.J.; Barrick, D.E. Least-squares methods for the extraction of surface currents from CODAR crossed-loop data: Application at ARSLOE. IEEE J. Ocean. Eng. 2006, OE-8, 226–253. [Google Scholar] [CrossRef]
- Barrick, D.E. A coastal radar system for tsunami warning. Remote Sens. Environ. 1979, 8, 353–358. [Google Scholar] [CrossRef]
- Lipa, B.; Isaacson, J.; Nyden, B.; Barrick, D. Tsunami arrival detection with high frequency (HF) radar. Remote Sens. 2012, 4, 1448–1461. [Google Scholar] [CrossRef]
- Dzvonkovskaya, A. Ocean surface current measurements using HF radar during the 2011 Japan tsunami hitting Chilean coast. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium 2012, Munich, Germany, 22–27 July 2012; pp. 7605–7608. [Google Scholar]
- Lipa, B.; Barrick, D.; Diposaptono, S.; Isaacson, J.; Jena, B.K.; Nyden, B.; Rajesh, K.; Kumar, T.S. High Frequency (HF) Radar detection of the weak 2012 Indonesian tsunamis. Remote Sens. 2012, 4, 2944–2956. [Google Scholar] [CrossRef]
- Lipa, B.; Parikh, H.; Barrick, D.; Roarty, H.; Glenn, S. High Frequency Radar Observations of the June 2013 US East Coast Meteotsunami. Nat. Hazards. 2014, 74, 109–122. [Google Scholar] [CrossRef]
- Poli, P.; Shapiro, N.M. Rapid characterization of large volcanic eruptions: Measuring the impulse of the Hunga Tonga explosion from teleseismic waves. Geophys. Res. Lett. 2022, 49, 8. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Bourg, J.; Nyden, B. HF radar detection of tsunamis. J. Oceanogr. 2006, 2, 705–716. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Isaacson, J. Coastal Tsunami Warning with Deployed HF Radar Systems. In Tsunami; Mokhtari, M., Ed.; InTech: London, UK, 2016; Available online: http://www.intechopen.com/books/tsunami/coastal-tsunami-warning-with-deployed-hf-radar-systems (accessed on 15 November 2022). [CrossRef]
- Office of Coast Survey. Available online: https://www.charts.noaa.gov/InteractiveCatalog/nrnc.shtml (accessed on 20 April 2023).
- GEBCO Compilation Group. GEBCO 2021 Grid; NERC EDS British Oceanographic Data Centre NOC: Liverpool, UK, 2021. [Google Scholar] [CrossRef]
- Wright, C.; Hindley, N.; Alexander, M.J.; Barlow, M.; Hoffmann, L.; Mitchell, C.; Yue, J. Tonga eruption triggered waves propagating globally from surface to edge of space. Nature 2022, 609, 741–746. [Google Scholar] [CrossRef] [PubMed]
- Tide Gauge Water Levels. Available online: https://tidesandcurrents.noaa.gov/waterlevels.html?id=9412110 (accessed on 25 September 2022).
- Available online: https://en.wikipedia.org/wiki/2009_Samoa_earthquake_and_tsunami (accessed on 20 April 2023).
- Williams, D.A.; Horsburgh, K.J.; Schultz, D.M.; Hughes, C.W. Proudman Resonances with tides, bathymetry and variable atmospheric forcings. Nat. Hazards 2021, 106, 1169–1194. [Google Scholar] [CrossRef]
- Symons, G.J. (Ed.) The Eruption of Krakatoa and Subsequent Phenomena; Report to Royal Society; 1888; Available online: https://hdl.handle.net/2027/hvd.32044032825895 (accessed on 26 November 2022).
- Choi, B.H.; Pelinovsky, E.; Kim, K.O.; Lee, J.S. Simulation of the trans-oceanic tsunami propagation due to the 1883 Krakatau Volcanic eruption. Nat. Hazards Earth Syst. Sci. 2003, 3, 321. [Google Scholar] [CrossRef]
- Proudman, J. The effects on the sea of changes in atmospheric pressure. Geophys. Suppl. Mon. Not. R. Astron. Soc. 1929, 2, 197–209. [Google Scholar] [CrossRef]
- Vilibic, I. Numerical simulations of the Proudman resonance. Cont. Shelf Res. 2008, 28, 574–581. [Google Scholar] [CrossRef]
- Amores, A.; Monserrat, S.; Marcos, M.; Argüeso, D.; Villalonga, J.; Jordà, G.; Gomis, D. Numerical simulation of atmospheric Lamb waves generated by the 2022 Hunga-Tonga volcanic eruption. Geophys. Res. Lett. 2022, 49, e2022GL098240. [Google Scholar] [CrossRef]
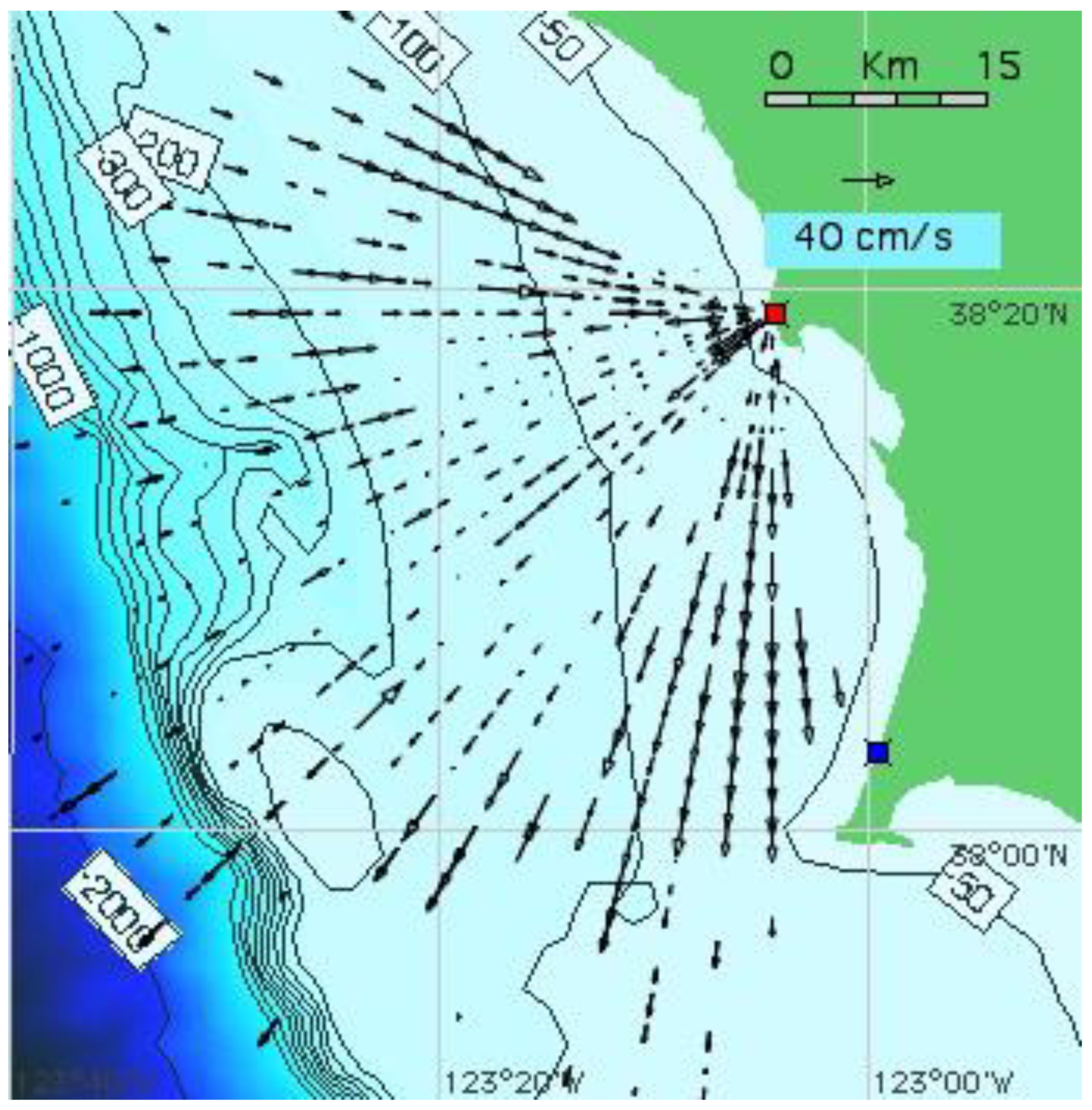

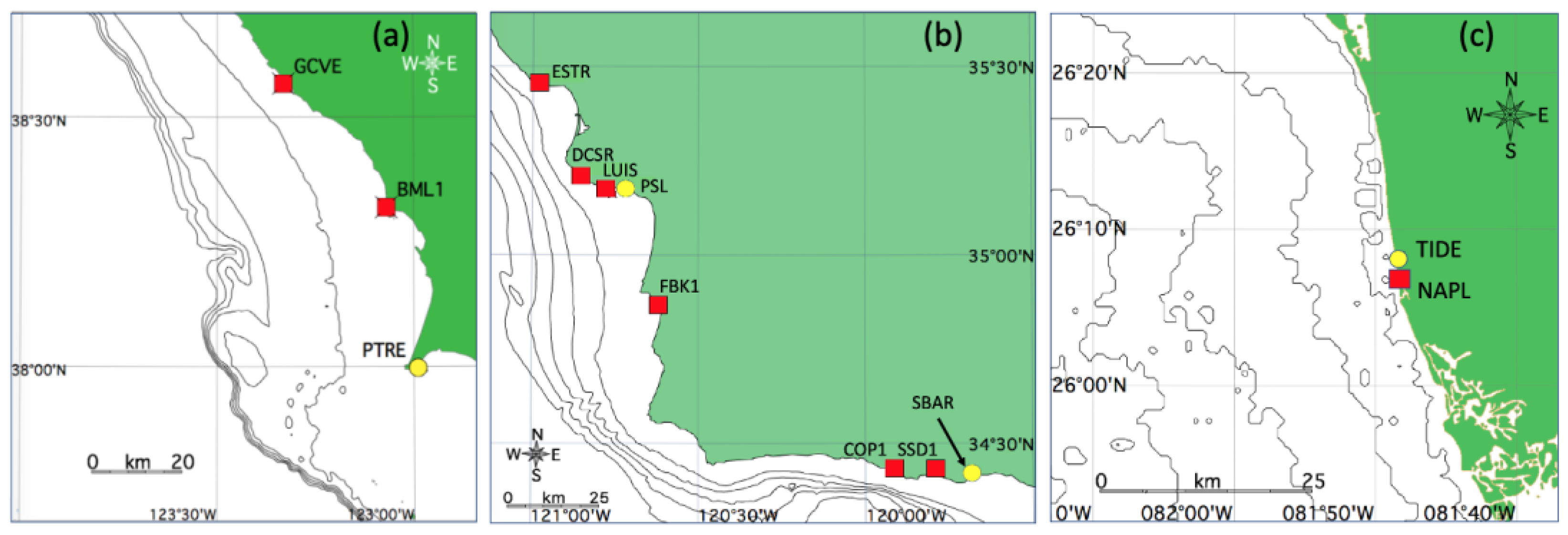

| GCVE | 38°34.031′N, 123°19.893′W |
| BML1 | 38°19.039′N, 123°04.348′W |
| ESTR | 35°27.585′N, 120°58.658′W |
| DCSR | 35°12.147′N, 120°50.765′W |
| LUIS | 35°09.649′N, 120°45.507′W |
| FBK1 | 34°52.185′N, 120°37.272′W |
| COP1 | 34°24.470′N, 119°52.700′W |
| SSD1 | 34°25.145′N, 119°35.798′W |
| NAPL | 26°09.729′N, 081°48.632′W |
| Site | Distance from Tonga | Lamb Wave Arrival Hours UTC | Radar Phase 1 Arrival Hours UTC | Radar Phase 2 Arrival Hours UTC | ||
|---|---|---|---|---|---|---|
| km | Expected | Observed | Observed | Expected | Observed | |
| GCVE | 8513 | 11.95 | 11.95 | 13.2 | 16.49 | 16.53 |
| BML1 | 8512 | 11.95 | 11.95 | 13.9 | 16.49 | 16.35 |
| ESTR | 8455 | 11.90 | 11.9 | 13.9 | 16.41 | 16.42 |
| DCSR | 8446 | 11.89 | 11.9 | - | 16.40 | 16.21 |
| LUIS | 8450 | 11.90 | 11.9 | 13.9 | 16.40 | 16.67 |
| FBK1 | 8440 | 11.89 | 11.9 | 12.4 | 16.39 | 16.07 |
| COP1 | 8462 | 11.91 | 11.9 | - | 16.42 | 15.96 |
| SSD1 | 8483 | 11.93 | 11.9 | 14.2 | 16.45 | 16.25 |
| NAPL | 11,341 | 14.51 | 14.4 | 17.4 | - | - |
| Radar Site | Avg Water Depth | Initial Wave Period | Max. del-v | Max. Wave Height | Est Wave Height, d = 5 m | Initial Tide Gauge Wave Height | Tide Gauge Site |
|---|---|---|---|---|---|---|---|
| m | h | cm/s, pp | m, pp | m | m | ||
| BML1 | 80 | 0.9 | 13 | 0.37 | 0.74 | 0.6 | Point Reyes |
| LUIS | 70 | 1.0 | 12 | 0.32 | 0.62 | 1.7 | Port San Luis |
| FBK1 | 50 | 0.8 | 15 | 0.34 | 0.61 | 0.7 | Estimate |
| SSD1 | 45 | 0.8 | 8 | 0.17 | 0.30 | 0.3 | Santa Barbara |
| GCVE | 90 | 0.7 | 7.5 | 0.23 | 0.47 | 1.0 | Arena Cove |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipa, B.; Barrick, D.; Whelan, C.; Losekoot, M.; Parikh, H. First Open-Coast HF Radar Observations of a 2-Phase Volcanic Tsunami, Tonga 2022. Remote Sens. 2023, 15, 2325. https://doi.org/10.3390/rs15092325
Lipa B, Barrick D, Whelan C, Losekoot M, Parikh H. First Open-Coast HF Radar Observations of a 2-Phase Volcanic Tsunami, Tonga 2022. Remote Sensing. 2023; 15(9):2325. https://doi.org/10.3390/rs15092325
Chicago/Turabian StyleLipa, Belinda, Donald Barrick, Chad Whelan, Marcel Losekoot, and Hardik Parikh. 2023. "First Open-Coast HF Radar Observations of a 2-Phase Volcanic Tsunami, Tonga 2022" Remote Sensing 15, no. 9: 2325. https://doi.org/10.3390/rs15092325
APA StyleLipa, B., Barrick, D., Whelan, C., Losekoot, M., & Parikh, H. (2023). First Open-Coast HF Radar Observations of a 2-Phase Volcanic Tsunami, Tonga 2022. Remote Sensing, 15(9), 2325. https://doi.org/10.3390/rs15092325




