Applying Time-Expended Sampling to Ensemble Assimilation of Remote-Sensing Data for Short-Term Predictions of Thunderstorms
Abstract
1. Introduction
2. WoFS and GSI-Based Rapid-Cycling EnKF
3. Event Overviews and Experiment Design
3.1. Event Overviews
3.1.1. Event on 28 April 2021
3.1.2. Event on 17 May 2021
3.1.3. Event on 23 May 2021
3.1.4. Event on 26 May 2021
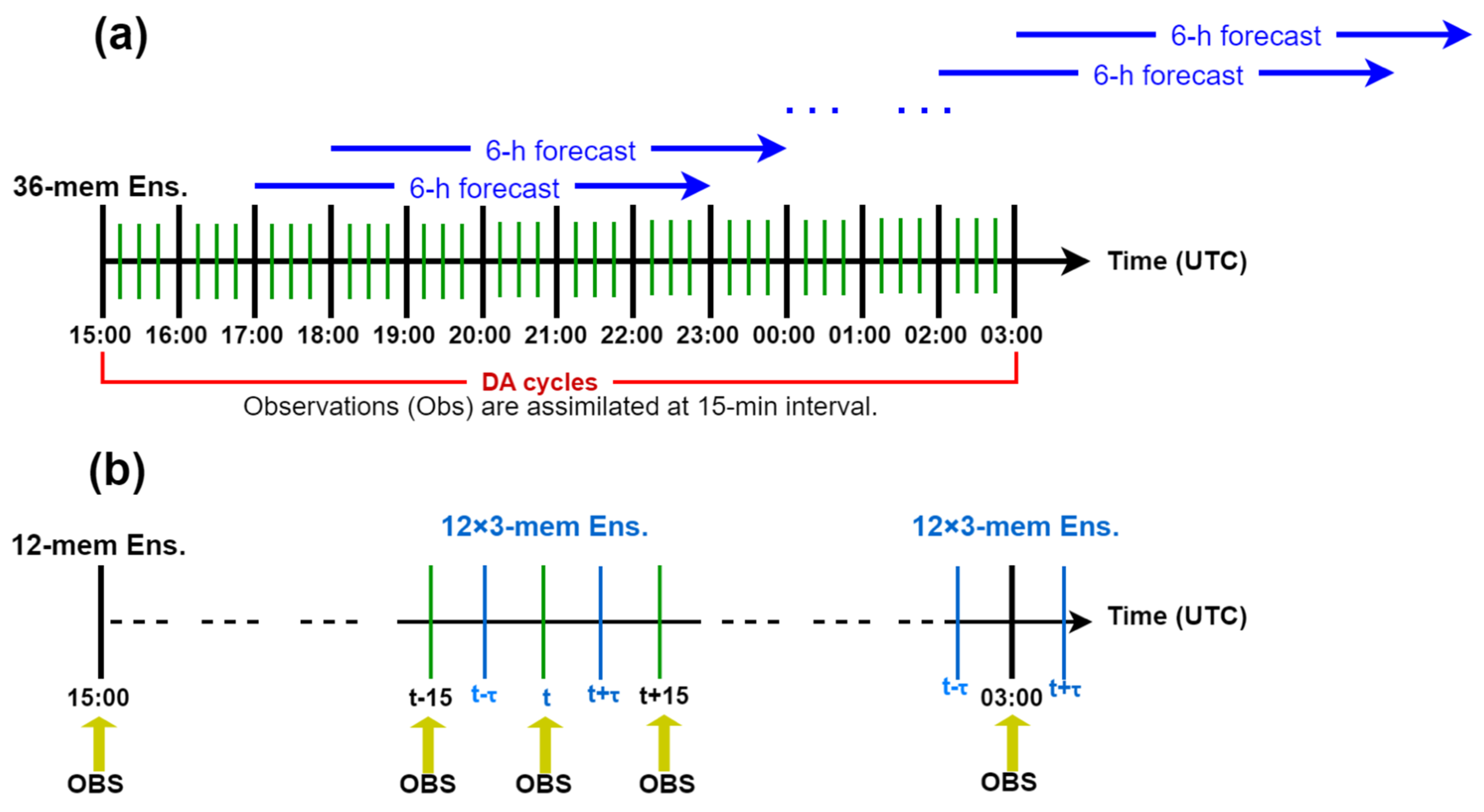
3.2. Description of TES and Experiment Design
4. Experiment Results and Comparisons
4.1. Assimilation Statistics
≈ σo2 + ∑m∑n[Hm(xn) − ∑nHm (xn)/N]2/[M(N − 1)] = σo2 + s2,
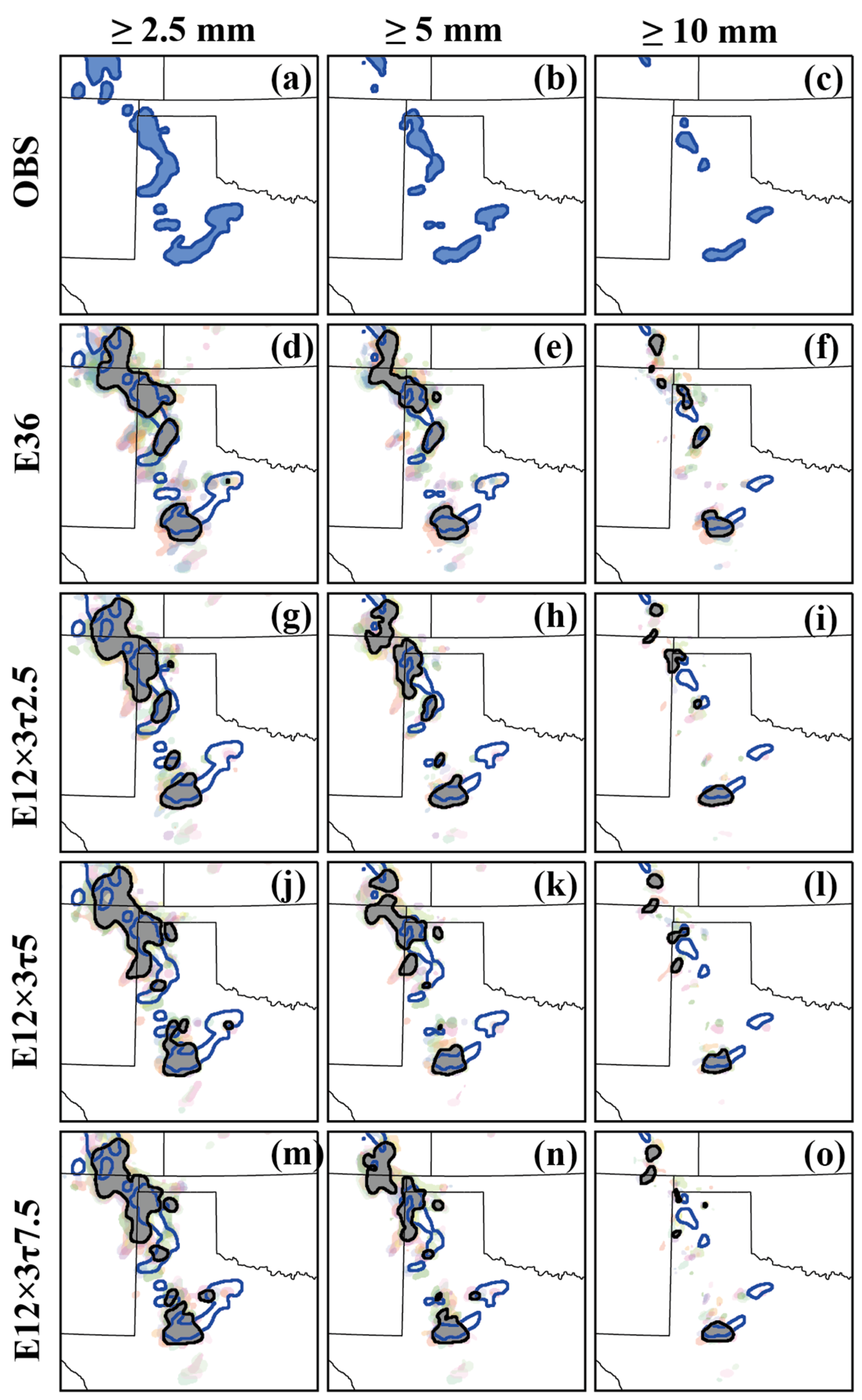
4.2. Forecast Performances
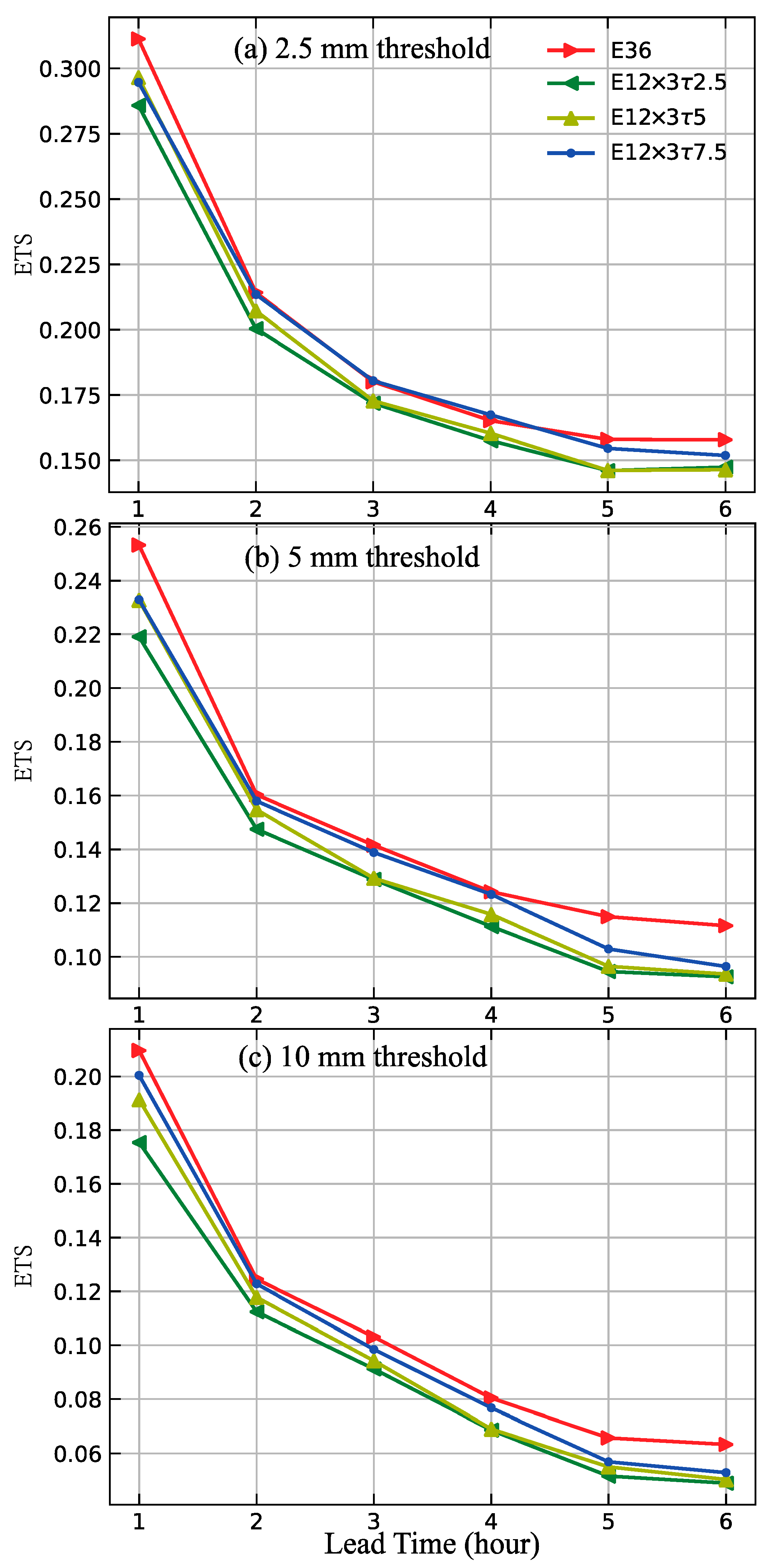
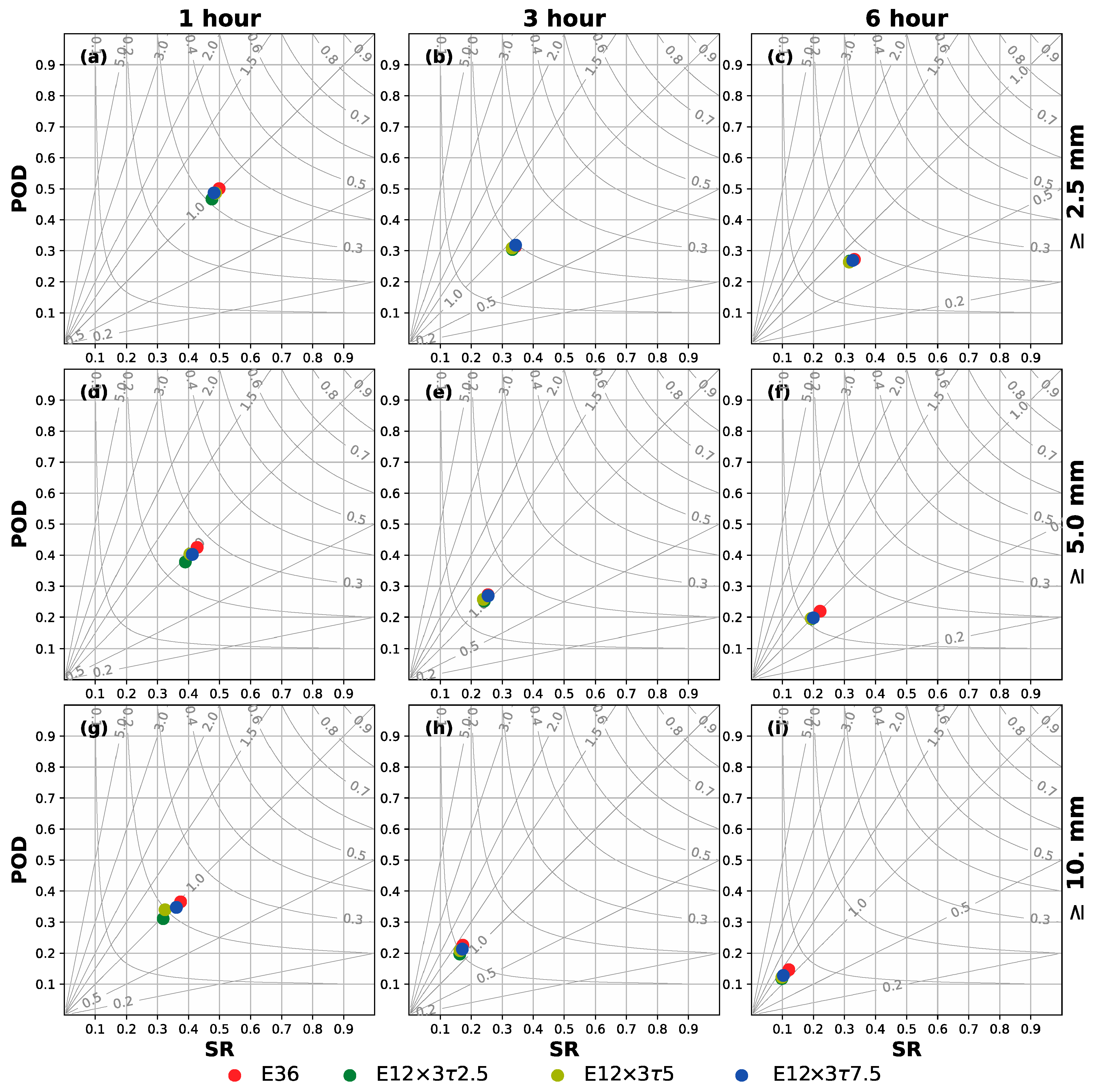
4.2.1. Overall Evaluation
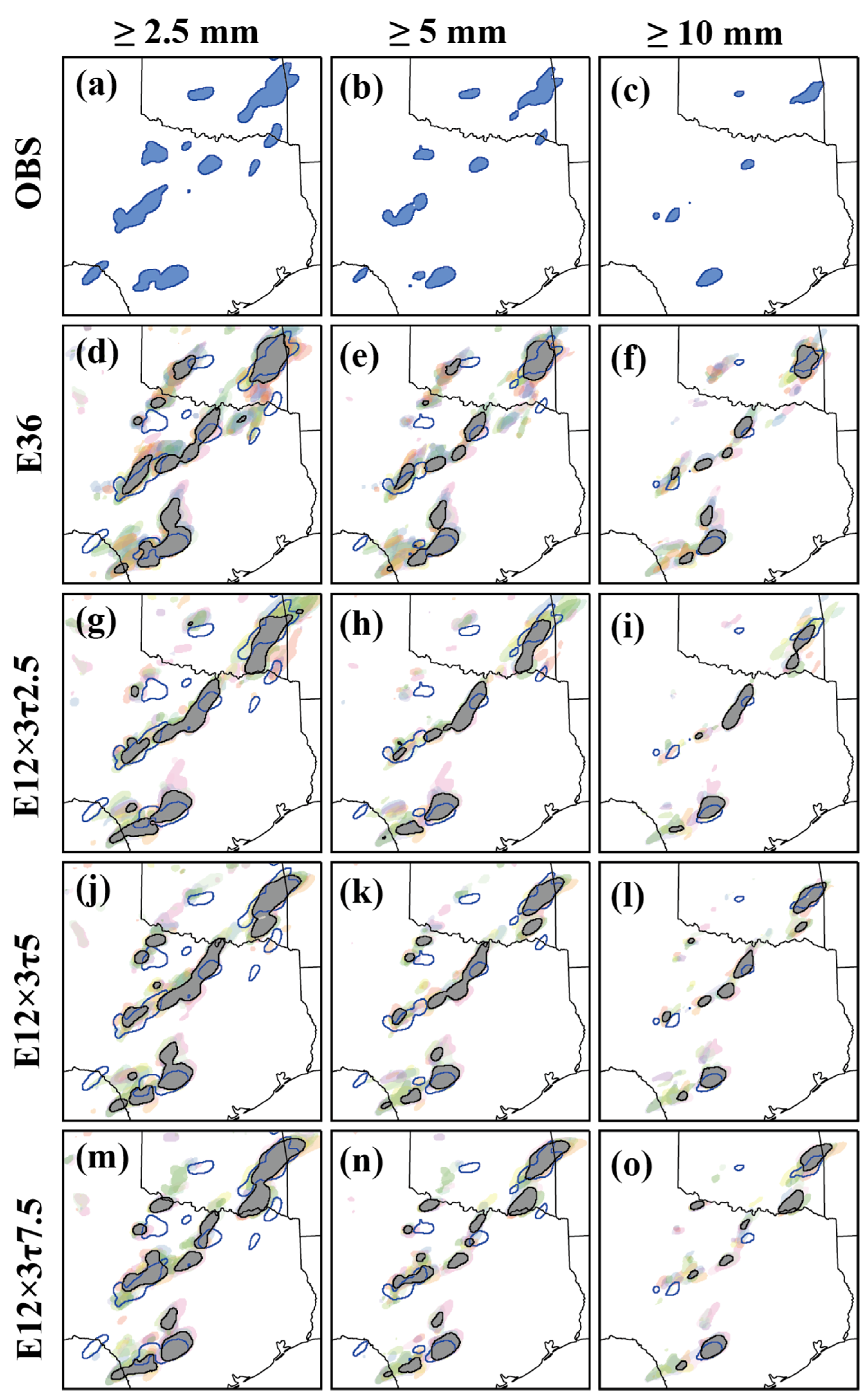
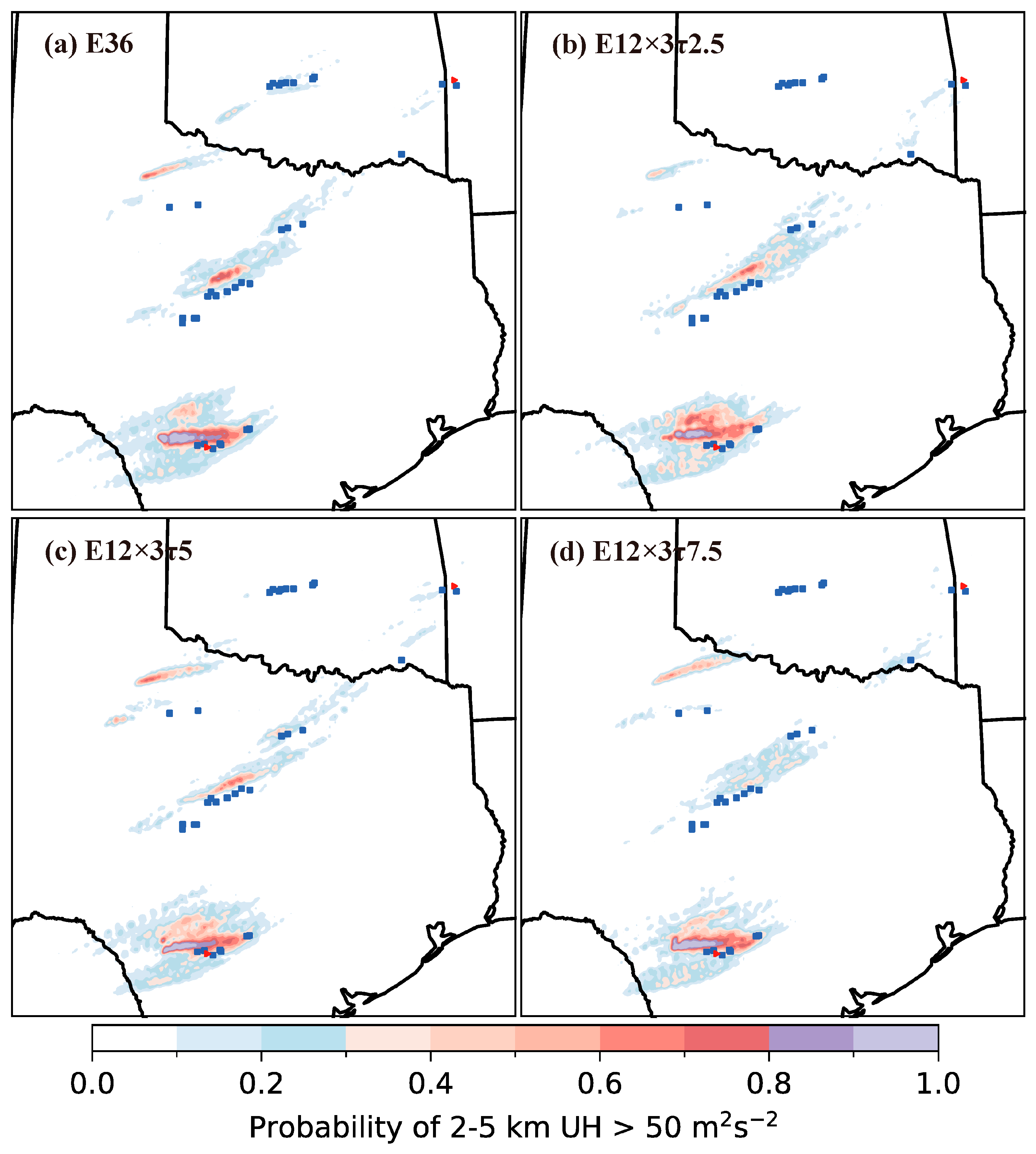
4.2.2. Best Forecast-Performance Case: 28 April 2021 Severe Storm Event
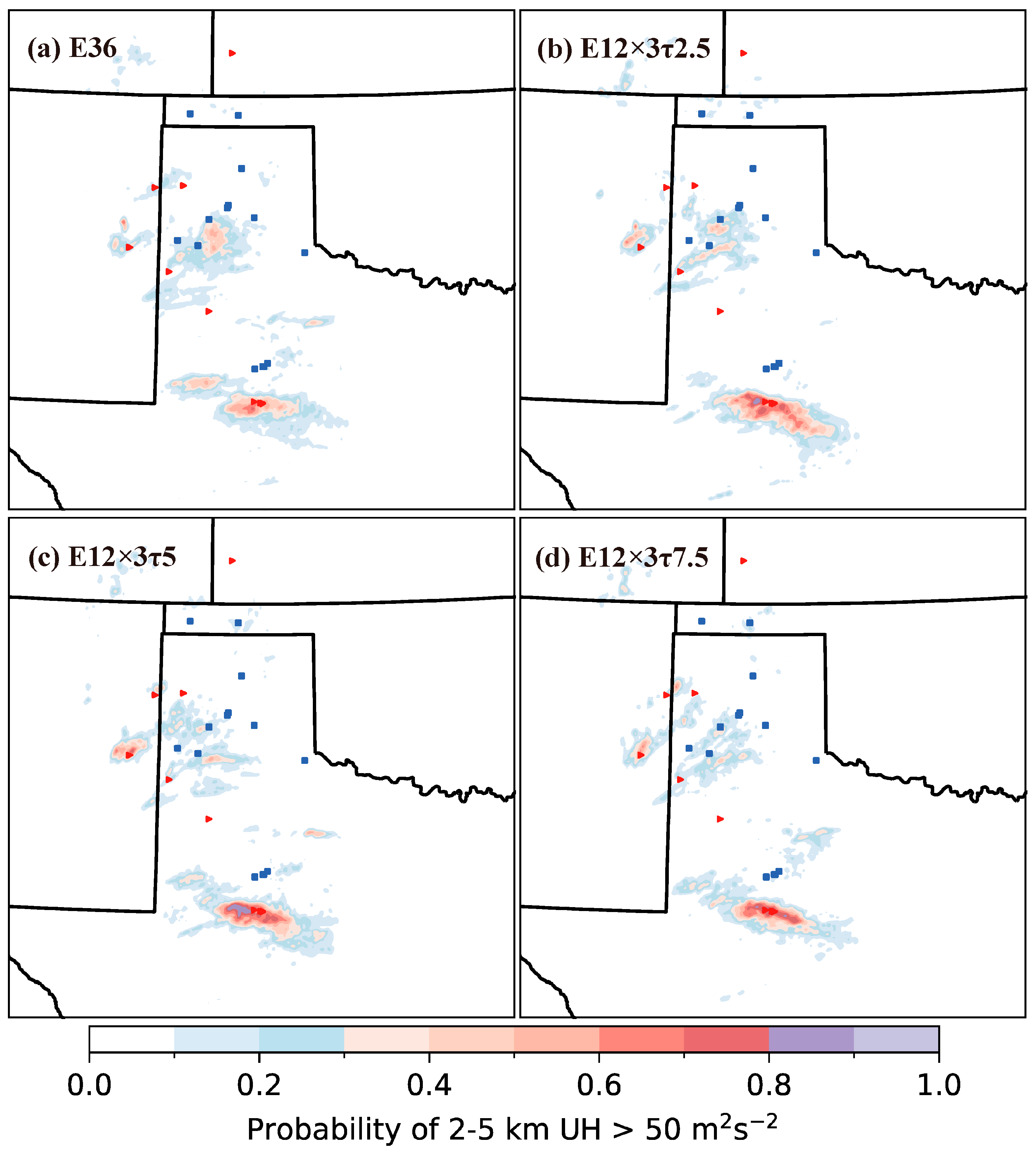
4.2.3. Worst Forecast-Performance Case: 17 May 2021 Severe Storm Event
5. Conclusions
- (i)
- Under various severe-weather conditions, represented by the four severe storm events considered in this study, TES can be successfully applied to the WoFS in assimilating remote-sensing data from radars and the geostationary satellite GOES-16, with improved computational efficiency and without compromising the quality of the analysis and subsequent short-term prediction of high-impact weather.
- (ii)
- With a wide range of severe-weather scenarios to capture, there is an optimal sampling-time interval τ, which can lead to better analyses and subsequent predictions. For the wide range of severe-weather scenarios (overviewed in Section 3.1 for the four severe storm events) in this study, the optimal sampling-time interval was found to be τ = T/2 (where T = 15 min is the assimilation-cycle-time window), although the quality of the analysis and the subsequent predictive capability were not sensitive to τ (selected between T/6 and T/2).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NOAA. Strategic plan for NOAA’s Office of Oceanic and Atmospheric Research. NOAA Rep. 2. 2014. Available online: https://research.noaa.gov/sites/oar/Documents/OARStrategicPlan.pdf (accessed on 25 April 2023).
- Stensrud, D.J.; Xue, M.; Wicker, L.J.; Kelleher, K.E.; Foster, M.P.; Schaefer, J.T.; Schneider, R.S.; Benjamin, S.; Weygandt, S.S.; Ferree, J.T.; et al. Convective-scale warn-on-forecast system: A vision for 2020. Bull. Am. Meteorol. Soc. 2009, 90, 1487–1500. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Wicker, L.J.; Xue, M.; Dawson, D.T.; Yussouf, N.; Wheatley, D.M.; Thompson, T.E.; Snook, N.A.; Smith, T.M.; Schenkman, A.D.; et al. Progress and challenges with Warn-on-Forecast. Atmos. Res. 2013, 123, 2–16. [Google Scholar] [CrossRef]
- Wheatley, D.M.; Knopfmeier, K.H.; Jones, T.A.; Creager, G.J. Storm-scale data assimilation and ensemble forecasting with the NSSL experimental warn-on-forecast system. Part I: Radar data experiments. Weather Forecast. 2015, 30, 1795–1817. [Google Scholar] [CrossRef]
- Jones, T.A.; Wang, X.; Skinner, P.; Johnson, A.; Wang, Y. Assimilation of GOES-13 imager clear-sky water vapor (6.5 μm) Radiances into a Warn-on-Forecast System. Mon. Weather Rev. 2018, 146, 1077–1107. [Google Scholar] [CrossRef]
- Flora, M.L.; Skinner, P.; Potvin, C.K.; Reinhart, A.E.; Jones, T.A.; Yussouf, N.; Knopfmeier, K.H. Object-based verification of short-term, storm-scale probabilistic mesocyclone guidance from an experimental Warn-on-Forecast System. Weather Forecast. 2019, 34, 1721–1739. [Google Scholar] [CrossRef]
- Yussouf, N.; Knopfmeier, K.H. Application of the Warn-on-Forecast system for flash-flood-producing heavy convective rainfall events. Q. J. R. Meteorol. Soc. 2019, 145, 2385–2403. [Google Scholar] [CrossRef]
- Jones, T.A.; Skinner, P.; Yussouf, N.; Knopfmeier, K.; Reinhart, A.; Wang, X.; Bedka, K.; Smith, W.; Palikonda, R. Assimilation of GOES-16 radiances and retrievals into the Warn-on-Forecast System. Mon. Weather Rev. 2020, 148, 1829–1859. [Google Scholar] [CrossRef]
- Guerra, J.E.; Skinner, P.S.; Clark, A.; Flora, M.; Matilla, B.; Knopfmeier, K.; Reinhart, A.E. Quantification of NSSL Warn-on-Forecast System accuracy by storm age using object-based verification. Weather Forecast. 2022, 37, 1973–1983. [Google Scholar] [CrossRef]
- Xu, Q.; Wei, L.; Lu, H.; Qiu, C.; Zhao, Q. Time-expanded sampling for ensemble-based filters: Assimilation experiments with a shallow-water equation model. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Xu, Q.; Lu, H.; Gao, S.; Xue, M.; Tong, M. Time-expanded sampling for ensemble Kalman filter: Assimilation experiments with simulated radar observations. Mon. Weather. Rev. 2008, 136, 2651–2667. [Google Scholar] [CrossRef]
- Gustafsson, N.; Bojarova, J.; Vignes, O. A hybrid variational ensemble data assimilation for the High Resolution Limited Area Model (HIRLAM). Nonlinear Process Geophys. 2014, 21, 303–323. [Google Scholar] [CrossRef]
- Huang, B.; Wang, X. On the use of cost-effective Valid-Time-Shifting (VTS) method to increase ensemble size in the GFS Hybrid 4DEnVar System. Mon. Weather. Rev. 2018, 146, 2973–2998. [Google Scholar] [CrossRef]
- Gasperoni, N.A.; Wang, X.; Wang, Y. Using a cost-effective approach to increase background ensemble member size within the GSI-Based EnVar System for improved radar analyses and forecasts of convective systems. Mon. Weather. Rev. 2022, 150, 667–689. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Q.; Yao, M.; Gao, S. Time-expanded sampling for ensemble-based filters: Assimilation experiments with real radar observations. Adv. Atmos. Sci. 2011, 28, 743–757. [Google Scholar] [CrossRef]
- Zhao, Q.; Xu, Q.; Jin, Y.; McLay, J.; Reynolds, C. Time-expanded sampling for ensemble-based data assimilation applied to conventional and satellite observations. Weather Forecast. 2015, 30, 855–872. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; National Center For Atmospheric Research Boulder Co Mesoscale and Microscale Meteorology Div: Boulder, CO, USA, 2008. [Google Scholar]
- Liu, H.; Hu, M.; Ge, G.; Zhou, C.; Stark, D.; Shao, H.; Newman, K.; Whitaker, J. Ensemble Kalman Filter (EnKF) User’s Guide Version 1.3-Compatible with GSI Community Release v3.7. 2018. Available online: https://dtcenter.org/community-code/ensemble-kalman-filter-system-enkf/documentation (accessed on 25 April 2023).
- Jones, T.A.; Otkin, J.A.; Stensrud, D.J.; Knopfmeier, K. Assimilation of satellite infrared radiances and doppler radar observations during a cool season observing system simulation experiment. Mon. Weather Rev. 2013, 141, 3273–3299. [Google Scholar] [CrossRef]
- McPherson, R.A.; Fiebrich, C.A.; Crawford, K.C.; Kilby, J.R.; Grimsley, D.L.; Martinez, J.E.; Basara, J.; Illston, B.G.; Morris, D.A.; Kloesel, K.A.; et al. Statewide monitoring of the mesoscale environment: A technical update on the Oklahoma Mesonet. J. Atmos. Ocean. Technol. 2007, 24, 301–321. [Google Scholar] [CrossRef]
- Weng, F. Advances in radiative transfer modeling in support of satellite data assimilation. J. Atmos. Sci. 2007, 64, 3799–3807. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M.; Wei, X.; Song, Y.; Toth, Z. Ensemble data assimilation with the NCEP Global forecast system. Mon. Weather Rev. 2008, 136, 463–482. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.W.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cocks, S.; Martinaitis, S.M.; et al. Multi-Radar Multi-Sensor (MRMS) quantitative precipitation estimation: Initial operating capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- Smith, T.M.; Lakshmanan, V.; Stumpf, G.J.; Ortega, K.; Hondl, K.; Cooper, K.; Calhoun, K.; Kingfield, D.; Manross, K.L.; Toomey, R.; et al. Multi-Radar Multi-Sensor (MRMS) severe weather and aviation products: Initial operating capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 1617–1630. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.; Dowell, D.C.; Grell, G.A.; et al. A north american hourly assimilation and model forecast cycle: The rapid refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Mansell, E.R.; Ziegler, C.L.; Bruning, E. Simulated electrification of a small thunderstorm with two-moment bulk microphysics. J. Atmos. Sci. 2010, 67, 171–194. [Google Scholar] [CrossRef]
- Pan, S.; Gao, J. A method for assimilating pseudo dewpoint temperature as a function of GLM flash extent density in GSI-based EnKF data assimilation system—A proof of concept study. Earth Space Sci. 2022, 9, 2378. [Google Scholar] [CrossRef]
- Clark, A.J. Generation of ensemble mean precipitation forecasts from convection-allowing ensembles. Weather Forecast. 2017, 32, 1569–1583. [Google Scholar] [CrossRef]
- Baldwin, M.E.; Mitchell, K.E. The NCEP hourly multisensor US precipitation analysis for operations and GCIP research. In Proceedings of the Preprints, 13th Conference on Hydrology, Long Beach, CA, USA, 13–17 January 1997; Volume 54, p. 55. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences. (International Geophysics), 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Press: Ames, IA, USA, 1989. [Google Scholar]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Kain, J.S.; Weiss, S.J.; Bright, D.R.; Baldwin, M.E.; Levit, J.J.; Carbin, G.W.; Schwartz, C.S.; Weisman, M.L.; Droegemeier, K.K.; Weber, D.B.; et al. Some practical considerations regarding horizontal resolution in the first generation of operational convection-allowing NWP. Weather Forecast. 2008, 23, 931–952. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, J.; Skinner, P.S.; Knopfmeier, K.; Jones, T.; Creager, G.; Heiselman, P.L.; Wicker, L.J. Test of a Weather-adaptive dual-resolution hybrid warn-on-forecast analysis and forecast system for several severe weather events. Weather Forecast. 2019, 34, 1807–1827. [Google Scholar] [CrossRef]






| Observation | Error Standard Deviation | Localization Radius (km) | Localization Depth ln(po/p) |
|---|---|---|---|
| Temperature | 1.0 (°K) | 60 | 0.85 |
| Dewpoint | 1.0 (°K) | 60 | 0.85 |
| U wind | 1.0 (m/s) | 60–100 | 0.85 |
| V wind | 1.0 (m/s) | 60–100 | 0.85 |
| Pressure | 0.75 (hPa) | 60 | 0.85 |
| Reflectivity | 5.0–7.0 (dBZ) | 18 | 0.8 |
| Radial velocity | 3.0 (m/s) | 18 | 0.8 |
| CWP | 0.025–0.2 (kg/m2) | 36 | 0.9 |
| BT62c | 1.25 (°K) | 36 | 4.0 |
| BT73c | 1.75 (°K) | 36 | 4.0 |
| Experiment Name | Description |
|---|---|
| E36 | Ns = 36 and M = 0 without TES |
| E12×3τ2.5 | Ns = 12 and M = 1 with TES and τ = 2.5 min |
| E12×3τ5 | Ns = 12 and M = 1 with TES and τ = 5 min |
| E12×3τ7.5 | Ns = 12 and M = 1 with TES and τ = 7.5 min |
| d (BIAS in °K) | D (RMSI in °K) | S (Spread in °K) | CR | ||||
|---|---|---|---|---|---|---|---|
| Prior | Posterior | Prior | Posterior | Prior | Posterior | ||
| BT62c | |||||||
| E36 | 0.26 | −0.001 | 1.173 | 0.555 | 1.05 | 0.497 | 1.533 |
| E12×3τ2.5 | 0.26 | 0.008 | 1.211 | 0.626 | 1.038 | 0.484 | 1.448 |
| E12×3τ5 | 0.254 | −0.001 | 1.184 | 0.602 | 1.06 | 0.492 | 1.482 |
| E12×3τ7.5 | 0.256 | −0.018 | 1.175 | 0.566 | 1.146 | 0.501 | 1.532 |
| BT73c | |||||||
| E36 | 0.643 | 0.246 | 1.527 | 0.816 | 1.233 | 0.586 | 1.727 |
| E12×3τ2.5 | 0.628 | 0.249 | 1.569 | 0.893 | 1.225 | 0.564 | 1.671 |
| E12×3τ5 | 0.614 | 0.251 | 1.497 | 0.861 | 1.232 | 0.574 | 1.725 |
| E12×3τ7.5 | 0.676 | 0.242 | 1.574 | 0.820 | 1.385 | 0.595 | 1.736 |
| Reflectivity | |||||||
| E36 | 4.738 | 3.642 | 11.205 | 8.656 | 4.589 | 1.658 | 0.737 |
| E12×3τ2.5 | 4.83 | 3.815 | 11.484 | 9.019 | 4.814 | 1.608 | 0.724 |
| E12×3τ5 | 4.429 | 3.302 | 10.97 | 8.26 | 5.373 | 1.699 | 0.788 |
| E12×3τ7.5 | 4.338 | 2.978 | 10.529 | 7.697 | 5.899 | 1.741 | 0.851 |
| Forecast Lead Time | 1 h | 3 h | 6 h | |
|---|---|---|---|---|
| Threshold | 2.5 mm | 0.342 | 0.094 | 0.109 |
| 5 mm | 0.842 | 0.314 | 0.621 | |
| 10 mm | 0.868 | 0.307 | 0.749 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Gao, J.; Xu, Q.; Ran, L. Applying Time-Expended Sampling to Ensemble Assimilation of Remote-Sensing Data for Short-Term Predictions of Thunderstorms. Remote Sens. 2023, 15, 2358. https://doi.org/10.3390/rs15092358
Zhang H, Gao J, Xu Q, Ran L. Applying Time-Expended Sampling to Ensemble Assimilation of Remote-Sensing Data for Short-Term Predictions of Thunderstorms. Remote Sensing. 2023; 15(9):2358. https://doi.org/10.3390/rs15092358
Chicago/Turabian StyleZhang, Huanhuan, Jidong Gao, Qin Xu, and Lingkun Ran. 2023. "Applying Time-Expended Sampling to Ensemble Assimilation of Remote-Sensing Data for Short-Term Predictions of Thunderstorms" Remote Sensing 15, no. 9: 2358. https://doi.org/10.3390/rs15092358
APA StyleZhang, H., Gao, J., Xu, Q., & Ran, L. (2023). Applying Time-Expended Sampling to Ensemble Assimilation of Remote-Sensing Data for Short-Term Predictions of Thunderstorms. Remote Sensing, 15(9), 2358. https://doi.org/10.3390/rs15092358






