Estimation of Land Deformation and Groundwater Storage Dynamics in Shijiazhuang–Baoding–Cangzhou–Hengshui Using Multi-Temporal Interferometric Synthetic Aperture Radar
Abstract
:1. Introduction
2. Study Region and Data
2.1. Study Region
2.2. Data
2.2.1. InSAR Datasets
2.2.2. Hydraulic Head
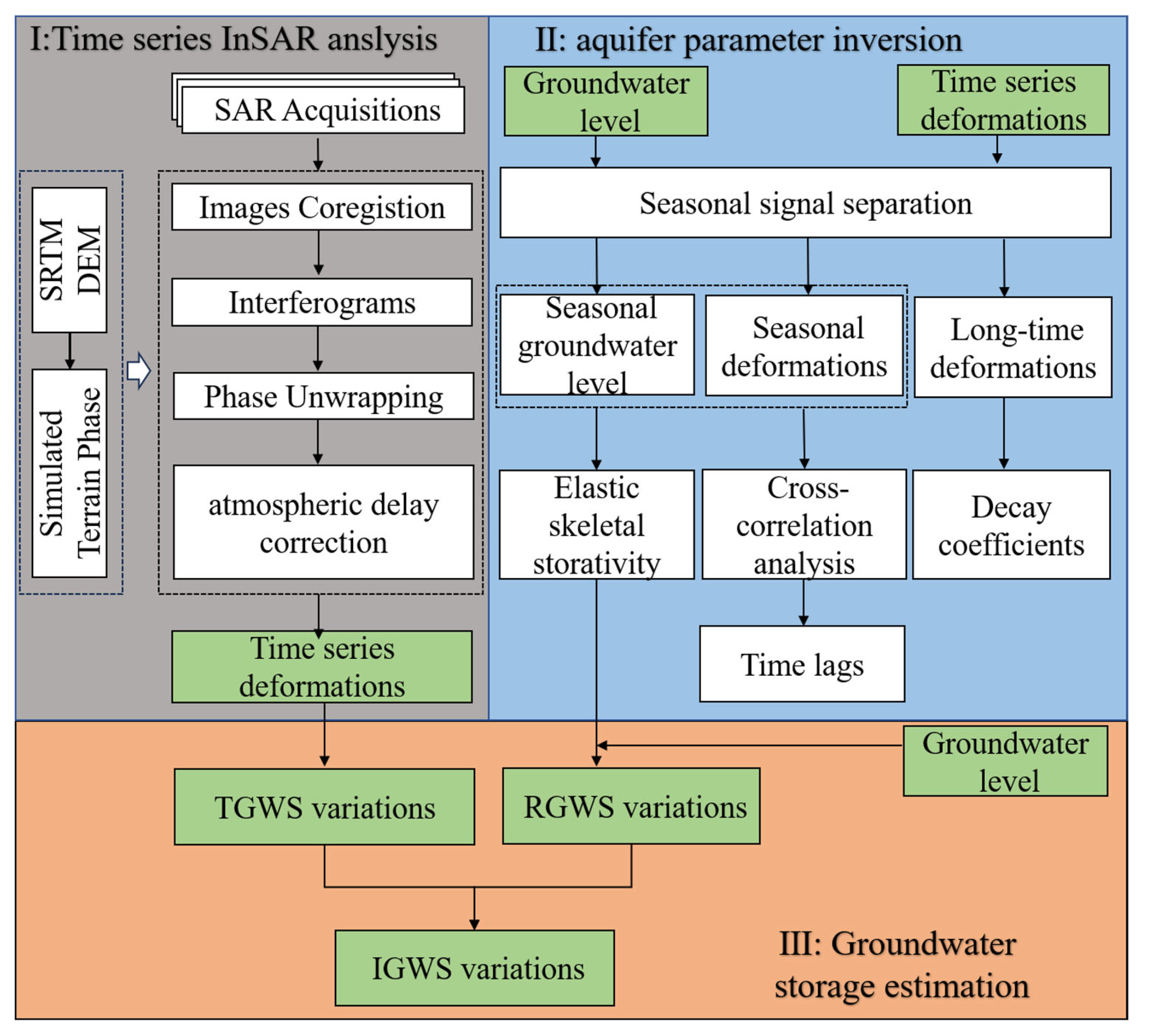
3. Method
3.1. Time-Series InSAR Data Processing
3.2. Aquifer Parameter Inversion
3.3. Aquifer Groundwater Storage (GWS) Estimation
4. Results
4.1. Land Deformation Monitoring Results and Analysis
4.2. Seasonal Deformation Results and Analysis
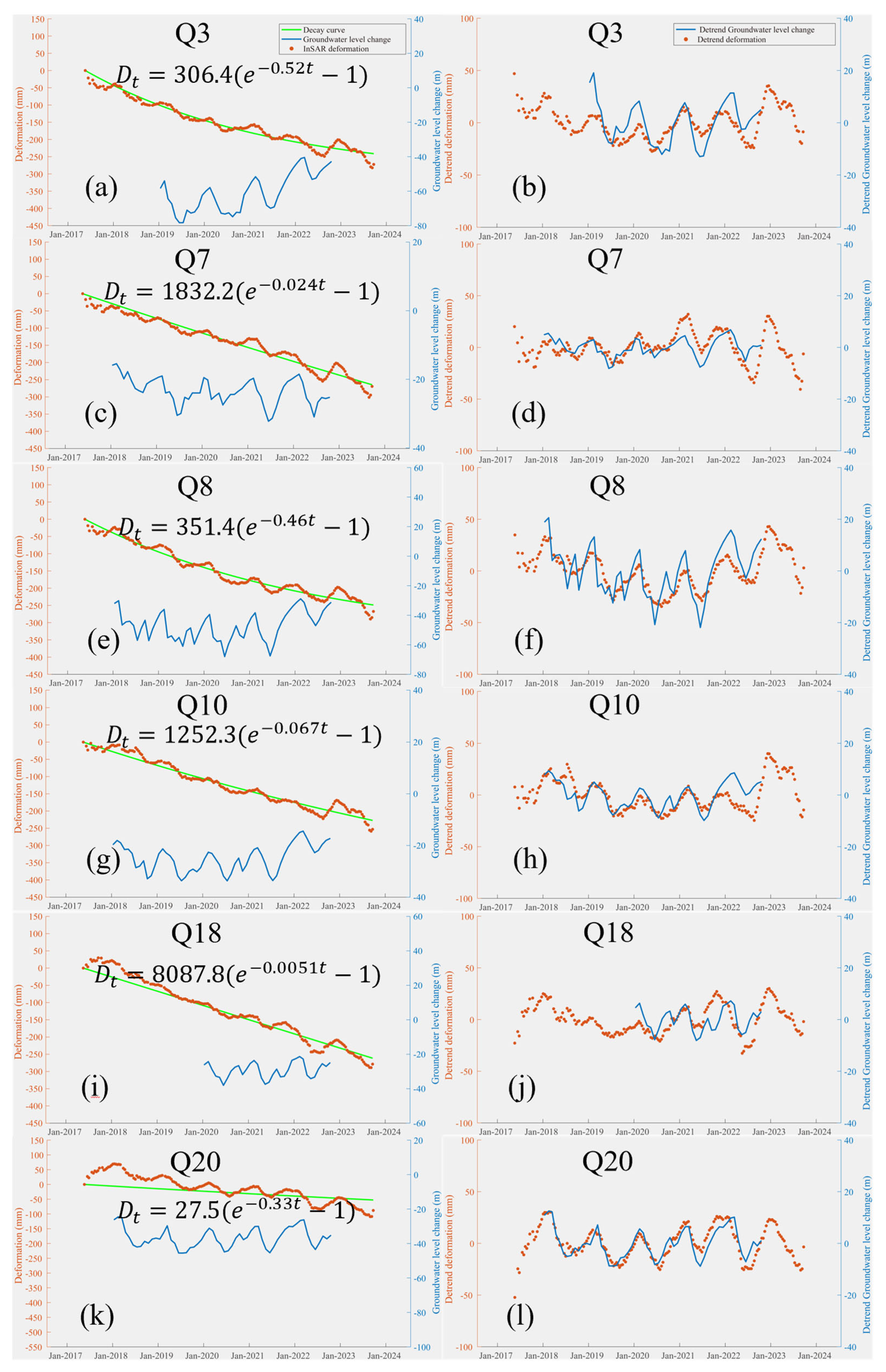
4.3. Aquifer Parameters (Ske) Estimation
4.4. GWS Parameter Estimation
5. Discussion
5.1. The Relationship between Heavy Rainfall and Deformation
5.2. Advantages and Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herrera-Garcia, G.; Ezquerro, P.; Tomas, R.; Bejar-Pizarro, M.; Lopez-Vinielles, J.; Rossi, M.; Mateos, R.M.; Carreon-Freyre, D.; Lambert, J.; Teatini, P.; et al. Mapping the global threat of land subsidence. Science 2021, 371, 34–36. [Google Scholar] [CrossRef]
- Jeanne, P.; Farr, T.G.; Rutqvist, J.; Vasco, D.W. Role of agricultural activity on land subsidence in the San Joaquin Valley, California. J. Hydrol. 2019, 569, 462–469. [Google Scholar] [CrossRef]
- Hoffmann, J.; Galloway, D.L.; Zebker, H.A. Inverse modeling of interbed storage parameters using land subsidence observations, Antelope Valley, California. Water Resour. Res. 2003, 39, 1031. [Google Scholar] [CrossRef]
- Amelung, C.C. Land subsidence in central Mexico detected by ALOS InSAR time-series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar]
- Motagh, M.; Shamshiri, R.; Haghighi, M.H.; Wetzel, H.-U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Halipu, A.; Wang, X.; Iwasaki, E.; Yang, W.; Kondoh, A. Quantifying Water Consumption through the Satellite Estimation of Land Use/Land Cover and Groundwater Storage Changes in a Hyper-Arid Region of Egypt. Remote Sens. 2022, 14, 2608. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Xue, Y.; Wang, Z.; Yao, Y.; Yan, X.; Wang, H. Land subsidence and uplift due to long-term groundwater extraction and artificial recharge in Shanghai, China. Hydrogeol. J. 2015, 23, 1851–1866. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Z.; Xu, B.; Gui, R.; Hu, J.; Yang, C.; Yang, Q.; Xiong, T. Coupling the Relationship between Land Subsidence and Groundwater Level, Ground Fissures in Xi’an City Using Multi-Orbit and Multi-Temporal InSAR. Remote Sens. 2023, 15, 3567. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, X.; Sun, Q.; Wang, H.; Hu, J. Characterizing Spatiotemporal Patterns of Land Deformation in the Santa Ana Basin, Los Angeles, from InSAR Time Series and Independent Component Analysis. Remote Sens. 2022, 14, 2624. [Google Scholar] [CrossRef]
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhu, L.; Zhang, C.; Huang, Z.; Li, Z.; Wang, H.; Chaofan, Z. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef]
- Shi, M.; Gong, H.; Gao, M.; Chen, B.; Zhou, C. Recent Ground Subsidence in the North China Plain, China, Revealed by Sentinel-1A Datasets. Remote Sens. 2020, 12, 3579. [Google Scholar] [CrossRef]
- Wang, L.; Jia, B.; Xie, Z.; Wang, B.; Liu, S.; Li, R.; Liu, B.; Wang, Y.; Chen, S. Impact of groundwater extraction on hydrological process over the Beijing-Tianjin-Hebei region, China. J. Hydrol. 2022, 609, 127689. [Google Scholar] [CrossRef]
- Dong, J.; Lai, S.; Wang, N.; Wang, Y.; Zhang, L.; Liao, M. Multi-scale deformation monitoring with Sentinel-1 InSAR analyses along the Middle Route of the South-North Water Diversion Project in China. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102324. [Google Scholar] [CrossRef]
- Zhang, K.; Ge, L.; Li, X.; Ng, A.H.-M. Monitoring ground surface deformation over the North China Plain using coherent ALOS PALSAR differential interferograms. J. Geod. 2013, 87, 253–265. [Google Scholar] [CrossRef]
- Xiao, R.; Yu, C.; Li, Z.; Song, C.; He, X. General survey of large-scale land subsidence by GACOS-corrected InSAR stacking: Case study in North China Plain. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 213–218. [Google Scholar] [CrossRef]
- Su, G.; Wu, Y.; Zhan, W.; Zheng, Z.; Chang, L.; Wang, J. Spatiotemporal evolution characteristics of land subsidence caused by groundwater depletion in the North China plain during the past six decades. J. Hydrol. 2021, 600, 126678. [Google Scholar] [CrossRef]
- Gerald, W.; Bawden, W.T.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature 2001, 412, 812–815. [Google Scholar]
- Shi, G.; Ma, P.; Hu, X.; Huang, B.; Lin, H. Surface response and subsurface features during the restriction of groundwater exploitation in Suzhou (China) inferred from decadal SAR interferometry. Remote Sens. Environ. 2021, 256, 112327. [Google Scholar] [CrossRef]
- Amelung, F.; Galloway, D.L.; Bell, J.W.; Zebker, H.A.; Laczniak, R.J. Sensing the ups and downs of Las Vegas: InSAR reveals structural control of land subsidence and aquifer-system deformation. Geology 1999, 27, 483–486. [Google Scholar] [CrossRef]
- Chaussard, E.; Bürgmann, R. Remote Sensing of Ground Deformation for Monitoring Groundwater Management Practices: Application to the Santa Clara Valley During the 2012-2015 California Drought: Groundwater Monitoring With InSAR. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Chaussard, E.; Bürgmann, R.; Shirzaei, M.; Fielding, E.J.; Baker, B. Predictability of hydraulic head changes and characterization of aquifer-system and fault properties from InSAR-derived ground deformation. J. Geophys. Res. Solid Earth 2014, 119, 6572–6590. [Google Scholar] [CrossRef]
- Hoffmann, J.R.; Zebker, H.A.; Galloway, D.L.; Amelung, F. Seasonal subsidence and rebound in Las Vegas Valley, Nevada, observed by Synthetic Aperture Radar Interferometry. Water Resour. Res. 2001, 37, 1551–1566. [Google Scholar] [CrossRef]
- Hu, X.; Bürgmann, R. Aquifer deformation and active faulting in Salt Lake Valley, Utah, USA. Earth Planet. Sci. Lett. 2020, 547, 116471. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, T.; Tang, W.; Jiang, M.; Jiang, H.; Yang, C.; Zhan, W.; Ming, Z.; Zhang, S. Inferring decelerated land subsidence and groundwater storage dynamics in Tianjin–Langfang using Sentinel-1 InSAR. Int. J. Digit. Earth 2022, 15, 1526–1546. [Google Scholar] [CrossRef]
- Peng, M.; Lu, Z.; Zhao, C.; Motagh, M.; Bai, L.; Conway, B.D.; Chen, H. Mapping land subsidence and aquifer system properties of the Willcox Basin, Arizona, from InSAR observations and independent component analysis. Remote Sens. Environ. 2022, 271, 112894. [Google Scholar] [CrossRef]
- Pride, S.R.; Vasco, D.W.; Flekkoy, E.G.; Holtzman, R. Dispersive transport and symmetry of the dispersion tensor in porous media. Phys. Rev. E 2017, 95, 043103. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.G.; Hashemi, H.; Chen, J.; Knight, R. Apportioning deformation among depth intervals in an aquifer system using InSAR and head data. Hydrogeol. J. 2021, 29, 2475–2486. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hudnut, K.W.; Ingebritsen, S.E.; Phillips, S.P.; Peltzer, G.; Rogez, F.; Rosen, P.A. Detection of aquifer system compaction and land subsidence using interferometric synthetic aperture radar, Antelope Valley, Mojave Desert, California. Water Resour. Res. 1998, 34, 2573–2585. [Google Scholar] [CrossRef]
- Qu, F.; Lu, Z.; Zhang, Q.; Bawden, G.W.; Kim, J.-W.; Zhao, C.; Qu, W. Mapping ground deformation over Houston–Galveston, Texas using multi-temporal InSAR. Remote Sens. Environ. 2015, 169, 290–306. [Google Scholar] [CrossRef]
- Su, G.; Xiong, C.; Zhang, G.; Wang, Y.; Shen, Q.; Chen, X.; An, H.; Qin, L. Coupled processes of groundwater dynamics and land subsidence in the context of active human intervention, a case in Tianjin, China. Sci. Total Environ. 2023, 903, 166803. [Google Scholar] [CrossRef]
- Chen, M.; Tomás, R.; Li, Z.; Motagh, M.; Li, T.; Hu, L.; Gong, H.; Li, X.; Yu, J.; Gong, X. Imaging Land Subsidence Induced by Groundwater Extraction in Beijing (China) Using Satellite Radar Interferometry. Remote Sens. 2016, 8, 468. [Google Scholar] [CrossRef]
- Yu, X.; Wang, G.; Hu, X.; Liu, Y.; Bao, Y. Land subsidence in Tianjin, China: Before and after the south-to-north water diversion. Remote Sens. 2023, 15, 1647. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Yu, J.; Fan, Q.; Si, J.; Zhu, W.; Song, M. Interpretation of the Spatiotemporal Evolution Characteristics of Land Deformation in Beijing during 2003–2020 Using Sentinel, ENVISAT, and Landsat Data. Remote Sens. 2022, 14, 2242. [Google Scholar] [CrossRef]
- Falabella, F.; Serio, C.; Masiello, G.; Zhao, Q.; Pepe, A. A Multigrid InSAR Technique for Joint Analyses at Single-Look and Multi-Look Scales. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4014905. [Google Scholar] [CrossRef]
- Lauknes, T.R.; Zebker, H.A.; Larsen, Y. InSAR Deformation Time Series Using an L1-Norm Small-Baseline Approach. IEEE Trans. Geosci. Remote Sens. 2010, 49, 536–546. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 2007, 112(B7). [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Jiang, L.; Bai, L.; Zhao, Y.; Cao, G.; Wang, H.; Sun, Q. Combining InSAR and Hydraulic Head Measurements to Estimate Aquifer Parameters and Storage Variations of Confined Aquifer System in Cangzhou, North China Plain. Water Resour. Res. 2018, 54, 8234–8252. [Google Scholar] [CrossRef]
- Terzaghi, K. Principles of soil mechanics: IV Settlement and consolidation of clay. Eng. News-Rec. 1925, 95, 874–878. [Google Scholar]
- Miller, M.M.; Shirzaei, M. Spatiotemporal characterization of land subsidence and uplift in Phoenix using InSAR time series and wavelet transforms. J. Geophys. Res. Solid Earth 2015, 120, 5822–5842. [Google Scholar] [CrossRef]
- Zhaoji, Z.; Yuhong, F.; Zongyu, C.; Zongzhuang, Z.; Zhenhua, X.; Yabin, W.; Jinxiang, M.; Lizhi, Y.; Jingli, S.; Menggui, J. Investigation and Evaluation of Sustainable Utilization of Groundwater in North China Plain; Geological Publishing House: Beijing, China, 2009. [Google Scholar]
- Murray, K.D.; Lohman, R.B. Short-lived pause in Central California subsidence after heavy winter precipitation of 2017. Sci. Adv. 2018, 4, eaar8144. [Google Scholar] [CrossRef] [PubMed]

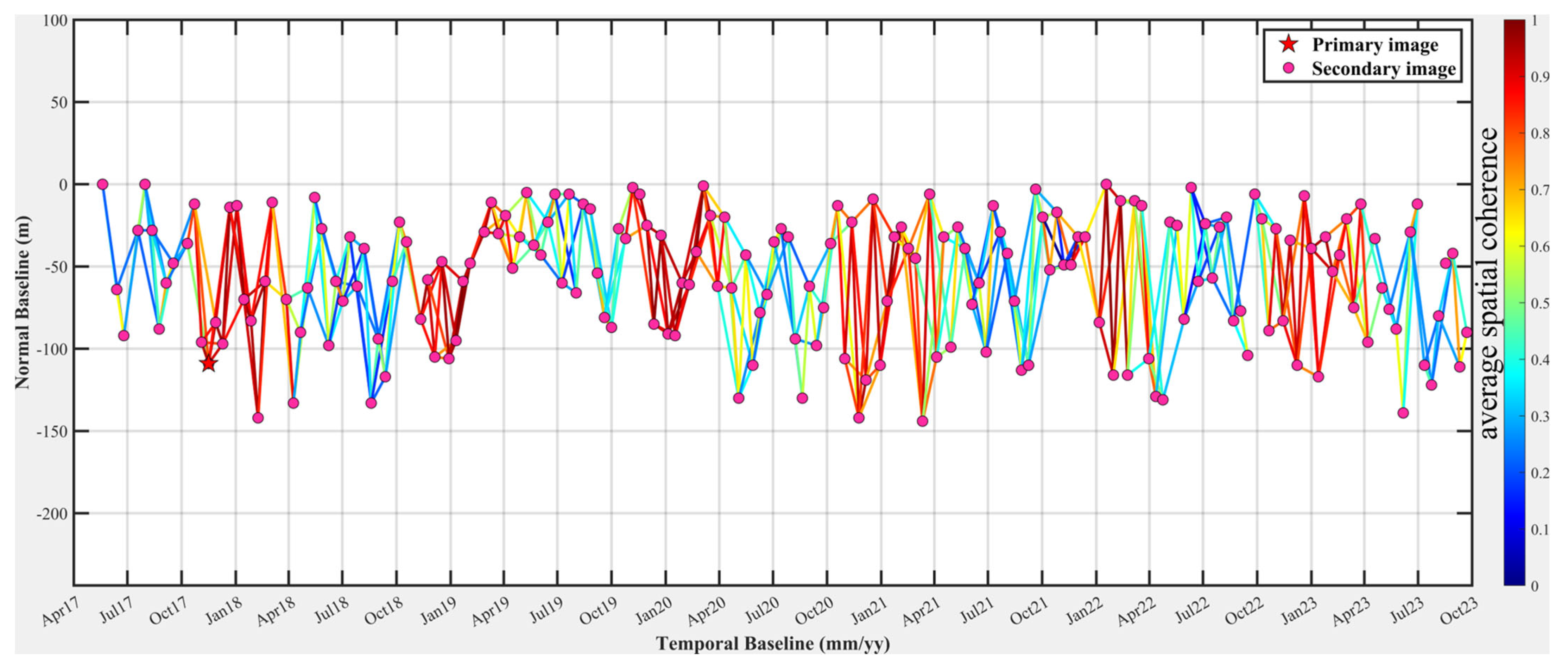


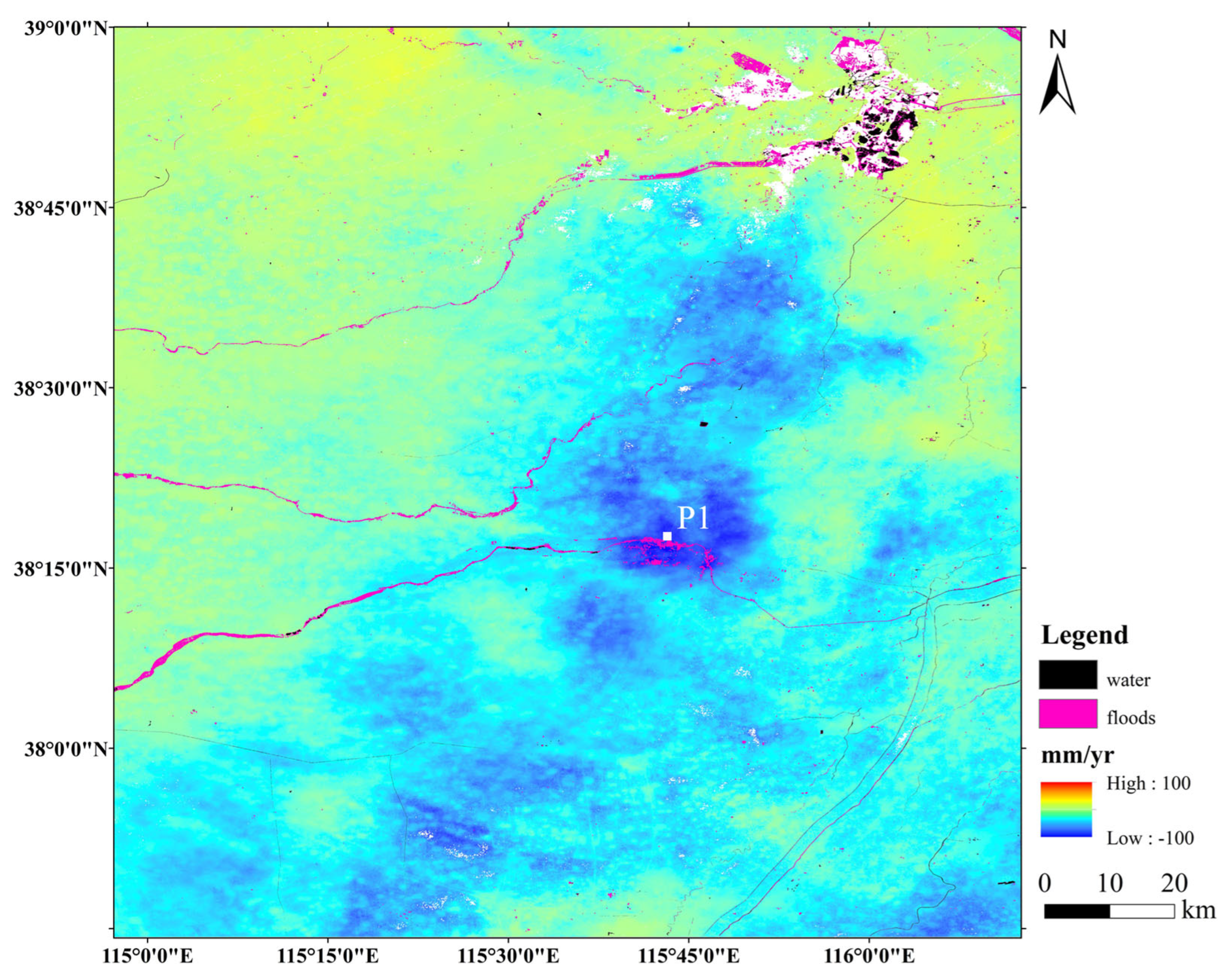
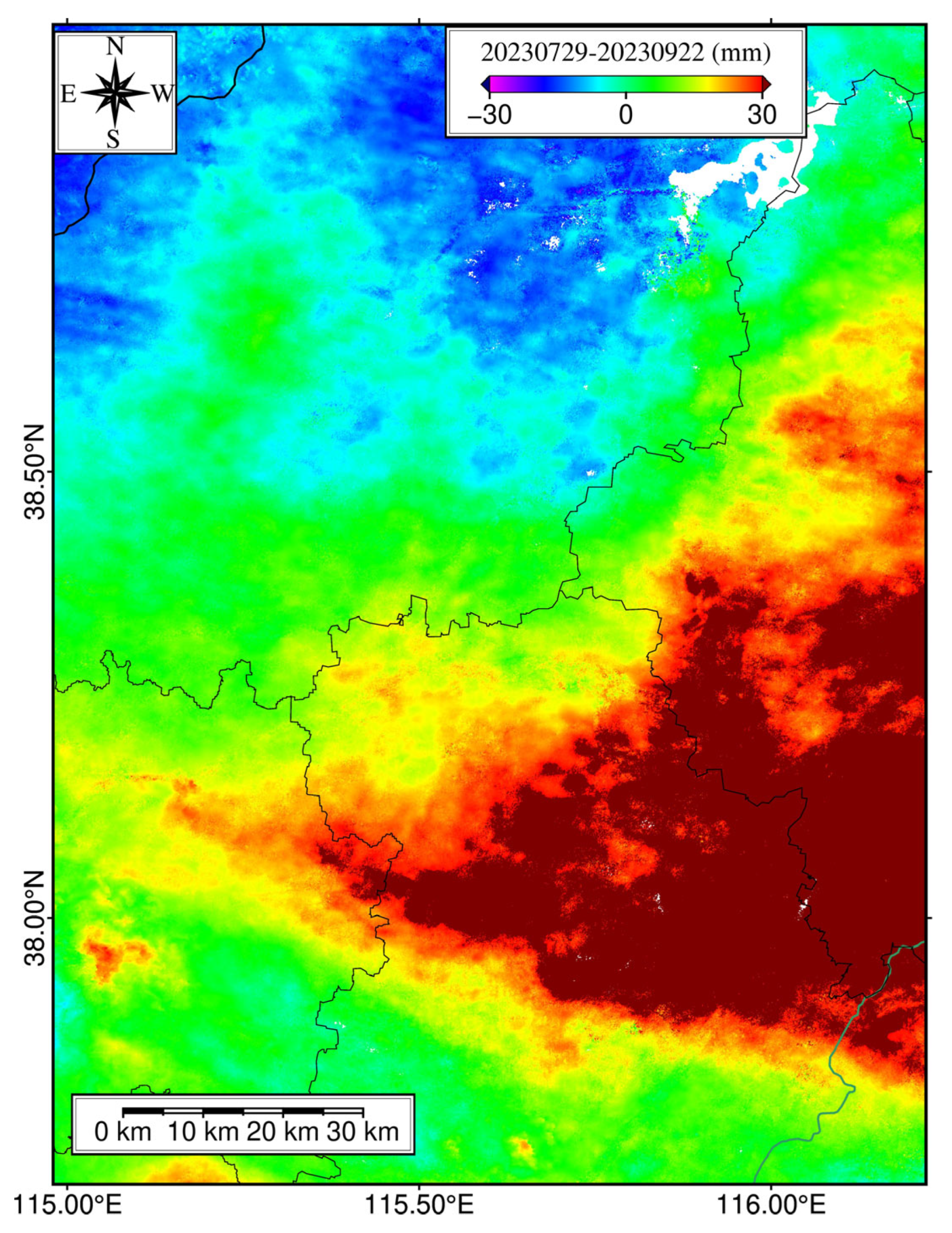

| Sensor | Band | Wavelength (cm) | Incidence Angle (°) | Heading (°) | Track | Polarization | Pass Direction | Number of Images | Date Range |
|---|---|---|---|---|---|---|---|---|---|
| S1 | C | 5.6 | 39.3 | −12.9 | 142 | VV | Ascending | 187 | 20/05/2017–22/09/2023 |
| Station | Time Lag (Day) | Correlation | Ske (10−3) | Station | Time Lag (Day) | Correlation | Ske (10−3) |
|---|---|---|---|---|---|---|---|
| Q1 | 46 | 0.45 | 2.32 ± 0.033 | Q11 | 192 | 0.37 | 6.53 ± 0.035 |
| Q2 | 54 | 0.57 | 2.02 ± 0.042 | Q12 | 33 | 0.64 | 3.24 ± 0.086 |
| Q3 | 21 | 0.62 | 1.21 ± 0.031 | Q13 | 55 | 0.43 | 2.36 ± 0.016 |
| Q4 | 15 | 0.58 | 2.34 ± 0.019 | Q14 | 129 | 0.39 | 2.65 ± 0.017 |
| Q5 | 133 | 0.66 | 4.48 ± 0.036 | Q15 | 45 | 0.76 | 15.27 ± 0.044 |
| Q6 | 27 | 0.58 | 1.02 ± 0.016 | Q16 | 61 | 0.57 | 11.04 ± 0.036 |
| Q7 | 19 | 0.53 | 3.45 ± 0.035 | Q17 | 47 | 0.71 | 13.82 ± 0.046 |
| Q8 | 18 | 0.74 | 1.77 ± 0.014 | Q18 | 23 | 0.67 | 2.42 ± 0.038 |
| Q9 | 26 | 0.66 | 1.78 ± 0.099 | Q19 | 127 | 0.47 | 5.08 ± 0.079 |
| Q10 | 22 | 0.71 | 1.90 ± 0.025 | Q20 | 5 | 0.88 | 2.69 ± 0.026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Zhang, X.; Hu, J.; Gui, R.; Yang, L. Estimation of Land Deformation and Groundwater Storage Dynamics in Shijiazhuang–Baoding–Cangzhou–Hengshui Using Multi-Temporal Interferometric Synthetic Aperture Radar. Remote Sens. 2024, 16, 1724. https://doi.org/10.3390/rs16101724
Yang Q, Zhang X, Hu J, Gui R, Yang L. Estimation of Land Deformation and Groundwater Storage Dynamics in Shijiazhuang–Baoding–Cangzhou–Hengshui Using Multi-Temporal Interferometric Synthetic Aperture Radar. Remote Sensing. 2024; 16(10):1724. https://doi.org/10.3390/rs16101724
Chicago/Turabian StyleYang, Qiuhong, Xing Zhang, Jun Hu, Rong Gui, and Liuming Yang. 2024. "Estimation of Land Deformation and Groundwater Storage Dynamics in Shijiazhuang–Baoding–Cangzhou–Hengshui Using Multi-Temporal Interferometric Synthetic Aperture Radar" Remote Sensing 16, no. 10: 1724. https://doi.org/10.3390/rs16101724
APA StyleYang, Q., Zhang, X., Hu, J., Gui, R., & Yang, L. (2024). Estimation of Land Deformation and Groundwater Storage Dynamics in Shijiazhuang–Baoding–Cangzhou–Hengshui Using Multi-Temporal Interferometric Synthetic Aperture Radar. Remote Sensing, 16(10), 1724. https://doi.org/10.3390/rs16101724






