Analysis of Lake Area Dynamics and Driving Forces in the Jianghan Plain Based on GEE and SEM for the Period 1990 to 2020
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Experimental Design
2.2. Data Source and Materials
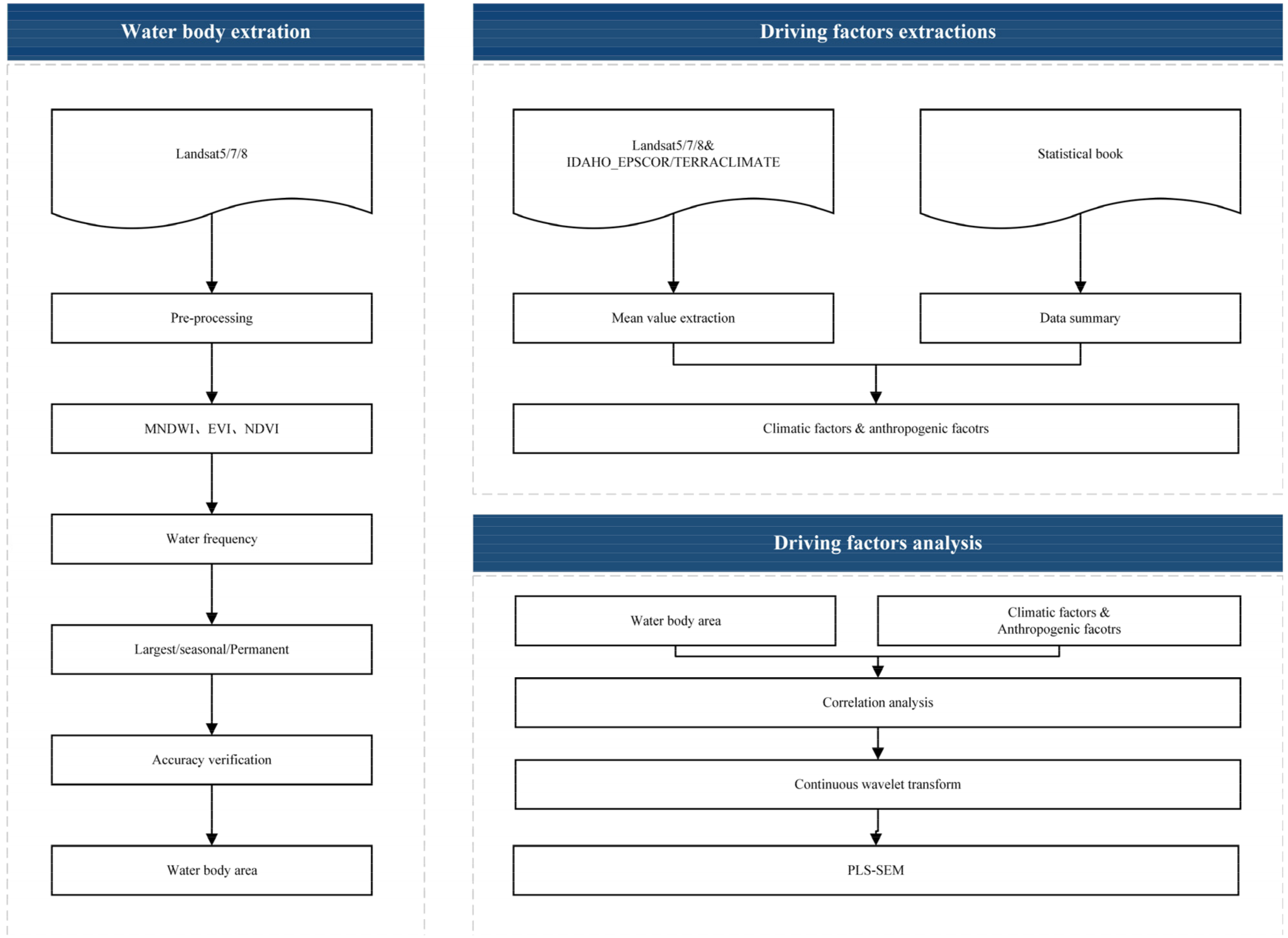
2.3. The Extraction of Lakes
2.4. Method of Obtaining the Driving Factor
2.5. Mann–Kendall Trend Test and Mutability Test
2.6. Continuous Wavelet Transform
2.7. Pearson Correlation Analysis and PLE-SEM
2.8. Conceptual Framework and Procedures of the Study
3. Results
3.1. Evaluation of Water Body Extraction Accuracy
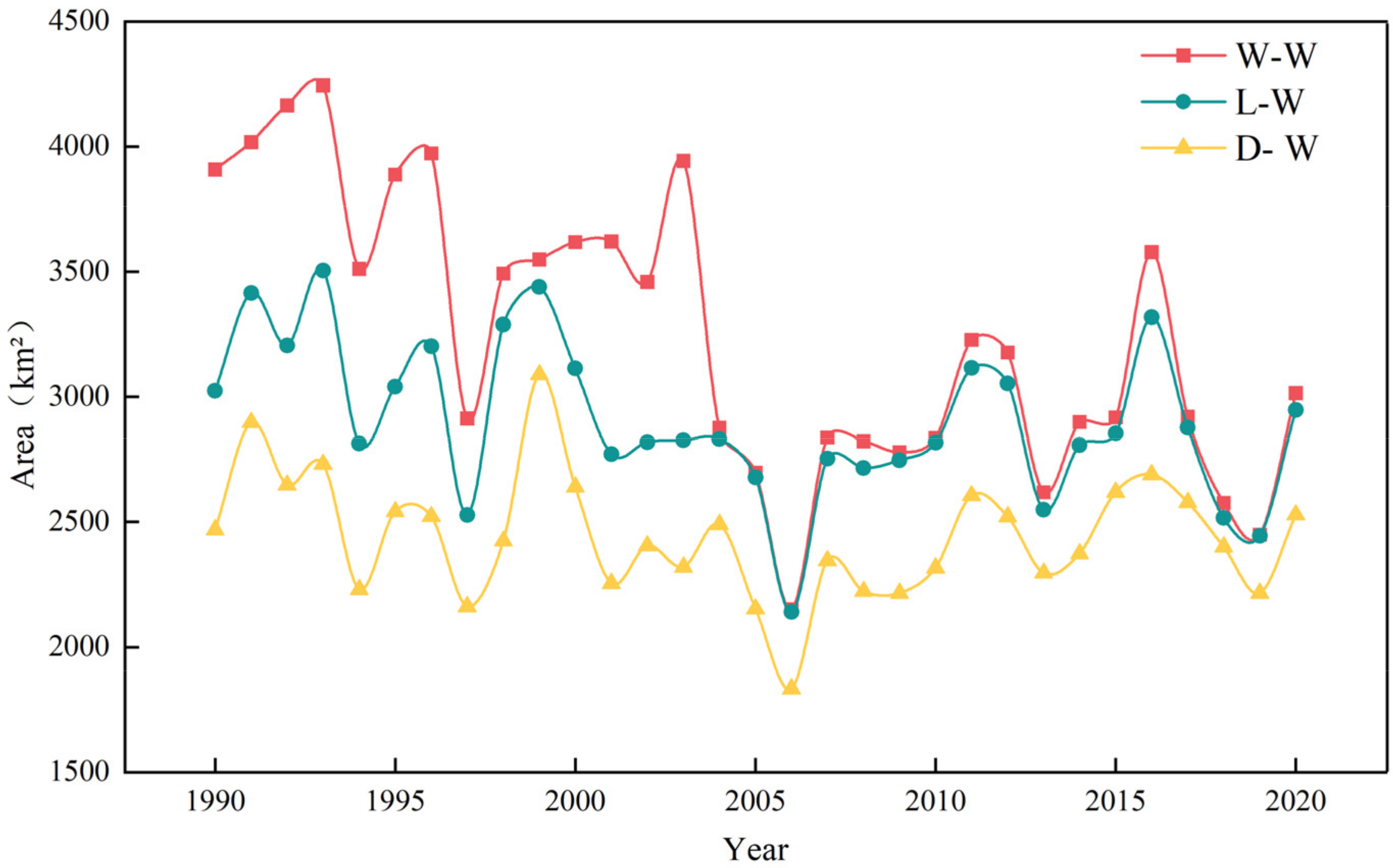
3.2. Characteristics of Changes in Area of the Lakes of Jianghan Plain
3.3. The Pearson Correlation between Changes in Lake Area and Driving Factors
3.3.1. The Pearson Correlation between the Area of the Wet Seasonal Lake and the Driving Factors
3.3.2. The Pearson Correlation between the Area of Level Seasonal Lakes and Driving Factors
3.3.3. The Pearson Correlation between the Area of Dry Seasonal Lakes and Driving Factors
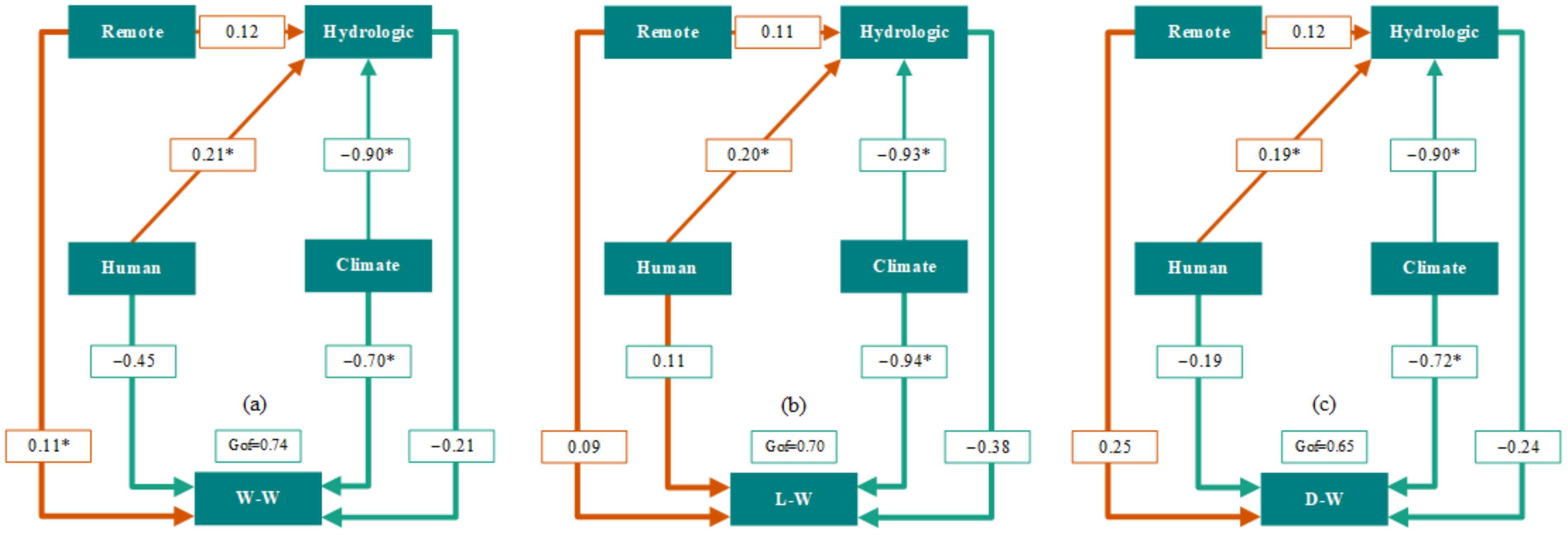
3.4. Drivers of Water Body Area Based on PLS-SEM
3.4.1. The Wet Seasonal Lake Structural Equation Model
3.4.2. The Level Seasonal Lake Structural Equation Model
3.4.3. The Dry Seasonal Lake Structural Equation Model
4. Discussion
4.1. Water Extraction
4.2. Driving Factors of Water Area Change
4.3. Applicability of Structural Equation Models
4.4. Limitations of the Study and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Van De Giesen, N. Earth’s Surface Water Change over the Past 30 Years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Jiang, Z.; Jiang, W.; Ling, Z.; Wang, X.; Peng, K.; Wang, C. Surface Water Extraction and Dynamic Analysis of Baiyangdian Lake Based on the Google Earth Engine Platform Using Sentinel-1 for Reporting SDG 6.6.1 Indicators. Water 2021, 13, 138. [Google Scholar] [CrossRef]
- Bo, Y.; Zhou, F.; Zhao, J.; Liu, J.; Liu, J.; Ciais, P.; Chang, J.; Chen, L. Additional Surface-Water Deficit to Meet Global Universal Water Accessibility by 2030. J. Clean. Prod. 2021, 320, 128829. [Google Scholar] [CrossRef]
- Koning, C.O. Vegetation Patterns Resulting from Spatial and Temporal Variability in Hydrology, Soils, and Trampling in an Isolated Basin Marsh, New Hampshire, USA. Wetlands 2005, 25, 239–251. [Google Scholar] [CrossRef]
- Robledano, F.; Esteve, M.A.; Farinós, P.; Carreño, M.F.; Martínez-Fernández, J. Terrestrial Birds as Indicators of Agricultural-Induced Changes and Associated Loss in Conservation Value of Mediterranean Wetlands. Ecol. Indic. 2010, 10, 274–286. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-Resolution Mapping of Global Surface Water and Its Long-Term Changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, F.; Shi, J.; Chan, N.W.; Cai, Y.; Cheng, C.; An, C.; Wang, W.; Liu, C. Analysis of Surface Water Area Dynamics and Driving Forces in the Bosten Lake Basin Based on GEE and SEM for the Period 2000 to 2021. Env. Sci. Pollut. Res. 2024, 31, 9333–9346. [Google Scholar] [CrossRef] [PubMed]
- Khandelwal, A.; Karpatne, A.; Marlier, M.E.; Kim, J.; Lettenmaier, D.P.; Kumar, V. An Approach for Global Monitoring of Surface Water Extent Variations in Reservoirs Using MODIS Data. Remote Sens. Environ. 2017, 202, 113–128. [Google Scholar] [CrossRef]
- Li, L.; Vrieling, A.; Skidmore, A.; Wang, T.; Turak, E. Monitoring the Dynamics of Surface Water Fraction from MODIS Time Series in a Mediterranean Environment. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 135–145. [Google Scholar] [CrossRef]
- Lu, S.; Jia, L.; Zhang, L.; Wei, Y.; Baig, M.H.A.; Zhai, Z.; Meng, J.; Li, X.; Zhang, G. Lake Water Surface Mapping in the Tibetan Plateau Using the MODIS MOD09Q1 Product. Remote Sens. Lett. 2017, 8, 224–233. [Google Scholar] [CrossRef]
- Ranghetti, L.; Busetto, L.; Crema, A.; Fasola, M.; Cardarelli, E.; Boschetti, M. Testing Estimation of Water Surface in Italian Rice District from MODIS Satellite Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 284–295. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, K.; Zhou, Y.; Liu, X.; Qin, B. Monitoring the River Plume Induced by Heavy Rainfall Events in Large, Shallow, Lake Taihu Using MODIS 250m Imagery. Remote Sens. Environ. 2016, 173, 109–121. [Google Scholar] [CrossRef]
- Jia, K.; Jiang, W.; Li, J.; Tang, Z. Spectral Matching Based on Discrete Particle Swarm Optimization: A New Method for Terrestrial Water Body Extraction Using Multi-Temporal Landsat 8 Images. Remote Sens. Environ. 2018, 209, 1–18. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M. Spatiotemporal Patterns and Effects of Climate and Land Use on Surface Water Extent Dynamics in a Dryland Region with Three Decades of Landsat Satellite Data. Sci. Total Environ. 2019, 658, 1574–1585. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Chen, Y.; Xu, T.; Liu, R.; Shi, K.; Huang, C. Super-Resolution Mapping of Wetland Inundation from Remote Sensing Imagery Based on Integration of Back-Propagation Neural Network and Genetic Algorithm. Remote Sens. Environ. 2015, 164, 142–154. [Google Scholar] [CrossRef]
- Wang, X.; Xie, S.; Zhang, X.; Chen, C.; Guo, H.; Du, J.; Duan, Z. A Robust Multi-Band Water Index (MBWI) for Automated Extraction of Surface Water from Landsat 8 OLI Imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 73–91. [Google Scholar] [CrossRef]
- Hardy, A.; Ettritch, G.; Cross, D.; Bunting, P.; Liywalii, F.; Sakala, J.; Silumesii, A.; Singini, D.; Smith, M.; Willis, T.; et al. Automatic Detection of Open and Vegetated Water Bodies Using Sentinel 1 to Map African Malaria Vector Mosquito Breeding Habitats. Remote Sens. 2019, 11, 593. [Google Scholar] [CrossRef]
- Schwatke, C.; Scherer, D.; Dettmering, D. Automated Extraction of Consistent Time-Variable Water Surfaces of Lakes and Reservoirs Based on Landsat and Sentinel-2. Remote Sens. 2019, 11, 1010. [Google Scholar] [CrossRef]
- Steinhausen, M.J.; Wagner, P.D.; Narasimhan, B.; Waske, B. Combining Sentinel-1 and Sentinel-2 Data for Improved Land Use and Land Cover Mapping of Monsoon Regions. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 595–604. [Google Scholar] [CrossRef]
- Wang, C.; Jia, M.; Chen, N.; Wang, W. Long-Term Surface Water Dynamics Analysis Based on Landsat Imagery and the Google Earth Engine Platform: A Case Study in the Middle Yangtze River Basin. Remote Sens. 2018, 10, 1635. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Oliphant, A.J.; Thenkabail, P.S.; Teluguntla, P.; Xiong, J.; Gumma, M.K.; Congalton, R.G.; Yadav, K. Mapping Cropland Extent of Southeast and Northeast Asia Using Multi-Year Time-Series Landsat 30-m Data Using a Random Forest Classifier on the Google Earth Engine Cloud. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 110–124. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine Applications Since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef]
- Hird, J.; DeLancey, E.; McDermid, G.; Kariyeva, J. Google Earth Engine, Open-Access Satellite Data, and Machine Learning in Support of Large-Area Probabilistic Wetland Mapping. Remote Sens. 2017, 9, 1315. [Google Scholar] [CrossRef]
- Ismail, M.A.; Waqas, M.; Ali, A.; Muzzamil, M.M.; Abid, U.; Zia, T. Enhanced Index for Water Body Delineation and Area Calculation Using Google Earth Engine: A Case Study of the Manchar Lake. J. Water Clim. Chang. 2022, 13, 557–573. [Google Scholar] [CrossRef]
- Zou, Z.; Xiao, X.; Dong, J.; Qin, Y.; Doughty, R.B.; Menarguez, M.A.; Zhang, G.; Wang, J. Divergent Trends of Open-Surface Water Body Area in the Contiguous United States from 1984 to 2016. Proc. Natl. Acad. Sci. USA 2018, 115, 3810–3815. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.R.; Li, M.; Wang, G.W. Characterizing Surface Water Changes across the Tibetan Plateau Based on Landsat Time Series and LandTrendr Algorithm. Eur. J. Remote Sens. 2022, 55, 251–262. [Google Scholar] [CrossRef]
- Deng, Y.; Jiang, W.; Tang, Z.; Ling, Z.; Wu, Z. Long-Term Changes of Open-Surface Water Bodies in the Yangtze River Basin Based on the Google Earth Engine Cloud Platform. Remote Sens. 2019, 11, 2213. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M.; Stehman, S.V.; Kommareddy, A. Surface Water Extent Dynamics from Three Decades of Seasonally Continuous Landsat Time Series at Subcontinental Scale in a Semi-Arid Region. Remote Sens. Environ. 2016, 178, 142–157. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, S.; Qin, X.; Zhao, N.; Liang, L. Mapping of Urban Surface Water Bodies from Sentinel-2 MSI Imagery at 10 m Resolution via NDWI-Based Image Sharpening. Remote Sens. 2017, 9, 596. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Ling, F.; Liu, Y.; Fang, F. Spatio-Temporal Change Detection of Ningbo Coastline Using Landsat Time-Series Images during 1976–2015. ISPRS Int. J. Geo-Inf. 2017, 6, 68. [Google Scholar] [CrossRef]
- Cavallo, C.; Papa, M.N.; Gargiulo, M.; Palau-Salvador, G.; Vezza, P.; Ruello, G. Continuous Monitoring of the Flooding Dynamics in the Albufera Wetland (Spain) by Landsat-8 and Sentinel-2 Datasets. Remote Sens. 2021, 13, 3525. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A New Technique for Surface Water Mapping Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 Algorithms in Data Mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Assoc Comp Machinery XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Belgiu, M.; Dragut, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, J.; Xiao, X.; Liu, R.; Zou, Z.; Zhao, G.; Ge, Q. Continuous Monitoring of Lake Dynamics on the Mongolian Plateau Using All Available Landsat Imagery and Google Earth Engine. Sci. Total Environ. 2019, 689, 366–380. [Google Scholar] [CrossRef] [PubMed]
- Shipley, B. A New Inferential Test for Path Models Based on Directed Acyclic Graphs. Struct. Equ. Model. A Multidiscip. J. 2000, 7, 206–218. [Google Scholar] [CrossRef]
- Tenenhaus, M.; Amato, S.; Vinzi, V.E. A Global Goodness-of-Fit Index for PLS Structural Equation Modelling. Proc. XLII SIS Sci. Meet. 2004, 1, 739–742. [Google Scholar]
- Wang, W.; Zhang, F.; Zhao, Q.; Liu, C.; Jim, C.Y.; Johnson, V.C.; Tan, M.L. Determining the Main Contributing Factors to Nutrient Concentration in Rivers in Arid Northwest China Using Partial Least Squares Structural Equation Modeling. J. Environ. Manag. 2023, 343, 118249. [Google Scholar] [CrossRef] [PubMed]
- Hair, J.F.; Ringle, C.M.; Sarstedt, M. PLS-SEM: Indeed a Silver Bullet. J. Mark. Theory Pract. 2011, 19, 139–152. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, M.; Wang, D.; Zhang, Y.; Shang, B.; Ma, X. Applying Social Cognitive Theory in Predicting Physical Activity Among Chinese Adolescents: A Cross-Sectional Study With Multigroup Structural Equation Model. Front. Psychol. 2022, 12, 695241. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ma, L.; Zhang, Y.; Chen, N.; Wang, W. Spatiotemporal Dynamics of Wetlands and Their Driving Factors Based on PLS-SEM: A Case Study in Wuhan. Sci. Total Environ. 2022, 806, 151310. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, T.; Chandran, V.G.R.; Klobas, J.E.; Liñán, F.; Kokkalis, P. Entrepreneurship Education Programmes: How Learning, Inspiration and Resources Affect Intentions for New Venture Creation in a Developing Economy. Int. J. Manag. Educ. 2020, 18, 100327. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, F.; Tan, M.L.; Kung, H.-T.; Shi, J.; Zhao, Q.; Wang, W.; Duan, P.; An, C.; Cai, Y.; et al. Characteristics of Dissolved Organic Matter and Its Relationship with Water Quality along the Downstream of the Kaidu River in China. Water 2022, 14, 3544. [Google Scholar] [CrossRef]
- Chang, T.; Li, J.; Guo, X.; Li, Y. The Spatial-Temporal Characteristics and Driving Forces Analysis of Water Area Landscape Pattern Changes on the Jianghan Plain. Adv. Water Sci. 2023, 34, 21–32. [Google Scholar]
- Wei, W.; Tang, L.; Ma, R. Evolution and Controlling Factors of Wetlands in Jianghan Plain. Saf. Environ. Eng. 2021, 28, 25–33. [Google Scholar]
- Feng, W.; Feng, C.; Chen, J. Effect of Human Activities and Association Rules Mining on Spatiotemporal Evolution in Jianghan Lake Group. J. Appl. Sci. 2018, 36, 958–968. [Google Scholar]
- Song, L.; Song, C.; Luo, S.; Chen, T.; Liu, K.; Zhang, Y.; Ke, L. Integrating ICESat-2 Altimetry and Machine Learning to Estimate the Seasonal Water Level and Storage Variations of National-Scale Lakes in China. Remote Sens. Environ. 2023, 294, 113657. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Beguería, S.; López-Moreno, J. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Wang, B.; Wu, R.; Lau, K. Interannual Variability of the Asian Summer Monsoon: Contrasts between the Indian and the Western North Pacific-East Asian Monsoons. J. Clim. 2001, 14, 4073–4090. [Google Scholar] [CrossRef]
- Li, J.; Zeng, Q. A Unified Monsoon Index. Geophys. Res. Lett. 2002, 29, 115. [Google Scholar] [CrossRef]
- Hurrell, J. Decadal trends in the north-atlantic oscillation—Regional temperatures and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
- Enfield, D.; Mestas-Nuñez, A.; Trimble, P. The Atlantic Multidecadal Oscillation and Its Relation to Rainfall and River Flows in the Continental US. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, Z.; Chen, B.; Gong, P.; Xu, B.; Fu, H. A Prolonged Artificial Nighttime-Light Dataset of China (1984–2020). Sci. Data 2024, 11, 414. [Google Scholar] [CrossRef] [PubMed]
- Zha, Y.; Gao, J.; Ni, S. Use of Normalized Difference Built-up Index in Automatically Mapping Urban Areas from TM Imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Chen, T.; Song, C.; Fan, C.; Cheng, J.; Duan, X.; Wang, L.; Liu, K.; Deng, S.; Che, Y. A Comprehensive Data Set of Physical and Human-Dimensional Attributes for China’s Lake Basins. Sci. Data 2022, 9, 519. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Determining the Most Accurate Program for the Mann-Kendall Method in Detecting Climate Mutation. Theor. Appl. Clim. 2020, 142, 847–854. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; He, H.; Xu, J.; Jin, Y. Detecting Global Vegetation Changes Using Mann-Kendal (MK) Trend Test for 1982–2015 Time Period. Chin. Geogr. Sci. 2018, 28, 907–919. [Google Scholar] [CrossRef]
- Martínez, B.; Gilabert, M.A. Vegetation Dynamics from NDVI Time Series Analysis Using the Wavelet Transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
- Quiroz, R. Improving Daily Rainfall Estimation from NDVI Using a Wavelet Transform. Environ. Model. 2011, 26, 201–209. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, S.; Liu, Y.; Tian, L. Identifying the Urban-Rural Fringe Using Wavelet Transform and Kernel Density Estimation: A Case Study in Beijing City, China. Environ. Model. Softw. 2016, 83, 286–302. [Google Scholar] [CrossRef]
- Yu, T.; Abulizi, A.; Xu, Z.; Jiang, J.; Akbar, A.; Ou, B.; Xu, F. Evolution of Environmental Quality and Its Response to Human Disturbances of the Urban Agglomeration in the Northern Slope of the Tianshan Mountains. Ecol. Indic. 2023, 153, 110481. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall Test Modified by Effective Sample Size to Detect Trend in Serially Correlated Hydrological Series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Jöreskog, K.G.; Sörbom, D. Recent Developments in Structural Equation Modeling. J. Mark. Res. 1982, 19, 404–416. [Google Scholar] [CrossRef]
- Gómez, C.; White, J.C.; Wulder, M.A. Optical Remotely Sensed Time Series Data for Land Cover Classification: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. A Meta-Analysis of Remote Sensing Research on Supervised Pixel-Based Land-Cover Image Classification Processes: General Guidelines for Practitioners and Future Research. Remote Sens. Environ. 2016, 177, 89–100. [Google Scholar] [CrossRef]
- Ksenak, L.; Pukanska, K.; Bartos, K.; Blistan, P. Assessment of the Usability of SAR and Optical Satellite Data for Monitoring Spatio-Temporal Changes in Surface Water: Bodrog River Case Study. Water 2022, 14, 299. [Google Scholar] [CrossRef]
- Lai, X.; Jiang, J.; Huang, Q. Water Storage Effects of Three Gorges Project on Water Regime of Poyang Lake. J. Hydroelectr. Eng. 2012, 31, 132–136+148. [Google Scholar]
- Tian, B.; Wu, C.; Mu, X.; Gao, P.; Zhao, G.; Yin, D. Analysis on the Characteristics and Driving Factors of Water Area Change in Poyang Lake During Flood Season Under Long Time Series. Res. Soil. Water Conserv. 2021, 28, 212–217. [Google Scholar]
- Wu, C.; Tian, B.; Gao, P.; Mu, X.; Zhao, G.; Yin, D. Characteristics and Driving Factors of Water Area Change of Poyang Lake During Dry Season in Recent 40Years. J. Soil Water Conserv. 2021, 35, 177–184+189. [Google Scholar]
- Wang, J.; Li, M.; Wang, L.; She, J.; Zhu, L.; Li, X. Long-Term Lake Area Change and Its Relationship with Climate in the Endorheic Basins of the Tibetan Plateau. Remote Sens. 2021, 13, 5125. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, S.; Wang, G.; Wang, H. Quantitative Assessment of Water Stage Changes of Poyang Lake in Dry Period and Its Influencing Factors. J. Hydroelectr. Eng. 2020, 39, 1–10. [Google Scholar]
- Guo, Z.; Huang, F.; Guo, L.; Wu, Y. Study on Driving Factors of Temporal and Spatial Evolution of Water Level in Poyang Lake. J. Hydroelectr. Eng. 2020, 39, 25–36. [Google Scholar]



| Factor Type | Driving Factor | Resolution | Data Sources | Date |
|---|---|---|---|---|
| Human factor | Gross domestic product (GDP) | https://data.cnki.net/yearbook | 1990–2020 | |
| Human factor | Population (POP) | https://data.cnki.net/yearbook | 1990–2020 | |
| Human factor | Crop area (CROP) | https://data.cnki.net/yearbook | 1990–2020 | |
| Human factor | Night light index (LIGHTS) | 1000 m | https://poles.tpdc.ac.cn/ | 1990–2020 |
| Human factor | Normalized difference vegetation index (NDVI) | 30 m | https://landsat.gsfc.nasa.gov/ | 1990–2020 |
| Human factor | Normalized difference Built-up index (NDBI) | 30 m | https://landsat.gsfc.nasa.gov/ | 1990–2020 |
| Climatic factor | Actual evapotranspiration (AET) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Climate water deficit (DEF) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Drought severity index (PDSI) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Maximum temperature (TMMX) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Minimum temperature (TMMN) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Cumulative precipitation (PR) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Reference evapotranspiration (PET) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Climatic factor | Vapor pressure deficit (VPD) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Hydrologic factor | Runoff (RO) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Hydrologic factor | Soil moisture content (SOIL) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Hydrologic factor | Downward surface shortwave radiation (SRAD) | 4638.3 m | Earth Engine’s public data/IDAHO_EPSCOR/ TERRACLIMATE | 1990–2020 |
| Remote factor | Indian Summer Monsoon Index (ISM) | http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html; | 1990–2020 | |
| Remote factor | Western North Pacific Monsoon Index (WNP) | http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html; | 1990–2020 | |
| Remote factor | East Asian summer monsoon Index (EASM) | http://ljp.gcess.cn/dct/page/1 | 1990–2020 | |
| Remote factor | North Atlantic oscillation (NAO) | https://psl.noaa.gov/data/correlation/nao.data | 1990–2020 | |
| Remote factor | Atlantic Multidecadal Oscillation (AMO) | https://psl.noaa.gov/data/correlation/amon.us.data | 1990–2020 |
| Samples | Google Earth | Total | User’s Accuracy | ||
|---|---|---|---|---|---|
| Water | Non-Water | ||||
| Landsat | Water body | 943 | 57 | 1000 | 94.30% |
| Non-water body | 60 | 940 | 1000 | 94.00% | |
| Total | 1003 | 997 | 2000 | Overall accuracy = 94.15% | |
| Producer’s accuracy | 94.02% | 94.28% | Kappa coefficient = 0.861 | ||
| Name | Block | W-W | L-W | D-W |
|---|---|---|---|---|
| GDP | Human | 0.323 | 0.276 | 0.154 |
| LIGHTS | Human | 0.529 | 0.547 | 0.742 |
| NDVI | Human | 0.221 | 0.254 | 0.159 |
| EASM | Remote | 1.000 | 1.000 | 1.000 |
| PDSI | Climate | −0.232 | 0.210 | 0.210 |
| TMMX | Climate | 0.178 | −0.172 | −0.156 |
| TMMN | Climate | 0.134 | −0.124 | −0.113 |
| PR | Climate | −0.202 | 0.229 | 0.230 |
| PET | Climate | 0.263 | −0.273 | −0.278 |
| VPD | Climate | 0.258 | −0.257 | −0.270 |
| SOIL | Hydrologic | 0.296 | 0.282 | 0.284 |
| RO | Hydrologic | 0.453 | 0.465 | 0.454 |
| SRAD | Hydrologic | −0.375 | −0.376 | −0.385 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, M.; Liu, Y. Analysis of Lake Area Dynamics and Driving Forces in the Jianghan Plain Based on GEE and SEM for the Period 1990 to 2020. Remote Sens. 2024, 16, 1892. https://doi.org/10.3390/rs16111892
He M, Liu Y. Analysis of Lake Area Dynamics and Driving Forces in the Jianghan Plain Based on GEE and SEM for the Period 1990 to 2020. Remote Sensing. 2024; 16(11):1892. https://doi.org/10.3390/rs16111892
Chicago/Turabian StyleHe, Minghui, and Yi Liu. 2024. "Analysis of Lake Area Dynamics and Driving Forces in the Jianghan Plain Based on GEE and SEM for the Period 1990 to 2020" Remote Sensing 16, no. 11: 1892. https://doi.org/10.3390/rs16111892
APA StyleHe, M., & Liu, Y. (2024). Analysis of Lake Area Dynamics and Driving Forces in the Jianghan Plain Based on GEE and SEM for the Period 1990 to 2020. Remote Sensing, 16(11), 1892. https://doi.org/10.3390/rs16111892







