Evaluating the Performance of the Enhanced Ross-Li Models in Characterizing BRDF/Albedo/NBAR Characteristics for Various Land Cover Types in the POLDER Database
Abstract
:1. Introduction
2. Materials and Methods
2.1. POLDER BRDF Database
2.2. Enhanced Ross-Li BRDF Models
2.3. Evaluation Methods of the Enhanced Ross-Li Models
3. Results and Analysis
3.1. Evaluating the Enhanced Ross-Li Models to Characterize the BRDF Characteristics
3.2. Analysis of BRDF Parameter Characteristics of the Enhanced Ross-Li Models
3.3. Comparison of Albedo Retrieval Results Using the Enhanced Ross-Li Models
3.4. Comparative Analysis of NBAR Inversion Results from the Enhanced Ross-Li Models
4. Discussion
5. Conclusions
- (1)
- Both enhanced Ross-Li models exhibit high fitting accuracy in characterizing the POLDER BRDF characteristics across 16 land cover types. However, for SI, the RTLSRC model demonstrates relatively poor fitting accuracy (RMSE = ~0.056). In contrast, the RTLSRCS model demonstrates a notable enhancement in accuracy compared to the RTLSRC model (RMSE = ~0.030), with the RTLSRCS model reducing the NRMSE values by approximately 2.34%. For DNF and BSV, the RTLSRCS model exhibits noticeable improvements over the RTLSRC model, with the overall NRMSE decreasing by 0.43% and 0.37%, respectively. For other land cover types, the improvement in fitting accuracy of the RTLSRCS model relative to the RTLSRC model is limited. While the RTLSRCS model is suitable for various IGBP types, the accuracy of the RTLSRC model is notably reduced for IGBP types with high reflectance and strong forward reflection characteristics.
- (2)
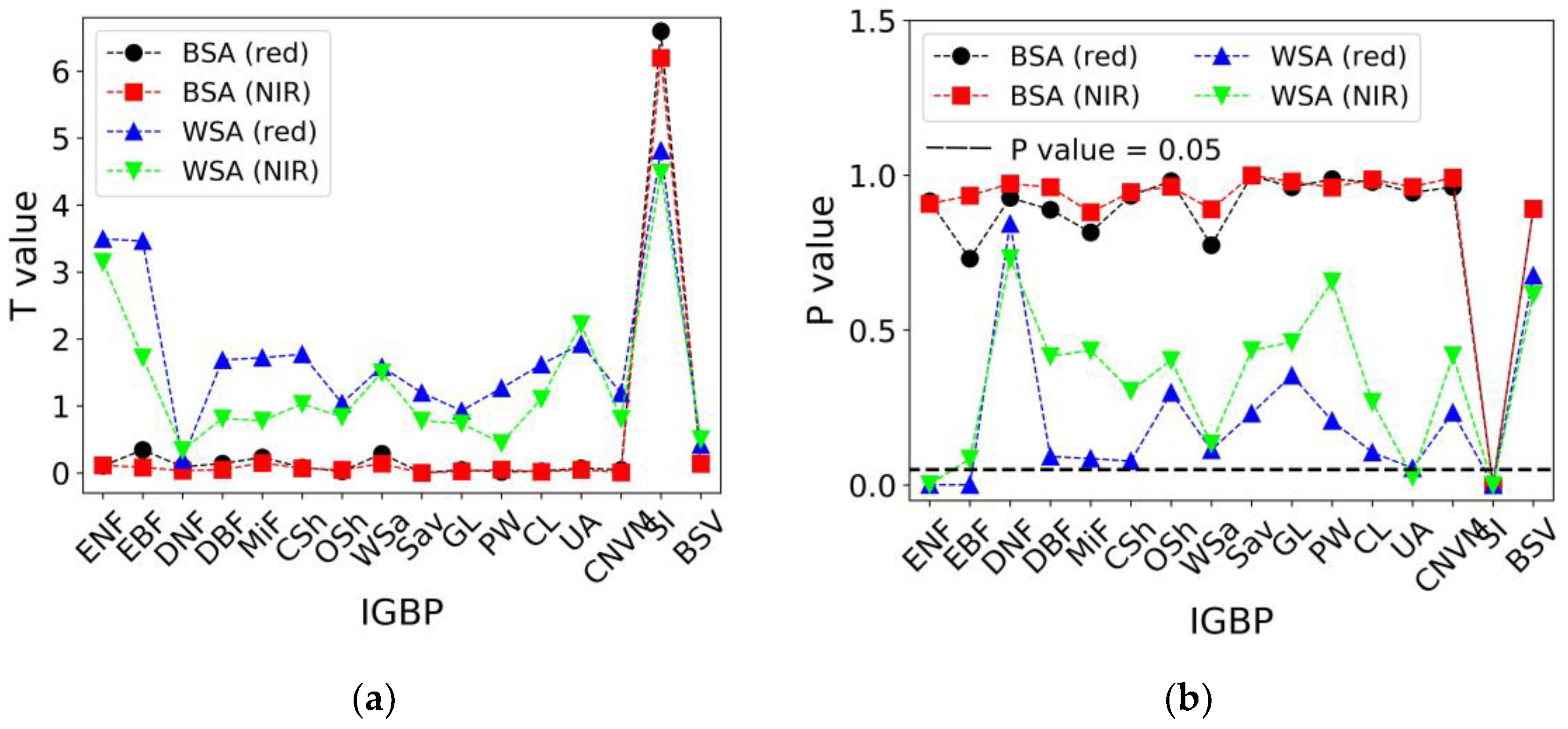
- The RTLSRC and RTLSRCS models exhibit highly consistent albedo inversion across various land cover types (R2 > 0.9), particularly in BSA and blue-sky albedo, except for SI. However, significant differences in shortwave WSA inversion persist between these two models for ENF, EBF, Csh, WSa, CL, UA, and SI (p < 0.05), with NRMSE values of approximately 8.2%, 3.7%, 6.1%, 3.4%, 3.0%, 5.5%, and 3.3%, respectively. Additionally, compared to the RTLSRCS model, the RTLSRC model demonstrates a notable underestimation in albedo inversion for SI, with an approximate underestimation of 0.013 in shortwave blue-sky albedo inversion.
- (3)
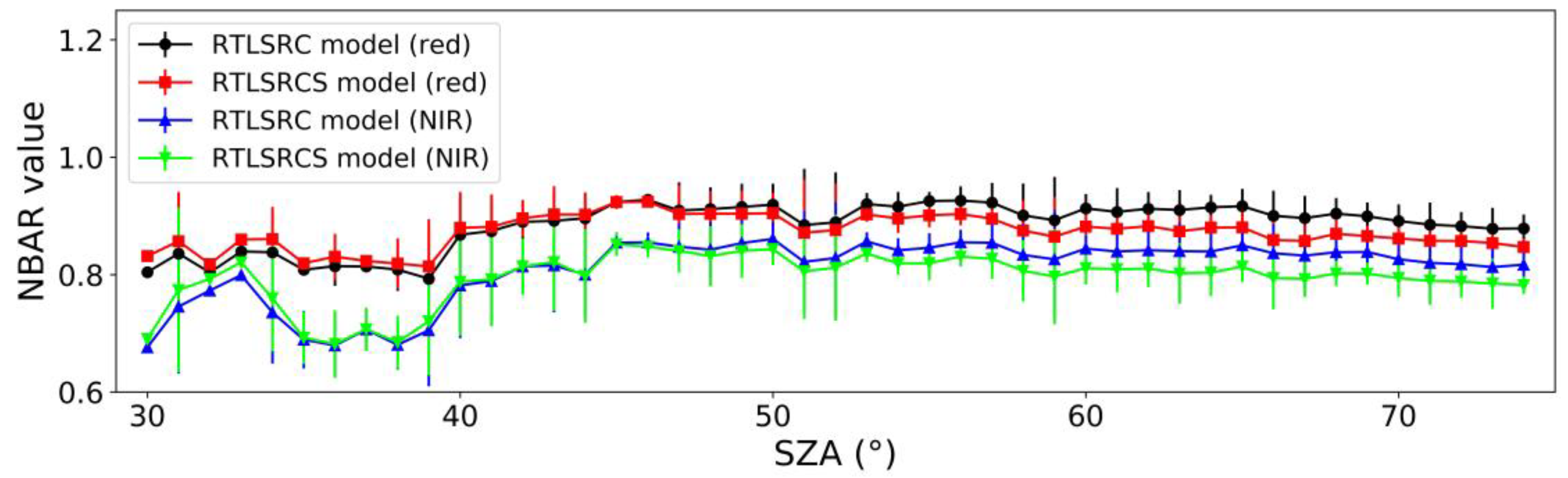
- The NABAR values inverted by these two models are nearly identical across the other 15 land cover types. However, the consistency of NBAR results between these two models is relatively poor for SI. Overall, the RTLSRC model tends to overestimate compared to the RTLSRCS model, with a noticeable bias of approximately 0.024. In addition, these two models show significant differences in the inverted NBAR values with varying SZA (p < 0.05). Therefore, the RTLSRCS model is suitable for characterizing the BRDF/Albedo/NBAR characteristics across various IGBP types. Conversely, using the RTLSRC model is not recommended for characterizing BRDF/Albedo/NBAR features for SI, as the model is not suitable for this land cover type.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jacquemoud, S. Inversion of the PROSPECT + SAIL canopy reflectance model from AVIRIS equivalent spectra, theoretical study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Jacquemoud, S. Modeling spectral and bidirectional soil reflectance. Remote Sens. Environ. 1992, 41, 123–132. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.; Deschamps, P.Y. A bidirectional reflectance model of the earths surface for the correction of remote-sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Dong, Y.; Qu, Y.; Zhang, X.; Xiong, C.; He, D.; Yin, S.; Cui, L.; Chang, Y. An assessment of the performance of two snow kernels in characterizing snow scattering properties. Int. J. Remote Sens. 2019, 40, 6315–6335. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Dong, Y.; Zhang, X.; Peltoniemi, J.I.; Mei, L.; Guo, J.; Yin, S.; Chang, Y.; Xie, R. Evaluation of the snow albedo retrieved from the snow kernel improved the Ross-Roujean BRDF model. Remote Sens. 2019, 11, 1611. [Google Scholar] [CrossRef]
- Bablet, A.; Vu, P.V.H.; Jacquemoud, S.; Viallefont-Robinet, F.; Fabre, S.; Briottet, X.; Sadeghi, M.; Whiting, M.L.; Baret, F.; Tian, J. MARMIT: A multilayer radiative transfer model of soil reflectance to estimate surface soil moisture content in the solar domain 400–2500 nm. Remote Sens. Environ. 2018, 217, 1–17. [Google Scholar] [CrossRef]
- Jiao, Z.; Dong, Y.; Schaaf, C.B.; Chen, J.M.; Román, M.; Wang, Z.; Zhang, H.; Ding, A.; Erb, A.; Hill, M.J.; et al. An algorithm for the retrieval of the clumping index (CI) from the MODIS BRDF product using an adjusted version of the kernel-driven BRDF model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Bréon, F.; Maignan, F. A BRDF-BPDF database for the analysis of Earth target reflectances. Earth Syst. Sci. Data 2017, 9, 31–45. [Google Scholar] [CrossRef]
- Gatebe, C.K.; King, M.D. Airborne spectral BRDF of various surface types (ocean, vegetation, snow, desert, wetlands, cloud decks, smoke layers) for remote sensing applications. Remote Sens. Environ. 2016, 179, 131–148. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Ding, A.; Ma, H.; Liang, S.; He, T. Extension of the Hapke model to the spectral domain to characterize soil physical properties. Remote Sens. Environ. 2022, 269, 112843. [Google Scholar] [CrossRef]
- Bréon, F.; Vermote, E. Correction of MODIS surface reflectance time series for BRDF effects. Remote Sens. Environ. 2012, 125, 1–9. [Google Scholar] [CrossRef]
- He, T.; Liang, S.; Wang, D.; Cao, Y.; Min, F. Evaluating land surface albedo estimation from Landsat MSS, TM, ETM+, and OLI data based on the unified direct estimation approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Sun, Q.; Erb, A.M.; Li, Z.; Schaaf, C.B.; Zhang, X.; Román, M.O.; Scott, R.L.; Zhang, Q.; et al. Evaluation of the VIIRS BRDF, Albedo and NBAR products suite and an assessment of continuity with the long-term MODIS record. Remote Sens. Environ. 2017, 201, 256–274. [Google Scholar] [CrossRef]
- Jiao, Z.; Hill, M.J.; Schaaf, B.C.; Zhang, H.; Wang, Z.; Li, X. An Anisotropic Flat Index (AFX) to derive BRDF archetypes from MODIS. Remote Sens. Environ. 2014, 141, 168–187. [Google Scholar] [CrossRef]
- Dupiau, A.; Jacquemoud, S.; Briottet, X.; Fabre, S.; Viallefont-Robinet, F.; Philpot, W.; Di Biagio, C.; Hébert, M.; Formenti, P. MARMIT-2: An improved version of the MARMIT model to predict soil reflectance as a function of surface water content in the solar domain. Remote Sens. Environ. 2022, 272, 112951. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy 1. Theory. J. Geophys. Res. 1981, 4, 3039–3054. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy 7. The single particle phase function hockey stick relation. Icarus 2012, 221, 1079–1083. [Google Scholar] [CrossRef]
- Jiang, C.; Fang, H. GSV: A general model for hyperspectral soil reflectance simulation. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101932. [Google Scholar] [CrossRef]
- Verhoef, W.; Christiaan, V.; Middleton, E.M. Hyperspectral radiative transfer modeling to explore the combined retrieval of biophysical parameters and canopy fluorescence from FLEX-Sentinel-3 tandem mission multi-sensor data. Remote Sens. Environ. 2018, 204, 942–963. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F. PROSPECT+SAIL models, A review of use for vegetation characterization. Remote Sens. Environ. 2009, 1131, 56–66. [Google Scholar] [CrossRef]
- Ding, A.; Liang, S.; Jiao, Z.; Ma, H.; Kokhanovsky, A.A.; Peltoniemi, J.I. Improving the asymptotic radiative transfer model to better characterize the pure snow hyperspectral bidirectional reflectance. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4303916. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Bréon, F.M. Validation of an analytical snow BRDF model using parasol multi-angular and multispectral observations. IEEE Trans. Geosci. Remote Sens. 2012, 9, 928–932. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Lamare, M.; Di Mauro, B.; Picard, G.; Arnaud, L.; Dumont, M.; Tuzet, F.; Brockmann, C.; Box, J.E. On the reflectance spectroscopy of snow. Cryosphere 2018, 12, 2371–2382. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Xiong, C.; Shi, J. Simulating polarized light scattering in terrestrial snow based on bicontinuous random medium and monte carlo ray tracing. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 177–189. [Google Scholar] [CrossRef]
- Kimmel, B.W.; Baranoski, G.V.G. A novel approach for simulating light interaction with particulate materials, application to the modeling of sand spectral properties. Opt. Express 2007, 15, 9755–9777. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, W.S.; Zhang, H. A seven-parameter BRDF model with double-peak characteristic suitable for sandy soil. Math. Probl. Eng. 2018, 2018, 9398608. [Google Scholar] [CrossRef]
- Han, Z.; Gu, X.; Zuo, X.; Bi, K.; Shi, S. Semi-empirical models for the bidirectional water-leaving radiance, an analysis of a turbid inland lake. Front. Environ. Sci. 2022, 9, 818557. [Google Scholar] [CrossRef]
- Kuusk, A. A two-layer canopy reflectance model. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 1–9. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.P.; Li, L. LESS, large-scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2018, 221, 695–706. [Google Scholar] [CrossRef]
- Chen, S.; Xiao, P.; Zhang, X.; Qi, J.; Yin, G.; Ma, W.; Liu, H. Simulating snow-covered forest bidirectional reflectance by extending hybrid geometric optical–radiative transfer model. Remote Sens. Environ. 2023, 296, 113713. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, A.; Kokhanovsky, A.; Schaaf, C.; Bréon, F.; Dong, Y.; Wang, Z.; Liu, Y.; Zhang, X.; Yin, S.; et al. Development of a snow kernel to better model the anisotropic reflectance of pure snow in a kernel-driven BRDF model framework. Remote Sens. Environ. 2019, 55, 198–209. [Google Scholar] [CrossRef]
- Qu, Y.; Liang, S.; Liu, Q.; Li, X.; Feng, Y.; Liu, S. Estimating Arctic sea-ice shortwave albedo from MODIS data. Remote Sens. Environ. 2016, 186, 32–46. [Google Scholar] [CrossRef]
- Jiao, Z.; Schaaf, C.B.; Dong, Y.; Román, M.; Hill, M.J.; Chen, J.M.; Wang, Z.; Zhang, H.; Saenz, E.; Poudyal, R.; et al. A method for improving hotspot directional signatures in BRDF models used for MODIS. Remote Sens. Environ. 2016, 186, 135–151. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Ding, A.; Zhang, H.; Zhang, X.; Li, Y.; He, D.; Yin, S.; Cui, L. A modified version of the kernel-driven model for correcting the diffuse light of ground multi-angular measurements. Remote Sens. Environ. 2018, 210, 325–344. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Dong, Y.; Zhang, H.; Li, Y.; He, D.; Ding, A.; Yin, S.; Cui, L.; Chang, Y. Potential investigation of linking PROSAIL with the Ross-Li BRDF model for vegetation characterization. Remote Sens. 2018, 10, 421–437. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Cui, L.; Zhang, H.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Xie, R.; Guo, J. Assessment of the hotspot effect for the PROSAIL model with POLDER hotspot observations based on the hotspot-enhanced kernel-driven BRDF model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8048–8064. [Google Scholar] [CrossRef]
- Wu, S.; Wen, J.; Xiao, Q.; Liu, Q.; Hao, D.; Lin, X.; You, D. Derivation of kernel functions for kernel-driven reflectance model over sloping terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 396–409. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Zhang, X.; Dong, Y.; Kokhanovsky, A.A.; Guo, J.; Jiang, H. A practical approach to improve the MODIS MCD43A products in snow-covered areas. J. Remote Sens. 2023, 3, 0057. [Google Scholar] [CrossRef]
- Lacaze, R.; Fédèle, E.; Bréon, F.M. POLDER-3/PARASOL BRDF Databases User Manual. 2009. Available online: https://scholar.google.com/scholar_lookup?title=POLDER-3%2FPARASOL%20BRDF%20Databases%20User%20Manual&author=R.%20Lacaze&publication_year=2009 (accessed on 10 April 2024).
- Yang, P. Exploring the interrelated effects of soil background, canopy structure and sun-observer geometry on canopy photochemical reflectance index. Remote Sens. Environ. 2022, 279, 113133. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo: I. algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo, II. validation. Remote Sens. Environ. 2003, 84, 25–41. [Google Scholar] [CrossRef]
- Jiao, Z.; Zhang, X.; Bréon, F.; Dong, Y.; Schaaf, C.B.; Román, M.; Wang, Z.; Cui, L.; Yin, S.; Ding, A.; et al. The influence of spatial resolution on the angular variation patterns of optical reflectance as retrieved from MODIS and POLDER measurements. Remote Sens. Environ. 2018, 215, 371–385. [Google Scholar] [CrossRef]
- Chang, Y.; Jiao, Z.; Zhang, X.; Mei, L.; Dong, Y.; Yin, S.; Cui, L.; Ding, A.; Guo, J.; Xie, R.; et al. Assessment of improved ross-li brdf models emphasizing albedo estimates at large solar angles using polder data. IEEE Trans. Geosci. Remote Sens. 2020, 99, 1–19. [Google Scholar] [CrossRef]
- Gobron, N.; Widlowski, J.; Pinty, B. The 4TH Radiation Transfer Model Intercomparison: Using ISO-13528 for Proficiency Testing of Canopy Reflectance Models. J. Geophys. Res. Atmos. 2013, 118, 6869–6890. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Pinty, B.; Clerici, M.; Dai, Y.; De Kauwe, M.; De Ridder, K.; Kallel, A.; Kobayashi, H.; Lavergne, T.; Meister, W.N. RAMI4PILPS: An Intercomparison of Formulations for the Partitioning of Solar Radiation in Land Surface Models. J. Geophys. Res. Biogeosciences 2015, 116, 264–265. [Google Scholar] [CrossRef]
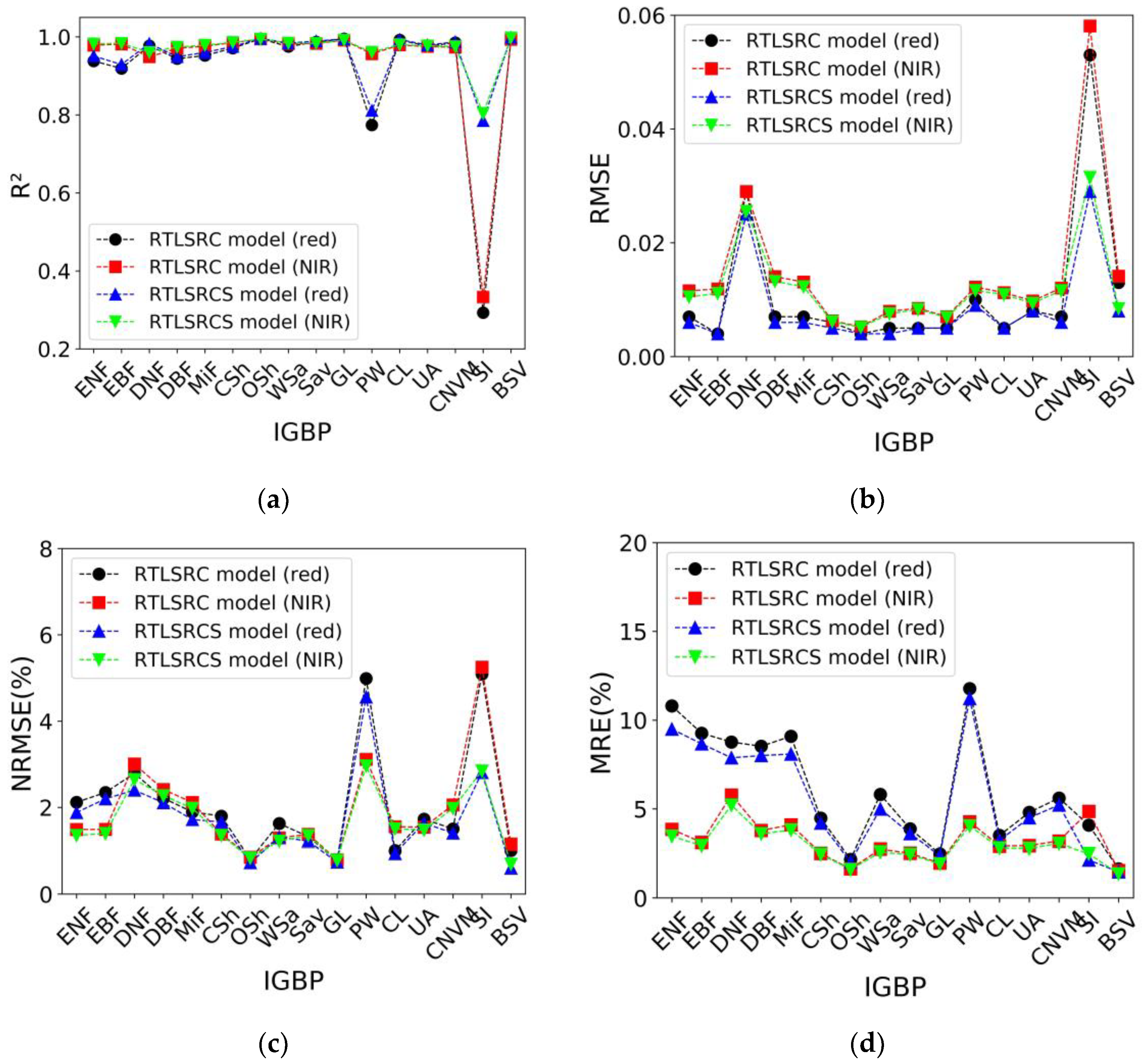
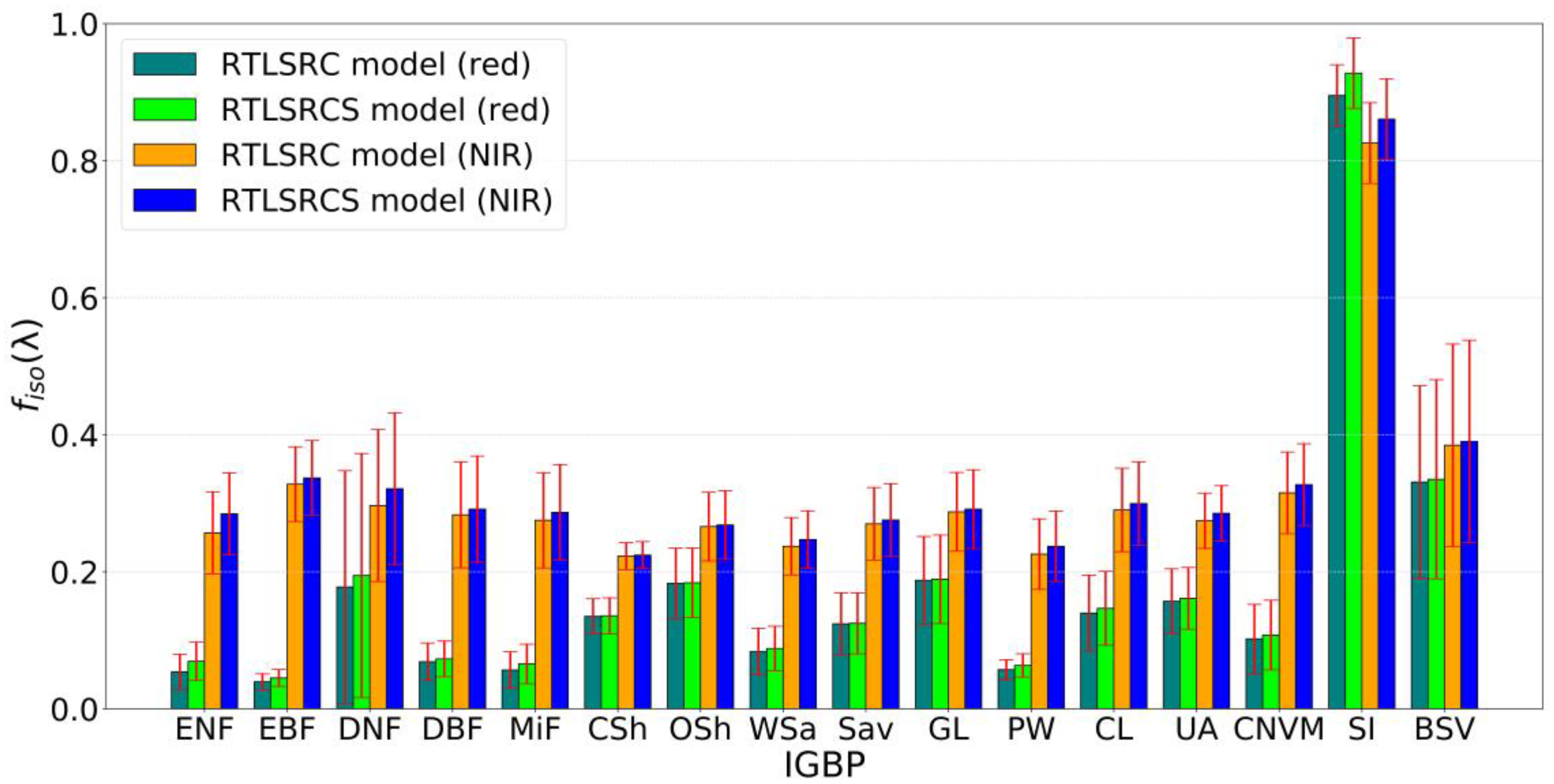
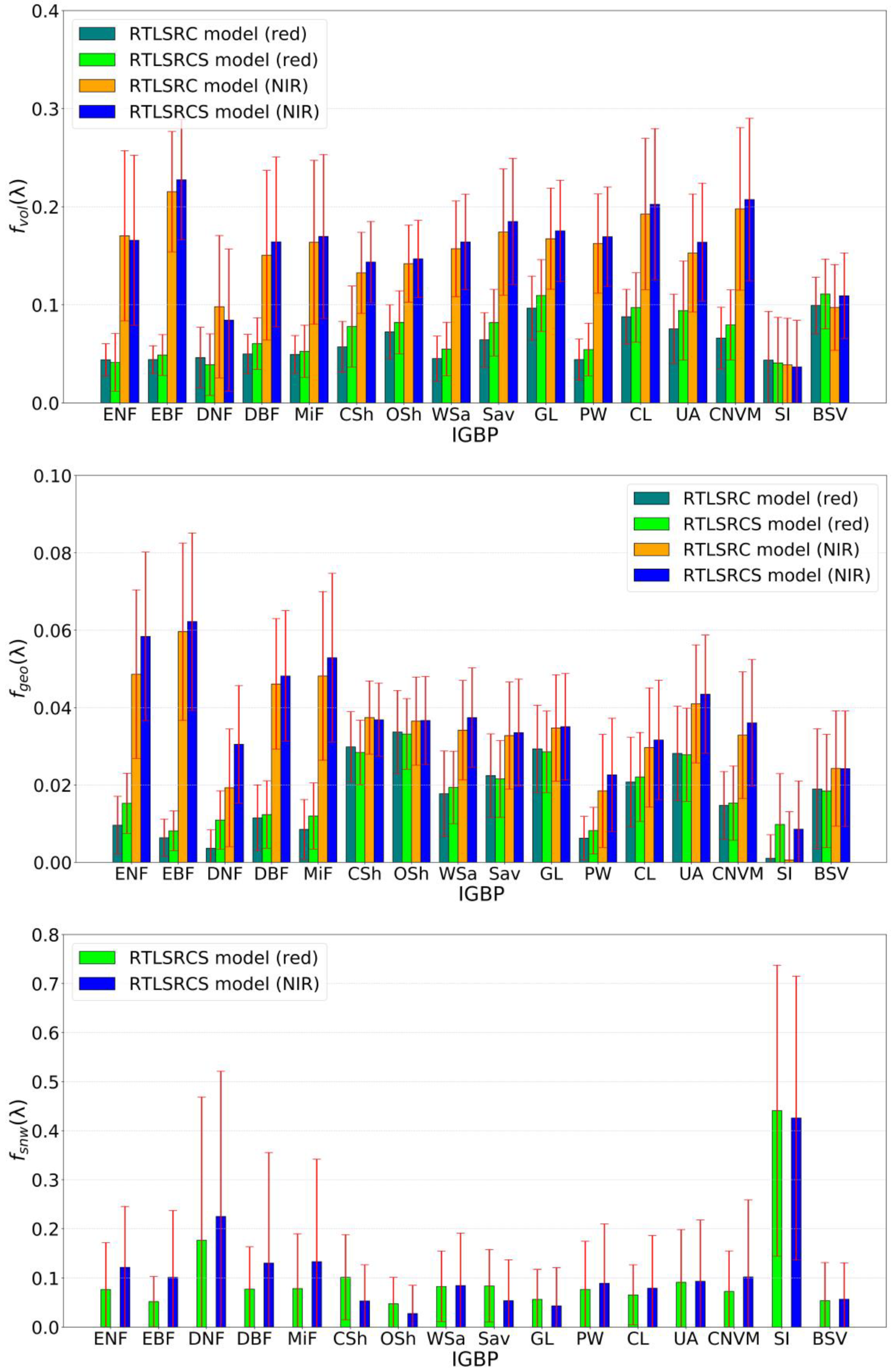


| IGBP | Screening Criteria | Number of Pixels | SZA (°) | VZA (°) | RAA (°) | Red | NIR |
|---|---|---|---|---|---|---|---|
| Evergreen Needleleaf Forests (ENF) | B3 < 0.2 | 579 | 48 ± 15 | 45 ± 2 | 166 ± 17 | 0.05 ± 0.02 | 0.22 ± 0.04 |
| Evergreen Broadleaf Forests (EBF) | B3 < 0.2 | 730 | 41 ± 11 | 45 ± 2 | 181 ± 20 | 0.04 ± 0.01 | 0.28 ± 0.04 |
| Deciduous Needleleaf Forests (DNF) | B3 < 0.6 | 336 | 53 ± 13 | 44 ± 3 | 170 ± 23 | 0.18 ± 0.17 | 0.29 ± 0.11 |
| Deciduous Broadleaf Forests (DBF) | B3 < 0.2 | 466 | 42 ± 12 | 45 ± 3 | 174 ± 21 | 0.06 ± 0.02 | 0.24 ± 0.06 |
| Mixed Forests (MiF) | B3 < 0.2 | 477 | 44 ± 13 | 45 ± 2 | 165 ± 16 | 0.05 ± 0.02 | 0.23 ± 0.06 |
| Closed Shrublands (CSh) | B3 < 0.2 | 212 | 39 ± 13 | 45 ± 2 | 184 ± 18 | 0.11 ± 0.02 | 0.19 ± 0.02 |
| Open Shrublands (OSh) | B3 < 0.4 | 1373 | 39 ± 12 | 45 ± 2 | 184 ± 16 | 0.15 ± 0.05 | 0.24 ± 0.05 |
| Woody Savannas (WSa) | B3 < 0.3 | 618 | 40 ± 11 | 44 ± 2 | 181 ± 19 | 0.07 ± 0.02 | 0.21 ± 0.04 |
| Savannas (Sav) | B3 < 0.3 | 498 | 37 ± 8 | 44 ± 2 | 185 ± 18 | 0.10 ± 0.04 | 0.24 ± 0.05 |
| Grasslands (GL) | B3 < 0.4 | 881 | 39 ± 14 | 44 ± 2 | 171 ± 17 | 0.16 ± 0.06 | 0.26 ± 0.06 |
| Permanent Wetlands (PW) | B3 < 0.3 | 78 | 41 ± 9 | 45 ± 3 | 176 ± 24 | 0.06 ± 0.01 | 0.22 ± 0.04 |
| Croplands (CL) | B3 < 0.3 | 874 | 40 ± 14 | 45 ± 2 | 171 ± 18 | 0.12 ± 0.05 | 0.27 ± 0.06 |
| Urban Areas (UA) | B3 < 0.3 | 631 | 39 ± 14 | 45 ± 2 | 172 ± 18 | 0.13 ± 0.04 | 0.24 ± 0.04 |
| Cropland Natural Vegetation Mosaics (CNVM) | B3 < 0.3 | 276 | 40 ± 14 | 45 ± 2 | 166 ± 18 | 0.09 ± 0.05 | 0.29 ± 0.05 |
| Snow and Ice (SI) | B1 > 0.4 | 945 | 62 ± 11 | 42 ± 3 | 191 ± 35 | 0.91 ± 0.04 | 0.84 ± 0.05 |
| Barren or Sparsely Vegetated (BSV) | B3 < 0.6 | 1600 | 34 ± 15 | 44 ± 1 | 174 ± 14 | 0.31 ± 0.15 | 0.36 ± 0.15 |
| IGBP | R2 | RMSE | Bias | NRMSE (%) | MRE (%) | T Value | p Value |
|---|---|---|---|---|---|---|---|
| ENF | 0.992 | 0.002 | 0.000 | 1.350 | 1.202 | 0.151 | 0.880 |
| EBF | 0.997 | 0.001 | 0.000 | 0.838 | 0.464 | 0.153 | 0.879 |
| DNF | 0.999 | 0.004 | −0.001 | 0.930 | 0.911 | 0.074 | 0.941 |
| DBF | 0.995 | 0.002 | 0.000 | 1.583 | 0.574 | 0.136 | 0.892 |
| MiF | 0.997 | 0.001 | 0.000 | 1.127 | 0.703 | 0.272 | 0.786 |
| CSh | 0.995 | 0.001 | 0.000 | 1.336 | 0.402 | 0.101 | 0.920 |
| OSh | 1.000 | 0.001 | 0.000 | 0.351 | 0.233 | 0.043 | 0.966 |
| WSa | 0.996 | 0.001 | 0.000 | 0.785 | 0.771 | 0.273 | 0.785 |
| Sav | 0.998 | 0.001 | 0.000 | 0.630 | 0.373 | 0.014 | 0.989 |
| GL | 1.000 | 0.001 | 0.000 | 0.248 | 0.220 | 0.045 | 0.965 |
| PW | 0.998 | 0.001 | 0.000 | 0.933 | 0.458 | 0.047 | 0.962 |
| CL | 0.999 | 0.001 | 0.000 | 0.475 | 0.366 | 0.035 | 0.972 |
| UA | 0.997 | 0.001 | 0.000 | 0.931 | 0.560 | 0.059 | 0.953 |
| CNVM | 0.998 | 0.001 | 0.000 | 0.628 | 0.412 | 0.037 | 0.970 |
| SI | 0.946 | 0.018 | −0.014 | 4.671 | 1.790 | 6.229 | 0.000 |
| BSV | 0.999 | 0.004 | −0.001 | 0.533 | 0.211 | 0.138 | 0.890 |
| IGBP | R2 | RMSE | Bias | NRMSE (%) | MRE (%) | T Value | p Value |
|---|---|---|---|---|---|---|---|
| ENF | 0.851 | 0.010 | −0.005 | 8.176 | 4.399 | 4.605 | 0.000 |
| EBF | 0.952 | 0.005 | −0.002 | 3.706 | 1.748 | 2.406 | 0.016 |
| DNF | 0.999 | 0.005 | −0.003 | 1.134 | 1.457 | 0.263 | 0.793 |
| DBF | 0.963 | 0.007 | −0.003 | 4.668 | 1.906 | 1.479 | 0.140 |
| MiF | 0.971 | 0.006 | −0.002 | 3.800 | 2.156 | 1.396 | 0.163 |
| CSh | 0.882 | 0.006 | −0.003 | 6.092 | 2.090 | 1.985 | 0.048 |
| OSh | 0.990 | 0.004 | −0.002 | 1.925 | 1.053 | 1.177 | 0.239 |
| WSa | 0.936 | 0.006 | −0.003 | 3.421 | 2.446 | 2.199 | 0.028 |
| Sav | 0.962 | 0.006 | −0.002 | 3.450 | 1.546 | 1.507 | 0.132 |
| GL | 0.993 | 0.004 | −0.002 | 1.647 | 1.207 | 1.054 | 0.292 |
| PW | 0.951 | 0.005 | −0.003 | 5.769 | 2.104 | 0.835 | 0.405 |
| CL | 0.976 | 0.006 | −0.003 | 2.995 | 1.772 | 2.085 | 0.037 |
| UA | 0.947 | 0.009 | −0.005 | 5.451 | 2.668 | 2.637 | 0.009 |
| CNVM | 0.960 | 0.007 | −0.004 | 3.665 | 2.033 | 1.683 | 0.093 |
| SI | 0.963 | 0.012 | −0.009 | 3.269 | 1.234 | 4.548 | 0.000 |
| BSV | 0.999 | 0.005 | −0.002 | 0.687 | 0.827 | 0.486 | 0.627 |
| IGBP | R2 | RMSE | Bias | NRMSE (%) | MRE (%) | T Value | p Value |
|---|---|---|---|---|---|---|---|
| ENF | 0.976 | 0.003 | −0.001 | 2.512 | 1.794 | 0.855 | 0.393 |
| EBF | 0.992 | 0.002 | 0.000 | 1.357 | 0.672 | 0.404 | 0.686 |
| DNF | 0.999 | 0.004 | −0.001 | 0.890 | 0.811 | 0.110 | 0.913 |
| DBF | 0.990 | 0.002 | 0.000 | 2.317 | 0.828 | 0.262 | 0.793 |
| MiF | 0.994 | 0.002 | 0.000 | 1.692 | 0.925 | 0.114 | 0.909 |
| CSh | 0.981 | 0.002 | −0.001 | 2.704 | 0.770 | 0.542 | 0.589 |
| OSh | 0.999 | 0.001 | 0.000 | 0.652 | 0.401 | 0.282 | 0.778 |
| WSa | 0.989 | 0.002 | 0.000 | 1.217 | 1.056 | 0.265 | 0.791 |
| Sav | 0.995 | 0.002 | 0.000 | 1.186 | 0.597 | 0.303 | 0.762 |
| GL | 0.999 | 0.001 | −0.001 | 0.509 | 0.421 | 0.253 | 0.800 |
| PW | 0.994 | 0.002 | 0.000 | 1.612 | 0.712 | 0.137 | 0.891 |
| CL | 0.997 | 0.002 | −0.001 | 0.970 | 0.633 | 0.495 | 0.621 |
| UA | 0.992 | 0.003 | −0.001 | 1.856 | 0.977 | 0.672 | 0.502 |
| CNVM | 0.993 | 0.002 | −0.001 | 1.276 | 0.725 | 0.437 | 0.662 |
| SI | 0.956 | 0.016 | −0.013 | 4.232 | 1.651 | 5.980 | 0.000 |
| BSV | 0.999 | 0.004 | −0.001 | 0.504 | 0.329 | 0.207 | 0.836 |
| IGBP | Bands | R2 | RMSE | Bias | NRMSE (%) | MRE (%) | T Value | p Value |
|---|---|---|---|---|---|---|---|---|
| LC15 | Red | 0.992 | 0.003 | 0.000 | 1.415 | 1.267 | 0.292 | 0.773 |
| NIR | 0.999 | 0.002 | 0.000 | 0.675 | 0.376 | 0.147 | 0.884 | |
| SI | Red | 0.832 | 0.030 | 0.023 | 8.015 | 2.933 | 11.044 | 0.000 |
| NIR | 0.882 | 0.032 | 0.025 | 6.450 | 3.434 | 10.321 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, A.; Jiao, Z.; Kokhanovsky, A.; Zhang, X.; Guo, J.; Zhao, P.; Zhang, M.; Jiang, H.; Xu, K. Evaluating the Performance of the Enhanced Ross-Li Models in Characterizing BRDF/Albedo/NBAR Characteristics for Various Land Cover Types in the POLDER Database. Remote Sens. 2024, 16, 2119. https://doi.org/10.3390/rs16122119
Ding A, Jiao Z, Kokhanovsky A, Zhang X, Guo J, Zhao P, Zhang M, Jiang H, Xu K. Evaluating the Performance of the Enhanced Ross-Li Models in Characterizing BRDF/Albedo/NBAR Characteristics for Various Land Cover Types in the POLDER Database. Remote Sensing. 2024; 16(12):2119. https://doi.org/10.3390/rs16122119
Chicago/Turabian StyleDing, Anxin, Ziti Jiao, Alexander Kokhanovsky, Xiaoning Zhang, Jing Guo, Ping Zhao, Mingming Zhang, Hailan Jiang, and Kaijian Xu. 2024. "Evaluating the Performance of the Enhanced Ross-Li Models in Characterizing BRDF/Albedo/NBAR Characteristics for Various Land Cover Types in the POLDER Database" Remote Sensing 16, no. 12: 2119. https://doi.org/10.3390/rs16122119
APA StyleDing, A., Jiao, Z., Kokhanovsky, A., Zhang, X., Guo, J., Zhao, P., Zhang, M., Jiang, H., & Xu, K. (2024). Evaluating the Performance of the Enhanced Ross-Li Models in Characterizing BRDF/Albedo/NBAR Characteristics for Various Land Cover Types in the POLDER Database. Remote Sensing, 16(12), 2119. https://doi.org/10.3390/rs16122119









