Ground-Based Hyperspectral Estimation of Maize Leaf Chlorophyll Content Considering Phenological Characteristics
Abstract
:1. Introduction
2. Materials and Methods
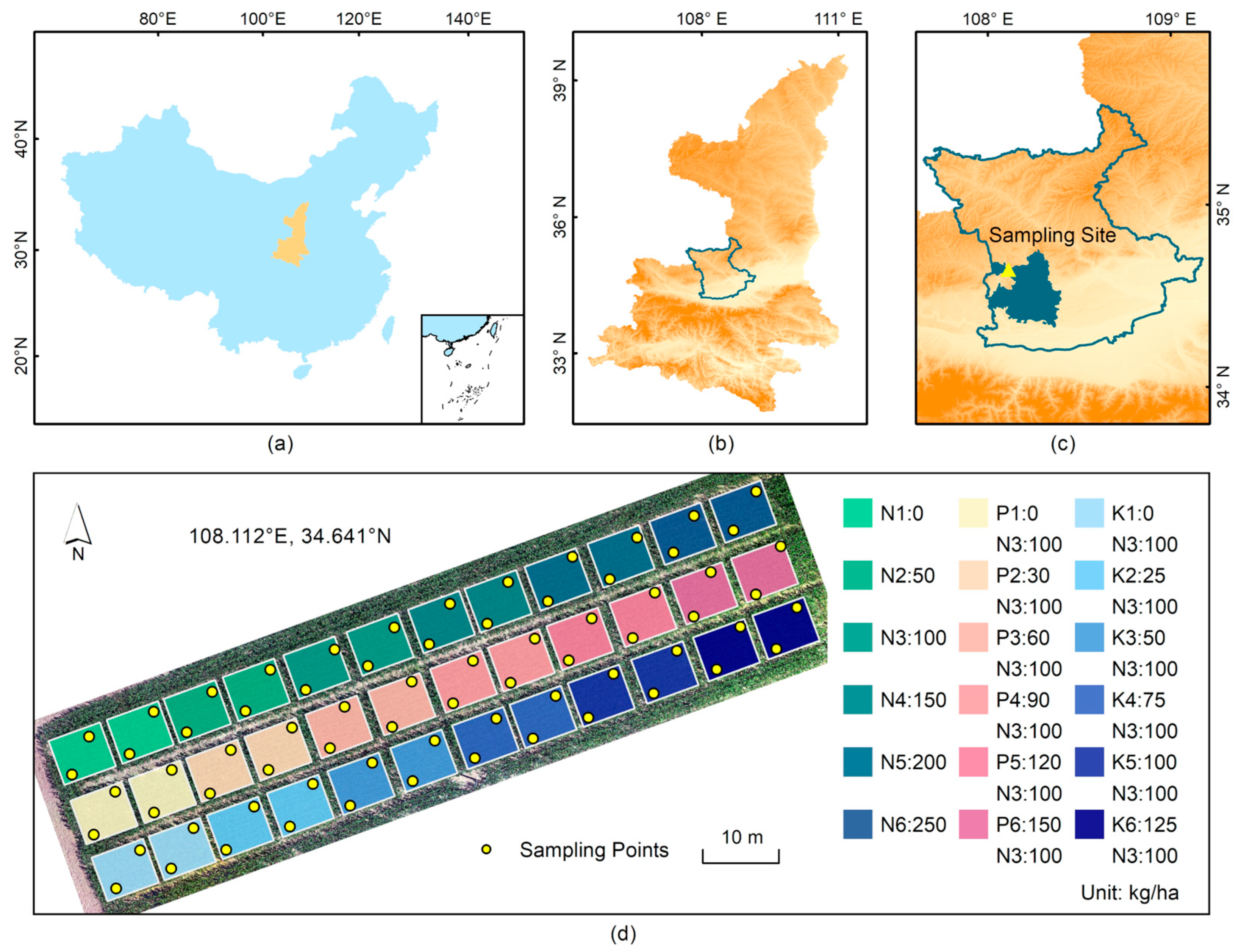
2.1. Experimental Design
2.2. Data Collection
2.2.1. Hyperspectral Data Acquisition
2.2.2. Leaf Chlorophyll Content Determination
2.3. Model-Independent Variable Determination
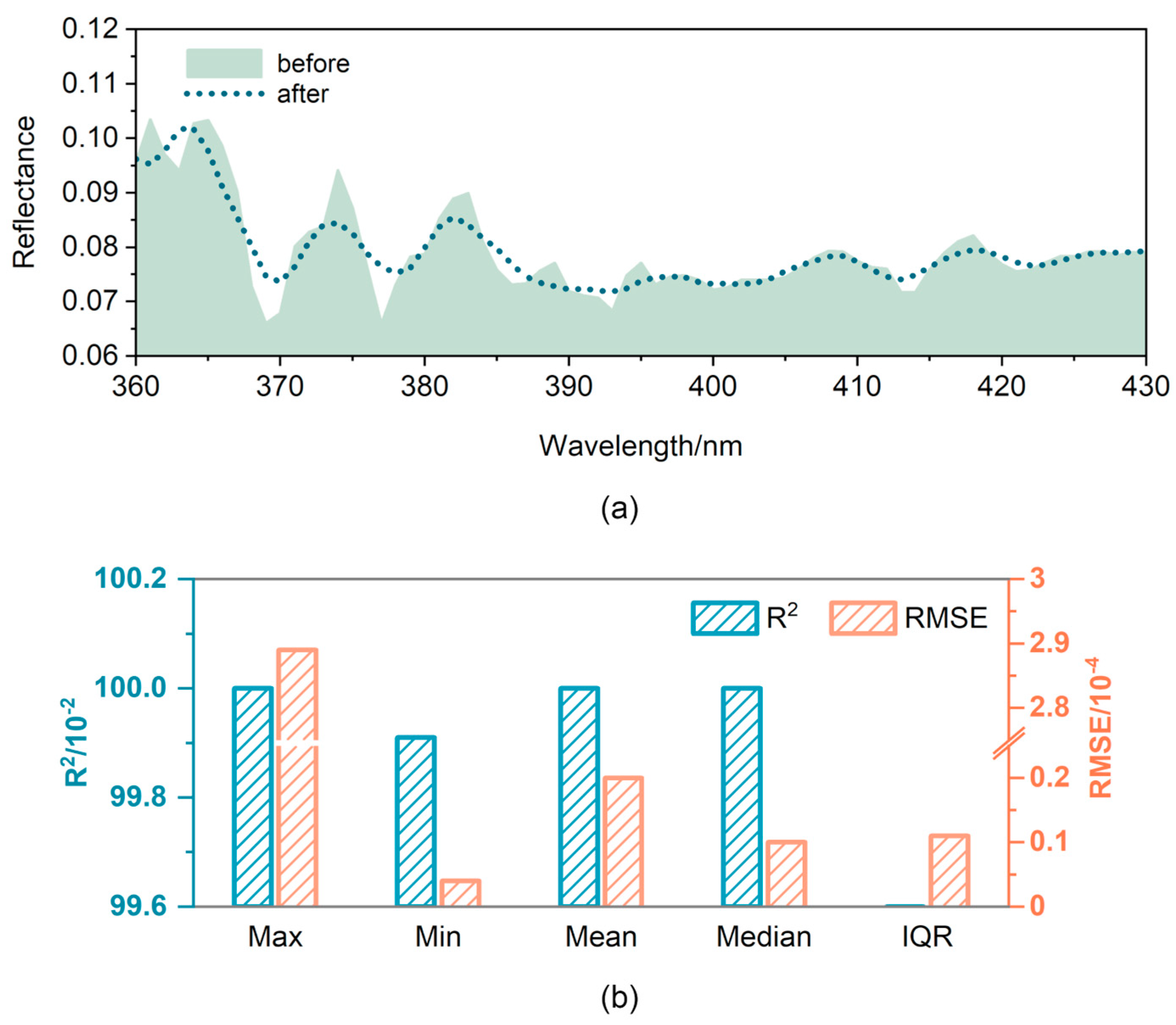
2.3.1. Spectral Denoising and Transformation
2.3.2. Spectral Indices (SIs) and Phenological Parameters (PPs)
2.3.3. Feature Variable Selection
2.4. Regression Analysis Method
2.5. Model Evaluation Metrics
3. Results
3.1. Statistical Analysis of LCC
3.2. Spectral Denoising
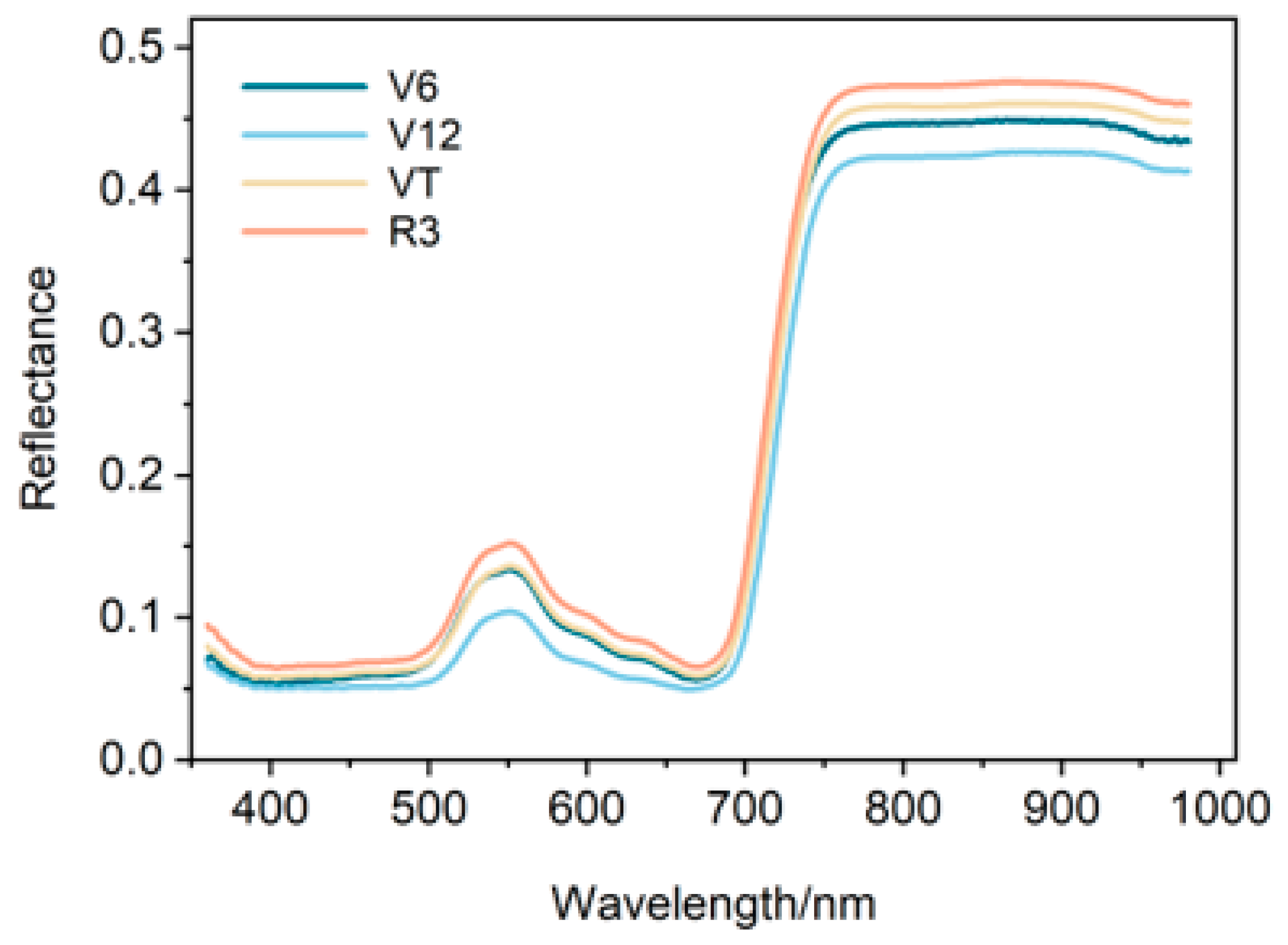
3.3. Spectral Curves of Maize Leaves
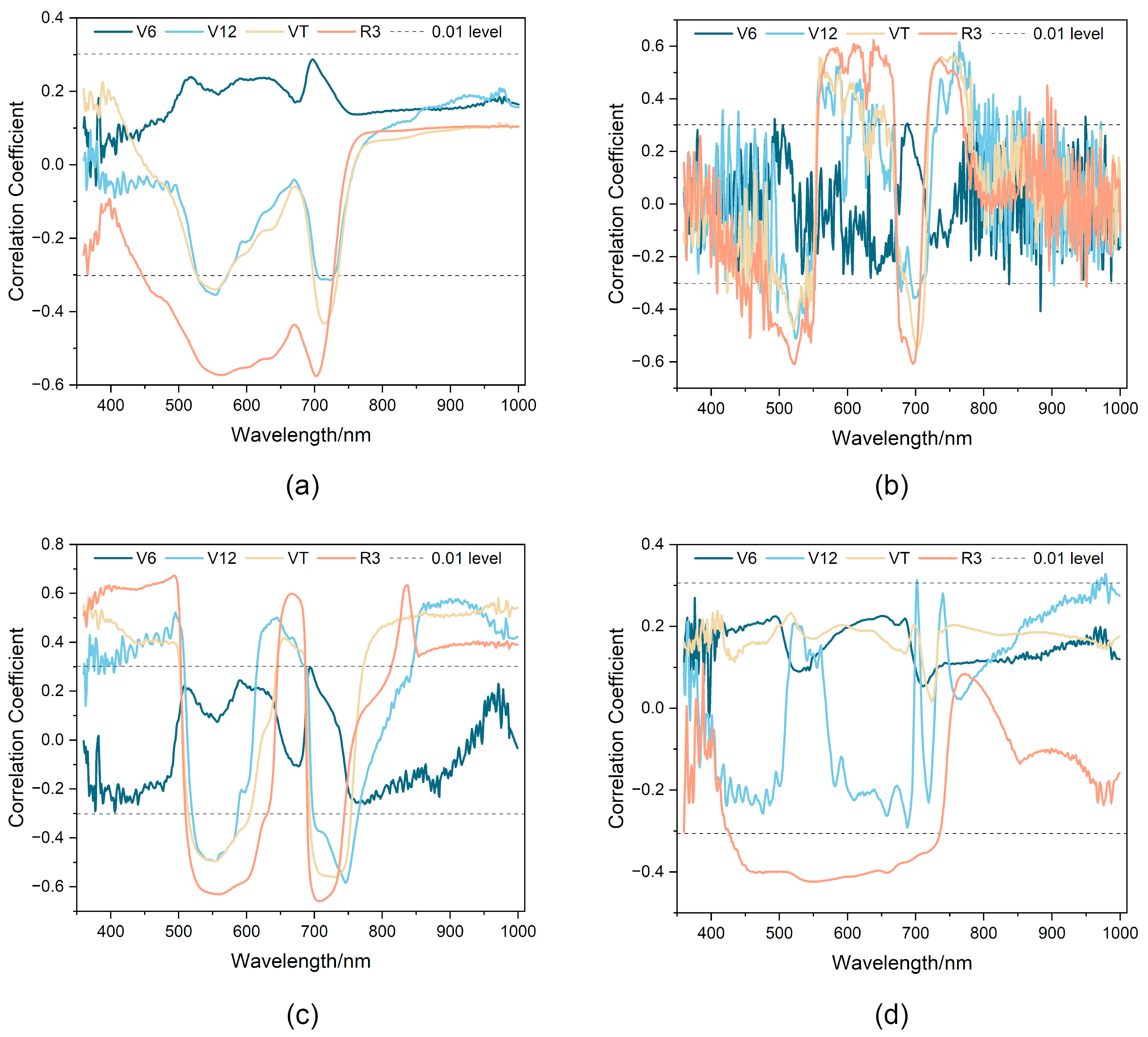
3.4. Correlation between LCC and Spectral Reflectance
3.4.1. Correlation between LCC and Single-Band Spectrum
3.4.2. Correlation of LCC with Classical SIs or PPs
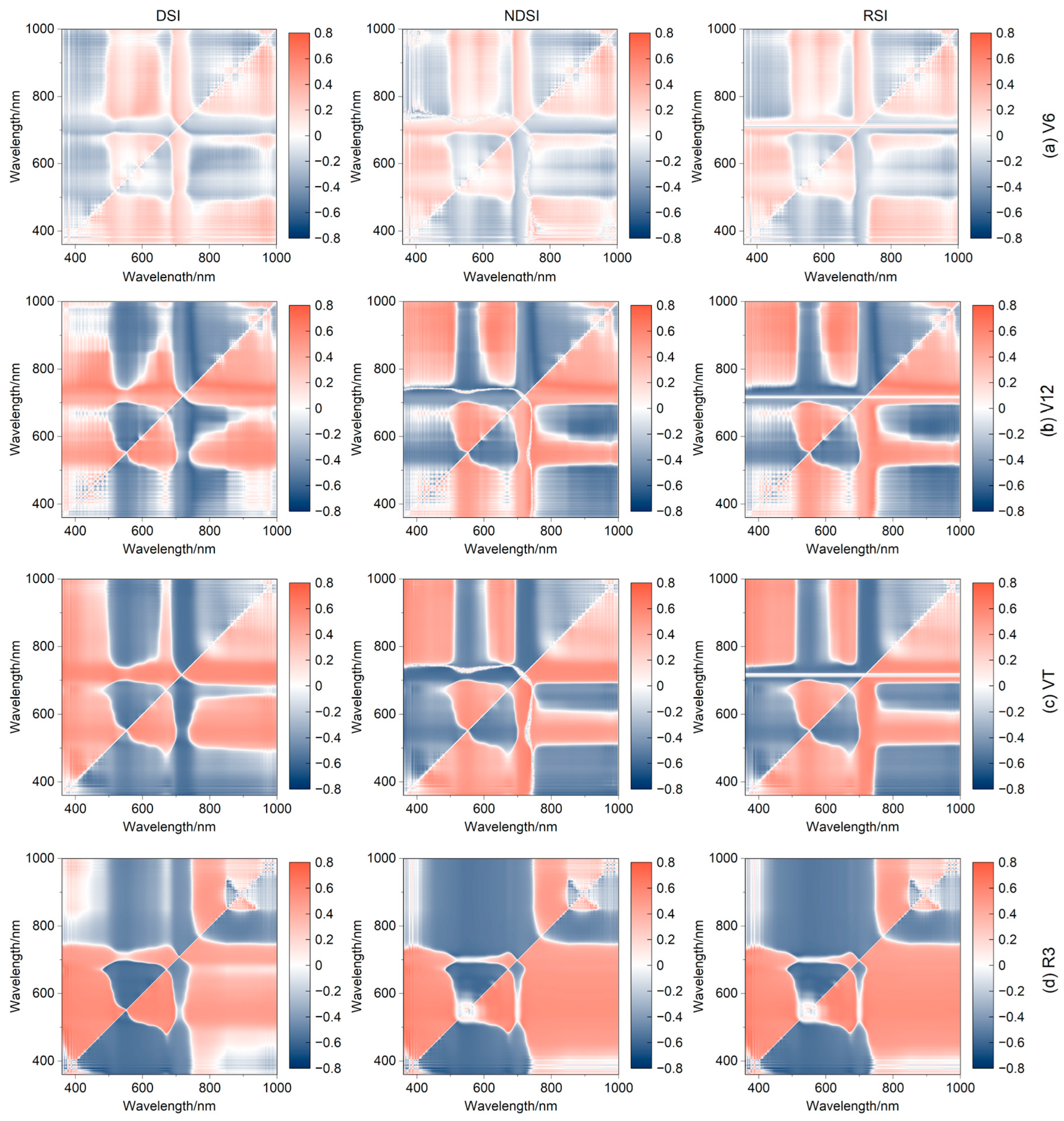
3.4.3. Correlation between LCC and SIc
3.5. Univariate Regression Model for LCC Estimation (LCC-UR)
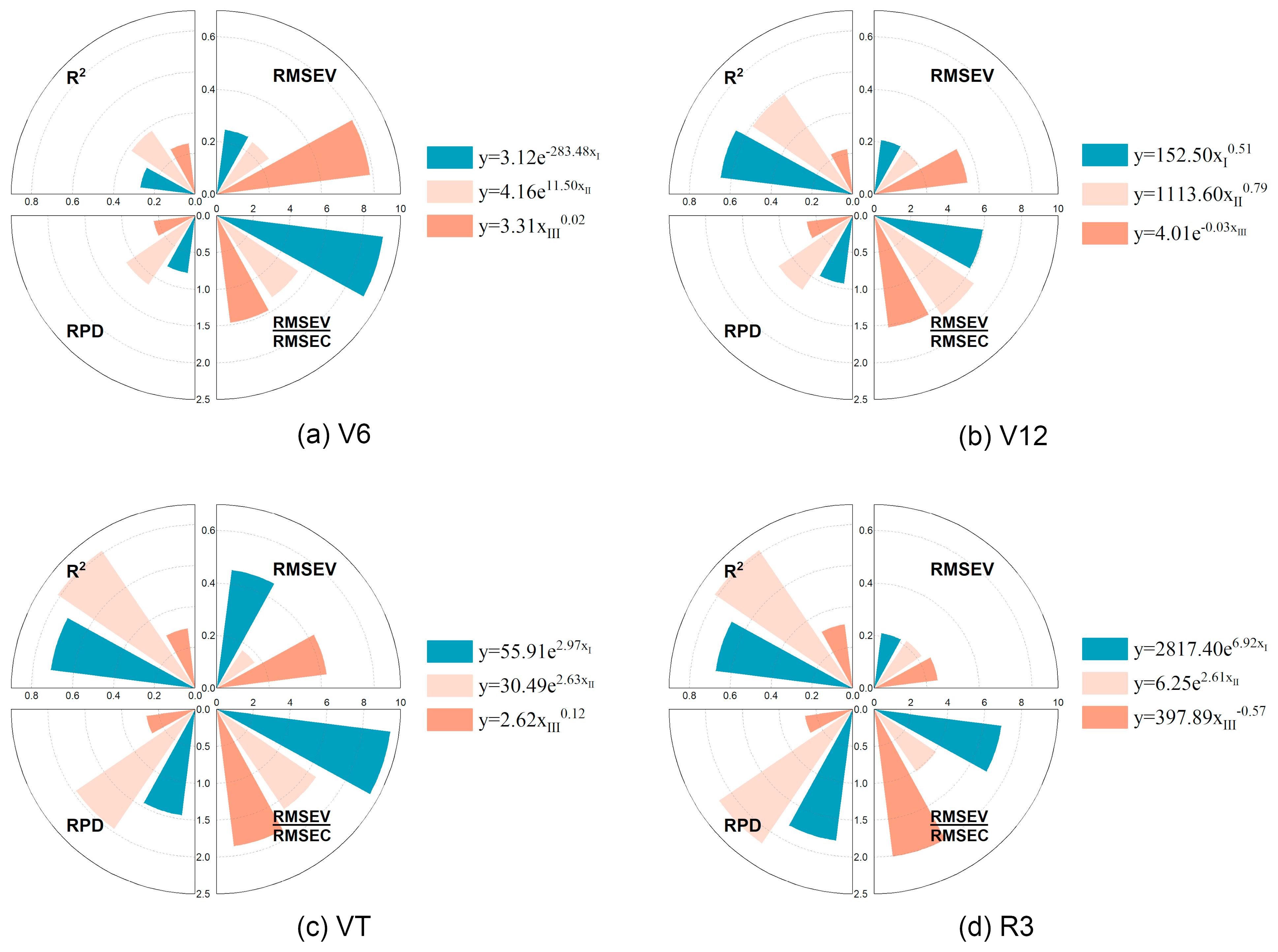
3.6. Multivariate Regression Model for LCC Estimation (LCC-MR)
3.6.1. Multivariate Linear Model
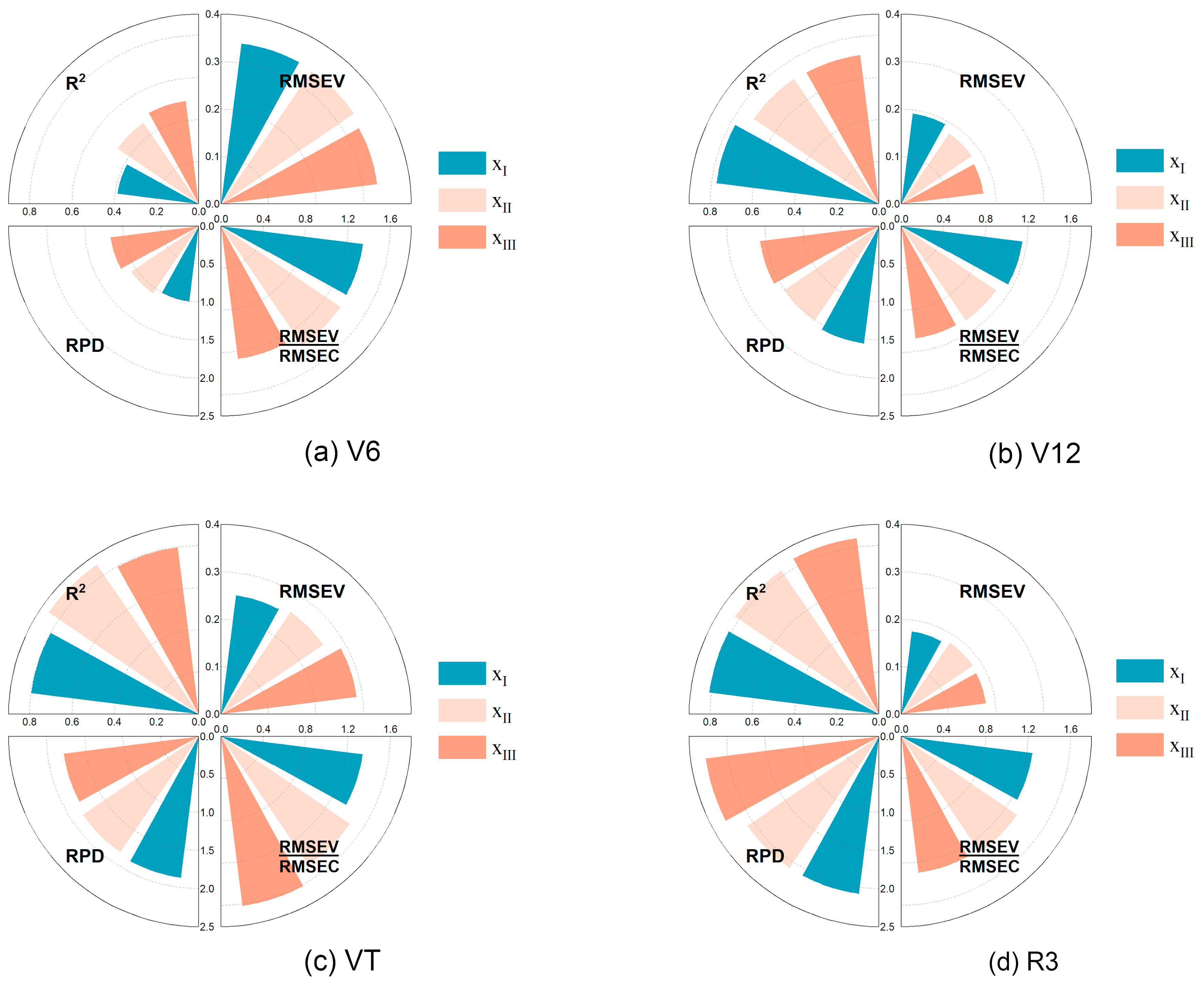
3.6.2. Machine Learning (ML) Model
4. Discussion
4.1. Effect of Spectral Transformations on Chlorophyll Estimation
4.2. Estimating Chlorophyll Using SIs, Rλ, and PPs
4.3. Effects of Different Growth Stages on Chlorophyll Estimation
4.4. Challenges and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Category | Concept | Abbreviations |
|---|---|---|
| broadband spectral indices | the green chlorophyll index | CIgreen |
| the red edge chlorophyll index | CIrededge | |
| the chlorophyll vegetation index | CVI | |
| the MERIS terrestrial chlorophyll index | MTCI | |
| critical growth stage of maize | milk-ripe stage | R3 |
| twelfth leaf stage or flare–opening stage | V12 | |
| sixth leaf stage or jointing stage | V6 | |
| tasseling stage | VT | |
| evaluation metrics | interquartile range | IQR |
| R-square | R2 | |
| root mean square error | RMSE | |
| root mean square error of calibration | RMSEC | |
| root mean square error of validation | RMSEV | |
| relative prediction deviation | RPD | |
| standard deviation | SD | |
| feature variable selection method | competitive adaptive reweighted sampling | CARS |
| genetic algorithm | GA | |
| successive projections algorithm | SPA | |
| uninformative variables elimination | UVE | |
| fundamental variables | phenological parameters | PPs |
| sensitive bands | Rλ | |
| optimal spectral indices | SIc | |
| spectral indices | SIs | |
| machine learning | gradient-boosting decision trees | GBDTs |
| random forest | RF | |
| random forest regression | RFR | |
| support vector machine | SVM | |
| support vector regression | SVR | |
| extreme gradient boosting | XGBoost | |
| narrowband spectral indices | the modified chlorophyll absorption ratio index | MCARI |
| the modified simple ratio index | MSR | |
| the structure-insensitive pigment index | SIPI | |
| phenological parameters | amplitude of season | AOS |
| gross spring greenness | GSG | |
| net spring greenness | NSG | |
| the peak value of season | POS | |
| rate of growth | ROG | |
| regression models | machine learning regression models for LCC estimation | LCC-ML |
| multivariate regression models for LCC estimation | LCC-MR | |
| univariate regression models for LCC estimation | LCC-UR | |
| machine learning | ML | |
| machine learning regression | MLR | |
| spectral denoising method | Gaussian filter | GF |
| moving average | MA | |
| median filter | MF | |
| Savitzky–Golay | SG | |
| the original and transformed spectra | the discrete wavelet transform spectra | DWT |
| the first derivative spectra | FD | |
| the original spectra | OS | |
| the standard normal variate spectra | SNV | |
| other | leaf area index | LAI |
| leaf chlorophyll content | LCC | |
| near-infrared | NIR |
References
- Sid’ko, A.F.; Botvich, I.Y.; Pis’man, T.I.; Shevyrnogov, A.P. Estimation of the Chlorophyll Content and Yield of Grain Crops via Their Chlorophyll Potential. Biophysics 2017, 62, 456–459. [Google Scholar] [CrossRef]
- Wang, G.; Zeng, F.; Song, P.; Sun, B.; Wang, Q.; Wang, J. Effects of Reduced Chlorophyll Content on Photosystem Functions and Photosynthetic Electron Transport Rate in Rice Leaves. J. Plant Physiol. 2022, 272, 153669. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote Estimation of Crop and Grass Chlorophyll and Nitrogen Content Using Red-Edge Bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Houborg, R.; Fisher, J.B.; Skidmore, A.K. Advances in Remote Sensing of Vegetation Function and Traits. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 1–6. [Google Scholar] [CrossRef]
- Li, L.; Ren, T.; Ma, Y.; Wei, Q.; Wang, S.; Li, X.; Cong, R.; Liu, S.; Lu, J. Evaluating Chlorophyll Density in Winter Oilseed Rape (Brassica Napus L.) Using Canopy Hyperspectral Red-Edge Parameters. Comput. Electron. Agric. 2016, 126, 21–31. [Google Scholar] [CrossRef]
- Qiao, B.; He, X.; Liu, Y.; Zhang, H.; Zhang, L.; Liu, L.; Reineke, A.-J.; Liu, W.; Müller, J. Maize Characteristics Estimation and Classification by Spectral Data under Two Soil Phosphorus Levels. Remote Sens. 2022, 14, 493. [Google Scholar] [CrossRef]
- Elmetwalli, A.H.; Tyler, A.N. Estimation of Maize Properties and Differentiating Moisture and Nitrogen Deficiency Stress via Ground—Based Remotely Sensed Data. Agric. Water Manag. 2020, 242, 106413. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.; Yue, J.; Fan, Y.; Jin, X.; Zhao, Y.; Song, X.; Long, H.; Yang, G. Estimation of Potato Above-Ground Biomass Using UAV-Based Hyperspectral Images and Machine-Learning Regression. Remote Sens. 2022, 14, 5449. [Google Scholar] [CrossRef]
- Li, S. Spatial Variability and Relationship of Spectral Reflectance and Growth Status to Corn Canopy in the Different Growth Stage. In Proceedings of the 2018 International Conference on Mathematics, Modelling, Simulation and Algorithms (MMSA 2018), Chengdu, China, 25–26 March 2018; Atlantis Press: Chengdu, China, 2018. [Google Scholar]
- Pan, W.; Cheng, X.; Du, R.; Zhu, X.; Guo, W. Detection of Chlorophyll Content Based on Optical Properties of Maize Leaves. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2024, 309, 123843. [Google Scholar] [CrossRef]
- Gao, S.; Yan, K.; Liu, J.; Pu, J.; Zou, D.; Qi, J.; Mu, X.; Yan, G. Assessment of Remote-Sensed Vegetation Indices for Estimating Forest Chlorophyll Concentration. Ecol. Indic. 2024, 162, 112001. [Google Scholar] [CrossRef]
- Wan, L.; Ryu, Y.; Dechant, B.; Lee, J.; Zhong, Z.; Feng, H. Improving Retrieval of Leaf Chlorophyll Content from Sentinel-2 and Landsat-7/8 Imagery by Correcting for Canopy Structural Effects. Remote Sens. Environ. 2024, 304, 114048. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical Vegetation Indices for Monitoring Terrestrial Ecosystems Globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote Estimation of Nitrogen and Chlorophyll Contents in Maize at Leaf and Canopy Levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E. Comparing Narrow and Broad-Band Vegetation Indices to Estimate Leaf Chlorophyll Content in Planophile Crop Canopies. Precis. Agric. 2011, 12, 334–344. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating Chlorophyll Content from Hyperspectral Vegetation Indices: Modeling and Validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating Leaf Chlorophyll Content in Sugar Beet Canopies Using Millimeter- to Centimeter-Scale Reflectance Imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar] [CrossRef]
- Jiang, S.; Chang, Q.; Wang, X.; Zheng, Z.; Zhang, Y.; Wang, Q. Estimation of Anthocyanins in Whole-Fertility Maize Leaves Based on Ground-Based Hyperspectral Measurements. Remote Sens. 2023, 15, 2571. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate Change, Phenology, and Phenological Control of Vegetation Feedbacks to the Climate System. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting Crop Yield Using Remotely Sensed Vegetation Indices and Crop Phenology Metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Shen, M.; Wang, S.; Jiang, N.; Sun, J.; Cao, R.; Ling, X.; Fang, B.; Zhang, L.; Zhang, L.; Xu, X.; et al. Plant Phenology Changes and Drivers on the Qinghai–Tibetan Plateau. Nat. Rev. Earth Environ. 2022, 3, 633–651. [Google Scholar] [CrossRef]
- Gurung, R.B.; Breidt, F.J.; Dutin, A.; Ogle, S.M. Predicting Enhanced Vegetation Index (EVI) Curves for Ecosystem Modeling Applications. Remote Sens. Environ. 2009, 113, 2186–2193. [Google Scholar] [CrossRef]
- Shen, M.; Tang, Y.; Chen, J.; Yang, W. Specification of Thermal Growing Season in Temperate China from 1960 to 2009. Clim. Change 2012, 114, 783–798. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring Phenological Variability from Satellite Imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Xie, Y.; Wilson, A.M. Change Point Estimation of Deciduous Forest Land Surface Phenology. Remote Sens. Environ. 2020, 240, 111698. [Google Scholar] [CrossRef]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant Phenology and Global Climate Change: Current Progresses and Challenges. Glob. Change Biol. 2019, 25, 1922–1940. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A Review of Vegetation Phenological Metrics Extraction Using Time-Series, Multispectral Satellite Data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Keenan, T.F.; Gray, J.; Friedl, M.A.; Toomey, M.; Bohrer, G.; Hollinger, D.Y.; Munger, J.W.; O’Keefe, J.; Schmid, H.P.; Wing, I.S.; et al. Net Carbon Uptake Has Increased through Warming-Induced Changes in Temperate Forest Phenology. Nat. Clim. Change 2014, 4, 598–604. [Google Scholar] [CrossRef]
- Kc, K.; Zhao, K.; Romanko, M.; Khanal, S. Assessment of the Spatial and Temporal Patterns of Cover Crops Using Remote Sensing. Remote Sens. 2021, 13, 2689. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Y.; Zhang, Z.; Zhang, X.; Wu, Y.; Chen, J.M. Deriving Photosystem-Level Red Chlorophyll Fluorescence Emission by Combining Leaf Chlorophyll Content and Canopy Far-Red Solar-Induced Fluorescence: Possibilities and Challenges. Remote Sens. Environ. 2024, 304, 114043. [Google Scholar] [CrossRef]
- Kong, X.; Zhao, Y.; Xue, J.; Chan, J.C.-W. Hyperspectral Image Denoising Using Global Weighted Tensor Norm Minimum and Nonlocal Low-Rank Approximation. Remote Sens. 2019, 11, 2281. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Li, Z.-L.; Leng, P.; Yang, Q.; Duan, S.-B. Hyperspectral Estimation of Soil Organic Matter Content Using Different Spectral Preprocessing Techniques and PLSR Method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef]
- Pavlou, M.; Ambler, G.; Seaman, S.; De Iorio, M.; Omar, R.Z. Review and Evaluation of Penalised Regression Methods for Risk Prediction in Low-dimensional Data with Few Events. Stat. Med. 2016, 35, 1159–1177. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving Estimation of Summer Maize Nitrogen Status with Red Edge-Based Spectral Vegetation Indices. Field Crops Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Luo, L.; Chang, Q.; Gao, Y.; Jiang, D.; Li, F. Combining Different Transformations of Ground Hyperspectral Data with Unmanned Aerial Vehicle (UAV) Images for Anthocyanin Estimation in Tree Peony Leaves. Remote Sens. 2022, 14, 2271. [Google Scholar] [CrossRef]
- Zhai, L.; Wan, L.; Sun, D.; Abdalla, A.; Zhu, Y.; Li, X.; He, Y.; Cen, H. Stability Evaluation of the PROSPECT Model for Leaf Chlorophyll Content Retrieval. Int. J. Agric. Biol. Eng. 2021, 14, 189–198. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Z.; He, Y.; Zhang, W.; Tong, L. Study on Early Rice Blast Diagnosis Based on Unpre-Processed Raman Spectral Data. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 234, 118255. [Google Scholar] [CrossRef] [PubMed]
- Shen, P.; Ma, X.; Guan, H.; He, H.; Wang, F.; Yu, M.; Yang, C. A Fourier Transform-Based Calculation Method of Wilting Index for Soybean Canopy Using Multispectral Image. Agronomy 2022, 12, 1650. [Google Scholar] [CrossRef]
- Wiedemair, V.; Huck, C.W. Evaluation of the Performance of Three Hand-Held near-Infrared Spectrometer through Investigation of Total Antioxidant Capacity in Gluten-Free Grains. Talanta 2018, 189, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Shen, Q.; Xia, K.; Zhang, S.; Kong, C.; Hu, Q.; Yang, S. Hyperspectral Indirect Inversion of Heavy-Metal Copper in Reclaimed Soil of Iron Ore Area. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 222, 117191. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Hu, T.; Luo, L.; He, Q.; Zhang, S.; Li, M.; Cui, X.; Li, H. Rapid Estimation of Leaf Nitrogen Content in Apple-Trees Based on Canopy Hyperspectral Reflectance Using Multivariate Methods. Infrared Phys. Technol. 2020, 111, 103542. [Google Scholar] [CrossRef]
- Zhu, C.; Ding, J.; Zhang, Z.; Wang, Z. Exploring the Potential of UAV Hyperspectral Image for Estimating Soil Salinity: Effects of Optimal Band Combination Algorithm and Random Forest. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 279, 121416. [Google Scholar] [CrossRef]
- Wang, G.; Wang, W.; Fang, Q.; Jiang, H.; Xin, Q.; Xue, B. The Application of Discrete Wavelet Transform with Improved Partial Least-Squares Method for the Estimation of Soil Properties with Visible and Near-Infrared Spectral Data. Remote Sens. 2018, 10, 867. [Google Scholar] [CrossRef]
- Song, D.; Gao, D.; Sun, H.; Qiao, L.; Zhao, R.; Tang, W.; Li, M. Chlorophyll Content Estimation Based on Cascade Spectral Optimizations of Interval and Wavelength Characteristics. Comput. Electron. Agric. 2021, 189, 106413. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Feng, L. Phenology-Driven Land Cover Classification and Trend Analysis Based on Long-Term Remote Sensing Image Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1142–1156. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, J.; Xiao, Y.; Shi, Z.; Chen, S. Towards Optimal Variable Selection Methods for Soil Property Prediction Using a Regional Soil Vis-NIR Spectral Library. Remote Sens. 2023, 15, 465. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, M.; Agyekum, A.A.; Wu, J.; Chen, Q.; Zuo, M.; El-Seedi, H.R.; Tao, F.; Shi, J.; Ouyang, Q.; et al. Quantitative Detection of Apple Watercore and Soluble Solids Content by near Infrared Transmittance Spectroscopy. J. Food Eng. 2020, 279, 109955. [Google Scholar] [CrossRef]
- Jiang, G.; Zhou, S.; Cui, S.; Chen, T.; Wang, J.; Chen, X.; Liao, S.; Zhou, K. Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content. Sensors 2020, 20, 6325. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Klopfenstein, A.; Douridas, N.; Shearer, S. Integration of High Resolution Remotely Sensed Data and Machine Learning Techniques for Spatial Prediction of Soil Properties and Corn Yield. Comput. Electron. Agric. 2018, 153, 213–225. [Google Scholar] [CrossRef]
- Han, H.; Lee, S.; Kim, H.-C.; Kim, M. Retrieval of Summer Sea Ice Concentration in the Pacific Arctic Ocean from AMSR2 Observations and Numerical Weather Data Using Random Forest Regression. Remote Sens. 2021, 13, 2283. [Google Scholar] [CrossRef]
- Li, H.; Zhang, C.; Zhang, S.; Atkinson, P.M. Crop Classification from Full-Year Fully-Polarimetric L-Band UAVSAR Time-Series Using the Random Forest Algorithm. Int. J. Appl. Earth Obs. Geoinf. 2020, 87, 102032. [Google Scholar] [CrossRef]
- Wang, S.; Fu, G. Modelling Soil Moisture Using Climate Data and Normalized Difference Vegetation Index Based on Nine Algorithms in Alpine Grasslands. Front. Environ. Sci. 2023, 11, 1130448. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Guo, J.; Wang, G.; Wang, X. Research on Classification Method of High-Dimensional Class-Imbalanced Datasets Based on SVM. Int. J. Mach. Learn. Cybern. 2019, 10, 1765–1778. [Google Scholar] [CrossRef]
- Gu, B.; Sheng, V.S.; Tay, K.Y.; Romano, W.; Li, S. Incremental Support Vector Learning for Ordinal Regression. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1403–1416. [Google Scholar] [CrossRef]
- Lin, N.; Zhang, D.; Feng, S.; Ding, K.; Tan, L.; Wang, B.; Chen, T.; Li, W.; Dai, X.; Pan, J.; et al. Rapid Landslide Extraction from High-Resolution Remote Sensing Images Using SHAP-OPT-XGBoost. Remote Sens. 2023, 15, 3901. [Google Scholar] [CrossRef]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD Values of Summer Maize Using UAV Hyperspectral Data Based on Multiple Machine Learning Algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Zheng, C.; Abd-Elrahman, A.; Whitaker, V.; Dalid, C. Prediction of Strawberry Dry Biomass from UAV Multispectral Imagery Using Multiple Machine Learning Methods. Remote Sens. 2022, 14, 4511. [Google Scholar] [CrossRef]
- Birenboim, M.; Kengisbuch, D.; Chalupowicz, D.; Maurer, D.; Barel, S.; Chen, Y.; Fallik, E.; Paz-Kagan, T.; Shimshoni, J.A. Use of Near-Infrared Spectroscopy for the Classification of Medicinal Cannabis Cultivars and the Prediction of Their Cannabinoid and Terpene Contents. Phytochemistry 2022, 204, 113445. [Google Scholar] [CrossRef]
- Zhou, F.-Y.; Liang, J.; Lü, Y.-L.; Kuang, H.-X.; Xia, Y.-G. A Nondestructive Solution to Quantify Monosaccharides by ATR-FTIR and Multivariate Regressions: A Case Study of Atractylodes Polysaccharides. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 279, 121411. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the Composition of Mineral-Organic Mixes Using UV–Vis–NIR Diffuse Reflectance Spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Ta, N.; Chang, Q.; Zhang, Y. Estimation of Apple Tree Leaf Chlorophyll Content Based on Machine Learning Methods. Remote Sens. 2021, 13, 3902. [Google Scholar] [CrossRef]
- Li, Z.; Li, C.; Gao, Y.; Ma, W.; Zheng, Y.; Niu, Y.; Guan, Y.; Hu, J. Identification of Oil, Sugar and Crude Fiber during Tobacco (Nicotiana tabacum L.) Seed Development Based on near Infrared Spectroscopy. Biomass Bioenergy 2018, 111, 39–45. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Qiao, H.; Xu, C.; Guo, J.; Si, H.; Wang, J.; Xiong, S.; Ma, X. Estimation of Leaf Nitrogen Content in Winter Wheat Based on Continuum Removal and Discrete Wavelet Transform. Int. J. Remote Sens. 2023, 44, 5523–5547. [Google Scholar] [CrossRef]
- Fearn, T.; Riccioli, C.; Garrido-Varo, A.; Guerrero-Ginel, J.E. On the Geometry of SNV and MSC. Chemom. Intell. Lab. Syst. 2009, 96, 22–26. [Google Scholar] [CrossRef]
- Luo, L.; Chang, Q.; Wang, Q.; Huang, Y. Identification and Severity Monitoring of Maize Dwarf Mosaic Virus Infection Based on Hyperspectral Measurements. Remote Sens. 2021, 13, 4560. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, L.; Li, J.; Qi, J. A Comparative Analysis of Broadband and Narrowband Derived Vegetation Indices in Predicting LAI and CCD of a Cotton Canopy. ISPRS J. Photogramm. Remote Sens. 2007, 62, 25–33. [Google Scholar] [CrossRef]
- Ren, S.; Peichl, M. Enhanced Spatiotemporal Heterogeneity and the Climatic and Biotic Controls of Autumn Phenology in Northern Grasslands. Sci. Total Environ. 2021, 788, 147806. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chang, Q.; Chen, Y.; Liu, Y.; Jiang, D.; Zhang, Z. Hyperspectral Estimation of Chlorophyll Content in Apple Tree Leaf Based on Feature Band Selection and the CatBoost Model. Agronomy 2023, 13, 2075. [Google Scholar] [CrossRef]
- Khan, A.; Vibhute, A.D.; Mali, S.; Patil, C.H. A Systematic Review on Hyperspectral Imaging Technology with a Machine and Deep Learning Methodology for Agricultural Applications. Ecol. Inform. 2022, 69, 101678. [Google Scholar] [CrossRef]
- Guo, Y.; Xiao, Y.; Hao, F.; Zhang, X.; Chen, J.; De Beurs, K.; He, Y.; Fu, Y.H. Comparison of Different Machine Learning Algorithms for Predicting Maize Grain Yield Using UAV-Based Hyperspectral Images. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103528. [Google Scholar] [CrossRef]
- Gao, D.; Qiao, L.; An, L.; Zhao, R.; Sun, H.; Li, M.; Tang, W.; Wang, N. Estimation of Spectral Responses and Chlorophyll Based on Growth Stage Effects Explored by Machine Learning Methods. Crop J. 2022, 10, 1292–1302. [Google Scholar] [CrossRef]
- Xiaoyan, W.; Zhiwei, L.; Wenjun, W.; Jiawei, W. Chlorophyll Content for Millet Leaf Using Hyperspectral Imaging and an Attention-Convolutional Neural Network. Ciênc. Rural 2020, 50, e20190731. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf Area Index Estimation Model for UAV Image Hyperspectral Data Based on Wavelength Variable Selection and Machine Learning Methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef] [PubMed]
- Tunca, E.; Köksal, E.S.; Öztürk, E.; Akay, H.; Çetin Taner, S. Accurate Estimation of Sorghum Crop Water Content under Different Water Stress Levels Using Machine Learning and Hyperspectral Data. Environ. Monit. Assess. 2023, 195, 877. [Google Scholar] [CrossRef]
- Kosola, K.R.; Eller, M.S.; Dohleman, F.G.; Olmedo-Pico, L.; Bernhard, B.; Winans, E.; Barten, T.J.; Brzostowski, L.; Murphy, L.R.; Gu, C.; et al. Short-Stature and Tall Maize Hybrids Have a Similar Yield Response to Split-Rate vs. Pre-Plant N Applications, but Differ in Biomass and Nitrogen Partitioning. Field Crops Res. 2023, 295, 108880. [Google Scholar] [CrossRef]
- Széles, A.; Horváth, É.; Simon, K.; Zagyi, P.; Huzsvai, L. Maize Production under Drought Stress: Nutrient Supply, Yield Prediction. Plants 2023, 12, 3301. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wang, H.; Wu, Z.; Wang, S.; Sun, H.; Senthilnath, J.; Wang, J.; Robin Bryant, C.; Fu, Y. Modified Red Blue Vegetation Index for Chlorophyll Estimation and Yield Prediction of Maize from Visible Images Captured by UAV. Sensors 2020, 20, 5055. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chen, X.; Meng, H.; Miao, H.; Jiang, S.; Chang, Q. UAV Hyperspectral Data Combined with Machine Learning for Winter Wheat Canopy SPAD Values Estimation. Remote Sens. 2023, 15, 4658. [Google Scholar] [CrossRef]
- Yin, Q.; Zhang, Y.; Li, W.; Wang, J.; Wang, W.; Ahmad, I.; Zhou, G.; Huo, Z. Estimation of Winter Wheat SPAD Values Based on UAV Multispectral Remote Sensing. Remote Sens. 2023, 15, 3595. [Google Scholar] [CrossRef]
- Abbas, F.; Zhang, F.; Ismail, M.; Khan, G.; Iqbal, J.; Alrefaei, A.F.; Albeshr, M.F. Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques. Sensors 2023, 23, 6843. [Google Scholar] [CrossRef]
- Han, Y.; Tang, R.; Liao, Z.; Zhai, B.; Fan, J. A Novel Hybrid GOA-XGB Model for Estimating Wheat Aboveground Biomass Using UAV-Based Multispectral Vegetation Indices. Remote Sens. 2022, 14, 3506. [Google Scholar] [CrossRef]


| SIs | Equations/Definition | References |
|---|---|---|
| CIgreen | [14] | |
| CIrededge | [14] | |
| CVI | [15] | |
| GreenNDVI | [15] | |
| MTCI | [14] | |
| MCARI | [8] | |
| MCARI/OSAVI | [16] | |
| MSR | [16] | |
| OSAVI | [16] | |
| SIPI | [17] | |
| AOS | the difference between the maximum and the mean value line | [45] |
| GSG | the area enclosed by the time series and its endpoints | [45] |
| NSG | the area enclosed by the time series and its mean value line | [45] |
| POS | the maximum value of the time series | [45] |
| ROG | the average positive slope of the time series | [45] |
| Datasets | Growth Stages | Sample Numbers | Range | Mean | Standard Deviation | Coefficient of Variation/% |
|---|---|---|---|---|---|---|
| Calibration set | V6 | 53 | 2.13–4.24 | 3.27 | 0.44 | 13.56 |
| V12 | 54 | 1.99–4.72 | 3.43 | 0.54 | 15.73 | |
| VT | 53 | 2.41–4.68 | 3.59 | 0.53 | 14.82 | |
| R3 | 53 | 1.85–5.50 | 3.33 | 0.78 | 23.59 | |
| Validation set | V6 | 18 | 2.26–4.23 | 3.28 | 0.49 | 15.04 |
| V12 | 18 | 2.41–4.52 | 3.43 | 0.52 | 15.06 | |
| VT | 18 | 2.60–4.79 | 3.62 | 0.56 | 15.36 | |
| R3 | 18 | 1.77–5.49 | 3.38 | 0.85 | 25.29 |
| Growth Stages | Characteristic Variables | ||
|---|---|---|---|
| SIs | Rλ | PPs | |
| V6 | OS_RSI, OS_DSI, OS_NDSI, FD_OSAVI, FD_SIPI, FD_MSR, FD_RSI, FD_DSI, SNV_NDSI, DWT_MCARI/OSAVI | FD_R883 | FD_ROG |
| V12 | OS_DSI, FD_GreenNDVI, FD_DSI, DWT_MCARI, DWT_MCARI/OSAVI, DWT_CIgreen, DWT_GreenNDVI, DWT_RSI, DWT_DSI, DWT_NDSI | FD_R764 | DWT_AOS |
| VT | OS_RSI, OS_DSI, FD_MCARI, FD_DSI, SNV_MCARI/OSAVI, SNV_CIrededge, SNV_RSI, SNV_DSI, SNV_NDSI, DWT_MTCI | SNV_R367 | SNV_AOS |
| R3 | OS_DSI, OS_NDSI, FD_CIgreen, FD_RSI, FD_NDSI, SNV_RSI, SNV_DSI, SNV_NDSI, DWT_RSI, DWT_NDSI | SNV_R493 | DWT_NSG |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Jiang, S.; Miao, H.; Song, Z.; Yu, J.; Guo, S.; Chang, Q. Ground-Based Hyperspectral Estimation of Maize Leaf Chlorophyll Content Considering Phenological Characteristics. Remote Sens. 2024, 16, 2133. https://doi.org/10.3390/rs16122133
Guo Y, Jiang S, Miao H, Song Z, Yu J, Guo S, Chang Q. Ground-Based Hyperspectral Estimation of Maize Leaf Chlorophyll Content Considering Phenological Characteristics. Remote Sensing. 2024; 16(12):2133. https://doi.org/10.3390/rs16122133
Chicago/Turabian StyleGuo, Yiming, Shiyu Jiang, Huiling Miao, Zhenghua Song, Junru Yu, Song Guo, and Qingrui Chang. 2024. "Ground-Based Hyperspectral Estimation of Maize Leaf Chlorophyll Content Considering Phenological Characteristics" Remote Sensing 16, no. 12: 2133. https://doi.org/10.3390/rs16122133
APA StyleGuo, Y., Jiang, S., Miao, H., Song, Z., Yu, J., Guo, S., & Chang, Q. (2024). Ground-Based Hyperspectral Estimation of Maize Leaf Chlorophyll Content Considering Phenological Characteristics. Remote Sensing, 16(12), 2133. https://doi.org/10.3390/rs16122133








