Inversion of Forest Aboveground Biomass in Regions with Complex Terrain Based on PolSAR Data and a Machine Learning Model: Radiometric Terrain Correction Assessment
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. PolSAR Data and Pre-Processing
2.3. Ground-Measured Forest AGB
2.4. SRTM DEM
3. Methods
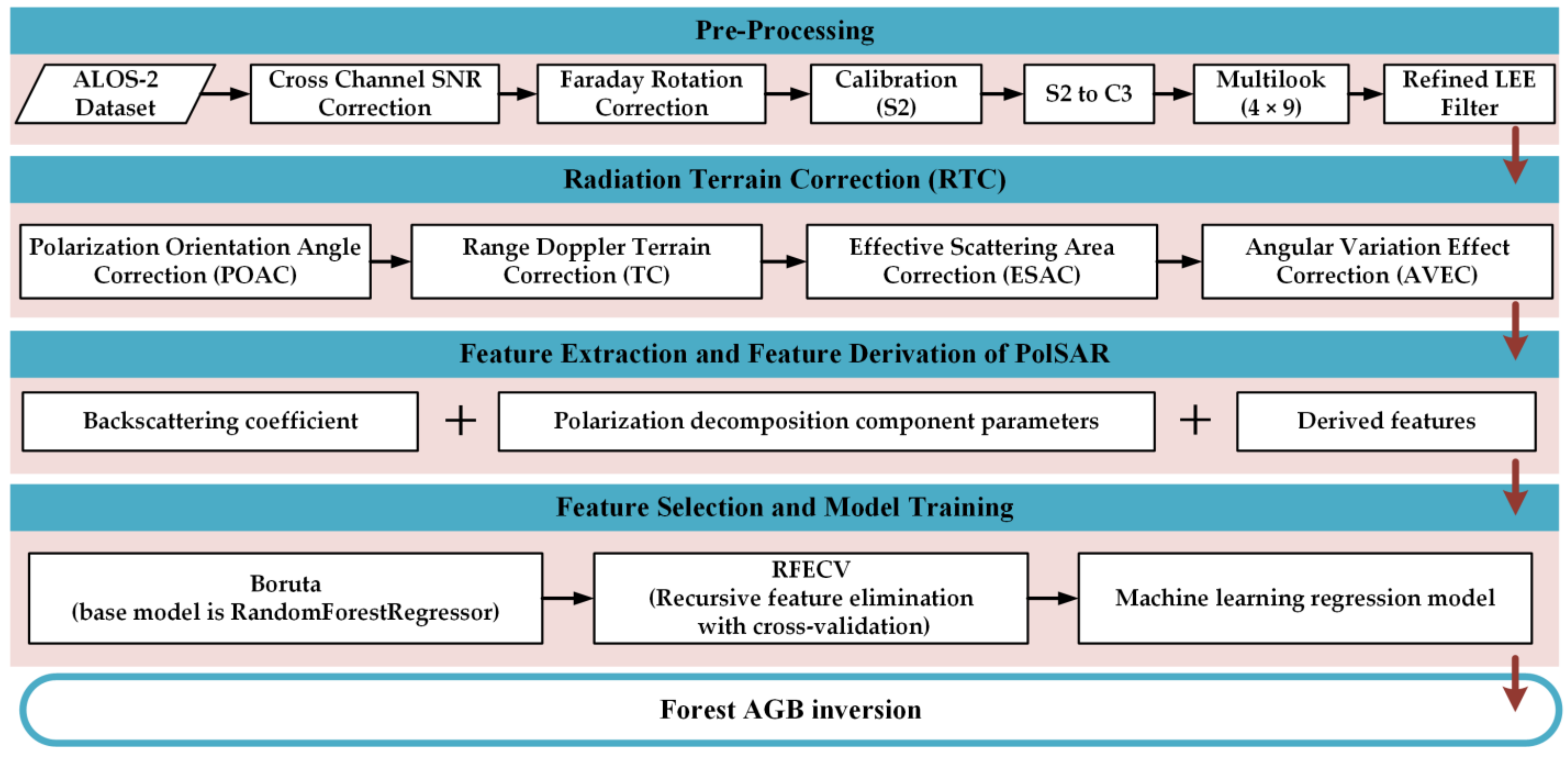
3.1. Radiometric Terrain Correction for PolSAR
3.1.1. Polarization Orientation Angle Correction
3.1.2. Effective Scattering Area Correction
3.1.3. Angular Variation Effect Correction
3.2. Feature Extraction and Feature Derivation of PolSAR
3.2.1. Backscattering Coefficient Features of PolSAR
3.2.2. Polarization Decomposition Features of PolSAR
3.3. Forest AGB Regression Modeling Algorithms and Model Evaluation
4. Results
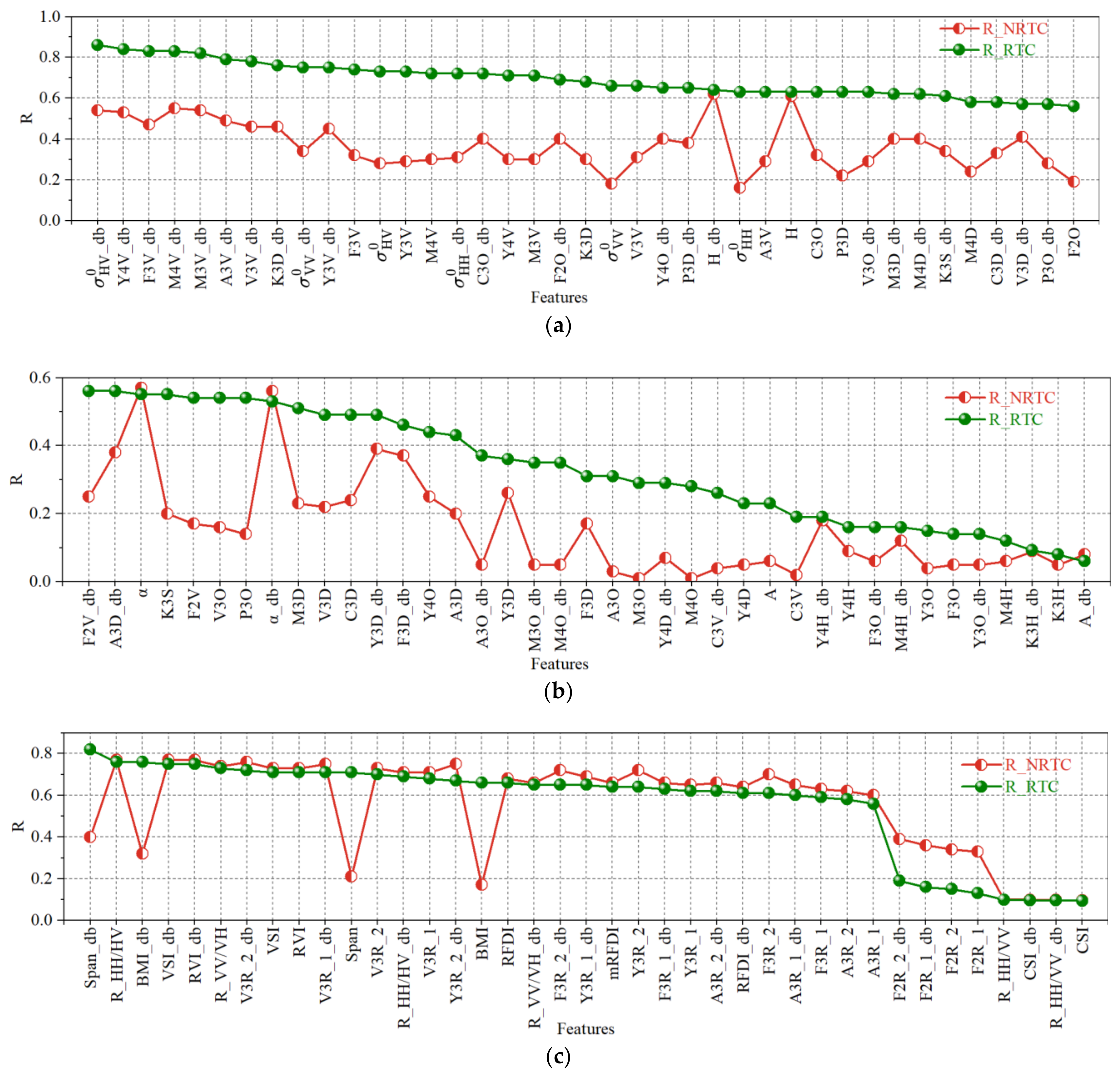
4.1. The Impact of Radiometric Terrain Correction on PolSAR Features
4.2. The Impact of Radiometric Terrain Correction on Polarization Decomposition Component
4.3. The Impact of Radiometric Terrain Correction on Regression Model Performance
5. Discussion
5.1. The Significance of Radiometric Terrain Correction
5.2. The Overcorrection of Radiometric Terrain Correction
5.3. Performance Comparison of Different Regression Models
5.4. Potential Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
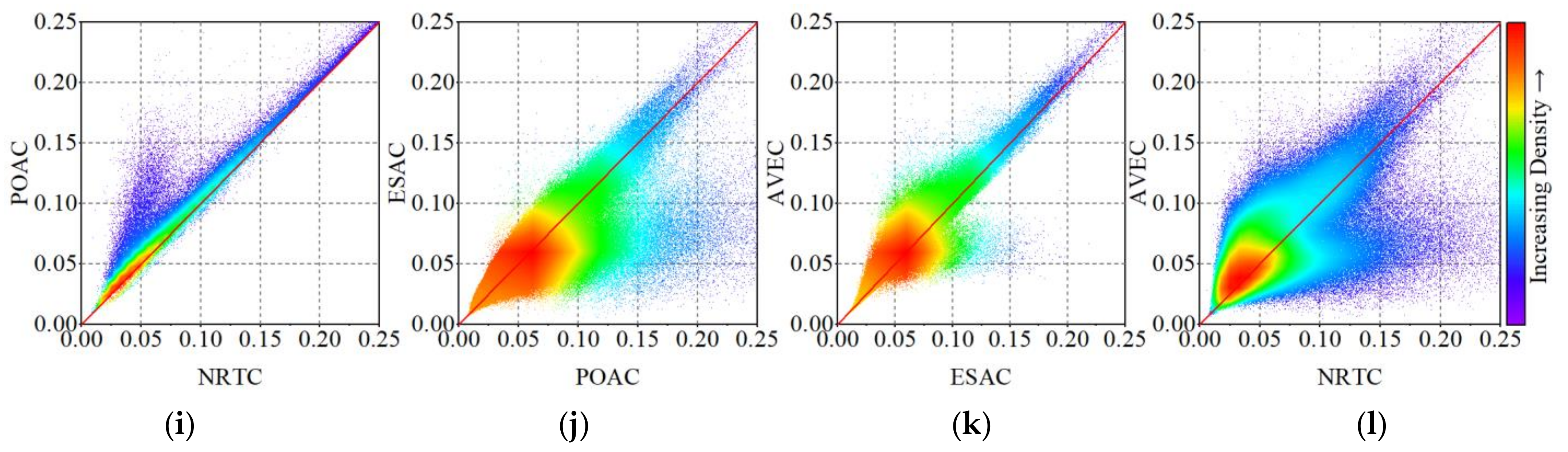
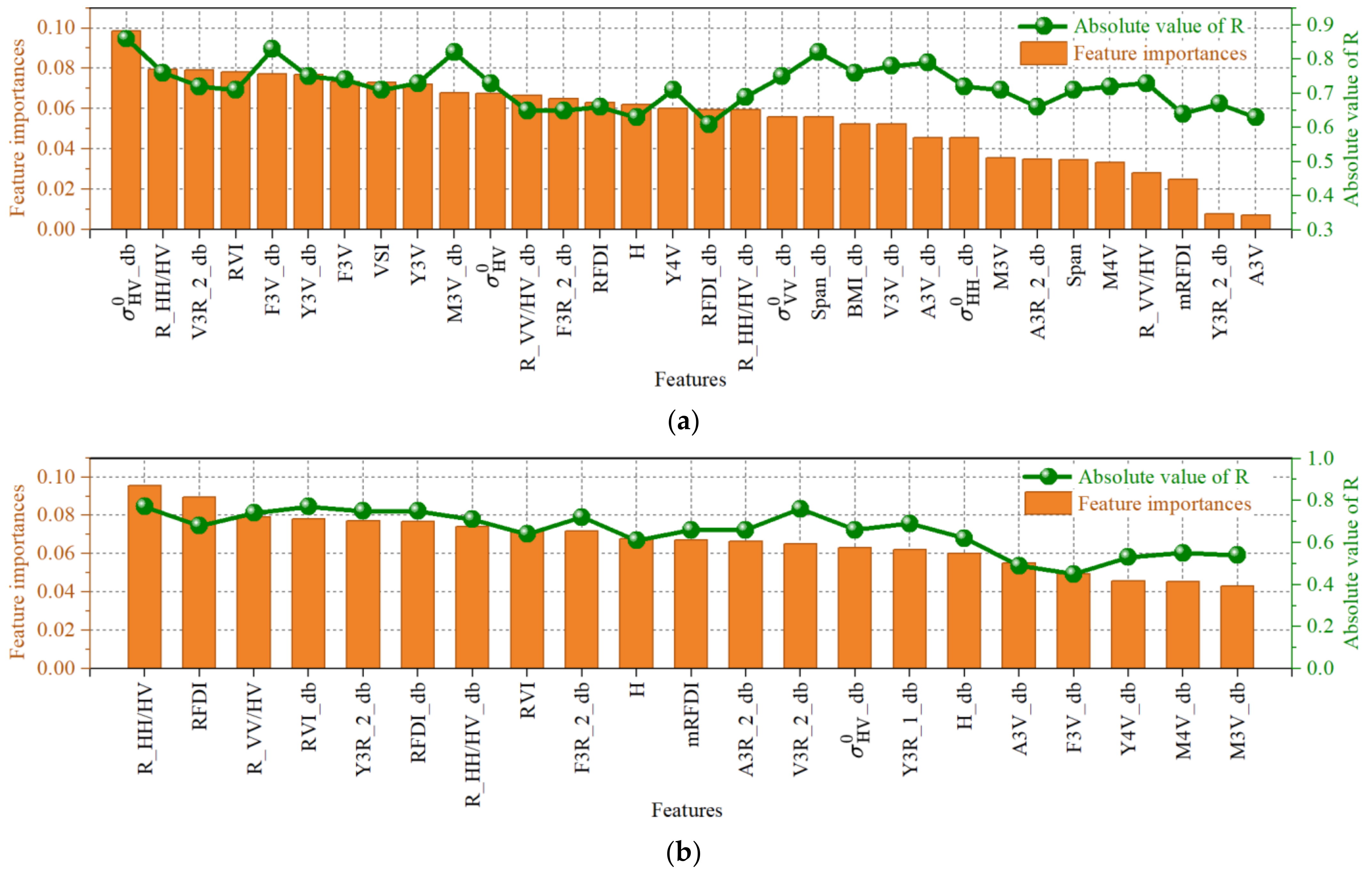

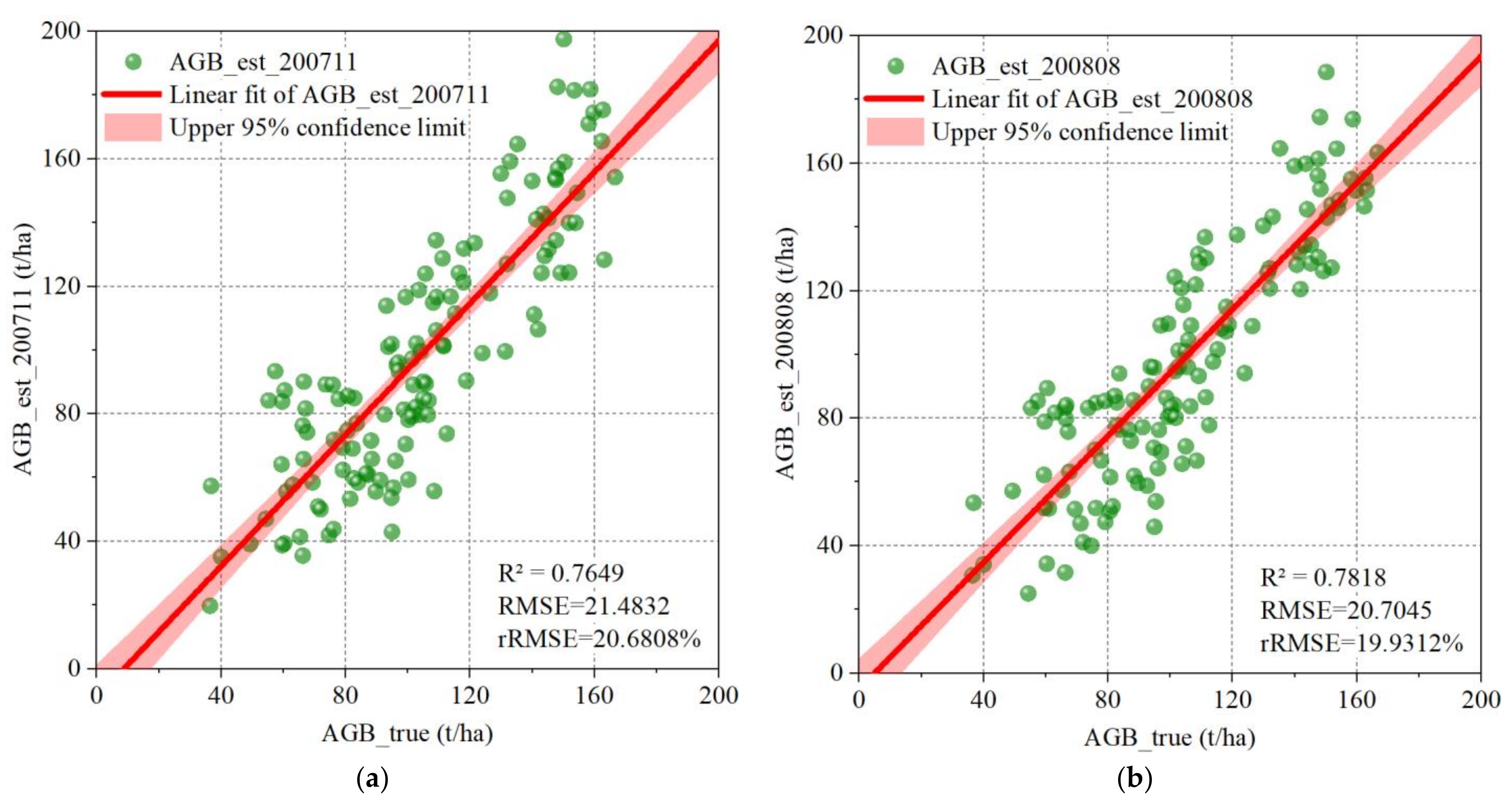
Appendix B
| ID | Features | NRTC/RTC | Significance | ||
|---|---|---|---|---|---|
| R_200711 | R_200725 | R_200808 | |||
| 1 | 0.12/0.58 | 0.16/0.63 | 0.14/0.60 | -/** | |
| 2 | 0.25/0.70 | 0.28/0.73 | 0.27/0.71 | */** | |
| 3 | 0.15/0.61 | 0.18/0.66 | 0.17/0.62 | -/** | |
| 4 | Span | 0.18/0.66 | 0.21/0.71 | 0.20/0.69 | -/** |
| 5 | R_HH/VV | −0.09/−0.09 | −0.10/−0.10 | −0.10/−0.10 | -/- |
| 6 | R_HH/HV | −0.74/−0.73 | −0.77/−0.76 | −0.76/−0.75 | **/** |
| 7 | R_VV/VH | −0.70/−0.69 | −0.74/−0.73 | −0.72/−0.70 | **/** |
| 8 | BMI | 0.14/0.62 | 0.17/0.66 | 0.15/0.65 | -/** |
| 9 | VSI | 0.70/0.67 | 0.73/0.71 | 0.71/0.68 | **/** |
| 10 | RVI | 0.70/0.67 | 0.73/0.71 | 0.71/0.68 | **/** |
| 11 | CSI | 0.091/0.089 | 0.096/0.094 | 0.096/0.095 | -/- |
| 12 | RFDI | −0.65/−0.64 | −0.68/−0.66 | −0.67/−0.65 | **/** |
| 13 | mRFDI | −0.63/−0.61 | −0.66/−0.64 | −0.65/−0.62 | **/** |
| 14 | F2O | 0.14/0.51 | 0.19/0.56 | 0.16/0.53 | -/** |
| 15 | F2V | 0.14/0.51 | 0.17/0.54 | 0.14/0.52 | -/** |
| 16 | F3D | 0.15/0.30 | 0.17/0.31 | 0.19/0.34 | -/* |
| 17 | F3O | 0.04/0.11 | 0.05/0.14 | 0.03/0.10 | -/- |
| 18 | F3V | 0.30/0.72 | 0.32/0.74 | 0.31/0.74 | */** |
| 19 | Y3D | 0.22/0.34 | 0.26/0.36 | 0.24/0.35 | -/* |
| 20 | Y3O | −0.03/0.10 | −0.04/0.15 | −0.04/0.11 | -/- |
| 21 | Y3V | 0.25/0.69 | 0.29/0.73 | 0.28/0.70 | -/** |
| 22 | Y4D | −0.04/0.21 | −0.05/0.23 | −0.04/0.21 | -/- |
| 23 | Y4O | −0.24/−0.44 | −0.25/−0.44 | −0.27/−0.45 | -/* |
| 24 | Y4V | 0.31/0.71 | 0.30/0.71 | 0.30/0.70 | */** |
| 25 | Y4H | 0.08/0.15 | 0.09/0.16 | 0.09/0.18 | -/- |
| 26 | M3D | 0.21/0.49 | 0.23/0.51 | 0.20/0.51 | -/** |
| 27 | M3O | 0.01/0.25 | 0.01/0.29 | 0.01/0.28 | -/- |
| 28 | M3V | 0.32/0.72 | 0.30/0.71 | 0.35/0.74 | */** |
| 29 | M4D | 0.25/0.60 | 0.24/0.58 | 0.22/0.57 | -/** |
| 30 | M4O | 0.01/0.28 | 0.01/0.28 | 0.01/0.30 | -/- |
| 31 | M4V | 0.29/0.71 | 0.30/0.72 | 0.32/0.74 | */** |
| 32 | M4H | 0.06/0.13 | 0.06/0.12 | 0.09/0.15 | -/- |
| 33 | A3D | 0.22/0.45 | 0.20/0.43 | 0.18/0.40 | -/* |
| 34 | A3O | 0.03/0.32 | 0.03/0.31 | 0.03/0.30 | -/- |
| 35 | A3V | 0.31/0.64 | 0.29/0.63 | 0.30/0.63 | -/** |
| 36 | V3D | 0.20/0.46 | 0.22/0.49 | 0.22/0.51 | -/* |
| 37 | V3O | 0.15/0.54 | 0.16/0.54 | 0.18/0.55 | -/** |
| 38 | V3V | 0.32/0.68 | 0.31/0.66 | 0.31/0.65 | */** |
| 39 | H | 0.61/0.62 | 0.61/0.63 | 0.60/0.63 | **/** |
| 40 | A | −0.07/−0.23 | −0.06/−0.23 | −0.07/−0.25 | -/- |
| 41 | α | 0.55/0.51 | 0.57/0.55 | 0.57/0.56 | **/** |
| 42 | C3D | 0.24/0.48 | 0.24/0.49 | 0.26/0.50 | -/* |
| 43 | C3O | 0.30/0.60 | 0.32/0.63 | 0.31/0.60 | -/** |
| 44 | C3V | −0.01/0.15 | −0.02/0.19 | −0.02/0.20 | -/- |
| 45 | K3S | 0.18/0.52 | 0.20/0.55 | 0.21/0.55 | -/** |
| 46 | K3D | 0.31/0.70 | 0.30/0.68 | 0.30/0.67 | */** |
| 47 | K3H | 0.05/0.08 | 0.05/0.08 | 0.05/0.07 | -/- |
| 48 | P3D | 0.20/0.60 | 0.22/0.63 | 0.22/0.65 | -/** |
| 49 | P3O | 0.13/0.52 | 0.14/0.54 | 0.15/0.55 | -/** |
| 50 | A3R_1 | 0.60/0.55 | 0.60/0.56 | 0.61/0.58 | **/** |
| 51 | A3R_2 | 0.62/0.59 | 0.62/0.58 | 0.63/0.60 | **/** |
| 52 | F2R_1 | −0.31/−0.12 | −0.33/−0.13 | −0.37/−0.15 | -/- |
| 53 | F2R_2 | −0.32/−0.15 | −0.34/−0.15 | −0.38/−0.17 | -/- |
| 54 | F3R_1 | 0.61/0.58 | 0.63/0.59 | 0.59/0.55 | **/** |
| 55 | F3R_2 | 0.69/0.60 | 0.70/0.61 | 0.71/0.61 | **/** |
| 56 | V3R_1 | 0.70/0.66 | 0.71/0.68 | 0.69/0.66 | **/** |
| 57 | V3R_2 | 0.72/0.70 | 0.73/0.70 | 0.71/0.69 | **/** |
| 58 | Y3R_1 | 0.65/0.61 | 0.65/0.62 | 0.64/0.60 | **/** |
| 59 | Y3R_2 | 0.70/0.64 | 0.72/0.64 | 0.70/0.63 | **/** |
| 60 | 0.30/0.70 | 0.31/0.72 | 0.31/0.71 | */** | |
| 61 | 0.50/0.81 | 0.54/0.86 | 0.52/0.82 | **/** | |
| 62 | 0.32/0.72 | 0.34/0.75 | 0.34/0.73 | */** | |
| 63 | Span_db | 0.38/0.79 | 0.40/0.82 | 0.40/0.80 | */** |
| 64 | R_HH/VV_db | −0.01/−0.01 | −0.098/−0.096 | −0.10/−0.10 | -/- |
| 65 | R_HH/HV_db | −0.57/−0.65 | −0.71/−0.69 | −0.70/−0.67 | **/** |
| 66 | R_VV/VH_db | −0.62/−0.60 | −0.66/−0.65 | −0.64/−0.63 | **/** |
| 67 | BMI_db | 0.30/0.73 | 0.32/0.76 | 0.30/0.75 | */** |
| 68 | VSI_db | 0.75/0.74 | 0.77/0.75 | 0.78/0.76 | **/** |
| 69 | RVI_db | 0.75/0.74 | 0.77/0.75 | 0.78/0.76 | **/** |
| 70 | CSI_db | 0.10/0.09 | 0.099/0.097 | 0.10/0.10 | -/- |
| 71 | RFDI_db | −0.62/−0.60 | −0.64/−0.61 | −0.65/−0.62 | **/** |
| 72 | mRFDI_db | NaN/NaN | NaN/NaN | NaN/NaN | -/- |
| 73 | F2O_db | 0.36/0.66 | 0.40/0.69 | 0.38/0.67 | */** |
| 74 | F2V_db | 0.23/0.53 | 0.25/0.56 | 0.25/0.54 | -/** |
| 75 | F3D_db | 0.35/0.45 | 0.37/0.46 | 0.38/0.48 | */* |
| 76 | F3O_db | −0.05/0.14 | −0.06/0.16 | −0.04/0.11 | -/- |
| 77 | F3V_db | 0.45/0.81 | 0.47/0.83 | 0.46/0.83 | */** |
| 78 | Y3D_db | 0.36/0.47 | 0.39/0.49 | 0.37/0.47 | */* |
| 79 | Y3O_db | −0.03/0.10 | −0.05/0.14 | −0.05/0.12 | -/- |
| 80 | Y3V_db | 0.42/0.72 | 0.45/0.75 | 0.43/0.72 | */** |
| 81 | Y4D_db | −0.05/0.27 | −0.07/0.29 | −0.05/0.27 | -/- |
| 82 | Y4O_db | −0.39/−0.65 | −0.40/−0.65 | −0.42/−0.67 | */** |
| 83 | Y4V_db | 0.54/0.84 | 0.53/0.84 | 0.53/0.83 | **/** |
| 84 | Y4H_db | 0.16/0.17 | 0.18/0.19 | 0.18/0.20 | -/- |
| 85 | M3D_db | 0.39/0.60 | 0.40/0.62 | 0.38/0.62 | */** |
| 86 | M3O_db | 0.04/0.32 | 0.05/0.35 | 0.05/0.34 | -/* |
| 87 | M3V_db | 0.55/0.83 | 0.54/0.82 | 0.58/0.85 | **/** |
| 88 | M4D_db | 0.41/0.63 | 0.40/0.62 | 0.39/0.60 | */** |
| 89 | M4O_db | 0.05/0.35 | 0.05/0.35 | 0.05/0.37 | -/* |
| 90 | M4V_db | 0.55/0.82 | 0.55/0.83 | 0.56/0.85 | **/** |
| 91 | M4H_db | 0.12/0.17 | 0.12/0.16 | 0.15/0.18 | -/- |
| 92 | A3D_db | 0.39/0.57 | 0.38/0.56 | 0.35/0.52 | */** |
| 93 | A3O_db | 0.05/0.38 | 0.05/0.37 | 0.04/0.35 | -/* |
| 94 | A3V_db | 0.50/0.79 | 0.49/0.79 | 0.49/0.80 | **/** |
| 95 | V3D_db | 0.38/0.55 | 0.41/0.57 | 0.41/0.59 | */** |
| 96 | V3O_db | 0.28/0.63 | 0.29/0.63 | 0.30/0.64 | -/** |
| 97 | V3V_db | 0.46/0.79 | 0.46/0.78 | 0.45/0.76 | **/** |
| 98 | H_db | 0.62/0.63 | 0.62/0.64 | 0.61/0.64 | **/** |
| 99 | A_db | −0.09/−0.06 | 0.08/−0.06 | 0.09/−0.08 | -/- |
| 100 | α_db | 0.54/0.50 | 0.56/0.53 | 0.56/0.54 | **/** |
| 101 | C3D_db | 0.33/0.57 | 0.33/0.58 | 0.35/0.59 | */** |
| 102 | C3O_db | 0.37/0.70 | 0.40/0.72 | 0.38/0.70 | */** |
| 103 | C3V_db | 0.02/0.23 | 0.04/0.26 | 0.04/0.27 | -/- |
| 104 | K3S_db | 0.31/0.58 | 0.34/0.61 | 0.35/0.61 | */** |
| 105 | K3D_db | 0.47/0.78 | 0.46/0.76 | 0.46/0.75 | */** |
| 106 | K3H_db | 0.09/0.09 | 0.089/0.092 | 0.09/0.09 | -/- |
| 107 | P3D_db | 0.35/0.63 | 0.38/0.65 | 0.38/0.67 | */** |
| 108 | P3O_db | 0.27/0.55 | 0.28/0.57 | 0.28/0.58 | -/** |
| 109 | A3R_1_db | 0.65/0.59 | 0.65/0.60 | 0.66/0.63 | **/** |
| 110 | A3R_2_db | 0.66/0.63 | 0.66/0.62 | 0.67/0.64 | **/** |
| 111 | F2R_1_db | −0.32/−0.15 | −0.36/−0.16 | −0.39/−0.18 | */- |
| 112 | F2R_2_db | −0.39/−0.19 | −0.39/−0.19 | −0.39/−0.19 | */- |
| 113 | F3R_1_db | 0.64/0.62 | 0.66/0.63 | 0.61/0.60 | **/** |
| 114 | F3R_2_db | 0.71/0.64 | 0.72/0.65 | 0.73/0.65 | **/** |
| 115 | V3R_1_db | 0.73/0.69 | 0.75/0.71 | 0.73/0.70 | **/** |
| 116 | V3R_2_db | 0.75/0.72 | 0.76/0.72 | 0.75/0.71 | **/** |
| 117 | Y3R_1_db | 0.69/0.64 | 0.69/0.65 | 0.67/0.62 | **/** |
| 118 | Y3R_2_db | 0.73/0.67 | 0.75/0.67 | 0.73/0.66 | **/** |
| Model | R2_RTC | R2_NRTC | rRMSE_RTC (%) | rRMSE_NRTC (%) |
|---|---|---|---|---|
| BysRidge | 0.86334 | 0.69453 | 18.11756 | 22.89453 |
| ARD | 0.86213 | 0.71534 | 18.31867 | 22.57860 |
| Lasso | 0.85586 | 0.68453 | 18.13603 | 23.37506 |
| ElasticNet | 0.84783 | 0.68124 | 18.51316 | 22.56761 |
| Ridge | 0.84704 | 0.64753 | 18.74611 | 23.45273 |
| CatBoost | 0.82521 | 0.73013 | 18.14501 | 22.43760 |
| XGBoost | 0.82202 | 0.74273 | 19.01550 | 21.37638 |
| AdaBoost | 0.81934 | 0.69574 | 18.37307 | 22.45734 |
| ET | 0.79859 | 0.70750 | 18.56786 | 22.89376 |
| RF | 0.78988 | 0.68545 | 18.53375 | 22.45703 |
References
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote Sensing of the Terrestrial Carbon Cycle: A Review of Advances over 50 Years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Sugden, A.; Smith, J.; Pennisi, E. The Future of Forests. Science 2008, 320, 1435. [Google Scholar] [CrossRef]
- Lu, D. The Potential and Challenge of Remote Sensing-based Biomass Estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS Mission: Mapping Global Forest Biomass to Better Understand the Terrestrial Carbon Cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Migolet, P.; Goïta, K.; Pambo, A.F.K.; Mambimba, A.N. Estimation of the Total Dry Aboveground Biomass in the Tropical Forests of Congo Basin Using Optical, LiDAR, and Radar Data. Gisci. Remote Sens. 2022, 59, 431–460. [Google Scholar] [CrossRef]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest Aboveground Biomass Mapping and Estimation across Multiple Spatial Scales Using Model-Based Inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A Tutorial on Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Soja, M.J.; Quegan, S.; d’Alessandro, M.M.; Banda, F.; Scipal, K.; Tebaldini, S.; Ulander, L.M.H. Mapping Above-Ground Biomass in Tropical Forests with Ground-Cancelled P-Band SAR and Limited Reference Data. Remote Sens. Environ. 2021, 253, 112153. [Google Scholar] [CrossRef]
- Tsokas, A.; Rysz, M.; Pardalos, P.M.; Dipple, K. SAR Data Applications in Earth Observation: An Overview. Expert Syst. Appl. 2022, 205, 117342. [Google Scholar] [CrossRef]
- Yan, X.; Li, J.; Smith, A.R.; Yang, D.; Ma, T.; Su, Y.; Shao, J. Evaluation of Machine Learning Methods and Multi-Source Remote Sensing Data Combinations to Construct Forest above-Ground Biomass Models. Int. J. Digit. Earth 2023, 16, 4471–4491. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Qi, J.; Chen, J.; Giannico, V. Estimating Aboveground Biomass in Subtropical Forests of China by Integrating Multisource Remote Sensing and Ground Data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of Multi-Resource Remotely Sensed Data and Allometric Models for Forest Aboveground Biomass Estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, D.; Chen, Q.; Keller, M.; Moran, E.; dos-Santos, M.N.; Bolfe, E.L.; Batistella, M. Examining Effective Use of Data Sources and Modeling Algorithms for Improving Biomass Estimation in a Moist Tropical Forest of the Brazilian Amazon. Int. J. Digit. Earth 2017, 10, 996–1016. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L.; Wang, L. Stacked Sparse Autoencoder Modeling Using the Synergy of Airborne LiDAR and Satellite Optical and SAR Data to Map Forest Above-Ground Biomass. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
- Liao, Z.; He, B.; Quan, X.; Van Dijk, A.I.J.M.; Qiu, S.; Yin, C. Biomass Estimation in Dense Tropical Forest Using Multiple Information from Single-Baseline P-Band PolInSAR Data. Remote Sens. Environ. 2019, 221, 489–507. [Google Scholar] [CrossRef]
- Solberg, S.; Hansen, E.H.; Gobakken, T.; Næssset, E.; Zahabu, E. Biomass and InSAR Height Relationship in a Dense Tropical Forest. Remote Sens. Environ. 2017, 192, 166–175. [Google Scholar] [CrossRef]
- Zeng, P.; Zhang, W.; Li, Y.; Shi, J.; Wang, Z. Forest Total and Component Above-Ground Biomass (AGB) Estimation through C- and L-Band Polarimetric SAR Data. Forests 2022, 13, 442. [Google Scholar] [CrossRef]
- Luo, H.; Qin, S.; Li, J.; Lu, C.; Yue, C.; Ou, G. High-Density Forest AGB Estimation in Tropical Forest Integrated with PolInSAR Multidimensional Features and Optimized Machine Learning Algorithms. Ecol. Indic. 2024, 160, 111878. [Google Scholar] [CrossRef]
- Chowdhury, T.A.; Thiel, C.; Schmullius, C. Growing Stock Volume Estimation from L-Band ALOS PALSAR Polarimetric Coherence in Siberian Forest. Remote Sens. Environ. 2014, 155, 129–144. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. The Potential of ALOS PALSAR Backscatter and InSAR Coherence for Forest Growing Stock Volume Estimation in Central Siberia. Remote Sens. Environ. 2016, 173, 258–273. [Google Scholar] [CrossRef]
- Eini-Zinab, S.; Maghsoudi, Y.; Sayedain, S.A. Assessing the Performance of Indicators Resulting from Three-Component Freeman–Durden Polarimetric SAR Interferometry Decomposition at P-and L-Band in Estimating Tropical Forest Aboveground Biomass. Int. J. Remote Sens. 2020, 41, 433–454. [Google Scholar] [CrossRef]
- Tebaldini, S. Single and Multipolarimetric SAR Tomography of Forested Areas: A Parametric Approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2375–2387. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Zhang, J.; Chen, H.; Chen, E.; Zhao, L.; Zhao, D. Tropical Forest AGB Estimation Based on Structure Parameters Extracted by TomoSAR. Int. J. Appl. Earth Obs. Geoinf. 2023, 121, 103369. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Zhu, J.; Fu, H.; Han, W.; Xie, H. Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data. Forests 2023, 14, 2303. [Google Scholar] [CrossRef]
- Thapa, B.; Lovell, S.; Wilson, J. Remote Sensing and Machine Learning Applications for Aboveground Biomass Estimation in Agroforestry Systems: A Review. Agroforest. Syst. 2023, 97, 1097–1111. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An Evaluation of Eight Machine Learning Regression Algorithms for Forest Aboveground Biomass Estimation from Multiple Satellite Data Products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest Biomass Estimation from Airborne LiDAR Data Using Machine Learning Approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, C.; Zhang, G.; Yang, Z.; Pang, Z.; Luo, Y. A Novel Framework for Forest Above-Ground Biomass Inversion Using Multi-Source Remote Sensing and Deep Learning. Forests 2024, 15, 456. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep Learning Based Retrieval of Forest Aboveground Biomass from Combined LiDAR and Landsat 8 Data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef]
- Oehmcke, S.; Li, L.; Trepekli, K.; Revenga, J.C.; Nord-Larsen, T.; Gieseke, F.; Igel, C. Deep Point Cloud Regression for Above-Ground Forest Biomass Estimation from Airborne LiDAR. Remote Sens. Environ. 2024, 302, 113968. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping Forest Aboveground Biomass in the Northeastern United States with ALOS PALSAR Dual-Polarization L-Band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Peregon, A.; Yamagata, Y. The Use of ALOS/PALSAR Backscatter to Estimate above-Ground Forest Biomass: A Case Study in Western Siberia. Remote Sens. Environ. 2013, 137, 139–146. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature Extraction for Hyperspectral Image Classification: A Review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Nesha, M.K.; Hussin, Y.A.; Van Leeuwen, L.M.; Sulistioadi, Y.B. Modeling and Mapping Aboveground Biomass of the Restored Mangroves Using ALOS-2 PALSAR-2 in East Kalimantan, Indonesia. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102158. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Le Toan, T.; Villard, L.; Mathieu, R.; Naidoo, L.; Asner, G.P. An Above-Ground Biomass Map of African Savannahs and Woodlands at 25 m Resolution Derived from ALOS PALSAR. Remote Sens. Environ. 2018, 206, 156–173. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground Biomass Retrieval in Tropical Forests—The Potential of Combined X- and L-Band SAR Data Use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Loew, A.; Mauser, W. Generation of Geometrically and Radiometrically Terrain Corrected SAR Image Products. Remote Sens. Environ. 2007, 106, 337–349. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, E.; Li, Z.; Zhang, W.; Gu, X. Three-Step Semi-Empirical Radiometric Terrain Correction Approach for PolSAR Data Applied to Forested Areas. Remote Sens. 2017, 9, 269. [Google Scholar] [CrossRef]
- Nie, Y.; Hu, Y.; Sa, R.; Fan, W. Inversion of Forest above Ground Biomass in Mountainous Region Based on PolSAR Data after Terrain Correction: A Case Study from Saihanba, China. Remote Sens. 2024, 16, 846. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, J.; Wang, C.; Lin, H.; Long, J.; Zhao, L.; Fu, H.; Liu, Z. Forest Growing Stock Volume Estimation in Subtropical Mountain Areas Using PALSAR-2 L-Band PolSAR Data. Forests 2019, 10, 276. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Marino, A.; Zeng, P.; Ji, Y.; Zhao, H.; Huang, G.; Wang, M. Forest Total and Component Biomass Retrieval via GA-SVR Algorithm and Quad-Polarimetric SAR Data. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103275. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Li, W.; Liang, S. A Proposed Ensemble Feature Selection Method for Estimating Forest Aboveground Biomass from Multiple Satellite Data. Remote Sens. 2023, 15, 1096. [Google Scholar] [CrossRef]
- Karachristos, K.; Koukiou, G.; Anastassopoulos, V. A Review on PolSAR Decompositions for Feature Extraction. J. Imaging 2024, 10, 75. [Google Scholar] [CrossRef]
- Shang, Z.; Lian, Z.; Li, M.; Han, K.; Zheng, H. Machine-Learning-Assisted Multi-Objective Optimization in Vertical Zone Refining of Ultra-High Purity Indium. Sep. Purif. Technol. 2023, 305, 122430. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature Selection in Machine Learning: A New Perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Xu, L.; Saatchi, S.S.; Yang, Y.; Myneni, R.B.; Frankenberg, C.; Chowdhury, D.; Bi, J. Satellite Observation of Tropical Forest Seasonality: Spatial Patterns of Carbon Exchange in Amazonia. Environ. Res. Lett. 2015, 10, 084005. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Sarram, M.A.; Gharaghani, S.; Chahooki, M.A.Z. A Survey on Semi-Supervised Feature Selection Methods. Pattern Recognit. 2017, 64, 141–158. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature Selection. ACM Comput. Surv. 2018, 50, 1–45. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A Survey on Feature Selection Methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Islam, M.R.; Lima, A.A.; Das, S.C.; Mridha, M.F.; Prodeep, A.R.; Watanobe, Y. A Comprehensive Survey on the Process, Methods, Evaluation, and Challenges of Feature Selection. IEEE Access 2022, 10, 99595–99632. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, L.; Li, Y.; Shi, J.; Yan, M.; Ji, Y. Forest Above-Ground Biomass Inversion Using Optical and SAR Images Based on a Multi-Step Feature Optimized Inversion Model. Remote Sens. 2022, 14, 1608. [Google Scholar] [CrossRef]
- Hsu, H.-H.; Hsieh, C.-W.; Lu, M.-D. Hybrid Feature Selection by Combining Filters and Wrappers. Expert Syst. Appl. 2011, 38, 8144–8150. [Google Scholar] [CrossRef]
- Li, X.; Ren, J. MICQ-IPSO: An Effective Two-Stage Hybrid Feature Selection Algorithm for High-Dimensional Data. Neurocomputing 2022, 501, 328–342. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.; Tien Bui, D. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of Sample Size, Data Type and Prediction Method for Remote Sensing-Based Estimations of Aboveground Forest Biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Schlund, M.; Scipal, K.; Quegan, S. Assessment of a Power Law Relationship Between P-Band SAR Backscatter and Aboveground Biomass and Its Implications for BIOMASS Mission Performance. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2018, 11, 3538–3547. [Google Scholar] [CrossRef]
- Sugimoto, R.; Kato, S.; Nakamura, R.; Tsutsumi, C.; Yamaguchi, Y. Deforestation Detection Using Scattering Power Decomposition and Optimal Averaging of Volume Scattering Power in Tropical Rainforest Regions. Remote Sens. Environ. 2022, 275, 113018. [Google Scholar] [CrossRef]
- Fu, X.; Jiang, D.; Wang, L.; Gao, X.; Qian, D. Study on Biomass of Larixprincipis Rupprechtiiin Saihanba Mechanized Forestry Centre. For. Ecol. Sci. 2015, 30, 113–116. [Google Scholar] [CrossRef]
- Jin, A. Study on the Biomass of the Main Trees at Bayingzhuang Forest Land in Hebei Province. Master’s Thesis, Beijing Forestry University, Beijing, China, 2012. [Google Scholar]
- Chu, C. Study on the Growth of Scotch Pine Plantations and the Variation of Soil Nutrients in Saihanba Aera. Master’s Thesis, Hebei Agricultural University, Baoding, China, 2016. [Google Scholar]
- Cao, J. Above- and Belowground Carbon Pools in Different Ages of Chinese Pine and Oriental Arborvitae Plantation Forests in Northern Mountain Areas of Beijing. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2011. [Google Scholar]
- Yang, L. The Build Study of Acer Truncatum Bunge Biomass Calculation Model in Western Hills of Beijing. Master’s Thesis, Beijing Forestry University, Beijing, China, 2012. [Google Scholar]
- Lee, J.-S.; Schuler, D.L.; Ainsworth, T.L.; Krogager, E.; Kasilingam, D.; Boerner, W.-M. On the Estimation of Radar Polarization Orientation Shifts Induced by Terrain Slopes. IEEE Trans. Geosci. Remote Sens. 2002, 40, 30–41. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Pottier, E.; Ferro-Famil, L. Unsupervised Terrain Classification Preserving Polarimetric Scattering Characteristics. IEEE Trans. Geosci. Remote Sens. 2004, 42, 722–731. [Google Scholar] [CrossRef]
- Gonçalves, F.G.; Santos, J.R.; Treuhaft, R.N. Stem Volume of Tropical Forests from Polarimetric Radar. Int. J. Remote Sens. 2011, 32, 503–522. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual Polarimetric Radar Vegetation Index for Crop Growth Monitoring Using Sentinel-1 SAR Data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Pope, K.O.; Rey-Benayas, J.M.; Paris, J.F. Radar Remote Sensing of Forest and Wetland Ecosystems in the Central American Tropics. Remote Sens. Environ. 1994, 48, 205–219. [Google Scholar] [CrossRef]
- Kim, Y.; Van Zyl, J.J. A Time-Series Approach to Estimate Soil Moisture Using Polarimetric Radar Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2519–2527. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; White, L.J.T.; Abernethy, K.A.; Jeffery, K.J.; Lewis, S.L.; Collins, M.; Lefsky, M.A.; Leal, M.E.; Woodhouse, I.H.; et al. Mapping Tropical Forest Biomass with Radar and Spaceborne LiDAR in Lopé National Park, Gabon: Overcoming Problems of High Biomass and Persistent Cloud. Biogeosciences 2012, 9, 179–191. [Google Scholar] [CrossRef]
- Chhabra, A.; Rüdiger, C.; Yebra, M.; Jagdhuber, T.; Hilton, J. RADAR-Vegetation Structural Perpendicular Index (R-VSPI) for the Quantification of Wildfire Impact and Post-Fire Vegetation Recovery. Remote Sens. 2022, 14, 3132. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a Two-Component Scattering Model to Polarimetric SAR Data From Forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A Three-Component Scattering Model for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-Component Power Decomposition for Polarimetric SAR Data Based on Adaptive Volume Scatter Modeling. Remote Sens. 2012, 4, 1559–1572. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-Component Scattering Model for Polarimetric SAR Image Decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-Based Decomposition of Polarimetric SAR Covariance Matrices Constrained for Nonnegative Eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar] [CrossRef]
- Yang, J.; Peng, Y.-N.; Yamaguchi, Y.; Yamada, H. On Huynen’s Decomposition of a Kennaugh Matrix. IEEE Geosci. Remote Sens. Lett. 2006, 3, 369–372. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharya, A.; Ratha, D.; Mandal, D.; Frery, A.C. Target Characterization and Scattering Power Decomposition for Full and Compact Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3981–3998. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharya, A.; Frery, A.C.; Lopez-Martinez, C.; Rao, Y.S. A Model-Free Four Component Scattering Power Decomposition for Polarimetric SAR Data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2021, 14, 3887–3902. [Google Scholar] [CrossRef]
- Cloude, S.R. Target Decomposition Theorems in Radar Scattering. Electron. Lett. 1985, 21, 22–24. [Google Scholar] [CrossRef]
- Krogager, E. New Decomposition of the Radar Target Scattering Matrix. Electron. Lett. 1990, 26, 1525. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An Entropy Based Classification Scheme for Land Applications of Polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Demirci, S.; Kirik, O.; Ozdemir, C. Interpretation and Analysis of Target Scattering from Fully-Polarized ISAR Images Using Pauli Decomposition Scheme for Target Recognition. IEEE Access 2020, 8, 155926–155938. [Google Scholar] [CrossRef]
- Liu, Z.; Michel, O.O.; Wu, G.; Mao, Y.; Hu, Y.; Fan, W. The Potential of Fully Polarized ALOS-2 Data for Estimating Forest Above-Ground Biomass. Remote Sens. 2022, 14, 669. [Google Scholar] [CrossRef]
- Chang, Q.; Zwieback, S.; DeVries, B.; Berg, A. Application of L-Band SAR for Mapping Tundra Shrub Biomass, Leaf Area Index, and Rainfall Interception. Remote Sens. Environ. 2022, 268, 112747. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Park, S.-E. The Effect of Topography on Target Decomposition of Polarimetric SAR Data. Remote Sens. 2015, 7, 4997–5011. [Google Scholar] [CrossRef]
- Lee, J.-S.; Ainsworth, T.L. The Effect of Orientation Angle Compensation on Coherency Matrix and Polarimetric Target Decompositions. IEEE Trans. Geosci. Remote Sens. 2011, 49, 53–64. [Google Scholar] [CrossRef]
- Li, H.; Li, Q.; Wu, G.; Chen, J.; Liang, S. The Impacts of Building Orientation on Polarimetric Orientation Angle Estimation and Model-Based Decomposition for Multilook Polarimetric SAR Data in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5520–5532. [Google Scholar] [CrossRef]
- Chowdhury, T.; Thiel, C.; Schmullius, C.; Stelmaszczuk-Górska, M. Polarimetric Parameters for Growing Stock Volume Estimation Using ALOS PALSAR L-Band Data over Siberian Forests. Remote Sens. 2013, 5, 5725–5756. [Google Scholar] [CrossRef]
- Soja, M.J.; Sandberg, G.; Ulander, L.M.H. Regression-Based Retrieval of Boreal Forest Biomass in Sloping Terrain Using P-Band SAR Backscatter Intensity Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2646–2665. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.M.H.; Wallerman, J.; Fransson, J.E.S. Measurements of Forest Biomass Change Using P-Band Synthetic Aperture Radar Backscatter. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6047–6061. [Google Scholar] [CrossRef]
- De Almeida, C.T.; Galvão, L.S.; Aragão, L.E.d.O.C.e.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.d.S.; Sato, L.Y.; Lopes, A.P.; Graça, P.M.L.d.A.; Silva, C.V.d.J.; et al. Combining LiDAR and Hyperspectral Data for Aboveground Biomass Modeling in the Brazilian Amazon Using Different Regression Algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Luckman, A. A Study of the Relationship between Radar Backscatter and Regenerating Tropical Forest Biomass for Spaceborne SAR Instruments. Remote Sens. Environ. 1997, 60, 1–13. [Google Scholar] [CrossRef]
- Kc, Y.B.; Liu, Q.; Saud, P.; Xu, C.; Gaire, D.; Adhikari, H. Driving Factors and Spatial Distribution of Aboveground Biomass in the Managed Forest in the Terai Region of Nepal. Forests 2024, 15, 663. [Google Scholar] [CrossRef]
- Narvaes, I.d.S.; dos Santos, J.R.; Bispo, P.d.C.; Graça, P.M.d.A.; Guimarães, U.S.; Gama, F.F. Estimating Forest Above-Ground Biomass in Central Amazonia Using Polarimetric Attributes of ALOS/PALSAR Images. Forests 2023, 14, 941. [Google Scholar] [CrossRef]
- Waqar, M.; Sukmawati, R.; Ji, Y.; Sri Sumantyo, J. Tropical PeatLand Forest Biomass Estimation Using Polarimetric Parameters Extracted from RadarSAT-2 Images. Land 2020, 9, 193. [Google Scholar] [CrossRef]
- Tian, L.; Wu, X.; Tao, Y.; Li, M.; Qian, C.; Liao, L.; Fu, W. Review of Remote Sensing-Based Methods for Forest Aboveground Biomass Estimation: Progress, Challenges, and Prospects. Forests 2023, 14, 1086. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Data formats and processing level | CEOS level 1.1 | Observation mode | HBQ |
| Observation date of scene center | 27.8054° | Radar wavelength | 0.2424525 m |
| Length of range direction | 49.8 km | Range resolution | 2.860844 m |
| Length of azimuth direction | 69.3 km | Azimuth resolution | 2.642742 m |
| Orbit direction | Ascending | Range pixel | 8392 |
| Observation direction | Right looking | Azimuth pixel | 26,105 |
| Tree Species | Allometric Equation | Ref. |
|---|---|---|
| Larix principis-rupprechtii | W = 0.1431 · DBH2.2193 | [60] |
| Betula platyphylla | W = 0.0330 · DBH2.9314 | [61] |
| Pinus sylvestris var. mongolica | W = 0.0930 · DBH2.3429 | [62] |
| Pinus tabuliformis | W = 0.0520 · DBH2.5830 | [63] |
| Acer truncatum | W = 0.1260 · DBH2.3830 | [64] |
| Count | Min (t/ha) | Max (t/ha) | Mean (t/ha) | SD (t/ha) |
|---|---|---|---|---|
| 132 | 36.39 | 166.58 | 103.88 | 32.31 |
| Features | Symbol | Equation | Symbol (dB) | Source |
|---|---|---|---|---|
| Span | Span | Span_db | [67] | |
| Co-Pol HH/VV Ratio | R_HH/VV | R_HH/VV_db | [67] | |
| Cross-Pol HH/HV Ratio | R_HH/HV | R_HH/HV_db | [67] | |
| Cross-Pol VV/VH Ratio | R_VV/VH | R_VV/VH_db | [68] | |
| Biomass Index | BMI | BMI_db | [69] | |
| Volume Scattering Index | VSI | VSI_db | [69] | |
| Canopy Structure Index | CSI | CSI_db | [69] | |
| Radar Vegetation Index | RVI | RVI_db | [70] | |
| Radar Forest Degradation Index | RFDI | RFDI_db | [71] | |
| modified RFDI | mRFDI | mRFDI_db | [72] |
| Decomposition Methods | Abbreviation | Symbol | Source |
|---|---|---|---|
| Freeman two-component | FRE2 | F2V, F2O | [73] |
| Freeman three-component | FRE3 | F3V, F3D, F3O | [74] |
| Yamaguchi three-component | YAM3 | Y3V, Y3D, Y3O | [75] |
| Yamaguchi four-component | YAM4 | Y4V, Y4D, Y4O, Y4H | [76] |
| Van Zyl three-component | VAZ3 | V3V, V3D, V3O | [77] |
| An and Yang three-component | ANY3 | A3V, A3D, A3O | [78] |
| Model-free three-component | MF3CF | M3V, M3D, M3O | [79] |
| Model-free four-component | MF4CF | M4V, M4D, M4O, M4H | [80] |
| Cloude three-component | CLD3 | C3V, C3D, C3O | [81] |
| Krogager three-component | KRO3 | K3S, K3D, K3H | [82] |
| H-A-alpha | HAα | H, A, α | [83] |
| Pauli three-component | PAU3 | P3D, P3O | [84] |
| Symbol | Equation | Symbol (dB) | Source |
|---|---|---|---|
| F2R_1 | F2R_1_db | [85] | |
| F3R_1 | F3R_1_db | [85] | |
| A3R_1 | A3R_1_db | [85] | |
| V3R_1 | V3R_1_db | [85] | |
| Y3R_1 | Y3R_1_db | [85] | |
| F2R_2 | F2R_2_db | [86] | |
| F3R_2 | F3R_2_db | [86] | |
| A3R_2 | A3R_2_db | [86] | |
| V3R_2 | V3R_2_db | [86] | |
| Y3R_2 | Y3R_2_db | [86] |
| Model | Python Package | Module | Estimator | Category |
|---|---|---|---|---|
| Ridge | scikit-learn (v1.4.2) | sklearn.linear_model | Ridge | linear |
| Lasso | scikit-learn (v1.4.2) | sklearn.linear_model | Lasso | linear |
| ElasticNet | scikit-learn (v1.4.2) | sklearn.linear_model | ElasticNet | linear |
| BysRidge | scikit-learn (v1.4.2) | sklearn.linear_model | BayesianRidge | linear |
| ARD | scikit-learn (v1.4.2) | sklearn.linear_model | ARDRegression | linear |
| RF | scikit-learn (v1.4.2) | sklearn.ensemble | RandomForestRegressor | non-parametric |
| ET | scikit-learn (v1.4.2) | sklearn.ensemble | ExtraTreesRegressor | non-parametric |
| AdaBoost | scikit-learn (v1.4.2) | sklearn.ensemble | AdaBoostRegressor | non-parametric |
| XGBoost | xgboost (v2.0.3) | xgboost | XGBRegressor | non-parametric |
| CatBoost | catboost (v1.2.3) | catboost | CatBoostRegressor | non-parametric |
| Algorithm | Boruta | RFECV | RF | Optuna |
|---|---|---|---|---|
| package | Boruta (v0.3) | scikit-learn (v1.4.2) | scikit-learn (v1.4.2) | Optuna (v3.6.0) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Sa, R.; Chumachenko, S.; Hu, Y.; Wang, Y.; Fan, W. Inversion of Forest Aboveground Biomass in Regions with Complex Terrain Based on PolSAR Data and a Machine Learning Model: Radiometric Terrain Correction Assessment. Remote Sens. 2024, 16, 2229. https://doi.org/10.3390/rs16122229
Nie Y, Sa R, Chumachenko S, Hu Y, Wang Y, Fan W. Inversion of Forest Aboveground Biomass in Regions with Complex Terrain Based on PolSAR Data and a Machine Learning Model: Radiometric Terrain Correction Assessment. Remote Sensing. 2024; 16(12):2229. https://doi.org/10.3390/rs16122229
Chicago/Turabian StyleNie, Yonghui, Rula Sa, Sergey Chumachenko, Yifan Hu, Youzhu Wang, and Wenyi Fan. 2024. "Inversion of Forest Aboveground Biomass in Regions with Complex Terrain Based on PolSAR Data and a Machine Learning Model: Radiometric Terrain Correction Assessment" Remote Sensing 16, no. 12: 2229. https://doi.org/10.3390/rs16122229
APA StyleNie, Y., Sa, R., Chumachenko, S., Hu, Y., Wang, Y., & Fan, W. (2024). Inversion of Forest Aboveground Biomass in Regions with Complex Terrain Based on PolSAR Data and a Machine Learning Model: Radiometric Terrain Correction Assessment. Remote Sensing, 16(12), 2229. https://doi.org/10.3390/rs16122229









