Global Navigation Satellite System/Inertial Measurement Unit/Camera/HD Map Integrated Localization for Autonomous Vehicles in Challenging Urban Tunnel Scenarios
Abstract
1. Introduction
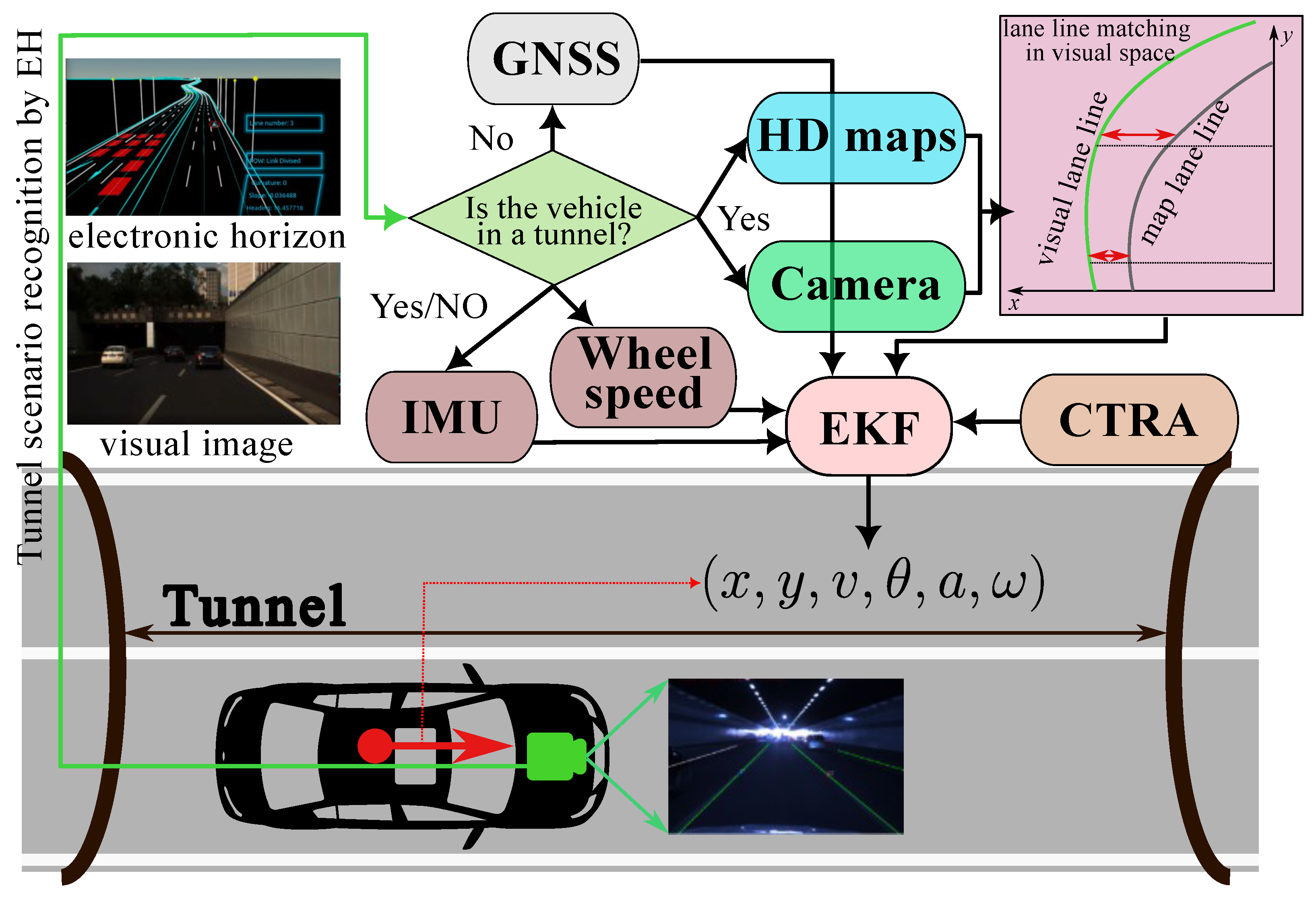
- EKF-Based Multiple-Sensor and HD Map Fusion Framework with Electronic Horizon: We propose an EKF-based fusion framework that integrates multiple sensors and HD maps via an EH to achieve lane-level localization in challenging urban tunnel scenes using mass-production-level sensors. Our system leverages HD maps and an EH to complement the GNSS and IMU sensors. We firstly use an improved BiSeNet to recognize lane lines from images captured by an on-board camera; these lane lines are then matched with HD map data managed by the EH module. The accurate geometric information obtained from this matching process is then used to correct the EKF estimations in GNSS-denied tunnel scenarios.
- Improving GNSS Integrity with HD Maps and EH Technologies: We enhance GNSS integrity in automotive applications by using HD maps and EH technologies to identify GNSS-denied scenarios. This allows us to flexibly switch between sensor measurements derived from the GNSS, camera, and HD maps based on the current scenario.
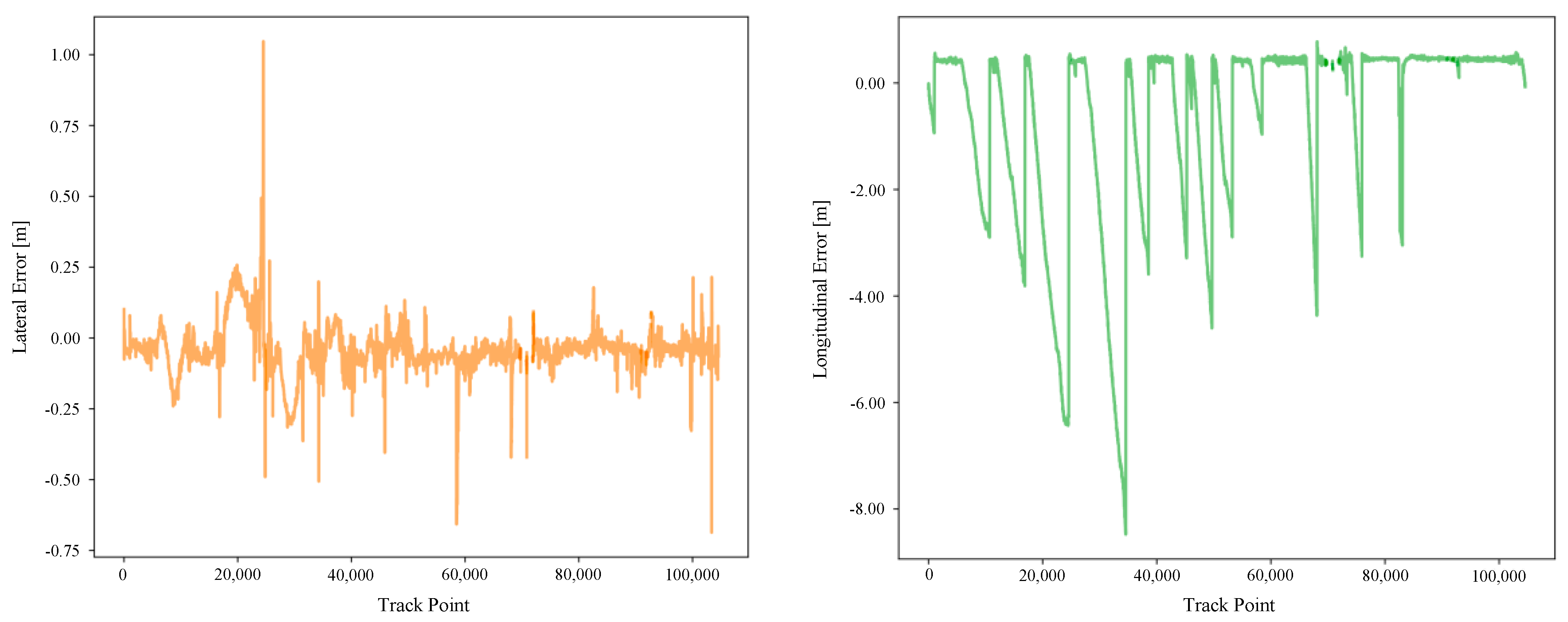
- Comprehensive Evaluation: The proposed method is evaluated using a challenging urban route where 35% of roads are within tunnels, lacking GNSS signals. The experimental results demonstrate that 99% of lateral localization errors are less than 0.29 m and 90% of longitudinal localization errors are less than 3.25 m, ensuring reliable lane-level localization throughout the entire trip.
2. Related Work
3. System Overview
- 1.
- Initial Position Acquisition: A GNSS (e.g., GPS) is used to acquire the initial position.
- 2.
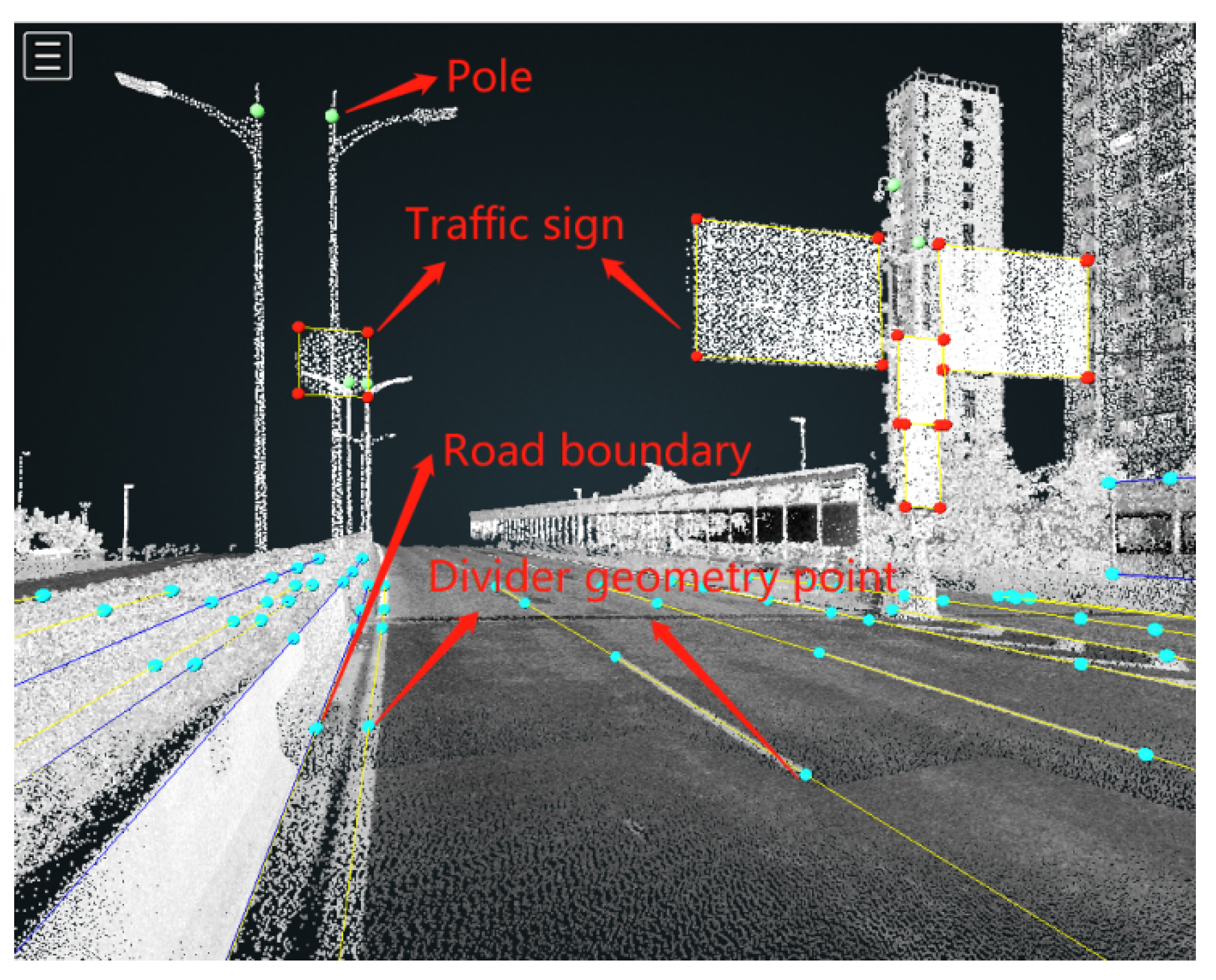
- HD Map Data Loading: An electronic horizon (EH) module is utilized to load sub-HD map data.
- 3.
- Lane Line Recognition and Representation: An improved BiSeNet (iBiSeNet) is used to recognize lane lines from camera images. These lane lines are then represented by cubic polynomials fitted using a weighted least squares (WLS) method.
- 4.
- Lane Line Matching and Pose Correction: The lane lines extracted from images are matched to the corresponding segments in HD maps using the Levenberg–Marquardt (LM) method. Consequently, accurate pose corrections are derived from the HD maps.
- 5.
- Motion Inference: Simultaneously with steps 1–4, IMU and vehicle wheel speedometer data are employed to infer vehicular motion based on the initial location.
- 6.
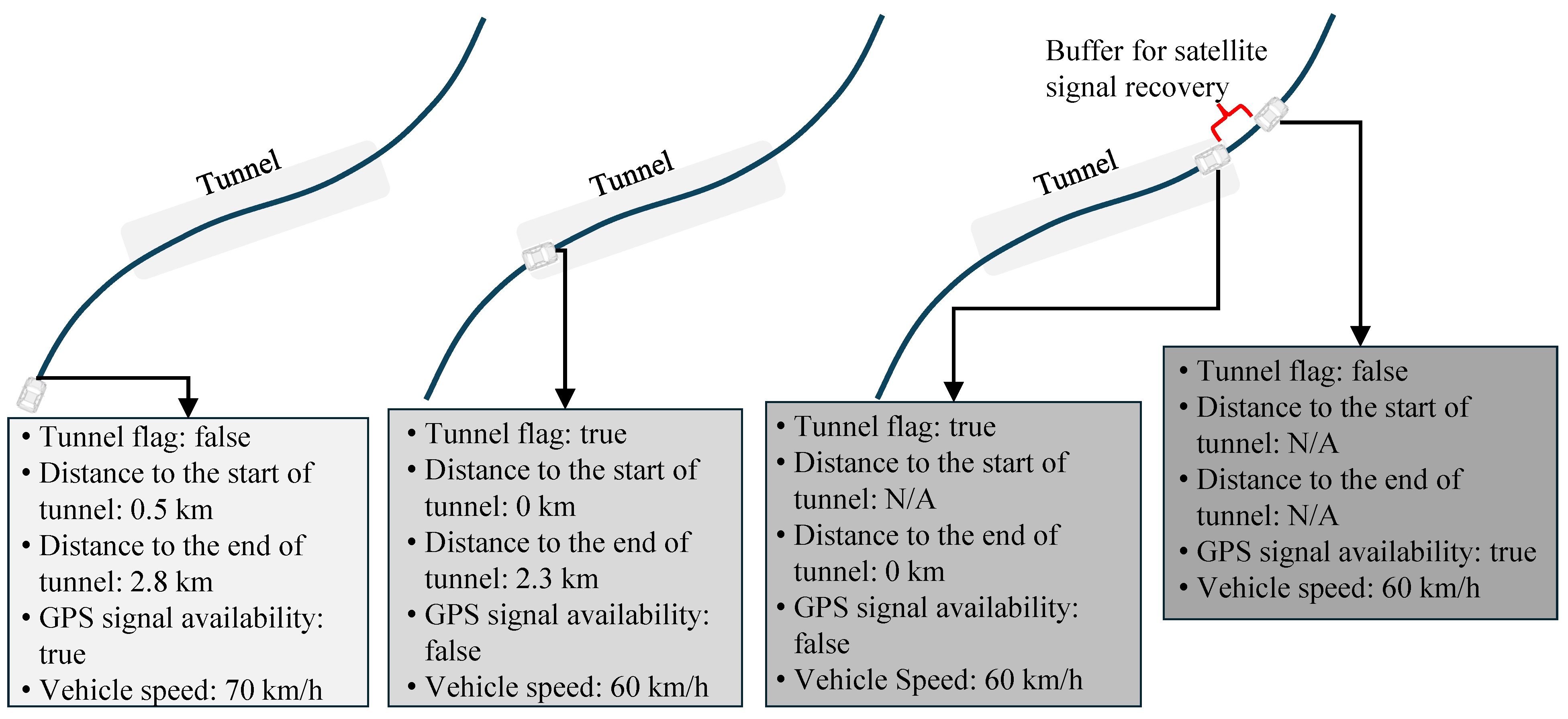
- Tunnel Scenario Identification: According to the sub-HD map constructed by the EH and the current vehicular position, tunnel scenarios are identified. If the vehicle is within a tunnel, camera and HD map matching is applied at 30 Hz; otherwise, GNSS measurements are used at 10 Hz.
- 7.
- Localization Update: The localization result is updated through the EKF, and the optimal pose is set as the initial pose at the next time step.
4. GNSS/IMU/Camera/HD Map Integrated Localization
4.1. Road Scenario Identification Based on Electronic Horizon
4.2. Lane Line Recognition Based on Deep Learning Method
- We incorporate both local attention and multi-scale attention mechanisms, in contrast to the original BiSeNet, which uses only classic attention.
- We restore images by 4 times, 4 times, and 8 times deconvolution in the last three output steps, whereas the original BiSeNet employs 8 times, 8 times, and 16 times upsampling in its last three output layers.
4.3. Matching between Visual Lane Lines and HD Map Lane Lines
4.4. Multi-Source Information Fusion for Vehicular Localization Using EKF
- If a vehicle is outside a tunnel, the position measurements are directly derived from the GNSS at 10 Hz:
- If the vehicle is driving in a tunnel, where the GNSS signals are unavailable, the vehicle’s pose measurements are obtained through vision-and-HD-map matching at 30 Hz:
- The IMU and wheel speed measurements, which remain obtainable, are directly used to update the vehicle’s acceleration, yaw rate, and velocity at 100 Hz:
5. Experiments
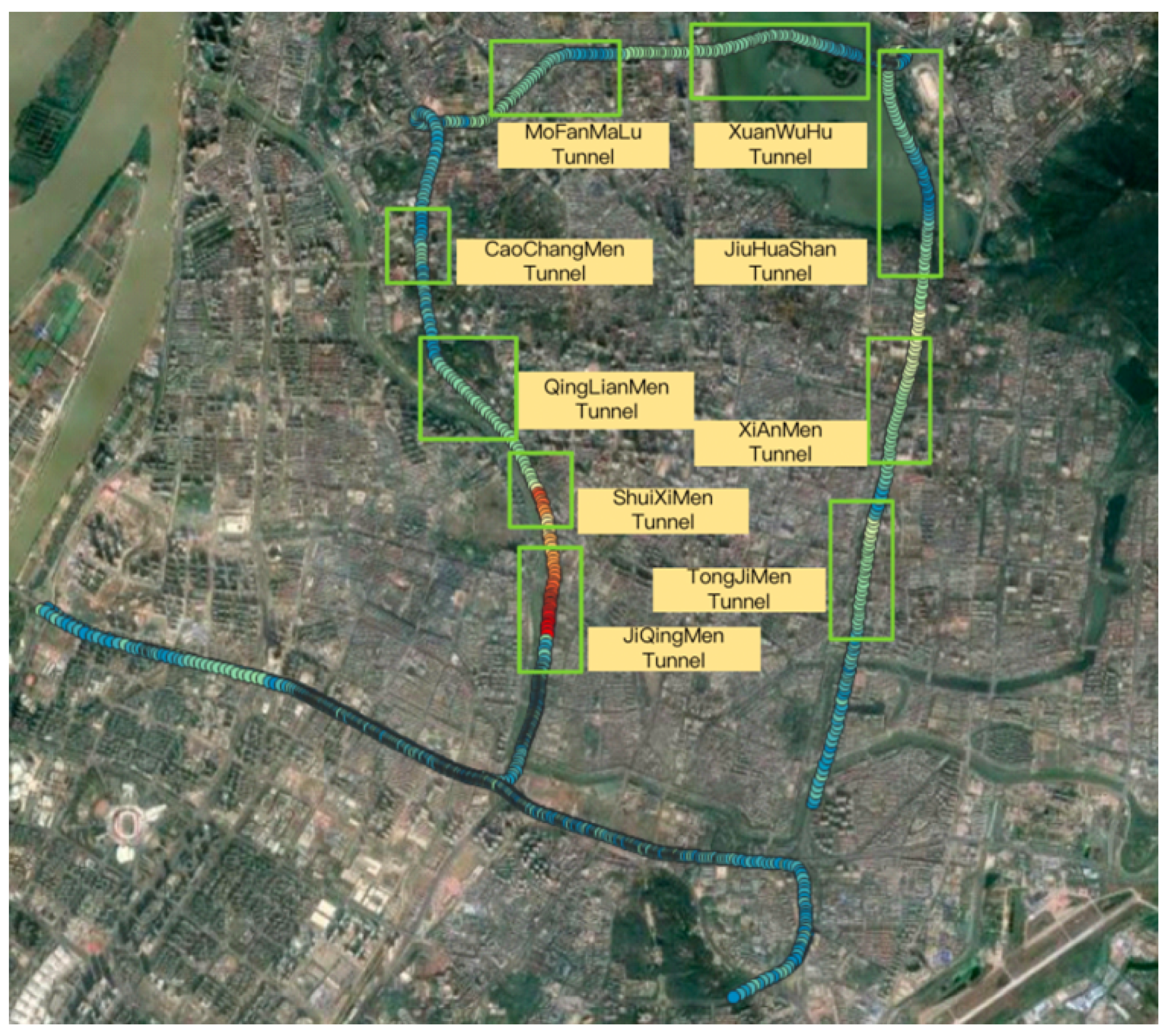
5.1. Experimental Configurations
5.2. Error Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Groves, P.D. Principles of gnss, inertial, and multisensor integrated navigation systems, [book review]. IEEE Aerosp. Electron. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Jackson, J.; Davis, B.; Gebre-Egziabher, D. A performance assessment of low-cost rtk gnss receivers. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 642–649. [Google Scholar]
- Binder, Y.I. Dead reckoning using an attitude and heading reference system based on a free gyro with equatorial orientation. Gyroscopy And Navig. 2017, 8, 104–114. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Zaminpardaz, S.; Teunissen, P.J. Analysis of galileo iov+ foc signals and e5 rtk performance. GPS Solut. 2017, 21, 1855–1870. [Google Scholar] [CrossRef]
- Qin, H.; Peng, Y.; Zhang, W. Vehicles on rfid: Error-cognitive vehicle localization in gps-less environments. IEEE Trans. Veh. 2017, 66, 9943–9957. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive kalman filter for integrated ins/gps navigation of autonomous vehicles. Mech. Syst. Signal Process. 2018, 100, 605–616. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Loam: Lidar odometry and mapping in real-time. In Robotics: Science and Systems; The MIT Press: Berkeley, CA, USA, 2014; Volume 2, pp. 1–9. [Google Scholar]
- Joshi, A.; James, M.R. Generation of accurate lane-level maps from coarse prior maps and lidar. IEEE Intell. Transp. Syst. 2015, 7, 19–29. [Google Scholar] [CrossRef]
- Chen, A.; Ramanandan, A.; Farrell, J.A. High-precision lane-level road map building for vehicle navigation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 1035–1042. [Google Scholar]
- Nedevschi, S.; Popescu, V.; Danescu, R.; Marita, T.; Oniga, F. Accurate ego-vehicle global localization at intersections through alignment of visual data with digital map. IEEE Trans. Intell. Transp. Syst. 2012, 14, 673–687. [Google Scholar] [CrossRef]
- Strijbosch, W. Safe autonomous driving with high-definition maps. ATZ Worldw. 2018, 120, 28–33. [Google Scholar] [CrossRef]
- Varnhagen, R. Electronic Horizon: A Map as a Sensor and Predictive Control; SAE Technical Paper: Warrendale, PA, USA, 2017. [Google Scholar]
- Horita, Y.; Schwartz, R.S. Extended electronic horizon for automated driving. In Proceedings of the 2015 14th International Conference on ITS Telecommunications (ITST), Copenhagen, Denmark, 2–4 December 2015; pp. 32–36. [Google Scholar]
- Ress, C.; Etemad, A.; Kuck, D.; Requejo, J. Electronic horizon-providing digital map data for adas applications. In Proceedings of the 2nd International Workshop on Intelligent Vehicle Control Systems (IVCS), Madeira, Portugal, 11–15 May 2008; Volume 2008, pp. 40–49. [Google Scholar]
- Ress, C.; Balzer, D.; Bracht, A.; Durekovic, S.; Löwenau, J. Adasis protocol for advanced in-vehicle applications. In Proceedings of the 15th World Congress on Intelligent Transport Systems, New York, NY, USA, 16–20 November 2008; Volume 7. [Google Scholar]
- Durekovic, S.; Smith, N. Architectures of map-supported adas. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 207–211. [Google Scholar]
- Wiesner, C.A.; Ruf, M.; Sirim, D.; Klinker, G. Visualisation of the electronic horizon in head-up-displays. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR-Adjunct), Merida, Mexico, 19–23 September 2016; pp. 87–89. [Google Scholar]
- Gao, B.; Hu, G.; Zhu, X.; Zhong, Y. A robust cubature kalman filter with abnormal observations identification using the mahalanobis distance criterion for vehicular ins/gnss integration. Sensors 2019, 19, 5149. [Google Scholar] [CrossRef]
- Gao, G.; Gao, B.; Gao, S.; Hu, G.; Zhong, Y. A hypothesis test-constrained robust kalman filter for ins/gnss integration with abnormal measurement. IEEE Trans. Veh. Technol. 2022, 72, 1662–1673. [Google Scholar] [CrossRef]
- Gao, G.; Zhong, Y.; Gao, S.; Gao, B. Double-channel sequential probability ratio test for failure detection in multisensor integrated systems. IEEE Trans. Instrum. Meas. 2021, 70, 3514814. [Google Scholar] [CrossRef]
- Cvišić, I.; Marković, I.; Petrović, I. Soft2: Stereo visual odometry for road vehicles based on a point-to-epipolar-line metric. IEEE Trans. Robot. 2022, 39, 273–288. [Google Scholar] [CrossRef]
- Fraundorfer, F.; Scaramuzza, D. Visual odometry: Part i: The first 30 years and fundamentals. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. The Kitti Vision Benchmark Suite. Available online: http://www.cvlibs.net/datasets/kitti (accessed on 24 May 2024).
- Schreiber, M.; Knöppel, C.; Franke, U. Laneloc: Lane marking based localization using highly accurate maps. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast, QLD, Australia, 23–26 June 2013; pp. 449–454. [Google Scholar]
- Dickmanns, E.D.; Zapp, A. A curvature-based scheme for improving road vehicle guidance by computer vision. In Mobile Robots I; SPIE: Bellingham, WA, USA, 1987; Volume 727, pp. 161–168. [Google Scholar]
- Gruyer, D.; Belaroussi, R.; Revilloud, M. Map-aided localization with lateral perception. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 674–680. [Google Scholar]
- Xiao, Z.; Yang, D.; Wen, F.; Jiang, K. A unified multiple-target positioning framework for intelligent connected vehicles. Sensors 2019, 19, 1967. [Google Scholar] [CrossRef] [PubMed]
- Cui, D.; Xue, J.; Zheng, N. Real-time global localization of robotic cars in lane level via lane marking detection and shape registration. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1039–1050. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, D.; Wen, T.; Jiang, K.; Yan, R. Monocular localization with vector hd map (mlvhm): A low-cost method for commercial ivs. Sensors 2020, 20, 1870. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xue, C.; Zhou, Y.; Wen, F.; Zhang, H. Visual semantic localization based on hd map for autonomous vehicles in urban scenarios. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11255–11261. [Google Scholar]
- Wen, T.; Xiao, Z.; Wijaya, B.; Jiang, K.; Yang, M.; Yang, D. High precision vehicle localization based on tightly-coupled visual odometry and vector hd map. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 672–679. [Google Scholar]
- Guo, C.; Lin, M.; Guo, H.; Liang, P.; Cheng, E. Coarse-to-fine semantic localization with hd map for autonomous driving in structural scenes. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 1146–1153. [Google Scholar]
- Wen, T.; Jiang, K.; Wijaya, B.; Li, H.; Yang, M.; Yang, D. Tm 3 loc: Tightly-coupled monocular map matching for high precision vehicle localization. IEEE Trans. Intell. Transp. 2022, 23, 20268–20281. [Google Scholar] [CrossRef]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. Bisenet: Bilateral segmentation network for real-time semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 325–341. [Google Scholar]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. Bisenet v2: Bilateral network with guided aggregation for real-time semantic segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Wan, G.; Yang, X.; Cai, R.; Li, H.; Zhou, Y.; Wang, H.; Song, S. Robust and precise vehicle localization based on multi-sensor fusion in diverse city scenes. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4670–4677. [Google Scholar]
- Wu, C.-H.; Su, W.-H.; Ho, Y.-W. A study on gps gdop approximation using support-vector machines. IEEE Trans. Instrum. Meas. 2010, 60, 137–145. [Google Scholar] [CrossRef]
- Aboutaleb, A.; El-Wakeel, A.S.; Elghamrawy, H.; Noureldin, A. Lidar/riss/gnss dynamic integration for land vehicle robust positioning in challenging gnss environments. Remote Sens. 2020, 12, 2323. [Google Scholar] [CrossRef]
- Skog, I.; Handel, P. In-car positioning and navigation technologies-a survey. IEEE Trans. Intell. Transp. Syst. 2009, 10, 4–21. [Google Scholar] [CrossRef]
- Lecce, V.D.; Amato, A. Route planning and user interface for an advanced intelligent transport system. IET Intell. Transp. Syst. 2011, 5, 149–158. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, M.; Liu, J. Real-time hd map change detection for crowdsourcing update based on mid-to-high-end sensors. Sensors 2021, 21, 2477. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.; Youn, J.; Sull, S. Efficient lane detection based on spatiotemporal images. IEEE Trans. Intell. Transp. Syst. 2015, 17, 289–295. [Google Scholar] [CrossRef]
- Caprile, B.; Torre, V. Using vanishing points for camera calibration. Int. J. Comput. Vis. 1990, 4, 127–139. [Google Scholar] [CrossRef]
- Moré, J.J. The levenberg-marquardt algorithm: Implementation and theory. In Numerical Analysis: Proceedings of the Biennial Conference, Dundee, UK, 28 June–1 July 1977; Springer: Cham, Switzerland, 2006; pp. 105–116. [Google Scholar]
- Hu, G.; Xu, L.; Gao, B.; Chang, L.; Zhong, Y. Robust unscented kalman filter based decentralized multi-sensor information fusion for ins/gnss/cns integration in hypersonic vehicle navigation. IEEE Trans. Instrum. Meas. 2023, 72, 8504011. [Google Scholar] [CrossRef]
- Tao, L.; Watanabe, Y.; Yamada, S.; Takada, H. Comparative evaluation of kalman filters and motion models in vehicular state estimation and path prediction. J. Navig. 2021, 74, 1142–1160. [Google Scholar] [CrossRef]
- Tao, L.; Watanabe, Y.; Takada, H. Geo-spatial and temporal relation driven vehicle motion prediction: A geographic perspective. IEEE Trans. Intell. Veh. 2024. early access. [Google Scholar] [CrossRef]
- Liu, J.; Gao, K.; Guo, W.; Cui, J.; Guo, C. Role, path, and vision of “5g+ bds/gnss”. Satell. Navig. 2020, 1, 23. [Google Scholar] [CrossRef]







| Method | Recall | Pixel Accuracy | IOU | Speed |
|---|---|---|---|---|
| Ours | 92.42% | 96.81% | 89.69% | 31 FPS |
| BiSeNet | – | – | 74.70% | 65.5 FPS |
| Tunnel | JiQingMen | ShuiXiMen | QingLiangMen | CaoChangMen | MoFanMaLu |
| Tunnel Length | 0.59 km | 0.56 km | 0.87 km | 0.74 km | 1.45 km |
| Tunnel | XuanWuHu | JiuHuaShan | XiAnMen | TongJiMen | Total tunnel length |
| Tunnel Length | 2.66 km | 2.78 km | 1.77 km | 1.44 km | 12.86 km |
| Route length | 36.38 km | 12.86/36.38 = 35% | |||
| Item | Lateral Error (m) | Longitudinal Error (m) | Yaw Error (Degree) |
|---|---|---|---|
| MAE | 0.041 | 0.701 | 0.899 |
| StD | 0.086 | 1.827 | 0.669 |
| Percentile | Lateral MAE (m) | Longitudinal MAE (m) | Yaw MAE (Degree) |
|---|---|---|---|
| 50% | 0.051 | 0.454 | 0.890 |
| 75% | 0.078 | 1.452 | 1.028 |
| 80% | 0.087 | 2.039 | 1.072 |
| 85% | 0.103 | 2.671 | 1.132 |
| 90% | 0.138 | 3.251 | 1.233 |
| 95% | 0.203 | 4.869 | 1.474 |
| 99% | 0.299 | 7.111 | 3.758 |
| Item | Lateral Error (m) | Longitudinal Error (m) | Yaw Error (Degree) |
|---|---|---|---|
| MAE | 4.638 | 16.546 | 2.960 |
| StD | 20.851 | 59.208 | 0.575 |
| Percentile | Lateral MAE (m) | Longitudinal MAE (m) | Yaw MAE (Degree) |
|---|---|---|---|
| 50% | 0.152 | 1.227 | 2.882 |
| 75% | 3.845 | 33.454 | 3.273 |
| 80% | 6.466 | 51.796 | 3.378 |
| 85% | 10.806 | 70.849 | 3.486 |
| 90% | 19.039 | 98.656 | 3.660 |
| 95% | 45.293 | 152.676 | 4.207 |
| 99% | 126.262 | 231.995 | 4.774 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, L.; Zhang, P.; Gao, K.; Liu, J. Global Navigation Satellite System/Inertial Measurement Unit/Camera/HD Map Integrated Localization for Autonomous Vehicles in Challenging Urban Tunnel Scenarios. Remote Sens. 2024, 16, 2230. https://doi.org/10.3390/rs16122230
Tao L, Zhang P, Gao K, Liu J. Global Navigation Satellite System/Inertial Measurement Unit/Camera/HD Map Integrated Localization for Autonomous Vehicles in Challenging Urban Tunnel Scenarios. Remote Sensing. 2024; 16(12):2230. https://doi.org/10.3390/rs16122230
Chicago/Turabian StyleTao, Lu, Pan Zhang, Kefu Gao, and Jingnan Liu. 2024. "Global Navigation Satellite System/Inertial Measurement Unit/Camera/HD Map Integrated Localization for Autonomous Vehicles in Challenging Urban Tunnel Scenarios" Remote Sensing 16, no. 12: 2230. https://doi.org/10.3390/rs16122230
APA StyleTao, L., Zhang, P., Gao, K., & Liu, J. (2024). Global Navigation Satellite System/Inertial Measurement Unit/Camera/HD Map Integrated Localization for Autonomous Vehicles in Challenging Urban Tunnel Scenarios. Remote Sensing, 16(12), 2230. https://doi.org/10.3390/rs16122230







