A New Retrieval Algorithm of Fractional Snow over the Tibetan Plateau Derived from AVH09C1
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. AVHRR Dataset
2.3. MODIS Dataset
2.4. Ground Observations and Reanalysis Dataset
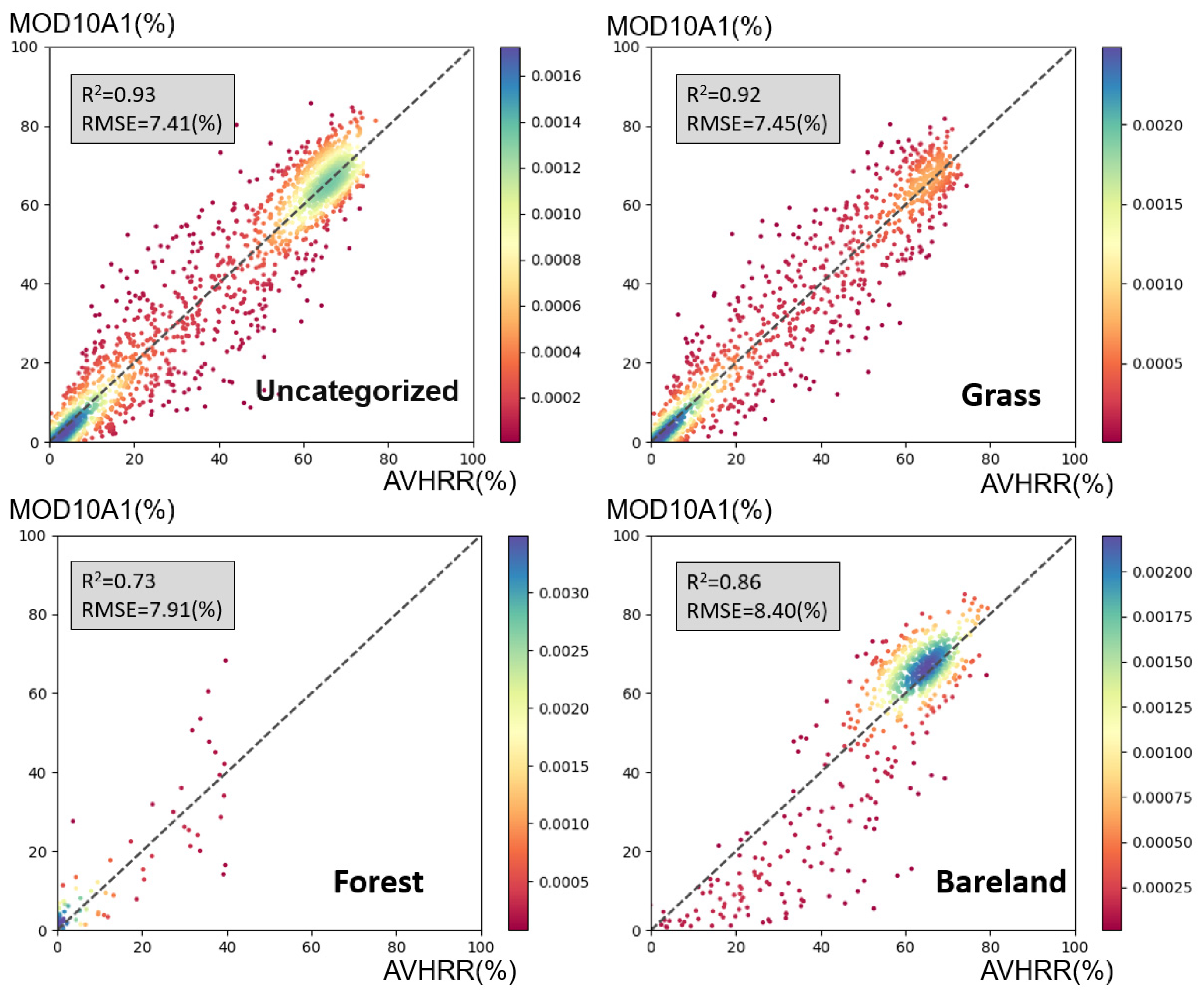
2.5. Land-Cover Type
3. Methods
3.1. Cloud Detection
3.2. Inversion Algorithm of AVHRR FSC
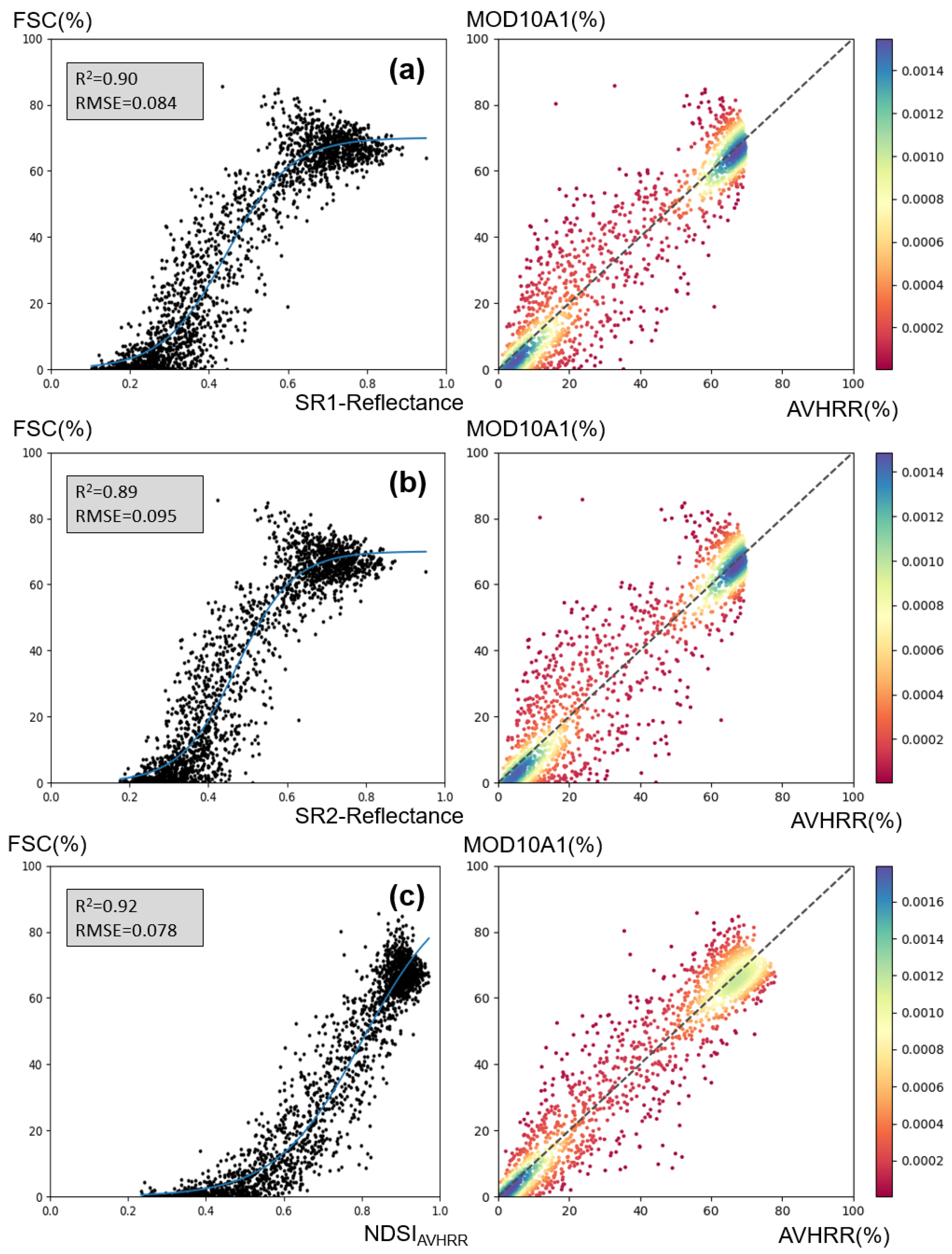
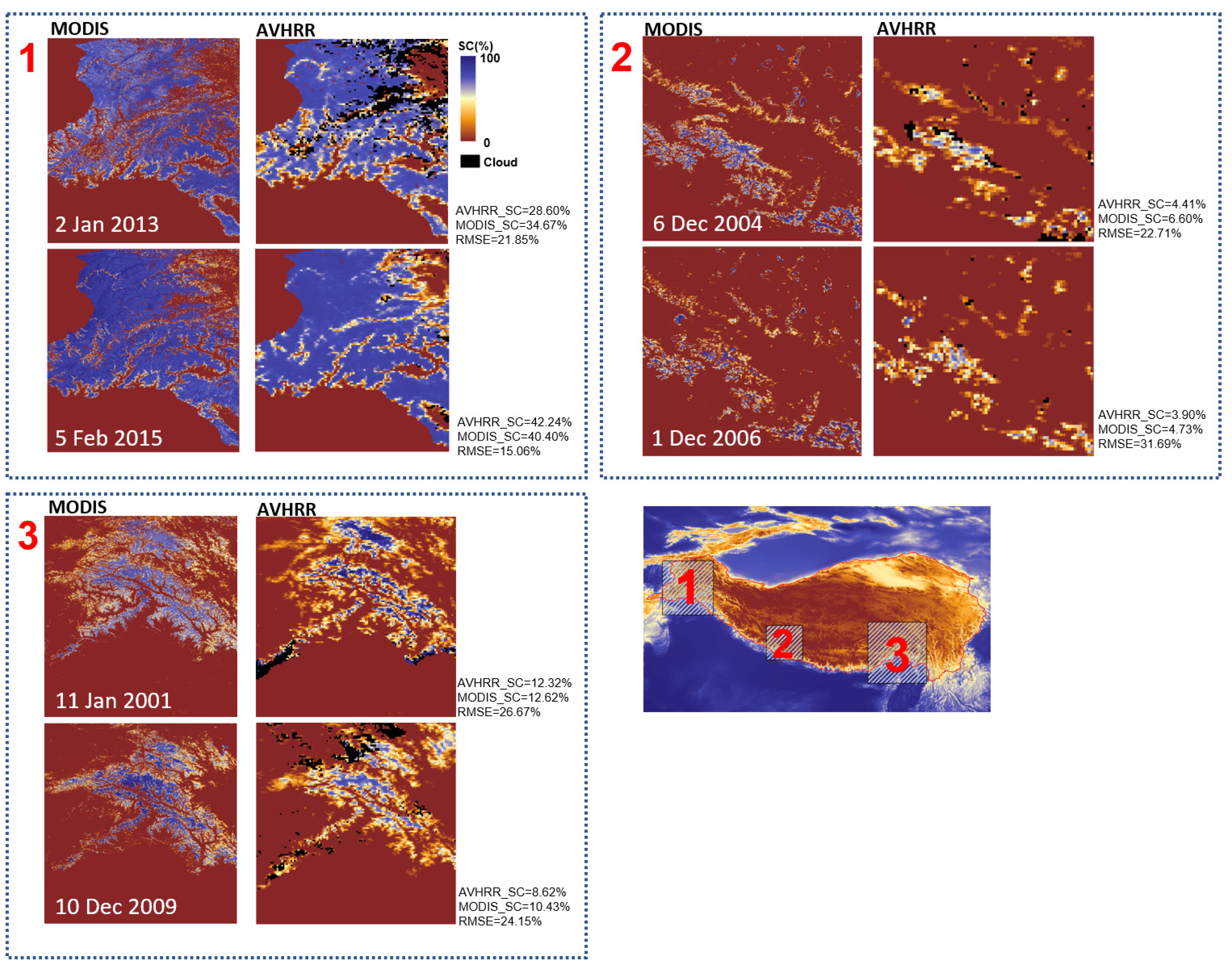
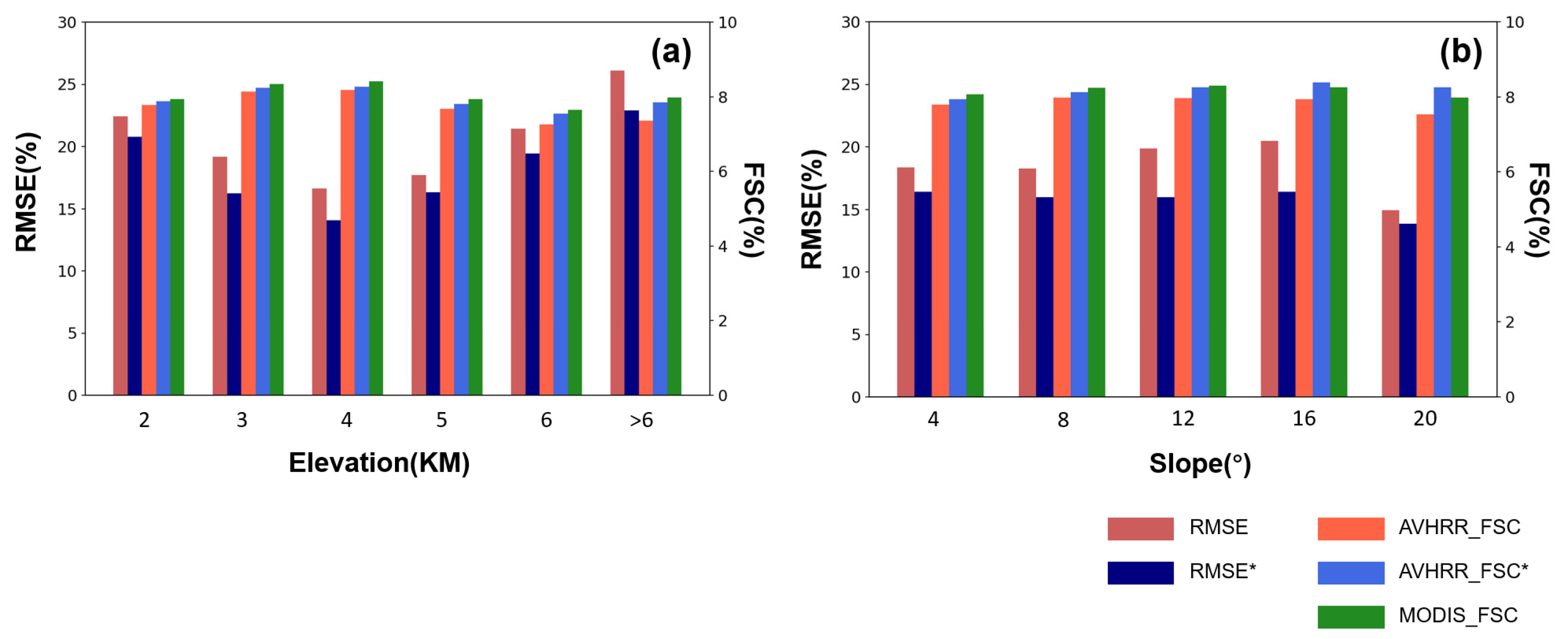
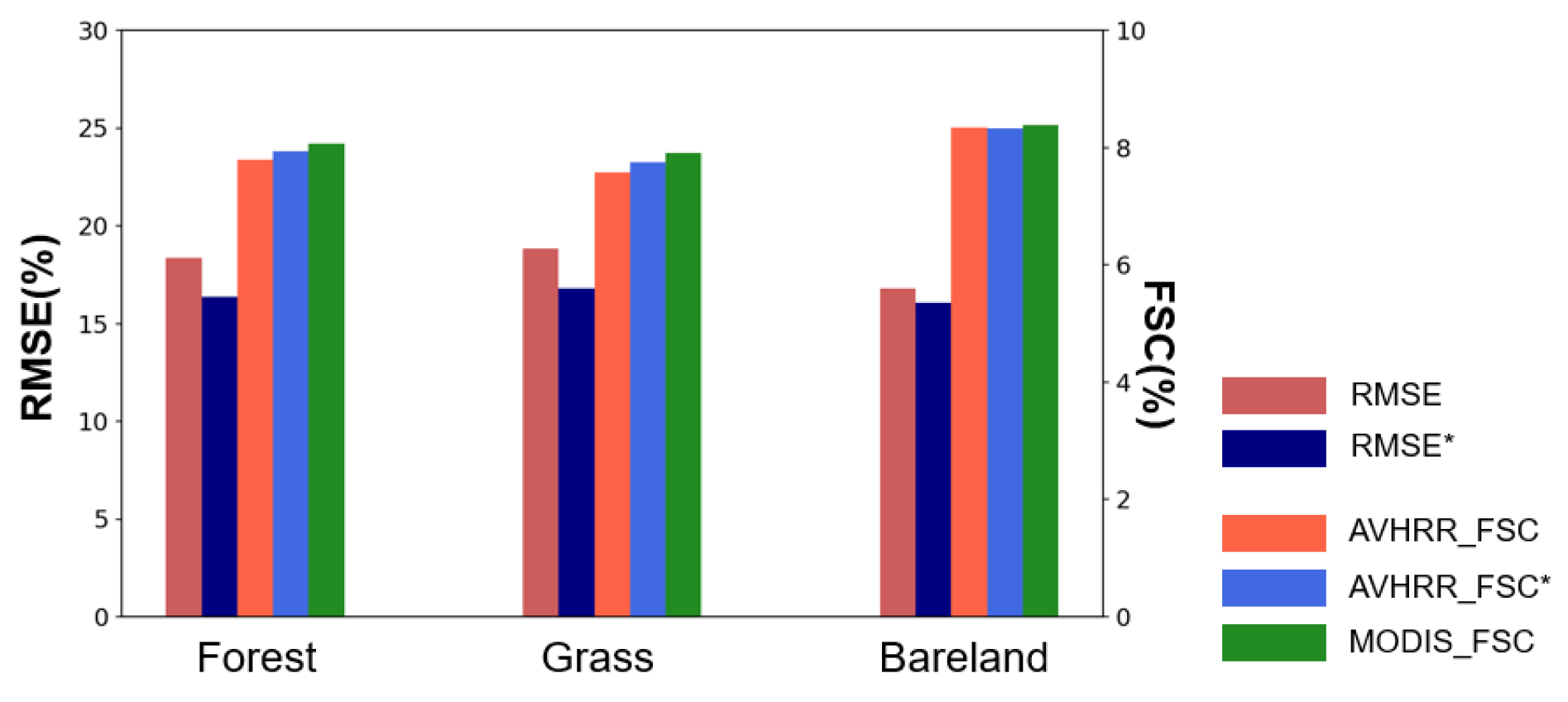
4. Accuracies of the AVHRR FSC Product
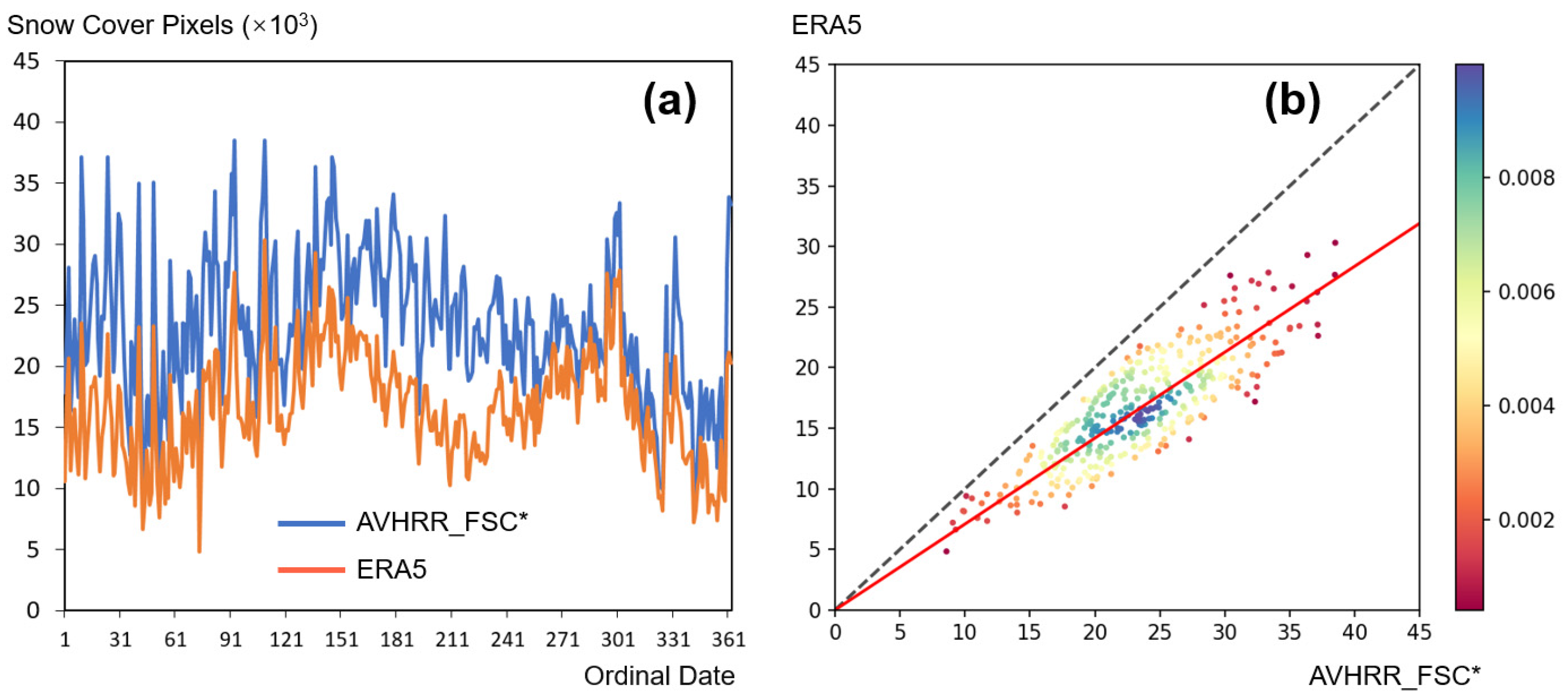
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simpson, J.J.; Stitt, J.R.; Sienko, M. Improved Estimates of the Areal Extent of Snow Cover from AVHRR Data. J. Hydrol. 1998, 204, 1–23. [Google Scholar] [CrossRef]
- Kelly, R.E.J.; Chang, A.T.C. Development of a Passive Microwave Global Snow Depth Retrieval Algorithm for Special Sensor Microwave Imager (SSM/I) and Advanced Microwave Scanning Radiometer-EOS (AMSR-E) Data. Radio Sci. 2003, 38, 41. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS Snow-Cover Products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Román, M.O. Overview of NASA’s MODIS and Visible Infrared Imaging Radiometer Suite (VIIRS) Snow-Cover Earth System Data Records. Earth Syst. Sci. Data 2017, 9, 765–777. [Google Scholar] [CrossRef]
- Marchane, A.; Jarlan, L.; Hanich, L.; Boudhar, A.; Gascoin, S.; Tavernier, A.; Filali, N.; Le Page, M.; Hagolle, O.; Berjamy, B. Assessment of Daily MODIS Snow Cover Products to Monitor Snow Cover Dynamics over the Moroccan Atlas Mountain Range. Remote Sens. Environ. 2015, 160, 72–86. [Google Scholar] [CrossRef]
- Hüsler, F.; Jonas, T.; Riffler, M.; Musial, J.P.; Wunderle, S. A Satellite-Based Snow Cover Climatology (1985–2011) for the European Alps Derived from AVHRR Data. Cryosph. 2014, 8, 73–90. [Google Scholar] [CrossRef]
- Helfrich, S.R.; McNamara, D.; Ramsay, B.H.; Baldwin, T.; Kasheta, T. Enhancements to, and Forthcoming Developments in the Interactive Multisensor Snow and Ice Mapping System (IMS). Hydrol. Process. An Int. J. 2007, 21, 1576–1586. [Google Scholar] [CrossRef]
- Robinson, D.A.; Dewey, K.F.; Heim, R.R. Global Snow Cover Monitoring: An Update. Bull.-Am. Meteorol. Soc. 1993, 74, 1689–1696. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Liang, T. Evaluation of MODIS Snow Cover and Cloud Mask and Its Application in Northern Xinjiang, China. Remote Sens. Environ. 2008, 112, 1497–1513. [Google Scholar] [CrossRef]
- Stroeve, J.; Box, J.E.; Gao, F.; Liang, S.; Nolin, A.; Schaaf, C. Accuracy Assessment of the MODIS 16-Day Albedo Product for Snow: Comparisons with Greenland in Situ Measurements. Remote Sens. Environ. 2005, 94, 46–60. [Google Scholar] [CrossRef]
- Solberg, R.; Wangensteen, B.; Amlien, J.; Koren, H.; Metsämäki, S.; Nagler, T.; Luojus, K.; Pulliainen, J. A New Global Snow Extent Product. In Proceedings of the Proceedings of ESA Living Planet Symposium, ESA Special Publication SP-686, Bergen, Norway, 26 June–2 July 2010. [Google Scholar]
- Ramsay, B.H. The Interactive Multisensor Snow and Ice Mapping System. Hydrol. Process. 1998, 12, 1537–1546. [Google Scholar] [CrossRef]
- Hall, D.K.; Salomonson, V.V.; Riggs, G.A. MODIS/Terra Snow Cover 8-Day L3 Global 500m Grid; Version 5; Tile h12v12; National Snow and Ice Data Center: Boulder, CO, USA, 2006. [Google Scholar]
- Riggs, G.A.; Hall, D.K.; Román, M.O. MODIS Snow Products Collection 6 User Guide; National Snow and Ice Data Center: Boulder, CO, USA, 2015; Volume 66. [Google Scholar]
- Zhao, Q.; Hao, X.; He, D.; Wang, J.; Li, H.; Wang, X. The Relationship between the Temporal and Spatial Changes of Snow Cover and Climate and Vegetation in Northern Xinjiang from 1980 to 2019. Remote Sens. Technol. Appl. 2022, 36, 1247–1258. [Google Scholar]
- Qiu, B.; Li, W.; Wang, X.; Shang, L.; Song, C.; Guo, W.; Zhang, Y. Satellite-Observed Solar-Induced Chlorophyll Fluorescence Reveals Higher Sensitivity of Alpine Ecosystems to Snow Cover on the Tibetan Plateau. Agric. For. Meteorol. 2019, 271, 126–134. [Google Scholar] [CrossRef]
- Alkama, R.; Forzieri, G.; Duveiller, G.; Grassi, G.; Liang, S.; Cescatti, A. Vegetation-Based Climate Mitigation in a Warmer and Greener World. Nat. Commun. 2022, 13, 606. [Google Scholar] [CrossRef]
- Khlopenkov, K.V.; Trishchenko, A.P. SPARC: New Cloud, Snow, and Cloud Shadow Detection Scheme for Historical 1-Km AVHHR Data over Canada. J. Atmos. Ocean. Technol. 2007, 24, 322–343. [Google Scholar] [CrossRef]
- Hüsler, F.; Jonas, T.; Wunderle, S.; Albrecht, S. Validation of a Modified Snow Cover Retrieval Algorithm from Historical 1-Km AVHRR Data over the European Alps. Remote Sens. Environ. 2012, 121, 497–515. [Google Scholar] [CrossRef]
- Zhou, H.; Aizen, E.; Aizen, V. Deriving Long Term Snow Cover Extent Dataset from AVHRR and MODIS Data: Central Asia Case Study. Remote Sens. Environ. 2013, 136, 146–162. [Google Scholar] [CrossRef]
- Hori, M.; Sugiura, K.; Kobayashi, K.; Aoki, T.; Tanikawa, T.; Kuchiki, K.; Niwano, M.; Enomoto, H. A 38-Year (1978–2015) Northern Hemisphere Daily Snow Cover Extent Product Derived Using Consistent Objective Criteria from Satellite-Borne Optical Sensors. Remote Sens. Environ. 2017, 191, 402–418. [Google Scholar] [CrossRef]
- Chen, X.; Long, D.; Liang, S.; He, L.; Zeng, C.; Hao, X.; Hong, Y. Developing a Composite Daily Snow Cover Extent Record over the Tibetan Plateau from 1981 to 2016 Using Multisource Data. Remote Sens. Environ. 2018, 215, 284–299. [Google Scholar] [CrossRef]
- Hao, X.; Huang, G.; Che, T.; Ji, W.; Sun, X.; Zhao, Q.; Zhao, H.; Wang, J.; Li, H.; Yang, Q. The NIEER AVHRR Snow Cover Extent Product over China - A Long-Term Daily Snow Record for Regional Climate Research. Earth Syst. Sci. Data 2021, 13, 4711–4726. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Chen, G.; Yang, Q.; Wang, B.; Ma, Y.; Shen, M. Complex Responses of Spring Alpine Vegetation Phenology to Snow Cover Dynamics over the Tibetan Plateau, China. Sci. Total Environ. 2017, 593, 449–461. [Google Scholar] [CrossRef]
- Ranzi, R.; Grossi, G.; Bacchi, B. Ten Years of Monitoring Areal Snowpack in the Southern Alps Using NOAA-AVHRR Imagery, Ground Measurements and Hydrological Data. Hydrol. Process. 1999, 13, 2079–2095. [Google Scholar] [CrossRef]
- Wang, L.; Sharp, M.; Brown, R.; Derksen, C.; Rivard, B. Evaluation of Spring Snow Covered Area Depletion in the Canadian Arctic from NOAA Snow Charts. Remote Sens. Environ. 2005, 95, 453–463. [Google Scholar] [CrossRef]
- Harrison, A.R.; Lucas, R.M. Multi-Spectral Classification of Snow Using NOAA AVHRR Imagery. Int. J. Remote Sens. 1989, 10, 907–916. [Google Scholar] [CrossRef]
- Pu, Z.; Xu, L.; Salomonson, V.V. MODIS/Terra Observed Seasonal Variations of Snow Cover over the Tibetan Plateau. Geophys. Res. Lett. 2007, 34, L06706. [Google Scholar] [CrossRef]
- You, Q.; Wu, T.; Shen, L.; Pepin, N.; Zhang, L.; Jiang, Z.; Wu, Z.; Kang, S.; AghaKouchak, A. Review of Snow Cover Variation over the Tibetan Plateau and Its Influence on the Broad Climate System. Earth-Sci. Rev. 2020, 201, 103043. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Csiszar, I.; Eidenshink, J.; Myneni, R.; Baret, F.; Masuoka, E.; Wolfe, R.; Claverie, M. NOAA Climate Data Record (CDR) of AVHRR Surface Reflectance; Version 5; NOAA National Centers for Environmental Information: Washington, DC, USA, 2019. [Google Scholar]
- Franch, B.; Vermote, E.F.; Roger, J.-C.; Murphy, E.; Becker-Reshef, I.; Justice, C.; Claverie, M.; Nagol, J.; Csiszar, I.; Meyer, D. A 30+ Year AVHRR Land Surface Reflectance Climate Data Record and Its Application to Wheat Yield Monitoring. Remote Sens. 2017, 9, 296. [Google Scholar] [CrossRef] [PubMed]
- Rittger, K.; Painter, T.H.; Dozier, J. Assessment of Methods for Mapping Snow Cover from MODIS. Adv. Water Resour. 2013, 51, 367–380. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, H.; Chen, Y.; Liu, H.; Liu, L.; Huang, H.; Liu, K. Mapping Snow Cover Variations Using a MODIS Daily Cloud-Free Snow Cover Product in Northeast China. J. Appl. Remote Sens. 2014, 8, 84681. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Lu, N.; Yao, T.; Liang, T. Toward Advanced Daily Cloud-Free Snow Cover and Snow Water Equivalent Products from Terra–Aqua MODIS and Aqua AMSR-E Measurements. J. Hydrol. 2010, 385, 23–35. [Google Scholar] [CrossRef]
- Tong, J.; Déry, S.J.; Jackson, P.L. Interrelationships between MODIS/Terra Remotely Sensed Snow Cover and the Hydrometeorology of the Quesnel River Basin, British Columbia, Canada. Hydrol. Earth Syst. Sci. 2009, 13, 1439–1452. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Lei, Y.; Letu, H.; Shang, H.; Shi, J. Cloud Cover over the Tibetan Plateau and Eastern China: A Comparison of ERA5 and ERA-Interim with Satellite Observations. Clim. Dyn. 2020, 54, 2941–2957. [Google Scholar] [CrossRef]
- Lei, Y.; Pan, J.; Xiong, C.; Jiang, L.; Shi, J. Snow Depth and Snow Cover over the Tibetan Plateau Observed from Space in against ERA5: Matters of Scale. Clim. Dyn. 2023, 60, 1523–1541. [Google Scholar] [CrossRef]
- Shreve, C.M.; Okin, G.S.; Painter, T.H. Indices for Estimating Fractional Snow Cover in the Western Tibetan Plateau. J. Glaciol. 2009, 55, 737–745. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote Sensing of Snow–a Review of Available Methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Solberg, R.; Hiltbrunner, D.; Koskinen, J.; Guneriussen, T.; Rautiainen, K.; Hallikainen, M. Snow Algorithms and Products-Review and Recommendations for Research and Development; Norwegian Computing Center: Oslo, Norway, 1997. [Google Scholar]
- Zhu, J.; Cao, S.; Shang, G.; Shi, J.; Wang, X.; Zheng, Z.; Liu, C.; Yang, H.; Xie, B. Subpixel Snow Mapping Using Daily AVHRR/2 Data over Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 2899. [Google Scholar] [CrossRef]
- Orsolini, Y.; Wegmann, M.; Dutra, E.; Liu, B.; Balsamo, G.; Yang, K.; de Rosnay, P.; Zhu, C.; Wang, W.; Senan, R. Evaluation of Snow Depth and Snow Cover over the Tibetan Plateau in Global Reanalyses Using in Situ and Satellite Remote Sensing Observations. Cryosph. 2019, 13, 2221–2239. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. Validation of MODIS Snow Cover Images over Austria. Hydrol. Earth Syst. Sci. 2006, 10, 679–689. [Google Scholar] [CrossRef]
- Simic, A.; Fernandes, R.; Brown, R.; Romanov, P.; Park, W. Validation of VEGETATION, MODIS, and GOES+ SSM/I Snow-cover Products over Canada Based on Surface Snow Depth Observations. Hydrol. Process. 2004, 18, 1089–1104. [Google Scholar] [CrossRef]
- Metsämäki, S.; Vepsäläinen, J.; Pulliainen, J.; Sucksdorff, Y. Improved Linear Interpolation Method for the Estimation of Snow-Covered Area from Optical Data. Remote Sens. Environ. 2002, 82, 64–78. [Google Scholar] [CrossRef]
- Veitinger, J.; Sovilla, B.; Purves, R.S. Influence of Snow Depth Distribution on Surface Roughness in Alpine Terrain: A Multi-Scale Approach. Cryosph. 2014, 8, 547–569. [Google Scholar] [CrossRef]
- Parajka, J.; Dadson, S.; Lafon, T.; Essery, R. Evaluation of Snow Cover and Depth Simulated by a Land Surface Model Using Detailed Regional Snow Observations from Austria. J. Geophys. Res. Atmos. 2010, 115, D24117. [Google Scholar] [CrossRef]
- Wu, X.; Naegeli, K.; Premier, V.; Marin, C.; Ma, D.; Wang, J.; Wunderle, S. Evaluation of Snow Extent Time Series Derived from Advanced Very High Resolution Radiometer Global Area Coverage Data (1982–2018) in the Hindu Kush Himalayas. Cryosph. 2021, 15, 4261–4279. [Google Scholar] [CrossRef]
- Pan, F.; Jiang, L.; Zheng, Z.; Wang, G.; Cui, H.; Zhou, X.; Huang, J. Retrieval of Fractional Snow Cover over High Mountain Asia Using 1 Km and 5 Km AVHRR/2 with Simulated Mid-Infrared Reflective Band. Remote Sens. 2022, 14, 3303. [Google Scholar] [CrossRef]
- Jing, Y.; Shen, H.; Li, X.; Guan, X. A Two-Stage Fusion Framework to Generate a Spatio–Temporally Continuous MODIS NDSI Product over the Tibetan Plateau. Remote Sens. 2019, 11, 2261. [Google Scholar] [CrossRef]
- Huang, X.; Deng, J.; Wang, W.; Feng, Q.; Liang, T. Impact of Climate and Elevation on Snow Cover Using Integrated Remote Sensing Snow Products in Tibetan Plateau. Remote Sens. Environ. 2017, 190, 274–288. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Foster, J.L.; Kumar, S. V Development and Evaluation of a Cloud-Gap-Filled MODIS Daily Snow-Cover Product. Remote Sens. Environ. 2010, 114, 496–503. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Arsenault, K.R.; Getirana, A.; Mocko, D.; Liu, Y. Quantifying the Added Value of Snow Cover Area Observations in Passive Microwave Snow Depth Data Assimilation. J. Hydrometeorol. 2015, 16, 1736–1741. [Google Scholar] [CrossRef]
- Klein, A.G.; Barnett, A.C. Validation of Daily MODIS Snow Cover Maps of the Upper Rio Grande River Basin for the 2000–2001 Snow Year. Remote Sens. Environ. 2003, 86, 162–176. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy Assessment of the MODIS Snow Products. Hydrol. Process. An Int. J. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]



| Band | Abbreviation | Wavelength (μm) | Description |
|---|---|---|---|
| SREFL_CH1 | SR1 | 0.58~0.68 | Surface reflectance at 0.64 μm |
| SREFL_CH2 | SR2 | 0.725~1.00 | Surface reflectance at 0.86 μm |
| SREFL_CH3 | SR3 | 3.55~3.93 | Surface reflectance at 3.75 μm |
| BT_CH3 | BT3 | 3.55~3.93 | Brightness temperature at 3.75 μm |
| BT_CH4 | BT4 | 10.30~11.30 | Brightness temperature at 11.0 μm |
| BT_CH5 | BT5 | 11.50~12.50 | Brightness temperature at 12.0 μm |
| Dataset | Date | Spatial Resolution | Temporal Resolution | Description |
|---|---|---|---|---|
| AVHRR | Year: 1982~2020 | 0.05° | Daily | Surface reflectance: AVH09C1 |
| MODIS | Training: 13 Feb 2003 6 Jan 2004 28 Mar 2007 5 Jan 2010 14 Jan 2010 16 Mar 2011 | 500 m | Daily | Fractional Snow Cover: MOD10A1 |
| Predicting: 11 Jan 2001 6 Dec 2004 1 Dec 2006 10 Dec 2009 2 Jan 2013 5 Feb 2015 | ||||
| DEM/Slop | \ | 30 m Resampled to 0.05° | \ | |
| LUCC | Year: 2000~2020 | 0.05° | Yearly | Land-Cover Type: MCD12C1 |
| Ground snow-depth records | Year: 2000~2012 | Points | Daily | Depth greater than 1 cm is considered valid. |
| Reanalysis dataset | Year: 2012 | 0.05° | daily | ERA5 snow cover dataset |
| Target | Switch | DEM | SR1 | SR2 | SR3 | SR1-SR2 | NDVI | NDSI | BT4(K) | BT3-BT4 | BT3-BT4 | BT4-BT5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DEM > 300 m&BT11 < 260 K | On | <3000 | ≥240 | >14.5 | >19.5 | |||||||
| On | ≥300 | ≥240 | >15.5 | >20 | ||||||||
| On | <240 | >21.5 | >31 | |||||||||
| On | >0.1 | >−0.02 | <0.88 | >25.5 | >33.5 | |||||||
| Off | >0.5 | >288 | ||||||||||
| Off | >310 | |||||||||||
| DEM < 300 m&BT11 ≥ 260 K | On | <260 | >14 | >16 | ||||||||
| On | >−0.02 | <310 | >10.5 | >16.5 | ||||||||
| On | >0.3 | >−0.02 | <293 | >11.5 | >17.5 | |||||||
| On | >0.4 | >−0.03 | <293 | >11.5 | >18 | >−1 | ||||||
| On | >0.4 | <278 | >11.5 | >19.5 | >−1 | |||||||
| On | >0.3 | >0.2 | <263 | >11.5 | >18 | |||||||
| Off | >0.5 | >288 | ||||||||||
| Off | >310 | |||||||||||
| Off | >1000 | <0.4 | <−0.04 | >275 |
| Year | AVHRRsnow~Stationsnow | AVHRRnon-snow~Stationsnow | AVHRRsnow~Stationnon-snow | AVHRRnon-now~Stationnon-snow | K | Recall |
|---|---|---|---|---|---|---|
| 2000 | 2007 | 17,183 | 423 | 15,169 | 0.07 | 0.83 |
| 2001 | 1615 | 17,730 | 350 | 15,276 | 0.06 | 0.82 |
| 2002 | 1748 | 17,749 | 286 | 15,010 | 0.06 | 0.86 |
| 2003 | 1252 | 16,970 | 276 | 12,265 | 0.04 | 0.82 |
| 2004 | 1532 | 18,666 | 329 | 13,521 | 0.04 | 0.82 |
| 2005 | 2324 | 18,896 | 392 | 13,261 | 0.07 | 0.86 |
| 2006 | 2038 | 18,702 | 579 | 13,673 | 0.05 | 0.79 |
| 2007 | 1447 | 17,211 | 334 | 16,267 | 0.05 | 0.81 |
| 2008 | 2412 | 18,060 | 287 | 14,598 | 0.08 | 0.90 |
| 2009 | 1687 | 17,178 | 344 | 16,115 | 0.06 | 0.83 |
| 2010 | 1079 | 17,772 | 346 | 16,367 | 0.03 | 0.76 |
| 2011 | 2123 | 17,394 | 766 | 15,786 | 0.06 | 0.73 |
| 2012 | 3737 | 16,459 | 1943 | 13,810 | 0.06 | 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Xu, L.; Li, Y. A New Retrieval Algorithm of Fractional Snow over the Tibetan Plateau Derived from AVH09C1. Remote Sens. 2024, 16, 2260. https://doi.org/10.3390/rs16132260
Yin H, Xu L, Li Y. A New Retrieval Algorithm of Fractional Snow over the Tibetan Plateau Derived from AVH09C1. Remote Sensing. 2024; 16(13):2260. https://doi.org/10.3390/rs16132260
Chicago/Turabian StyleYin, Hang, Liyan Xu, and Yihang Li. 2024. "A New Retrieval Algorithm of Fractional Snow over the Tibetan Plateau Derived from AVH09C1" Remote Sensing 16, no. 13: 2260. https://doi.org/10.3390/rs16132260
APA StyleYin, H., Xu, L., & Li, Y. (2024). A New Retrieval Algorithm of Fractional Snow over the Tibetan Plateau Derived from AVH09C1. Remote Sensing, 16(13), 2260. https://doi.org/10.3390/rs16132260







