Multi-Instrument Observations of the Ionospheric Response Caused by the 8 April 2024 Total Solar Eclipse
Abstract
:1. Introduction
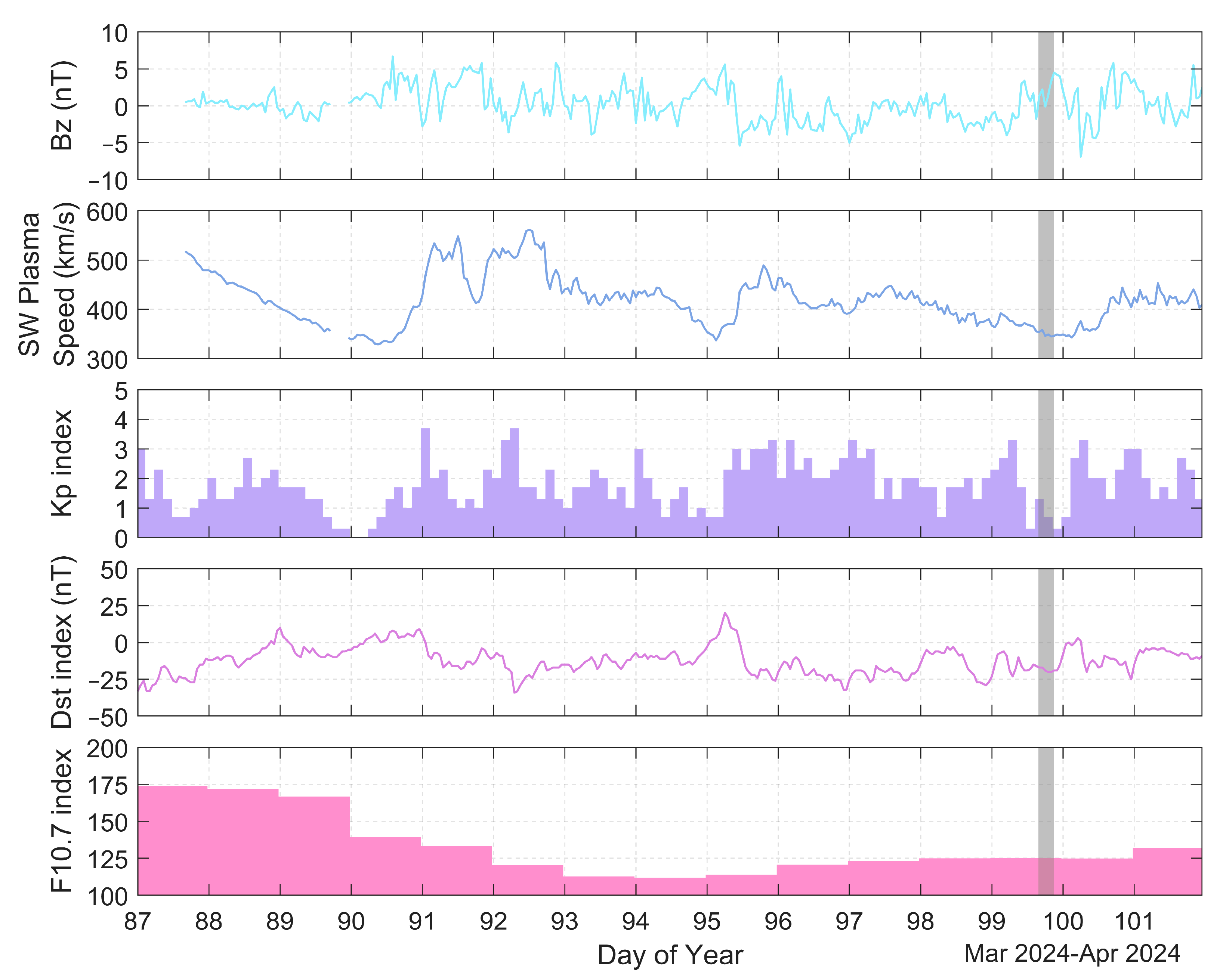
2. Data and Methods
2.1. Data Sources
2.2. Methods and Statistical Indicators
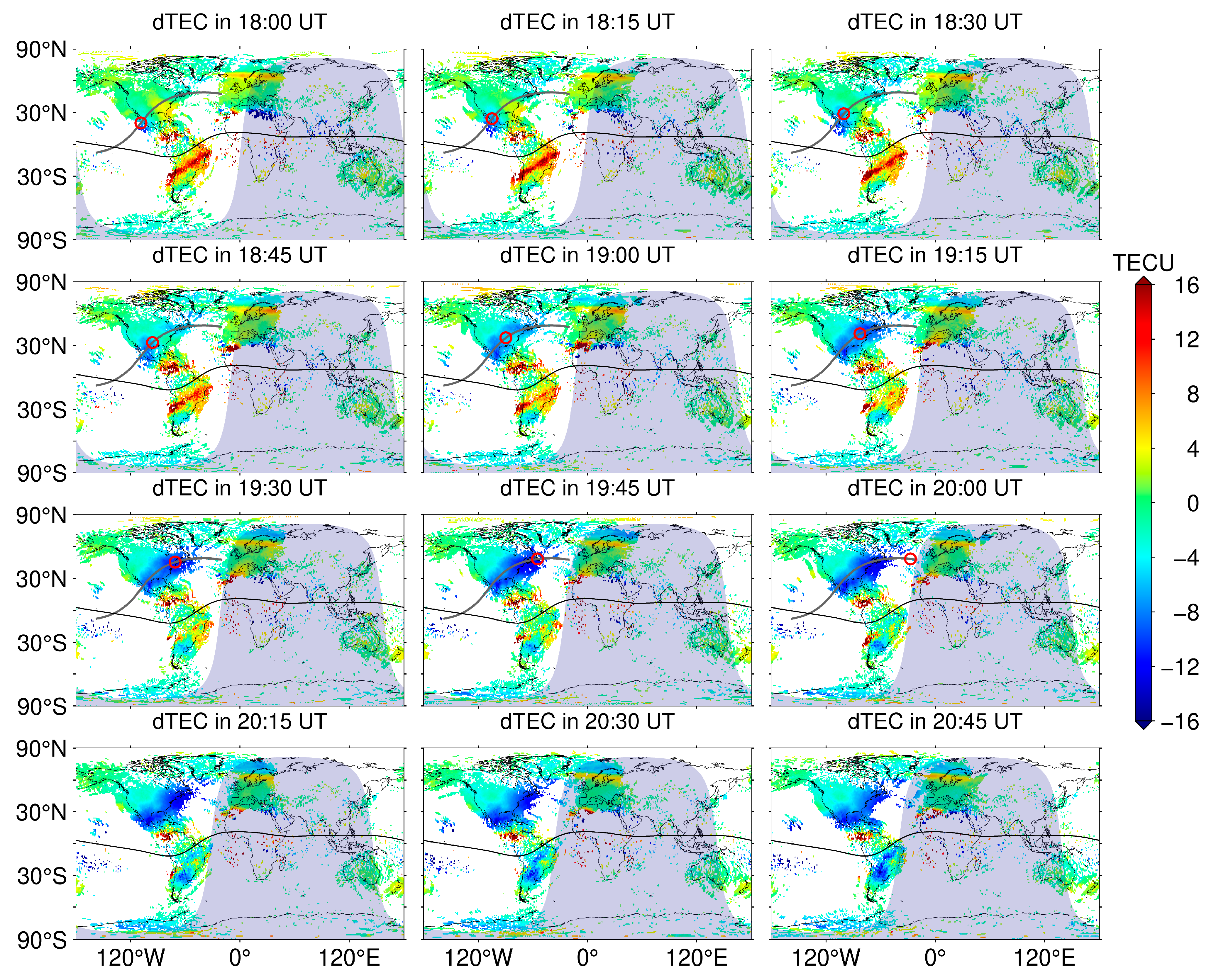
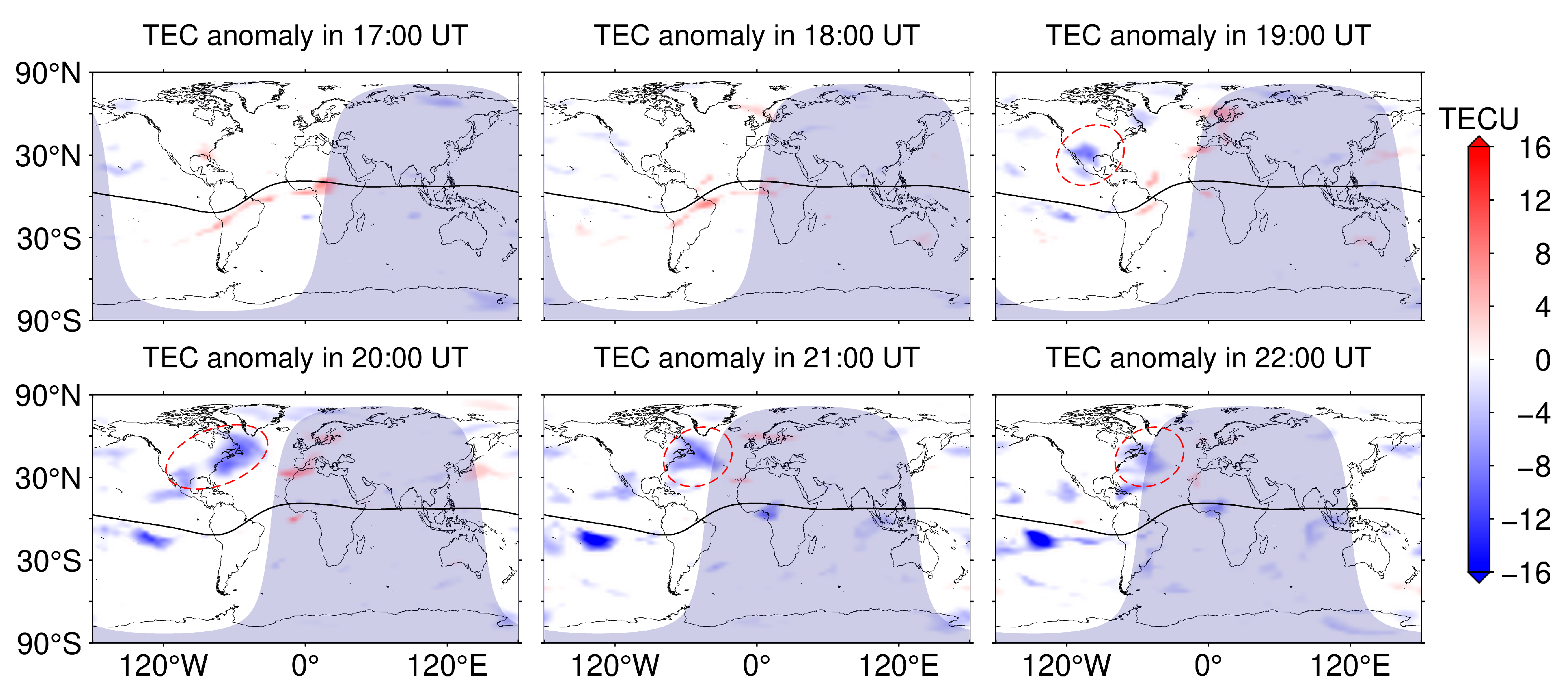
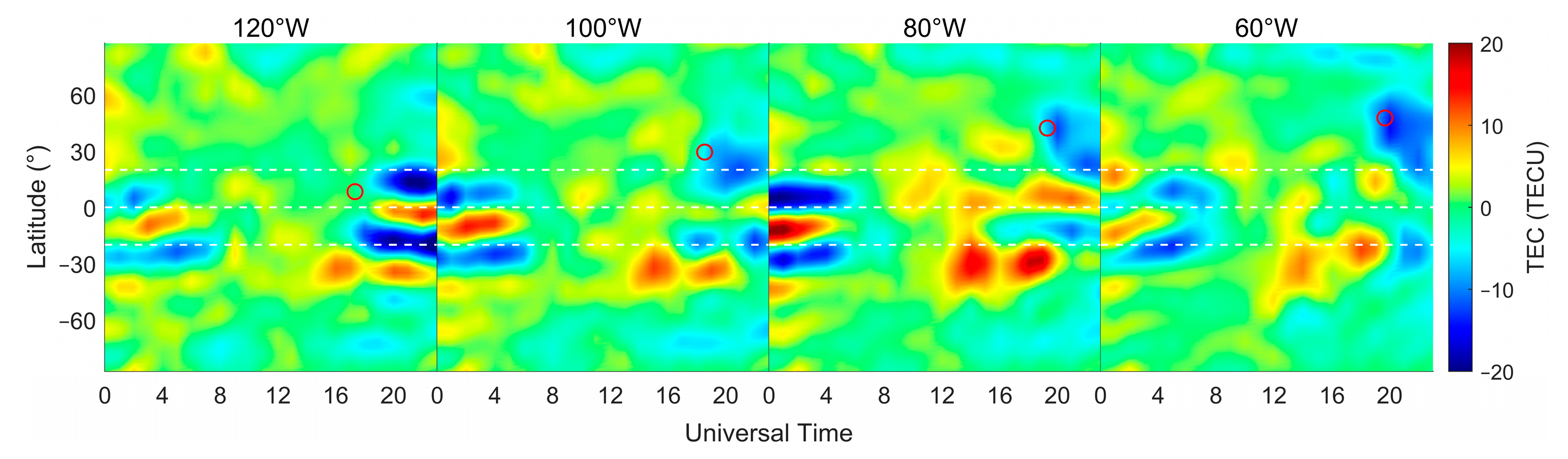
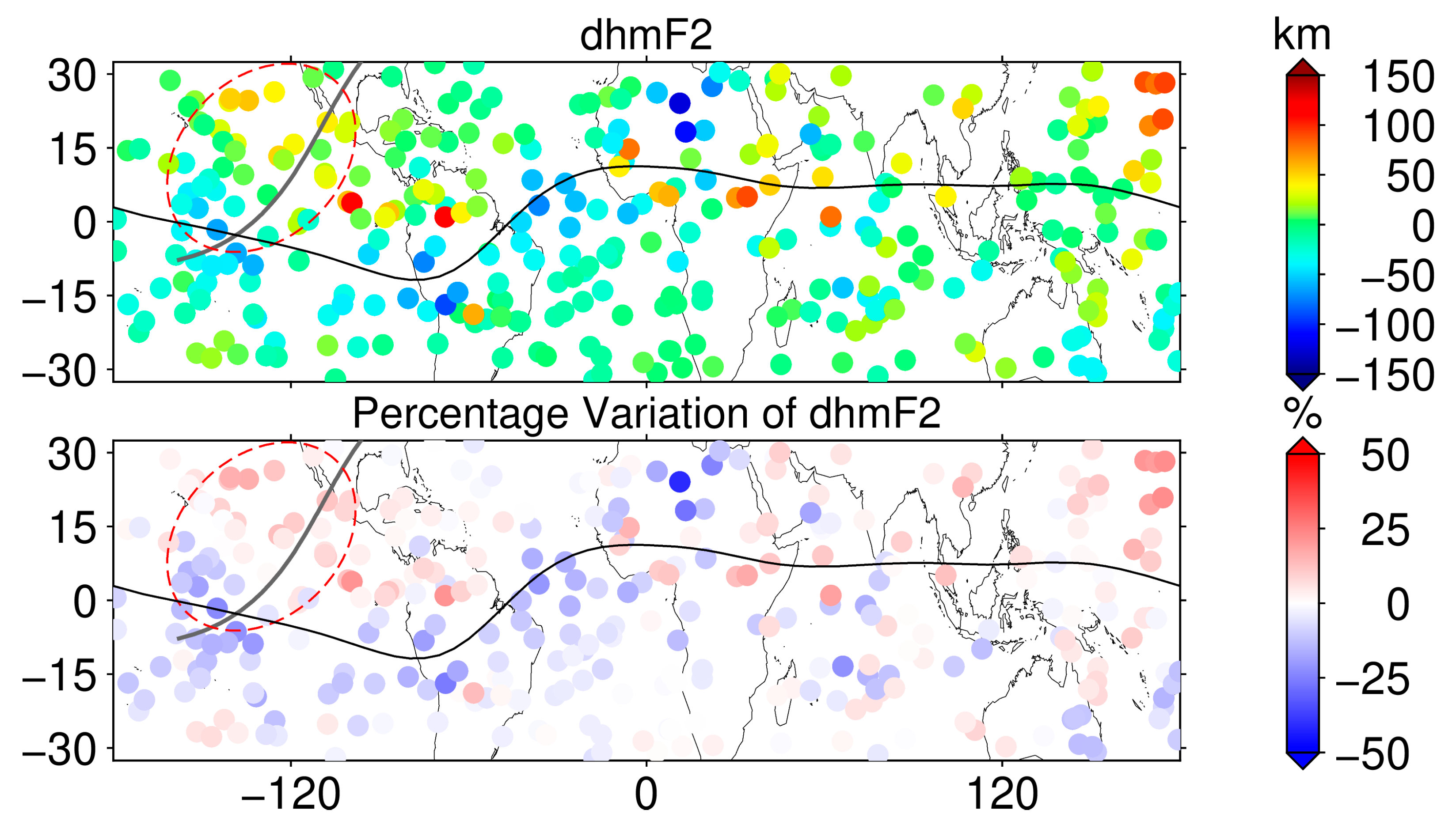
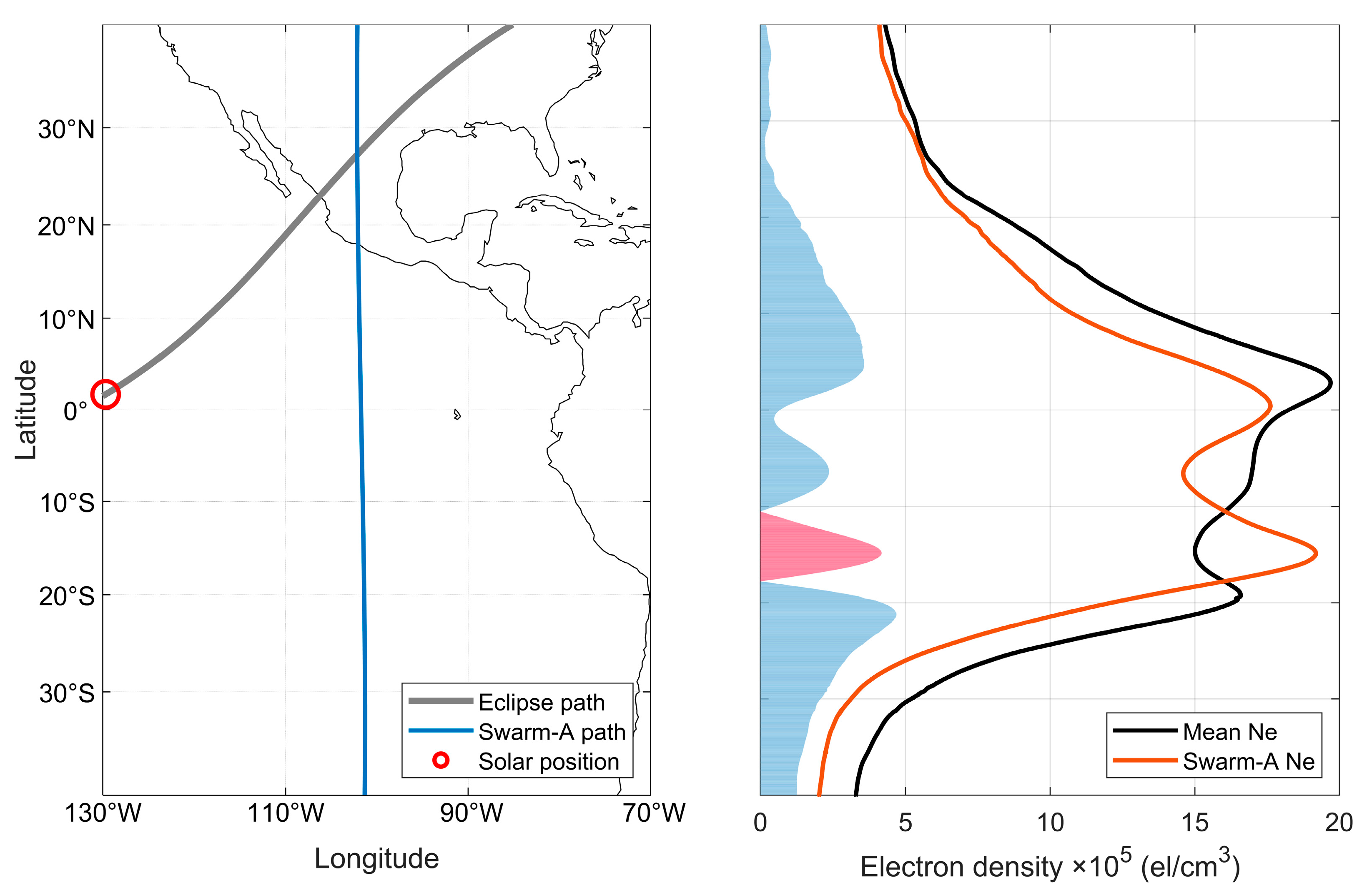
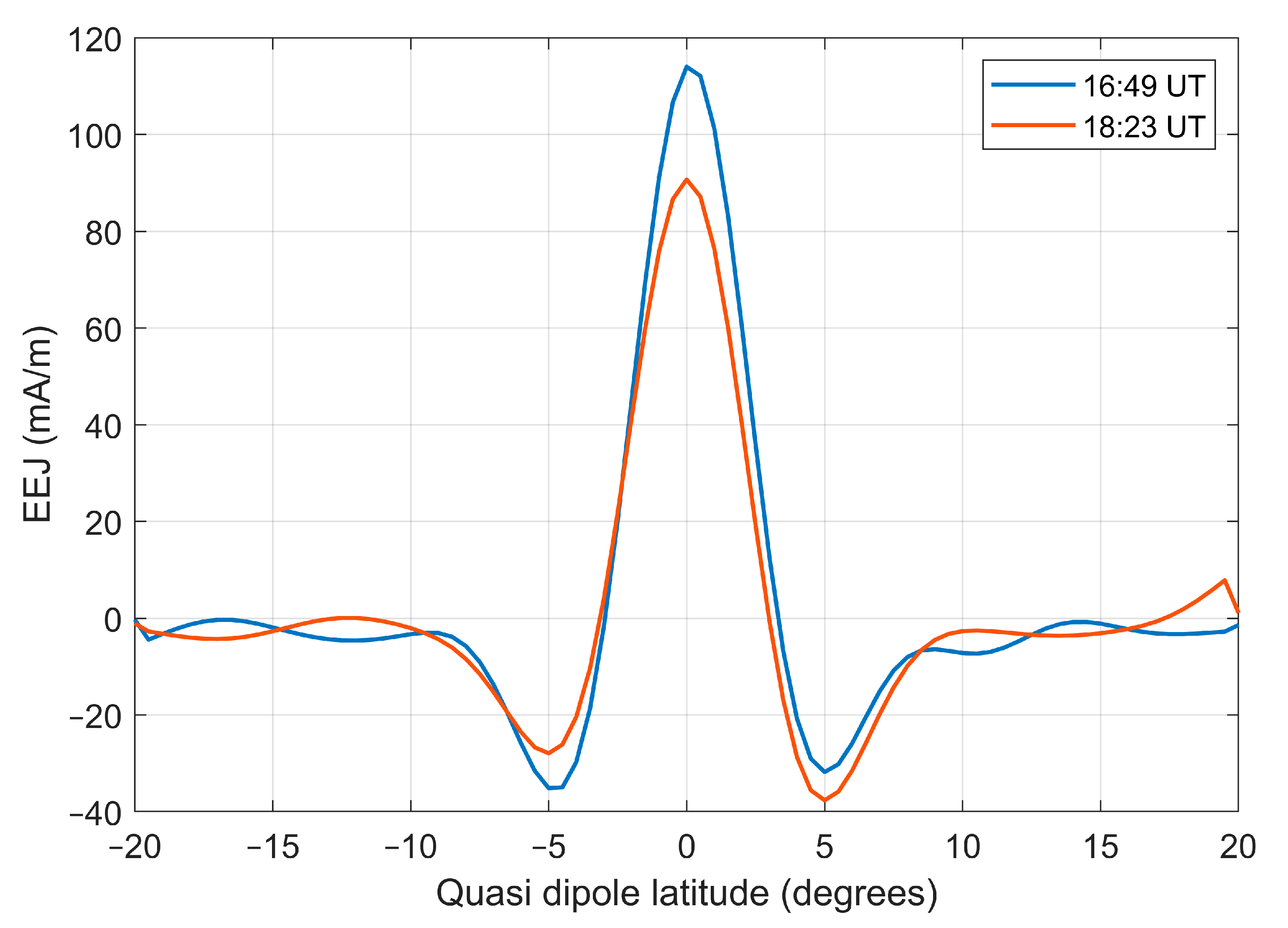
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, J.; Zhang, Y.; Li, W.; Han, B.; Zhao, Z.; Zhang, T.; Huang, R. Analysis of ionospheric TEC response to solar and geomagnetic activities at different solar activity stages. Adv. Space Res. 2023, 71, 2225–2239. [Google Scholar] [CrossRef]
- Davis, C.J.; Lockwood, M.; Bell, S.A.; Smith, J.A.; Clarke, E.M. Ionospheric measurements of relative coronal brightness during the total solar eclipses of 11 August 1999 and 9 July 1945. Ann. Geophys. 2000, 18, 182–190. [Google Scholar] [CrossRef]
- Klimenko, V.V.; Bessarab, F.S.; Korenkov, Y.N. Numerical simulation of effects of the 11 August 1999 solar eclipse in the outer ionosphere. Cosm. Res. 2007, 45, 102–109. [Google Scholar] [CrossRef]
- Le, H.; Liu, L.; Yue, X.; Wan, W. The midlatitude F2 layer during solar eclipses: Observations and modeling. J. Geophys. Res. Space Phys. 2008, 113, A08309. [Google Scholar] [CrossRef]
- Müller-Wodarg, I.C.F.; Aylward, A.D.; Lockwood, M. Effects of a mid-latitude solar eclipse on the thermosphere and ionosphere—A modelling study. Geophys. Res. Lett. 1998, 25, 3787–3790. [Google Scholar] [CrossRef]
- Huba, J.D.; Drob, D. SAMI3 prediction of the impact of the 21 August 2017 total solar eclipse on the ionosphere/plasmasphere system. Geophys. Res. Lett. 2017, 44, 5928–5935. [Google Scholar] [CrossRef]
- Dang, T.; Lei, J.; Wang, W.; Zhang, B.; Burns, A.; Le, H.; Wu, Q.; Ruan, H.; Dou, X.; Wan, W. Global Responses of the Coupled Thermosphere and Ionosphere System to the August 2017 Great American Solar Eclipse. J. Geophys. Res. Space Phys. 2018, 123, 7040–7050. [Google Scholar] [CrossRef]
- Martínez-Ledesma, M.; Bravo, M.; Urra, B.; Souza, J.; Foppiano, A. Prediction of the Ionospheric Response to the 14 December 2020 Total Solar Eclipse Using SUPIM-INPE. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028625. [Google Scholar] [CrossRef]
- Bravo, M.A.; Molina, M.G.; Martínez-Ledesma, M.; de Haro Barbás, B.; Urra, B.; Elías, A.; Souza, J.; Villalobos, C.; Namour, J.H.; Ovalle, E.; et al. Ionospheric response modeling under eclipse conditions: Evaluation of 14 December 2020, total solar eclipse prediction over the South American sector. Front. Astron. Space Sci. 2022, 9, 1021910. [Google Scholar] [CrossRef]
- Klobuchar, J.A.; Whitney, H.E. Ionospheric electron content measurements during a solar eclipse. J. Geophys. Res. 1965, 70, 1254–1257. [Google Scholar] [CrossRef]
- Farges, T.; Jodogne, J.C.; Bamford, R.; Le Roux, Y.; Gauthier, F.; Vila, P.M.; Altadill, D.; Sole, J.G.; Miro, G. Disturbances of the western European ionosphere during the total solar eclipse of 11 August 1999 measured by a wide ionosonde and radar network. J. Atmos. Sol. Terr. Phys. 2001, 63, 915–924. [Google Scholar] [CrossRef]
- Jakowski, N.; Stankov, S.M.; Wilken, V.; Borries, C.; Altadill, D.; Chum, J.; Buresova, D.; Boska, J.; Sauli, P.; Hruska, F.; et al. Ionospheric behavior over Europe during the solar eclipse of 3 October 2005. J. Atmos. Sol. Terr. Phys. 2008, 70, 836–853. [Google Scholar] [CrossRef]
- Chen, G.; Qi, H.; Ning, B.; Zhao, Z.; Yao, M.; Deng, Z.; Li, T.; Huang, S.; Feng, W.; Wu, J.; et al. Nighttime ionospheric enhancements induced by the occurrence of an evening solar eclipse. J. Geophys. Res. Space Phys. 2013, 118, 6588–6596. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Dandenault, P.B.; Galkin, I.A.; Hamel, R.; Richards, P.G. Investigation of the Electron Density Variation during the 21 August 2017 Solar Eclipse. Geophys. Res. Lett. 2018, 45, 1253–1261. [Google Scholar] [CrossRef]
- Pezzopane, M.; Pietrella, M.; Pignalberi, A.; Tozzi, R. 20 March 2015 solar eclipse influence on sporadic E layer. Adv. Space Res. 2015, 56, 2064–2072. [Google Scholar] [CrossRef]
- Harjosuwito, J.; Husin, A.; Dear, V.; Muhamad, J.; Faturahman, A.; Bahar, A.; Erlansyah; Syetiawan, A.; Pradipta, R. Ionosonde and GPS total electron content observations during the 26 December 2019 annular solar eclipse over Indonesia. Ann. Geophys. 2023, 41, 147–172. [Google Scholar] [CrossRef]
- Emelyanov, L.Y.; Bogomaz, O.V.; Chernogor, L.F.; Domnin, I.F. Response of the mid-latitude ionosphere to the solar eclipse on 25 October 2022: Results of F2–layer vertical sounding. Adv. Space Res. 2024, 73, 2338–2354. [Google Scholar] [CrossRef]
- Vogrinčič, R.; Lara, A.; Borgazzi, A.; Raulin, J.P. Effects of the Great American Solar Eclipse on the lower ionosphere observed with VLF waves. Adv. Space Res. 2020, 65, 2148–2157. [Google Scholar] [CrossRef]
- Mendes Da Costa, A.; Paes Leme, N.M.; Rizzo Piazza, L. Lower ionosphere effect observed during the 30 June 1992 total solar eclipse. J. Atmos. Terr. Phys. 1995, 57, 13–17. [Google Scholar] [CrossRef]
- Pal, S.; Maji, S.K.; Chakrabarti, S.K. First ever VLF monitoring of the lunar occultation of a solar flare during the 2010 annular solar eclipse and its effects on the D-region electron density profile. Planet. Space Sci. 2012, 73, 310–317. [Google Scholar] [CrossRef]
- Guha, A.; De, B.K.; Choudhury, A.; Roy, R. Spectral character of VLF sferics propagating inside the Earth-ionosphere waveguide during two recent solar eclipses. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Venkatesham, K.; Singh, R.; Maurya, A.K.; Dube, A.; Kumar, S.; Phanikumar, D.V. The 22 July 2009 Total Solar Eclipse: Modeling D Region Ionosphere Using Narrowband VLF Observations. J. Geophys. Res. Space Phys. 2019, 124, 616–627. [Google Scholar] [CrossRef]
- Hoque, M.M.; Wenzel, D.; Jakowski, N.; Gerzen, T.; Berdermann, J.; Wilken, V.; Kriegel, M.; Sato, H.; Borries, C.; Minkwitz, D. Ionospheric response over Europe during the solar eclipse of March 20, 2015. J. Space Weather Space Clim. 2016, 6, A36. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Z.; Yang, G.; Zhou, C.; Yao, M.; Li, T.; Huang, S.; Li, N. Enhancement and HF Doppler observations of sporadic-E during the solar eclipse of 22 July 2009. J. Geophys. Res. Space Phys. 2010, 115, A09325. [Google Scholar] [CrossRef]
- Chernogor, L.F. Effects of solar eclipses in the ionosphere: Results of Doppler sounding: 1. Experimental data. Geomagn. Aeron. 2012, 52, 768–778. [Google Scholar] [CrossRef]
- Manju, G.; Sridharan, R.; Ravindran, S.; Madhav Haridas, M.K.; Pant, T.K.; Sreelatha, P.; Mohan Kumar, S.V. Rocket borne in-situ Electron density and Neutral Wind measurements in the equatorial ionosphere—Results from the January 2010 annular solar eclipse campaign from India. J. Atmos. Sol. Terr. Phys. 2012, 86, 56–64. [Google Scholar] [CrossRef]
- Hairston, M.R.; Mrak, S.; Coley, W.R.; Burrell, A.; Holt, B.; Perdue, M.; Depew, M.; Power, R. Topside Ionospheric Electron Temperature Observations of the 21 August 2017 Eclipse by DMSP Spacecraft. Geophys. Res. Lett. 2018, 45, 7242–7247. [Google Scholar] [CrossRef]
- Valdés-Abreu, J.C.; Díaz, M.; Bravo, M.; Stable-Sánchez, Y. IonosphericTotal Electron Content Changes during the 15 February 2018 and 30 April 2022 Solar Eclipses over South America and Antarctica. Remote Sens. 2023, 15, 4810. [Google Scholar] [CrossRef]
- MacPherson, B.; González, S.A.; Sulzer, M.P.; Bailey, G.J.; Djuth, F.; Rodriguez, P. Measurements of the topside ionosphere over Arecibo during the total solar eclipse of February 26, 1998. J. Geophys. Res. Space Phys. 2000, 105, 23055–23067. [Google Scholar] [CrossRef]
- Goncharenko, L.P.; Erickson, P.J.; Zhang, S.-R.; Galkin, I.; Coster, A.J.; Jonah, O.F. Ionospheric Response to the Solar Eclipse of 21 August 2017 in Millstone Hill (42N) Observations. Geophys. Res. Lett. 2018, 45, 4601–4609. [Google Scholar] [CrossRef]
- Domnin, I.F.; Yemel’yanov, L.Y.; Kotov, D.V.; Lyashenko, M.V.; Chernogor, L.F. Solar eclipse of August 1, 2008, above Kharkov: 1. Results of incoherent scatter observations. Geomagn. Aeron. 2013, 53, 113–123. [Google Scholar] [CrossRef]
- Aa, E.; Zhang, S.-R.; Erickson, P.J.; Wang, W.; Coster, A.J. 3-D Ionospheric Electron Density Variations during the 2017 Great American Solar Eclipse: A Revisit. Atmosphere 2023, 14, 1379. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Palamartchouk, K.S.; Perevalova, N.P.; Chernukhov, V.V.; Lukhnev, A.V.; Zalutsky, V.T. Ionospheric effects of the solar eclipse of March 9, 1997, as deduced from GPS data. Geophys. Res. Lett. 1998, 25, 465–468. [Google Scholar] [CrossRef]
- Baran, L.W.; Ephishov, I.I.; Shagimuratov, I.I.; Ivanov, V.P.; Lagovsky, A.F. The response of the ionospheric total electron content to the solar eclipse on August 11, 1999. Adv. Space Res. 2003, 31, 989–994. [Google Scholar] [CrossRef]
- Ding, F.; Wan, W.; Ning, B.; Liu, L.; Le, H.; Xu, G.; Wang, M.; Li, G.; Chen, Y.; Ren, Z.; et al. GPS TEC response to the 22 July 2009 total solar eclipse in East Asia. J. Geophys. Res. Space Phys. 2010, 115, A07308. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I. Ionospheric Total Electron Content Response to the Great American Solar Eclipse of 21 August 2017. Geophys. Res. Lett. 2018, 45, 1199–1208. [Google Scholar] [CrossRef]
- Şentürk, E.; Arqim Adil, M.; Saqib, M. Ionospheric total electron content response to annular solar eclipse on June 21, 2020. Adv. Space Res. 2021, 67, 1937–1947. [Google Scholar] [CrossRef]
- Chernogor, L.F.; Mylovanov, Y.B.; Zhdanko, Y.H. Response of total electron content to the 25 October 2022 partial solar eclipse from high to low latitudes in the Euro-Asian region. Adv. Space Res. 2024. [Google Scholar] [CrossRef]
- Zhai, C.; Dang, T.; Yao, Y.; Kong, J.; Chen, Y.; Cheng, X. Three-Dimensional Ionospheric Evolution and Asymmetry of the Electron Density Depletion Generated by the 21 June 2020 Annular Solar Eclipse. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031725. [Google Scholar] [CrossRef]
- Aa, E.; Coster, A.J.; Zhang, S.-R.; Vierinen, J.; Erickson, P.J.; Goncharenko, L.P.; Rideout, W. 2-D Total Electron Content and 3-D Ionospheric Electron Density Variations during the 14 October 2023 Annular Solar Eclipse. J. Geophys. Res. Space Phys. 2024, 129, e2024JA032447. [Google Scholar] [CrossRef]
- He, L.; Heki, K.; Wu, L. Three-Dimensional and Trans-Hemispheric Changes in Ionospheric Electron Density Caused by the Great Solar Eclipse in North America on 21 August 2017. Geophys. Res. Lett. 2018, 45, 10933–10940. [Google Scholar] [CrossRef]
- Chen, C.H.; Lin, C.C.H.; Lee, C.J.; Liu, J.Y.; Saito, A. Ionospheric responses on the 21 August 2017 solar eclipse by using three-dimensional GNSS tomography. Earth Planets Space 2022, 74, 173. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Liu, J.-Y.; Lin, C.C.; Chou, M.-Y. The Ionospheric Three-Dimensional Electron Density Variations Induced by the 21 August 2017 Total Solar Eclipse by Using Global Ionospheric Specification. Remote Sens. 2023, 15, 3887. [Google Scholar] [CrossRef]
- Chen, G.; Wang, J.; Reinisch, B.W.; Li, Y.; Gong, W. Disturbances in Sporadic-E during the Great Solar Eclipse of August 21, 2017. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028986. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Erickson, P.J.; Vierinen, J.; Aa, E.; Rideout, W.; Coster, A.J.; Goncharenko, L.P. Conjugate Ionospheric Perturbation During the 2017 Solar Eclipse. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028531. [Google Scholar] [CrossRef]
- Rideout, W.; Coster, A. Automated GPS processing for global total electron content data. GPS Solut. 2006, 10, 219–228. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Galkin, I.A. Global Ionospheric Radio Observatory (GIRO). Earth Planets Space 2011, 63, 377–381. [Google Scholar] [CrossRef]
- Heelis, R.A.; Stoneback, R.A.; Perdue, M.D.; Depew, M.D.; Morgan, W.A.; Mankey, M.W.; Lippincott, C.R.; Harmon, L.L.; Holt, B.J. Ion Velocity Measurements for the Ionospheric Connections Explorer. Space Sci. Rev. 2017, 212, 615–629. [Google Scholar] [CrossRef] [PubMed]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Knudsen, D.; Haagmans, R. Swarm—An Earth Observation Mission investigating Geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Lomidze, L.; Knudsen, D.J.; Burchill, J.; Kouznetsov, A.; Buchert, S.C. Calibration and Validation of Swarm Plasma Densities and Electron Temperatures Using Ground-Based Radars and Satellite Radio Occultation Measurements. Radio Sci. 2018, 53, 15–36. [Google Scholar] [CrossRef]
- Yuan, Y. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS. Ph.D. Thesis, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan, China, 2002. (In Chinese). [Google Scholar]
- Feng, J.; Yuan, Y.; Zhang, T.; Zhang, Z.; Meng, D. Analysis of Ionospheric Anomalies before the Tonga Volcanic Eruption on 15 January 2022. Remote Sens. 2023, 15, 4879. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. NAVIGATION 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Wu, C.; Ridley, A.J.; Goncharenko, L.; Chen, G. GITM-Data Comparisons of the Depletion and Enhancement during the 2017 Solar Eclipse. Geophys. Res. Lett. 2018, 45, 3319–3327. [Google Scholar] [CrossRef]
- Le, H.; Liu, L.; Ren, Z.; Chen, Y.; Zhang, H. Effects of the 21 June 2020 Solar Eclipse on Conjugate Hemispheres: A Modeling Study. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028344. [Google Scholar] [CrossRef]
- Choudhary, R.K.; St.-Maurice, J.P.; Ambili, K.M.; Sunda, S.; Pathan, B.M. The impact of the 15 January 2010, annular solar eclipse on the equatorial and low latitude ionospheric densities. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, T.; Zhang, X.; Yuan, Y.; Wang, Y.; Ma, Y. Multi-Instrument Observations of the Ionospheric Response Caused by the 8 April 2024 Total Solar Eclipse. Remote Sens. 2024, 16, 2451. https://doi.org/10.3390/rs16132451
Zhang H, Zhang T, Zhang X, Yuan Y, Wang Y, Ma Y. Multi-Instrument Observations of the Ionospheric Response Caused by the 8 April 2024 Total Solar Eclipse. Remote Sensing. 2024; 16(13):2451. https://doi.org/10.3390/rs16132451
Chicago/Turabian StyleZhang, Hui, Ting Zhang, Xinyu Zhang, Yunbin Yuan, Yifan Wang, and Yutang Ma. 2024. "Multi-Instrument Observations of the Ionospheric Response Caused by the 8 April 2024 Total Solar Eclipse" Remote Sensing 16, no. 13: 2451. https://doi.org/10.3390/rs16132451
APA StyleZhang, H., Zhang, T., Zhang, X., Yuan, Y., Wang, Y., & Ma, Y. (2024). Multi-Instrument Observations of the Ionospheric Response Caused by the 8 April 2024 Total Solar Eclipse. Remote Sensing, 16(13), 2451. https://doi.org/10.3390/rs16132451






