Refining Spatial and Temporal XCO2 Characteristics Observed by Orbiting Carbon Observatory-2 and Orbiting Carbon Observatory-3 Using Sentinel-5P Tropospheric Monitoring Instrument NO2 Observations in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Used for Reconstructing XCO2
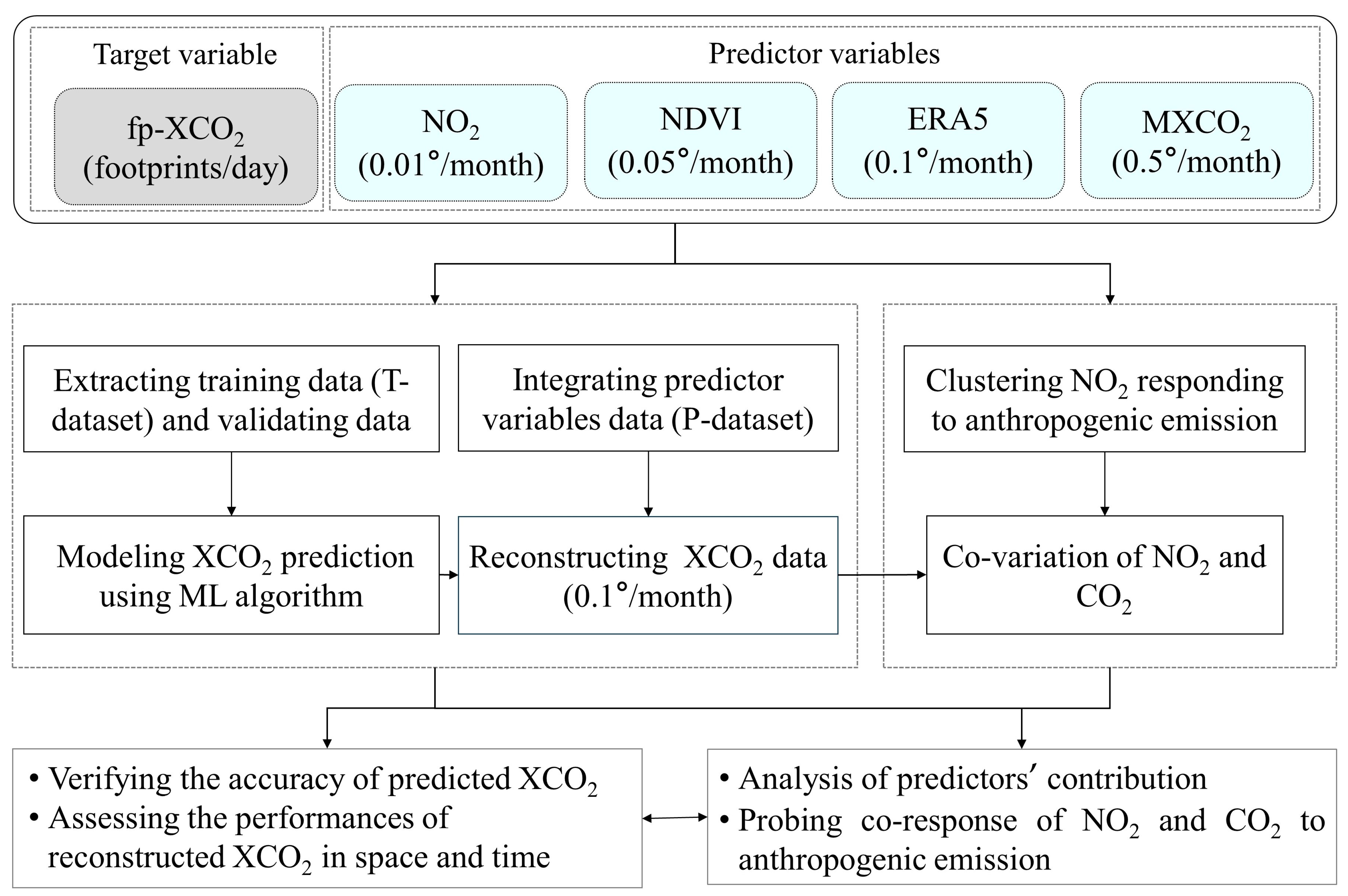
2.2. Methodology
2.2.1. Modeling XCO2 Prediction and Reconstructing XCO2 in Space and Time
2.2.2. Evaluation of Reconstructed XCO2 and Effects of NO2 Constraints
3. Results
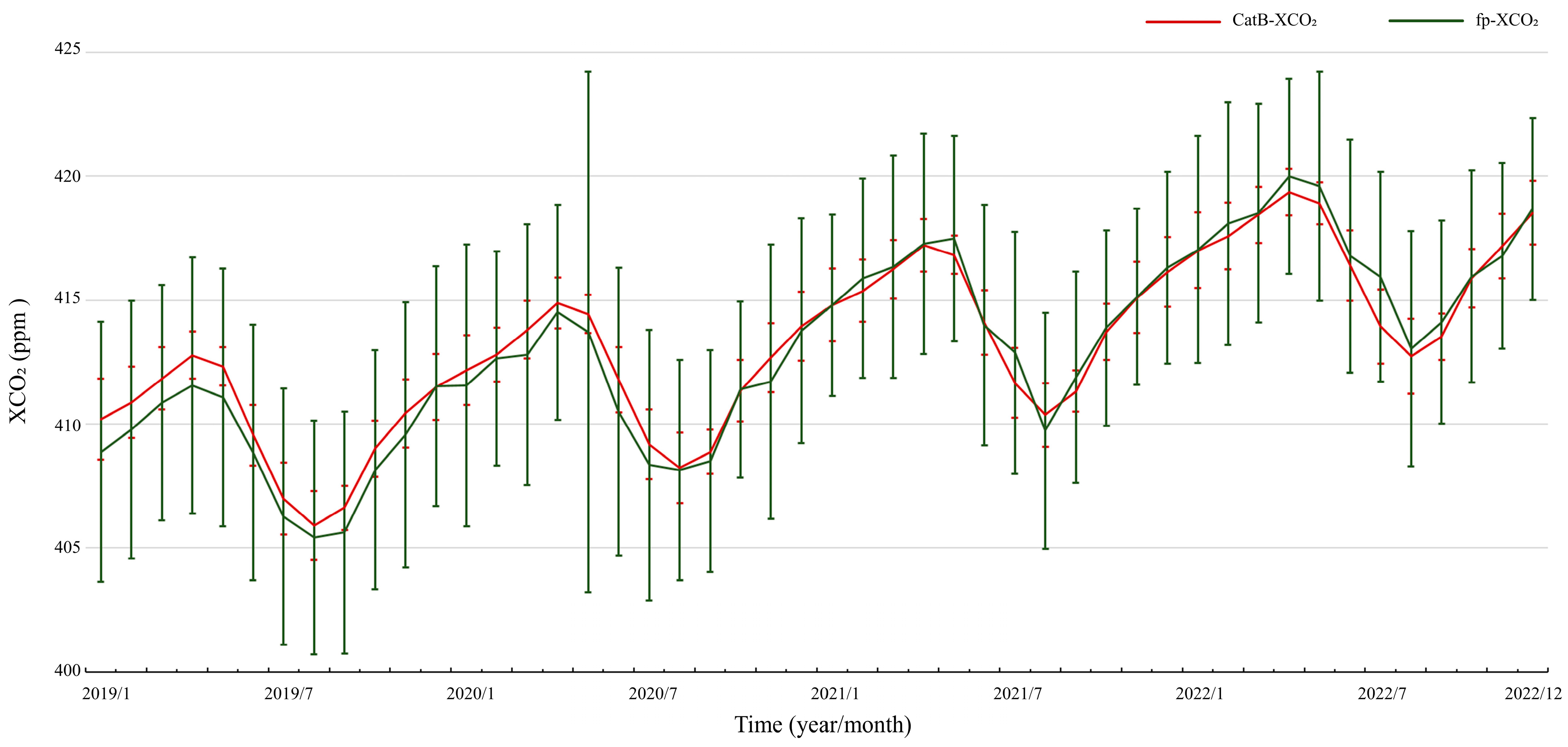
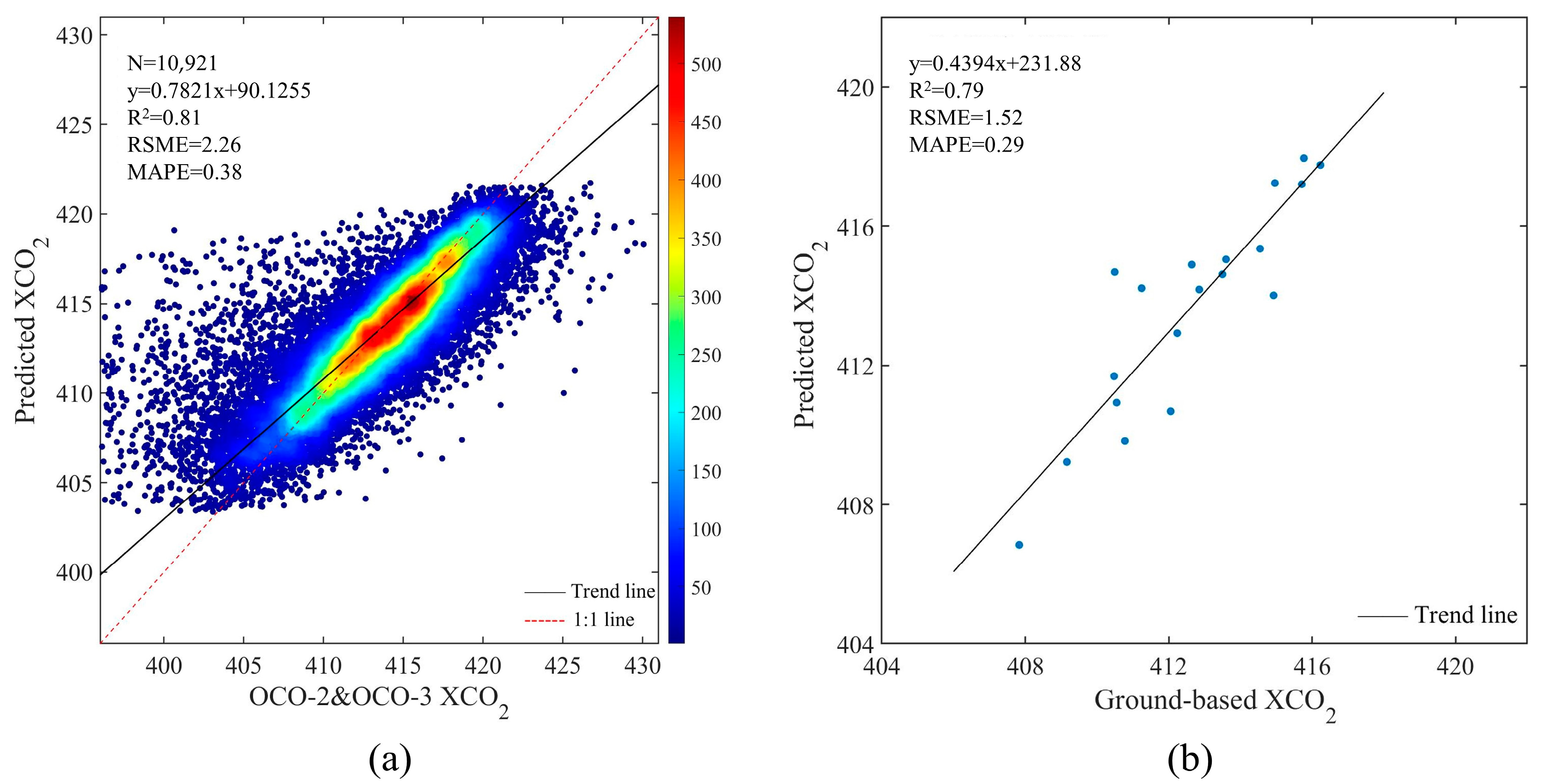
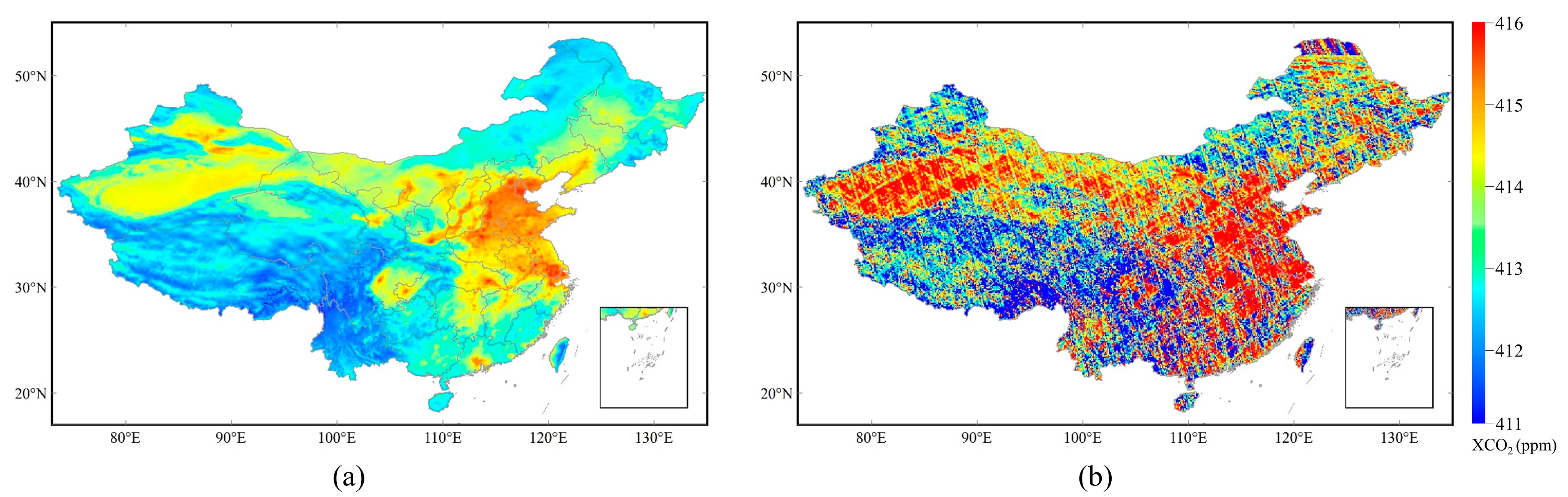
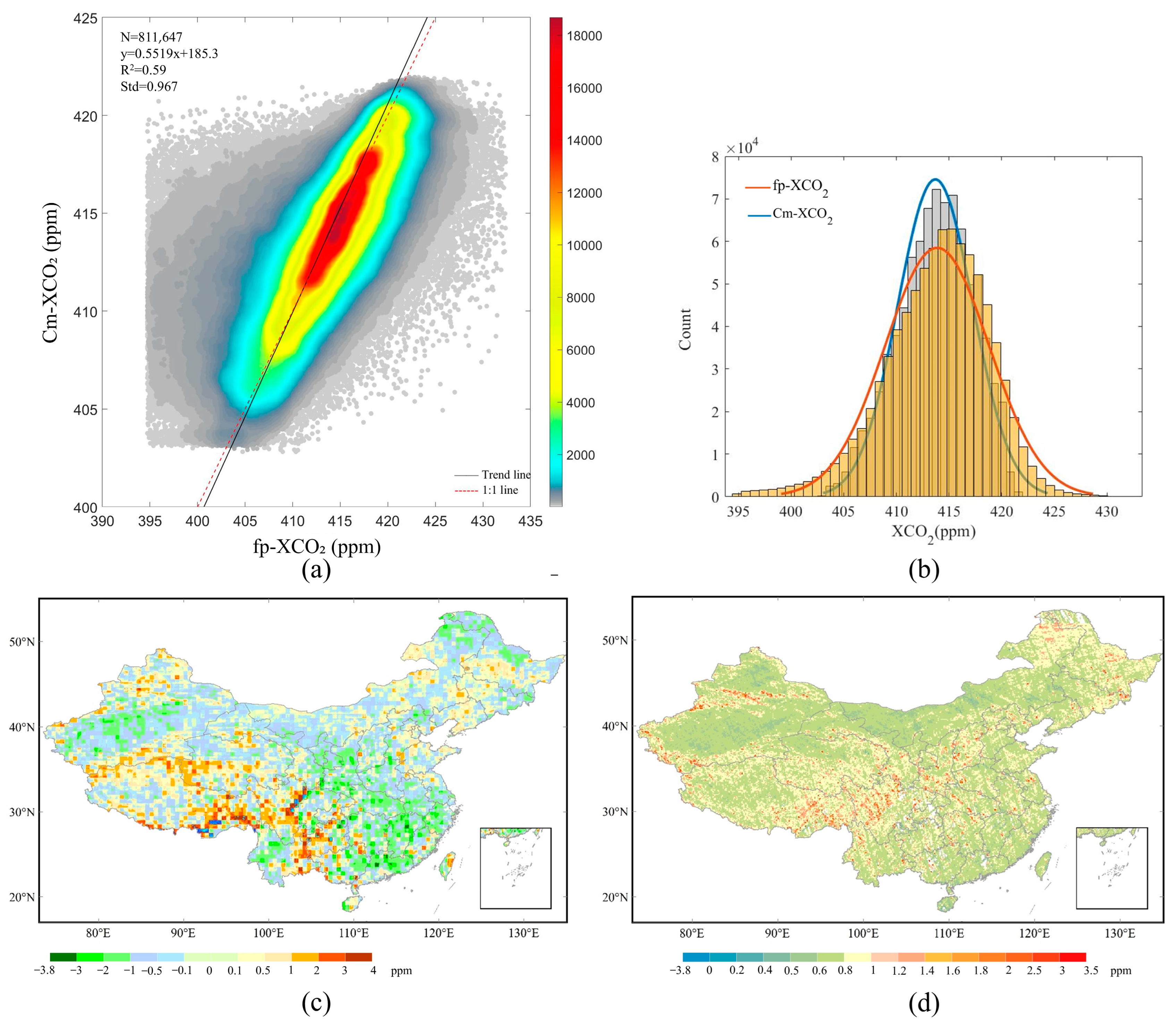
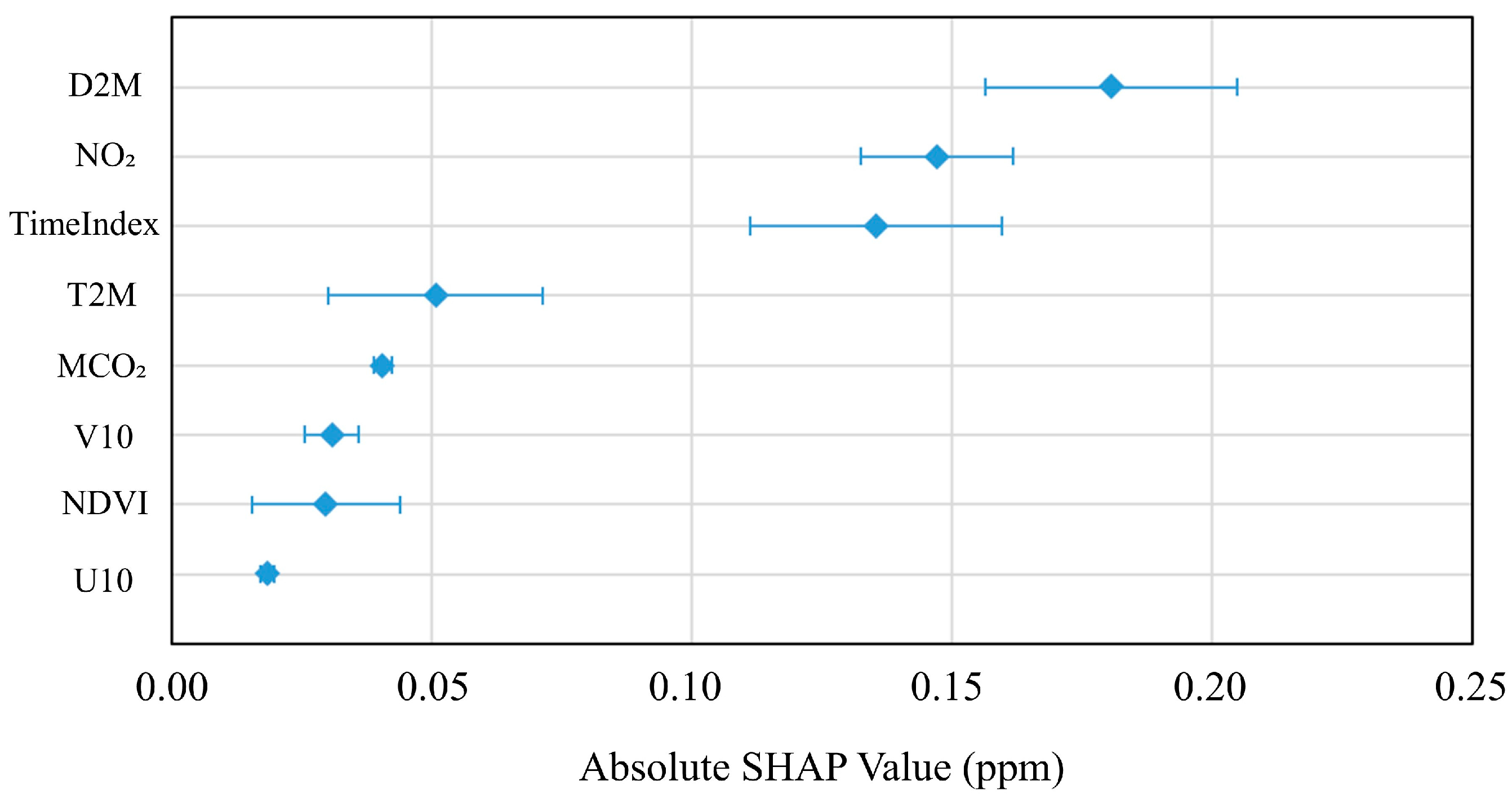
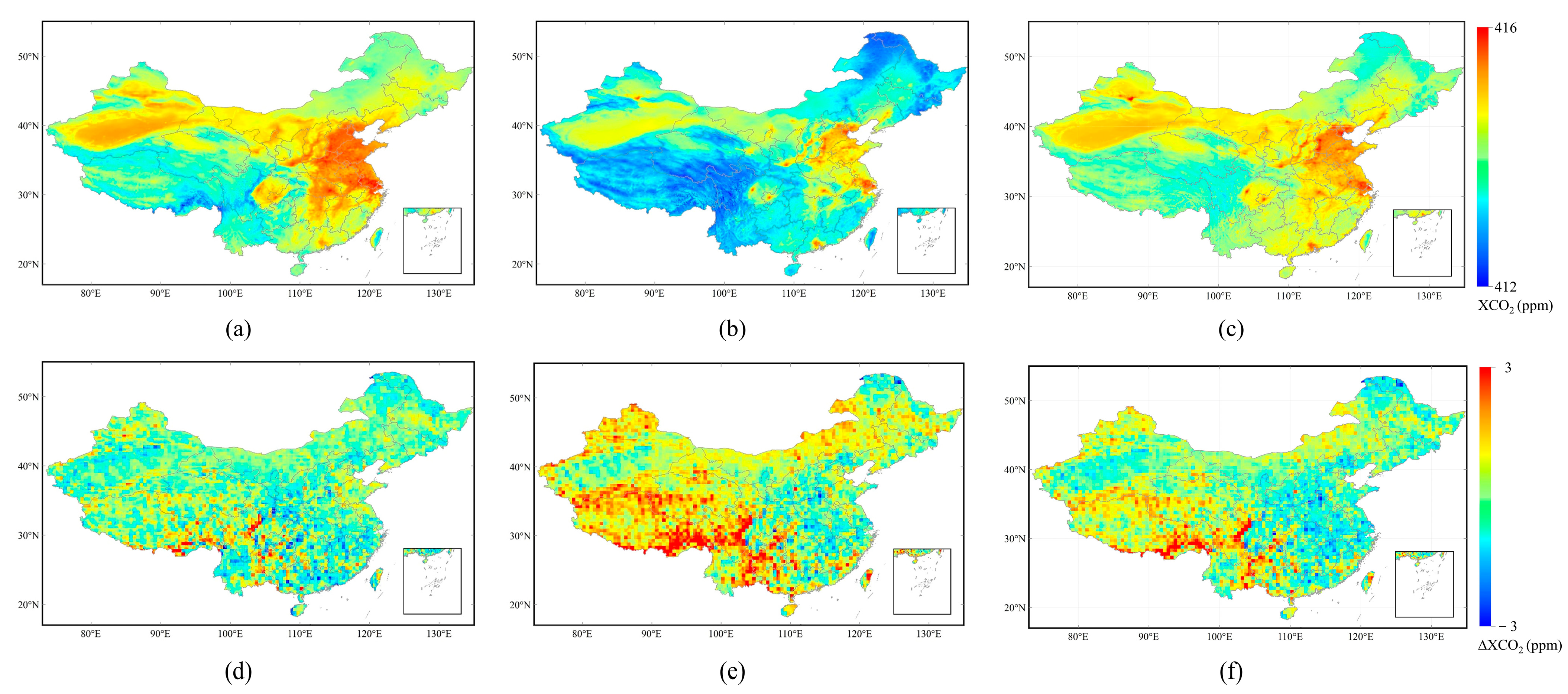
3.1. Model Prediction Accuracy and Performance of the Reconstructed XCO2
3.1.1. Accuracy of the XCO2 Predictions
3.1.2. Performance of the Model Predictions
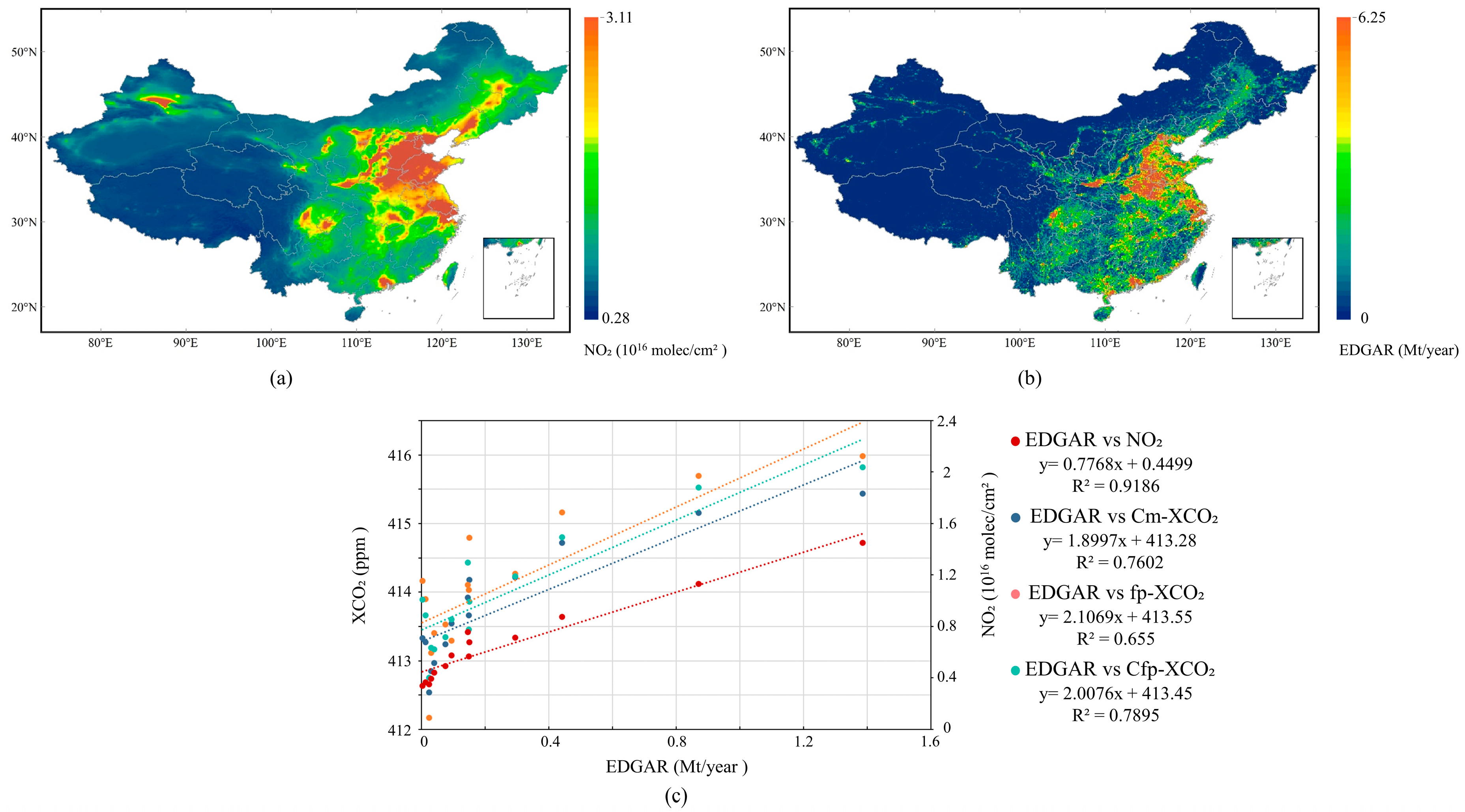
3.2. Co-Variation of CO2 and NO2 to Anthropogenic CO2 Emissions
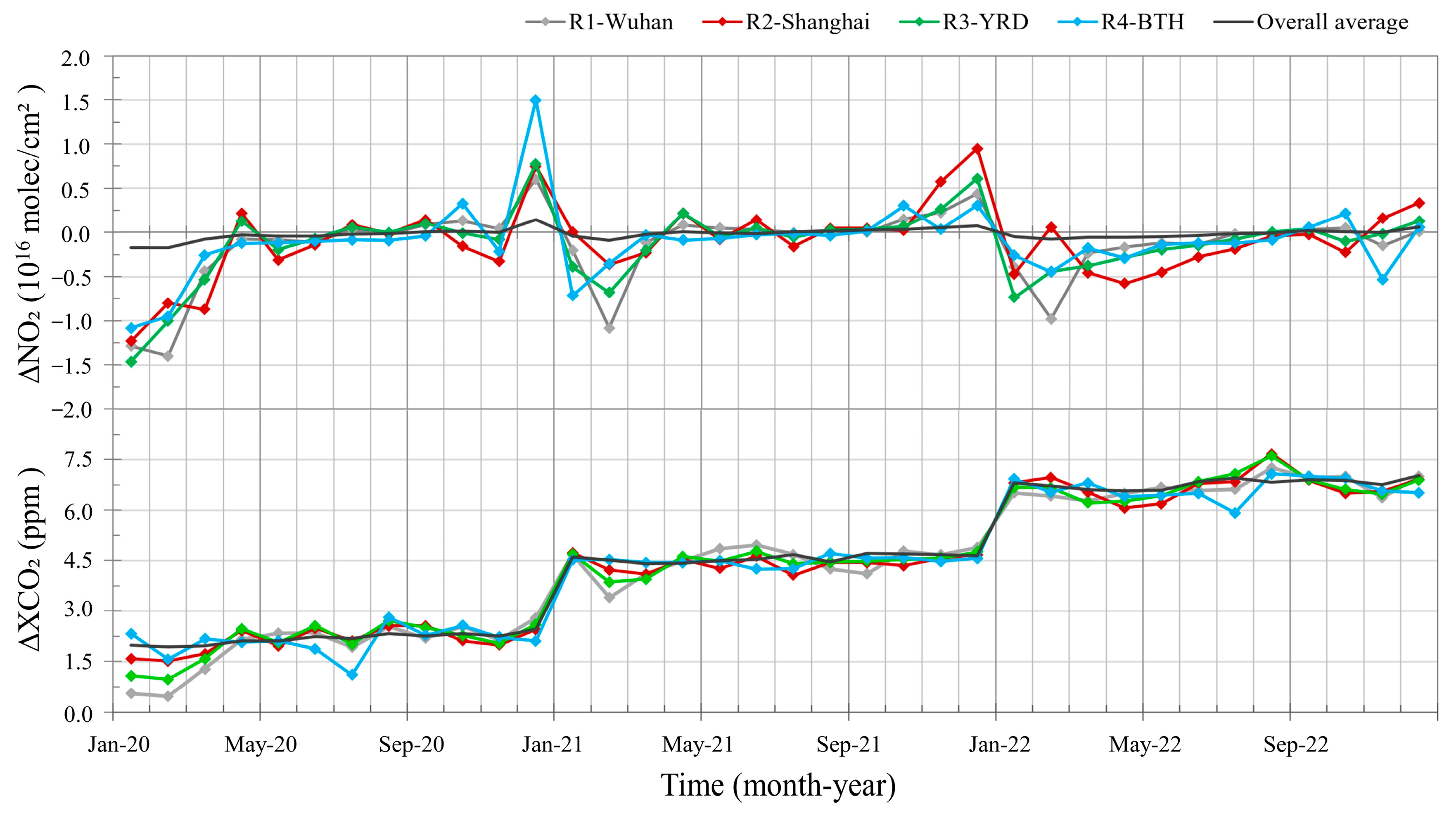
3.2.1. NO2 Constraints Enhancing the XCO2 Response to Anthropogenic Emissions
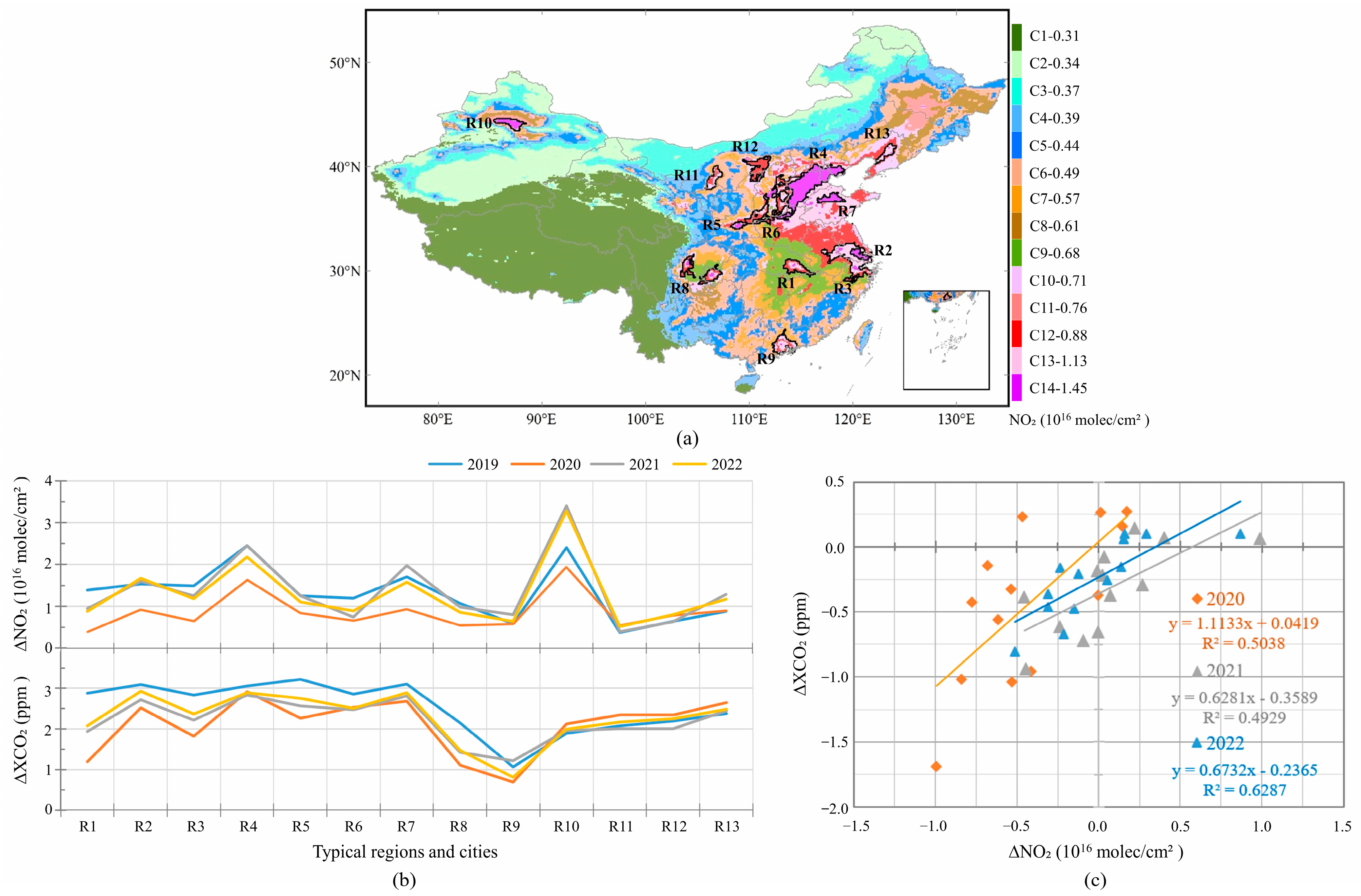
3.2.2. Co-Response of NO2 and CO2 Concentrations to Anthropogenic Emissions under Special Scenarios of Human Activity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Wang, H.; Liu, Z.; Zhang, Y.; Yu, Z.; Chen, C. Impact of Different Urban Canopy Models on Air Quality Simulation in Chengdu, Southwestern China. Atmos. Environ. 2021, 267, 118775. [Google Scholar] [CrossRef]
- Hsueh, Y.-H.; Li, K.-F.; Lin, L.-C.; Bhattacharya, S.K.; Laskar, A.H.; Liang, M.-C. East Asian CO2 Level Change Caused by Pacific Decadal Oscillation. Remote Sens. Environ. 2021, 264, 112624. [Google Scholar] [CrossRef]
- Liang, M.; Zhang, Y.; Ma, Q.; Yu, D.; Chen, X.; Cohen, J.B. Dramatic Decline of Observed Atmospheric CO2 and CH4 during the COVID-19 Lockdown over the Yangtze River Delta of China. J. Environ. Sci. 2023, 124, 712–722. [Google Scholar] [CrossRef]
- Fang, S.; Du, R.; Qi, B.; Ma, Q.; Zhang, G.; Chen, B.; Li, J. Variation of Carbon Dioxide Mole Fraction at a Typical Urban Area in the Yangtze River Delta, China. Atmos. Res. 2022, 265, 105884. [Google Scholar] [CrossRef]
- Fu, Y.; Sun, W.; Luo, F.; Zhang, Y.; Zhang, X. Variation Patterns and Driving Factors of Regional Atmospheric CO2 Anomalies in China. Environ. Sci. Pollut. Res. 2022, 29, 19390–19403. [Google Scholar] [CrossRef]
- Wang, W.; He, J.; Feng, H.; Jin, Z. High-Coverage Reconstruction of XCO2 Using Multisource Satellite Remote Sensing Data in Beijing–Tianjin–Hebei Region. Int. J. Environ. Res. Public Health 2022, 19, 10853. [Google Scholar] [CrossRef]
- Crisp, D.; Fisher, B.M.; O’Dell, C.; Frankenberg, C.; Basilio, R.; Bösch, H.; Brown, L.R.; Castano, R.; Connor, B.; Deutscher, N.M.; et al. The ACOS CO2 Retrieval Algorithm–Part II: Global XCO2 Data Characterization. Atmos. Meas. Tech. 2012, 5, 687–707. [Google Scholar] [CrossRef]
- Nakajima, M.; Kuze, A.; Suto, H. The Current Status of GOSAT and the Concept of GOSAT-2. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XVI, Edinburgh, UK, 24–27 September 2012; Meynart, R., Neeck, S.P., Shimoda, H., Eds.; SPIE: Bellingham, WA, USA, 2012; p. 853306. [Google Scholar]
- Kataoka, F.; Crisp, D.; Taylor, T.; O’Dell, C.; Kuze, A.; Shiomi, K.; Suto, H.; Bruegge, C.; Schwandner, F.; Rosenberg, R.; et al. The Cross-Calibration of Spectral Radiances and Cross-Validation of CO2 Estimates from GOSAT and OCO-2. Remote Sens. 2017, 9, 1158. [Google Scholar] [CrossRef]
- Jin, C.; Xue, Y.; Jiang, X.; Zhao, L.; Yuan, T.; Sun, Y.; Wu, S.; Wang, X. A Long-Term Global XCO2 Dataset: Ensemble of Satellite Products. Atmos. Res. 2022, 279, 106385. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Z.; Cai, Z.; Wang, L.; Gu, Z.; Xu, Y.; Zhao, J. Analysis of the Spatial–Temporal Distribution Characteristics of NO2 and Their Influencing Factors in the Yangtze River Delta Based on Sentinel-5P Satellite Data. Atmosphere 2022, 13, 1923. [Google Scholar] [CrossRef]
- Zhang, L.; Li, T.; Wu, J. Deriving Gapless CO2 Concentrations Using a Geographically Weighted Neural Network: China, 2014–2020. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103063. [Google Scholar] [CrossRef]
- Zeng, Z.; Lei, L.; Hou, S.; Ru, F.; Guan, X.; Zhang, B. A Regional Gap-Filling Method Based on Spatiotemporal Variogram Model of CO2 Columns. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3594–3603. [Google Scholar] [CrossRef]
- Sheng, M.; Lei, L.; Zeng, Z.-C.; Rao, W.; Zhang, S. Detecting the Responses of CO2 Column Abundances to Anthropogenic Emissions from Satellite Observations of GOSAT and OCO-2. Remote Sens. 2021, 13, 3524. [Google Scholar] [CrossRef]
- Zhang, S.; Lei, L.; Sheng, M.; Song, H.; Li, L.; Guo, K.; Ma, C.; Liu, L.; Zeng, Z. Evaluating Anthropogenic CO2 Bottom-Up Emission Inventories Using Satellite Observations from GOSAT and OCO-2. Remote Sens. 2022, 14, 5024. [Google Scholar] [CrossRef]
- Uddin, M.S.; Czajkowski, K.P. Performance Assessment of Spatial Interpolation Methods for the Estimation of Atmospheric Carbon Dioxide in the Wider Geographic Extent. J. Geovis. Spat. Anal. 2022, 6, 10. [Google Scholar] [CrossRef]
- He, C.; Ji, M.; Li, T.; Liu, X.; Tang, D.; Zhang, S.; Luo, Y.; Grieneisen, M.L.; Zhou, Z.; Zhan, Y. Deriving Full-Coverage and Fine-Scale XCO2 Across China Based on OCO-2 Satellite Retrievals and CarbonTracker Output. Geophys. Res. Lett. 2022, 49, e2022GL098435. [Google Scholar] [CrossRef]
- Wu, C.; Ju, Y.; Yang, S.; Zhang, Z.; Chen, Y. Reconstructing Annual XCO2 at a 1 Km × 1 Km Spatial Resolution across China from 2012 to 2019 Based on a Spatial CatBoost Method. Environ. Res. 2023, 236, 116866. [Google Scholar] [CrossRef]
- Kallio, J.; Tervonen, J.; Räsänen, P.; Mäkynen, R.; Koivusaari, J.; Peltola, J. Forecasting Office Indoor CO2 Concentration Using Machine Learning with a One-Year Dataset. Build. Environ. 2021, 187, 107409. [Google Scholar] [CrossRef]
- Zhao, Z.; Xie, F.; Ren, T.; Zhao, C. Atmospheric CO2 Retrieval from Satellite Spectral Measurements by a Two-Step Machine Learning Approach. J. Quant. Spectrosc. Radiat. Transf. 2022, 278, 108006. [Google Scholar] [CrossRef]
- Finch, D.; Palmer, P.; Zhang, T. Automated Detection of Atmospheric NO2 Plumes from Satellite Data: A Tool to Help Infer Anthropogenic Combustion Emissions. Atmos. Meas. Tech. 2021, 15, 721–733. [Google Scholar] [CrossRef]
- Hakkarainen, J.; Ialongo, I.; Oda, T.; Szeląg, M.E.; O’Dell, C.W.; Eldering, A.; Crisp, D. Building a Bridge: Characterizing Major Anthropogenic Point Sources in the South African Highveld Region Using OCO-3 Carbon Dioxide Snapshot Area Maps and Sentinel-5P/TROPOMI Nitrogen Dioxide Columns. Environ. Res. Lett. 2023, 18, 035003. [Google Scholar] [CrossRef]
- Saw, G.K.; Dey, S.; Kaushal, H.; Lal, K. Tracking NO2 Emission from Thermal Power Plants in North India Using TROPOMI Data. Atmos. Environ. 2021, 259, 118514. [Google Scholar] [CrossRef]
- Fuentes Andrade, B.; Buchwitz, M.; Reuter, M.; Bovensmann, H.; Richter, A.; Boesch, H.; Burrows, J.P. A Method for Estimating Localized CO2 Emissions from Co-Located Satellite XCO2 and NO2 Images. Atmos. Meas. Tech. 2024, 17, 1145–1173. [Google Scholar] [CrossRef]
- Goldberg, D.L.; Lu, Z.; Oda, T.; Lamsal, L.N.; Liu, F.; Griffin, D.; McLinden, C.A.; Krotkov, N.A.; Duncan, B.N.; Streets, D.G. Exploiting OMI NO2 Satellite Observations to Infer Fossil-Fuel CO2 Emissions from U.S. Megacities. Sci. Total Environ. 2019, 695, 133805. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Berezin, E.V.; Ciais, P.; Broquet, G.; Zhuravlev, R.V.; Janssens-Maenhout, G. Estimation of Fossil-Fuel CO2 Emissions Using Satellite Measurements of “Proxy” Species. Atmos. Chem. Phys. 2016, 16, 13509–13540. [Google Scholar] [CrossRef]
- Liu, F.; Duncan, B.N.; Krotkov, N.A.; Lamsal, L.N.; Beirle, S.; Griffin, D.; McLinden, C.A.; Goldberg, D.L.; Lu, Z. A Methodology to Constrain Carbon Dioxide Emissions from Coal-Fired Power Plants Using Satellite Observations of Co-Emitted Nitrogen Dioxide. Atmos. Chem. Phys. 2020, 20, 99–116. [Google Scholar] [CrossRef]
- He, Q.; Ye, T.; Wang, W.; Luo, M.; Song, Y.; Zhang, M. Spatiotemporally Continuous Estimates of Daily 1-Km PM2.5 Concentrations and Their Long-Term Exposure in China from 2000 to 2020. J. Environ. Manag. 2023, 342, 118145. [Google Scholar] [CrossRef]
- Park, H.; Jeong, S.; Park, H.; Labzovskii, L.D.; Bowman, K.W. An Assessment of Emission Characteristics of Northern Hemisphere Cities Using Spaceborne Observations of CO2, CO, and NO2. Remote Sens. Environ. 2021, 254, 112246. [Google Scholar] [CrossRef]
- Hakkarainen, J.; Ialongo, I.; Maksyutov, S.; Crisp, D. Analysis of Four Years of Global XCO2 Anomalies as Seen by Orbiting Carbon Observatory-2. Remote Sens. 2019, 11, 850. [Google Scholar] [CrossRef]
- Liu, D.; Lei, L.; Guo, L.; Zeng, Z.-C. A Cluster of CO2 Change Characteristics with GOSAT Observations for Viewing the Spatial Pattern of CO2 Emission and Absorption. Atmosphere 2015, 6, 1695–1713. [Google Scholar] [CrossRef]
- Wang, W.; Tian, Y.; Liu, C.; Sun, Y.; Liu, W.; Xie, P.; Liu, J.; Xu, J.; Morino, I.; Velazco, V.A.; et al. Investigating the Performance of a Greenhouse Gas Observatory in Hefei, China. Atmos. Meas. Tech. 2017, 10, 2627–2643. [Google Scholar] [CrossRef]
- Ciais, P.; Dolman, A.J.; Bombelli, A.; Duren, R.; Peregon, A.; Rayner, P.J.; Miller, C.; Gobron, N.; Kinderman, G.; Marland, G.; et al. Current Systematic Carbon-Cycle Observations and the Need for Implementing a Policy-Relevant Carbon Observing System. Biogeosciences 2014, 11, 3547–3602. [Google Scholar] [CrossRef]
- Yang, E.G.; Kort, E.A.; Ott, L.E.; Oda, T.; Lin, J.C. Using Space-Based CO 2 and NO 2 Observations to Estimate Urban CO2 Emissions. JGR Atmos. 2023, 128, e2022JD037736. [Google Scholar] [CrossRef]
- Ebi, K.L.; Anderson, C.L.; Hess, J.J.; Kim, S.-H.; Loladze, I.; Neumann, R.B.; Singh, D.; Ziska, L.; Wood, R. Nutritional Quality of Crops in a High CO2 World: An Agenda for Research and Technology Development. Environ. Res. Lett. 2021, 16, 064045. [Google Scholar] [CrossRef]
- Warren, J.M.; Jensen, A.M.; Ward, E.J.; Guha, A.; Childs, J.; Wullschleger, S.D.; Hanson, P.J. Divergent Species-specific Impacts of Whole Ecosystem Warming and Elevated CO2 on Vegetation Water Relations in an Ombrotrophic Peatland. Glob. Change Biol. 2021, 27, 1820–1835. [Google Scholar] [CrossRef]
- European Commission; Joint Research Centre. Fossil CO2 Emissions of All World Countries: 2018 Report; Publications Office: Luxembourg, 2018. [Google Scholar]
- He, Z.; Lei, L.; Welp, L.; Zeng, Z.-C.; Bie, N.; Yang, S.; Liu, L. Detection of Spatiotemporal Extreme Changes in Atmospheric CO2 Concentration Based on Satellite Observations. Remote Sens. 2018, 10, 839. [Google Scholar] [CrossRef]
- Chen, S.; Mihara, K.; Wen, J. Time Series Prediction of CO2, TVOC and HCHO Based on Machine Learning at Different Sampling Points. Build. Environ. 2018, 146, 238–246. [Google Scholar] [CrossRef]
- Kalra, S.; Lamba, R.; Sharma, M. Machine Learning Based Analysis for Relation between Global Temperature and Concentrations of Greenhouse Gases. J. Inf. Optim. Sci. 2020, 41, 73–84. [Google Scholar] [CrossRef]
- Siabi, Z.; Falahatkar, S.; Alavi, S.J. Spatial Distribution of XCO2 Using OCO-2 Data in Growing Seasons. J. Environ. Manag. 2019, 244, 110–118. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Eldering, A.; Wennberg, P.O.; Crisp, D.; Gunson, M.R.; Fisher, B.; Frankenberg, C.; Kiel, M.; Lindqvist, H.; Mandrake, L.; et al. Improved Retrievals of Carbon Dioxide from Orbiting Carbon Observatory-2 with the Version 8 ACOS Algorithm. Atmos. Meas. Tech. 2018, 11, 6539–6576. [Google Scholar] [CrossRef]
- Massie, S.T.; Sebastian Schmidt, K.; Eldering, A.; Crisp, D. Observational Evidence of 3-D Cloud Effects in OCO-2 CO2 Retrievals. JGR Atmos. 2017, 122, 7064–7085. [Google Scholar] [CrossRef]
- Van Geffen, J.; Boersma, K.F.; Eskes, H.; Sneep, M.; Ter Linden, M.; Zara, M.; Veefkind, J.P. S5P TROPOMI NO2 Slant Column Retrieval: Method, Stability, Uncertainties and Comparisons with OMI. Atmos. Meas. Tech. 2020, 13, 1315–1335. [Google Scholar] [CrossRef]
- Fan, C.; Li, Z.; Li, Y.; Dong, J.; Van Der, A.R.; De Leeuw, G. Variability of NO2 Concentrations over China and Effect on Air Quality Derived from Satellite and Ground-Based Observations. Atmos. Chem. Phys. 2021, 21, 7723–7748. [Google Scholar] [CrossRef]
- Fioletov, V.; McLinden, C.A.; Griffin, D.; Krotkov, N.; Liu, F.; Eskes, H. Quantifying Urban, Industrial, and Background Changes in NO2 during the COVID-19 Lockdown Period Based on TROPOMI Satellite Observations. Atmos. Chem. Phys. 2022, 22, 4201–4236. [Google Scholar] [CrossRef]
- Veefkind, J.P.; Aben, I.; McMullan, K.; Förster, H.; De Vries, J.; Otter, G.; Claas, J.; Eskes, H.J.; De Haan, J.F.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES Mission for Global Observations of the Atmospheric Composition for Climate, Air Quality and Ozone Layer Applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Guo, M.; Wang, X.; Li, J.; Wang, H.; Tani, H. Examining the Relationships between Land Cover and Greenhouse Gas Concentrations Using Remote-Sensing Data in East Asia. Int. J. Remote Sens. 2013, 34, 4281–4303. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Y.; Wang, Q.; Guan, B. Climate, CO2, and Anthropogenic Drivers of Accelerated Vegetation Greening in the Haihe River Basin. Remote Sens. 2022, 14, 268. [Google Scholar] [CrossRef]
- Chen, X.; He, Q.; Ye, T.; Liang, Y.; Li, Y. Decoding Spatiotemporal Dynamics in Atmospheric CO2 in Chinese Cities: Insights from Satellite Remote Sensing and Geographically and Temporally Weighted Regression Analysis. Sci. Total Environ. 2024, 908, 167917. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Noël, S.; Gier, B.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Anand, J.; Parker, R.J.; et al. Computation and Analysis of Atmospheric Carbon Dioxide Annual Mean Growth Rates from Satellite Observations during 2003–2016. Atmos. Chem. Phys. 2018, 18, 17355–17370. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, C.; Zhang, L.; Palm, M.; Notholt, J.; Yin, H.; Vigouroux, C.; Lutsch, E.; Wang, W.; Shan, C.; et al. Fourier Transform Infrared Time Series of Tropospheric HCN in Eastern China: Seasonality, Interannual Variability, and Source Attribution. Atmos. Chem. Phys. 2020, 20, 5437–5456. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Quart. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and Scaled Difference Vegetation Index Retrievals of Vegetation Fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Chatterjee, A.; Payne, V.; Eldering, A.; Rosenberg, R.; Kiel, M.; Fisher, B.; Nelson, R.; Dang, L.; Rodrigues, G.K.; O’Dell, C.; et al. Orbiting Carbon Observatory-3 (OCO-3) Data Quality Statement: Level 2 Forward and Retrospective Processing Data Release 10 (V10 and V10r), V10.4 Lite Files; California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar]
- Keely, W.R.; Mauceri, S.; Crowell, S.; O’Dell, C.W. A Nonlinear Data-Driven Approach to Bias Correction of XCO 2 for NASA’s OCO-2 ACOS Version 10. Atmos. Meas. Tech. 2023, 16, 5725–5748. [Google Scholar] [CrossRef]
- Zhang, J. China Greenhouse Gas Bulletin 2022 post. China Meteorological News, 6 December 2023. [Google Scholar]


| Acronym | Parameter | Source | Resolution | Product | |
|---|---|---|---|---|---|
| Space | Time | ||||
| fp-XCO2 | XCO2 retrievals | OCO-2 | 2.25 km × 1.29 km | 16 days | OCO-2 _L2_Lite_FP_11r |
| OCO-3 | 2.25 km × 1.29 km | 16 days | OCO-3 _L2_Lite_FP_10.4r | ||
| NO2 | Atmospheric NO2 column | TROPOMI-S5P | 0.01° | Monthly | Sentinel-5P OFFL NO2: Offline Nitrogen Dioxide |
| NDVI | Normalized-difference vegetation index | MODIS | 0.05° | Monthly | MOD13C2 |
| D2M | 2 m dewpoint temperature | ERA5— fifth-generation ECMWF atmospheric reanalysis | 0.1° | Monthly | Complete ERA5 global atmospheric reanalysis |
| T2M | 2 m temperature | ||||
| U10 | 10 m U-wind component | ||||
| V10 | 10 m V-wind component | ||||
| MXCO2 | Mapping XCO2 | Mapped geostatistical method using XCO2 retrievals | 0.5° | Monthly | Global land 0.5° mapping XCO2 dataset using satellite observations of GOSAT, OCO-2, and OCO-3 from 2009 to 2022 |
| T-XCO2 | Ground-based XCO2 data | TCCON | Point | - | TCCON data from Hefei (PRC) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Lei, L.; Sheng, M.; Ji, Z.; Song, H. Refining Spatial and Temporal XCO2 Characteristics Observed by Orbiting Carbon Observatory-2 and Orbiting Carbon Observatory-3 Using Sentinel-5P Tropospheric Monitoring Instrument NO2 Observations in China. Remote Sens. 2024, 16, 2456. https://doi.org/10.3390/rs16132456
Guo K, Lei L, Sheng M, Ji Z, Song H. Refining Spatial and Temporal XCO2 Characteristics Observed by Orbiting Carbon Observatory-2 and Orbiting Carbon Observatory-3 Using Sentinel-5P Tropospheric Monitoring Instrument NO2 Observations in China. Remote Sensing. 2024; 16(13):2456. https://doi.org/10.3390/rs16132456
Chicago/Turabian StyleGuo, Kaiyuan, Liping Lei, Mengya Sheng, Zhanghui Ji, and Hao Song. 2024. "Refining Spatial and Temporal XCO2 Characteristics Observed by Orbiting Carbon Observatory-2 and Orbiting Carbon Observatory-3 Using Sentinel-5P Tropospheric Monitoring Instrument NO2 Observations in China" Remote Sensing 16, no. 13: 2456. https://doi.org/10.3390/rs16132456
APA StyleGuo, K., Lei, L., Sheng, M., Ji, Z., & Song, H. (2024). Refining Spatial and Temporal XCO2 Characteristics Observed by Orbiting Carbon Observatory-2 and Orbiting Carbon Observatory-3 Using Sentinel-5P Tropospheric Monitoring Instrument NO2 Observations in China. Remote Sensing, 16(13), 2456. https://doi.org/10.3390/rs16132456






