Ranging Offset Calibration and Moving Average Filter Enhanced Reliable UWB Positioning in Classic User Environments
Abstract
1. Introduction
- We introduced a ranging offset calibration and moving average filter into the prior residual-based robust extended Kalman filter, which can provide higher accuracy and reliability for UWB positioning solutions.
- This paper has provided a convenient ranging offset calibration scheme, which can effectively improve the positioning accuracy only by using a short period of static UWB observation.
- This paper constructs a robust weight function-based selective moving average filter to smooth the UWB results, by which the UWB positioning accuracy will be hardly influenced by the NLOS-polluted UWB ranges at previous epochs.
- Three sets of UWB datasets from classic user scenarios (indoor, outdoor, and transform areas) are used to investigate the performance of the presented UWB positioning method.
2. Methods
2.1. Conventional UWB Positioning Model
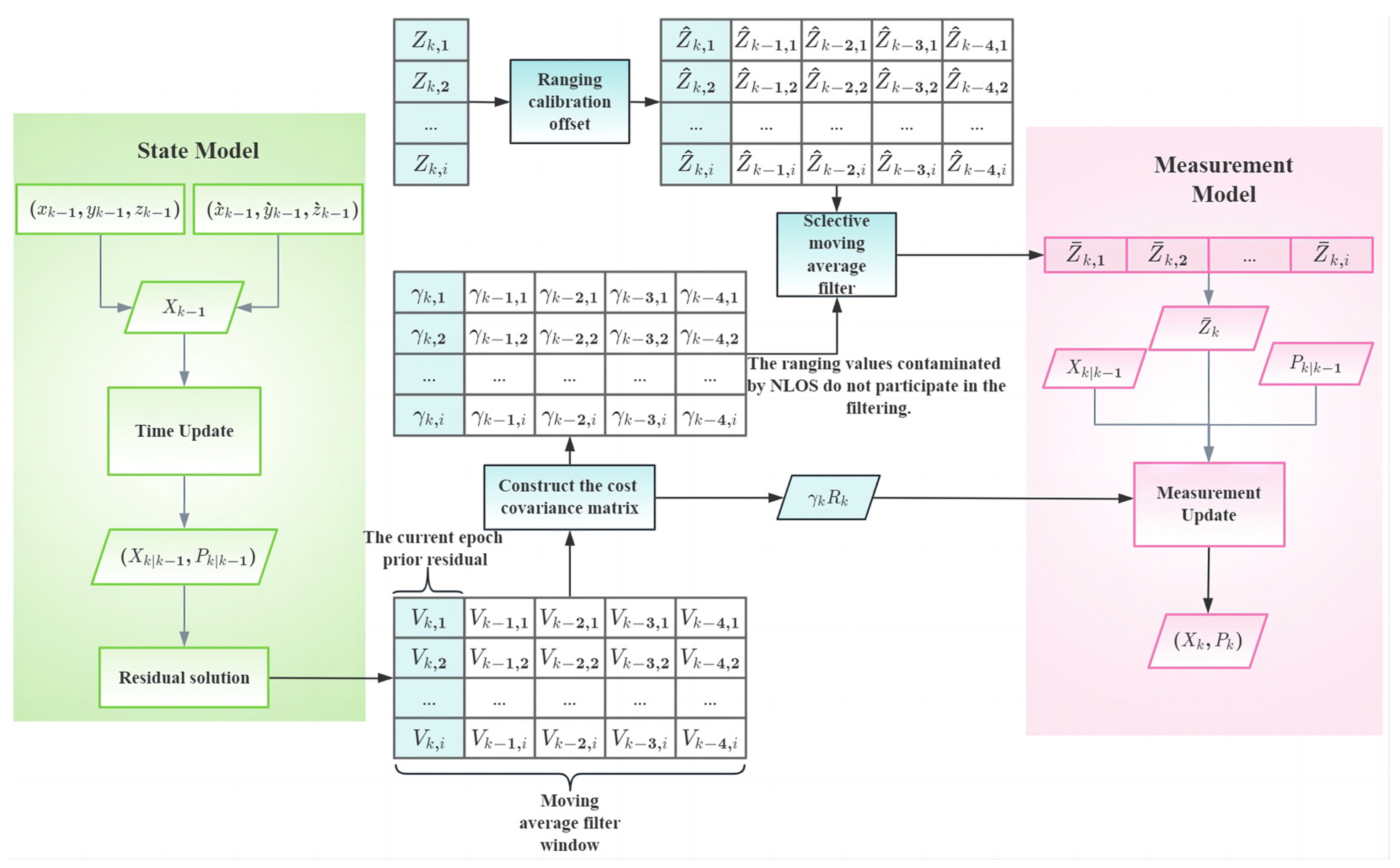
2.2. UWB Ranging Offset Calibration Model
2.3. Prior Residual-Based Robust Algorithm
2.4. Moving Average Filter Model
2.5. Algorithm Overview
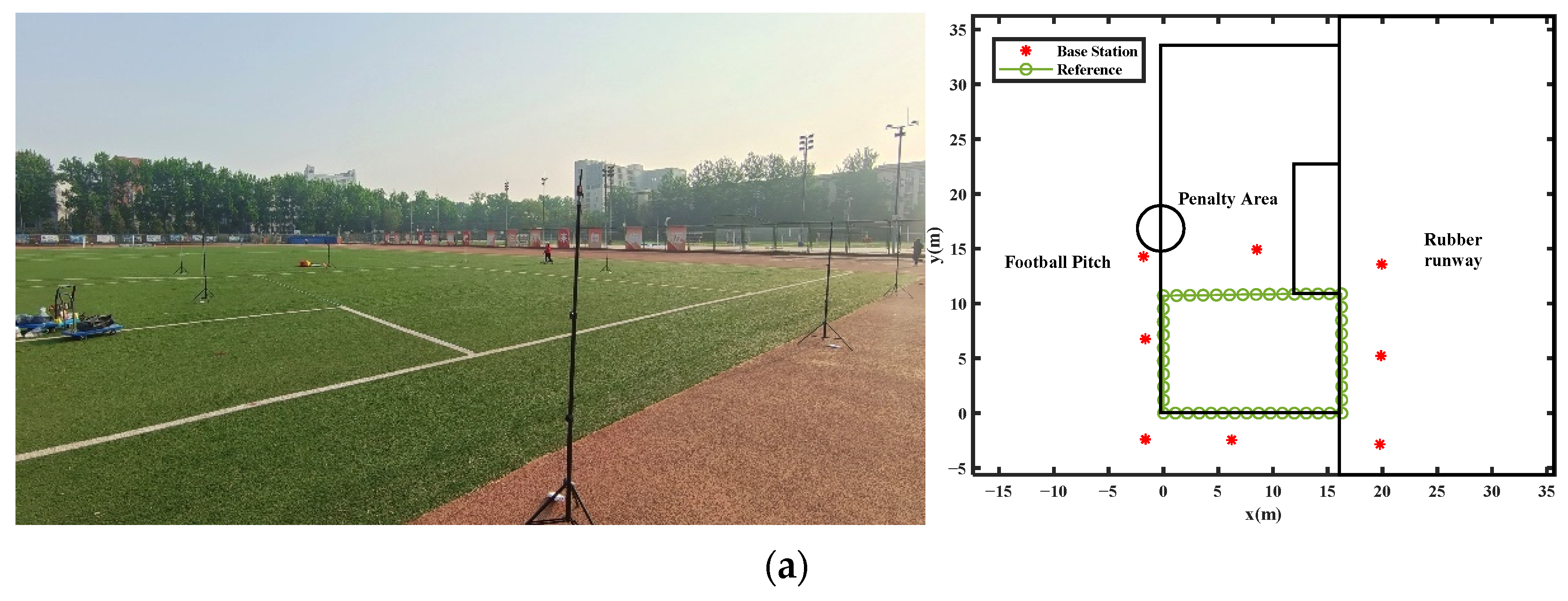
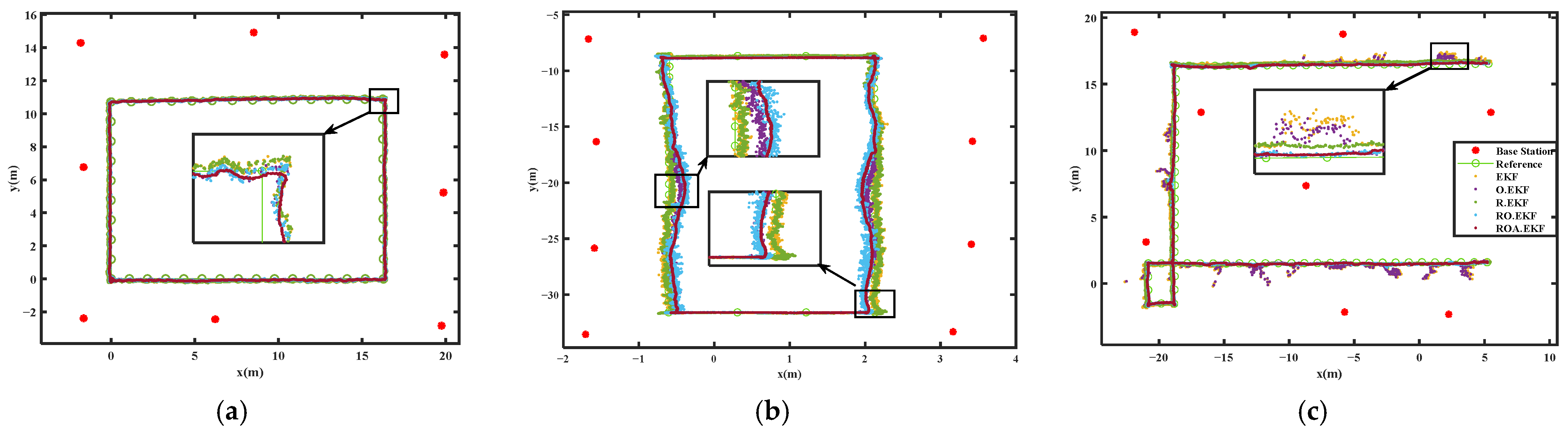
3. Experiments and Results
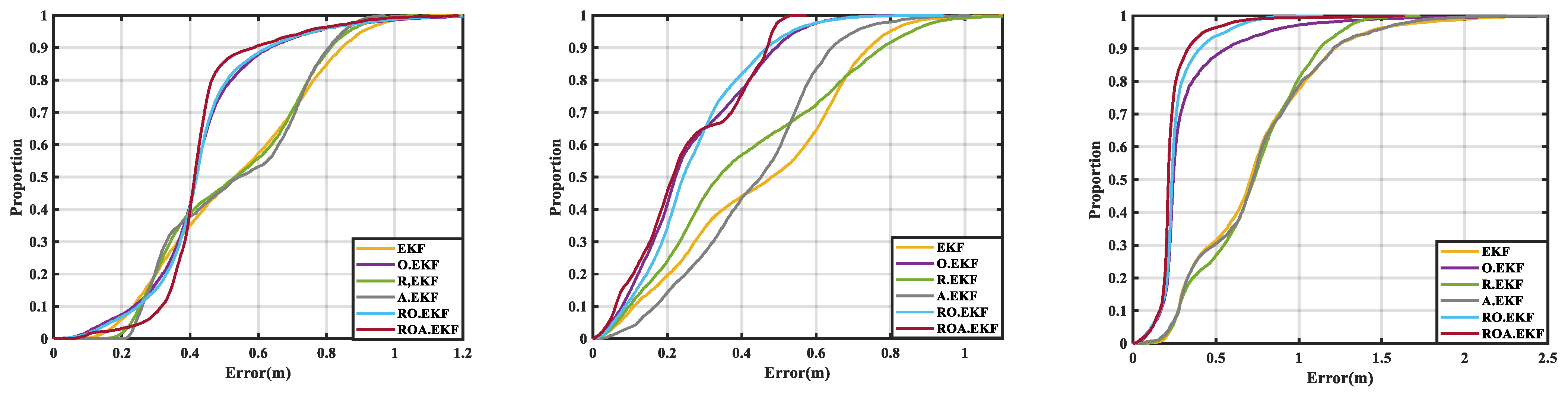
3.1. UWB Positioning Accuracy Evaluation Method
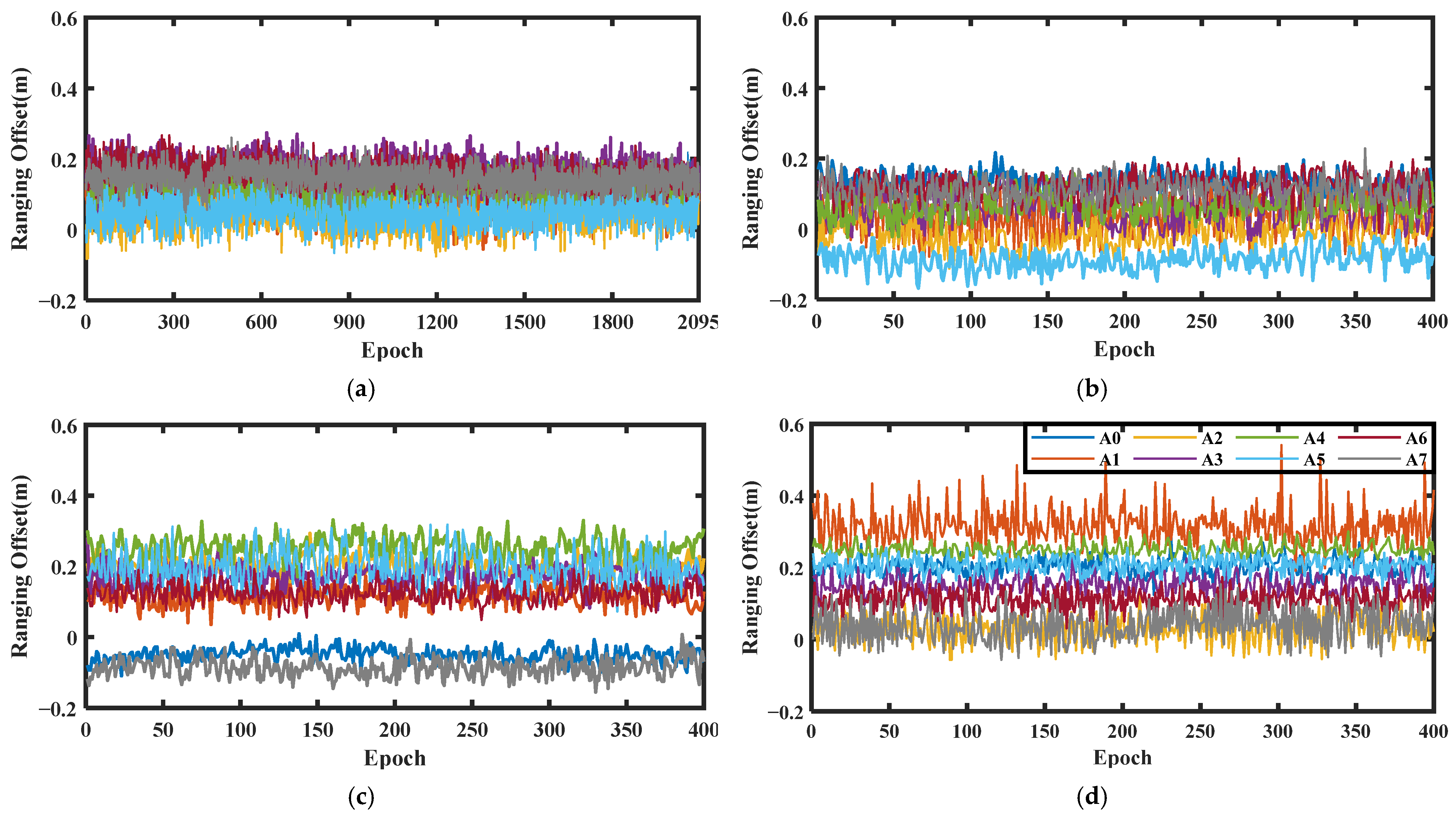
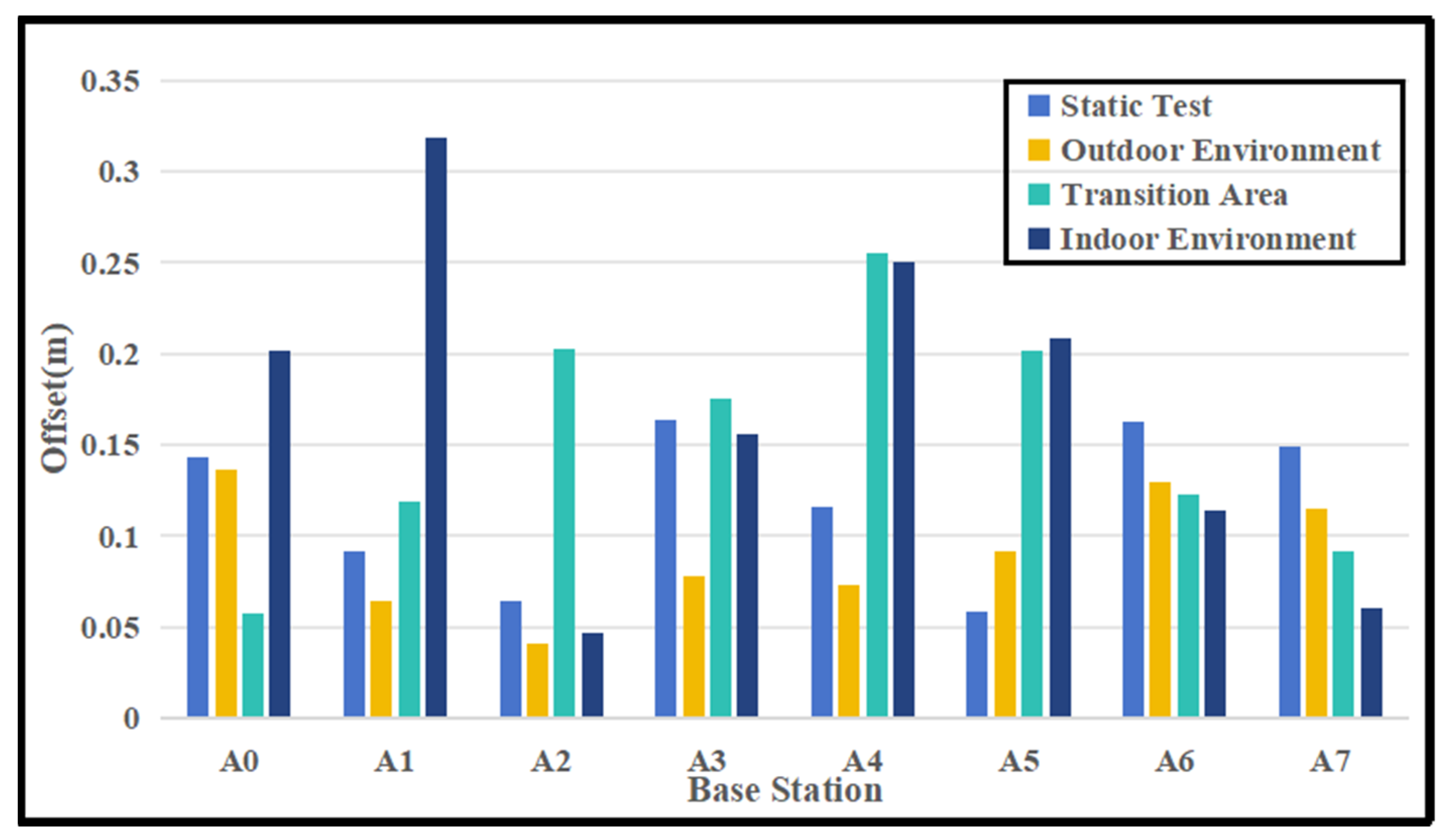
3.2. UWB Ranging Data Quality Analysis
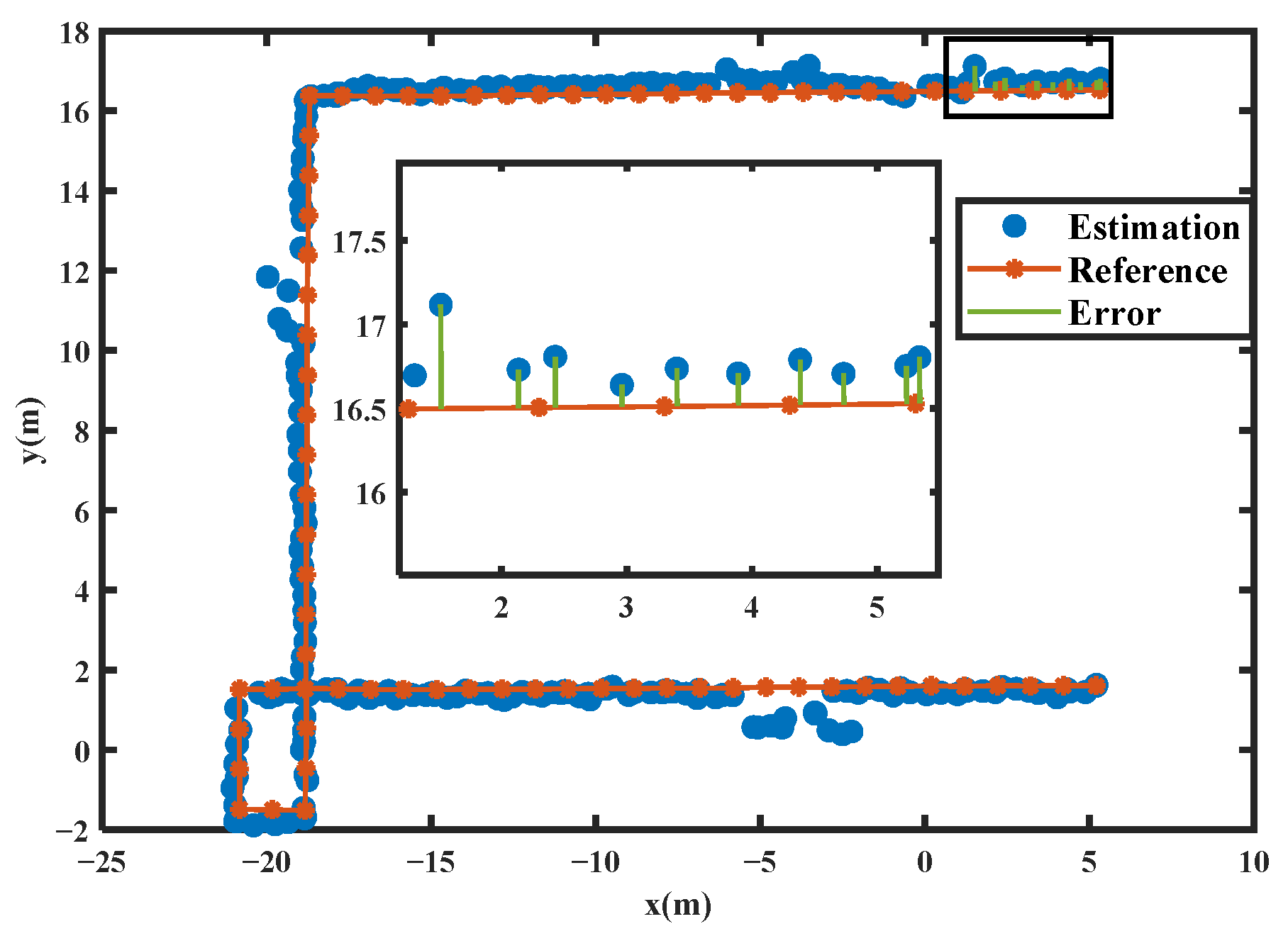
3.3. UWB Positioning Accuracy Analysis
3.3.1. UWB Ranging Offset Calibration Algorithm Enhanced UWB Positioning
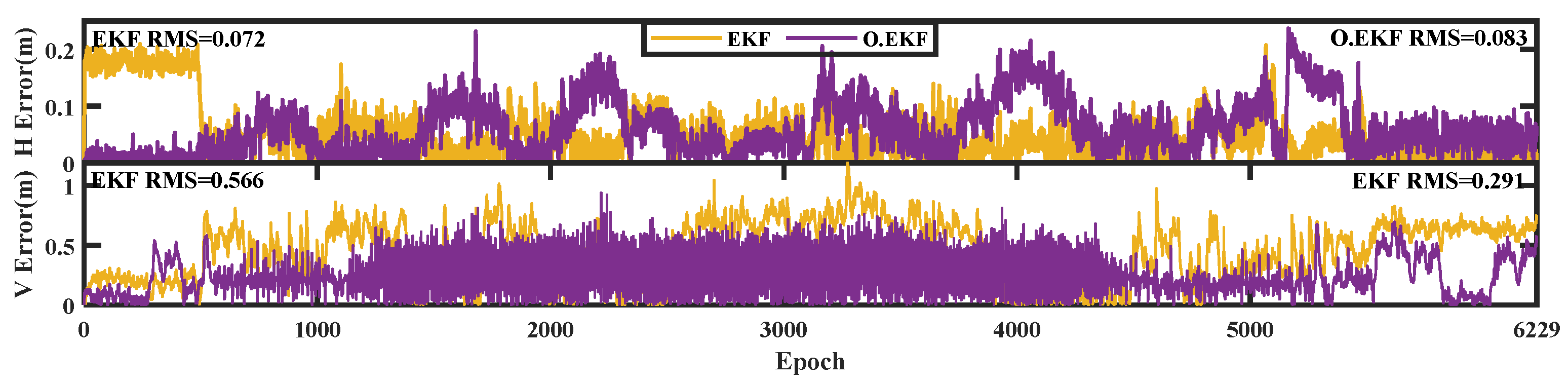
3.3.2. Prior Residual-Based Robust Theory Enhanced UWB Positioning
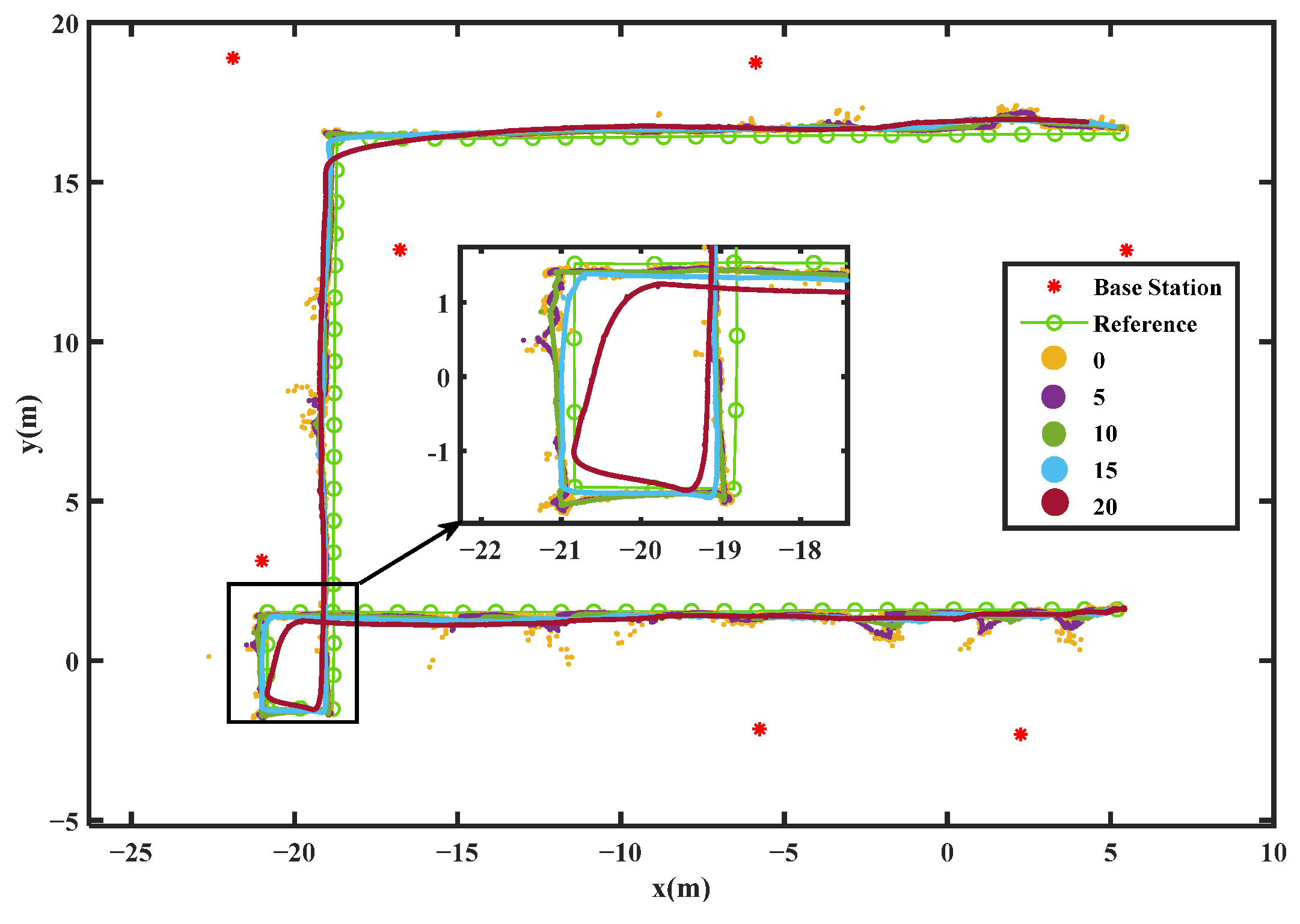
3.3.3. Moving Average Filter Enhanced UWB Positioning
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teunissen, P.J.G. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef]
- Lachapelle, G. GNSS indoor location technologies. J. Glob. Position. Syst. 2004, 3, 2–11. [Google Scholar] [CrossRef]
- Ghinamo, G.; Detoma, E.; Cavallo, D.; Boiero, G.; Lovisolo, P.; Torre, A.D. Analysis of the Accuracy of Indoor GNSS Measurements and Positioning Solution. In Proceedings of the European Navigation Conference 2008, Toulouse, France, 22–25 April 2008. [Google Scholar]
- Zhe, H.; Petovello, M.; Ling, P.; Olesen, D.M. Evaluation of GPS/BDS indoor positioning performance and enhancement. Adv. Space Res. 2017, 59, 870–876. [Google Scholar]
- Mautz, R. Indoor Positioning Technologies. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2012. [Google Scholar]
- Dabove, P.; Pietra, V.D.; Piras, M.; Jabbar, A.A.; Kazim, S.A. Indoor positioning using Ultra-wide band (UWB) technologies: Positioning accuracies and sensors’ performances. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 26 April 2018; pp. 175–184. [Google Scholar]
- Ledergerber, A.; D’Andrea, R. Ultra-wideband range measurement model with Gaussian processes. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Kohala Coast, HI, USA, 27–30 August 2017; pp. 1929–1934. [Google Scholar]
- Wang, Y.; Yang, X.; Zhao, Y.; Liu, Y.; Cuthbert, L. Bluetooth positioning using RSSI and triangulation methods. In Proceedings of the 2013 IEEE 10th Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2013; pp. 837–842. [Google Scholar]
- Cheng, Y.; Zhou, T. UWB Indoor Positioning Algorithm Based on TDOA Technology. In Proceedings of the 2019 10th International Conference on Information Technology in Medicine and Education (ITME), Qingdao, China, 23–25 August 2019; pp. 777–782. [Google Scholar]
- Tian, Z.; Wang, Z.; Li, Z.; Zhou, M. RTIL: A Real-Time Indoor Localization System by Using Angle of Arrival of Commodity WiFi Signal. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; pp. 1–6. [Google Scholar]
- Schmid, L.; Salido-Monzú, D.; Wieser, A. Accuracy Assessment and Learned Error Mitigation of UWB ToF Ranging. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–8. [Google Scholar]
- Mahfouz, M.R.; Fathy, A.E.; Kuhn, M.J.; Wang, Y. Recent trends and advances in UWB positioning. In Proceedings of the 2009 IEEE MTT-S International Microwave Workshop on Wireless Sensing, Local Positioning, and RFID, Cavtat, Croatia, 24–25 September 2009; pp. 1–4. [Google Scholar]
- Poulose, A.; Eyobu, O.S.; Kim, M.; Han, D.S. Localization Error Analysis of Indoor Positioning System Based on UWB Measurements. In Proceedings of the 2019 Eleventh International Conference on Ubiquitous and Future Networks (ICUFN), Zagreb, Croatia, 2–5 July 2019; pp. 84–88. [Google Scholar]
- Dierenbach, K.; Ostrowski, S.; Jozkow, G.; Toth, C.K.; Grejner-Brzezinska, D.A.; Koppanyi, Z. UWB for navigation in GNSS compromised environments. In Proceedings of the 28th international technical meeting of the satellite division of the institute of navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; pp. 2380–2389. [Google Scholar]
- Yang, G.; Zhao, L.; Dai, Y.; Xu, Y. A KFL-TOA UWB indoor positioning method for complex environment. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 3010–3014. [Google Scholar]
- Park, J.W.; Nam, S.C.; Choi, H.B.; Ko, Y.E.; Ko, Y.B. Improving deep learning-based UWB LOS/NLOS identification with transfer learning: An empirical approach. Electronics 2020, 9, 1714. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.J.; García-Naya, J.A.; Suárez-Casal, P. Environmental cross-validation of NLOS machine learning classification/mitigation with low-cost UWB positioning systems. Sensors 2019, 19, 5438. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Gao, Z.; Xu, Q.; Yang, C.; Li, Y. Comprehensive Evaluation of Robust and Tight Integration of UWB and Low-cost IMU. IEEE Sens. J. 2023, 23, 26411–26422. [Google Scholar] [CrossRef]
- Denis, B.; Keignart, J.; Daniele, N. Impact of NLOS propagation upon ranging precision in UWB systems. In Proceedings of the IEEE Conference on Ultra Wideband Systems and Technologies, Reston, VA, USA, 16–19 November 2003; pp. 379–383. [Google Scholar]
- Dong, M. A low-cost NLOS identification and mitigation method for UWB ranging in static and dynamic environments. IEEE Commun. Lett. 2021, 25, 2420–2424. [Google Scholar] [CrossRef]
- Nguyen, D.T.A.; Lee, H.G.; Jeong, E.R.; Lee, H.L.; Joung, J. Deep learning-based localization for UWB systems. Electronics 2020, 9, 1712. [Google Scholar] [CrossRef]
- Tian, Q.; Kevin, I.; Wang, K.; Salcic, Z. An INS and UWB fusion approach with adaptive ranging error mitigation for pedestrian tracking. IEEE Sens. J. 2020, 20, 4372–4381. [Google Scholar] [CrossRef]
- Smaoui, N.; Gnawali, O.; Kim, K. Study and mitigation of platform related uwb ranging errors. In Proceedings of the 2020 International Conference on COMmunication Systems & NETworkS (COMSNETS), Bengaluru, India, 7–11 January 2020; pp. 346–353. [Google Scholar]
- Borhan, N.; Saleh, I.; Yunus, A.; Rahiman, W.; Novaliendry, D. Reducing UWB Indoor Localization Error Using the Fusion of Kalman Filter with Moving Average Filter. In Proceedings of the 2023 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 17 June 2023; pp. 55–59. [Google Scholar]
- Guo, S.; Zhang, Y.; Gui, X.; Han, L. An Improved PDR/UWB Integrated System for Indoor Navigation Applications. IEEE Sens. J. 2020, 20, 8046–8061. [Google Scholar] [CrossRef]
- Liu, T.; Li, B.; Chen, G.; Yang, L.; Qiao, J.; Chen, W. Tightly Coupled Integration of GNSS/UWB/VIO for Reliable and Seamless Positioning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2116–2128. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Liu, F.; Zhang, J.; Yang, D.; Li, B. An Emergency Seamless Positioning Technique Based on ad hoc UWB Networking Using Robust EKF. Sensors 2019, 19, 3135. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Han, H.; Wang, J.; Yu, H.; Yang, D. A Robust Extended Kalman Filter Applied to Ultrawideband Positioning. Math. Probl. Eng. 2020, 2020, 1809262. [Google Scholar] [CrossRef]
- Ghanem, E.; O’Keefe, K.; Klukas, R. Testing vehicle-to-vehicle relative position and attitude estimation using multiple UWB ranging. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar]
- Jiang, Y.; Pan, S.; Meng, Q.; Zhang, M.; Gao, W.; Ma, C. Performance Analysis of Robust Tightly Coupled GNSS/INS Integration Positioning Based on M Estimation in Challenging Environments. In Proceedings of the China Satellite Navigation Conference (CSNC 2022) Proceedings, Singapore, 25 May 2022; pp. 400–414. [Google Scholar]
- Li, Y.; Gao, Z.; Xu, Q.; Yang, C. Comprehensive Evaluations of NLOS and Linearization Errors on UWB Positioning. Appl. Sci. 2023, 13, 6187. [Google Scholar] [CrossRef]
- Koswatta, R.; Karmakar, N.C. Moving average filtering technique for signal processing in digital section of UWB chipless RFID reader. In Proceedings of the 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 7–10 December 2010; pp. 1304–1307. [Google Scholar]







| Parameter | Value |
|---|---|
| Antenna type | External antenna |
| Maximum range coverage | <500 m |
| Recommended range coverage | <300 m |
| Update rate (Hz) | 20 |
| Delay (ms) | <50 |
| Ranging accuracy (m) | 0.1 |
| Optimal frequency band (MHz) | [3744, 4243] [4243, 4742] |
| Ranging scheme | TOA (Time-of-Arrive) |
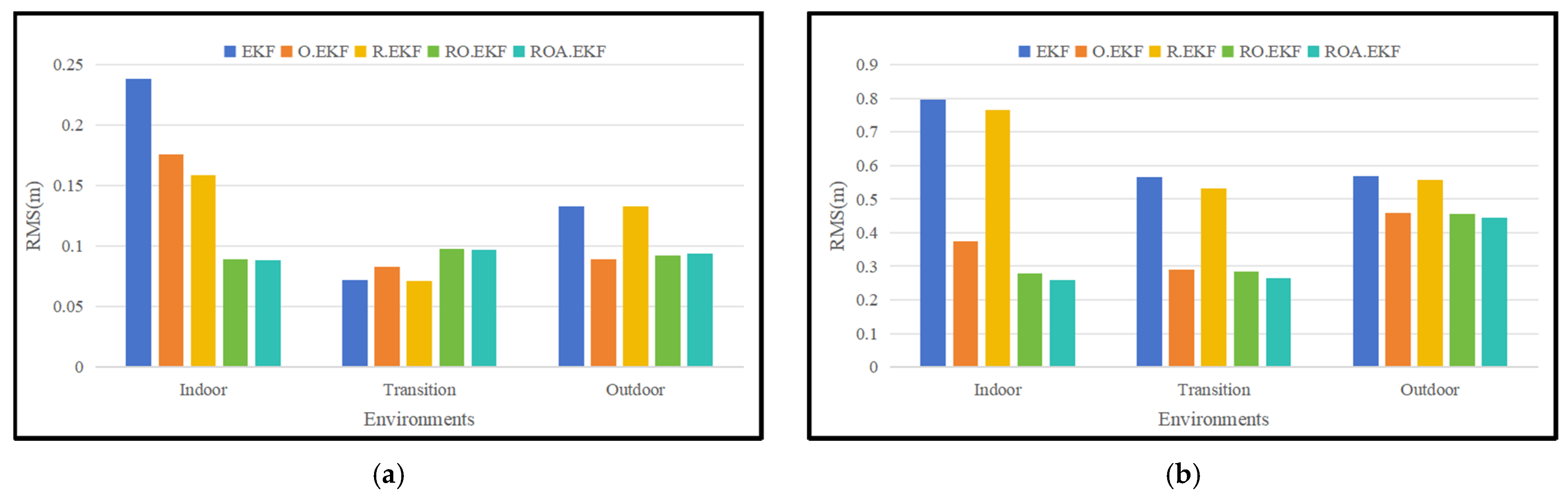
| RMS (m) | Indoor | Transition | Outdoor | |||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | |
| EKF | 0.238 | 0.795 | 0.072 | 0.566 | 0.133 | 0.569 |
| O.EKF | 0.176 | 0.373 | 0.083 | 0.291 | 0.089 | 0.458 |
| RO.EKF | 0.089 | 0.279 | 0.098 | 0.284 | 0.092 | 0.455 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Gao, Z.; Li, Y.; Lv, S.; Liu, J.; Yang, C. Ranging Offset Calibration and Moving Average Filter Enhanced Reliable UWB Positioning in Classic User Environments. Remote Sens. 2024, 16, 2511. https://doi.org/10.3390/rs16142511
Liu J, Gao Z, Li Y, Lv S, Liu J, Yang C. Ranging Offset Calibration and Moving Average Filter Enhanced Reliable UWB Positioning in Classic User Environments. Remote Sensing. 2024; 16(14):2511. https://doi.org/10.3390/rs16142511
Chicago/Turabian StyleLiu, Junhao, Zhouzheng Gao, Yan Li, Siao Lv, Jia Liu, and Cheng Yang. 2024. "Ranging Offset Calibration and Moving Average Filter Enhanced Reliable UWB Positioning in Classic User Environments" Remote Sensing 16, no. 14: 2511. https://doi.org/10.3390/rs16142511
APA StyleLiu, J., Gao, Z., Li, Y., Lv, S., Liu, J., & Yang, C. (2024). Ranging Offset Calibration and Moving Average Filter Enhanced Reliable UWB Positioning in Classic User Environments. Remote Sensing, 16(14), 2511. https://doi.org/10.3390/rs16142511








